Abstract
The 5th generation (5G) wireless networks propose to address a variety of usage scenarios, such as enhanced mobile broadband (eMBB), massive machine-type communications (mMTC), and ultra-reliable low-latency communications (URLLC). Due to the exponential increase in the user equipment (UE) devices of wireless communication technologies, 5G and beyond networks (B5G) expect to support far higher user density and far lower latency than currently deployed cellular technologies, like long-term evolution-Advanced (LTE-A). However, one of the critical challenges for B5G is finding a clever way for various channel access mechanisms to maintain dense UE deployments. Random access channel (RACH) is a mandatory procedure for the UEs to connect with the evolved node B (eNB). The performance of the RACH directly affects the performance of the entire network. Currently, RACH uses a uniform distribution-based (UD) random access to prevent a possible network collision among multiple UEs attempting to access channel resources. However, in a UD-based channel access, every UE has an equal chance to choose a similar contention preamble close to the expected value, which causes an increase in the collision among the UEs. Therefore, in this paper, we propose a Poisson process-based RACH (2PRACH) alternative to a UD-based RACH. A Poisson process-based distribution, such as exponential distribution, disperses the random preambles between two bounds in a Poisson point method, where random variables occur continuously and independently with a constant parametric rate. In this way, our proposed 2PRACH approach distributes the UEs in a probability distribution of a parametric collection. Simulation results show that the shift of RACH from UD-based channel access to a Poisson process-based distribution enhances the reliability and lowers the network’s latency.
1. Introduction
An enormous increase in the demand for capacity in mobile communication devices has led wireless communication industries to prepare to support up to a thousand-fold increase in total internet traffic [1,2,3]. The 3rd Generation Partnership Project (3GPP) suggests that connecting the user equipment (UE) to an existing cellular network, such as Long-Term Evolution-Advanced (LTE-A), 5th generation (5G), and beyond 5G (B5G) networks [4], requires the higher layer connections between the UEs. In general, a considerable amount of data needs to be distributed from many UEs on a 5G network. In this way, the UEs perform a random access (RA) mechanism for transmitting resource requests to the base station, known as evolved Node B (eNB) [5]. The UEs execute RA using the physical random access channel (RACH) through a four-step handshake process. Several UEs attempt to communicate over the same channel resources in a dense UE deployment. The UEs contend to control the common radio resources, which creates a massive collision problem. Due to simultaneous UE channel access, preamble collisions can obstruct the RA process. The problem of successful RA is crucial due to the increasingly growing number of connected UEs in the network [6]. A standard 5G network consists of two parts: the enhanced packet core (EPC) network and the radio access network (RAN) [7]. A high-level architecture of a typical 5G network with linked UEs’ connectivity is shown in Figure 1, where the UEs are linked to the eNBs. The EPC is responsible for the ultimate regulation of mobile devices and creating an Internet Protocol (IP) packet transmission path. The RAN is responsible for wireless networking and radio resource usage. The RAN, which provides the requisite protocols for the user and control plane to communicate with mobile devices (UEs) in 5G network, is composed of eNBs. The eNBs are interconnected through the X2 interface. In addition, the eNB is connected to the EPC using an S1 interface [8].
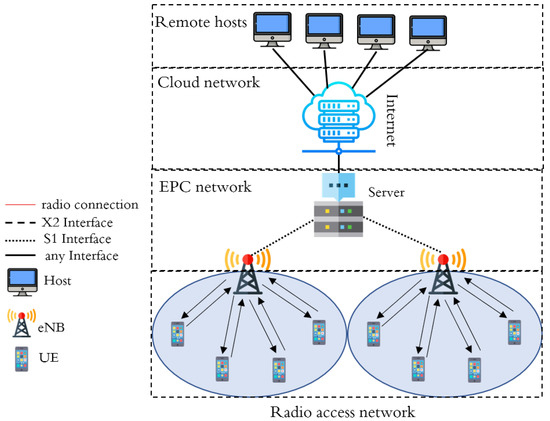
Figure 1.
A typical user equipment (UE) communication in a 5th generation (5G) network.
In a standard 5G network, the minimal resource scheduling unit for downlink (DL) and uplink (UL) transmission is referred to as a resource block (RB). An RB consists of 12 subcarriers in the frequency domain (FD), each size of 180kHz and one subframe in the time domain (TD), length of 1 ms. This time-frequency resource is called RACH, and it is the RB on which RA is performed. RA helps UEs initialize an association, known as a contention-based RA (CB-RA) method [9]. In a CB-RA, UEs utilize preambles to launch the RA transmission attempt. There is a total of 64 preambles divided into two categories; preambles of contention-free RA (CF-RA) and preambles of CB-RA. For CF-RA, the eNB incorporates a few preambles and designates specific preambles for various UEs. Residual preambles are used for CB-RA, where every UE randomly chooses one preamble from a set of predefined uniform random variables (RV) [7].
This uniform distribution (UD) of RVs is used to prevent the inevitable collisions in the 5G network when multiple UEs attempts to access the channel resources. However, in a UD-based channel access mechanism, every UE has an equal chance to choose an identical contention preamble close to the mean value of the UD, that is, for a lower bound a and an upper bound b, which may cause an increase in a collision among the UEs. However, we may use a Poisson process-based distribution, which expresses the probability of a given RV of events independently and distributively occurring in a fixed interval of time or space with a known constant rate. Figure 2 shows a random variable (X) between a uniform random value and a Poisson process-based random value (that is an ED). In a Poisson process-based method, an ED distributes random values between two boundaries. Random variables exist constantly and independently with a constant average rate of , for the as a constant rate parameter.
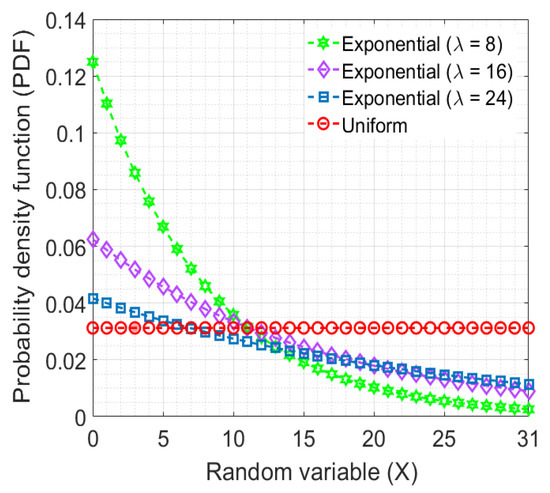
Figure 2.
Uniform distribution-based and Poisson process-based (that is, exponential with ) random value dispersion.
Contributions of the Paper
The motive to introduce a Poisson process-based RA framework is to spread the UEs in a parametric set of a probability distribution. The parametric distribution approach allows the system to disperse RVs exponentially. Therefore, in this paper, we suggest using RVs with Poisson distribution, such as a continuous exponential distribution (ED). The proposed mechanism is named as Poisson process-based RACH (2PRACH). The contributions of this paper are twofold:
- This paper assesses the strengths of Poisson distribution RVs as compared to the uniform distribution RVs.
- We propose a 2PRACH mechanism, which suggests replacing UD with ED in random access mechanism for 5G/B5G networks.
The rest of the paper is organized as follows. In Section 2, we present related work on enhancing the existing RACH procedure in 5G cellular networks. Section 3 describes the existing RACH mechanism in 5G networks. In Section 4, we present our proposed 2PRACH mechanism for random access in 5G networks. Simulation results and performance evaluation is discussed in Section 5. Finally, in Section 6, a conclusion is given, along with future work considerations.
2. Related Research Works
In related research contributions, many researchers have proposed mechanisms to decrease the delay at the RACH procedure. One of the proposals from 3GPP is an early data transmission (EDT) as a feature of the Release 15 specification [8]. According to EDT, data transmission services from the UL channel are sent sooner, enabling data packet transmission to be piggybacked with the RACH system. In Reference [9], authors gave some underlying findings on the execution of EDT, showing that it shows improvements at the edge of the network in-data packet latency by 85 ms. Condoluci et al. [10] conducted performance studies to show that a two-way handshake RACH mechanism is based on an exceptionally structured RA preamble that guarantees a 10–50% delay reduction for 5G macro-cell networks and 50–70% femtocell 5G networks compared to the standard RACH method. A specific RACH resource method for ultra-reliable low-latency communications (URLLC)-related traffic is proposed in Reference [11], designated as resource allocation priorities. Authors propose that by reserving RA preambles twice the amount of URLLC-based UE requests, a channel access latency of less than 10 ms can be obtained for of URLLC-based UEs. Jiang et al. [12] developed a stochastic geometry model for evaluating the effect of diversity by repeating RA preambles to increase the probability of success in RACH. Their analysis shows that repetition of the RA preamble leads to inefficient use of wireless channel resources in considerably dense UE implementation. Besides, Vural et al. [13] submitted that the benefits of using multiple RA preambles in the RACH process could be seen for smaller preamble group size, up to 20 as the resource usage saturates with repeated transmissions. Their analysis shows that repetition of the RA preamble leads to inefficient use of wireless channel resources in considerably dense UE implementation. Furthermore, Vural et al. [14] showed that the benefits of using multiple RA preambles in the RACH method could be seen for smaller preamble group size, which is up to 20 as resource usage saturates with repeated transmissions. Therefore, RA improvements include short transmission slots of 5G numerology, the quicker transmission of UL data packets, efficient backoff times, and dedicated resource allocation for URLLC applications to reduce the channel access latency. However, maintaining high reliability needs progressively channel resources, such as consistency, diversity redundancy, and retransmission, while extending latency over URLLC application requirements. The authors propose a novel RA enhancement in Reference [15], including parallel RA preambles, dynamic, reserved RA preambles, and enhanced backoff mechanisms to diminish the channel collision probability. Arouk et al. [16] developed an analytical method to model RACH procedure output in machine type communication (MTC) networks, which is also a promising 5G network. Their proposed model is essentially used with any system to manage congestion that affects RA procedure. In Reference [17], the authors recommend avoiding the RACH cycle without needing network synchronization to achieve smooth mobility. Their proposed generalized RACH-less handover scheme reduces the latency considerably. Ali et. al. [18] proposed a contention-resolution-based RACH (CRB-RACH) system that dynamically adapts backoff times to allow further improvements compared to a fixed-back-off scheme. Hsu et al. [19] propose a random-access scheme for multi-radio access technologies (RAT), named Multi-RAT RA, which uses traffic offloading configuration parameters utilizing the licensed and unlicensed bands. Although the authors achieve a higher average success probability with their proposed Multi-RAT RA scheme, the use of dual or multiple RATs is required to complete this efficiency. Liu et al. [20] enhanced the RACH procedure by obtaining the approximate characterization of UEs’ interference in a wireless system. Their derived analytical expression of success probability helps to consider the channel collision and the preamble transmission. The authors further extend their proposed RACH success probability analysis for multiple time slots by modeling the queue evolution. In Reference [21], the authors address excessive congestion and channel collision in the RACH due to massive users’ access. They propose a dynamic adjustment of the backoff parameters based on the number of contending devices. The vibrant use of backoff parameters in a RACH scheme achieves the enhanced channel access success probability for statics access and random access with a slight increase in the access delay. Another work in Reference [22] proposes a Timing Advance-based Preamble Resource Expansion (TAPRE) scheme for RACH procedure, which adjusts time slot for preamble transmission to reduce the collision probability effectively. The authors achieved this with a Resource Allocation Wait (RAW) protocol, which efficiently reduces RA failures. However, these works considered enhancing the existing uniform distribution-based RACH mechanism.
Problem Statement
The aforementioned related research works propose significant changes to currently implemented RACH, which improve its performance in various applications and context. However, neither of the works propose to replace UD and discusses the limitations posed by the UD distribution. It has been observed that with the continuous evolution of wireless communication technologies and the massive increase in connected devices, UD-based channel access mechanisms have already been proved less efficient. One of the reasons behind the still use of UD-based mechanisms is the backward compatibility and ease of use. However, due to channel scarcity and resource constraints, we need to move on to better options. Keeping this in mind, in this paper, we expand the capabilities of the current RACH by implying Poisson process-based exponential distribution. As described earlier, from Figure 2, the users’ dispersion in the earlier channel access slots allows the system to permit early channel access with low collision chances.
3. Existing Contention-Based Random-Access Mechanism
When a UE is switched on or awakens, it initially synchronizes with the DL channels by reading the primary synchronization signal (PSS) and secondary synchronization signal (SSS) from the eNB. The UE separates the Master Information Block (MIB) at that point, which contains data on the DL and UL carriers’ configuration so that the eNB receives data from the Sender Information Block (SIB). All RA parameters are included in this SIB, such as the number of available RA slots, RA preamble classes, and preamble setup. Subsequently, UEs generate CB-RA transmission attempts in order to decode the SIB. For association initialization in a 5G network, the CB-RA conducts four main phases. Figure 3 shows a CB-RA procedure in a 5G network.
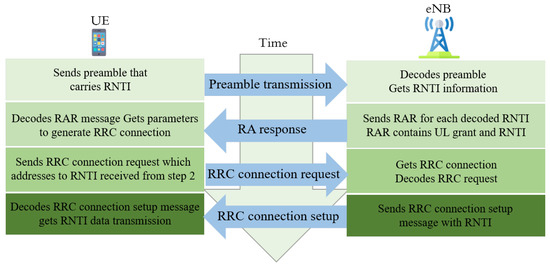
Figure 3.
Contention-based random access (RA) procedure in a 5G network.
3.1. Preamble Transmission (UE → eNB)
By choosing a randomly generated one of the accessible CB preambles from a uniform distribution, a UE initiates CB-RA and sends it to the eNB at the next available RACH slot. The eNB regularly broadcasts SIB messages that encourage the UEs to select a good preamble from them. The physical properties of RA preamble in a PRACH contain the RA radio network temporary identification (RNTI) and the preamble data configuration. The UE waits for an RA response (RAR) window once the preamble is submitted.
3.2. Random Access Response (RAR) (eNB → UE)
The eNB calculates the power delay profile (PDP) of the obtained preamble on the PRACH. A predefined threshold is tested for this calculated PDP, and, if it is found to be greater than the threshold, it is called an active RA preamble. The eNB decodes the RNTI for each active RA preamble to discover the RA slot where the preamble has been submitted. Later, the eNB sends a RAR message to the decoded UEs on the DL control message channel. The RAR message includes a timing advance (TA) instruction to synchronize eventual UL transmissions, a UL resource award for radio resource channel (RRC) requirements, and a short RNTI, which could be made stable at the collision resolution period (CRP). However, if different UEs transmit a similar preamble at a similar RA slot, a collision occurs.
3.3. RRC Connection Request (UE → eNB)
Channel services are delegated to the UE as specified in the previous step; hence, the UE sends an RRC link request and a scheduling request to eNB. In step 3, a message is forwarded to the temporary RNTI assigned in Step 2 of the RAR message and conveys either a particular RNTI if the eNB already has one RRC-associated UE, or an initial UE identity, or a randomly chosen number. However, colliding UEs seek to retransmit RA channel requests using the same UL procedure due to a collision in phase 2; consequently, further collisions occur in the network.
3.4. RRC Connection Setup (eNB → UE)
This phase is also known as CRP, in which an eNB acknowledges the UE after decoding the RRC request. RRC link configuration messages are sent using the dedicated RNTI. After this, an acknowledgment is submitted by the active UEs to the eNB and proceed with data transmission. However, once the limit of retransmission attempts is approached, the colliding UEs must wait to begin a new CB-RA process.
4. Proposed Poisson Process-Based RACH (2PRACH) Mechanism
Since, a very few numbers of preambles for CB-RA are used in each RA slot. The use of uniformly distributed random variable-based RA for preamble collection has a restriction on assembling contending UEs close to an estimated mean value of , resulting in higher collisions after a long run or concurrently accessing multiple UEs. Therefore, we recommend that a Poisson process-based RACH (2PRACH) can be used instead of UD-based RACH. A continues exponential distribution is one of the probability distributions which deals with the time events in a Poisson process. The probability density function (PDF), , of such an exponential distribution with a random variable x (preamble in a RACH) and constant parameter can be defined as,
In this equation, is the constant rate parameter of a Poisson process-based exponential distribution. A Poisson process-based exponentially distributed random variable X with a constant rate parameter allows UEs to stay with the boundaries of mean given by:
which is evident to make sense that, if a UE try to access the channel at an average rate of per data frame transmission, then the UE expects to wait for every next transmission attempt. In addition, the variance of such a UE with random variable X to access the channel resources is given by,
Hence, the standard deviation of the UE remains same as of its mean value. In 2PRACH mechanism, every UE follow the memory-lessness property of the ED. According to this property, a time domain ED random variable, for example T, follows the relation given by:
This relationship can be formulated by considering the tail distribution, that is the complementary distribution function, and is given by,
Thus, the time spent by the UE waiting to access the channel relative to its previous or initial time is conditioned on its failure to access the resources at timeslot i, while the remaining channel access time is distributed same as the original unconditional distribution. This can be explained as, if a UE fails to access the channel at timeslot i, the conditional property that channel access will take place at least after j timeslot and is equal to the unconditional probability of accessing the resources more than j timeslot after the i timeslots.
5. Performance Evaluation
The proposed 2PRACH approach decreases the collision incidence and improves the performance rate of the existing RA of the UE association without altering the 3GPP recommended RA procedure. We conducted simulations in a discrete-event network simulator release 3.30.1 (ns-3.30.1) [23] to evaluate the performance of the 2PRACH approach. The network topology used in simulations includes a radio access network part of a typical UE communication, as shown in Figure 1. The proposed approach’s efficiency is measured in terms of network stability (reliability) and end-to-end latency. These two evaluation parameters are tested for three different scenarios. First, we conducted simulations with increasing number of UEs in the network, that is . Later, we assess the efficiency with varying data packet sizes and interarrival packet speeds. The objective of conducting simulations of various packet sizes and rates of interarrival is to evaluate the impact on the proposed mechanism’s real data transmissions. We observe from Figure 2 that the users’ distribution tends towards the similar density function as of a uniform distribution. Therefore, one can choose the average rate parameter () according to the conditions and requirements. In this paper, we use as our rate parameter, which distributes the users near the initial channel access slots. Detailed simulation parameters and their used values are described in Table 1.

Table 1.
Simulation parameters and their values.
Figure 4 compares the efficiency of our proposed 2PRACH mechanism with the existing uniform distribution-based RACH procedure, and the CRB-RACH mechanism [18], where the number of contending UEs varies. In Figure 4a, we show that the 2PRACH mechanism achieves higher reliability than existing RACH and CRB-RACH procedures, also in dense UEs deployments, which is 64 UEs. Similarly, the network’s end-to-end latency is also reduced for the proposed 2PRACH mechanism, as shown in Figure 4b. In the 2PRACH scheme, improved reliability and reduced latency are evident that for a denser UE environment, choosing earlier RA preambles with a constant parametric rate decreases collision among the UEs. The improved efficiency is because a Poisson process-based distribution manages the number of events in a fixed time frame and the time between occurrences of those successive events. It fits our RACH scheme’s settings because it is one of the distributions with the “lack-of-memory” property. It means that, after waiting to access the channel without successful transmission, the probability of a UE to access the channel in the next contention is the same as was the probability (in previous transmission attempt) of accessing the channel in the following two transmission attempts. Thus, as a UE in the system continues to wait, the chance of successful transmission neither increases nor decreases based on the parameter selected. Although the CRB-RACH procedure improves the efficiency compared to the existing RACH with the use of dynamic backoff adjustment, due to the use of uniformly distributed backoff parameters, it achieves lesser reliability and higher latency as compared to 2PRACH. The efficiency of the proposed 2PRACH mechanism is also measured with various data packet sizes. The motivation to evaluate an RA process with different data frame sizes is that the UEs’ channel capital occupancy time very much depends upon the data frame size to transmit. Figure 5a,b show the effect on the network’s stability and latency of various data frame sizes. The figures reveal that the 2PRACH procedure works well for both; reliability and end-to-end latency relative to existing UD-based RACH when considering the different types of data frame sizes.
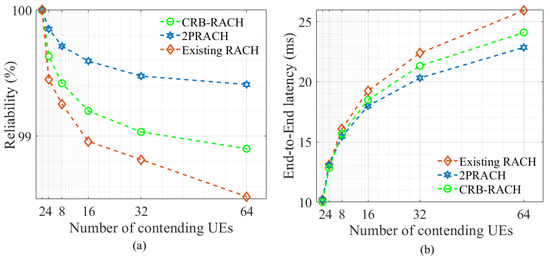
Figure 4.
Performance comparison of process-based random access channel (2PRACH) with existing random access channel (RACH) and contention-resolution-based RACH (CRB-RACH) procedures with the varying number of contending UEs, where (a) network reliability (%), and (b) end-to-end latency (ms).
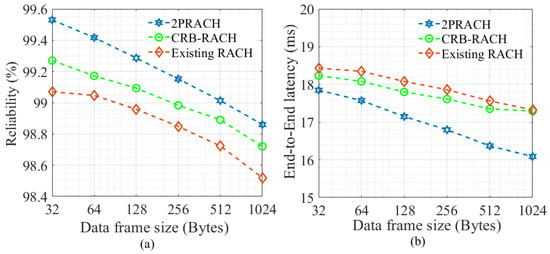
Figure 5.
Performance comparison of 2PRACH with existing RACH and CRB-RACH procedures with varying data frame sizes, where (a) network reliability (%), and (b) end-to-end latency (ms).
However, the influence of data frame interarrival rate has fewer effects on the network’s stability and latency efficiency, as seen in Figure 6a,b, respectively. The importance of using a Poisson process-based distribution is evident from the figures (that is, Figure 4, Figure 5 and Figure 6). The main purpose of the proposed 2PRACH for the RA procedure is to enable the UEs in the network to carry out their initialization of the association more effectively, where reliability is accomplished by reducing network collisions.
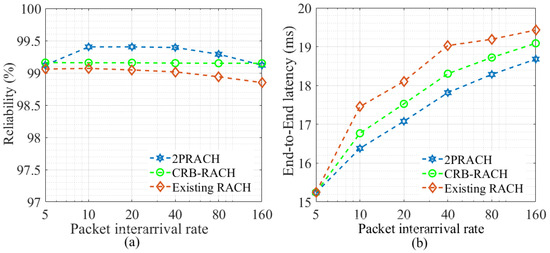
Figure 6.
Performance comparison of 2PRACH with existing RACH and CRB-RACH procedures with varying packet interarrival rate, where (a) network reliability (%), and (b) end-to-end latency (ms).
5.1. Discussion on the Substantial Impact
As we described above in the problem statement section, neither of the related research works propose to replace the traditional uniform distribution-based channel access procedure due to its ease of use and backward compatibility. Therefore, the limitations and challenges posed by the uniform distribution are always ignored. Our proposed 2PRACH protocol expands the current RACH capabilities by implying parametric channel access, which is a more dynamic and robust technique. It opens new ways for researchers and industrialists to think beyond the conventional RACH mechanism and overcome the channel scarcity challenges. As shown in the results, the achieved higher reliability, and the reduced latency proves that the shift of the RACH mechanism from a uniform distribution to a Poisson process-based mechanism has potentials for the next-generation 5G and beyond networks.
5.2. Limitations of the Work
In our current article, we focus on highlighting the issues related to the currently in-use RACH mechanism due to a uniform distribution-based channel access. We propose using a Poisson process-based RACH mechanism to enhance the channel access in terms of increased reliability and reduced end-to-end delays, which is evaluated based on several simulations and experiments. However, it is more convincing for the readers to see the match of analytical results with the simulation results. We understand the importance of comparing analytical results with simulation results to affirm the performance improvement of the proposed solution. However, our current manuscript does not include such analytical modeling due to the related complexities in designing a Markov Chain-based analytical model for our proposed solution. We are already working to fix this limitation and hope to develop a novel analytical model for Poisson process-based channel access mechanisms.
6. Conclusions and Future Work
One of the challenges for 5G cellular communication networks is to provide effective channel connectivity, especially for denser UE scenarios. In a 5G network, the random access channel (RACH) procedure is the core channel access mechanism to set up the wireless communication association between a UE and eNB. However, the efficiency of the currently deployed RACH system is greatly affected by the rise in the number of contending UEs in a network. It is due to the limited available channel contention preamble set. The selection of contention preambles based on the uniformly distributed random-access mechanism of the RACH system is one reason for this efficiency loss. In a uniform distribution, each UE has an equal opportunity to select identical contention preambles close to the mean value of the distribution, creating a rise in collisions among the UEs. Since there is only a single contention stage for the UEs to access the channel, we may consider alternate solutions to allow the UEs to access the channel as early as possible. For this purpose, we propose a Poisson process-based RACH, named 2PRACH, which is based on continuous exponential distribution. The proposed 2PRACH distributes contention preambles between two bounds in a Poisson point method, in which random variables exist continuously and independently with a constant average rate allowing UEs to access the channel resources at their earliest slots. In this way, the 2PRACH mechanism distributes the UEs in a parametric collection of the probability distribution. The performance evaluation results of simulation experiments show that 2PRACH significantly improves the reliability of the network. The increased reliability is achieved due to the enhanced capacity of the UEs to transmit their data packets. At the same time, the long waiting period of the uniformly distributed preamble is eliminated to achieve reduced latency, as well.
In the future, we plan to apply a reinforcement learning-enabled framework to improve the efficiency of 2PRACH. The behaviorist appraisal feature of reinforcement learning models is the incentive to incorporate reinforcement-learning to refine the RA procedure in 5G networks. Besides, we are also working to develop a novel analytical model for Poisson process-based channel access mechanisms.
Author Contributions
Conceptualization, methodology, validation, A.O.A. and R.A.; formal analysis, resources, data curation, D.A. and A.A.; writing—original draft preparation, A.O.A. and R.A.; writing—review and editing, D.A. and A.A.; supervision, project administration, T.K.; funding acquisition, R.A. and T.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, Saudi Arabia grant number RG-2-611-41. The APC was funded by King Abdulaziz University, Saudi Arabia and Sejong University, Korea.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
This work was supported by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant No. (RG-2-611-41). The author, therefore, gratefully acknowledge DSR technical 440 and financial support.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 3GPP | Third Generation Partnership Project |
| CB | Contention-based |
| CED | Continuous Exponential Distribution |
| CF | Contention-free |
| CRP | Contention Resolution Period |
| DL | Down-link |
| DUD | Discrete Uniform Distribution |
| eNB | Evolved Node B |
| EPC | Evolved Packet Core |
| LTE-A | Long Term Evolution-Advanced |
| MIB | Master Information Block |
| Probability Density Function | |
| PDP | Power Delay Profile |
| PRACH | Physical Random Access Channel |
| PSS | Primary Synchronization Signal |
| RA | Random Access |
| RAN | Radio Access Network |
| RAR | RA response |
| RL | Reinforcement Learning |
| RNTI | Radio Network Temporary Identity |
| RRC | Radio Resource Connection |
| SIB | System Information Block |
| SSS | Secondary Synchronization Signal |
| TA | Timing Advance |
| UE | User Equipment |
| UL | Up-link |
References
- Rangan, S.; Rappaport, T.S.; Erkip, E. Millimeter-wave cellular wireless networks: Potentials and challenges. Proc. IEEE 2014, 102, 366–385. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Gutierrez, F.; Ben-Dor, E.; Murdock, J.N.; Qiao, Y.; Tamir, J.I. Broadband millimeter-wave propagation measurements and models using adaptive-beam antennas for outdoor Urban cellular communications. IEEE Trans. Antennas Propag. 2013, 61, 1850–1859. [Google Scholar] [CrossRef]
- Hong, W.; Baek, K.-H.; Lee, Y.; Kim, Y.; Ko, S.-T. Study and prototyping of practically large-scale mmWave antenna systems for 5G cellular devices. IEEE Commun. Mag. 2014, 52, 63–69. [Google Scholar] [CrossRef]
- 3GPP. Study on Scenarios and Requirements for Next-Generation Access Technologies (Release 14); V14.2.0; Rep. TR 38.913; 3GPP: Sophia Antipolis, France, 2017. [Google Scholar]
- Bajracharya, R.; Shrestha, R.; Ali, R.; Musaddiq, A.; Kim, S.W. LWA in 5G: State-of-the-art architecture, opportunities, and research challenges. IEEE Commun. Mag. 2018, 56, 134–141. [Google Scholar] [CrossRef]
- Misic, V.B.; Misic, J. Machine-to-Machine Communications: Architectures, Technology, Standards, and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- 3GPP. TS 36.300 V11.2.0—Evolved Universal Terrestrial Radio Access (E-UTRA) and Evolved Universal Terrestrial Radio Access Network (EUTRAN); Overall Description; 3GPP: Sophia Antipolis, France, 2012. [Google Scholar]
- 3GPP. TS 38.300, NR; Overall Description; Stage-2; Release 15, v15.1.0; 3GPP: Sophia Antipolis, France, 2018. [Google Scholar]
- Hoglund, A.; Van, D.P.; Tirronen, T.; Liberg, O.; Sui, Y.; Yavuz, E.A. 3GPP Release 15 Early Data Transmission. IEEE Commun. Stand. Mag. 2018, 2, 90–96. [Google Scholar] [CrossRef]
- Condoluci, M.; Dohler, M.; Araniti, G.; Molinaro, A.; Sachs, J. Enhanced Radio Access and Data Transmission Procedures Facilitating Industry Compliant Machine Type Communications over LTE-based 5G Networks. IEEE Wirel. Commun. 2016, 23, 56–63. [Google Scholar] [CrossRef]
- Chen, Y.-J.; Cheng, L.-Y.; Wang, L.-C. Prioritized Resource Reservation for Reducing RA Delay in 5G URLLC. In Proceedings of the 2017 IEEE 28th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Montreal, QC, Canada, 8–13 October 2017; pp. 1–5. [Google Scholar]
- Jiang, N.; Deng, Y.; Condoluci, M.; Guo, W.; Nallanathan, A.; Dohler, M. RACH Preamble Repetition in NB-IoT Network. IEEE Commun. Lett. 2018, 22, 1244–1247. [Google Scholar] [CrossRef]
- Vural, S.; Wang, N.; Foster, G.; Tafazolli, R. Success Probability of Multiple-Preamble Based Single-Attempt Random Access to Mobile Networks. IEEE Commun. Lett. 2017, 21, 1755–1758. [Google Scholar] [CrossRef]
- Thota, J.; Aijaz, A. On Performance Evaluation of Random-Access Enhancements for 5G uRLLC. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Arouk, O.; Ksentini, A. General Model for RACH Procedure Performance Analysis. IEEE Commun. Lett. 2016, 20, 372–375. [Google Scholar] [CrossRef]
- Choi, J.; Shin, D. Generalized RACH-Less Handover for Seamless Mobility in 5G and Beyond Mobile Networks. IEEE Wirel. Commun. Lett. 2019, 8, 1264–1267. [Google Scholar] [CrossRef]
- Choi, J. On the Adaptive Determination of the Number of Preambles in RACH for MTC. IEEE Commun. Lett. 2016, 20, 1385–1388. [Google Scholar] [CrossRef]
- Ali, M.S.; Hossain, E.; Kim, D.I. LTE/LTE-A Random Access for Massive Machine-Type Communications in Smart Cities. IEEE Commun. Mag. 2017, 55, 76–83. [Google Scholar] [CrossRef]
- Hsu, C.; Das, K.; Jorguseski, L. Multi-RAT Random Access Scheme Utilising Combined Licensed and Unlicensed Spectrum for Massive Machine-Type Communications. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, Y.; Jiang, N.; Elkashlan, M.; Nallanathan, A. Analysis of Random Access in NB-IoT Networks with Three Coverage Enhancement Groups: A Stochastic Geometry Approach. IEEE Trans. Wirel. Commun. 2021, 20, 549–564. [Google Scholar] [CrossRef]
- Althumali, H.D.; Othman, M.; Noordin, N.K.; Hanapi, Z.M. Dynamic Backoff Collision Resolution for Massive M2M Random Access in Cellular IoT Networks. IEEE Access 2020, 8, 201345–201359. [Google Scholar] [CrossRef]
- Lee, B.-H.; Lee, H.-S.; Moon, S.; Lee, J.-W. Enhanced Random Access for Massive Machine Type Communications. IEEE Internet Things J. 2020. [Google Scholar] [CrossRef]
- NS-3, A Discrete-Event Network Simulator Release 3.30.1. Available online: https://www.nsnam.org/doxygen/group_lte.html (accessed on 1 January 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).