An Extended Finite Element Method (XFEM) Study on the Elastic T-Stress Evaluations for a Notch in a Pipe Steel Exposed to Internal Pressure
Abstract
1. Introduction
2. Materials and Methods
2.1. K-T Approach
- T-stress enhances the possibility of crack opening stresses in the context of small crack [26];
- T-stress influences the plastic zone. Jayadevan [3] highlighted that plastic zone is affected by the variation of T-stress. The plastic area escalates with the upsurge in the absolute value of T-stress and changes its form. Sobotka et al. [4] demonstrated the deviation in the plastic wake with various T-stress which depends on plastic wakes height (hpw).
- Propagation’s direction: Fayed et al. [6] analyzed the impact of T-stress on the propagation’s direction by Maximum Tangential Stress (MTS). The principle of MTS is in the crack propagation direction which is in line with that of maximum tangential stress. MTS only considers the term singularity. Therefore, the direction of crack does not coincide with the initial directions of the crack. This behavior shows that the tangential stress is affected by the T-Stress. MTS becomes generalized maximum tangential stress (GMTS), which considers the T-stress in the expression of stress.
- T-stress has an impact on crack initiation angle. Shahani [1] analyzed the consequence of the T-stress on the angle of initiation of crack propagation. The study has shown that a negative T value declines the angle of crack initiation, and a positive T value enhances it.
- T-Stress is of prime significance when ensuring the stability of the direction of crack propagation, such as T negative gives a stable direction, and for T positive it is unstable [5].
2.2. Extended Finite Elements
- H(x): The Heaviside enrichment function,
- F(x): Enrichment functions near the crack front.
- N: Interpolation function of finite element. : Number of nodes enriched with Heaviside function. : Number of knots enriched near the crack front.
2.3. Geometry
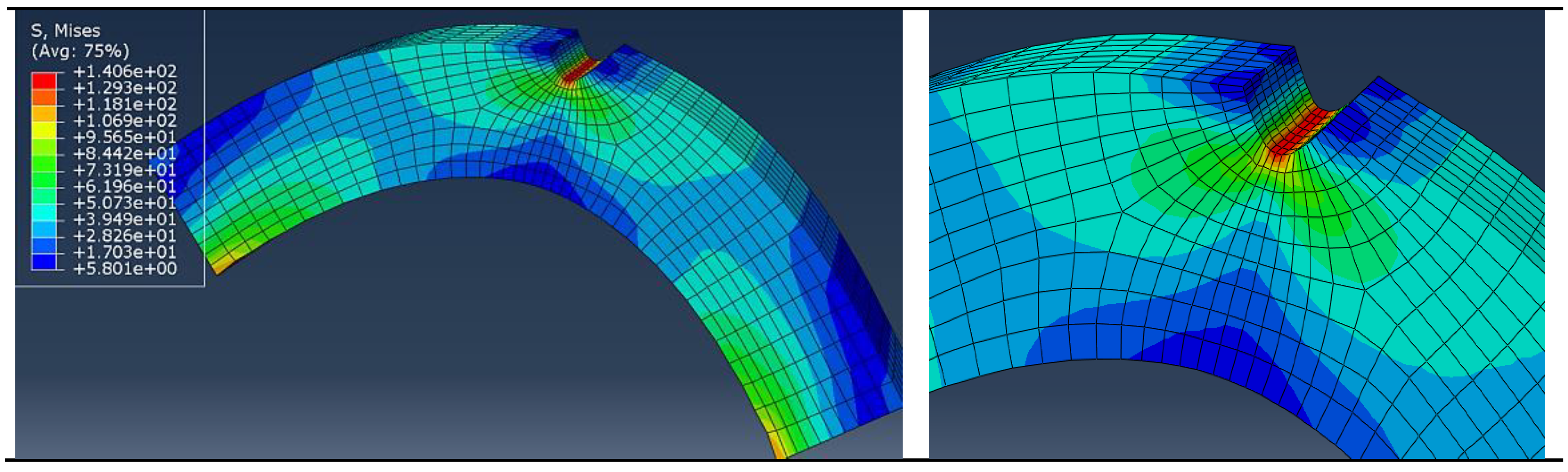
3. Results
4. Discussion
5. Conclusions
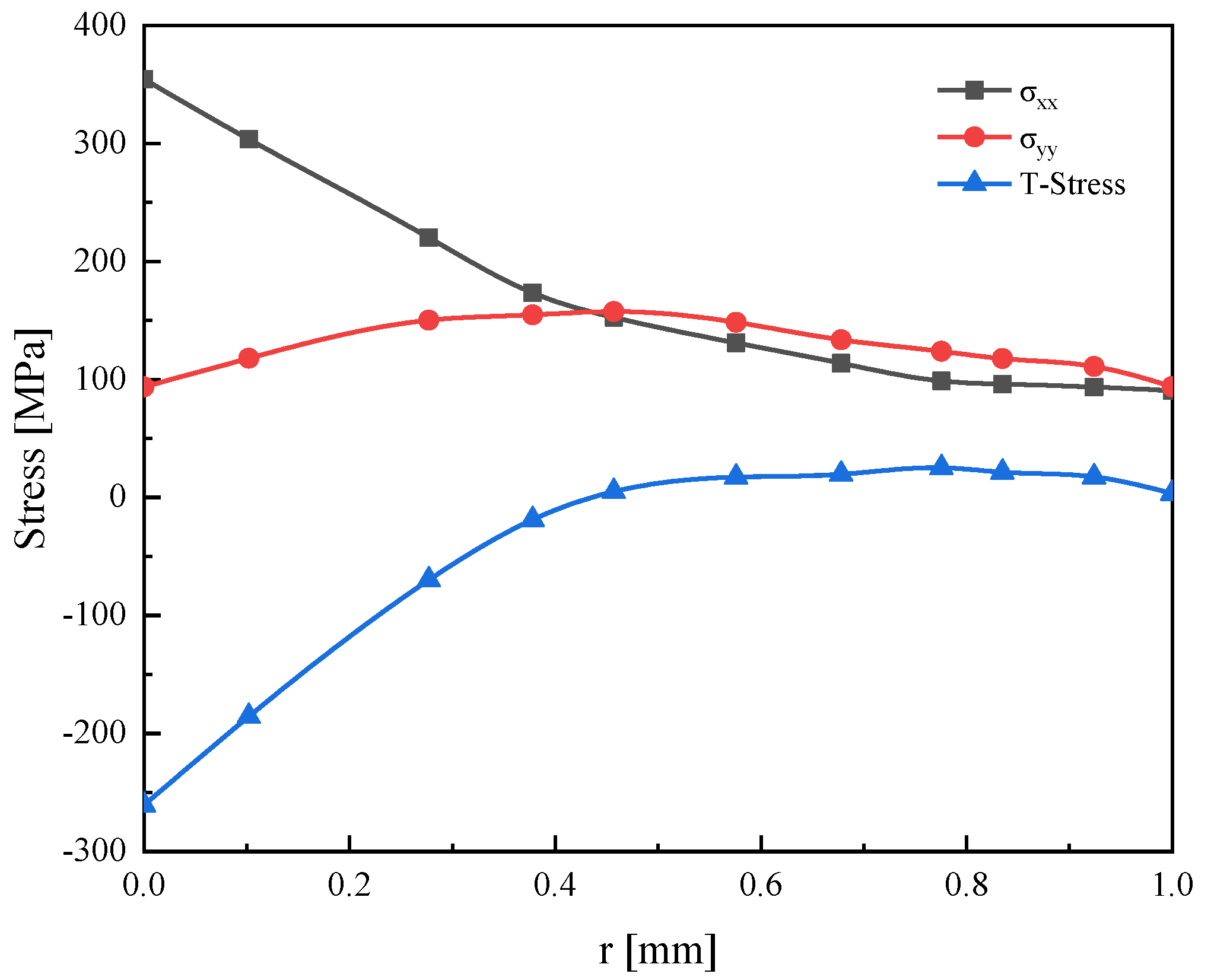
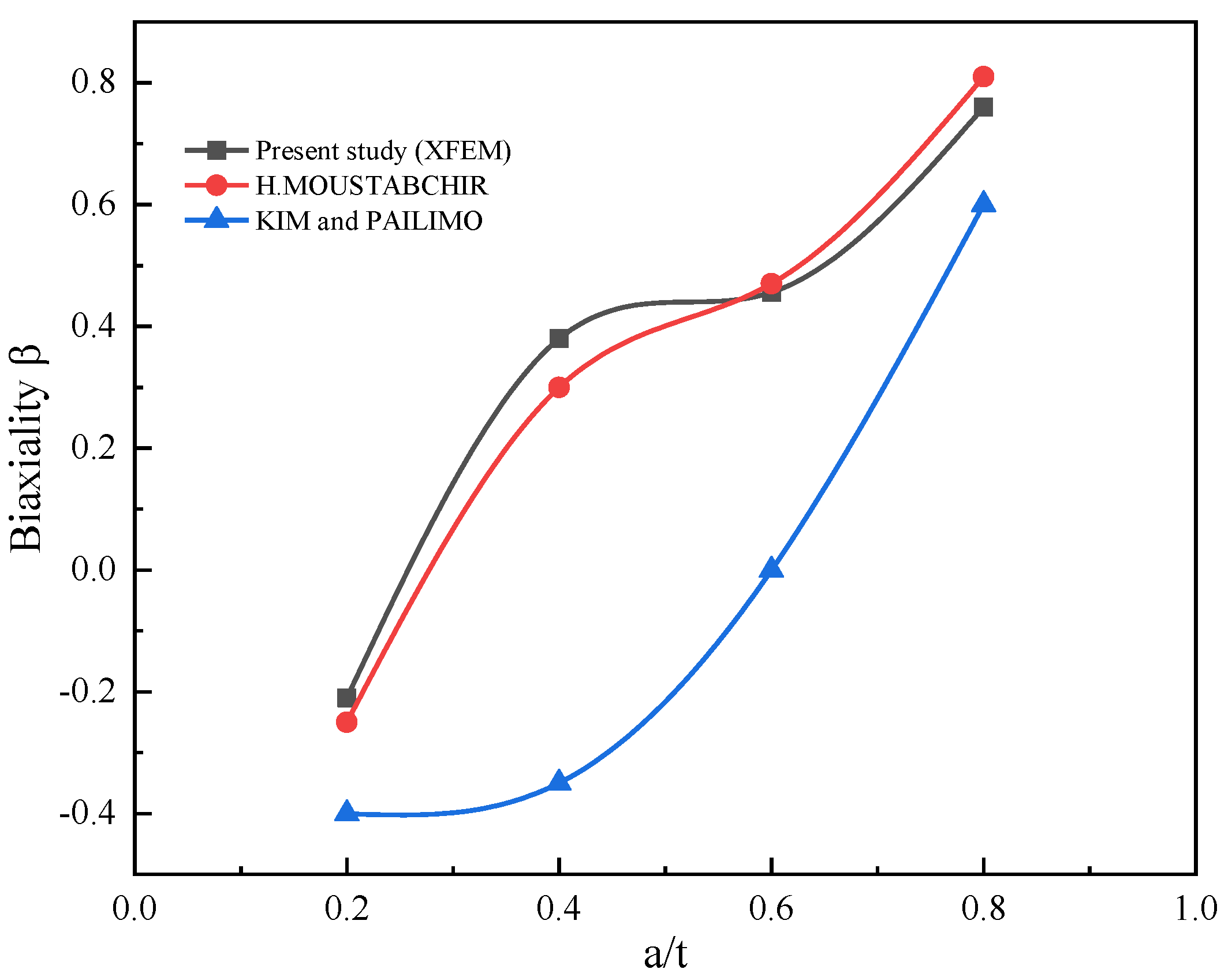
- To study the influence of geometry and notch size on the T-stress, authors have approached the biaxiality as a function of a/t. The evaluation endorsed that biaxiality increases with the increasing a/t which is in accord with president results.
- The integration of biaxiality allowed us to determine the state of the crack initiation, and we can say that the pipe is safe in the used conditions.
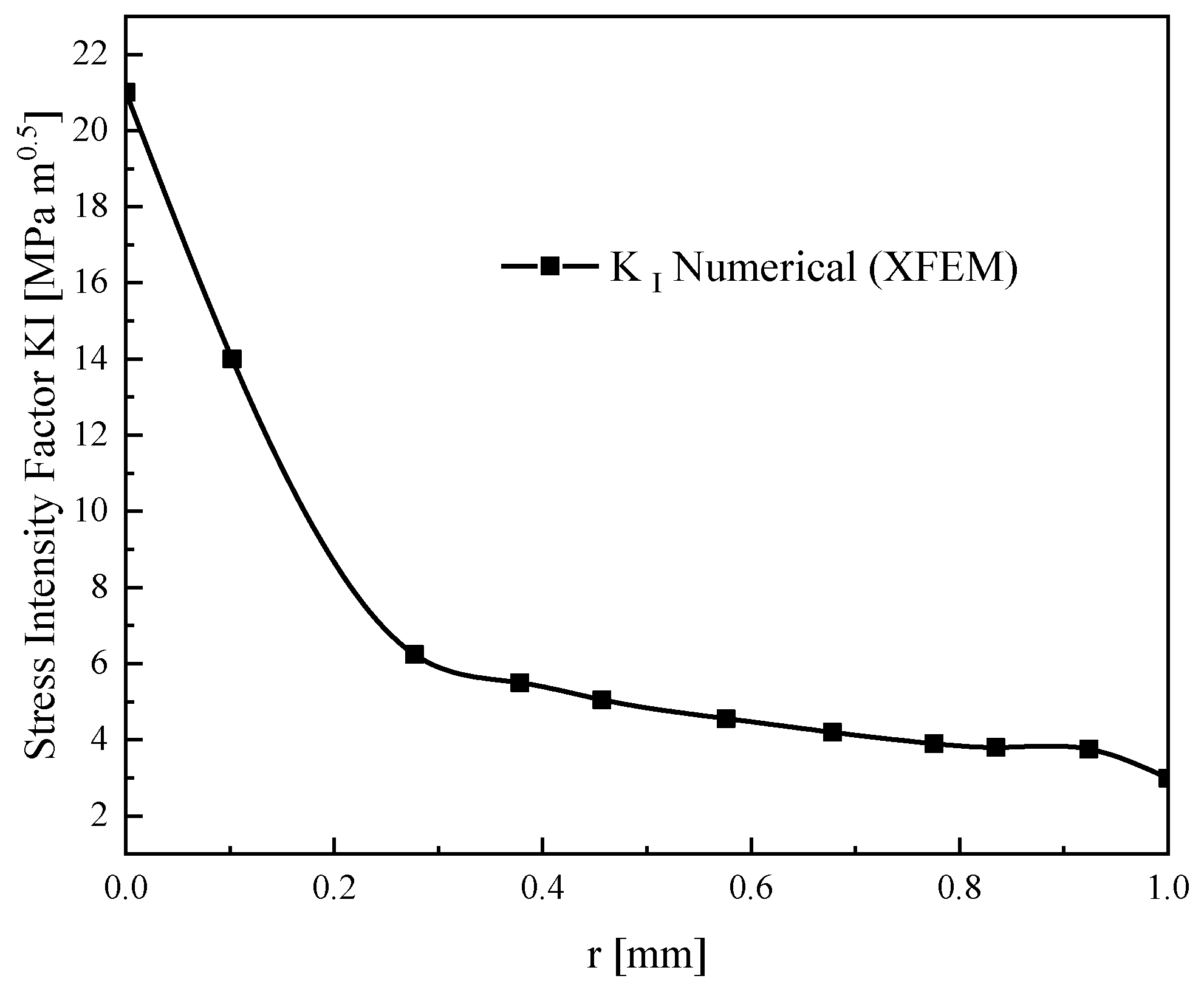
- The SIF alone does not characterize the behavior of notches. T-stress is obtained by Stress Difference Method (SDM) along with the notch in mode I. SDM is an efficient and simple method to calculate the fracture parameters.
- With ABAQUS-based investigations, the numerical results achieved by X-FEM are in good agreement with the Moustabchir result [39]. The implementation of X-FEM in the presence of a notch corrected the problems of the standard finite element method. The advantage of the X-FEM is that the mesh is independent of the notch.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shahani, A.; Tabatabaei, S. Effect of T-stress on the fracture of a four point bend specimen. Mater. Des. 2009, 30, 2630–2635. [Google Scholar] [CrossRef]
- Hamam, R.; Pommier, S.; Bumbieler, F. Mode I fatigue crack growth under biaxial loading. Int. J. Fatigue 2005, 27, 1342–1346. [Google Scholar] [CrossRef]
- Jayadevan, K.; Narasimhan, R.; Ramamurthy, T.; Dattaguru, B. Effect of T-stress and loading rate on crack initiation in rate sensitive plastic materials. Int. J. Solids Struct. 2002, 39, 1757–1775. [Google Scholar] [CrossRef]
- Sobotka, J.; Dodds, R. T-stress effects on steady crack growth in a thin, ductile plate under small-scale yielding conditions: Three-dimensional modeling. Eng. Fract. Mech. 2011, 78, 1182–1200. [Google Scholar] [CrossRef]
- Cotterell, B.; Rice, J. Slightly curved or kinked cracks. Int. J. Fract. 1980, 16, 155–169. [Google Scholar] [CrossRef]
- Fayed, A.S. Numerical Analysis of Crack Initiation Direction in Quasi-brittle Materials: Effect of T-Stress. Arab. J. Sci. Eng. 2019, 44, 7667–7676. [Google Scholar] [CrossRef]
- Nejati, M.; Ghouli, S.; Ayatollahi, M.R. Crack tip asymptotic fields in anisotropic planes: Importance of higher order terms. Appl. Math. Model. 2021, 91, 837–862. [Google Scholar] [CrossRef]
- Chen, X.; Yue, Z. Mode-I pressurized axisymmetric penny-shaped crack in graded interfacial zone with variable modulus and Poisson’s ratio. Eng. Fract. Mech. 2020, 235, 107164. [Google Scholar] [CrossRef]
- Toshio, N.; Parks, D.M. Determination of elastic T-stress along three-dimensional crack fronts using an interaction integral. Int. J. Solids Struct. 1992, 29, 1597–1611. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, S.; Han, S.; Fan, L. T-stress evaluation for multiple cracks in FGMs by the numerical manifold method and the interaction integral. Theor. Appl. Fract. Mech. 2020, 105, 102436. [Google Scholar] [CrossRef]
- Nakamura, N.; Kawabata, T.; Takashima, Y.; Yanagimoto, F. Effect of the stress field on crack branching in brittle material. Theor. Appl. Fract. Mech. 2020, 108, 102583. [Google Scholar] [CrossRef]
- Hancock, J.W.; Renter, W.G.; Parks, D.M. Constraint and Toughness Parameterized by T. In Constraint Effects in Fracture; Hackett, E., Schwalbe, K., Dodds, R., Eds.; ASTM International: West Concord, PA, USA, 1993; pp. 21–40. [Google Scholar]
- Matvienko, Y. The effect of crack-tip constraint in some problems of fracture mechanics. Eng. Fail. Anal. 2020, 110, 104413. [Google Scholar] [CrossRef]
- Moes, J.N.; Dolbow, T.B. A Finite Element Method for Crack Growth without Remeshing; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1999. [Google Scholar] [CrossRef]
- Wang, C.; Huang, Z.; Wu, Y.-S. Coupled numerical approach combining X-FEM and the embedded discrete fracture method for the fluid-driven fracture propagation process in porous media. Int. J. Rock Mech. Min. Sci. 2020, 130, 104315. [Google Scholar] [CrossRef]
- Shu, Y.; Li, Y.; Duan, M.; Yang, F. An X-FEM approach for simulation of 3-D multiple fatigue cracks and application to double surface crack problems. Int. J. Mech. Sci. 2017, 130, 331–349. [Google Scholar] [CrossRef]
- Liang, Y.-J.; McQuien, J.S.; Iarve, E.V. Implementation of the regularized extended finite element method in Abaqus framework for fracture modeling in laminated composites. Eng. Fract. Mech. 2020, 230, 106989. [Google Scholar] [CrossRef]
- Akhondzadeh, S.; Khoei, A.; Broumand, P. An efficient enrichment strategy for modeling stress singularities in isotropic composite materials with X-FEM technique. Eng. Fract. Mech. 2017, 169, 201–225. [Google Scholar] [CrossRef]
- Nagashima, T.; Suemasu, H. X-FEM analyses of a thin-walled composite shell structure with a delamination. Comput. Struct. 2010, 88, 549–557. [Google Scholar] [CrossRef]
- El Fakkoussi, S.; Moustabchir, H.; Elkhalfi, A.; Pruncu, C.I. Computation of the stress intensity factor KI for external longitudinal semi-elliptic cracks in the pipelines by FEM and XFEM methods. Int. J. Interact. Des. Manuf. 2018, 13, 545–555. [Google Scholar] [CrossRef]
- Llavori, I. A coupled crack initiation and propagation numerical procedure for combined fretting wear and fretting fa-tigue lifetime assessment. Theor. Appl. Fract. Mech. 2019, 101, 294–305. [Google Scholar] [CrossRef]
- Meliani, H.M. Mécanique de la Rupture d’Entaille par l’Approche Globale: Estimation des Contraintes de Confinements dans des Structures Portant des Entailles; Editions Universitaires Européennes: Saarbrücken, Germany, 2010. [Google Scholar]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press LLC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Ravera, R.J.; Sih, G.C. Transient Analysis of Stress Waves around Cracks under Antiplane Strain. J. Acoust. Soc. Am. 1970, 47, 875–881. [Google Scholar] [CrossRef]
- Yu, P.; Wang, Q.; Zhang, C.; Zhao, J. Elastic T -stress and I-II mixed mode stress intensity factors for a through-wall crack in an inner-pressured pipe. Int. J. Press. Vessel. Pip. 2018, 159, 67–72. [Google Scholar] [CrossRef]
- Brugier, F. Modèle Condensé de Plasticité Pour la Fissuration et Influence de la Contrainte T; Université Paris-Saclay (ComUE): Saint-Aubin, France, 2017; Available online: https://www.theses.fr/2017SACLN028 (accessed on 20 January 2021).
- Gupta, M.; Alderliesten, R.; Benedictus, R. A review of T-stress and its effects in fracture mechanics. Eng. Fract. Mech. 2015, 134, 218–241. [Google Scholar] [CrossRef]
- Kfouri, A.P. Some evaluations of the elastic T-term using Eshelby’s method. Int. J. Fract. 1986, 30, 301–315. [Google Scholar] [CrossRef]
- Yang, B.; Ravi-Chandar, K. Evaluation of elastic T-stress by the stress dierence method. Eng. Fract. Mech. 1999, 64, 589–605. [Google Scholar] [CrossRef]
- Du, Z. eXtended Finite Element Method (XFEM) in Abaqus; Simulia: Jhonston, RI, USA, 2009. [Google Scholar]
- Xie, Y.; Cao, P.; Jin, J.; Wang, M. Mixed mode fracture analysis of semi-circular bend (SCB) specimen: A numerical study based on extended finite element method. Comput. Geotech. 2017, 82, 157–172. [Google Scholar] [CrossRef]
- Yixiu, S.; Yazhi, L. A Simple and Efficient X-FEM Approach for Non-planar Fatigue Crack Propagation. Procedia Struct. Integr. 2016, 2, 2550–2557. [Google Scholar] [CrossRef][Green Version]
- Nasri, K.; Zenasni, M. Fatigue crack growth simulation in coated materials using X-FEM. Comptes Rendus Mécanique 2017, 345, 271–280. [Google Scholar] [CrossRef]
- Savenkov, E.B.; Borisov, V.E.; Kritskiy, B.V. Surface Representation with Closest Point Projection in the X-FEM. Math. Model. Comput. Simul. 2020, 12, 36–52. [Google Scholar] [CrossRef]
- Angioni, S.; Visrolia, A.; Meo, M. Combining X-FEM and a multilevel mesh superposition method for the analysis of thick composite structures. Compos. Part B Eng. 2012, 43, 559–568. [Google Scholar] [CrossRef]
- Koutsawa, Y.; Belouettar, S.; Makradi, A.; Tiem, S. X-FEM implementation of VAMUCH: Application to active structural fiber multi-functional composite materials. Compos. Struct. 2012, 94, 1297–1304. [Google Scholar] [CrossRef]
- Schiavone, A.; Abeygunawardana-Arachchige, G.; Silberschmidt, V.V. Crack initiation and propagation in ductile specimens with notches: Experimental and numerical study. Acta Mech. 2015, 227, 203–215. [Google Scholar] [CrossRef]
- Patria, K.; Bambang, B.; Muhammad, F. XFEM Based Fracture Analysis of Single Notch Reactive Powder Concrete Specimen Subjected to Three Point Bending Test; Web of Conferences; EDP Sciences: Paris, France, 2020; p. 05027. [Google Scholar] [CrossRef]
- Moustabchir, H.; Arbaoui, J.; Zitouni, A.; Hariri, S.; Dmytrakh, I. Numerical analysis of stress intensity factor and T-stress in pipeline of steel P264GH submitted to loading conditions. J. Theor. Appl. Mech. 2015, 53, 665–672. [Google Scholar] [CrossRef]
- Kim, J.-H.; Paulino, G.H. T-stress, mixed-mode stress intensity factors, and crack initiation angles in functionally graded materials: A unified approach using the interaction integral method. Comput. Methods Appl. Mech. Eng. 2003, 192, 1463–1494. [Google Scholar] [CrossRef]
- Bouchard, P.-O.; Bernacki, M.; Parks, D.M. Analysis of stress intensity factors and T-stress to control crack propagation for kerf-less spalling of single crystal silicon foils. Comput. Mater. Sci. 2013, 69, 243–250. [Google Scholar] [CrossRef]
- Sherry, A.H.; France, C.C.; Goldthorpe, M.R. Compendium of t-stress solutions for two and three dimensional cracked geometries. Fatigue Fract. Eng. Mater. Struct. 1995, 18, 141–155. [Google Scholar] [CrossRef]
- Ayatollahi, M.; Pavier, M.; Smith, D. Determination of T-stress from finite element analysis for mode I and mixed mode I/II loading. Int. J. Fract. 1998, 91, 283–298. [Google Scholar] [CrossRef]
- Bouledroua, O.; Meliani, M.H.; Pluvinage, G. A Review of T-Stress Calculation Methods in Fracture Mechanics Computation. Nat. Technol. 2016, 11, 20. [Google Scholar]
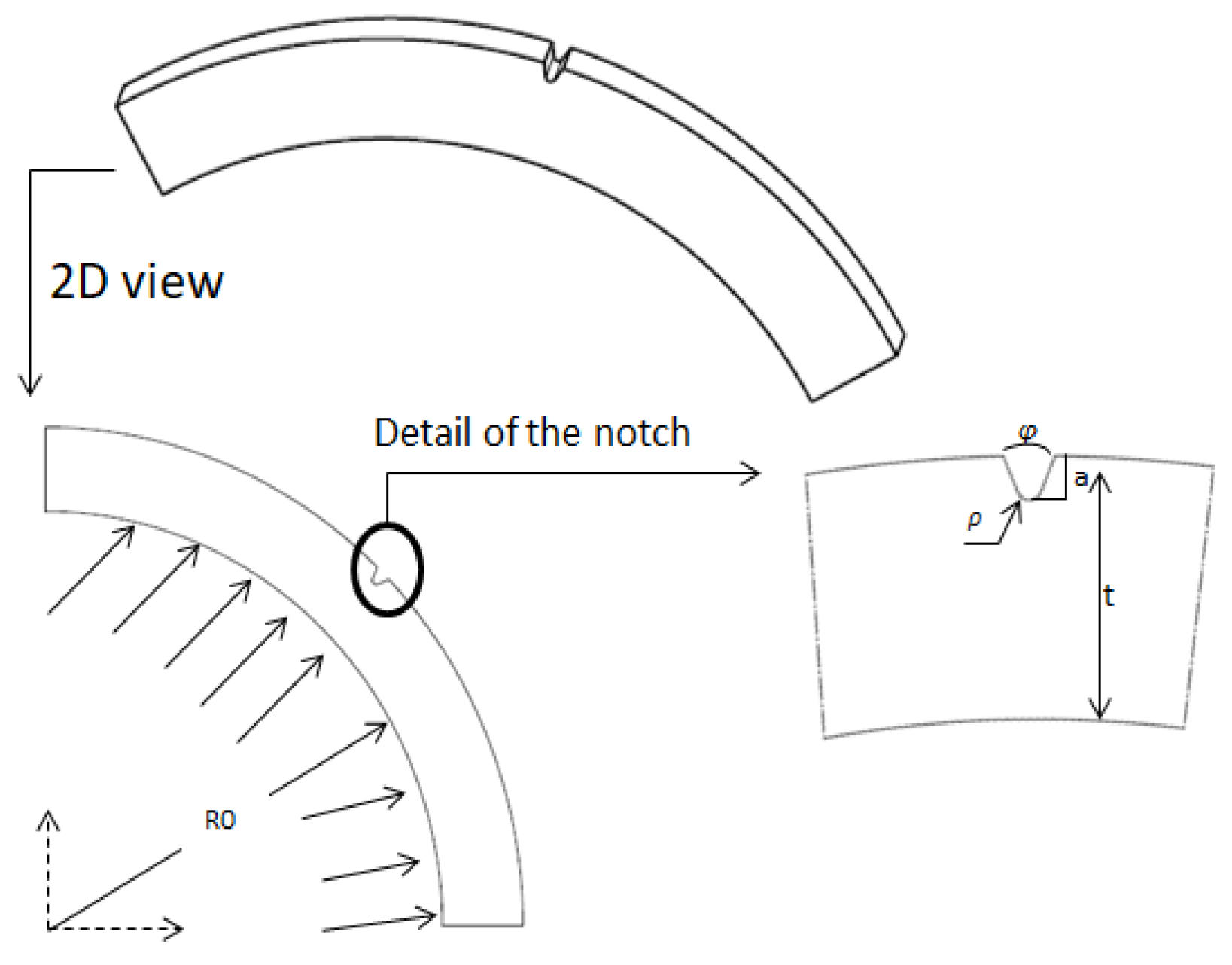

| Ri [mm] | P [MPa] | φ [deg] | a [mm] | t [mm] | ρ [mm] |
|---|---|---|---|---|---|
| 213.45 | 15 | 45 | 1.22–4.88 | 6.1 | 0.15 |
| Young’s Modulus | Poisson’s Ratio | Yield Stress | Elongation to Fracture |
|---|---|---|---|
| 207,000 MPa | 0.3 | 430 MPa | 35% |
| Material | C | Mn | S | Si | P | Al |
|---|---|---|---|---|---|---|
| Tested | 0.135 | 0.665 | 0.002 | 0.195 | 0.027 | 0.027 |
| Steel P264GH (Standard EN10028.2–92) | 0.18 | 1 | 0.015 | 0.4 | 0.025 | 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yakoubi, K.; Montassir, S.; Moustabchir, H.; Elkhalfi, A.; Pruncu, C.I.; Arbaoui, J.; Farooq, M.U. An Extended Finite Element Method (XFEM) Study on the Elastic T-Stress Evaluations for a Notch in a Pipe Steel Exposed to Internal Pressure. Mathematics 2021, 9, 507. https://doi.org/10.3390/math9050507
Yakoubi K, Montassir S, Moustabchir H, Elkhalfi A, Pruncu CI, Arbaoui J, Farooq MU. An Extended Finite Element Method (XFEM) Study on the Elastic T-Stress Evaluations for a Notch in a Pipe Steel Exposed to Internal Pressure. Mathematics. 2021; 9(5):507. https://doi.org/10.3390/math9050507
Chicago/Turabian StyleYakoubi, Khadija, Soufiane Montassir, Hassane Moustabchir, Ahmed Elkhalfi, Catalin Iulian Pruncu, Jamal Arbaoui, and Muhammad Umar Farooq. 2021. "An Extended Finite Element Method (XFEM) Study on the Elastic T-Stress Evaluations for a Notch in a Pipe Steel Exposed to Internal Pressure" Mathematics 9, no. 5: 507. https://doi.org/10.3390/math9050507
APA StyleYakoubi, K., Montassir, S., Moustabchir, H., Elkhalfi, A., Pruncu, C. I., Arbaoui, J., & Farooq, M. U. (2021). An Extended Finite Element Method (XFEM) Study on the Elastic T-Stress Evaluations for a Notch in a Pipe Steel Exposed to Internal Pressure. Mathematics, 9(5), 507. https://doi.org/10.3390/math9050507








