Anti-Fuzzy Multi-Ideals of Near Ring

Abstract

Recently, fuzzy multisets have come to the forefront of scientists’ interest and have been used for algebraic structures such as groups, rings, and near rings. In this paper, we first summarize the knowledge about algebraic structure of fuzzy multisets such as fuzzy multi-subnear rings and fuzzy multi-ideals of near rings. Then we recall the results from our related previous work, where we defined different operations on fuzzy multi-ideals of near rings and we generalized some known results for fuzzy ideals of near rings to fuzzy multi-ideals of near rings. Finally, we define anti-fuzzy multi-subnear rings (multi-ideals) of near rings and study their properties.

1. Introduction

In 1938 Dresher and Ore laid the foundations of the theory of multigroups [1]. In 1965, Zadeh [2] proposed fuzzy sets as a mathematical model of vagueness where elements belong to a given set to some degree that is typically a number between 0 and 1 inclusive. A multiset, as defined by Yager [3] in 1987, is a collection of elements with the possibility that an element may occur more than once. Multiplicity in the multiset is the number of times an element occurs in the multiset. It is evident that a multiset in which every element has a multiplicity of exactly one is a set, i.e., its elements are pairwise different [4]. As a combination of the two concepts—multisets and fuzzy sets—Yager [3] defined fuzzy multisets or fuzzy bags. The latter are fuzzy subsets whose elements may occur more than once.

Biswas [5] introduced anti-fuzzy subgroups and then the anti-fuzzification of algebraic structures started to grow. In particular, a link between near rings and anti-fuzzy sets was established by Kim and Jun [6], where they studied the notion of anti-fuzzy R-subgroups of near rings. Later on, Kim et al. [7] introduced the notion of anti-fuzzy ideals of near rings and investigated some related properties. Davvaz studied the fuzzy ideals of near rings in [8]. Ferrero and Ferrero-Cotti presented some development in near rings in 2002, see [9].

In [10], the authors combined the notion of near rings with fuzzy multisets and defined fuzzy multi-subnear rings (multi-ideals) of near rings. In our paper, we combine the notion of near rings with fuzzy multisets [11] to define anti-fuzzy multi-subnear rings (multi-ideals) of near rings.

The aim of this paper is to highlight the connection between fuzzy multisets and algebraic structures from an anti-fuzzification point of view. Moreover, this research proposes the generalization of the results known for anti-fuzzy ideals of near rings. It is known that the notion of fuzzy multiset is well entrenched in solving many real life problems. So, the algebraic structure defined concerning them in this paper could help to approach these issues from a different position. The benefit of this paper is the link found between algebraic structures and fuzzy multisets by introducing anti-fuzzy multi-ideals of near rings and studying their properties.

The paper is organized as follows: After an Introduction, Section 2 briefly reviews some preliminary results related to near rings and fuzzy multisets that are used throughout the paper. Section 3 presents some previous results on fuzzy multi-subnear rings (multi-ideals) of near rings. Finally, Section 4 defines anti-fuzzy multi-subnear rings (multi-ideals) of near rings and investigates some of their properties.

2. Preliminaries

Here we recall the results related to near rings (see [12,13,14]), fuzzy multisets (see [3,15,16,17,18]) that are used throughout the paper; the approach of hyperstructures as hyper ring and hyper ideals can be found, e.g., in [19,20,21,22].

A near ring is an algebraic structure that looks like a ring where it allows one distributive law to be satisfied (either left or right) [12,23,24]. Let R be a non-empty set. Then $(R,+,·)$ is called a near ring if: $(R,+)$ is a group; $(R,·)$ is a semigroup; and if the Left distributive law $x·(y+z)=x·y+x·z$ for all $x,y,z\in R$ is valid. Moreover, it is evident that every ring is a near ring.

Definition 1.

[12] Let $(R,+,·)$ be a near ring.

1. 

A non-empty subset S of R is called a subnear ring of R if $(S,+,·)$ is a near ring.

2. 

A subnear ring I of R is called an ideal of R if:

(a) 

$x+y-x\in I$ for all $x\in R$ and $y\in I$;

(b) 

$x·y\in I$ for all $x\in R$ and $y\in I$;

(c) 

$(x+a)·y-x·y\in I$ for all $x,y\in R$ and $a\in I$.

3. 

It is called simple if R has no proper non-trivial ideals.

A multiset (or bag) is a set containing repeated elements. A fuzzy multiset is a generalization of a fuzzy set. Yager in [3] introduced it under the name fuzzy bag.

A crisp bag describes the number of elements in the fuzzy bag. The definition and main results concerning the fuzzy set are overtaken from [2].

Definition 2.

[17] Let X be a non-empty set and Q be the set of all crisp multisets drawn from the interval $[0,1]$. A fuzzy multiset A drawn from X is represented by a function $C{M}_A:X\to Q$.

The value $C{M}_A\left(x\right)$, mentioned above, is a crisp multiset drawn from $[0,1]$. For each $x\in X$, $C{M}_A\left(x\right)$ is defined as the decreasingly ordered sequence of elements and it is denoted by:

$$\left({\mu }_A^1\left(x\right),{\mu }_A^2\left(x\right),\dots ,{\mu }_A^p\left(x\right)\right):{\mu }_A^1\left(x\right)\ge {\mu }_A^2\left(x\right)\ge \dots \ge {\mu }_A^p\left(x\right).$$

A fuzzy set on a set X can be understood as a special case of fuzzy multiset where $CM\left(x\right)=\left({\mu }_A^1\left(x\right)\right)$ for all $x\in X$.

Definition 3.

[18] Let X be a non-empty set and $A,B$ be fuzzy multisets of X with fuzzy count functions $C{M}_A,C{M}_B$, respectively. Then:

1. 

$A\subseteq B$if$C{M}_A\left(x\right)\le C{M}_B\left(x\right)$for all$x\in X$;

2. 

$A=B$if$C{M}_A\left(x\right)=C{M}_B\left(x\right)$for all$x\in X$(i.e.,$C{M}_A\left(x\right)\le C{M}_B\left(x\right)$and$C{M}_B\left(x\right)\le C{M}_A\left(x\right)$for all$x\in X$);

3. 

the fuzzy multiset$A\cap B$is defined as$C{M}_{A\cap B}\left(x\right)=C{M}_A\left(x\right)\wedge C{M}_B\left(x\right)$;

4. 

the fuzzy multiset$A\cup B$is defined as$C{M}_{A\cup B}\left(x\right)=C{M}_A\left(x\right)\vee C{M}_B\left(x\right)$.

In Definition 3, if $C{M}_A\left(x\right)=({\mu }_A^1\left(x\right),\dots ,{\mu }_A^p\left(x\right))$ and $C{M}_B\left(x\right)=\left({\mu }_B^1\left(x\right),\dots ,{\mu }_B^r\left(x\right)\right)$ then:

• $C{M}_A\left(x\right)\le C{M}_B\left(x\right)$ means that ${\mu }_A^i\left(x\right)\le {\mu }_B^i\left(x\right)$ for all $i=1,\dots ,\max \{p,r\}$;
• $C{M}_A\left(x\right)\wedge C{M}_B\left(x\right)=(\min \left({\mu }_A^1\left(x\right),{\mu }_B^1\left(x\right)\right),\dots ,\min ({\mu }_A^{\max (p,r)}\left(x\right),{\mu }_B^{\max (p,r)}\left(x\right)\left)\right)$;
• $C{M}_A\left(x\right)\vee C{M}_B\left(x\right)=\left(\max \left({\mu }_A^1\left(x\right),{\mu }_B^1\left(x\right)\right),\dots ,\max \left({\mu }_A^{\max (p,r)}\left(x\right),{\mu }_B^{\max (p,r)}\left(x\right)\right)\right)$.

3. Fuzzy Multi-Ideal of Near Rings

This section combines the notions of fuzzy multiset [4,25] and fuzzy ideals of near rings to define fuzzy multi-ideals of near rings. It presents several results related to the new defined concept. Since every fuzzy set can be considered as a fuzzy multiset then some of the results in this section can be considered as a generalization for those in [26] that are related to fuzzy ideals of near rings.

Definition 4.

[10] Let $(R,+,·)$ be a near ring. A fuzzy multiset A (with fuzzy count function $C{M}_A$) over R is a fuzzy multi-subnear ring of R if for all $x,y\in R$, the following conditions hold.

1. 

$C{M}_A\left(x\right)\wedge C{M}_A\left(y\right)\le C{M}_A(x-y)$;

2. 

$C{M}_A\left(x\right)\wedge C{M}_A\left(y\right)\le C{M}_A(x·y)$.

Definition 5.

[10] Let $(R,+,·)$ be a near ring. A fuzzy multiset A (with fuzzy count function $C{M}_A$) over R is a fuzzy multi-ideal of R if for all $x,y\in R$, the following conditions hold.

1. 

$C{M}_A\left(x\right)\wedge C{M}_A\left(y\right)\le C{M}_A(x-y)$;

2. 

$C{M}_A\left(x\right)\wedge C{M}_A\left(y\right)\le C{M}_A(x·y)$;

3. 

$C{M}_A\left(y\right)\le C{M}_A(x+y-x)$;

4. 

$C{M}_A\left(y\right)\le C{M}_A(x·y)$;

5. 

$C{M}_A\left(a\right)\le C{M}_A((x+a)y-xy)$for all$a\in R$.

Proposition 1.

[10] Let $(R,+,·)$ be a near ring with zero element $0\in R$ and A be a fuzzy multi-ideal of R. Then

1. 

$C{M}_A\left(x\right)\le C{M}_A\left(0\right)$;

2. 

$C{M}_A(-x)=C{M}_A\left(x\right)$;

3. 

$C{M}_A(x+y-x)=C{M}_A\left(y\right)$;

4. 

$C{M}_A\left(a\right)\le C{M}_A\left(x\right)$for all$x\in <a>=\{r·a:r\in R\}$.,

5. 

${\bigwedge }_{1\le i\le n}C{M}_A\left(x_i\right)\le C{M}_A(x_1+\dots +x_n)$for all$x_i\in R$.

Remark 1.

Let$(R,+,·)$be a near ring with zero element$0\in R$and A be a fuzzy multiset of R with$C{M}_A\left(x\right)=C{M}_A\left(0\right)$for all$x\in R$. Then A is a fuzzy multi-ideal of R and it is called the constant fuzzy multi-ideal.

Next, we deal with some operations on fuzzy multi-subnear rings (multi-ideals) of near rings such as intersection, union, and product.

Proposition 2.

[10] Let $(R,+,·)$ be a near ring and $A,B$ be fuzzy multi-subnear rings of R. Then $A\cap B$ is a fuzzy multi-subnear ring of R.

Corollary 1.

[10] Let $(R,+,·)$ be a near ring and $A_i$ be a fuzzy multi-subnear ring of R for $i=1,\dots ,n$. Then ${\bigcap }_{i=1}^n{A}_i$ is a fuzzy multi-subnear ring of R.

Proposition 3.

[10] Let $(R,+,·)$ be a near ring and $A,B$ be fuzzy multi-ideals of R. Then $A\cap B$ is a fuzzy multi-ideal of R.

Corollary 2.

[10] Let $(R,+,·)$ be a near ring and $A_i$ be a fuzzy multi-ideal of R for $i=1,\dots ,n$. Then ${\bigcap }_{i=1}^n{A}_i$ is a fuzzy multi-ideal of R.

Proposition 4.

[10] Let $R,S$ be near rings with fuzzy multisets $A,B$, respectively. If $A,B$ are fuzzy multi-subnear rings (multi-ideals) of $R,S$ then $A\times B$ is fuzzy multi-subnear rings (multi-ideal) of $R\times S$, where $C{M}_{A\times B}\left((r,s)\right)=C{M}_A\left(r\right)\wedge C{M}_B\left(s\right)$ for all $(r,s)\in R\times S$.

Proposition 5.

[10] Let $R_i$ be near rings with fuzzy multiset $A_i$ for $i=1,\dots ,n$. If $A_i$ is a fuzzy multi-subnear ring (multi-ideal) of $R_i$ then ${\prod }_{i=1}^n{A}_i$ is a fuzzy multi-ideal of ${\prod }_{i=1}^n{R}_i$, where $C{M}_{{\prod }_{i=1}^n{A}_i}\left((r_1,\cdots ,r_n)\right)={\bigwedge }_{i=1}^{n}C{M}_{A_i}\left(r_i\right)$ for all $(r_1,\cdots ,r_n)\in {\prod }_{i=1}^n{R}_i$.

Notation 1.

Let$(R,+,·)$be a near ring, A be a fuzzy multiset of R, and$C{M}_A\left(x\right)=({\mu }_A^1\left(x\right),{\mu }_A^2\left(x\right),\dots ,{\mu }_A^p\left(x\right))$. Then

• $C{M}_A\left(x\right)=0$if${\mu }_A^1\left(x\right)=0$,
• $C{M}_A\left(x\right)>0$if${\mu }_A^1\left(x\right)>0$,
• $C{M}_A\left(x\right)=\underline{1}$if$C{M}_A\left(x\right)=(\underset{s\mathrm{times}}{\underbrace{1,\dots ,1}})$where

  $$s=\max \{k\in \mathbb{N}:C{M}_A\left(y\right)=({\mu }_A^1\left(y\right),{\mu }_A^2\left(y\right),\dots ,{\mu }_A^k\left(y\right)),{\mu }_A^k\left(y\right)\ne 0,y\in R\}.$$

Definition 6.

[10] Let $(R,+,·)$ be a near ring and A be a fuzzy multiset of H. Then $A_{\star }=\{x\in R:C{M}_A\left(x\right)>0\}$ and $A^{\star }=\{x\in R:C{M}_A\left(x\right)=C{M}_A\left(0\right)\}$.

Proposition 6.

[10] Let $(R,+,·)$ be a near ring and A be a fuzzy multi-subnear ring (multi-ideal) of R. Then $A_{\star }$ is either the empty set or a subnear ring (ideal) of R.

Proposition 7.

[10] Let $(R,+,·)$ be a near ring with a fuzzy multi-ideal A. Then the fuzzy multiset of $P_n\left(R\right)$ defined as $CM(a_0+a_{1}x+\dots +a_{n}x)=C{M}_A\left(a_0\right)$ is a fuzzy multi-ideal of $P_n\left(R\right)$.

Notation 2.

Let$(R,+,·)$be a near ring, A be a fuzzy multiset of R and$C{M}_A\left(x\right)=({\mu }_A^1\left(x\right),{\mu }_A^2\left(x\right),\dots ,{\mu }_A^p\left(x\right))$. We say that$C{M}_A\left(x\right)\ge (t_1,\dots ,t_k)$if$p\ge k$and${\mu }_A^i\left(x\right)\ge t_i$for all$i=1,\dots ,k$. If$C{M}_A\left(x\right)\ngeqq (t_1,\dots ,t_k)$and$(t_1,\dots ,t_k)\ngeqq C{M}_A\left(x\right)$then we say that$C{M}_A\left(x\right)$and$(t_1,\dots ,t_k)$are not comparable.

Notation 3.

Let$(R,+,·)$be a near ring, A a fuzzy multiset of R with fuzzy count function$CM$, and$t=(t_1,\dots ,t_k)$where$t_i\in [0,1]$for$i=1,\dots ,k$and$t_1\ge t_2\ge \dots \ge t_k$. Then$C{M}^t=\{x\in R:CM\left(x\right)\ge t\}$.

Theorem 1.

[10] Let $(R,+,·)$ be a near ring, A a fuzzy multiset of R with fuzzy count function $CM$ and $t=(t_1,\dots ,t_k)$ where $t_i\in [0,1]$ for $i=1,\dots ,k$ and $t_1\ge t_2\ge \dots \ge t_k$. Then A is a fuzzy multi-subnear ring of R if and only if $C{M}_t$ is either the empty set or a subnear ring of R.

Theorem 2.

[10] Let $(R,+,·)$ be a near ring, A a fuzzy multiset of R with fuzzy count function $CM$ and $t=(t_1,\dots ,t_k)$ where $t_i\in [0,1]$ for $i=1,\dots ,k$ and $t_1\ge t_2\ge \dots \ge t_k$. Then A is a fuzzy multi-ideal of R if and only if $C{M}_t$ is either the empty set or an ideal of R.

Corollary 3.

[10] Let $(R,+,·)$ be a near ring. If every subnear ring of R is an ideal of R then every fuzzy multi-subnear ring of R is a fuzzy multi-ideal of R.

Proposition 8.

[10] Let $(R,+,·)$ be a near ring and I be an ideal of R. Then $I=C{M}_t$ for some fuzzy multi-ideal $CM$ of R, $t=(t_1,\dots ,t_k)$ where $t_i\in [0,1]$ for $i=1,\dots ,k$ and $t_1\ge t_2\ge \dots \ge t_k$.

Corollary 4.

[10] Let $(R,+,·)$ be a near ring. Then R has at least one fuzzy multi-ideal beside the constant fuzzy multi-ideal.

Definition 7.

Let$(R,+,·)$be a near ring, A and B be fuzzy multi-subnear rings (ideals) of R with fuzzy count functions$C{M}_A$and$C{M}_B$, respectively. If for all$x,y\in R$:

1. 

$C{M}_A\left(x\right)=C{M}_A\left(y\right)$if and only if$C{M}_B\left(x\right)=C{M}_B\left(y\right)$,

2. 

$C{M}_A\left(x\right)\le C{M}_A\left(y\right)$if and only if$C{M}_B\left(x\right)\le C{M}_B\left(y\right)$, and

3. 

$C{M}_A\left(x\right),C{M}_A\left(y\right)$are not comparable if and only if$C{M}_B\left(x\right),C{M}_B\left(y\right)$are not comparable then A and B are equivalent fuzzy multi-subnear rings (ideals) of R.

4. Anti-Fuzzy Multi-Ideals of Near Rings

This section defines the complement of a fuzzy multiset and discusses some of its properties. Moreover, we introduce anti-fuzzy multi-subnear rings (multi-ideals) of near rings and prove some results related to the new defined concepts.

Definition 8.

Let$(R,+,·)$be a near ring. A fuzzy multiset A (with count function$C{M}_A$) over R is an anti-fuzzy multi-subnear ring of R if for all$x,y\in R$, the following conditions hold.

1. 

$C{M}_A\left(x\right)\vee C{M}_A\left(y\right)\ge C{M}_A(x-y)$;

2. 

$C{M}_A\left(x\right)\vee C{M}_A\left(y\right)\ge C{M}_A(x·y)$.

Definition 9.

Let$(R,+,·)$be a near ring. A fuzzy multiset A (with count function$C{M}_A$) over R is an anti-fuzzy multi-ideal of R if for all$x,y\in R$, the following conditions hold.

1. 

$C{M}_A\left(x\right)\vee C{M}_A\left(y\right)\ge C{M}_A(x-y)$;

2. 

$C{M}_A\left(x\right)\vee C{M}_A\left(y\right)\ge C{M}_A(x·y)$;

3. 

$C{M}_A\left(y\right)\ge C{M}_A(x+y-x)$;

4. 

$C{M}_A\left(y\right)\ge C{M}_A(x·y)$;

5. 

$C{M}_A\left(a\right)\ge C{M}_A((x+a)y-xy)$for all$a\in R$.

Proposition 9.

Let$(R,+,·)$be a near ring with zero element$0\in R$and A be an anti-fuzzy multi-ideal of R. Then

1. 

$C{M}_A\left(x\right)\ge C{M}_A\left(0\right)$;

2. 

$C{M}_A(-x)=C{M}_A\left(x\right)$;

3. 

$C{M}_A(x+y-x)=C{M}_A\left(y\right)$;

4. 

$C{M}_A\left(a\right)\ge C{M}_A\left(x\right)$for all$x\in <a>$.

Proof. 

The proof is straightforward. □

Definition 10.

Let R be a non-empty set. Let A be a fuzzy multiset of R. The complement of A will be denoted$A^{\prime }$and it is a fuzzy multiset defined as: For all$x\in R$,

$$C{M}_{A^{\prime }}\left(x\right)=\underline{1}-C{M}_A\left(x\right).$$

Example 1.

Let$R=\{a,b,c\}$be a set. Let A be a fuzzy multiset and the fuzzy count function$CM$be defined as:$CM\left(a\right)=0,CM\left(b\right)=(1,1,1,1),CM\left(c\right)=(0.5,0.3,0.1)$. Then$A^{\prime }=\{(1,1,1,1)/a,(1,0.9,0.7,0.5)/c\}$.

Proposition 10.

Let R be a non-empty set, A be a fuzzy multiset of R, and$x,y\in R$. Then

$$C{M}_A\left(x\right)\le C{M}_A\left(y\right)\mathit{if}\mathit{and}\mathit{only}\mathit{if}\underline{1}-C{M}_{A^{\prime }}\left(y\right)\le \underline{1}-C{M}_{A^{\prime }}\left(x\right).$$

Proof. 

Let $C{M}_A\left(x\right)=({\mu }_A^1\left(x\right),{\mu }_A^2\left(x\right),\dots ,{\mu }_A^m\left(x\right))\le C{M}_A\left(y\right)=({\mu }_A^1\left(y\right),{\mu }_A^2\left(y\right),\dots ,{\mu }_A^n\left(y\right))$ and $s=\max \{k\in \mathbb{N}:C{M}_A\left(y\right)=({\mu }_A^1\left(y\right),{\mu }_A^2\left(y\right),\dots ,{\mu }_A^k\left(y\right)),{\mu }_A^k\left(y\right)\ne 0,y\in R\}$. It is clear that $s\ge m$ and $s\ge n$. Then $\underline{1}-C{M}_{A^{\prime }}\left(y\right)=(1-{\mu }_A^s\left(y\right),\dots ,1-{\mu }_A^n\left(y\right),\dots ,1-{\mu }_A^1\left(y\right))$. Since $C{M}_A\left(x\right)\le C{M}_A\left(y\right)$, it follows that ${\mu }_A^i\left(x\right)\le {\mu }_A^i\left(y\right)$ for all $i=1,\dots ,s$. The latter implies that $1-{\mu }_A^i\left(y\right)\le 1-{\mu }_A^i\left(x\right)$ for all $i=1,\dots ,s$. Thus, $\underline{1}-C{M}_{A^{\prime }}\left(y\right)\le \underline{1}-C{M}_{A^{\prime }}\left(x\right)$. Similarly, we can prove that if $\underline{1}-C{M}_{A^{\prime }}\left(y\right)\le \underline{1}-C{M}_{A^{\prime }}\left(x\right)$ then $C{M}_A\left(x\right)\le C{M}_A\left(y\right)$. □

Proposition 11.

Let R be a non-empty set,$A,B$fuzzy multisets of R,$s=\max \{k\in \mathbb{N}:C{M}_A\left(y\right)=({\mu }_A^1\left(y\right),{\mu }_A^2\left(y\right),\dots ,{\mu }_A^k\left(y\right)),{\mu }_A^k\left(y\right)\ne 0,y\in R\}$, and$s^{\prime }=\max \{k\in \mathbb{N}:C{M}_B\left(y\right)=({\mu }_B^1\left(y\right),{\mu }_B^2\left(y\right),\dots ,{\mu }_B^k\left(y\right)),{\mu }_B^k\left(y\right)\ne 0,y\in R\}$. Then

1. 

if$s=s^{\prime }$and$A\subseteq B$then$B^{\prime }\subseteq A^{\prime }$;

2. 

if$A=B$then$A^{\prime }=B^{\prime }$.

Proof. 

(1) We have $C{M}_{A^{\prime }}\left(x\right)=(1-{\mu }_A^s\left(x\right),\dots ,1-{\mu }_A^1\left(x\right))$ and $C{M}_{B^{\prime }}\left(x\right)=(1-{\mu }_B^s\left(x\right),\dots ,1-{\mu }_B^1\left(x\right))$. Since $A\subseteq B$, it follows that ${\mu }_A^i\left(x\right)\le {\mu }_B^i\left(x\right)$ for all $i=1,\dots ,s$. The latter implies that $1-{\mu }_B^i\left(x\right)\le 1-{\mu }_A^i\left(x\right)$ for all $i=1,\dots ,s$. Thus, $C{M}_{B^{\prime }}\left(x\right)\le C{M}_{A^{\prime }}\left(x\right)$.

(2) Since $A=B$, it follows that $s=s^{\prime }$, $A\subseteq B$, and $B\subseteq A$. By (1), we get that $B^{\prime }\subseteq A^{\prime }$ and $A^{\prime }\subseteq B^{\prime }$. Thus, $A^{\prime }=B^{\prime }$. □

Remark 2.

Let R be a non-empty set,$A,B$fuzzy multisets of R,$s=\max \{k\in \mathbb{N}:C{M}_A\left(y\right)=({\mu }_A^1\left(y\right),{\mu }_A^2\left(y\right),\dots ,{\mu }_A^k\left(y\right)),{\mu }_A^k\left(y\right)\ne 0,y\in R\}$, and$s^{\prime }=\max \{k\in \mathbb{N}:C{M}_B\left(y\right)=({\mu }_B^1\left(y\right),{\mu }_B^2\left(y\right),\dots ,{\mu }_B^k\left(y\right)),{\mu }_B^k\left(y\right)\ne 0,y\in R\}$. If$s\ne s^{\prime }$and$A\subseteq B$then$B^{\prime }\subseteq A^{\prime }$may not hold.

Remark 2 can be illustrated by the following example.

Example 2.

Let$R=\{d,e\}$. Moreover, let$A=\left\{\right(1,0.5)/d,(0.7,0.6)/e\}$,$B=\left\{\right(1,0.5,0.4)/d,$$(0.7,0.6)/e\}$be fuzzy multisets of R. It is clear that$A\subseteq B$and$s=2\ne 3=s^{\prime }$. Having$A^{\prime }=\{\left(0.5\right)/d,(1,0.4,0.3)/e\}$and$B^{\prime }=\{(0.6,0.5)/d,(0.4,0.3)/e\}$implies that$B^{\prime }⊈A^{\prime }$.

Proposition 12.

Let R be a non-empty set,$A,B$fuzzy multisets of R,$s=\max \{k\in \mathbb{N}:C{M}_A\left(y\right)=({\mu }_A^1\left(y\right),{\mu }_A^2\left(y\right),\dots ,{\mu }_A^k\left(y\right)),{\mu }_A^k\left(y\right)\ne 0,y\in R\}$, and$s^{\prime }=\max \{k\in \mathbb{N}:C{M}_B\left(y\right)=({\mu }_B^1\left(y\right),{\mu }_B^2\left(y\right),\dots ,{\mu }_B^k\left(y\right)),{\mu }_B^k\left(y\right)\ne 0,y\in R\}$. Then

1. 

${\left(A^{\prime }\right)}^{\prime }=A$;

2. 

$A^{\prime }\cap B^{\prime }\subseteq {(A\cup B)}^{\prime }$;

3. 

${(A\cap B)}^{\prime }\subseteq A^{\prime }\cup B^{\prime }$.

Proof. 

(1) Having $C{M}_{A^{\prime }}\left(x\right)=(1-{\mu }_A^s\left(x\right),\dots ,1-{\mu }_A^1\left(x\right))$ for every $x\in R$ implies that $C{M}_{{\left(A^{\prime }\right)}^{\prime }}\left(x\right)=(1-(1-{\mu }_A^1\left(x\right)),\dots ,1-(1-{\mu }_A^s\left(x\right)))=C{M}_A\left(x\right)$.

(2) Without loss of generality, let $s\ge s^{\prime }$. Having

$$C{M}_{A\cup B}\left(x\right)=(\max ({\mu }_A^1\left(x\right),{\mu }_B^1\left(x\right)),\dots ,\max ({\mu }_A^s\left(x\right),{\mu }_B^s\left(x\right)))$$

implies that $C{M}_{{(A\cup B)}^{\prime }}\left(x\right)=(1-\max ({\mu }_A^s\left(x\right),{\mu }_B^s\left(x\right)),\dots ,1-\max ({\mu }_A^1\left(x\right),{\mu }_B^1\left(x\right)))$. However, $1-\max ({\mu }_A^i\left(x\right),{\mu }_B^i\left(x\right))=\min (1-{\mu }_A^i\left(x\right),1-{\mu }_B^i\left(x\right))$. The latter implies that $C{M}_{{(A\cup B)}^{\prime }}\left(x\right)=(\min (1-{\mu }_A^s\left(x\right),1-{\mu }_B^s\left(x\right)),\dots ,\min (1-{\mu }_A^{s^{\prime }}\left(x\right),1-{\mu }_B^{s^{\prime }}\left(x\right)),\dots \min (1-{\mu }_A^1\left(x\right),1-{\mu }_B^1\left(x\right)))\ge (\min (1-{\mu }_A^{s^{\prime }}\left(x\right),1-{\mu }_B^{s^{\prime }}\left(x\right)),\dots ,\min (1-{\mu }_A^1\left(x\right),1-{\mu }_B^1\left(x\right)))=C{M}_{A^{\prime }\cap B^{\prime }}\left(x\right)$.

(3) Without loss of generality, let $s\ge s^{\prime }$. Having

$$C{M}_{A\cap B}\left(x\right)=(\min ({\mu }_A^1\left(x\right),{\mu }_B^1\left(x\right)),\dots ,\min ({\mu }_A^{s^{\prime }}\left(x\right),{\mu }_B^{s^{\prime }}\left(x\right)))$$

implies that $C{M}_{{(A\cap B)}^{\prime }}\left(x\right)=(1-\min ({\mu }_A^{s^{\prime }}\left(x\right),{\mu }_B^{s^{\prime }}\left(x\right)),\dots ,1-\min ({\mu }_A^1\left(x\right),{\mu }_B^1\left(x\right)))$. However, $1-\min ({\mu }_A^i\left(x\right),{\mu }_B^i\left(x\right))=\max (1-{\mu }_A^i\left(x\right),1-{\mu }_B^i\left(x\right))$. The latter implies that $C{M}_{{(A\cap B)}^{\prime }}\left(x\right)=(\max (1-{\mu }_A^{s^{\prime }}\left(x\right),1-{\mu }_B^{s^{\prime }}\left(x\right)),\dots ,\max (1-{\mu }_A^1\left(x\right),1-{\mu }_B^1\left(x\right)))$ $\le (\max (1-{\mu }_A^s\left(x\right),1-{\mu }_B^s\left(x\right)),\dots ,\max (1-{\mu }_A^1\left(x\right),1-{\mu }_B^1\left(x\right)))=C{M}_{A^{\prime }\cup B^{\prime }}\left(x\right)$. □

Remark 3.

Let R be a non-empty set,$A,B$fuzzy multisets of R. Then$A^{\prime }\cap B^{\prime }={(A\cup B)}^{\prime }$and${(A\cap B)}^{\prime }=A^{\prime }\cup B^{\prime }$may not hold.

We illustrate Remark 3 by the following example.

Example 3.

Let$R=\{a,b,c\}$and$A,B$be fuzzy multisets of R with

$$A=\left\{\right(0.4,0.3)/a,(0.5,0.2,0.1)/c\},B=\left\{\right(0.4,0.3,0.3,0.3)/a\}.$$

One can easily see that:

$$A^{\prime }\cup B^{\prime }=\{(1,0.7,0.7,0.6)/a,(1,1,1,1)/b,(1,1,1,1)/c\}$$

$$\ne \{(0.7,0.6)/a,(1,1)/b,(1,1)/c\}={(A\cap B)}^{\prime },$$

and that

$${(A\cup B)}^{\prime }=\{(0.7,0.7,0.7,0.6)/a,(1,1,1,1)/b,(1,0.9,0.8,0.5)/c\}$$

$$\ne \{(0.7,0.7,0.6)/a,(1,1,1)/b,(0.9,0.8,0.5)/c\}=A^{\prime }\cap B^{\prime }.$$

Remark 4.

Let$(R,+,·)$be a near ring and A be the constant fuzzy multiset of R. Then A is an anti-fuzzy multi-ideal of R.

Next, we deal with some operations on anti-fuzzy multi-subnear rings (anti-fuzzy multi-ideals) of near rings.

Proposition 13.

Let$(R,+,·)$be a near ring and$A,B$be anti-fuzzy multi-subnear rings (anti-fuzzy multi-ideals) of R. Then$A\cup B$is an anti fuzzy multi-subnear ring (anti-fuzzy multi-ideal) of R.

Proof. 

The proof is similar to that of Proposition 2 and Proposition 3. □

Corollary 5.

Let$(R,+,·)$be a near ring and$A_i$be an anti-fuzzy multi-subnear ring (multi-ideal) of R for$i=1,\dots ,n$. Then${\cup }_{i=1}^n{A}_i$is an anti-fuzzy multi-subnear ring (multi-ideal) of R.

Proof. 

The proof follows by using induction and Proposition 13. □

Remark 5.

Let$A,B$be anti-fuzzy multi-ideals of a near ring R. Then$A\cap B$may not be an anti-fuzzy multi-ideal of R.

We illustrate Remark 5 by the following example.

Example 4.

Let$(\mathbb{Z},+,·)$be the near ring of integers under standard addition ”+” and with ”·” defined by$x·y=y$for all$x,y\in \mathbb{Z}$. Let$A,B$be the anti-fuzzy multi-ideals of$\mathbb{Z}$given by:

$$C{M}_A\left(x\right)=\left\{\begin{array}{c}0ifxisamultipleof3;\hfill \\ (1,0.4,0.4,0.1)otherwise.\hfill \end{array}\right.$$

$$C{M}_B\left(x\right)=\left\{\begin{array}{c}(0.3,0.2,0.2)ifxisaneveninteger;\hfill \\ (0.3,0.3,0.3)otherwise.\hfill \end{array}\right.$$

Having$C{M}_{A\cap B}\left(3\right)=0,C{M}_{A\cap B}\left(2\right)=(0.3,0.2,0.2),C{M}_{A\cap B}\left(1\right)=(0.3,0.3,0.3)$,$1=3-2$, and$C{M}_{A\cap B}\left(1\right)=(0.3,0.3,0.3)\nleqq C{M}_{A\cap B}\left(3\right)\vee C{M}_{A\cap B}\left(2\right)=(0.3,0.2,0.2)$implies that$A\cap B$is not an anti-fuzzy multi-ideal of$\mathbb{Z}$.

Proposition 14.

Let X be a non-empty set and A a fuzzy multiset of X. Then for all$x,y\in X$,

1. 

$\underline{1}-CM\left(x\right)\wedge CM\left(y\right)=(\underline{1}-CM\left(x\right))\vee (\underline{1}-CM\left(y\right))$;

2. 

$\underline{1}-CM\left(x\right)\vee CM\left(y\right)=(\underline{1}-CM\left(x\right))\wedge (\underline{1}-CM\left(y\right))$.

Proof. 

The proof is straightforward. □

Theorem 3.

Let$(R,+,·)$be a near ring and A be a fuzzy multiset of R. Then A is a fuzzy multi-subnear ring (multi-ideal) of R if and only if$A^{\prime }$is an anti-fuzzy multi-subnear ring (multi-ideal) of R.

Proof. 

Let A be a fuzzy multi-ideal of R and $x,y\in R$. We need to prove that conditions of Definition 9 are satisfied for $A^{\prime }$. (1) $C{M}_{A^{\prime }}(x-y)=\underline{1}-C{M}_A(x-y)$. Having A a fuzzy multi-ideal of R implies that $C{M}_A(x-y)\ge C{M}_A\left(x\right)\wedge C{M}_A\left(y\right)$. The latter implies that $C{M}_{A^{\prime }}(x-y)\le (\underline{1}-C{M}_A\left(x\right))\vee (\underline{1}-C{M}_A\left(y\right))=C{M}_{A^{\prime }}\left(x\right)\vee C{M}_{A^{\prime }}\left(y\right)$. (2) $C{M}_{A^{\prime }}(x·y)=\underline{1}-C{M}_A(x·y)$. Having A a fuzzy multi-ideal of R implies that $C{M}_A(x·y)\ge C{M}_A\left(x\right)\wedge C{M}_A\left(y\right)$. The latter implies that $C{M}_{A^{\prime }}(x·y)\le (\underline{1}-C{M}_A\left(x\right))\vee (\underline{1}-C{M}_A\left(y\right))=C{M}_{A^{\prime }}\left(x\right)\vee C{M}_{A^{\prime }}\left(y\right)$. (3) $C{M}_{A^{\prime }}(x+y-x)=\underline{1}-C{M}_A(x+y-x)$. Having A a fuzzy multi-ideal of R implies that $C{M}_A(x+y-x)\ge C{M}_A\left(y\right)$. The latter implies that $C{M}_{A^{\prime }}(x+y-x)\le \underline{1}-C{M}_A\left(y\right)=C{M}_{A^{\prime }}\left(y\right)$. (4) $C{M}_{A^{\prime }}(x·y)=\underline{1}-C{M}_A(x·y)$. Having A a fuzzy multi-ideal of R implies that $C{M}_A(x·y)\ge C{M}_A\left(y\right)$. The latter implies that $C{M}_{A^{\prime }}(x·y)\le \underline{1}-C{M}_A\left(y\right)=C{M}_{A^{\prime }}\left(y\right)$. (5) Let $a\in R$. $C{M}_{A^{\prime }}((x+a)y-xy)=\underline{1}-C{M}_A((x+a)y-xy)$. Having A a fuzzy multi-ideal of R implies that $C{M}_A((x+a)y-xy)\ge C{M}_A\left(a\right)$. The latter implies that $C{M}_{A^{\prime }}((x+a)y-xy)\le \underline{1}-C{M}_A\left(a\right)=C{M}_{A^{\prime }}\left(a\right)$.

Conversely, let $A^{\prime }$ be an anti-fuzzy multi-ideal of R and $x,y\in R$. We need to prove that conditions of Definition 5 are satisfied for A. (1) $C{M}_A(x-y)=\underline{1}-C{M}_{A^{\prime }}(x-y)$. Having $A^{\prime }$ an anti-fuzzy multi-ideal of R implies that $C{M}_{A^{\prime }}(x-y)\le C{M}_{A^{\prime }}\left(x\right)\vee C{M}_{A^{\prime }}\left(y\right)$. The latter implies that $C{M}_A(x-y)\ge (\underline{1}-C{M}_{A^{\prime }}\left(x\right))\wedge (\underline{1}-C{M}_{A^{\prime }}\left(y\right))=C{M}_A\left(x\right)\wedge C{M}_A\left(y\right)$. (2) $C{M}_A(x·y)=\underline{1}-C{M}_{A^{\prime }}(x·y)$. Having $A^{\prime }$ an anti-fuzzy multi-ideal of R implies that $C{M}_{A^{\prime }}(x·y)\le C{M}_{A^{\prime }}\left(x\right)\vee C{M}_{A^{\prime }}\left(y\right)$. The latter implies that $C{M}_A(x·y)\ge (\underline{1}-C{M}_{A^{\prime }}\left(x\right))\wedge (\underline{1}-C{M}_{A^{\prime }}\left(y\right))=C{M}_A\left(x\right)\wedge C{M}_A\left(y\right)$ (3) $C{M}_A(x+y-x)=\underline{1}-C{M}_{A^{\prime }}(x+y-x)$. Having $A^{\prime }$ an anti-fuzzy multi-ideal of R implies that $C{M}_{A^{\prime }}(x+y-x)\le C{M}_{A^{\prime }}\left(y\right)$. The latter implies that $C{M}_A(x+y-x)\ge \underline{1}-C{M}_{A^{\prime }}\left(y\right)=C{M}_A\left(y\right)$. (4) $C{M}_A(x·y)=\underline{1}-C{M}_{A^{\prime }}(x·y)$. Having $A^{\prime }$ an anti-fuzzy multi-ideal of R implies that $C{M}_{A^{\prime }}(x+y-x)\le C{M}_{A^{\prime }}\left(y\right)$. The latter implies that $C{M}_A(x·y)\ge \underline{1}-C{M}_{A^{\prime }}\left(y\right)=C{M}_A\left(y\right)$. (5) Let $a\in R$. $C{M}_A((x+a)y-xy)=\underline{1}-C{M}_{A^{\prime }}((x+a)y-xy)$. Having $A^{\prime }$ an anti-fuzzy multi-ideal of R implies that $C{M}_{A^{\prime }}((x+a)y-xy)\le C{M}_{A^{\prime }}\left(a\right)$. The latter implies that $C{M}_A((x+a)y-xy)\ge \underline{1}-C{M}_{A^{\prime }}\left(a\right)=C{M}_A\left(a\right)$. □

Example 5.

Let$(R,+,·)$be the near ring defined by the following tables: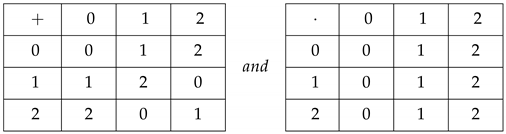

In [10], Al-Tahan et al. showed that

$$A=\left\{\right(1,1,0.6,0.6,0.1)/0,(0.8,0.4,0.2,0.1)/1,(0.8,0.4,0.2,0.1)/2\}$$

is a fuzzy multi-ideal of R. Theorem 3 asserts that

$$A^{\prime }=\{(0.9,0.4,0.4)/0,(1,0.9,0.8,0.6,0.2)/1,(1,0.9,0.8,0.6,0.2)/2\}$$

is an anti-fuzzy multi-ideal of R.

Corollary 6.

Let$(R,+,·)$be a near ring and A be a fuzzy multiset of R. Then A and$A^{\prime }$are fuzzy multi-ideals of R if and only if A is the constant fuzzy multi-ideal of R.

Proof. 

Let A be the constant fuzzy multi-ideal of R. Then A and $A^{\prime }$ are fuzzy multi-ideals of R.

Let A and $A^{\prime }$ be fuzzy multi-ideals of R. Then, for all $x\in R$, we have $C{M}_A\left(x\right)\le C{M}_A\left(0\right)$ and $\underline{1}-C{M}_A\left(x\right)=C{M}_{A^{\prime }}\left(x\right)\le C{M}_{A^{\prime }}\left(0\right)=\underline{1}-C{M}_A\left(0\right)$ (by Propositions 1 and 9). The latter and Proposition 10 imply that $C{M}_A\left(x\right)\le C{M}_A\left(0\right)$ and $C{M}_A\left(x\right)\ge C{M}_A\left(0\right)$. Thus, $C{M}_A\left(x\right)=C{M}_A\left(0\right)$. □

Corollary 7.

Let$(R,+,·)$be a near ring and A be a fuzzy multiset of R. Then A and$A^{\prime }$are anti-fuzzy multi-ideals of R if and only if A is the constant fuzzy multi-ideal of R.

Proof. 

The proof is similar to that of Corollary 6. □

Notation 4.

Let$(R,+,·)$be a near ring, A a fuzzy multiset of R with fuzzy count function$C{M}_A$, and$t=(t_1,\dots ,t_k)$where$t_i\in [0,1]$for$i=1,\dots ,k$and$t_1\ge t_2\ge \dots \ge t_k$. Then$C{M}_A^t=\{x\in R:CM\left(x\right)\le t\}$.

Theorem 4.

Let$(R,+,·)$be a near ring, A a fuzzy multiset of R with fuzzy count function$C{M}_A$and$t=(t_1,\dots ,t_k)$where$t_i\in [0,1]$for$i=1,\dots ,k$and$t_1\ge t_2\ge \dots \ge t_k$. Then A is an anti-fuzzy multi-subnear ring (multi-ideal) of R if and only if$C{M}_A^t$is either the empty set or a subnear ring (ideal) of R.

Proof. 

The proof is similar to that of Theorems 1 and 2. □

Proposition 15.

Let$(R,+,·)$be a near ring and I be an ideal of R. Then$I=C{M}^t$for some anti-fuzzy multi-ideal$CM$of R,$t=(t_1,\dots ,t_k)$where$t_i\in (0,1]$for$i=1,\dots ,k$and$t_1\ge t_2\ge \dots \ge t_k$.

Proof. 

Let $t=(t_1,\dots ,t_k)$ and $q=(t_1,\dots ,t_k,t_k)$ where $t_i\in (0,1]$ for $i=1,\dots ,k$ and define the fuzzy multiset A of R as follows:

$$CM\left(x\right)=\left\{\begin{array}{ll}t& \mathrm{if}x\in I,\\ q& \mathrm{otherwise}.\end{array}\right.$$

It is clear that $t<q$ and $I=C{M}^t$. We still need to prove that $CM$ is an anti-fuzzy multi-ideal of R. Using Theorem 4, it suffices to show that $C{M}^{\alpha }\ne \varnothing$ is an ideal of R for all $\alpha =(a_1,\dots ,a_s)$ with $a_i\in [0,1]$, $a_1\ne 0$, and $a_1\ge \dots \ge a_s$ for $i=1,\dots ,s$. One can easily see that

$$C{M}_{\alpha }=\left\{\begin{array}{ll}I& \mathrm{if}t\le \alpha <q,\\ R& \mathrm{if}\alpha \ge q,\\ \varnothing & \mathrm{if}\left(0\le \alpha <t\right)\mathrm{or}(\alpha \mathrm{and}t\mathrm{are}\mathrm{not}\mathrm{comparable}).\end{array}\right.$$

Thus, $C{M}^{\alpha }$ is either the empty set or an ideal of R. □

Remark 6.

Let$(R,+,·)$be a near ring and A and B be anti-fuzzy multi-subnear rings (ideals) of R with fuzzy count functions$C{M}_A$and$C{M}_B$, respectively. If for all$x,y\in R$:

1. 

$C{M}_A\left(x\right)=C{M}_A\left(y\right)$if and only if$C{M}_B\left(x\right)=C{M}_B\left(y\right)$,

2. 

$C{M}_A\left(x\right)\le C{M}_A\left(y\right)$if and only if$C{M}_B\left(x\right)\le C{M}_B\left(y\right)$, and

3. 

$C{M}_A\left(x\right),C{M}_A\left(y\right)$are not comparable if and only if$C{M}_B\left(x\right),C{M}_B\left(y\right)$are not comparable then A and B are equivalent anti-fuzzy multi-subnear rings (ideals) of R.

Example 6.

Let$(R,+,·)$be any non-trivial near ring with identity$0\in R$. Then

$$C{M}_A\left(x\right)=\left\{\begin{array}{c}0ifx=0;\hfill \\ (1,0.4,0.4,0.3)otherwise.\hfill \end{array}\right.$$

and

$$C{M}_B\left(x\right)=\left\{\begin{array}{c}(0.3,0.3,0.2)ifx=0;\hfill \\ (1,0.7,0.3)otherwise.\hfill \end{array}\right.$$

are equivalent anti-fuzzy multi-ideals of R.

In what follows, when we say that a near ring has a certain number of anti-fuzzy multi-ideals we mean that it has a certain number of non-equivalent fuzzy multi-ideals.

Corollary 8.

Let$(R,+,·)$be a near ring. Then R has at least one anti-fuzzy multi-ideal beside the constant anti-fuzzy multi-ideal.

Proof. 

Let $(R,+,·)$ be a near ring. Then R has at least two ideals: R and $\left\{0\right\}$. With $\left\{0\right\}$ as an ideal of R and using Proposition 15, we get that $\left\{0\right\}=C{M}^t$ for some $t=(t_1,\dots ,t_k)$. One can define the anti-fuzzy multi-ideal corresponding to $\left\{0\right\}$ as:

$$CM\left(x\right)=\left\{\begin{array}{ll}t& \mathrm{if}x=0\\ q& \mathrm{otherwise},\end{array}\right.$$

where $q>t$. □

Corollary 9.

Let$(R,+,·)$be a simple near ring. Then R has only two non-equivalent anti-fuzzy multi-ideals.

Example 7.

Let p be a prime natural number and$({\mathbb{Z}}_p,+,·)$be the near ring of integers modulo p under standard addition “+" modulo p and “·" defined by$x·y=y$for all$x,y\in {\mathbb{Z}}_p$. Since${\mathbb{Z}}_p$is a simple near ring, it follows by means of Corollary 9 that it has only two non-equivalent anti-fuzzy multi-ideals.

5. Conclusions

This paper found a new link between algebraic structures and fuzzy multisets by introducing anti-fuzzy multi-ideals of near rings and studying their properties. The various basic operations, definitions and theorems related to anti-fuzzy multi-ideals of near rings have been discussed. The results in this paper can be considered as a generalization of the results known for anti-fuzzy ideals of near rings. Moreover, our results are considered as a generalization for anti-fuzzy ideals of rings. This is because every ring is a near ring.

The aim of this paper was to highlight the connection between fuzzy multisets and algebraic structures from an anti-fuzzification point of view. It is well known that the concept of fuzzy multiset is well established in dealing with many real life problems. So, the algebraic structure defined concerning them in this paper would help to approach these problems with a different perspective. The benefit of the paper is the link found between algebraic structures and fuzzy multisets by introducing anti-fuzzy multi-ideals of near rings and studying their properties.