A New Approach for Approximate Solution of ADE: Physical-Based Modeling of Carriers in Doping Region

Abstract

The electric behavior in semiconductor devices is the result of the electric carriers’ injection and evacuation in the low doping region, N-. The carrier’s dynamic is determined by the ambipolar diffusion equation (ADE), which involves the main physical phenomena in the low doping region. The ADE does not have a direct analytic solution since it is a spatio-temporal second-order differential equation. The numerical solution is the most used, but is inadequate to be integrated into commercial electric circuit simulators. In this paper, an empiric approximation is proposed as the solution of the ADE. The proposed solution was validated using the final equations that were implemented in a simulator; the results were compared with the experimental results in each phase, obtaining a similarity in the current waveforms. Finally, an advantage of the proposed methodology is that the final expressions obtained can be easily implemented in commercial simulators.

1. Introduction

In recent years, several investigations have been carried out in the field of power device modeling with the aim of obtaining electrical simulations closer to their experimental measurements. The main problem that arises in obtaining a practical model is the proper description of the behavior of the chargers’ distribution in the N-region. To obtain the loads’ behavior model, the electron and hole currents that are injected during the switching phases need to be calculated.

The electric behavior in semiconductor devices is the result of the electrical chargers’ injection and evacuation in the low doping region, N-. The carrier dynamics is determined by the ambipolar diffusion equation (ADE) solution, where the expression involves the main physical phenomena in the low doping region.

In the literature, some ADE solution methodologies have been reported. However, an analytic solution cannot be obtained because it is a second-order differential equation that depends on time and distance [1,2]. The ADE solutions reported in the literature are classified into two methodologies: numerical solution and approximate solution. The numerical solution gives more exactitude; however, it is not suitable for electrical simulators in contrast with the approximate solution.

The approximate solution is suitable for designers of electrical circuits and can be mainly subdivided into the separation of variables, transformation techniques (Laplace, Fourier), and concentrated electrical chargers [3,4,5,6,7,8,9,10,11,12,13,14,15]; this last type of methodology is one of the most practical, efficient, and focuses mainly on the calculation and modeling of the carriers’ concentration in the N-region that allows the adequate description of the static and dynamic behavior of the semiconductor power devices.

In the literature, limited ADE solution methods based on the N-region modeling are presented. In [6,7,8,9,10,11,12,13,14,15,16,17], it is considered a discretization of the N-region, which includes the movement of the borders in space (xl and xr). In this solution, the authors used the Newton–Raphson method. However, it requires a pre-process of two to four iterations per simulation step; therefore, this solution is not suitable for implementation in electrical circuit simulators.

In [18,19], the use of a three-phase approximation for the turned-off condition was proposed. In each phase, a linearization of the gradient of the charges that occurred in the N-region was obtained; however, the models’ high complexity limited its implementation only to the SABER simulator.

In [20], the N-region was divided into five to ten subregions, where the concentration of carriers was approximated through a second-order polynomial equation with coefficients that varied in time. Due to its complexity, this solution is not suitable for implementation in a commercial electrical simulator.

In [21], to describe the dynamic behavior, the Rayleigh–Ritz method was used in combination with an approximation of the normalized position variable. In this, the final expressions obtained were in a function of time and were easy to solve; however, its implementation was limited only to the SABER simulator.

In [22,23], the ADE solution was presented using the finite element method, obtaining an electrical equivalent for an analogic solution; however, due to the use of the finite element method, its use in electrical circuit simulators becomes impractical.

In [24,25], a Fourier series-based ADE solution was obtained, where the methodology converted the ADE into a finite arrangement of first-order differential equations with variable Fourier coefficients. The accuracy of the model depends on the number of terms used. Therefore, its implementation in electrical circuit simulators is impractical.

In [26], the principle of physical modeling of a power diode was presented based in an approximate solution, however, only a two-dimensional variable analysis was presented.

In this paper, an empirical approximation of the ADE solution is proposed, presenting a detailed procedure and a three-dimensional variable analysis of the carriers’ behavior. It allows the simulation of the main physical phenomena associated with the low doping region in bipolar semiconductor devices, obtaining the carriers’ injection and evacuation of the N-region. The proposed solution solves the ADE as a function on the ambipolar diffusion length adjustment (L), which is achieved by using a simplified semi-theoretical approach. Some of the advantages of this modeling approach are listed below:

• Facility of implementation in circuit simulators through analog electrical components with the system of equations developed as a solution of the ADE.
• The mathematical procedure to solve the spatio-temporal second-order differential ADE equation is not complex in comparison to the numerical solutions proposed in the previous reported references.
• The calculation variables used in each expression are a function of time and space, ensuring an adequate approximation with experimental values.
• The developed model calculates the low doping zone width during the space charge accumulation, allowing the excess of the carriers’ injected calculation on the N-region.
• A three-dimensional variable analysis of the carriers’ behavior is presented.
• The results show that the proposed solution is robust for its integration in commercial electrical circuit simulators.
• The obtained solution ensures a balance between mathematical calculations and accuracy results that are appropriate for its use by electronic designers.
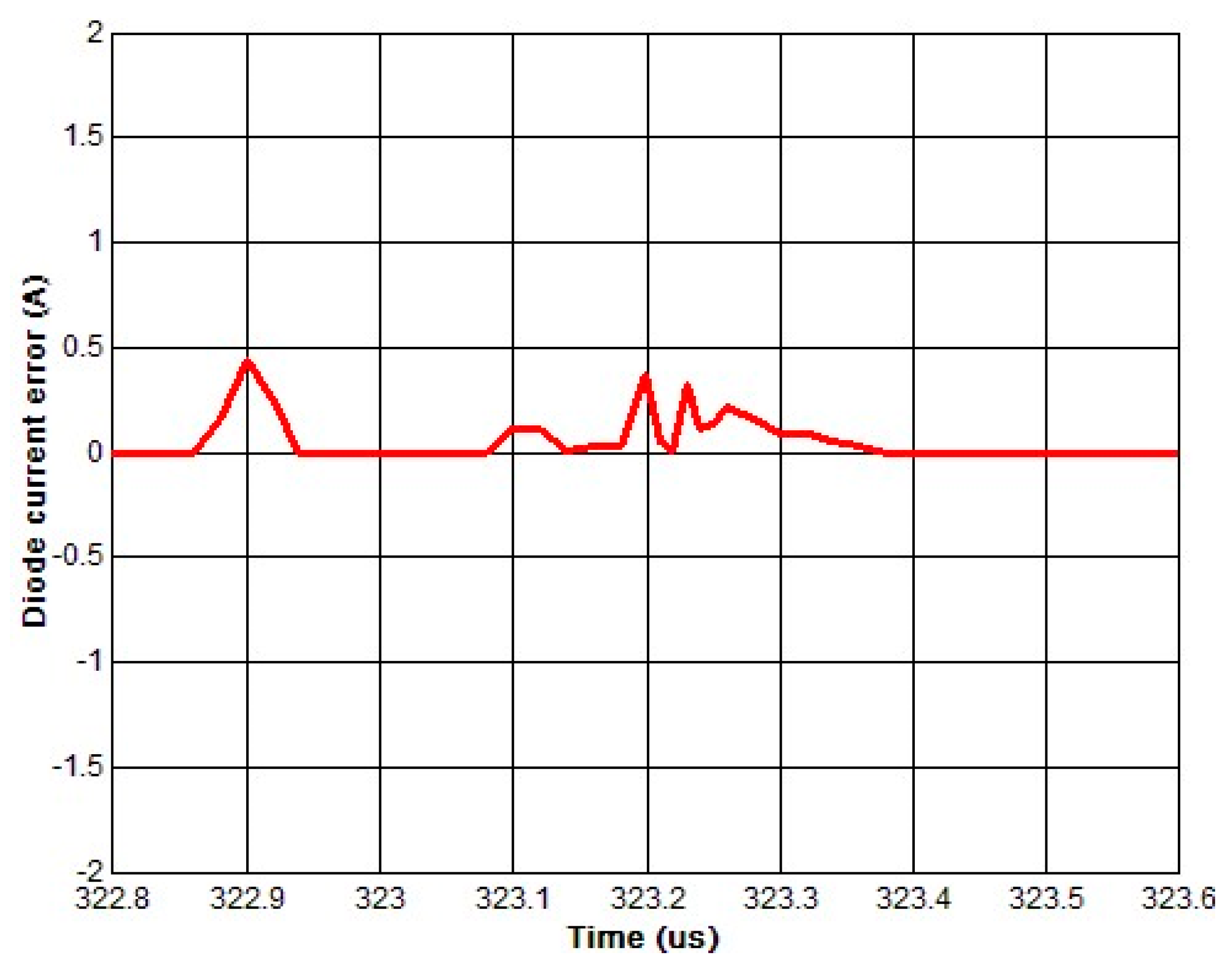
• A graphical and numerical estimated error is presented to validate the accuracy of the obtained results.

The rest of this paper is organized as follows. In Section 2, the development to obtain the ADE is presented. The proposed empirical solution is described in Section 3. In Section 4, the simulation results that validate the proposed solution methodology are presented, and finally, the conclusions of the developed work are presented in Section 5.

2. Ambipolar Diffusion Equation (ADE)

The diode was one of the first semiconductor devices developed for applications in power circuits. This type of device has two junctions (P+N- and N-N+) with a high doping profile and an intermediate region (N-) with a low doping profile. In this type of power device, the N-region is injected with carriers during the conduction phase, reducing this region’s resistance during current flow. However, the injection of a high concentration of minority carriers within the N-region causes two main problems during switching conditions: overvoltage during the change from its OFF state to ON state and reverse recovery during the change from its ON state to OFF state [1,2]. Therefore, the correct solution proposal of the ADE for its implementation in commercial simulators is essential.

The behavior of the N-region of a diode can be simplified as shown in Figure 1, where an injection of carriers takes place in the N-region through two injectors: anode and cathode. The net flow of electrons and holes (carriers) in the semiconductor devices generates the currents I_p(0,t), I_n(0,t), I_p(WB,t), and I_n(WB,t).

Figure 1. Charge distribution in the N-region.

2.1. Carrier Transport

The process in which the charge carriers, p(x,t) ≈ n(x,t) move is known as the carrier transport. The transport of the carrier is made through two basic mechanisms: drift and diffusion.

2.1.1. Drift Mechanisms

When an electric field, E (V/cm), is applied to the N-region, a drift movement in the direction of the electric field for holes (V_p) (opposite direction for electrons (V_n)) predominates over the disordered movement of the carriers by thermal agitation.

The drift movement is due to the carriers’ acceleration caused by the electric field. For small values of the electric field, the drift velocity is proportional to the applied electric field. The constant proportionality between the drift velocity and the electric field is called mobility, μ_n for electrons, and μ_p for holes [1,2].

The drift movement causes electrons and hole currents that are given by:

$$I_{n\_drift}=-q\cdot A\cdot n\cdot V_n=q\cdot A\cdot n\cdot {\mu }_n\cdot E\hspace{1em}(\mathrm{a}mps)$$

(1)

$$I_{p\_drift}=-q\cdot A\cdot p\cdot V_p=q\cdot A\cdot p\cdot {\mu }_p\cdot E\hspace{1em}(amps)$$

(2)

where A is the area of the N-region; n and p are the carriers; and V_n and V_p represent the average velocities of electrons and holes, respectively. The total drift current is the sum of electrons and hole currents caused by the electric field [1,2], which is given by,

$$I_{T\_drift}=q\cdot A\cdot \left(n\cdot {\mu }_n+\mu \cdot p_p\right)E\hspace{1em}[A]$$

(3)

2.1.2. Diffusion

When the carriers are not uniformly distributed in the semiconductor, there is a high concentration region movement to those of low concentration; it predominates over the carriers’ chaotic motion due to thermal agitation. The diffusion of an electron (or hole) from a high concentration region to a low concentration produces a flow of electrons (or holes). The electron and hole currents are proportional to their concentration gradients, which are expressed, in one dimension [1,2], as:

$$I_{n\_difusion}=q\cdot A\cdot D_n\cdot \frac{dn}{dx}$$

(4)

$$I_{p\_difusion}=-q\cdot A\cdot D_p\cdot \frac{dp}{dx}$$

(5)

where D_n and D_p (cm²/s) are the diffusion coefficients for electrons and holes, respectively. The total diffusion current is the contribution of electrons and hole currents,

$$I_{T\_diff}=q\cdot A\cdot D_n\cdot \frac{dn}{dx}-q\cdot A\cdot D_p\cdot \frac{dp}{dx}$$

(6)

There is a high injection of carriers in semiconductor power devices, where n ≈ p in the N-region, being dn/dx ≈ dp/dx. Equations (3) and (6) for the high injection condition are:

$$I_n(x)\approx \frac{b}{1+b}{I}_T+q\cdot A\cdot D\frac{dp}{dx}$$

(7)

$$I_p(x)\approx \frac{1}{1+b}{I}_T-q\cdot A\cdot D\frac{dp}{dx}$$

(8)

where $D=2\frac{D_n\cdot D_p}{D_n+D_p}$.

D is the ambipolar diffusion coefficient. Equations (7) and (8) are known as transport equations, which allow for calculating the current of electrons and holes for any x value along the N-region under high injection conditions.

2.2. Carrier Control Model

When the carrier concentration is disturbed from its equilibrium value (n_{(x = 0)}, p_{(x = 0)}), electrons and holes will try to return to equilibrium. In the injection of excess carriers, the return to equilibrium occurs through the process of recombination of the minority carriers injected with the majority carriers. In the case of the extraction of carriers, they will return to equilibrium through the electron-hole pair generation process. The time required to re-establish the equilibrium is known as the lifetime τ. The analytical expression that allows for calculating the current contribution due to changes in carrier concentration is the continuity equation for electrons and holes given by [1,2],

$$\frac{dn(x,t)}{dt}\approx -\frac{1}{q\cdot A}\frac{d{I}_n}{dx}+G_n-R_n$$

(9)

$$\frac{dp(x,t)}{dt}\approx -\frac{1}{q\cdot A}\frac{d{I}_p}{dx}+G_p-R_p$$

(10)

where G_n and G_p are the electrons and holes generation velocities, respectively. R_n and R_p are the recombination velocity of electron and hole, respectively.

The recombination velocities for electrons and holes, considering only the Shockley–Read–Hall recombination, SRH, and Δn ≈ Δp >> n_i, are given by [1,2],

$$R_p=\frac{p\left(x,t\right)}{{\tau }_p} \mathrm{and} R_n=\frac{n\left(x,t\right)}{{\tau }_n}$$

(11)

Equations (9) and (10) are rewritten, using Equation (11),

$$\frac{dn(x,t)}{dt}=-\frac{1}{q\cdot A}\frac{d{I}_n}{dx}-\frac{n(x,t)}{{\tau }_n}$$

(12)

$$\frac{dp(x,t)}{dt}=-\frac{1}{q\cdot A}\frac{d{I}_p}{dx}-\frac{p(x,t)}{{\tau }_p}$$

(13)

To obtain the carriers’ control, the equation is considered only p. If Equation (12) is integrated between the limits x = 0 and x = W_B, a new expression is obtained given by,

$${\displaystyle \underset{0}{\overset{W_B}{\int }}\frac{\partial I_p}{\partial x}dx}=-qA\cdot {\displaystyle \underset{0}{\overset{W_B}{\int }}\frac{p(x,t)}{{\tau }_p}dx}-qA\cdot {\displaystyle \underset{0}{\overset{W_B}{\int }}\frac{\partial p(x,t)}{\partial t}dx}$$

(14)

As:

$$Q_B=qA\cdot {\displaystyle \underset{0}{\overset{W_B}{\int }}p(x,t)\cdot dx}=qA{W}_B\cdot p(x,t)$$

(15)

$$\frac{d{Q}_B}{dt}=qA\cdot {\displaystyle \underset{0}{\overset{W_B}{\int }}\frac{\partial p(x,t)}{\partial t}dx}$$

(16)

combining Equations (14)–(16), which uses the value of the incoming current and the outgoing current of the N-region as a function of time, the carriers’ control expression is,

$$I{p}_{(0, t)}-I{p}_{(W_B, t)}=\frac{Q}{{\tau }_p}+\frac{dQ}{dt}$$

(17)

The equation that describes the dynamic and static behavior of the carriers in the N-region is obtained, combining Equations (8) and (17).

$$\frac{{\partial }^{2}p(x,t)}{\partial x^2}=\frac{p(x,t)}{L^2}+\frac{1}{D}\frac{\partial p(x,t)}{\partial t}$$

(18)

where $L=\sqrt{D\cdot \tau }$ is known as the ambipolar diffusion length. Equation (18) is known as the ADE.

The solution of Equation (18) allows obtaining the injection of currents and the resistance in the N-region, given, respectively, by,

$$I_{n(x,t)}=\frac{b\cdot I_T}{1+b}+qAD\cdot \frac{\partial p(x,t)}{\partial x}$$

(19)

$$I_{p(x,t)}=\frac{I_T}{1+b}-qAD\cdot \frac{\partial p(x,t)}{\partial x}$$

(20)

$$R_{N-}={\displaystyle \underset{0}{\overset{W_B}{\int }}\frac{dx}{qA\left({\mu }_{n}n+{\mu }_{p}p\right)}}=\frac{W_B}{qA\left({\mu }_{n}n+{\mu }_{p}p\right)}$$

(21)

With $n\approx N_D, p\approx p(x,t) and Q_0=qA{N}_D{W}_B{\mu }_n$

$$\begin{gathered} R_{N-}=\frac{W_B}{qA{N}_D{\mu }_n+qA\left({\mu }_n+{\mu }_p\right)p(x,t)}=\frac{W_B^2}{qA{N}_D{W}_B{\mu }_n+qA{W}_B\cdot p(x,t)\left({\mu }_n+{\mu }_p\right)} \\ =\frac{W_B^2}{Q_0{\mu }_n+Q_B\left({\mu }_n+{\mu }_p\right)} \end{gathered}$$

(22)

where Q₀ represents the stored carriers for thermodynamic equilibrium.

3. The Empirical Solution of the ADE

The N-regions’ behavior depends on two phases, known as static and dynamic phases.

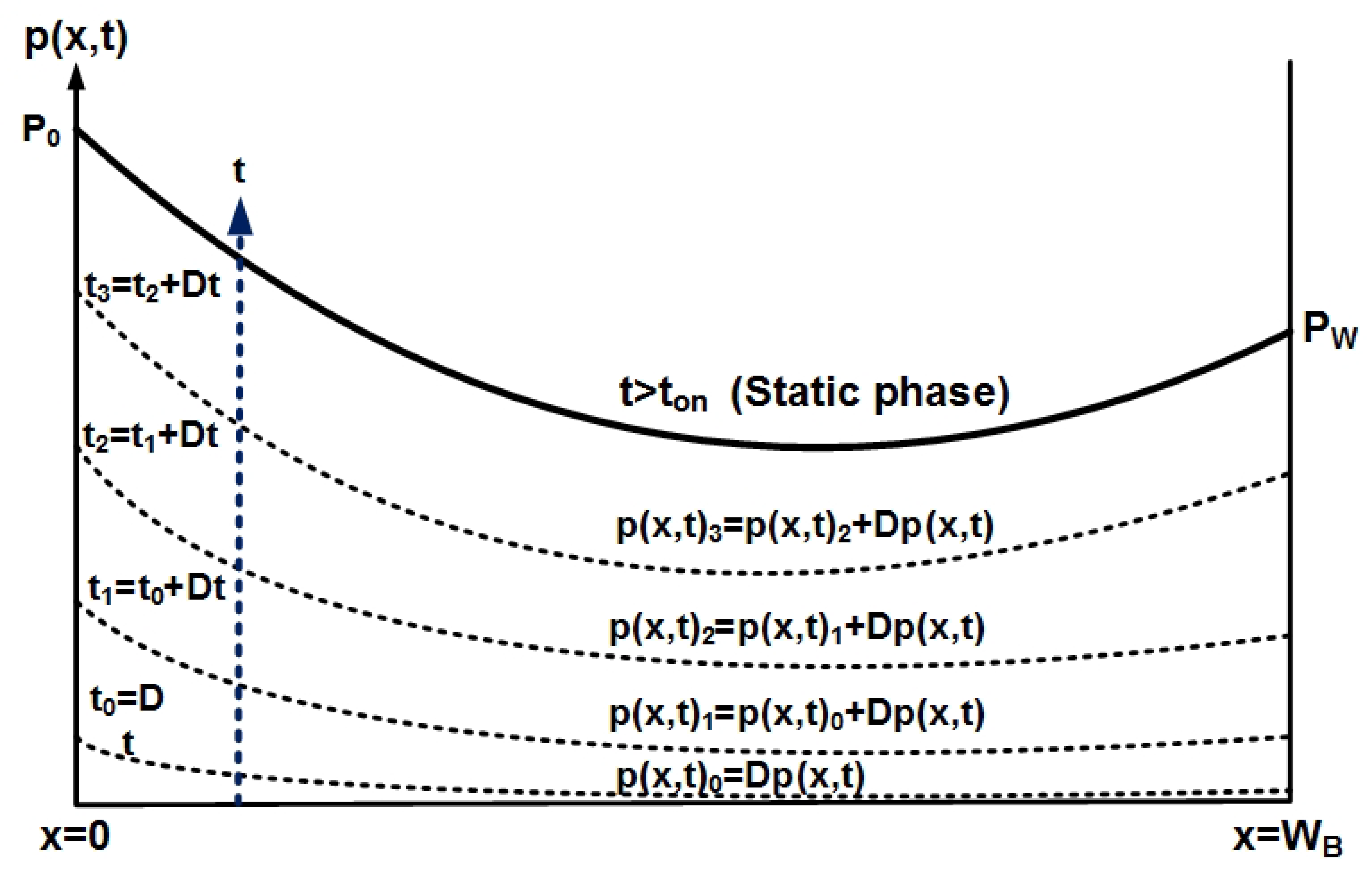
3.1. Static Phase

Under the static conditions: $\raisebox{1ex}{$\partial p(x,t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.=0$, the concentration of carriers will only depend on the variable x, hence Equation (18) can be expressed as:

$$\frac{d^{2}p(x)}{d{x}^2}-\frac{p(x)}{L_S^2}=0$$

(23)

On the other hand, considering the initial conditions of concentration P₀ and P_W at x = 0 and x = W_B, the solution of Equation (23) is given by

$$p(x)=\frac{P_W\cdot \sinh \left(\frac{x}{L_S}\right)+P_0\cdot \sinh \left(\frac{W_B-x}{L_S}\right)}{\sinh \left(\frac{W_B}{L_S}\right)}$$

(24)

Using Equation (24), the concentration gradients in the diode unions are given by,

$$\frac{\partial p(x)}{\partial x}|\begin{array}{c}\\ x=0\end{array}=\frac{1}{L_S}\frac{P_W-P_0\cdot \cosh \left(\frac{W_B}{L_S}\right)}{\sinh \left(\frac{W_B}{L_S}\right)}$$

(25)

$$\frac{\partial p(x)}{\partial x}|\begin{array}{c}\\ x=W_B\end{array}=\frac{1}{L_S}\frac{P_W\cdot \cosh \left(\frac{W_B}{L_S}\right)-P_0}{\sinh \left(\frac{W_B}{L_S}\right)}$$

(26)

According to Equations (25) and (26), the currents I_p(x) and I_n(WB) are

$$I_{p(x=0)}=\frac{I_T}{1+b}-\frac{q\cdot A\cdot D}{L_S}\frac{P_W-P_0\cdot \cosh \left(\frac{W_B}{L_S}\right)}{\sinh \left(\frac{W_B}{L_S}\right)}$$

(27)

$$I_{n(x=W_B)}=\frac{b\cdot I_T}{1+b}+\frac{q\cdot A\cdot D}{L_S}\frac{P_W\cdot \cosh \left(\frac{W_B}{L_S}\right)-P_0}{\sinh \left(\frac{W_B}{L_S}\right)}$$

(28)

The expression given by Equation (29) represents the solution of Equation (15) through p(x) = Δp(x), which is used to obtain the excess of carriers injected on the N-region by ∆p(x).

$$Q_{BS}(x)=\frac{q\cdot A\cdot L_S\cdot \left(P_0+P_W\right)\left[\cosh \left(\frac{W_B}{L_S}\right)-1\right]}{\sinh \left(\frac{W_B}{L_S}\right)}$$

(29)

as $tanh\left(\frac{x}{2}\right)=\frac{cosh\left(x\right)-1}{sin\left(x\right)}$, then

$$Q_{BS}(x)=q\cdot A\cdot L_S\cdot \left(P_0+P_W\right)\cdot \tanh \left(\frac{W_B}{2\cdot L_S}\right)$$

(30)

The Q_BS(x) given by Equation (30) allows a better approximation of the carriers’ dynamic in the N-region. As Q_BS(x) is known, R_N- is given by Equation (22).

3.2. Conduction Phase

This phase is divided into two states: activation and reverse blocking.

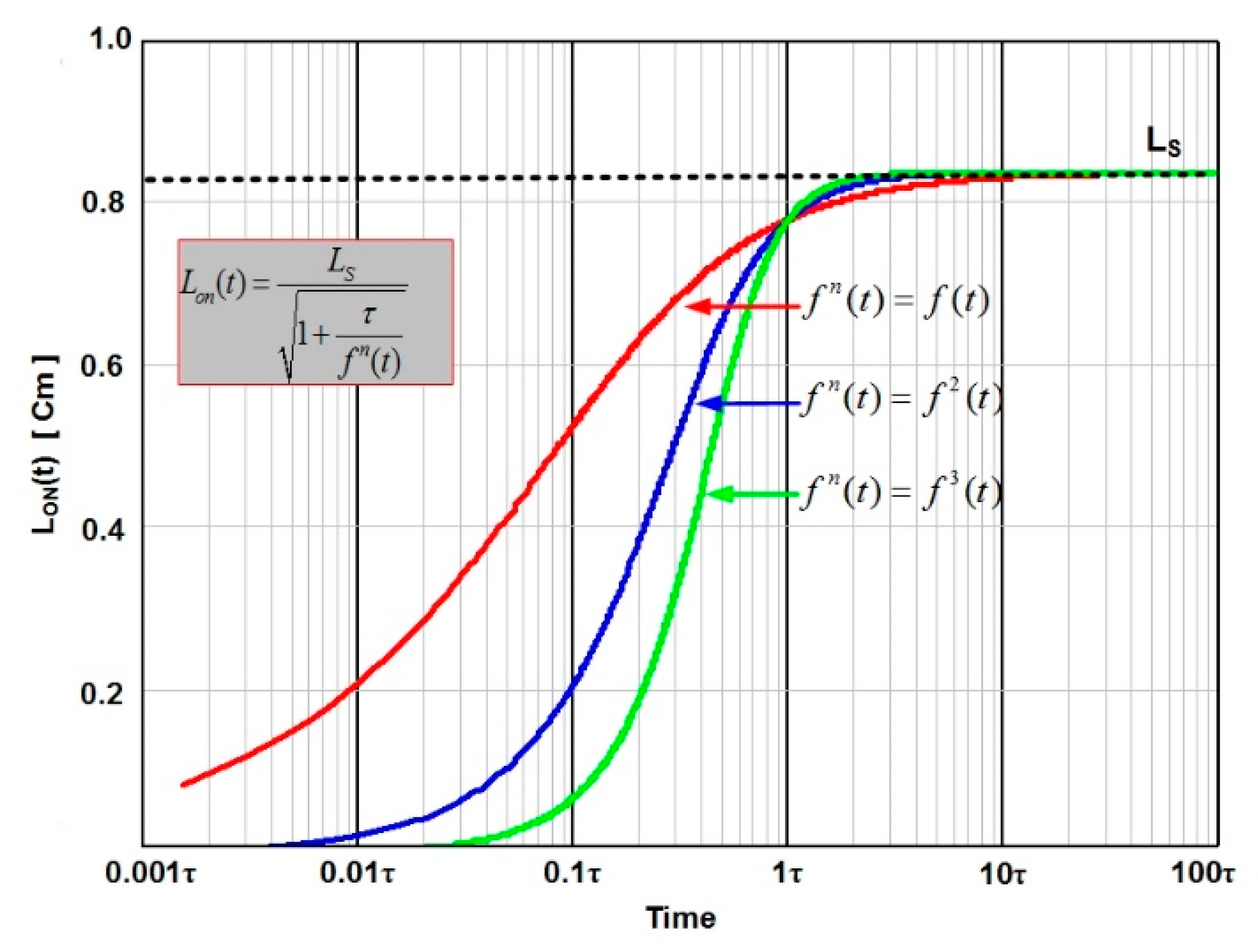
3.2.1. Activation

Figure 2 shows a typical carrier’s behavior during the activation phase, each time increment Δt is related with a non-linear increment in the concentration Δp(x,t); when the carriers’ increment is equal to zero, the activation phase ends. In this condition, any variation of Δt does not affect the carriers’ behavior; the previously analyzed condition $\raisebox{1ex}{$\partial p(x,t)$}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.\equiv 0$ is achieved.

Figure 2. Carriers installation in the N-region, in the activation phase.

As a result of the previous analysis, the increment of chargers in the N-region has a non-linear relationship inversely proportional to the time increment. This condition is formulated by:

$$\frac{\partial p(x,t)}{\partial t}\approx \frac{p(x,t)}{f^n(t)}$$

(31)

where fⁿ(t) is the time-dependent function. The ADE approximate solution requires the appropriate definition of the fⁿ(t) function.

The main contribution of this paper is an approximated solution of the ADE that can be implemented on electronic simulators; according to this approach, an empiric first-order approximation of function is included and given by

$$\frac{\partial p(x,t)}{\partial t}\approx \frac{p(x,t)}{f(t)}$$

(32)

therefore, the ADE is rewritten as

$$\frac{{\partial }^{2}p(x,t)}{\partial x^2}\approx \frac{p(x,t)}{D\cdot \tau }\left(1+\frac{\tau }{f(t)}\right)\approx \frac{p(x,t)}{L_{on}^2(x,t)}$$

(33)

where a new diffusion length is given by:

$$L_{on}(x,t)=\frac{L_S}{\sqrt{1+\frac{\tau }{f(t)}}}=\sqrt{\frac{L_S^2}{1+\frac{\tau }{t}}}$$

(34)

To calculate the excess of carriers injected into the N-region during the activation phase, combining Equations (33) and (15) with p(x,t) = Δp, a new expression is obtained given by:

$$Q_{on}(x,t)=q\cdot A\cdot L_{on}(t)\cdot \left(P_0+P_W\right)\cdot \tanh \left(\frac{x}{2\cdot L_{on}(t)}\right)$$

(35)

Figure 3 shows the L_on(t) response; this behavior considers a function approximation such as: fⁿ(t) = f(t) and fⁿ(t) = f²(t). In this way, the second-order approximation creates a fast evolution of L_on(t) to L_s that has a strong relation with the activation time.

Figure 3. L_on(t) response.

At the beginning of the activation phase, p(x,t) has a strong time dependence through ambipolar diffusion length L_on(t). At the end of the activation phase, called the static phase, p(x,t) is independent of the time since L_on(t→∞) = L_s. As the expression in Equation (33) is similar to Equation (23), the solution of p(x,t) with $L_{on}(t)$ is formulated by

$$p(x,t)=\frac{P_W\cdot \sinh \left(\frac{x}{L_{on}(t)}\right)+P_0\cdot \sinh \left(\frac{W_B-x}{L_{on}(t)}\right)}{\sinh \left(\frac{W_B}{L_{on}(t)}\right)}$$

(36)

With Equation (36), the concentration gradients in the diode unions are obtained using the transportation equations in a similar way as Equations (25)–(28).

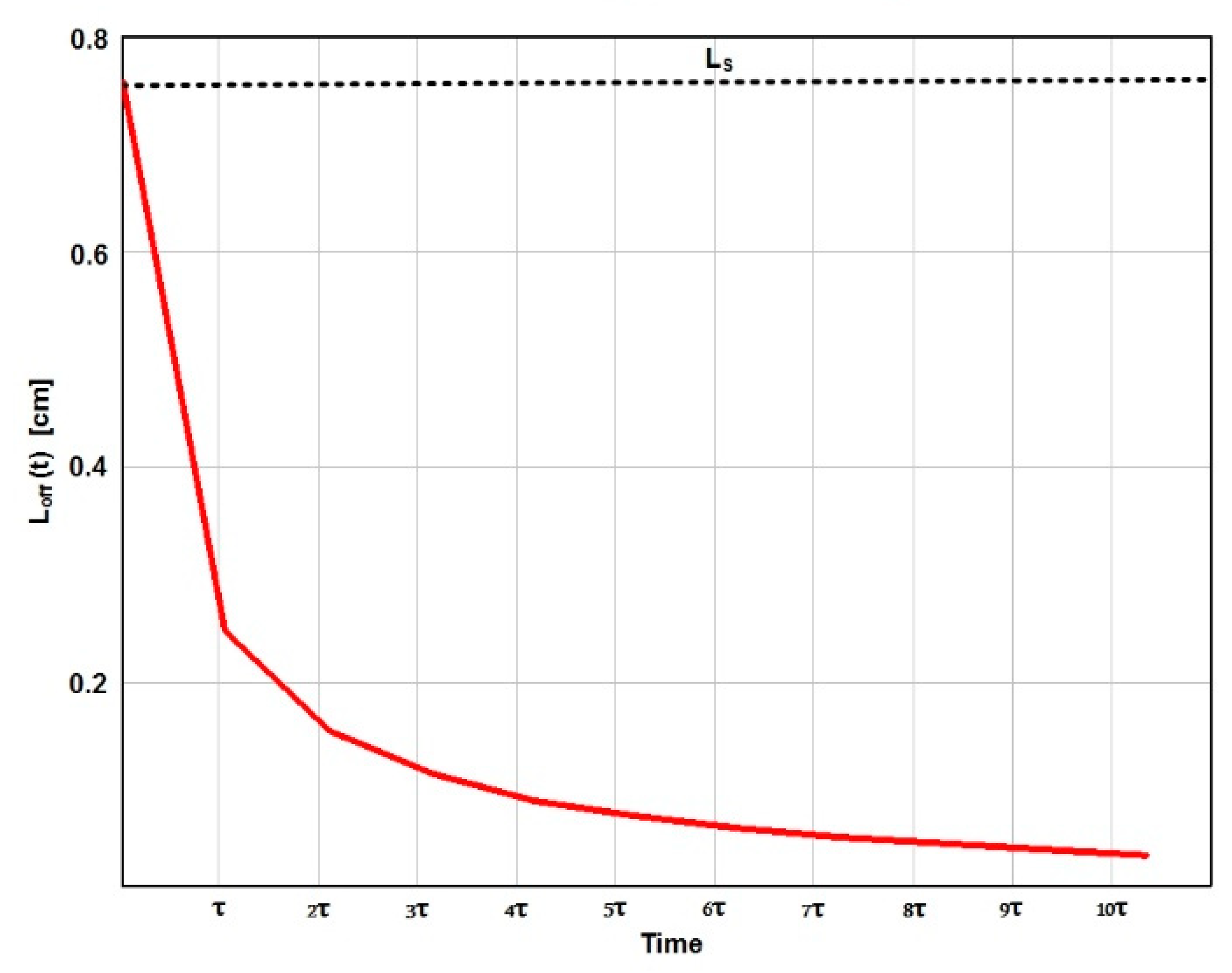
3.2.2. Blocking

In this condition, the excess of carriers Δp(x,t) stored on the N-region during the activation phase are evacuated by both injectors. To model the blocking condition, a new diffusion length as a function of the time is proposed; notice that L_off, which begins in the L_s value, decreases to zero; to satisfy this condition, L_off is formulated by:

$$L_{off}(t)=L_S-\sqrt{\frac{L_S^2}{1+\frac{\tau }{t}}}$$

(37)

Figure 4 shows the L_off as a function of time. Note that according to the expected condition, L_off decreases from L_s to zero.

Figure 4. L_off(t) response.

To quantify the carriers in the N-region during the inverse, the blocking phase was used Equation (38)

$$Q_{off}(x,t)=q\cdot A\cdot L_{off}(t)\cdot \left(P_0+P_W\right)\cdot \tanh \left(\frac{x}{2\cdot L_{off}(t)}\right)$$

(38)

Similar to the activation phase, p(x) as a function of L_off is given by Equation (39), which guarantees the evacuation of the N-region carriers.

$$p(x,t)=\frac{P_W\cdot \sinh \left(\frac{x}{L_{off}(t)}\right)+P_0\cdot \sinh \left(\frac{W_B-x}{L_{off}(t)}\right)}{\sinh \left(\frac{W_B}{L_{off}(t)}\right)}$$

(39)

with p(x,t) known, the concentration gradients in the diode unions are obtained to be used in the transportation equations in a similar way as Equations (25)–(28).

4. Simulation Results

In this section, the solution of ADE is given by Equations (24), (36) and (39), according to different phases: static, activation, and inverse blocking, and the data used were: A = 0.04 cm, W = 37 µm, τ_n = τ_p = 0.15 µs, µ_n = 947 cm²/Vs, µ_p = 108 cm²/Vs, and L_S = 0.73. The simulation results showed that the adopted empirical approximation could obtain a feasible and reduced equation to model the injection and evacuation of carriers in the N-region and are easily implemented on commercial and non-commercial electronic simulators.

4.1. Static Phase

Figure 5 shows the p(x) response to different injected carrier values to the N-region. To obtain the density of charge, we used the expressions reported in [27]. Table 1 shows the total injected current to the N-region and the carriers’ concentration, P₀, and P_W.

Figure 5. p(x) response in the static phase.

Table 1. Injected current vs. P₀ and P_W.

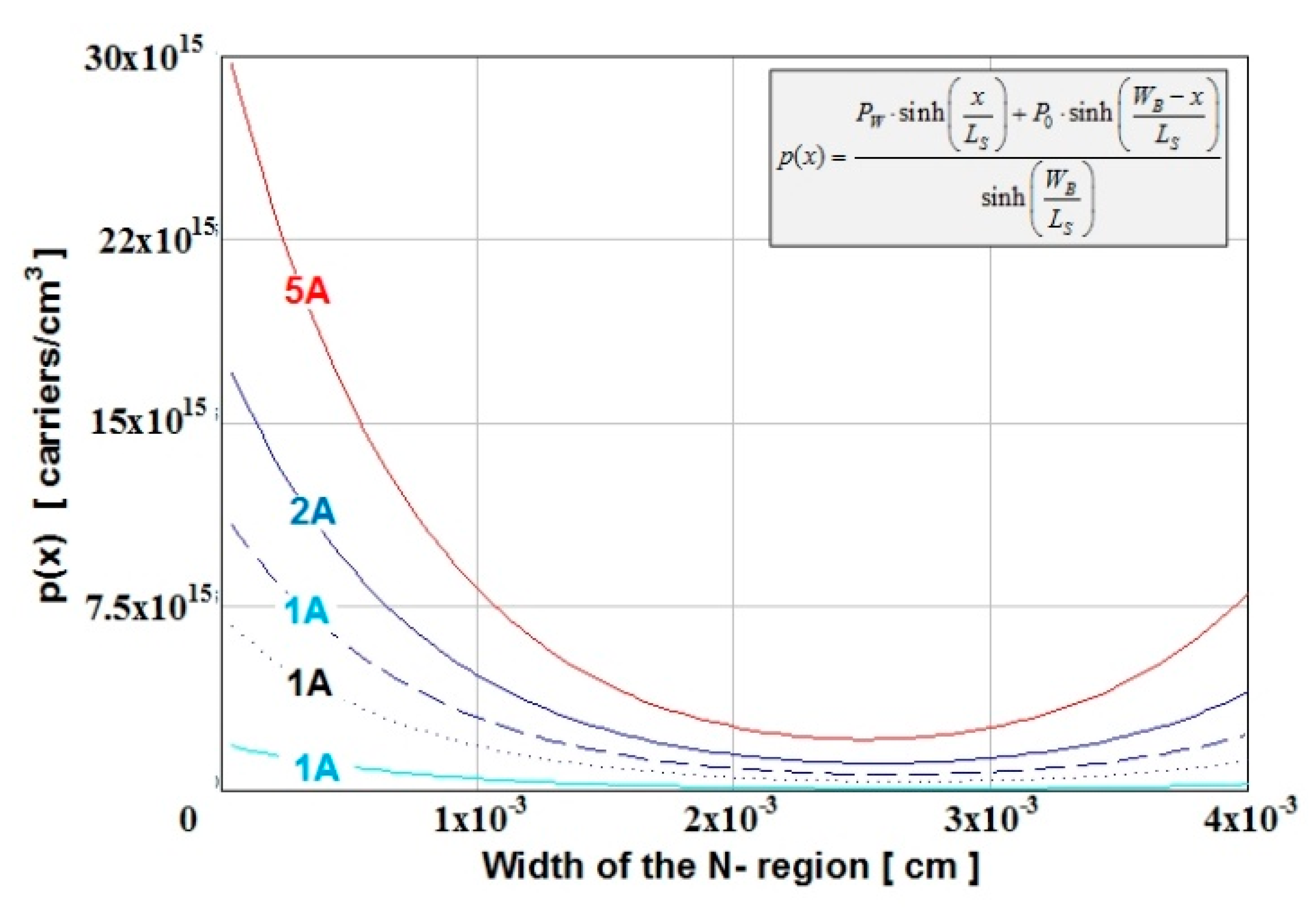
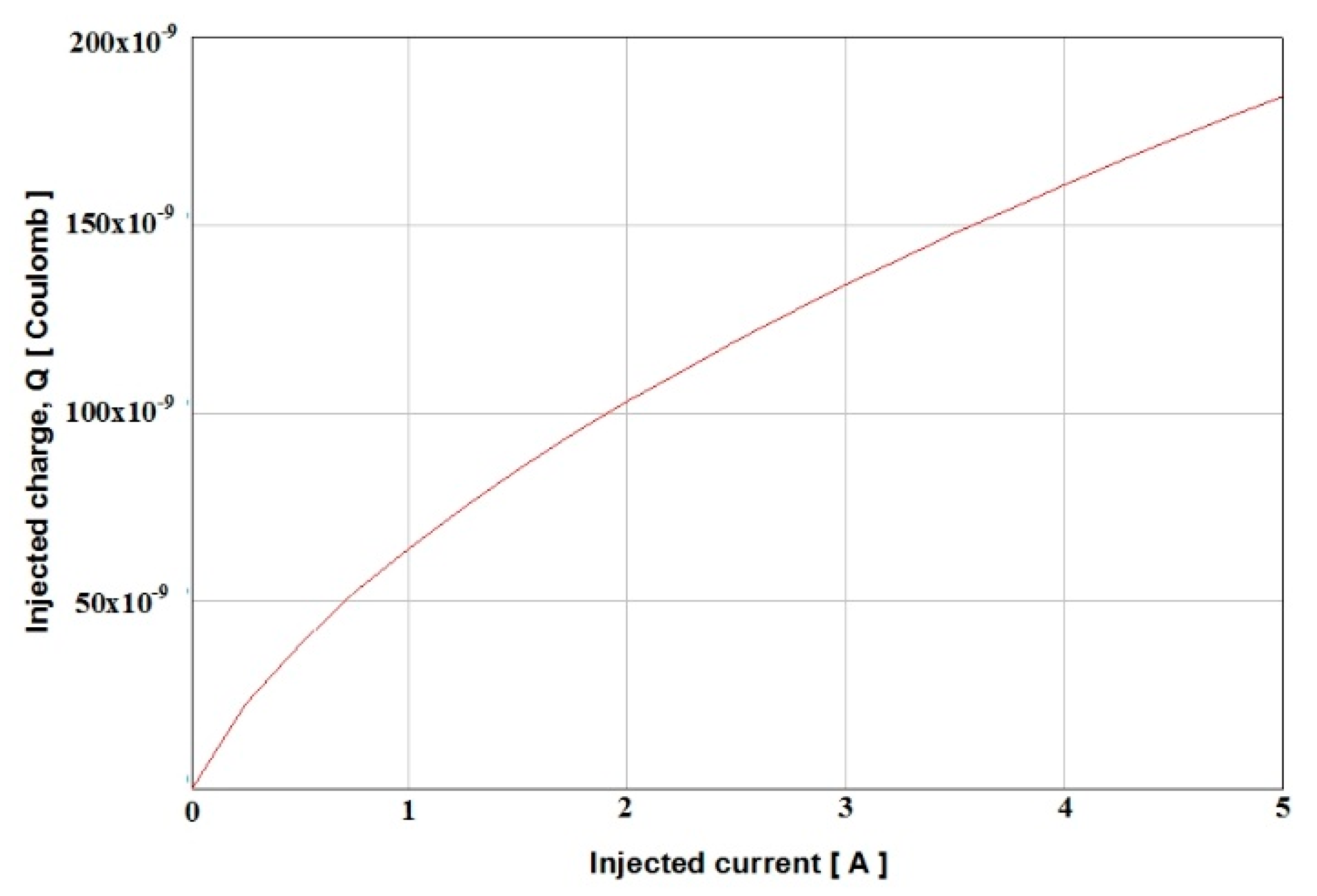
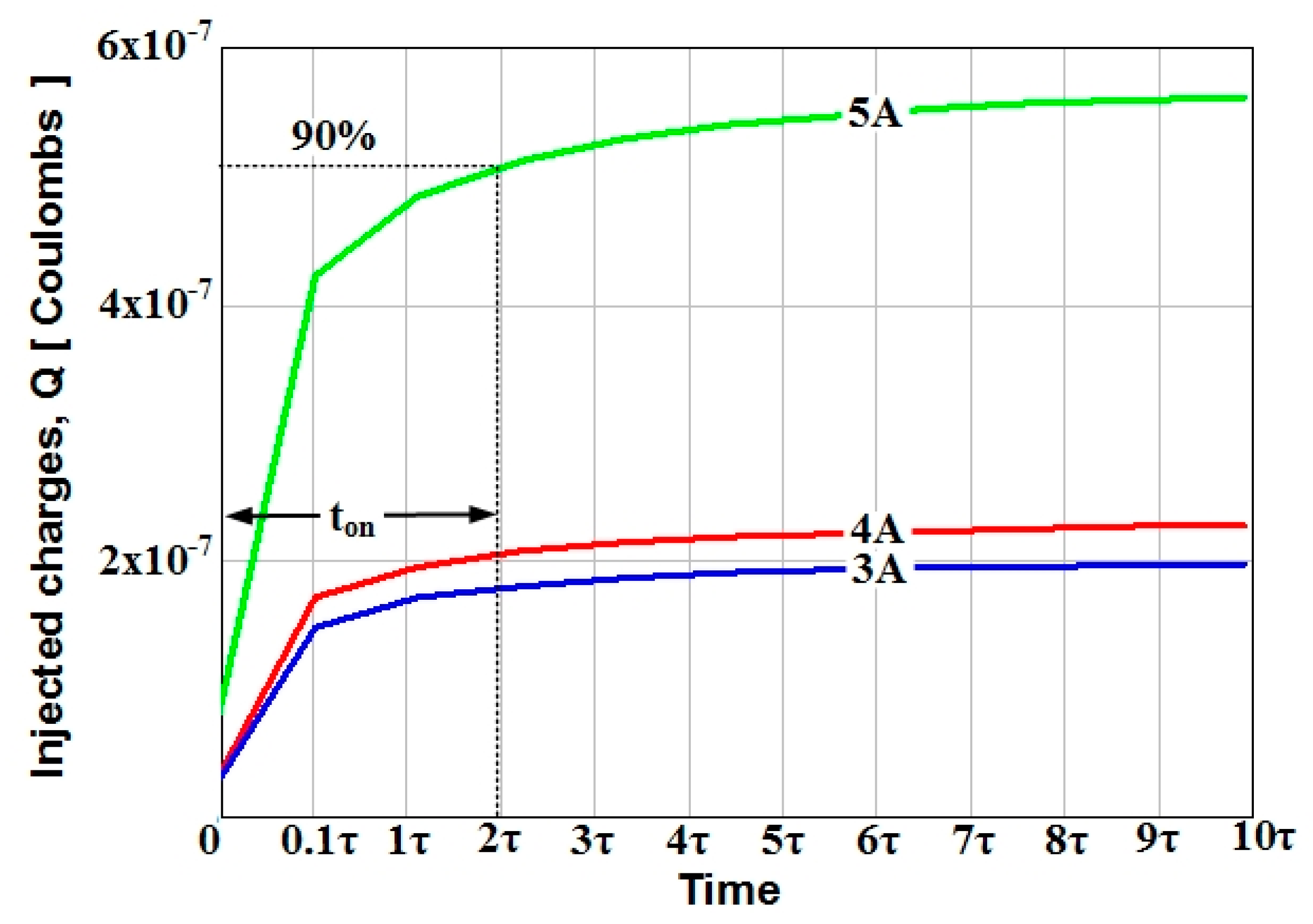
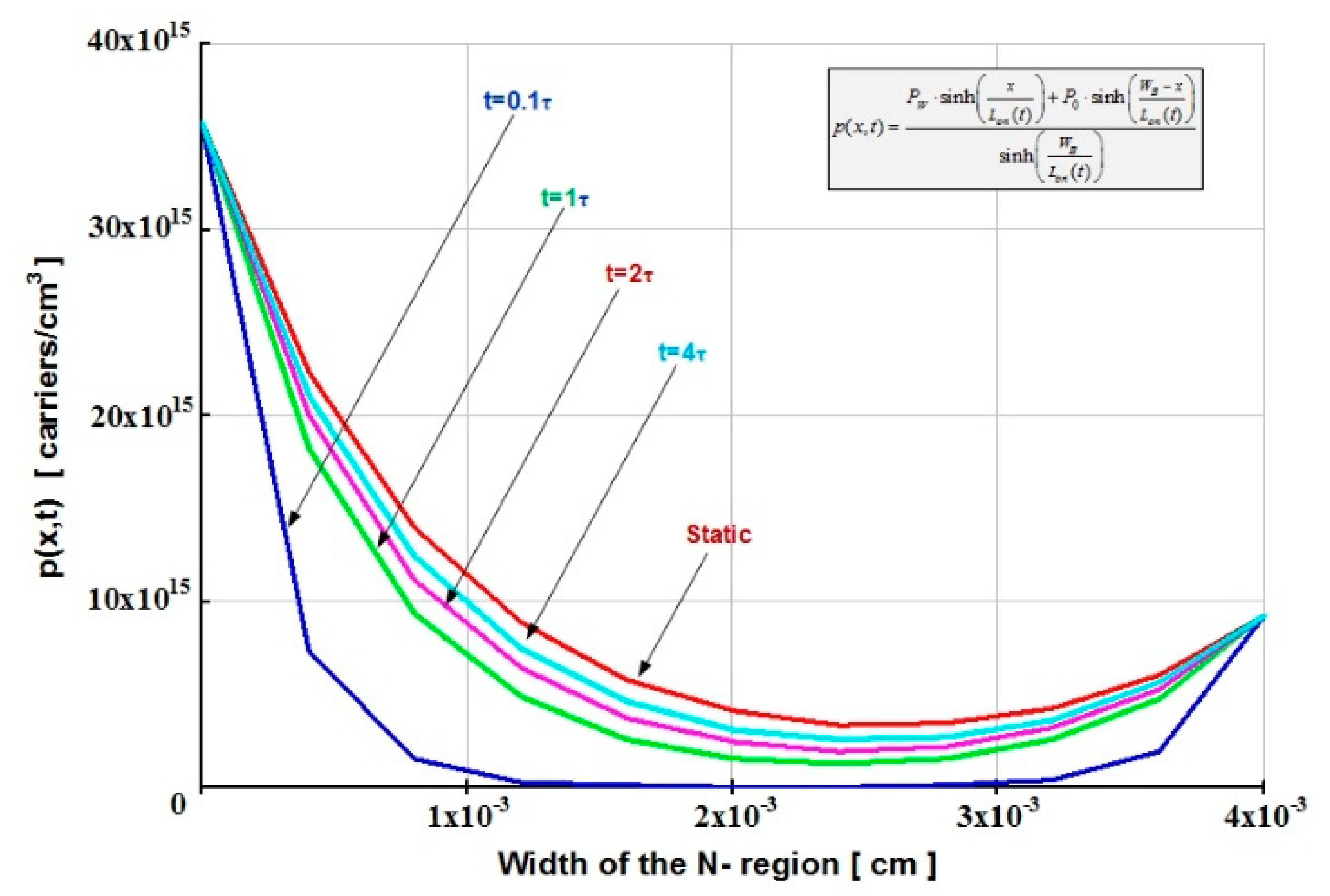
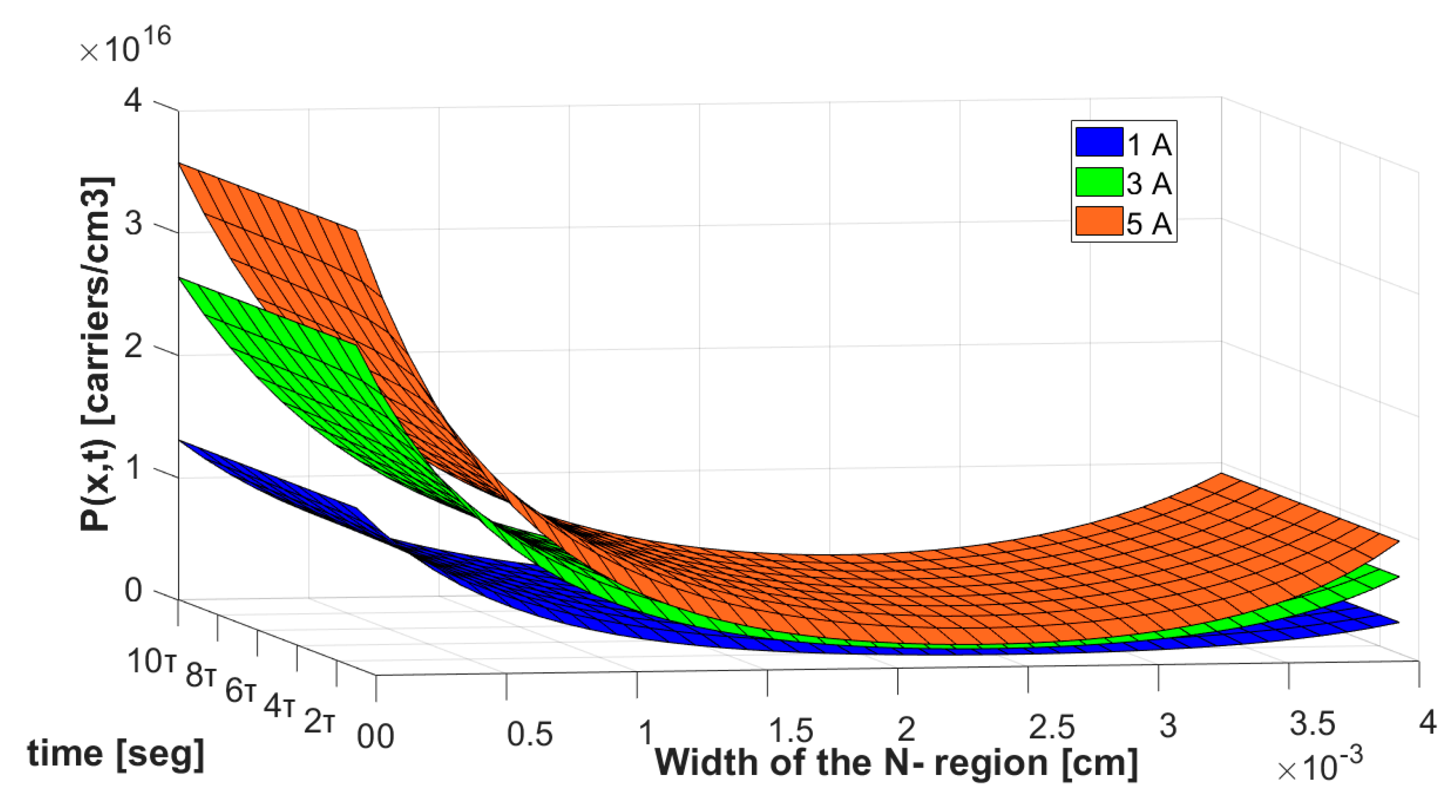
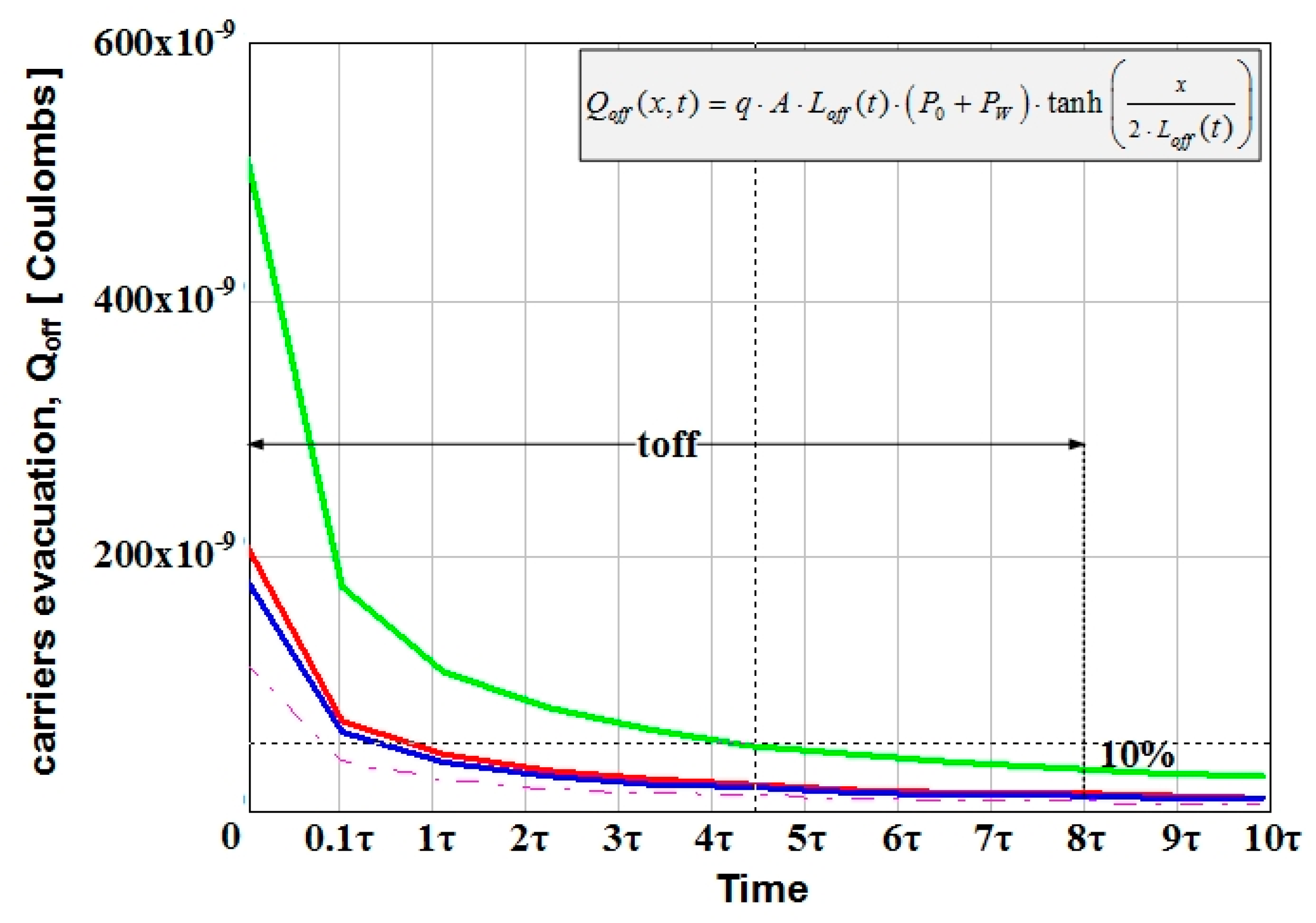
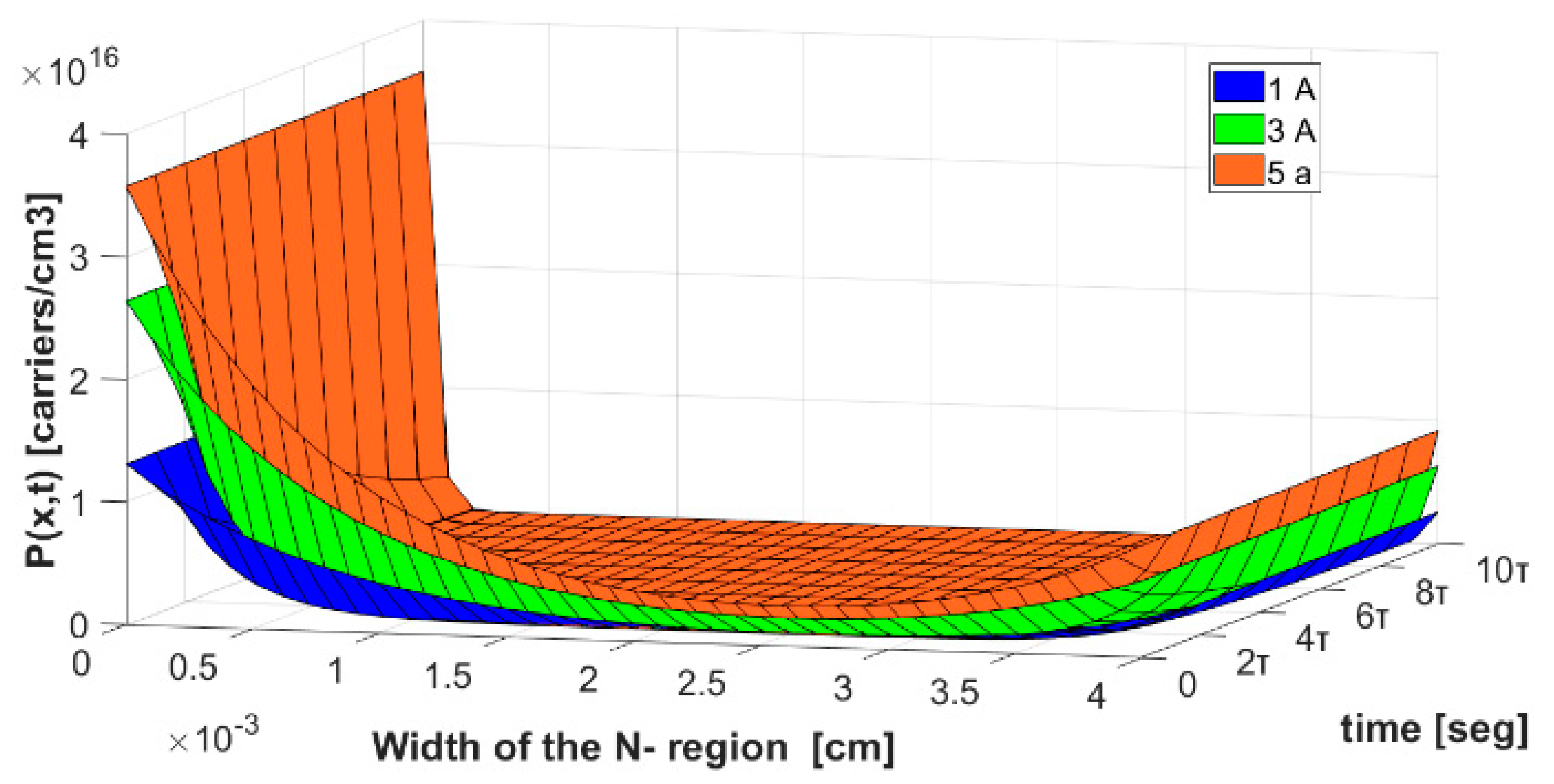
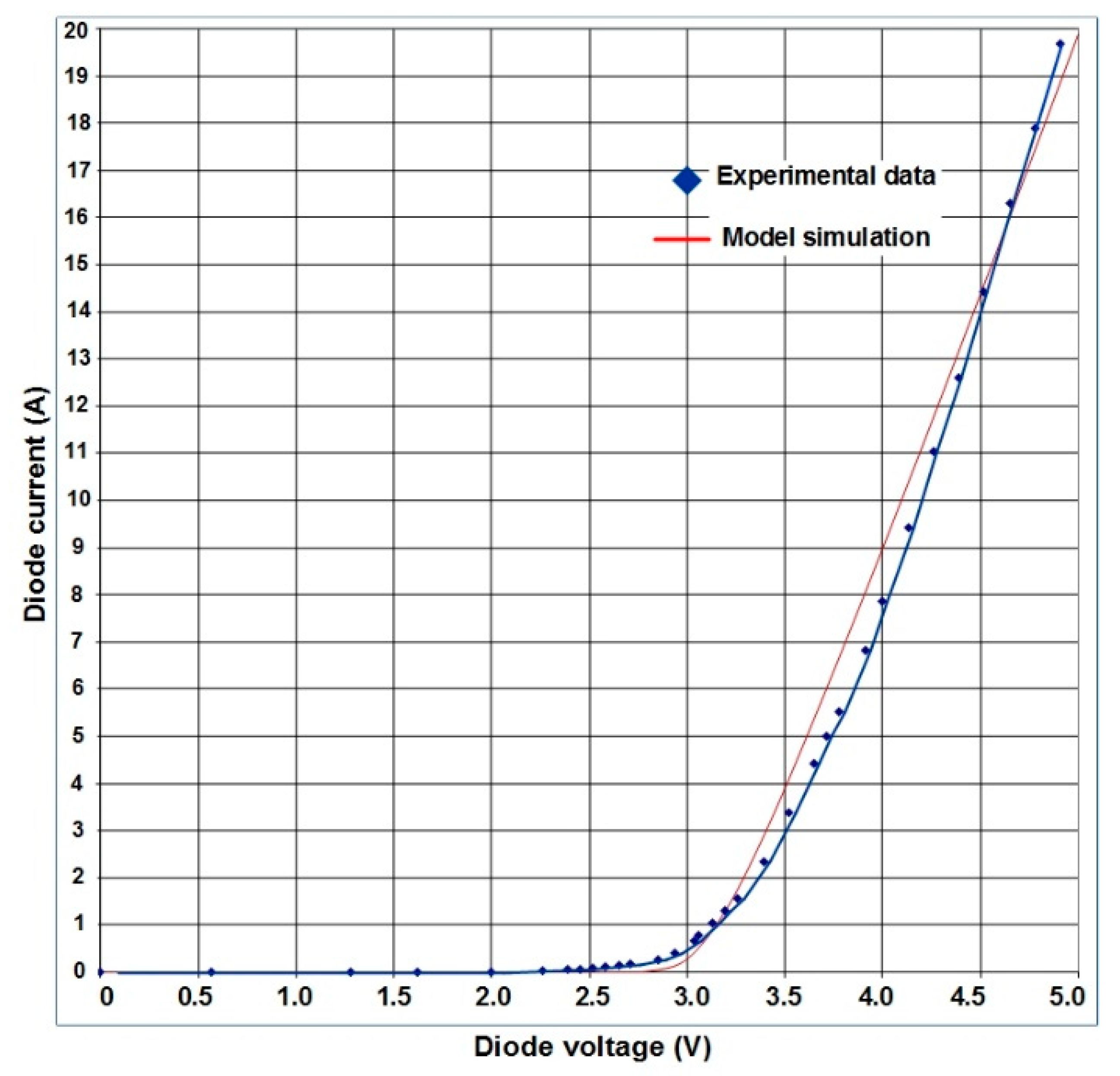
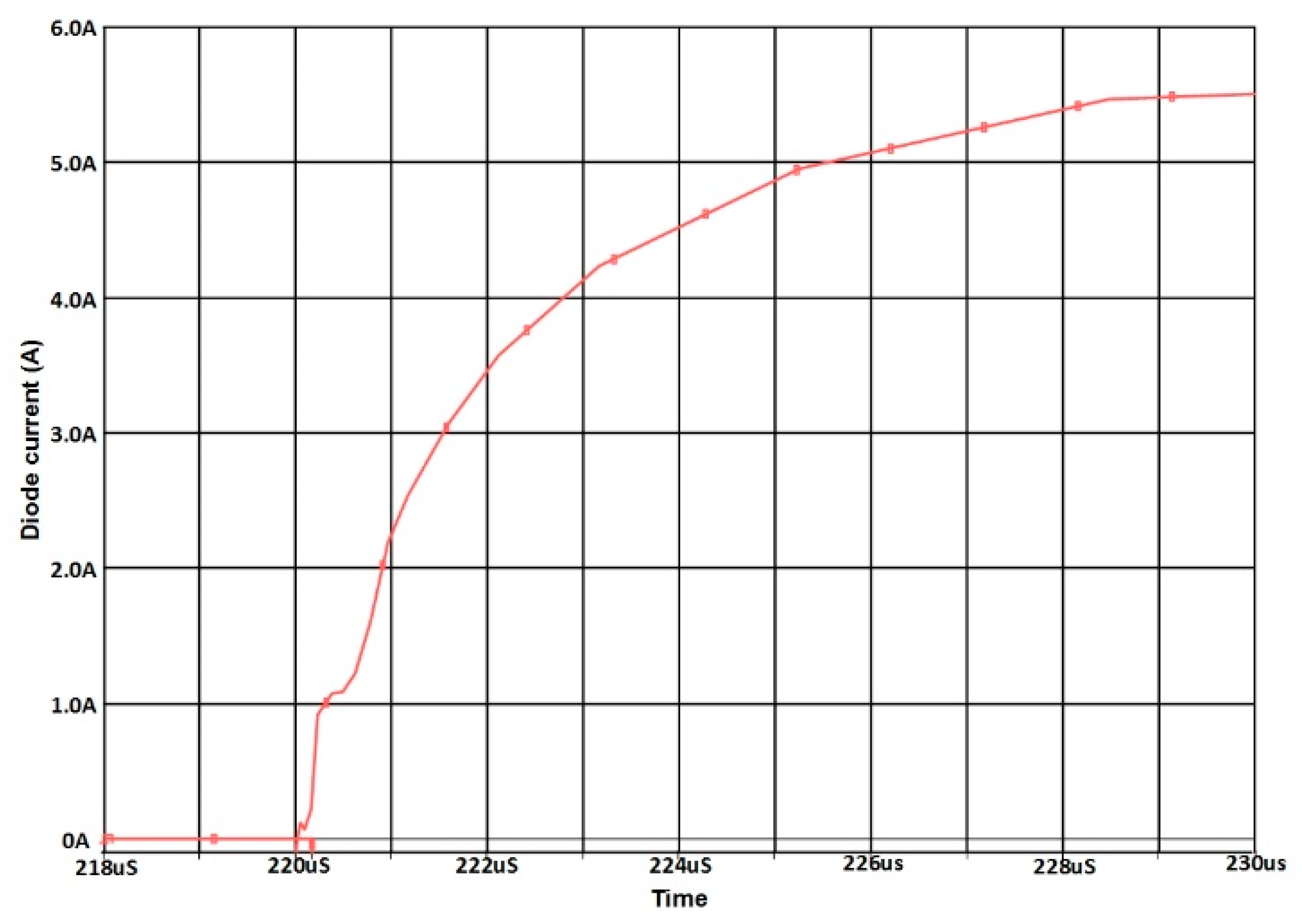
Current [A]	P0 [Charges/cm3]	PW [Charges/cm3]
0.5	8.043 × 1015	1.384 × 1015
1	1.310 × 1016	2.571 × 1015
1.5	1.712 × 1016	3.627 × 1015
2	2.056 × 1016	4.588 × 1015
2.5	2.362 × 1016	5.476 × 1015
3	2.640 × 1016	6.305 × 1015
3.5	2.897 × 1016	7.085 × 1015
4	3.137 × 1016	7.824 × 1015
4.5	3.362 × 1016	8.529 × 1015
5	3.576 × 1016	9.203 × 1015

Figure 5 shows the density of carriers injected to the N-region, which increases according to the total injected current. Figure 6 shows the relation between the current and the carriers injected into the N-region.

Figure 6. Q_B response in function of the injected current.

Figure 7 shows the N-region resistance response according to the injected current, which decreases according to the injected currents with a proportional increment. This behavior of the resistance has a substantial impact on the analysis of conduction losses in power semiconductors.

Figure 7. N-region resistance and injected current relation.

4.2. Conduction Phase

The conduction phase begins when a current, different to zero, is injected in the N-region; in this phase, the carriers’ density in the N-region depends on the time the current changes from zero to a maximum value when the static phase begins.

Figure 8 shows the injected carriers’ behavior for different maximum current values. At approximately t = 2τ, a value of 90% of I_MAX = 5 A is reached; this being the activation time of the semiconductor device, t_on, it can be verified that t_on is dependent on the maximum current injected into the device.

Figure 8. Q(t) behavior during the conduction phase.

Figure 9 shows the p(x,t) evolution for a current injection in the range of 0 A to 5 A. When the carriers’ injection time increases, the static phase is reached. According to the Figure 9, it can be considered that at t = 4τ, the static phase begins since the increment of p(x,t) is small.

Figure 9. p(x,t) behavior during the conduction phase.

Figure 10 shows the evolution of p(x,t) for a time range from 2τ to 10τ for a maximum current injection of 1 A, 3 A, and 5 A.

Figure 10. p(x,t) behavior for 5 A, 3 A, and 1 A.

4.3. Reverse Blocking Phase

The reverse blocking phase starts when the current in the N-region is reduced from a maximum (static) value to zero. In this phase, the carriers’ displacement is evaluated along the N-region. Figure 11 shows the carriers’ evacuation during the static phase from 5 A to 0 A.

Figure 11. Qoff behavior during the reverse blocking phase for different carriers’ evacuation.

At approximately t = 8τ, a value of 10% of I_MAX = 5 A was reached, which indicates the deactivation time of the semiconductor device, t_off. It can be verified that t_off is dependent on the maximum static current that is evacuated in the device and which is always greater than t_on.

Figure 12 shows the p(x,t) evolution for a current displacement from 5 A to 0 A; the evolution of p(x,t) from the static phase to zero was verified for different charge displacement times. For values of t greater than 10τ, it was considered that the reverse blocking had been reached since the decrements of p (x,t) were small.

Figure 12. p(x,t) behavior during the reverse blocking phase.

Figure 13 shows the p(x,t) evolution for a time range from 2τ to 10τ for a maximum current injection of 1 A, 3 A, and 5 A during the reverse blocking phase.

Figure 13. p(x,t) for 5 A, 3 A, and 1 A during the reverse blocking phase.

As shown in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13, the proposed ADE solution allows modeling the carrier’s injection behavior and the carrier’s evacuation in the N-region.

The proposed solution for modeling the chargers’ behavior in the N-region in a bipolar semiconductor device was used in the Orcad Pspice electrical circuit simulator, which allows the developed equations to be implemented easily, the characteristics are very similar to other simulators, and it is one of the simulators with greater acceptance and use in the electric area. The main results for the static, activation, and reverse blocking phases are shown in Figure 14, Figure 15 and Figure 16, respectively.

Figure 14. Static simulation and experimental data.

Figure 15. Turn-on phase simulation results.

Figure 16. Turn-off simulation and experimental data.

A straight comparison between the simulation and experimental results is presented to validate the proposed model obtaining similar current waveforms under static, turn-on, and turn-off conditions. As presented in the comparison of simulation results with the experimental data, adequate similarity was achieved for each phase of semiconductor device activation, which ensures a suitable model for use as a design tool prior to the realization of the experimental prototype.

In this paper, an empirical approximation of the ADE solution is presented, and its final equation was validated via a commercial electronic circuit simulator. To quantify the accuracy of the obtained results, the quadratic error was evaluated by Equation (40) for the turn-off phase, which is considered the most unstable due to its negative current impulse. Figure 17 shows the quadratic error between the experimental and simulated waveforms.

$$error(n)={\left[Exp(n)-Sim(n)\right]}^2$$

(40)

where n is a sample of time; error(n) is the quadratic error; and Exp(n) and Sim(n) are the experimental and simulation sampled data, respectively.

Figure 17. Turn-off phase error.

Additionally, the mean square error (MSE) was obtained with Equation (41), and the obtained value was 0.0620 for the turn-off phase.

$$MSE=\frac{1}{i}{\displaystyle \sum _{n=1}^i{\left[Exp(n)-Sim(n)\right]}^2}$$

(41)

where i is the number of samples.

5. Conclusions

An ambipolar diffusion equation solution using an empirical methodology was presented; this allowed for an adequate modeling of the injection and evacuation of carriers in the N-region. The method considers the main transport phenomena in the semiconductor material.

The proposed solution was validated using the final equations that were implemented in a simulator; the results were compared with experimental results in each phase, obtaining a similarity in the current waveforms.

An advantage of the proposed methodology is that the final expressions obtained can be easily implemented in any of the commercial simulators that has the option to integrate equations.

Finally, the proposed methodology was initially used in the p–n junction, but it can be implemented in bipolar current control devices such as the BJT, IGBT, and thyristor family.