Stochastic Modeling of Plant Virus Propagation with Biological Control
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Modeling
2.2. Stochastic Modeling
2.2.1. Continuous Time Markov Chain Models
2.2.2. Stochastic Differential Equations
2.3. A Plant-Virus Model with Biological Control
2.4. Numerical Methods
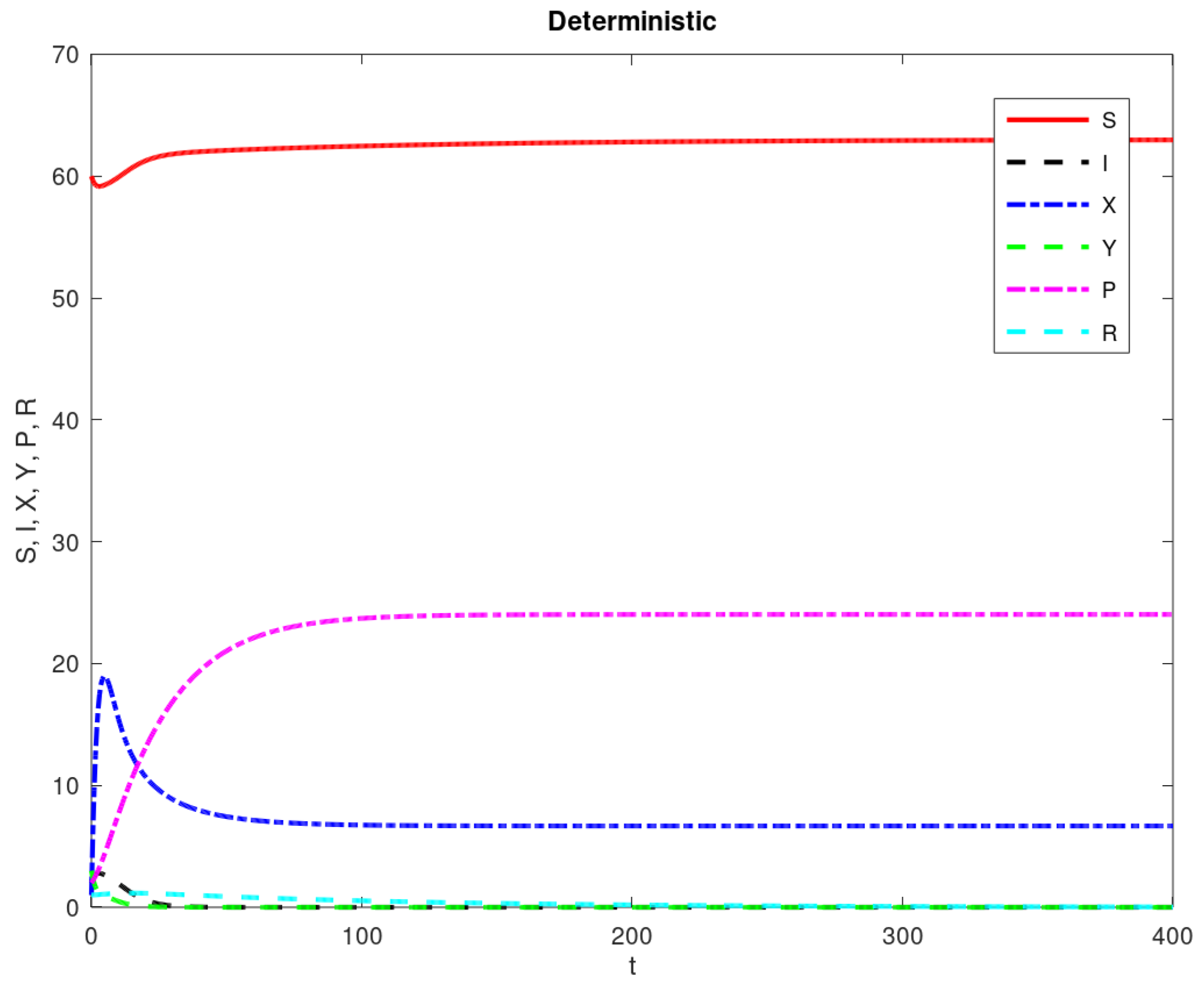
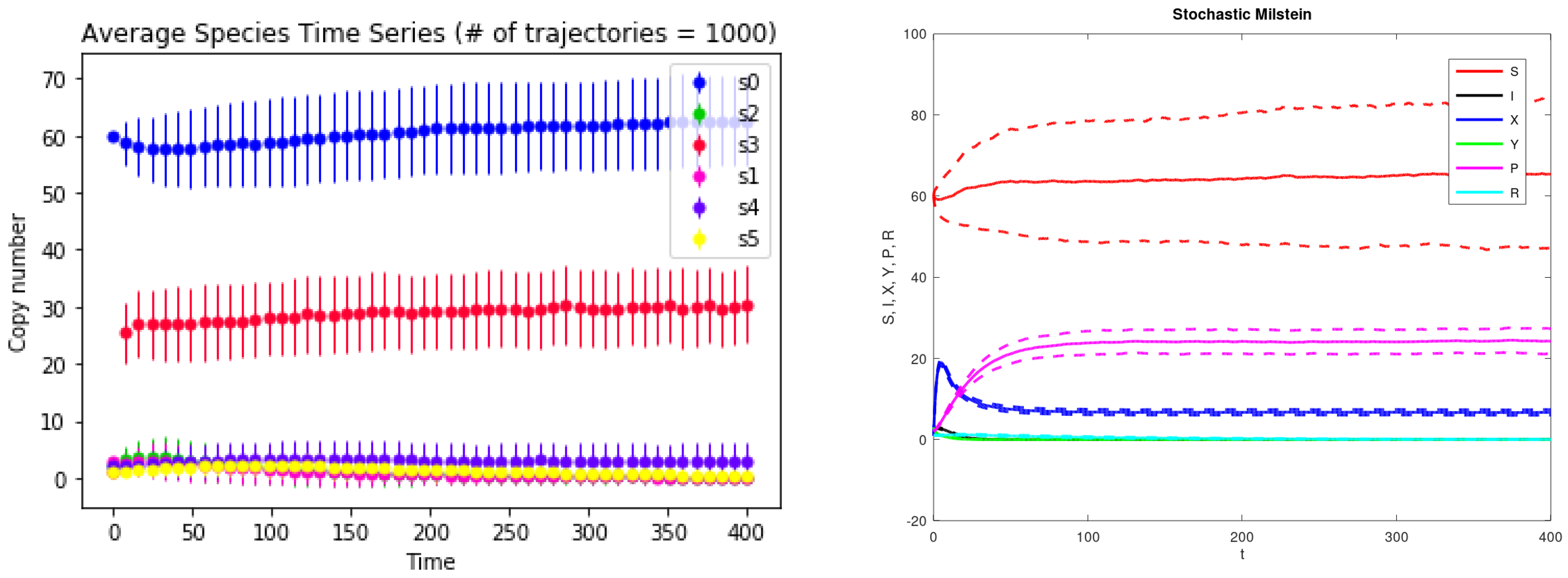
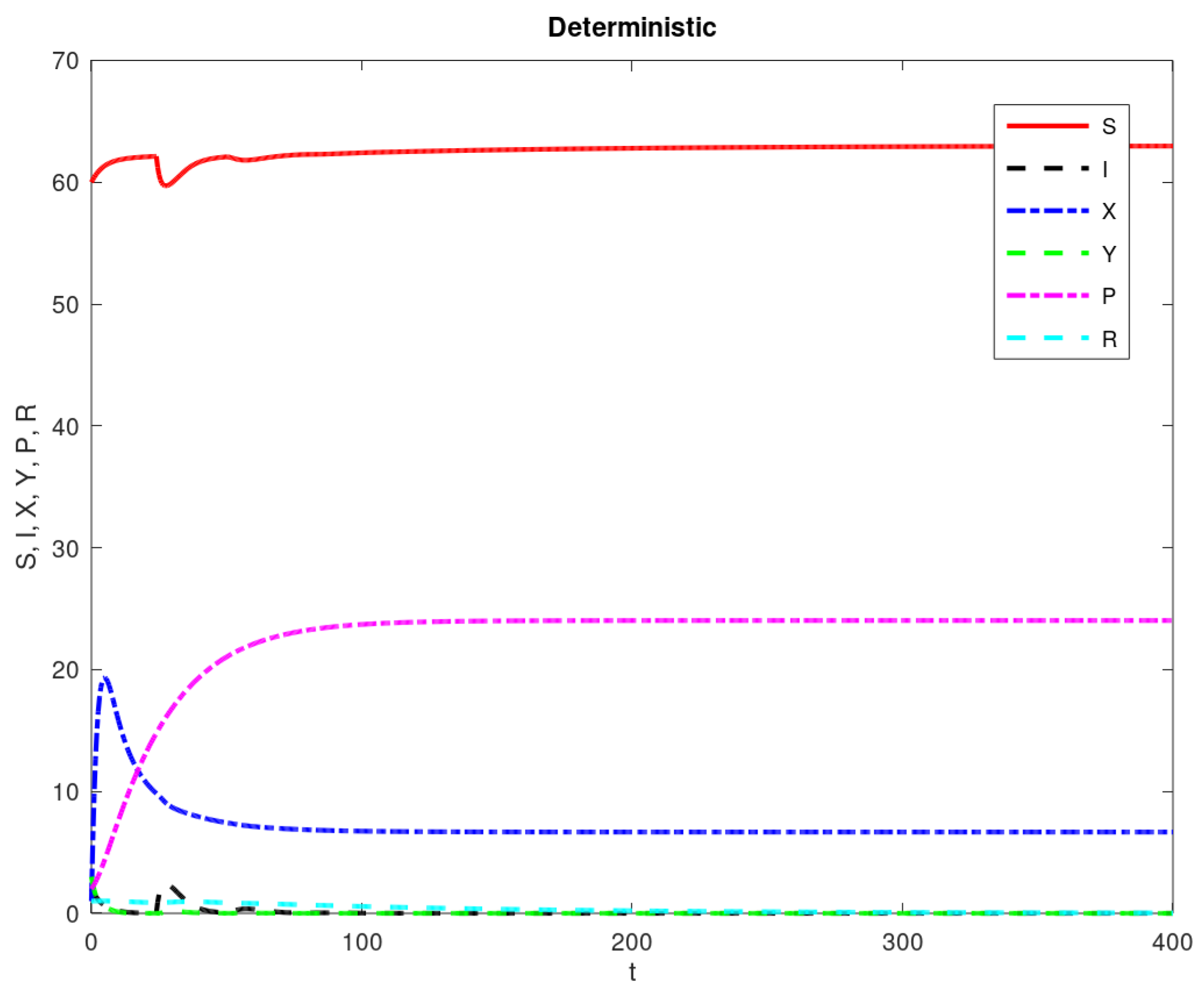
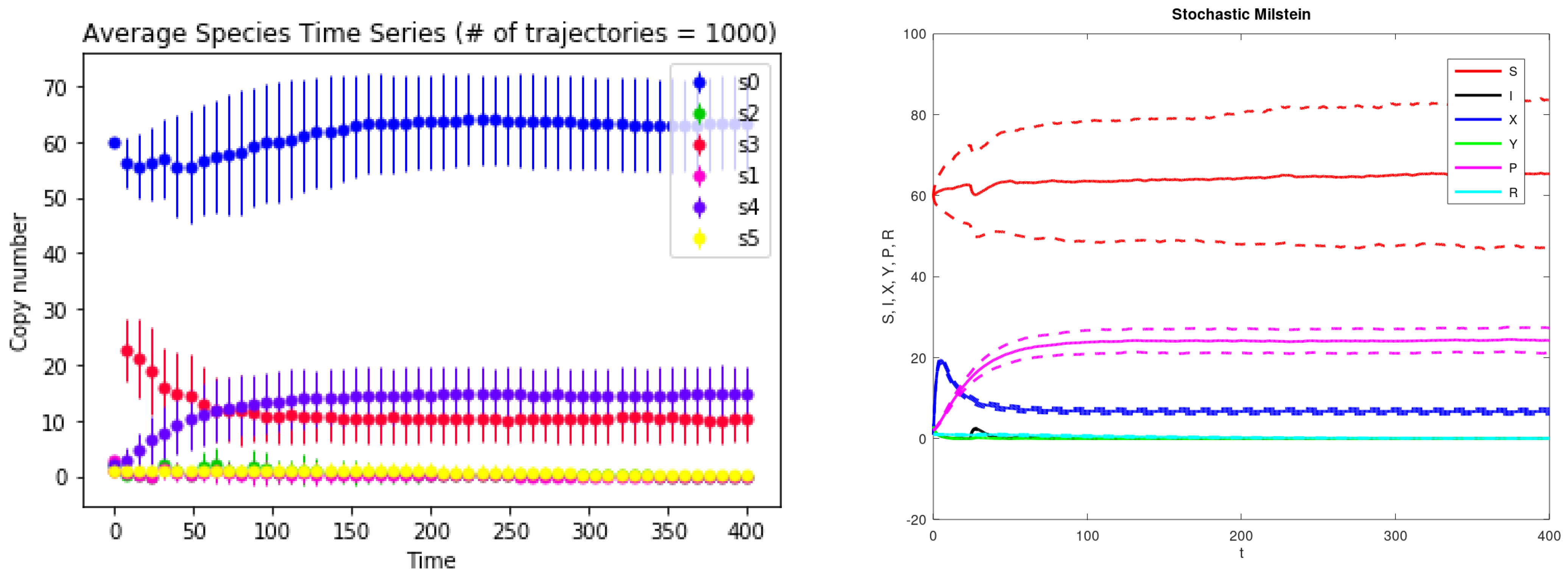
3. Results
4. Discussions
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Scholthof, K.B.G.; Adkins, S.; Czosnek, H.; Palukaitis, P.; Jacquot, E.; Hohn, T.; Hohn, B.; Saunders, K.; Candresse, T.; Ahlquist, P.; et al. Top 10 plant viruses in molecular plant pathology. Mol. Plant Pathol. 2011, 12, 938–954. [Google Scholar] [CrossRef] [PubMed]
- Fereres, A. Insect vectors as drivers of plant virus emergence. Curr. Opin. Virol. 2015, 10, 42–46. [Google Scholar] [CrossRef]
- Jeger, M.; Van Den Bosch, F.; Madden, L.; Holt, J. A model for analysing plant-virus transmission characteristics and epidemic development. Math. Med. Biol. A J. IMA 1998, 15, 1–18. [Google Scholar] [CrossRef]
- Jeger, M.; Holt, J.; Van Den Bosch, F.; Madden, L. Epidemiology of insect-transmitted plant viruses: Modelling disease dynamics and control interventions. Physiol. Entomol. 2004, 29, 291–304. [Google Scholar] [CrossRef]
- Van Maanen, A.; Xu, X.M. Modelling plant disease epidemics. Eur. J. Plant Pathol. 2003, 109, 669–682. [Google Scholar] [CrossRef]
- Anguelov, R.; Lubuma, J.; Dumont, Y. Mathematical analysis of vector-borne diseases on plants. In Proceedings of the 2012 IEEE 4th International Symposium on Plant Growth Modeling, Simulation, Visualization and Applications, Shanghai, China, 31 October–3 November 2012; pp. 22–29. [Google Scholar]
- Shi, R.; Zhao, H.; Tang, S. Global dynamic analysis of a vector-borne plant disease model. Adv. Differ. Equ. 2014, 2014, 59. [Google Scholar] [CrossRef]
- Meng, X.; Li, Z. The dynamics of plant disease models with continuous and impulsive cultural control strategies. J. Theor. Biol. 2010, 266, 29–40. [Google Scholar] [CrossRef]
- Al Basir, F.; Adhurya, S.; Banerjee, M.; Venturino, E.; Ray, S. Modelling the effect of incubation and latent periods on the dynamics of vector-borne plant viral diseases. Bull. Math. Biol. 2020, 82, 1–22. [Google Scholar] [CrossRef]
- Jackson, M.; Chen-Charpentier, B.M. Modeling plant virus propagation with delays. J. Comput. Appl. Math. 2017, 309, 611–621. [Google Scholar] [CrossRef]
- Jackson, M.; Chen-Charpentier, B.M. A model of biological control of plant virus propagation with delays. J. Comput. Appl. Math. 2018, 330, 855–865. [Google Scholar] [CrossRef]
- Chen-Charpentier, B.M.; Jackson, M. Direct and indirect optimal control applied to plant virus propagation with seasonality and delays. J. Comput. Appl. Math. 2020, 380, 112983. [Google Scholar] [CrossRef]
- Zhang, T.; Meng, X.; Song, Y.; Li, Z. Dynamical analysis of delayed plant disease models with continuous or impulsive cultural control strategies. Abstr. Appl. Anal. 2012, 2012. [Google Scholar] [CrossRef]
- Al Basir, F.; Takeuchi, Y.; Ray, S. Dynamics of a delayed plant disease model with Beddington-DeAngelis disease transmission. Math. Biosci. Eng. 2021, 18, 583–599. [Google Scholar] [CrossRef] [PubMed]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 23. [Google Scholar]
- Evans, L.C. An Introduction to Stochastic Differential Equations; American Mathematical Soc.: Providence, RI, USA, 2012; Volume 82. [Google Scholar]
- Ghanem, R.; Spanos, P.D. Polynomial Chaos in Stochastic Finite Elements. J. Appl. Mech. 1990, 57, 197–202. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener–Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Gibson, G.J. Markov chain Monte Carlo methods for fitting spatiotemporal stochastic models in plant epidemiology. J. R. Stat. Soc. Ser. C Appl. Stat. 1997, 46, 215–233. [Google Scholar] [CrossRef]
- Keeling, M.J.; Ross, J.V. On methods for studying stochastic disease dynamics. J. R. Soc. Interface 2008, 5, 171–181. [Google Scholar] [CrossRef]
- Qi, H.; Meng, X.; Chang, Z. Markov semigroup approach to the analysis of a nonlinear stochastic plant disease model. Electron. J. Differ. Equ. 2019, 2019, 1–19. [Google Scholar]
- Stollenwerk, N.; Briggs, K.M. Master equation solution of a plant disease model. Phys. Lett. A 2000, 274, 84–91. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Cao, Y.; Gillespie, D.T.; Petzold, L.R. Efficient step size selection for the tau-leaping simulation method. J. Chem. Phys. 2006, 124, 044109. [Google Scholar] [CrossRef]
- Hemberg, M.; Yaliraki, S.N.; Barahona, M. Stochastic kinetics of viral capsid assembly based on detailed protein structures. Biophys. J. 2006, 90, 3029–3042. [Google Scholar] [CrossRef][Green Version]
- Perlmutter, J.D.; Hagan, M.F. Mechanisms of virus assembly. Annu. Rev. Phys. Chem. 2015, 66, 217–239. [Google Scholar] [CrossRef] [PubMed]
- Allen, L. An Introduction to Mathematical Biology; Pearson-Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Gagniuc, P.A. Markov Chains: From Theory to Implementation and Experimentation; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Holling, C. The Components of Predation as Revealed by a Study of Small Mammal Predation of the European Pine Sawfly. Can. Entomol. 1959, 91, 293–320. [Google Scholar] [CrossRef]
- Fages, F.; Gay, S.; Soliman, S. Inferring reaction systems from ordinary differential equations. Theor. Comput. Sci. 2015, 599, 64–78. [Google Scholar] [CrossRef]
- Simon, C.M. The SIR dynamic model of infectious disease transmission and its analogy with chemical kinetics. PeerJ Phys. Chem. 2020, 2, e14. [Google Scholar] [CrossRef]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Fages, F.; Soliman, S. On robustness computation and optimization in BIOCHAM-4. In Proceedings of the International Conference on Computational Methods in Systems Biology, Brno, Czech Republic, 12–14 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 292–299. [Google Scholar]
- Ermentrout, B. Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students; Siam: Philadelphia, PA, USA, 2002; Volume 14. [Google Scholar]
- Gómez, H.F.; Hucka, M.; Keating, S.M.; Nudelman, G.; Iber, D.; Sealfon, S.C. Moccasin: Converting matlab ode models to sbml. Bioinformatics 2016, 32, 1905–1906. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Hucka, M.; Finney, A.; Sauro, H.M.; Bolouri, H.; Doyle, J.C.; Kitano, H.; Arkin, A.P.; Bornstein, B.J.; Bray, D.; Cornish-Bowden, A.; et al. The systems biology markup language (SBML): A medium for representation and exchange of biochemical network models. Bioinformatics 2003, 19, 524–531. [Google Scholar] [CrossRef]
- Soong, T.T. Random Differential Equations in Science and Engineering; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Pinsky, M.; Karlin, S. An Introduction to Stochastic Modeling; Academic Press: Burlington, MA, USA, 2010. [Google Scholar]
- Allen, L.J. An Introduction to Stochastic Processes with Applications to Biology; CRC Press: Hoboken, NJ, USA, 2010. [Google Scholar]
- Oksendal, B. Stochastic Differential Equations: An Introduction with Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- McQuarrie, D.A. Stochastic approach to chemical kinetics. J. Appl. Probab. 1967, 4, 413–478. [Google Scholar] [CrossRef]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; Elsevier: Amsterdam, The Netherlands, 1992; Volume 1. [Google Scholar]
- Gillespie, D.T. Stochastic Simulation of Chemical Kinetics. Annu. Rev. Phys. Chem. 2007, 58, 35–55. [Google Scholar] [CrossRef] [PubMed]
- Weber, M.F.; Frey, E. Master equations and the theory of stochastic path integrals. Rep. Prog. Phys. 2017, 80, 046601. [Google Scholar] [CrossRef] [PubMed]
- Gibson, M.A.; Bruck, J. Efficient exact stochastic simulation of chemical systems with many species and many channels. J. Phys. Chem. A 2000, 104, 1876–1889. [Google Scholar] [CrossRef]
- Van Gend, C.; Kummer, U. STODE-automatic stochastic simulation of systems described by differential equations. In Proceedings of the 2nd International Conference on Systems Biology, Pasadena, CA, USA, 4–7 November 2001; Volume 326, p. 333. [Google Scholar]
- COmplex PAthway SImulator (COPASI). Available online: http://copasi.org/ (accessed on 12 December 2020).
- Higham, D.J. Modeling and Simulating Chemical Reactions. SIAM Rev. 2008, 50, 347–368. [Google Scholar] [CrossRef]
- Allen, E. Modeling with Itô Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2007; Volume 22. [Google Scholar]
- Gray, A.; Greenhalgh, D.; Hu, L.; Mao, X.; Pan, J. A stochastic differential equation SIS epidemic model. SIAM J. Appl. Math. 2011, 71, 876–902. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiang, D.; Mao, X.; Gray, A. The threshold of a stochastic SIRS epidemic model in a population with varying size. Discret. Contin. Dyn. Syst. Ser. B 2015, 20, 1277–1295. [Google Scholar] [CrossRef][Green Version]
- Zhu, L.; Hu, H. A stochastic SIR epidemic model with density dependent birth rate. Adv. Differ. Equ. 2015, 2015, 330. [Google Scholar] [CrossRef]
- Rao, F. Dynamics analysis of a stochastic SIR epidemic model. Abstr. Appl. Anal. 2014, 2014, 356013. [Google Scholar] [CrossRef]
- Chang, Z.; Meng, X.; Zhang, T. A new way of investigating the asymptotic behaviour of a stochastic SIS system with multiplicative noise. Appl. Math. Lett. 2019, 87, 80–86. [Google Scholar] [CrossRef]
- Bellen, A.; Zennaro, M. Numerical Methods for Delay Differential Equations; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Shampine, L.F.; Thompson, S.; Kierzenka, J. Solving Delay Differential Equations with dde23. 2000. Available online: http://www.runet.edu/~thompson/webddes/tutorial.pdf (accessed on 12 December 2020).
- Alemneh, H.T.; Makinde, O.D.; Theuri, D.M. Optimal Control Model and Cost Effectiveness Analysis of Maize Streak Virus Pathogen Interaction with Pest Invasion in Maize Plant. Egypt. J. Basic Appl. Sci. 2020, 7, 180–193. [Google Scholar] [CrossRef]
- Bosque-Pérez, N.A. Eight decades of maize streak virus research. Virus Res. 2000, 71, 107–121. [Google Scholar] [CrossRef]
- Magenya, O.; Mueke, J.; Omwega, C. Significance and transmission of maize streak virus disease in Africa and options for management: A review. Afr. J. Biotechnol. 2008, 7, 4897–4910. [Google Scholar]
- Alemneh, H.T.; Makinde, O.D.; Mwangi Theuri, D. Ecoepidemiological Model and Analysis of MSV Disease Transmission Dynamics in Maize Plant. Int. J. Math. Math. Sci. 2019, 2019. [Google Scholar] [CrossRef]
- Mao, X.; Sabanis, S. Numerical solutions of stochastic di erential delay equations under local Lipschitz condition. J. Comput. Appl. Math. 2003, 151, 215–227. [Google Scholar] [CrossRef]
- Barrio, M.; Burrage, K.; Leier, A.; Tian, T. Oscillatory Regulation of Hes1: Discrete Stochastic Delay Modelling and Simulation. PLoS Comput. Biol. 2006, 2, e117. [Google Scholar] [CrossRef] [PubMed]
- Barbuti, R.; Caravagna, G.; Milazzo, P.; Maggiolo-Schettini, A. On the Interpretation of Delays in Delay Stochastic Simulation of Biological Systems. Electron. Proc. Theor. Comput. Sci. 2009, 6, 17–29. [Google Scholar] [CrossRef][Green Version]
- GNU. GNU Octave. Library Catalog. Available online: www.gnu.org (accessed on 12 December 2020).
- Maarleveld, T.R.; Olivier, B.G.; Bruggeman, F.J. StochPy: A Comprehensive, User-Friendly Tool for Simulating Stochastic Biological Processes. PLoS ONE 2013, 8, e79345. [Google Scholar] [CrossRef] [PubMed]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar]
- Mondal, S.; Mukherjee, S.; Bagchi, B. Mathematical modeling and cellular automata simulation of infectious disease dynamics: Applications to the understanding of herd immunity. J. Chem. Phys. 2020, 153, 114119. [Google Scholar] [CrossRef]
- Cummings, D.A.; Lessler, J. Infectious disease dynamics. In Infectious Disease Epidemiology: Theory and Practice; Nelson, K.E., Masters Williams, C., Eds.; Jones & Bartlett Publishers: Burlington, MA, USA, 2014; pp. 131–166. [Google Scholar]
- Funk, S.; Salathé, M.; Jansen, V.A. Modelling the influence of human behaviour on the spread of infectious diseases: A review. J. R. Soc. Interface 2010, 7, 1247–1256. [Google Scholar] [CrossRef]
- Rivers, C.M.; Lofgren, E.T.; Marathe, M.; Eubank, S.; Lewis, B.L. Modeling the impact of interventions on an epidemic of Ebola in Sierra Leone and Liberia. PLoS Curr. 2014, 6. [Google Scholar] [CrossRef]
- Begon, M.; Bennett, M.; Bowers, R.G.; French, N.P.; Hazel, S.; Turner, J. A clarification of transmission terms in host-microparasite models: Numbers, densities and areas. Epidemiol. Infect. 2002, 129, 147–153. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.J. A primer on stochastic epidemic models: Formulation, numerical simulation, and analysis. Infect. Dis. Model. 2017, 2, 128–142. [Google Scholar] [CrossRef] [PubMed]

| Parameter Name | Description | Value |
|---|---|---|
| K | Total plant host population | 63 P-unit |
| Infection rate of plants due to vectors | 0.01/day/P-unit | |
| Infection rate of vectors due to plants | 0.01/day/P-unit | |
| Saturation constant of plants due to vectors | 0.2/P-unit | |
| Saturation constant of vectors due to plants | 0.1/P-unit | |
| Natural death rate of plants | 0.01/day | |
| m | Natural death rate of vectors | 0.2974/day |
| Recovery rate of plants | 0.01/day | |
| Replenishing rate of vectors | 10 P-unit/day | |
| d | Death rate of infected plants due to the disease | 0.2/day |
| Contact rate between predators and healthy insects | 0.05/day/P-unit | |
| Contact rate between predators and infected insects | 0.05/day/P-unit | |
| Natural death rate of predators | 0.05/day | |
| Saturation of predators due to insects | 0.1/P-unit | |
| Recruiting rate of predators | 0.4 P-unit/day | |
| Conversion rate of predators due to insects | 0.1 | |
| Delay for plants | 24 days | |
| Delay for vectors | 1 day |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen-Charpentier, B. Stochastic Modeling of Plant Virus Propagation with Biological Control. Mathematics 2021, 9, 456. https://doi.org/10.3390/math9050456
Chen-Charpentier B. Stochastic Modeling of Plant Virus Propagation with Biological Control. Mathematics. 2021; 9(5):456. https://doi.org/10.3390/math9050456
Chicago/Turabian StyleChen-Charpentier, Benito. 2021. "Stochastic Modeling of Plant Virus Propagation with Biological Control" Mathematics 9, no. 5: 456. https://doi.org/10.3390/math9050456
APA StyleChen-Charpentier, B. (2021). Stochastic Modeling of Plant Virus Propagation with Biological Control. Mathematics, 9(5), 456. https://doi.org/10.3390/math9050456






