An Intelligent Algorithm for Solving the Efficient Nash Equilibrium of a Single-Leader Multi-Follower Game
Abstract
:1. Introduction
2. Preliminaries and Prerequisites
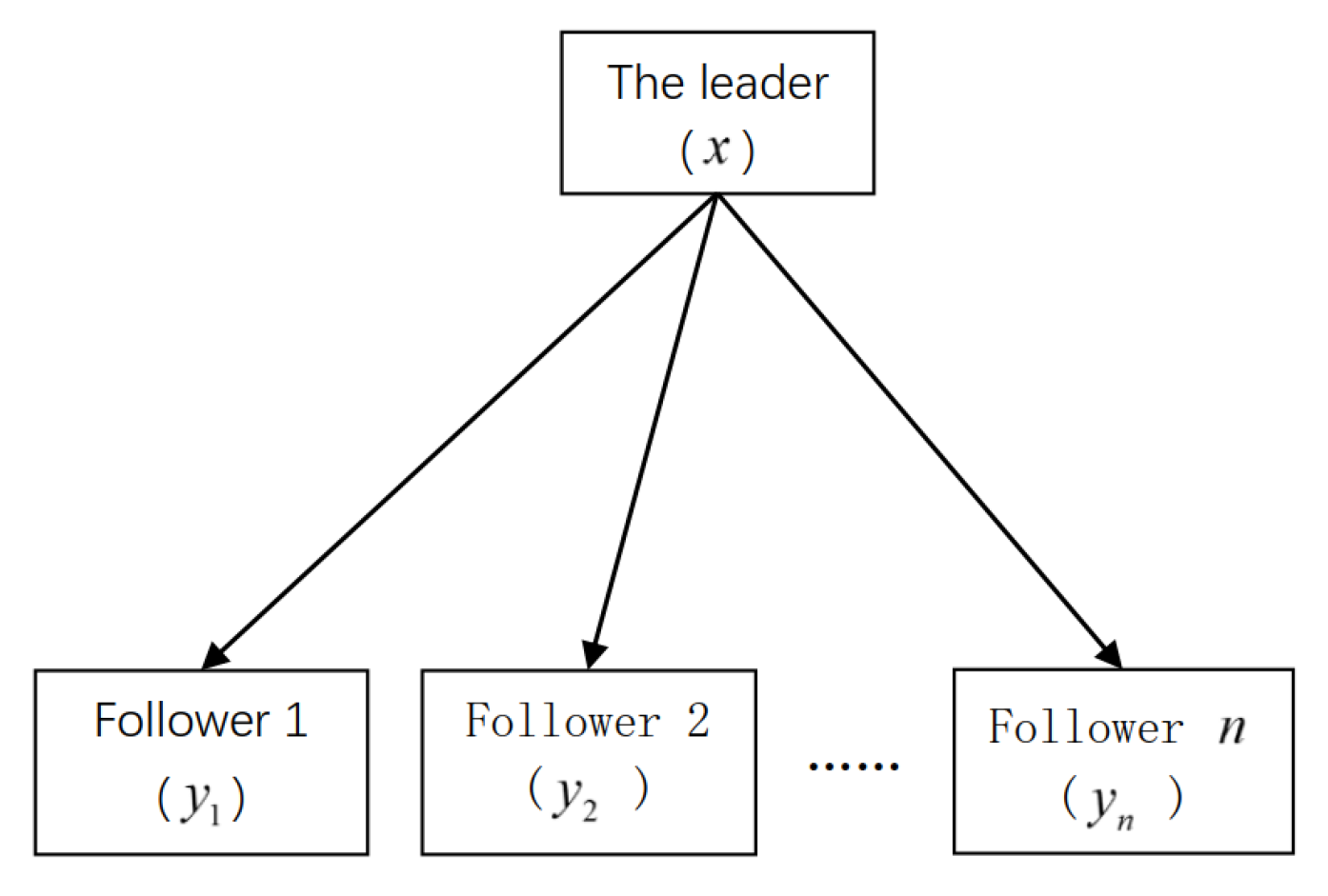
2.1. The Model of the Single-Leader Multi-Follower Game (SLMFG)
2.2. The Special Form of the SLMFG
- (a)
- The leader’s objective function and the leader’s feasible set G, are both continuous.
- (b)
- The followers’ objective functions and the followers’ constraint functions are both differentiable with local Lipschitz continuity.
- (c)
- For every follower , given any , each follower’s objective function is convex concerning , and the constraint function is convex with respect to .
2.3. The Definition of Efficient Nash Equilibrium
3. The Transformation of the SLMFG
3.1. The SLMFG Is Turned into a Nonlinear Equation Problem (NEP)
3.2. The Nonlinear Complementarity Problem (NCP) Is Converted into a Nonlinear Equation Problem (NEP)
4. The Design of Immune Particle Swarm Optimization (IPSO) Algorithm
4.1. The Particle Swarm Optimization (PSO) Algorithm
4.2. The Immune Particle Swarm Optimization (IPSO) Algorithm
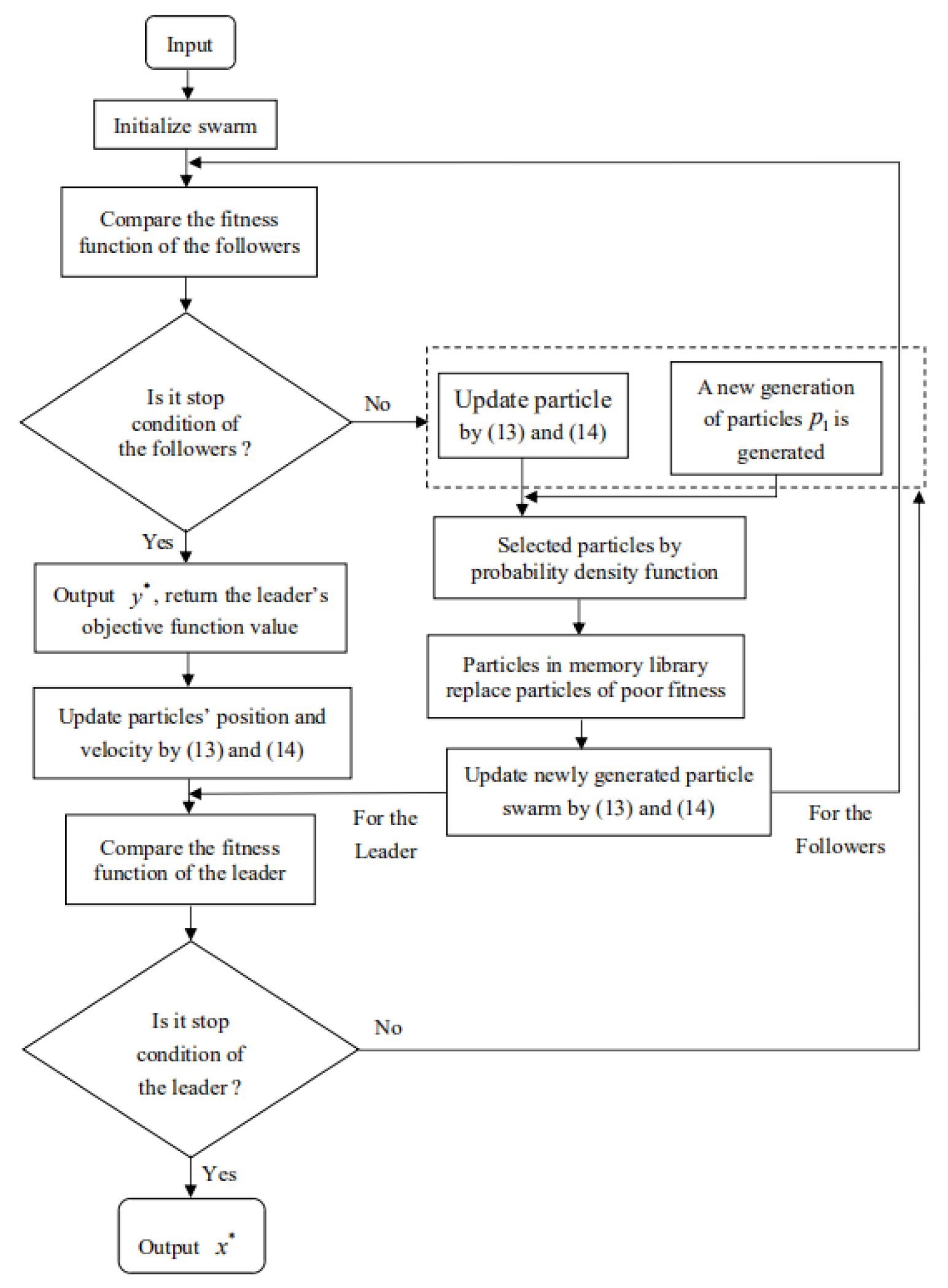
4.3. Implementation Steps of the IPSO Algorithm
- Step 1:
- Initialize the parameters. The maximum number of iterations for the followers is and the maximum number of iterations for the leader is . The acceleration constants are and , the inertia weight values are and , and the precision is . The size of the randomly generated population is M, and the initial value is randomly generated according to the feasible domain of the leader.
- Step 2:
- The IPSO algorithm can obtain the initial population by randomly generating the followers’ initial positions and initial velocities with the followers’ set-value mappings.
- Step 3:
- The algorithm is used to calculate each particle’s fitness function value for the followers and find the individual best position and population best position .
- Step 4:
- Equation (15) is used to compute the inertia weight w.
- Step 5:
- Step 6:
- Followers are randomly generated to obtain a new population with size Q.
- Step 7:
- We select population M from the new population through the probability concentration selection formulation Equation (20).
- Step 8:
- Step 9:
- By calculating the fitness value of particle ’s current position, ’s fitness value is compared with ’s fitness value. If , then ; otherwise, .
- Step 10:
- Each particle’s fitness function value for the followers is calculated, and the individual best position and population best position are found. Hence, we can compare the fitness value of the particle with the fitness value of the global ; if , then ; otherwise, .
- Step 11:
- Stopping condition of the followers: Does the maximum number of iterations or the precision satisfy the termination condition? If yes, we output the optimal particle (approximate solution of the followers); otherwise, we return to Step 4.
- Step 12:
- The followers’ optimal particle is returned as feedback to the leader.
- Step 13:
- The algorithm is used to calculate each particle’s fitness function value for the leader and find the individual best position and population best position .
- Step 14:
- Step 15:
- A new population number of size Q is randomly generated.
- Step 16:
- We choose population M from the new population through the probability concentration selection formula Equation (21).
- Step 17:
- Step 18:
- By calculating and comparing ’s fitness value with ’s fitness value, if , then ; otherwise, .
- Step 19:
- Each particle’s fitness function value for the leader is calculated, and the individual best position and population best position are found. Hence, we can compare the particle ’s fitness value with the global optimal particle ’s fitness value; if , then ; otherwise, .
- Step 20:
- Stopping condition for the leader: Is the maximum number of iterations achieved or is the precision ? If yes, we output the optimal particle ; otherwise, we return to Step 14.
- Step 21:
- Finally, if satisfies Definition 2, then denotes the efficient Nash equilibrium set of the SLMFG.
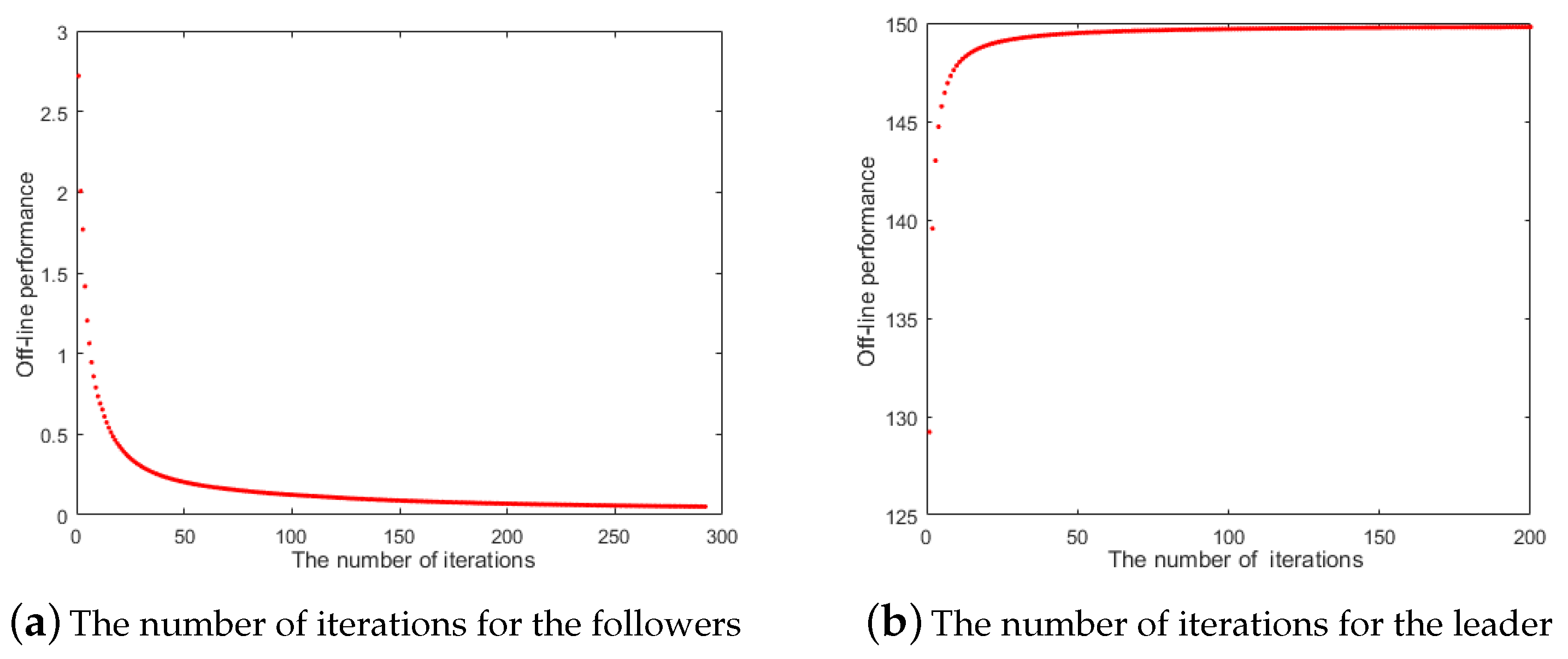
4.4. Performance Evaluation of the IPSO Algorithm
5. Numerical Experiment
- (0.000, 8.054, 1.946; 0.000, 0.000; 1.320, 6.734; 0.973, 0.973);
- (1.946, 0.000, 8.054; 0.973, 0.973; 0.000, 0.000; 1.320, 6.734); and
- (8.054, 1.946, 0.000; 6.734, 1.320; 0.973, 0.973; 0.000, 0.000).
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nash, J. Non-cooperative games. Ann. Math. 1951, 54, 286–295. [Google Scholar] [CrossRef]
- Nash, J. Equilibrium points in n-person games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takako, F.-G. Non-Cooperative Game Theory; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Bhatti, B.A.; Broadwater, R. Distributed Nash equilibrium seeking for a dynamic micro-grid energy trading game with non-quadratic payoffs. Energy 2020, 117709. [Google Scholar] [CrossRef]
- Anthropelos, M.; Boonen, T.J. Nash equilibria in optimal reinsurance bargaining. Insur. Math. Econ. 2020, 93, 196–205. [Google Scholar] [CrossRef]
- Campbell, D.E. Incentives: Motivation and the Economics of Information, 2nd ed.; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Yu, J.; Wang, H.L. An existence theorem for equilibrium points for multi-leader-follower games. Nonlinear TMA 2008, 69, 1775–1777. [Google Scholar] [CrossRef]
- Jia, W.S.; Xiang, S.W.; He, J.H.; Yang, Y. Existence and stability of weakly Pareto-Nash equilibrium for generalized multiobjective multi-leader-follower games. J. Glob. Optim. 2015, 61, 397–405. [Google Scholar] [CrossRef]
- Bucarey, L.V.; Casorrán, L.M.; Labbé, M.; Ordoñez, F.; Figueroa, O. Coordinating resources in Stackelberg security games. Eur. J. Oper. Res. 2019, 11, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Luo, X.; Liu, Y.F.; Liu, J.P.; Liu, X. Energy scheduling for a three-level integrated energy system based on energy hub models: A hierarchical Stackelberg game approach. Sustain. Cities Soc. 2020, 52, 101814. [Google Scholar] [CrossRef]
- Anbalagan, S.; Kumar, D.; Raja, G.; Balaji, A. SDN assisted Stackelberg game model for LTE-WiFi offloading in 5G networks. Digit. Commun. Netw. 2019, 5, 268–275. [Google Scholar] [CrossRef]
- Lee, M.L.; Nguyen, N.P.; Moonc, J. Leader-follower decentralized optimal control for large population hexarotors with tilted propellers: A Stackelberg game approach. J. Frankl. Inst. 2019, 356, 6175–6207. [Google Scholar] [CrossRef]
- Saberi, Z.; Saberi, M.; Hussain, O.; Chang, E. Stackelberg model based game theory approach for assortment andselling price planning for small scale online retailers. Future Gener. Comput. Syst. 2019, 100, 1088–1102. [Google Scholar] [CrossRef]
- Clempner, J.B.; Poznyak, A.S. Solving transfer pricing involving collaborative and non-cooperative equilibria in Nash and Stackelberg games: Centralized-Decentralized decision making. Comput. Econ. 2019, 54, 477–505. [Google Scholar] [CrossRef]
- Jie, Y.M.; Choo, K.K.R.; Li, M.C.; Chen, L.; Guo, C. Tradeoff gain and loss optimization against man-in-the-middle attacks based on game theoretic model. Future Gener. Comput. Syst. 2019, 101, 169–179. [Google Scholar] [CrossRef]
- Bard, J.F. Practical Bilevel Optimization: Algorithms and Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1998; pp. 193–386. [Google Scholar]
- Jeroslow, R.G. The polynomial hierarchy and a simple model for competitive analysis. Math. Program. 1985, 32, 146–164. [Google Scholar] [CrossRef]
- Gumus, Z.H.; Floudas, C.A. Global optimization of nonlinear bilevel programming problems. J. Glob. Optim. 2001, 20, 1–31. [Google Scholar] [CrossRef]
- Tutuko, B.; Nurmaini, S.; Sahayu, P. Optimal route driving for leader-follower using dynamic particle swarm optimization. In Proceedings of the 2018 International Conference on Electrical Engineering and Computer Science(ICECOS), Pangkal Pinang, Indonesia, 2–4 October 2018; pp. 45–49. [Google Scholar]
- Khanduzi, R.; Maleki, H.R. A novel bilevel model and solution algorithms for multi-period interdiction problem with fortification. Appl. Intell. 2018, 48, 2770–2791. [Google Scholar] [CrossRef]
- Liu, B.D. Stackelberg-Nash equilibrium for multilevel programming with multiple follows using genetic algorithms. Comput. Math. Appl. 1998, 36, 79–89. [Google Scholar] [CrossRef] [Green Version]
- Mahmoodi, A. Stackelberg-Nash equilibrium of pricing and inventory decisions in duopoly supply chains using a nested evolutionary algorithm. Appl. Soft Comput. J. 2020, 86, 105922. [Google Scholar] [CrossRef]
- Amouzegar, M.A. A global optimization method for nonlinear bilevel programming problems. Syst. Man Cybern. 1999, 29, 771–777. [Google Scholar] [CrossRef]
- Facchinei, F.; Fisher, A.; Piccialli, V. Generalized Nash equilibrium problems and Newton methods. Math. Program. 2009, 117, 163–194. [Google Scholar] [CrossRef]
- Li, Q. A Smoothing Newton Method for Generalized Nash Equilibrium Problems; Dalian University of Technology: Dalian, China, 2009. [Google Scholar]
- Izmailov, A.F.; Solodov, M.V. On error bounds and Newton-type methods for generalized Nash equilibrium problems. Comput. Optim. Appl. 2014, 59, 201–218. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the International Conference on Networks, Singapore, 27–30 August 2002; pp. 1942–1948. [Google Scholar]
- Shi, Y.; Eberhart, R.C. A modified particle swarm optimizer. In Proceedings of the IEEE International Conference on Evolutionary Computation, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Jiao, W.; Cheng, W.; Zhang, M.; Song, T. A simple and effective immune particle swarm optimization algorithm. In Advances in Swarm Intelligence; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Jiang, J.; Song, C.; Ping, H.; Zhang, C. Convergence analysis of self-adaptive immune particle swarm optimization algorithm. In Advances in Neural Networks-ISNN 2018; Lecture Notes in Computer Science; Huang, T., Lv, J., Sun, C., Tuzikov, A., Eds.; Springer: Cham, Switzerland, 2018; Volume 10878. [Google Scholar]
- Lu, G.; Tan, D.; Zhao, M. Improvement on regulating definition of antibody density of immune algorithm. In Proceedings of the International Conference on Neural Information Processing, Singapore, 18–22 November 2002; pp. 2669–2672. [Google Scholar]
- De Jong, K.A. Analysis of the Behavior of a Class of Genetic Adaptive System; University of Michigan: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Bard, J.F. Convex two-level optimization. Math. Program. 1988, 40, 15–27. [Google Scholar] [CrossRef]
- Li, H.; Wang, Y.P.; Jian, Y.C. A new genetic algorithm for nonlinear bilevel programming problem and its global convergence. Syst. Eng. Theory Pract. 2005, 3, 62–71. [Google Scholar]
| Times | Number of Iterations | Efficient Nash Equilibrium | Fitness Function Value |
|---|---|---|---|
| 1 | 285 | , | 21.8 × 10 |
| 2 | 274 | , | 2.2 × 10 |
| 3 | 276 | , | 27.7 × 10 |
| 4 | 292 | , | 44.6 × 10 |
| 5 | 288 | , | 27.9 × 10 |
| Times | Number of Iterations | Efficient Nash Equilibrium | Fitness Function Value |
|---|---|---|---|
| 1 | 75 | 150.445 | |
| 2 | 80 | 149.932 | |
| 3 | 84 | 150.000 | |
| 4 | 101 | 149.898 | |
| 5 | 150 | 151.022 |
| x | |||||
|---|---|---|---|---|---|
| (7, 3, 12, 18) | (0, 10) | (30, 0) | 6600 | 25 | 29 |
| (6.97, 3.03, 12.03, 17.97) | (0.1, 9.9) | (29.9, 0.1) | 6600 | 24.82 | 29.62 |
| (6.96, 3.04, 12.05, 17.95) | (0.15, 9.85) | (29.85, 0.15) | 6600 | 24.745 | 29.945 |
| (6.94, 3.06, 12.06, 17.94) | (0.2, 9.8) | (29.8, 0.2) | 6600 | 24.68 | 30.28 |
| (6.91, 3.09, 12.09, 17.91) | (0.3, 9.7) | (29.7, 0.3) | 6600 | 24.58 | 30.98 |
| (6.85, 3.15, 12.15, 17.85) | (0.5, 9.5) | (29.5, 0.5) | 6600 | 24.5 | 32.50 |
| (6.7, 3.3, 12.3, 17.7) | (1, 9) | (29, 1) | 6600 | 25 | 37 |
| (7.05, 3.13, 11.93, 17.89) | (0.26, 9.92) | (29.82, 0.00) | 6599.99 | 23.47 | 30.83 |
| ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| x | |||||||
|---|---|---|---|---|---|---|---|
| (1.946, 8.054, 0.000) | (0.973, 0.973) | (1.317, 6.737) | (0.000, 0.000) | 9.577 | 1.609 | 7.099 | 0.000 |
| (8.054, 1.946, 0.000) | (1.316, 6.738) | (0.973, 0.973) | (0.000, 0.000) | 9.577 | 7.099 | 1.609 | 0.000 |
| (0.000, 1.946, 8.054) | (0.000, 0.000) | (0.973, 0.973) | (6.319, 6.735) | 9.587 | 0.000 | 1.609 | 7.098 |
| (0.000, 8.054, 1.946) | (0.000, 0.000) | (1.320, 6.734) | (0.973, 0.973) | 9.593 | 0.000 | 7.098 | 1.609 |
| (1.946, 0.000, 8.054) | (0.973, 0.973) | (0.000, 0.000) | (1.320, 6.734) | 9.593 | 1.609 | 0.000 | 7.098 |
| (8.054, 1.946, 0.000) | (6.734, 1.320) | (0.973, 0.973) | (0.000, 0.000) | 9.593 | 7.098 | 1.609 | 0.000 |
| (1.946, 8.054, 0.000) | (0.973, 0.973) | (1.314, 6.378) | (0.000, 0.000) | 9.558 | 1.609 | 7.094 | 0.000 |
| ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.-P.; Jia, W.-S. An Intelligent Algorithm for Solving the Efficient Nash Equilibrium of a Single-Leader Multi-Follower Game. Mathematics 2021, 9, 454. https://doi.org/10.3390/math9050454
Liu L-P, Jia W-S. An Intelligent Algorithm for Solving the Efficient Nash Equilibrium of a Single-Leader Multi-Follower Game. Mathematics. 2021; 9(5):454. https://doi.org/10.3390/math9050454
Chicago/Turabian StyleLiu, Lu-Ping, and Wen-Sheng Jia. 2021. "An Intelligent Algorithm for Solving the Efficient Nash Equilibrium of a Single-Leader Multi-Follower Game" Mathematics 9, no. 5: 454. https://doi.org/10.3390/math9050454






