1. Introduction
Metaheuristics [
1,
2] are approximate techniques for optimization. Each metaheuristic was originally introduced for a certain type of optimization problem, for example, function optimization or combinatorial optimization (CO). However, nowadays one can find a metaheuristic variant for different types of optimization problems. Ant colony optimization (ACO) [
3,
4] is a metaheuristic algorithm originally introduced for solving CO problems. The inspiration of ACO was the foraging behavior of natural ant colonies and, in particular, the way in which ant colonies find short paths between their ant hive and food sources. Any ACO algorithm works roughly as follows. At each iteration, a pre-defined number of artificial ants derive solutions to the considered optimization problem. This is done in a probabilistic way, making use of two types of information: (1)
greedy information and (2)
pheromone values. Then, some of these solutions—typically the best ones—are used to update the pheromone values. This is done with the aim of changing the probability distribution used for generating solutions such that high-quality solutions can be found. In other words, ACO is an optimization technique based on learning from positive examples, henceforth called
positive learning. Most of the work on ACO algorithms from the literature focuses on solving CO problems, such as scheduling problems [
5], routing and path-planning problems [
6,
7], problems related to transportation [
8], and feature selection [
9]. Several well-known ACO variants were introduced in the literature over the years, including the
-
Ant System (MMAS) [
10], Ant Colony System (ACS) [
11], and the Rank-Based Ant System [
12], just to name a few of the most important ones.
As already mentioned above, ACO is strongly based on positive learning, which also holds for most other metaheuristics based on learning. By means of positive learning the algorithm tries to identify those solution components that are necessary for assembling high-quality solutions. Nevertheless, there is evidence in nature that learning from negative examples, henceforth called negative learning, can play a significant role in biological self-organizing systems:
Pharaoh ants (
Monomorium pharaonis), for example, use negative trail pheromone a ‘no entry’ signals in order to mark unrewarding foraging paths [
13,
14].
A different type of negative feedback caused by crowding at the food source was detected in colonies of
Lasius niger [
15]. This negative feedback enables the colony to maintain a flexible foraging system despite the strong positive feedback by the pheromone trails.
Another example concerns the use of anti-pheromone hydrocarbons used by male tsetse flies. They play an important role in tsetse communications [
16].
Honeybees (
Apis mellifera ligustica) were shown to mark flowers with scent and to strongly reject all recently visited flowers [
17].
Based on these examples, Schoonderwoerd et al. [
18] stated already in 1997 that it might be possible to improve ACOs’ performance with an additional mechanism that tries to identify undesirable components with the help of a negative feedback mechanisms.
1.1. Existing Approaches
In fact, the ACO research community has made several attempts to design such a negative learning mechanism. Maniezzo [
19] and Cordón et al. [
20] were presumably the first ones to make use of an active decrease of pheromone values associated to solution components appearing in low-quality solutions. Montgomery and Randall [
21] proposed three anti-pheromone strategies that were partially inspired by previous works that made use of several types of pheromones; see, for example, [
22]. In their first approach, the pheromone values of those solution components that belong to the worst solution at each iteration are decreased. Their second approach—in addition to the standard pheromone—makes explicit use of negative pheromones. Each ant has a specific bias—different to the one of the other ants—towards each of the two types of pheromone. Finally, their third approach uses a certain number of ants at each iteration in order to explore the use of solution components with lower pheromone values, without introducing dedicated anti-pheromones. Unfortunately, the presented experimental evaluation did not allow clear conclusions about a potential advantage of any of the three strategies over standard ACO. Different extensions of the approaches from [
21] were explored by Simons and Smith [
23]. The authors admitted, however, that nearly all their approaches proved to be counter-intuitive. Their only idea that showed to be useful to some extent was to make use of a rather high amount of anti-pheromone at the early stages of the search process.
In [
24], Rojas-Morales et al. presented an ACO variant for the multi dimensional knapsack problem based on opposite learning. The first algorithm phase serves for building anti-pheromone values with the intention to enable the algorithm during the second phase to avoid solution components that lead to low-quality solutions despite being locally attractive, due to a rather high heuristic value. Unfortunately, no consistent improvement over standard ACO could be observed in the results. In addition, earlier algorithm variants based on opposition-based learning were tested on four rather small TSP instances [
25]. Another application to the TSP was proposed in Ramos et al. [
26], where they proposed a method that uses a second-order coevolved compromise between positive and negative feedback. According to the authors, their method achieves better results than single positive feedback systems in the context of the TSP. Finally, the most successful strand of work on using negative learning in ACO deals with the application to constraint satisfaction problems (CSPs). Independently of each other, Ye et al. [
27] and Masukane and Mizuno [
28,
29] proposed negative feedback strategies for ACO algorithms in the context of CSPs. Both approaches make use of negative pheromone values in addition to the standard pheromone values. Moreover, in both works the negative pheromone values are updated at each iteration with the worst solution(s) generated at that iteration. The difference is basically to be found in the way in which the negative pheromone values are used for generating new solutions. Finally, we would also like to mention a very recent negative learning approach from the field of multi-objective optimization [
30].
1.2. Contribution and General Idea
When devising a negative feedback mechanism there are fundamentally two questions to be answered: (1) how to identify those solution components that should receive a negative feedback, and (2) how exactly to make use of the negative feedback. Concerning the first question, it can be observed that all the existing approaches mentioned in the previous section try to identify low-quality solution components on the basis of the solutions generated by the ACO algorithm itself. In contrast, the main idea of this article is to make use of an additional optimization technique for identifying these components. In particular, we test two possibilities in this work. The first one is the application of mathematical programming solvers—we used CPLEX—for solving opportunely defined sub-instances of the tackled problem instance. Second, we tested the use of an additional ACO algorithm that works independently of the main algorithm for solving the before-mentioned sub-instances.
We have tested this mechanism in a preliminary work [
31] by applying it to the so-called capacitated minimum dominating set problem (CapMDS), with excellent results. In this extended work we first describe the mechanism in general terms in the context of subset selection problems, which is a large class of CO problems. Subsequently, we demonstrate its application to two classical NP-hard combinatorial optimization problems: the minimum dominating set (MDS) problem [
32] and the multi dimensional knapsack problem (MDKP) [
33]. Our results show that, even though positive learning remains to be the most important form of learning, the incorporation of negative learning improves the obtained results significantly for subsets of problem instances with certain characteristics. Moreover, for comparison purposes we implement several negative learning approaches introduced for ACO in the related literature. The obtained results show that our mechanism outperforms all of them with statistical significance.
2. Preliminaries and Problem Definitions
Even though the negative learning mechanism presented in this work is general and can be incorporated into ACO algorithms for any CO problem, for the sake of simplicity this study is conducted in the context of subset selection problems. This important class of CO problems can formally be defined as follows:
Set C is a finite set of n items.
Function {TRUE, FALSE} decides if a subset is a feasible solution. Henceforth, let be the set of all feasible solutions.
The objective function assigns a value to each feasible solution.
The optimization goal might be minimization or maximization. Numerous well-known CO problems can be stated in terms of a subset selection problem. A prominent example is the symmetric traveling salesman problem (TSP). Hereby, the edges E of the complete TSP graph correspond to item set C. Moreover, a subset is evaluated by function F as a feasible solution if and only if the edges from S define a Hamiltonian cycle in G. Finally, given a feasible solution S, the objective function value of S is calculated as the sum of the distances of all edges from S. The optimization goal in the case of the TSP is minimization. In the following we explain both the MDS problem and the MDKP in terms of subset selection problems.
2.1. Minimum Dominating Set
The classical MDS problem—which is
-hard—can be stated as follows. Given is an undirected graph
, with
C being the set of vertices and
E the set of edges. Given a vertex
,
denotes the neighborhood of
in
G. A subset
is called a
dominating set if and only if for each vertex
the following holds: (1)
or (2) there is at least one
with
. The MDS requires finding a feasible solution of minimum cardinality. This problem is obviously a subset selection problem in which
C is the set of items,
for
evaluates to
TRUE if and only if
S is a dominating set of
G, and
. A standard integer linear programming (ILP) model for the MDS problem can be stated as follows.
subject to:
The model consists of a binary variable
for each vertex
. The objective function counts the selected vertices, and the constraints (
2) ensure that each vertex either belongs to the solution or has, at least, one neighbor that forms part of the solution. In the literature, there are many variants of the MDS problem. Examples include the minimum connected dominating set problem [
34], the minimum total dominating set problem [
35] and the minimum vertex weight dominating set problem [
36]. The currently best metaheuristic approach for solving the MDS problem is a two-goal local search with inference rules from [
37].
2.2. Multi Dimensional Knapsack Problem
The MDKP is also a classical
-hard CO problem that is often used as a test case for new algorithmic proposals (see, for example, [
38,
39,
40]). The problem can be stated as follows. Given is (1) a set
C =
of
n items and (2) a number of
m resources. The availability of each resource
k is limited by
, which is also called the capacity of resource
k. Moreover, each item
consumes a fixed amount
from each resource
(
resource consumption). Additionally, each item
comes with a profit
.
A candidate solution
is a valid solution if and only if, concerning all resources, the total amount consumed by the items in
S does not exceed the resource capacities. In other words, it is required that
for all
. Moreover, a valid solution
S is labeled
non-extensible, if no
can be added to
S without losing the property of being a valid solution. The problem requires to find a valid solution
S of maximum total profit (
). The standard ILP for the MDKP is stated in the following.
subject to:
This model is built on a binary variable
for each item
. Constraints (
5) are called the knapsack constraints. In general, the literature offers very successful exact solution techniques; see, for example, [
41,
42,
43]. However, devising heuristic solvers still remains to be a challenge. Among numerous metaheuristic proposals for the MDKP problem, the currently best performing ones are the DQPSO algorithm from [
44] and the TPTEA algorithm from [
45].
3. MMAS: The Baseline Algorithm
Many of the negative learning approaches for ACO cited in
Section 1.1 were introduced for different ACO variants. In order to ensure a fair comparison, we add both our own proposal as well as the approaches from the literature to the same standard ACO algorithm:
-
Ant System (MMAS) in the hypercube framework [
46], which is one of the most-used ACO versions from the last decade. In the following we first describe the standard MMAS algorithm in the hypercube framework for subset selection problems. This will be our baseline algorithm. Subsequently we describe the way in which the negative learning proposal from this paper and the chosen negative learning proposals from the literature are added to this baseline algorithm.
3.1. MMAS in the Hypercube Framework
The pheromone model in the context of subset selection problems consists of a pheromone value for each item , where C is the complete set of items. Remember that, in the context of the MDS, C is the set of vertices of the input graph, while C is the set of items in the case of the MDKP. The MMAS algorithm maintains three solutions throughout a run:
: the best solution generated at the current iteration, also called the iteration-best solution.
: the best solution generated since the last restart of the algorithm, also called the restart-best solution.
: the best-so-far solution, that is, the best solution found since the start of the algorithm.
Moreover, the algorithm makes use of a Boolean control variable {TRUE, FALSE} and the convergence factor for deciding on the pheromone update mechanism and on the question whether or not to restart the algorithm. At the start of the algorithm, solutions and are initialized to NULL, the convergence factor is set to zero, is set to FALSE and the pheromone values are all initilized to in function ; see lines 2 and 3 of Algorithm 1. Then, at each iteration, solutions are probabilistically generated in function Construct_Solution, based on pheromone information and on greedy information. The construction of solutions will be outlined in detail for both problems (MDS and MDKP) below. The generated solutions are stored in set , and the best one from is stored as ; see lines 5–10 of Algorithm 1. Then, the restart-best and best-so-far solutions— and —are updated with , if appropriate; lines 11 and 12. Afterward, the pheromone update is conducted in function , , , ,,) and the new value for the convergence factor is computed in function ); lines 13 and 14. Finally, based on the values of and , the algorithm might be restarted. Such a restart consists in re-initializing all pheromone values, in setting the restart-best solution to NULL, and to TRUE. In the following, the function for the pheromone update and for the calculation of the convergence factor are outlined in detail.
,
,
,
,
,
): the pheromone update that is described here is the same as in any other MMAS algorithm in the hypercube framework. First, the three solutions
,
, and
receive weights
,
and
, respectively. A standard setting of these weights, depending on
and
, is provided in
Table 1. It always holds that
. After having determined the solution weights, each pheromone value
is updated as follows:
where
Hereby,
is the so-called learning rate, and function
evaluates to 1 if and only if item
forms part of solution
S. Otherwise, the function evaluates to 0. Finally, after conducting this update, those pheromone values that exceed
are set to
, and those values that have dropped below
are set to
. Note that, in this way, a complete convergence of the algorithm is avoided. Finally, note that the learning mechanism represented by this pheromone update can clearly be labeled positive learning, because it makes use of the best solutions found for updating the pheromone values.
| Algorithm 1 MMAS in the hypercube framework (baseline algorithm) |
- 1:
input: a problem instance with the complete item set C - 2:
NULL, NULL, cf:= 0, FALSE - 3:
- 4:
while termination conditions not met do - 5:
- 6:
for k = 1, do - 7:
- 8:
- 9:
end for - 10:
best solution from - 11:
if better than then - 12:
if better than then - 13:
, , , ,,) - 14:
cf ) - 15:
if cf > 0.999 then - 16:
if TRUE then - 17:
NULL, and FALSE - 18:
- 19:
else - 20:
TRUE - 21:
end if - 22:
end if - 23:
end while - 24:
output:, the best solution found by the algorithm
|
): Just like the pheromone update, the computation of the convergence factor is a standard procedure that works in the same way for all MMAS algorithms in the hypercube framework:
Accordingly, the value of is zero in the case when all pheromone values are set to . The other extreme case is represented by all pheromone values having either value or . In this case, evaluates to one. Otherwise, has a value between 0 and 1. Herewith the description of all components of the baseline algorithm is completed.
3.1.1. Solution Construction for the MDS Problem
In the following we say that, if a vertex
is added to a solution
S under construction, then
covers itself and all its neighbors, that is, all
. Moreover, given a set
—that is, a solution under construction—we denote by
the set of uncovered neighbors of
. The solution construction mechanism is shown in Algorithm 2. It starts with an empty solution
. Then, at each step, exactly one of the vertices of those that do not yet form part of
S or that—with respect to
S—have uncovered neighbors (
) is chosen in function
and added to
S. The choice of a vertex in
is done as follows. First, a probability
is calculated for each
:
Hereby,
is the greedy information that we used. Then, a random number
is drawn. If
,
(to be added to
S) is selected such that
for all
. Otherwise,
is chosen by roulette-wheel-selection based on the calculated probabilities. Note that
is an important parameter of the algorithm.
| Algorithm 2 MDS solution construction |
- 1:
input: a graph G = (C, E) - 2:
- 3:
or - 4:
whiledo - 5:
- 6:
- 7:
or - 8:
end while - 9:
output: a valid solution S
|
3.1.2. Solution Construction for the MDKP
As in the MDS-case, the solution construction starts with an empty solution
, and at each construction step exactly one item
is selected from a set
. The definition of
in the case of the MDKP is as follows. An item
forms part of
if and only if (1)
, and (2)
is a valid solution. The probability
for an item
to be chosen at the current construction step is the same as in Equation (
9), just that the definition of the greedy information changes. In particular,
is defined as follows:
These greedy values are often called utility ratios in the related literature. Given the probabilities, the choice of an item is done exactly in the same way as outlined above in the case of the MDS problem.
4. Adding Negative Learning to MMAS
In the following we first describe our own proposal for adding negative learning to ACO. Subsequently, our implementations of some existing approaches from the literature are outlined.
4.1. Our Proposal
As mentioned in the introduction, for each negative learning mechanism there are two fundamental questions to be answered: (1) how is the negative information generated, maintained and updated, and (2) how is this information being used.
4.1.1. Information Maintenance
We maintain the information derived from negative learning by means of a second pheromone model , which consists of a pheromone value for each item . We henceforth refer to these values as the negative pheromone values. Whenever the pheromone values are (re-)initialized, the negative pheromone values are set to , which is in contrast to the standard pheromone values, which are set to 0.5 (see above).
4.1.2. Information Generation and Update
The generation of the information for negative learning is done by two new instructions, which are introduced between lines 9 and 10 of the baseline MMAS algorithm (Algorithm 1):
Function merges all solutions from , resulting in a subset . Then an optimization algorithm is applied to find the best-possible solution that only consists of items from . In this work we have experimented with two options:
Option 1: Application of the ILP solver CPLEX 12.10. In the case of the MDS problem, the ILP model from
Section 2.1 is used after adding an additional constraint
for all
. In the case of the MDKP, we use the ILP model from
Section 2.2 after replacing all occurrences of
C with
.
Option 2: Application of the baseline MMAS algorithm (Algorithm 1). In the case of both the MDS and the MDKP problem, this application of the baseline MMAS only considers items from for the construction of solutions. Moreover, this MMAS application uses its own pheromone values, parameter settings, etc. Finally, the best-so-far solution of this (inner) ACO is initialized with .
In both options, solution —which is returned by —is the best solution between and the best solution found by the optimization algorithm (CPLEX, respectively baseline MMAS) in the allotted computation time. This computation time is calculated on the basis of a maximum computation time ( CPU seconds) and the current value of the convergence factor, which is passed to function SolveSubinstance as a parameter. In particular, the allowed computation time (in seconds) is . This means that the available computation time for solving the sub-instance decreases with an increasing convergence factor value. The rationale behind this setting is that, when the convergence factor is low, the variance between solutions in is rather high and is therefore rather large, which means that more time is necessary to explore sub-instance .
The last action in function SolveSubinstance
is the update of the negative pheromone values based on solution
. This update only concerns the negative pheromone values of those components that form part of
. The update formula is as follows:
where
is the
negative learning rate and
if
, resp.
otherwise. In other words, the negative pheromone value of those components that do not form part of
is increased.
4.1.3. Information Use
The negative pheromone values are used in the context of the construction of solutions. In particular, Equation (
9) is replaced by the following one:
In this way, those items that have accumulated a rather high negative pheromone value (because they have not appeared in the solutions derived by CPLEX, respectively the (inner) MMAS algorithm, to the sub-instances of previous iterations) have a decreased probability to be chosen for solutions in the current iteration. Note that a very similiar formula was used already in [
27].
4.2. Proposals from the Literature
As mentioned before, the proposals from the literature were introduced in the context of several different ACO versions. In order to ensure a fair comparison, we reimplemented those proposals that we chose for comparison in the context of the baseline MMAS algorithm. In particular, we implemented four different approaches, which all share the following common feature. In addition to the iteration-best solution (
), the restart-best solution (
) and the best-so-far solution (
), these extensions of the baseline MMAS algorithm maintain the
iteration-worst solution (
), the
restart-worst solution (
) and the
worst-so-far solution (
). As in the case of
and
, solutions
and
are initialized to
NULL at the start of the algorithm. Then, the following three lines are introduced after line 12 of Algorithm 1:
| worst solution from |
| if worse than then |
| if worse than then |
The way in which these three additional solutions are used differs among the four implemented approaches.
4.2.1. Subtractive Anti-Pheromone
This idea is adopted from [
21], but has already been used in similar form in [
19,
20]. Our implementation of this idea is as follows. After the standard pheromone update of the baseline MMAS algorithm (see line 13 of Algorithm 1), the following is done. First, a set
B is generated by joining the items in solutions
,
and
, that is,
. Then, all those items in which the pheromone value receives an update from at least one of the solutions
,
, or
in the current iteration are removed from
B. That is:
| ifthen |
| ifthen |
| ifthen |
Afterward, the following additional update is applied:
In other words, the pheromone values of all those components that appear in “bad” solutions, but who do not form part of “good” solutions, are subject to a pheromone value decrease depending on the reduction rate . Finally, note that the solution construction procedure in this variant—which is henceforth labeled ACO-SAP—is exactly the same as in the baseline MMAS algorithm.
4.2.2. Explorer Ants
The explorer ants approach from [
21]—henceforth labeled A
CO-E
A—is very similar to the previously presented A
CO-S
AP approach. The only difference is in the construction of solutions. This approach has an additional paramete:
, the proportion of explorer ants. Given the number of ants (
) and
, the number of explorer ants
is calculated as follows:
At each iteration,
solution constructions are performed in the same way as in the baseline MMAS algorithm. The remaining
solution constructions make use of the following formula (instead of Equation (
9) for calculating the probabilities:
In other words, explorer ants make use of the opposite of the pheromone values for constructing solutions.
4.2.3. Preferential Anti-Pheromone
Like our own negative learning proposal, the preferential anti-pheromone approach from [
21] makes use of an additional set
of pheromone values. Remember that
contains a pheromone value
for each item
. These negative pheromone values are initilized at the start of the algorithm as well as when the algorithm is restarted, to a value of 0.5. Moreover, after the update of the standard pheromone values in line 13 of the baseline MMAS algorithm, exactly the same update is conducted for the negative pheromone values:
where
Hereby, is the negative learning rate, and function evaluates to 1 if and only if item forms part of solution S. Moreover, values , and are the same as the ones used for the udpate of the standard pheromone values. This means that the learning of the negative pheromone values is dependent on the dynamics of the learning of the standard pheromone values.
The standard pheromone values and the negative pheromone values are used as follows for the construction of solutions. The probabilities for the
a-th solution construction—where
—are determined as follows:
where
. This means that
for the first solution construction, which means that only the negative pheromones values are used. In the other extreme, it holds that
for the
-th solution construction, that is, only the standard pheromone values are used. All other solution constructions combine both pheromone types at different rates. Note that this preferential anti-pheromone approach is henceforth labeled A
CO-P
AP.
4.2.4. Second-Order Swarm Intelligence
Our implementation of the second-order swarm intelligence approach from [
26] works exactly like the A
CO-P
AP approach from the previous section for what concerns the definition and the update of the negative pheromone values. However, the way in which they are used is different. The item probabilities for the construction of solutions is calculated by the following formula:
where
is a parameter of the algorithm. Note that this approach is henceforth labeled A
CO2o.
4.3. Summary of the Tested Algorithms
In addition to the baseline MMAS algorithm (henceforth simply labeled ACO), and the four approaches from the literature (ACO-SAP, ACO-EA, ACO-PAP and ACO2o) we test the following six versions of the negative learning mechanism proposed in this paper:
A
CO-C
PL: The mechanism described in
Section 4.1 using option 1 (CPLEX) for solving sub-instances.
ACO-CPLneg: This algorithm is the same as ACO-CPL, with the exception that Equation (12) is not performed. This means that the algorithm does make use of solution for additional positive learning. Studying this variant will show if, by solely adding negative learning, the algorithm improves over the baseline ACO.
ACO-CPL: This algorithm is the same as ACO-CPL, apart from the fact that the update of the negative pheromone values is not performed. In this way, the algorithm only makes use of the additional positive learning mechanism obtained by adding solution to .
The remaining three algorithm variants are ACO-ACO, ACO-ACO and ACO-ACO. These algorithm variants are the same ones as ACO-CPL, ACO-CPL and ACO-CPL, except that they make use of option 2 (baseline ACO algorithm) for solving the corresponding sub-instances at each iteration.
A summary of the parameters that arise in these 11 algorithms is provided in
Table 2, together with a description of their function and the parameter value domains that were used for parameter tuning (which will be described in
Section 5.2). Moreover, an overview on the parameters that are involved in each of the 11 algorithms is provided in
Table 3.
5. Experimental Evaluation
The experiments concerning the MDS problem were performed on a cluster of machines with two Intel® Xeon® Silver 4210 CPUs with 10 cores of 2.20 GHz and 92 Gbytes of RAM. The MDKP experiments were conducted on a cluster of machines with Intel® Xeon® CPU 5670 CPUs with 12 cores (2.933 GHz) and at least 32 GB RAM. For solving the sub-instances in ACO-CPL, ACO-CPL and ACO-CPL we used CPLEX 12.10 in one-threaded mode.
5.1. Problem Instances
Concerning the MDS problem, we generated a benchmark instance set with instances of different sizes (number of vertices 10,000}), different densities (percentage of all possible edges ) and different graph types (random graphs and random geometric graphs). For each combination of n, d and graph type, 10 random instances were generated. This makes a total of 160 problem instances.
In the case of the MDKP we used a benchmark set of 90 problem instances with 500 items from the OR-Library (
http://people.brunel.ac.uk/~mastjjb/jeb/info.html, accessed on 20 January 2021). This set consists of 30 instances with 5, 10, and 30 resources. Moreover, each of these three subsets contains 10 instances with resource tightness 0.25, 0.5, and 0.75. Roughly, the higher the value of the resource tightness, the more items can be placed in the knapsack. These 90 problem instances are generally known to be the most difficult ones available in the literature for heuristic solvers.
5.2. Algorithm Tuning
The scientific parameter tuning tool irace [
47] was used for the purpose of parameter tuning. In particular we produced for each of the 11 algorithms (resp., algorithm versions) exactly one parameter value set for each problem (MDS problem vs. MDKP). For the purpose of tuning the algorithms for the MDS problem, we additionally generated for each combination of
n,
d (density), and graph type exactly one random instance. In other words, 16 problem instances were used for tuning, and the tuner was given a maximal budget of 2000 algorithm applications. In the context of tuning the algorithms for the MDKP, we randomly selected one of the 10 problem instances for each combination of “the number of resources” (5, 10, 30) and the instance tightness (0.25, 0.5, 0.75). Consequently, nine problem instances were used for tuning in the case of the MDKP. Remember that the parameter value domains considered for tuning are provided in
Table 2. The parameter values that were determined by irace for the 11 algorithms and for the two problems are provided in
Table 4 (MDS problem) and
Table 5 (MDKP).
5.3. Results
Using the previously determined parameter values, each of the 11 considered algorithms was applied 30 times—that is, with 30 different random seeds—to each of the 160 MDS problem instances. Hereby, 500 CPU seconds were chosen as a time limit for the graphs with 5000 nodes, whereas 1000 CPU seconds were chosen as a time limit for each run concerning the graphs with 10,000 nodes. Moreover, each algorithm was applied 100 times to each of the 90 MDKP instances. This was done with a time limit of 500 s per run. Note that, in this way, the same computational resources were given to all 11 algorithms in the context of both tackled problems. The choice of 100 runs per instance in the case of the MDKP was done in order to produce results that are comparable to the best existing approaches from the literature, which were also applied 100 times to each problem instance.
Due to space restrictions we present a comparative analysis of the 11 algorithms in terms of
critical difference (CD) plots [
48] and so-called
heatmaps. In order to produce the average ranks of all algorithms—both for the whole set of problem instances (per problem) as well as for instance subsets—the Friedman test was applied for the purpose of comparing the 11 approaches simultaneously. In this way we also obtained the rejection of the hypothesis that the 11 techniques perform equally. Subsequently, all pairwise algorithm comparisons were performed using the Nemenyi post-hoc test [
49]. The obtained results are shown graphically (CD plots and heatmaps). The CD plots show the average algorithm ranks (horizontal axis) with respect to the considered (sub-)set of instances. In those cases in which the performances of two algorithms are below the critical difference threshold—based on a significance level of 0.05—the two algorithms are considered as statistically equivalent. This is indicated by bold horizontal bars joining the markers of the respective algorithm variants.
5.3.1. Results for the MDS Problem
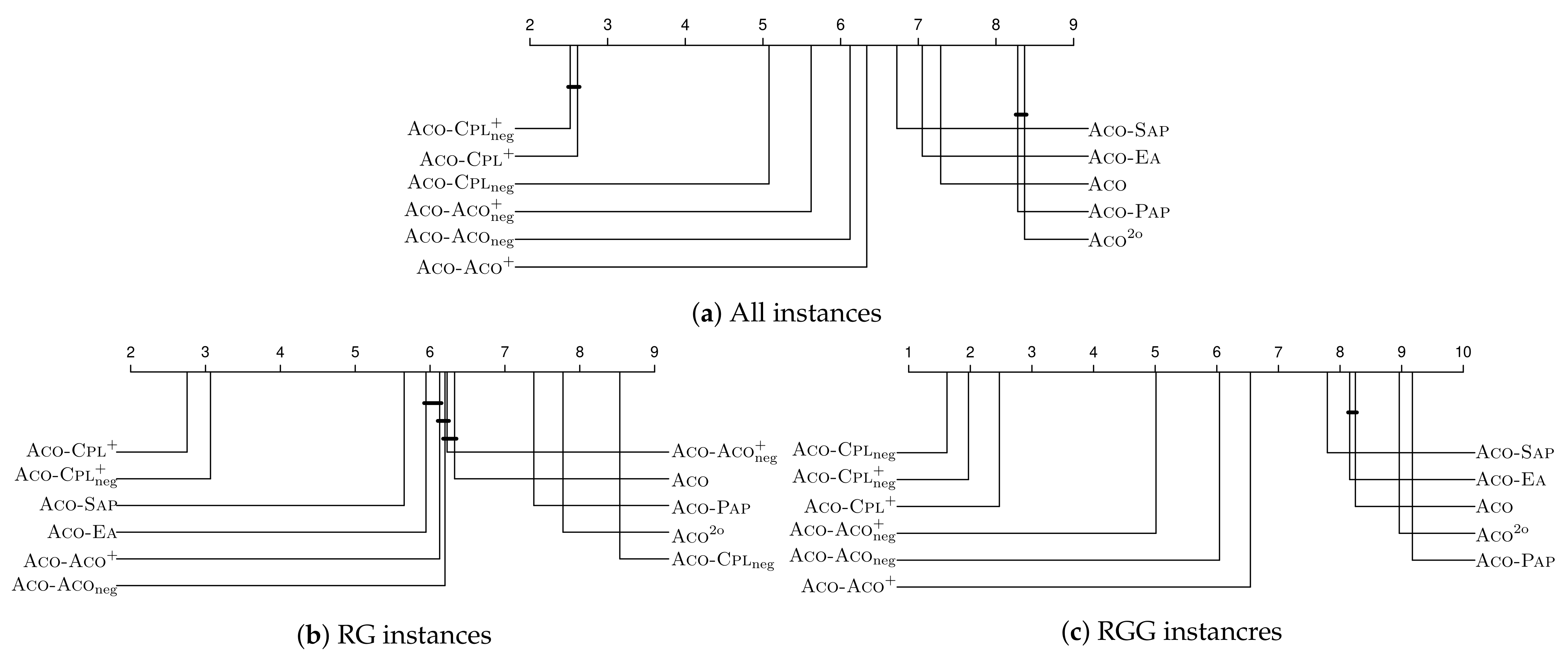
Figure 1a shows the CD plot for the whole set of 160 MDS instances, while
Figure 1b,c present more fine-grained results concerning random graphs (RGs) and random geometric graphs (RGGs), respectively. Furthermore, the heatmaps in
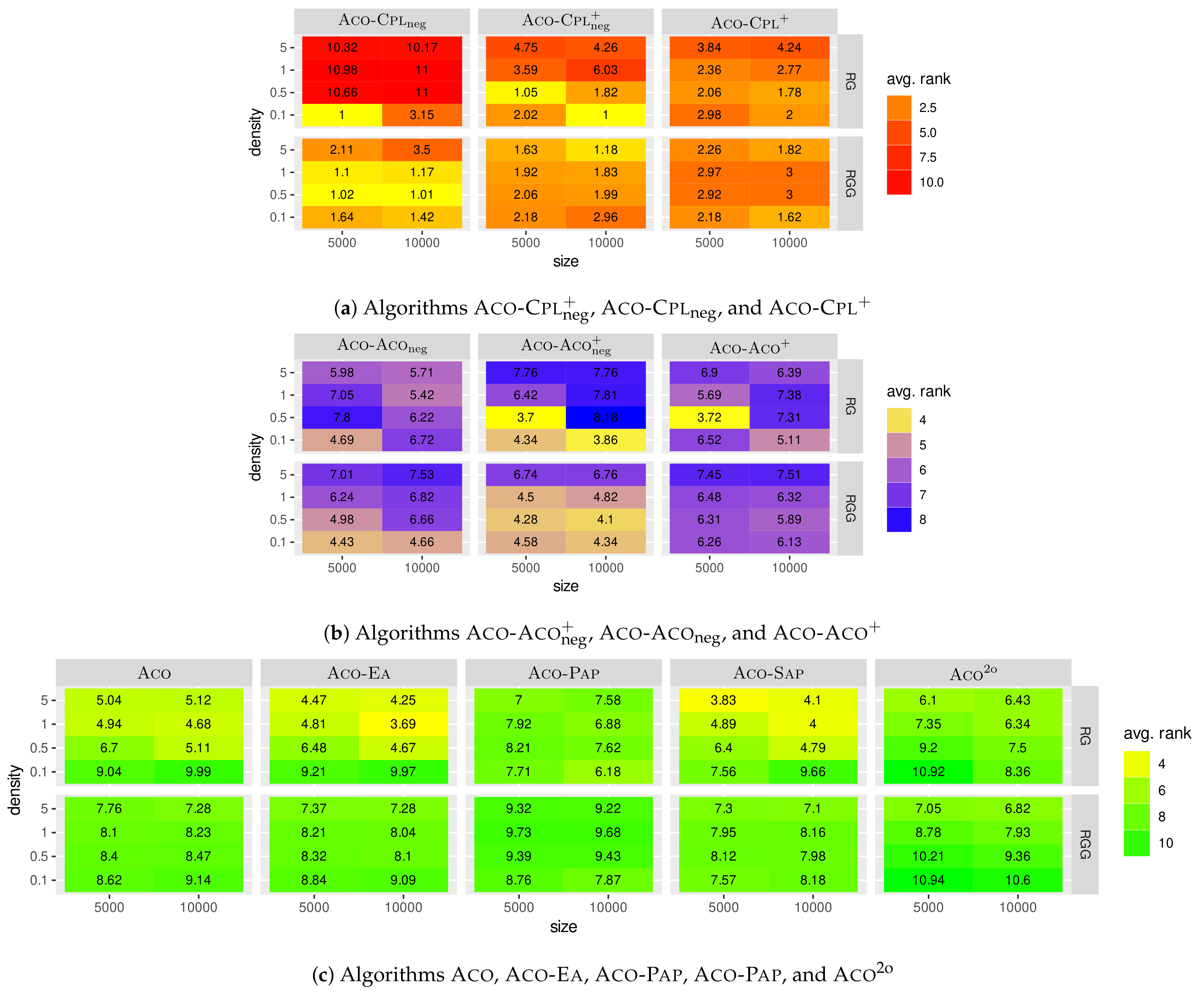
Figure 2 show the average ranks of the 11 algorithms in an even more fine-grained way. The graphic shows exactly one heatmap for each algorithm. The ones of algorithms A
CO-C
PL, A
CO-C
PL and A
CO-C
PL are shown in
Figure 2a, the ones of algorithms A
CO-A
CO, A
CO-A
CO and A
CO-A
CO in
Figure 2b, and the ones of the remaining five algorithms in
Figure 2c. The upper part of each heatmap shows the results for RGs, while the lower part concerns the results for RGGs. Each of these parts has two columns: the first one contains the results for the graphs with 5000 nodes, and the second one for the ones with 10,000 nodes. Moreover, each part has four rows, showing the results for the four considered graph densities. In general, the more yellow the cell of a heatmap, the better is the relative performance of the corresponding algorithm for the respective combination of features (graph type, graph size, and density).
The global CD plot from
Figure 1a allows to make the following observations:
All the six algorithm variants proposed in this paper significantly improve over the remaining five algorithm variants, that is, over the baseline MMAS (ACO) and over the four considered negative learning variants from the literature.
The three algorithm variants that make use of CPLEX for generating the negative feedback (option 1) outperform the other three variants (making use of option 2) with statistical significance. This shows the importance of the way in which the negative feedback is generated. In fact, the more accurate the negative feedback, the better the global performance of the algorithm.
Concerning the four negative learning mechanisms from the literature, it is shown that only ACO-SAP and ACO-EA are able to outperform the baseline MMAS algorithm. In contrast, ACO-PAP and ACO2o perform significantly worse than the baseline MMAS algorithm.
When comparing variants ACO-CPL and ACO-CPL with ACO-CPL, it can be observed that ACO-CPL has only a slight advantage over ACO-CPL (which is not statistically significant). This means that, even though negative learning is useful, the additional positive feedback obtained by making use of solution for updating solutions and is very powerful.
The comparison of the three algorithms making use of option 2 (ACO-ACO, ACO-ACO and ACO-ACO) shows a significant difference to the comparison concerning the three algorithms using option 1: the two versions that make use of negative learning (ACO-ACO and ACO-ACO) outperform the version without negative learning (ACO-ACO) with statistical significance. This can probably be explained by the lower quality of the positive feedback information, as solutions can be expected to be generally worse than solutions of the algorithm version using option 1.
When looking at the results in a more fine-grained way, the following can be observed:
Interestingly, the graph type seems to have a big influence on the relative behavior of the algorithms. In the case of RGs, for example, ACO-CPL is the clear winner of the comparison with ACO-CPL in second place. However, the really interesting aspect is that ACO-CPL finishes last with statistical significance. This means that negative learning seems even to be harmful in the case of RGs. On the contrary, ACO-CPL is the clear winner of the competition in the context of RGGs, with ACO-CPL finishing in second place (with statistical significance), and ACO-CPL only in third place. This means that, in the case of RGGs, negative learning is much more important than the additional positive feedback provided by solution , which even seems harmful.
Another interesting aspect is that, in the context of RGs, two negative learning versions from the literature (ACO-SAP and ACO-EA) clearly outperform our proposed negative learning variants using option 2.
The heatmaps from
Figure 2 also indicate some interesting tendencies. Negative learning in the context of our algorithm variants A
CO-C
PL, A
CO-C
PL, A
CO-A
CO and A
CO-A
CO seems to gain importance with an increasing sparsity of the graphs. On the other side, in the context of RGs, it is clearly shown that the relative quality of A
CO-S
AP and A
CO-E
A grows with increasing graph size (number of vertices) and with increasing density.
5.3.2. Results for the MDKP
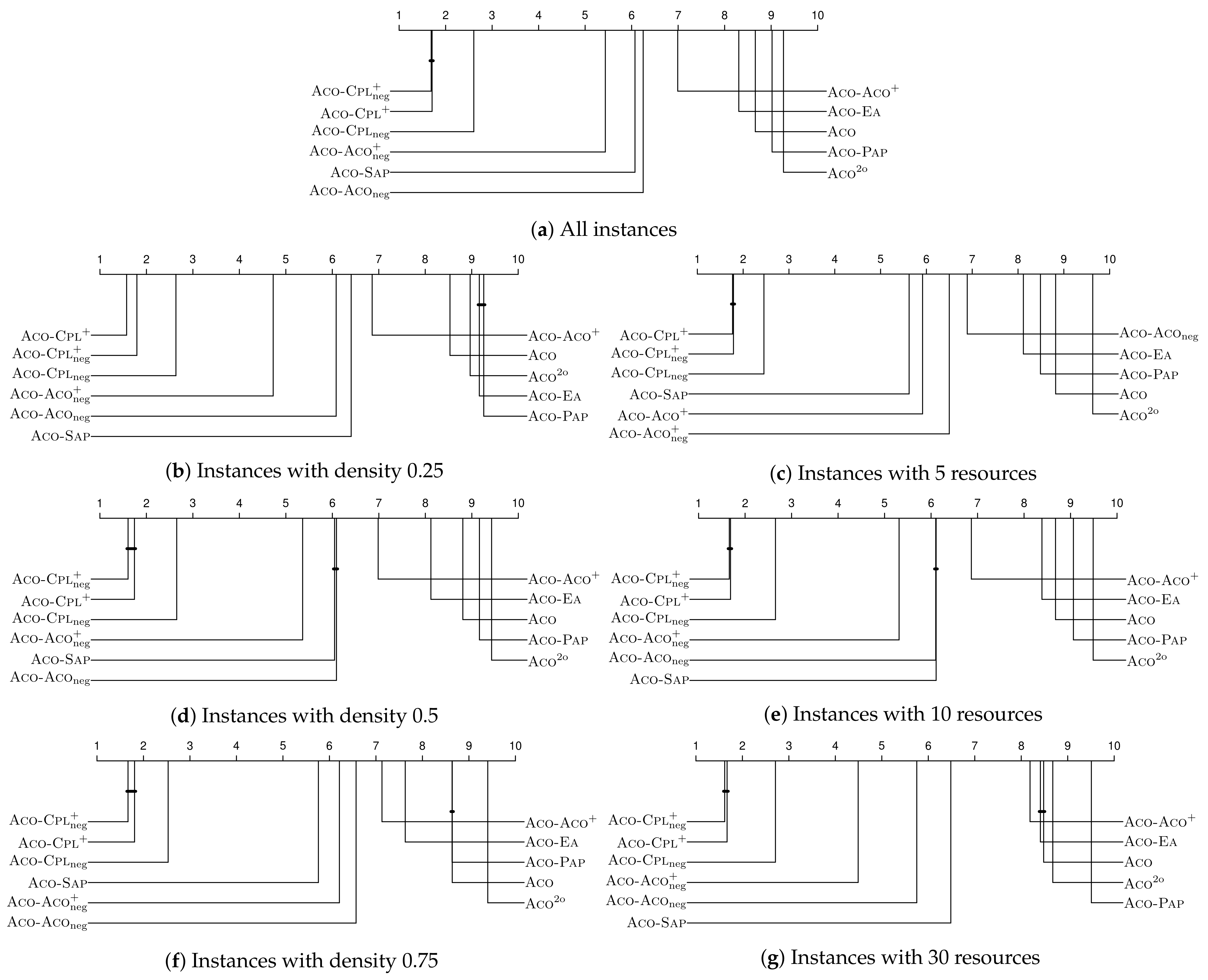
Figure 3a shows the CD plot for the whole set of 90 MDKP instances, while
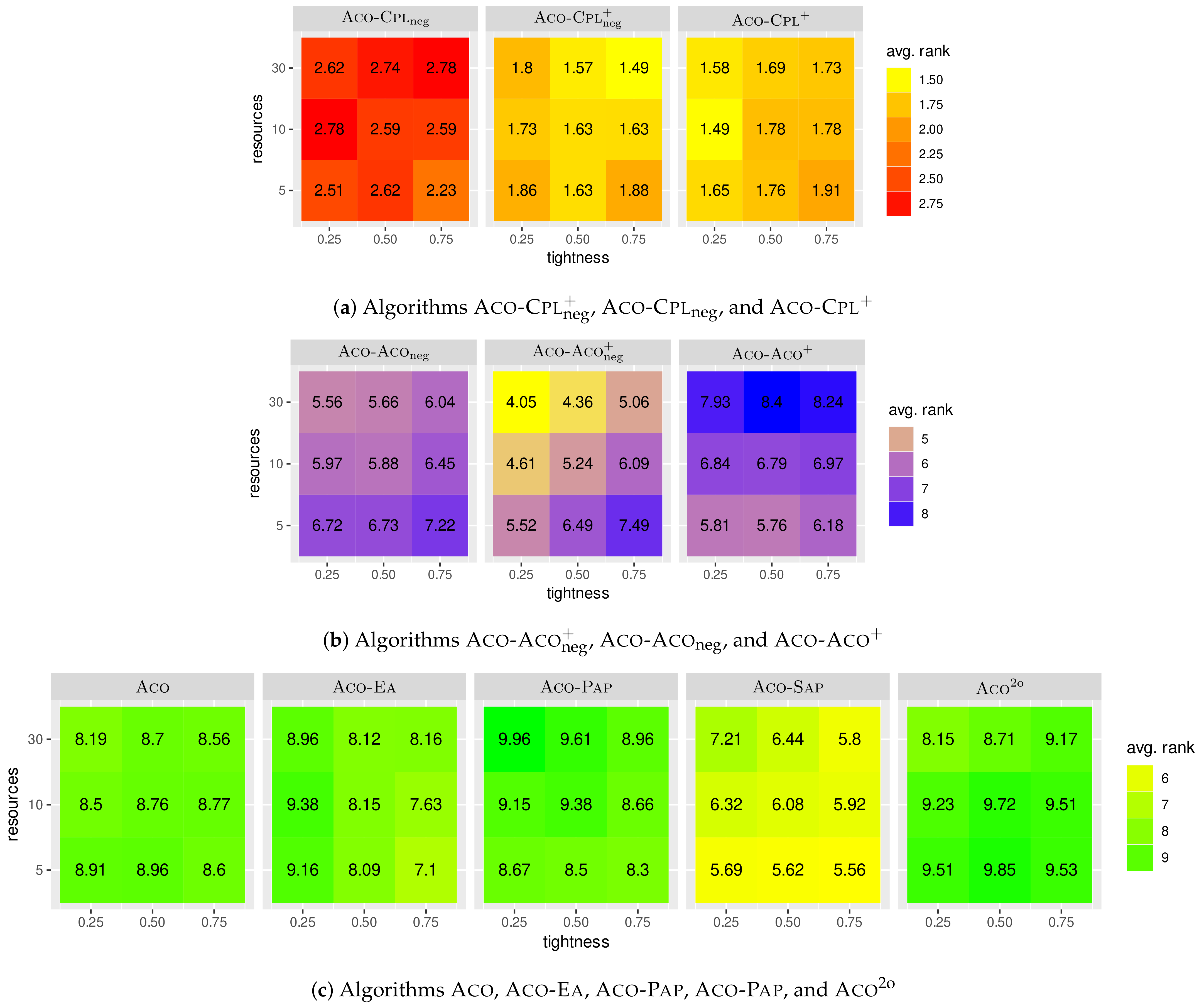
Figure 3b–g present more fine-grained results concerning instances with different numbers of resources and with a varying instance tightness. Again, the heatmaps in
Figure 4 complement this more fine-grained presentation of the results. The 11 algorithms are distributed in the same way as described in the context of the MDS problem into three heatmap graphics. Each heatmap (out of 11 heatmaps in total) has three rows: one for each number of resources (5, 10, 30). Moreover, each heatmap has three columns: one for each considered instance tightness (0.25, 0.5, 0.75). Interestingly, from a global point of view (
Figure 3a) the relative difference between the algorithm performances is very similar to the one observed for the MDS problem. In particular, our negative learning variants using option 1 perform best. Again, A
CO-C
PL has a slight advantage over A
CO-C
PL, which is—like in the case of the MDS problem—not statistically significant. Basically there is only one major difference to the results for the MDS problem: A
CO-S
AP, one of the negative learning variants from the literature, outperforms A
CO-A
CO and A
CO-A
CO.
When studying the results in a more fine-grained way, the following observations can be made:
The negative learning component of our algorithm proposal seems to gain importance with a growing number of resources. This can especially be observed for algorithm variants ACO-CPL, ACO-ACO and ACO-ACO. However, there is an interesting difference between ACO-CPL and ACO-ACO: while ACO-CPL improves with an increasing instance tightness, the opposite is the case for ACO-ACO.
Again, as in the case of the MDS problem, the relative performance of ACO-SAP, the best one of the negative learning variants chosen from the literature, is contrary to the relative performance of ACO-ACO. In other words, the relative performance of ACO-SAP improves with a decreasing number of resources and with an increasing instance tightness.
5.3.3. Comparison to the State-of-the-Art
Even though the objective of this study is not to outperform current state-of-the-art algorithms for the chosen problems, we are certainly interested to know how our globally best algorithm (ACO-CPL) performs in comparison to the state-of-the-art.
In the case of the MDS problem we chose for this purpose one of the classical benchmark sets, which was also used in one of the latest published works [
37]. This benchmark set is labeled UDG and consists of 120 graphs with numbers of vertices between 50 and 1000. For each of the six graph sizes, UDG contains graphs of two different densities. The benchmark set consists of 10 graphs per combination of graph size and graph density. Following the procedure from [
37], we applied A
CO-C
PL 10 times with a time limit of 1000 CPU seconds for each application to each of the 120 instances of set UDG. Note that we did not specifically tune the parameters of A
CO-C
PL. Instead, the same parameter values as in the previous section were used. The results are shown in a summarized way—as in [
37]—in
Table 6. In particular, each table row presents the results for the 10 instances of the respective instance family. For each of the six compared algorithms, the provided number is the average over the best solutions found for each of the 10 instances within 10 runs per instance. The best result per table row is indicated in bold face. Surprisingly, it can be observed that A
CO-C
PL matches the performance of the best two approaches. It is also worth mentioning that the five competitors of A
CO-C
PL in this table were all published since 2017 and are all based on local search. In particular, algorithm RLS
[
50] was shown to outperform all existing ACO and hyper-heuristic algorithms, which were the state-of-the-art before this recent start of focused research efforts on sophisticated local search algorithms. Concerning computation time, in [
37] it is stated that CC
FS requires on average 0.21 s, FastMWDS requires 0.83 s, and FastDS requires 22.19 s to obtain the best solutions of each run. A
CO-C
PL is somewhat slower by requiring on average 36.14 s.
In the context of the MDKP, we compare A
CO-C
PL to the current state-of-the-art algorithms: a sophisticated particle swarm optimization algorithm (DQPSO) from [
44], published in 2020, and a powerful evolutionary algorithm (TPTEA) from [
45], published in 2018. As these two algorithms—in their original papers—were applied to the 90 benchmark problems used in this work, it was not required to conduct additional experiments with A
CO-C
PL. A summarized comparison of the three algorithms is provided in
Table 7. Each row contains average results for the 10 problem instances for each combination of the number of resources (5, 10, 30) and the instance tightness (0.25, 0.5, 0.75). In particular, we show averages concerning the best solutions found (table columns 3–5), the average solution quality obtained (table columns 6–8), and the average computation times required (table columns 9–11). As in the case of the MDS problem, we were surprised to see that A
CO-C
PL can actually compete with current state-of-the-art algorithms. The state-of-the-art results were even improved by A
CO-C
PL in some cases, especially for what concerns medium instance tightness for 5 and 10 resources, and low instance tightness for 30 resources. Moreover, the computation time of A
CO-C
PL is much lower than that of TPTEA, and comparable to the one required by DQPSO.
6. Discussion and Conclusions
Metaheuristics based on learning—such as ant colony optimization, particle swarm optimization and evolutionary algorithms—are generally based on learning from positive examples, that is, they are based on positive learning. However, examples from nature show that learning from negative examples can be very beneficial. In fact, there have been several attempts during the last two decades to find a way to beneficially add negative learning to ant colony optimization. However, hardly any of the respective papers were able to show that the proposed mechanism was really useful. This is with the exception of the strand of work on constraint satisfaction problems. The goal of this work was, therefore, to devise a new negative learning mechanism for ant colony optimization and to show its usefulness. The main idea of our mechanism is that the negative feedback should not be extracted from the main ant colony optimization algorithm itself. Instead, it should be produced by an additional algorithmic component. In fact, after devising a new negative learning framework, we have tested two algorithmic options for producing the negative information: (1) making use of the mathematical programming solver CPLEX, and (2) making use of the baseline ACO algorithm, but in terms of additional applications for solving sub-instances of the original problem instances.
All considered algorithm variants were applied to two NP-hard combinatorial optimization problems from the class of subset selection problems: the minimum dominating set problem and the multi dimensional knapsack problem. Moreover, four negative learning mechanisms from the literature were implemented on the basis of the chosen baseline ACO algorithm in order to be able to compare our proposals with existing approaches. The obtained results have shown, first of all, that the proposed negative learning mechanism—especially when using CPLEX for producing the negative feedback information—is superior to the existing approaches from the literature. Second, we have shown that, even though negative learning is not useful for all problem instances, it can be very useful for subsets of problem instances with certain characteristics. In the context of the minimum dominating set problem, for example, this concerns rather sparse graphs, while for the multi dimensional knapsack problem the proposed negative learning mechanism was especially useful for problem instances with rather many resources. From a global point of view, it was also shown that it is generally not harmful to add negative learning, because the globally best-performing algorithm variant makes use of negative learning. Finally, we were even able to show that our globally best-performing algorithm variant is able to compete with current state-of-the-art algorithms for both considered problems.
Future lines for additional work include the following aspects. First, we aim to apply the proposed mechanism also to problems of a very different nature. Examples include scheduling and vehicle routing problems. Second, we aim at experimenting with other alternatives for producing the negative feedback information.
Author Contributions
Methodology, T.N. and C.B.; programming, T.N; writing—original draft, T.N. and C.B.; writing—review and editing, T.N. and C.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by project CI-SUSTAIN funded by the Spanish Ministry of Science and Innovation (PID2019-104156GB-I00).
Data Availability Statement
Both the problem instances used in this study and the detailed numerical results can be obtained from the corresponding author (C. Blum) on demand.
Acknowledgments
We acknowledge administrative and technical support by the Spanish National Research Council (CSIC).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. 2003, 35, 268–308. [Google Scholar] [CrossRef]
- Gendreau, M.; Potvin, J.Y. Handbook of Metaheuristics, 3rd ed.; International Series in Operations Research & Management Science; Springer: Berlin, Germany, 2019. [Google Scholar]
- Dorigo, M.; Stützle, T. Ant colony optimization: Overview and recent advances. In Handbook of Metaheuristics; Springer: Berlin, Germany, 2019; pp. 311–351. [Google Scholar]
- Dorigo, M.; Stützle, T. Ant Colony Optimization; MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Engin, O.; Güçlü, A. A new hybrid ant colony optimization algorithm for solving the no-wait flow shop scheduling problems. Appl. Soft Comput. 2018, 72, 166–176. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Alinaghian, M.; Hosseinabadi, A.A.R.; Sasi, M.B.; Sangaiah, A.K. An improved ant colony optimization for the multi-trip Capacitated Arc Routing Problem. Comput. Electr. Eng. 2019, 77, 457–470. [Google Scholar] [CrossRef]
- Zhang, D.; You, X.; Liu, S.; Pan, H. Dynamic Multi-Role Adaptive Collaborative Ant Colony Optimization for Robot Path Planning. IEEE Access 2020, 8, 129958–129974. [Google Scholar] [CrossRef]
- Jovanovic, R.; Tuba, M.; Voß, S. An efficient ant colony optimization algorithm for the blocks relocation problem. Eur. J. Oper. Res. 2019, 274, 78–90. [Google Scholar] [CrossRef]
- Peng, H.; Ying, C.; Tan, S.; Hu, B.; Sun, Z. An improved feature selection algorithm based on ant colony optimization. IEEE Access 2018, 6, 69203–69209. [Google Scholar] [CrossRef]
- Stützle, T.; Hoos, H.H. MAX–MIN ant system. Future Gener. Comput. Syst. 2000, 16, 889–914. [Google Scholar] [CrossRef]
- Dorigo, M.; Gambardella, L.M. Ant colony system: A cooperative learning approach to the traveling salesman problem. IEEE Trans. Evol. Comput. 1997, 1, 53–66. [Google Scholar] [CrossRef]
- Bullnheimer, B.; Hartl, R.R.; Strauss, C. A new rank-based version of the Ant System: A computational study. Central Eur. J. Oper. Res. 1999, 7, 25–38. [Google Scholar]
- Robinson, E.J.H.; Jackson, D.E.; Holcombe, M.; Ratnieks, F.L.W. ‘No entry’ signal in ant foraging. Nature 2005, 438, 442. [Google Scholar] [CrossRef]
- Robinson, E.J.H.; Jackson, D.E.; Holcombe, M.; Ratnieks, F.L.W. No entry signal in ant foraging (Hymenoptera: Formicidae): New insights from an agent-based model. Myrmecol. News 2007, 10, 120. [Google Scholar]
- Grüter, C.; Schürch, R.; Czaczkes, T.J.; Taylor, K.; Durance, T.; Jones, S.M.; Ratnieks, F.L.W. Negative Feedback Enables Fast and Flexible Collective Decision-Making in Ants. PLoS ONE 2012, 7, e44501. [Google Scholar] [CrossRef]
- Schlein, Y.; Galun, R.; Ben-Eliahu, M.N. Abstinons–Male-produced Deterrents of Mating in Flies. J. Chem. Ecol. 1981, 7, 285–290. [Google Scholar] [CrossRef]
- Giurfa, M. The repellent scent-mark of the honeybee Apis mellifera tigustica and its role as communication cue during foraging. Insectes Sociaux 1993, 40, 59–67. [Google Scholar] [CrossRef]
- Schoonderwoerd, R.; Holland, O.; Bruten, J.; Rothkrantz, L. Ant-Based Load Balancing in Telecommunications Networks. Adapt. Behav. 1997, 5, 169–207. [Google Scholar] [CrossRef]
- Maniezzo, V. Exact and approximate nondeterministic tree-search procedures for the quadratic assignment problem. INFORMS J. Comput. 1999, 11, 358–369. [Google Scholar] [CrossRef]
- Cordón, O.; Fernández de Viana, I.; Herrera, F.; Moreno, L. A New ACO Model Integrating Evolutionary Computation Concepts: The Best-Worst Ant System. In Proceedings of the ANTS 2000–Second International Workshop on Ant Algorithms, Brussels, Belgium, 8–9 September 2000; pp. 22–29. [Google Scholar]
- Montgomery, J.; Randall, M. Anti-pheromone as a Tool for Better Exploration of Search Space. In Proceedings of the ANTS 2002–3rd International Workshop on Ant Algorithms, Brussels, Belgium, 12–14 September 2002; Lecture Notes in Computer Science. Dorigo, M., Di Caro, G., Sampels, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2463, pp. 100–110. [Google Scholar]
- Iredi, S.; Merkle, D.; Middendorf, M. Bi-criterion optimization with multi colony ant algorithms. In Proceedings of the EMO 2001–International Conference on Evolutionary Multi-Criterion Optimization, Zurich, Switzerland, 7–9 March 2001; Lecture Notes in Computer Science. Zitzler, E., Deb, K., Thiele, L., Coello, C.A., Corne, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 1993, pp. 359–372. [Google Scholar]
- Simons, C.; Smith, J. Exploiting antipheromone in ant colony optimisation for interactive search-based software design and refactoring. In Proceedings of the GECCO 2016–Genetic and Evolutionary Computation Conference Companion, Denver, CO, USA, 20–24 July 2016; ACM: New York City, NY, USA, 2016; pp. 143–144. [Google Scholar]
- Rojas-Morales, N.; Riff, M.C.; Coello Coello, C.A.; Montero, E. A Cooperative Opposite-Inspired Learning Strategy for Ant-Based Algorithms. In Proceedings of the ANTS 2018–11th International Conference on Swarm Intelligence, Rome, Italy, 29–31 October 2018; Lecture Notes in Computer Science. Dorigo, M., Birattari, M., Blum, C., Christensen, A.L., Reina, A., Trianni, V., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 11172, pp. 317–324. [Google Scholar]
- Malisia, A.R.; Tizhoosh, H.R. Applying opposition-based ideas to the ant colony system. In Proceedings of the 2007 IEEE Swarm Intelligence Symposium, Honolulu, HI, USA, 1–5 April 2007; pp. 182–189. [Google Scholar]
- Ramos, V.; Rodrigues, D.M.S.; Louçã, J. Second Order Swarm Intelligence. In Proceedings of the Proceedings of HAIS 2013–International Conference on Hybrid Artificial Intelligence Systems, Salamanca, Spain, 11–13 September 2013; Pan, J.S., Polycarpou, M.M., Woźniak, M., de Carvalho, A.C.P.L.F., Quintián, H., Corchado, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 411–420. [Google Scholar]
- Ye, K.; Zhang, C.; Ning, J.; Liu, X. Ant-colony algorithm with a strengthened negative-feedback mechanism for constraint-satisfaction problems. Inf. Sci. 2017, 406–407, 29–41. [Google Scholar] [CrossRef]
- Masukane, T.; Mizuno, K. Solving Constraint Satisfaction Problems by Cunning Ants with multi-Pheromones. Int. J. Mach. Learn. Comput. 2018, 8, 361–366. [Google Scholar]
- Masukane, T.; Mizuno, K. Refining a Pheromone Trail Graph by Negative Feedback for Constraint Satisfaction Problems. In Proceedings of the TAAI 2019–International Conference on Technologies and Applications of Artificial Intelligence, Kaohsiung City, Taiwan, 21–23 November 2019; pp. 1–6. [Google Scholar]
- Ning, J.; Zhao, Q.; Sun, P.; Feng, Y. A multi-objective decomposition-based ant colony optimisation algorithm with negative pheromone. J. Exp. Theor. Artif. Intell. 2020, in press. [Google Scholar] [CrossRef]
- Nurcahyadi, T.; Blum, C. A New Approach for Making Use of Negative Learning in Ant Colony Optimization. In Proceedings of the ANTS 2020–12th International Conference on Swarm Intelligence, Barcelona, Spain, 26–28 October 2020; Lecture Notes in Computer Science. Dorigo, M., Stützle, T., Blesa, M.J., Blum, C., Hamann, H., Heinrich, M.K., Strobel, V., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 12421, pp. 16–28. [Google Scholar]
- Garey, M.R.; Johnson, D.S. Computers and Intractability; Freeman: San Francisco, CA, USA, 1979; Volume 174. [Google Scholar]
- Fréville, A. The multidimensional 0–1 knapsack problem: An overview. Eur. J. Oper. Res. 2004, 155, 1–21. [Google Scholar] [CrossRef]
- Li, R.; Hu, S.; Liu, H.; Li, R.; Ouyang, D.; Yin, M. Multi-Start Local Search Algorithm for the Minimum Connected Dominating Set Problems. Mathematics 2019, 7, 1173. [Google Scholar] [CrossRef]
- Yuan, F.; Li, C.; Gao, X.; Yin, M.; Wang, Y. A novel hybrid algorithm for minimum total dominating set problem. Mathematics 2019, 7, 222. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, J.; Liu, Y.; Lv, S.; Lai, Y.; Wang, J. Improved Memetic Algorithm for Solving the Minimum Weight Vertex Independent Dominating Set. Mathematics 2020, 8, 1155. [Google Scholar] [CrossRef]
- Cai, S.; Hou, W.; Wang, Y.; Luo, C.; Lin, Q. Two-goal Local Search and Inference Rules for Minimum Dominating Set. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, IJCAI-20, Yokohama, Japan, 11–17 July 2020; pp. 1467–1473. [Google Scholar] [CrossRef]
- Chu, P.C.; Beasley, J.E. A genetic algorithm for the multidimensional knapsack problem. Discret. Appl. Math. 1994, 49, 189–212. [Google Scholar]
- Wang, L.; Wang, S.Y.; Xu, Y. An effective hybrid EDA-based algorithm for solving multidiemnsional knapsack problems. Expert Syst. Appl. 2012, 39, 5593. [Google Scholar] [CrossRef]
- Kong, X.; Gao, L.; Ouyang, H.; Li, S. Solving large-scale multidimensional knapsack problems with a new binary harmony search algorithm. Comput. Oper. Res. 2015, 63, 7–22. [Google Scholar] [CrossRef]
- Vimont, Y.; Boussier, S.; Vasquez, M. Reduced costs propagation in an efficient implicit enumeration for the 01 multidimensional knapsack problem. J. Comb. Optim. 2008, 15, 165–178. [Google Scholar] [CrossRef]
- Boussier, S.; Vasquez, M.; Vimont, Y.; Hanafi, S.; Michelon, P. A multi-level search strategy for the 0–1 multidimensional knapsack problem. Discret. Appl. Math. 2010, 158, 97–109. [Google Scholar] [CrossRef]
- Mansini, R.; Speranza, M.G. Coral: An exact algorithm for the multidimensional knapsack problem. INFORMS J. Comput. 2012, 24, 399–415. [Google Scholar] [CrossRef]
- Lai, X.; Hao, J.K.; Fu, Z.H.; Yue, D. Diversity-preserving quantum particle swarm optimization for the multidimensional knapsack problem. Expert Syst. Appl. 2020, 149, 113310. [Google Scholar] [CrossRef]
- Lai, X.; Hao, J.K.; Glover, F.; Lü, Z. A two-phase tabu-evolutionary algorithm for the 0–1 multidimensional knapsack problem. Inf. Sci. 2018, 436, 282–301. [Google Scholar] [CrossRef]
- Blum, C.; Dorigo, M. The hyper-cube framework for ant colony optimization. IEEE Trans. Syst. Man Cybern. Part B 2004, 34, 1161–1172. [Google Scholar] [CrossRef]
- López-Ibánez, M.; Dubois-Lacoste, J.; Cáceres, L.P.; Birattari, M.; Stützle, T. The irace package: Iterated racing for automatic algorithm configuration. Oper. Res. Perspect. 2016, 3, 43–58. [Google Scholar] [CrossRef]
- Calvo, B.; Santafé, G. scmamp: Statistical Comparison of Multiple Algorithms in Multiple Problems. R J. 2016, 8, 248–256. [Google Scholar] [CrossRef]
- García, S.; Herrera, F. An Extension on “Statistical Comparisons of Classifiers over Multiple Data Sets” for all Pairwise Comparisons. J. Mach. Learn. Res. 2008, 9, 2677–2694. [Google Scholar]
- Chalupa, D. An order-based algorithm for minimum dominating set with application in graph mining. Inf. Sci. 2018, 426, 101–116. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, S.; Yin, M. Local search for minimum weight dominating set with two-level configuration checking and frequency based scoring function. J. Artif. Intell. Res. 2017, 58, 267–295. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, S.; Chen, J.; Yin, M. A Fast Local Search Algorithm for Minimum Weight Dominating Set Problem on Massive Graphs. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, IJCAI-18, Stockholm, Sweden, 13–19 July 2018; pp. 1514–1522. [Google Scholar]
- Fan, Y.; Lai, Y.; Li, C.; Li, N.; Ma, Z.; Zhou, J.; Latecki, L.J.; Su, K. Efficient local search for minimum dominating sets in large graphs. In Proceedings of the International Conference on Database Systems for Advanced Applications, Chiang Mai, Thailand, 22–25 April 2019; Springer: Berlin, Germany, 2019; pp. 211–228. [Google Scholar]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).