Double Roman Graphs in P(3k, k)

Abstract

A double Roman dominating function on a graph $G=(V,E)$ is a function $f:V\to \{0,1,2,3\}$ with the properties that if $f\left(u\right)=0$, then vertex u is adjacent to at least one vertex assigned 3 or at least two vertices assigned 2, and if $f\left(u\right)=1$, then vertex u is adjacent to at least one vertex assigned 2 or 3. The weight of f equals $w\left(f\right)={\sum }_{v\in V}f\left(v\right)$. The double Roman domination number ${\gamma }_{dR}\left(G\right)$ of a graph G is the minimum weight of a double Roman dominating function of G. A graph is said to be double Roman if ${\gamma }_{dR}\left(G\right)=3\gamma \left(G\right)$, where $\gamma \left(G\right)$ is the domination number of G. We obtain the sharp lower bound of the double Roman domination number of generalized Petersen graphs $P(3k,k)$, and we construct solutions providing the upper bounds, which gives exact values of the double Roman domination number for all generalized Petersen graphs $P(3k,k)$. This implies that $P(3k,k)$ is a double Roman graph if and only if either $k\equiv 0$ (mod 3) or $k\in \{1,4\}$.

1. Introduction

Let $G=(V,E)$ be a graph without loops and multiple edges, where $V=V\left(G\right)$ and $E=E\left(G\right)$ are the vertex set and edge set of G, respectively. If $uv\in E$, we say that vertices u and v are adjacent, and v is a neighbor of u. The neighborhood of u, $N\left(u\right)$ is the set of all neighbors of u, so $v\in N\left(u\right)$, and $u\in N\left(v\right)$. The set of consecutive integers between a and b with $a<b$ is denoted by $[a,b]=\{a,a+1,\cdots ,b\}$ and $[0,b-1]=\{0,1,\cdots ,b-1\}$ is abbreviated to $\left[b\right]$ for short. For convenience, we write $i=q^{+}$ when $i\ge q$ and, similarly, $i=q^{-}$ when $i\le q$.

A set D of vertices of G is a dominating set if every vertex in $V\setminus D$ has at least one neighbor in D. The domination number $\gamma \left(G\right)$ is the cardinality of a minimum dominating set of G. A double Roman dominating function (DRDF) on a graph $G=(V,E)$ is a function $f:V\to \{0,1,2,3\}$ with the properties that

• $f\left(u\right)=0$, then vertex u is adjacent to at least one vertex assigned 3 or at least two vertices assigned 2 under f;
• if $f\left(u\right)=1$, then vertex u is adjacent to at least one vertex assigned 2 or 3 under f.

In other words, if vertices represent provinces of Roman empire and DRDF represents roman legions, any province either must have a legion that protects it, or, it has to have at least two available legions in the neighborhood that may intervene without leaving the domestic province unprotected. The weight of f equals $w\left(f\right)={\sum }_{v\in V}f\left(v\right)$. The double Roman domination number ${\gamma }_{dR}\left(G\right)$ of a graph G is the minimum weight of a double Roman dominating function of G. A DRDF f is a ${\gamma }_{dR}$-function of G if $w\left(f\right)={\gamma }_{dR}\left(G\right)$. Given a double Roman dominating function f, we obtain a partition of the vertex set $V=V_0\cup V_1\cup V_2\cup V_3$, where $V_i=V_i^f=\left\{u\right|f\left(u\right)=i\}$. A vertex u is DR-dominated if it is either in $V_2\cup V_3$ or if $u\in V_1$ and it has a neighbor in $V_2\cup V_3$ or if $u\in V_0$ and u has at least one neighbor in $V_3$ or two neighbors in $V_2$. On the other hand, any partition $V=V_0\cup V_1\cup V_2\cup V_3$ in which every vertex is DR-dominated obviously gives rise to a double Roman dominating function.

Domination in graphs with its many varieties has been studied extensively in the past [1,2]. Roman domination and double Roman domination is a rather new variety of interest [3,4,5,6,7,8,9,10,11]. Very recently, double Roman domination for cardinal products of graphs was studied in [12], and double Roman trees were characterized in [13]. Cartesian products of certain circles are shown to be double Roman in [14]. It is known that the decision problem associated with ${\gamma }_{dR}\left(G\right)$ is NP-complete for bipartite and chordal graphs, undirected path graphs, chordal bipartite graphs, and circle graphs [15,16,17]. Closely related problems to double Roman domination were studied in [18,19,20].

In this work we will study DRDF on generalized Petersen graphs P(3k, k). More precisely, we will give exact values of the double Roman domination number for all generalized Petersen graphs P(3k, k).

Petersen graphs are among the most interesting examples when considering nontrivial graph invariants. The domination and its variations of generalized Petersen graphs have attracted considerable attention, see for example [21,22,23,24,25,26,27,28]. Let n and k be integers where $n\ge 3$, $k\ge 1$, and $k<\frac{n}{2}$. The generalized Petersen graph $P(n,k)$ is a graph with vertex set $U\cup I$ and edge set $E_1\cup E_2\cup E_3$, where $U=\{u_0,u_1,\cdots ,u_{n-1}\}$, $I=\{v_0,v_1,\cdots ,v_{n-1}\}$, $E_1=\left\{u_i{u}_{i+1}\right|i\in \left[n\right]\}$, $E_2=\left\{u_i{v}_i\right|i\in \left[n\right]\}$, $E_3=\left\{v_i{v}_{i+k}\right|i\in \left[n\right]\}$, and subscripts are reduced modulo n. If $n=3k$, we define $T_i=\{u_i,v_i,u_{i+k}$, $v_{i+k}$, $u_{i+2k}$, $v_{i+2k}\}$, for any integer i. Recalling that the subscripts are taken modulo n, it is clear that $T_{i+k}=T_i$; hence, the Petersen graph $P(3k,k)$ has exactly k distinct $T_i$, $i\in \left[k\right]$.

The rest of the paper is organized as follows. In the next section, we mention related previous work, give some more formal definitions, and we formally state our main result. The following sections provide the proof of Theorem 2. In Section 3, the upper bound and the small cases are elaborated. Section 4 is devoted to the proof of the lower bound. Concluding remarks are given in the last section.

2. Preliminaries and Main Result

Beeler et al. [4] initiated the study of the double Roman domination in graphs. They showed that $2\gamma \left(G\right)\le {\gamma }_{dR}\left(G\right)\le 3\gamma \left(G\right)$ and defined a graph G to be double Roman if ${\gamma }_{dR}\left(G\right)=3\gamma \left(G\right)$, where $\gamma \left(G\right)$ is the domination number of G. Among other things, Beeler et al. obtained the following result that we recall for a later reference:

Proposition 1

([4]). In a double Roman dominating function f of weight ${\gamma }_{dR}\left(G\right)$, no vertex needs to be assigned the value 1.

Zhao et al. [29] studied the domination number for the generalized Petersen graphs $P(ck,k)$ for integer constants $c\ge 3$. They obtained upper bound on $\gamma \left(P\right(ck,k\left)\right)$ for general c, and showed that

Theorem 1

([29]). $\gamma \left(P(3k,k)\right)=\lceil \frac{5k}{3}\rceil$ for any $k\ge 1$.

Note that by Proposition 1, we can restrict attention to the DRDF of a graph G with no vertex assigned the value 1. Furthermore, it is easy to see that DRDF of a given graph is not unique. For example, $P(3,1)$ has DRDF’s with value 3 on two vertices and DRDF’s with value 2 on three vertices. Here we will, without loss of generality, consider ${\gamma }_{dR}$-functions with minimal $|V_2|$. In Figure 1, a DRDF of $P(9,3)$ is given that has minimal number of vertices in $V_2$, in fact $|V_2|=0$. On the left (a), the usual drawing is given, while on the right (b), we introduce another way of drawing $P(3k,k)$ that will be used in the sequel. The vertices are organized according to the triangles, $T_i$. Vertices of triangle $T_0$ and its neighbors, $\{u_0,u_k,u_{2k},u_0,v_k,v_{2k}\}$, are indicated in Figure 1b.

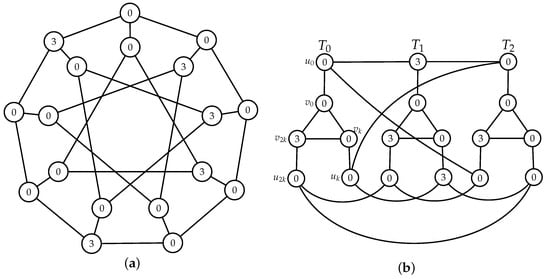
Figure 1. A double Roman dominating function (DRDF) of $P(9,3)$. Standard drawing (a) and alternative drawing used in this work (b).

In this paper, we provide the double Roman domination numbers of all Petersen graphs $P(3k,k)$ and characterize the double Roman graphs among them.

Below we prove Propositions 2 and 3 which imply our main result

Theorem 2.

$${\gamma }_{dR}\left(P(3k,k)\right)=\left\{\begin{array}{cc}5k+1,\hfill & \mathit{if}k\in \{1,2,4\},\hfill \\ 5k,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

and its corollary (using Theorem 1):

Corollary 1.

The generalized Petersen graph $P(3k,k)$ is a double Roman graph if and only if either $k\equiv 0$ (mod 3) or $k\in \{1,4\}$.

In the next section we recall the exact values of ${\gamma }_{dR}\left(P(3k,k)\right)$ for $k=1,2,3,4,5$ (Lemma 1) and give a sharp upper bound for the general case (Proposition 2). In Section 4 we provide a sharp lower bound (Proposition 3). Lemma 1, Proposition 2, and Proposition 3 together clearly imply Theorem 2.

3. The Upper Bound

In this section, we construct double Roman dominating functions establishing upper bounds for the double Roman dominating numbers. In fact, by Theorem 2 it turns out that these DRDFs are optimal.

First, let us consider $P(3k,k)$ for $k\le 5$. It is straightforward to check that the DRDF in Figure 1 and Figure 2 are optimal. We omit the details. For later reference, we state the observation as

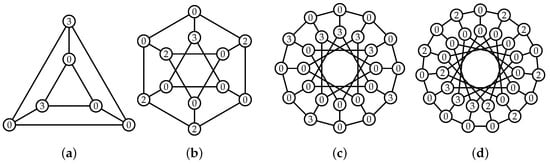
Figure 2. (a) A DRDF of $P(3,1)$; (b) A DRDF of $P(6,2)$; (c) A DRDF of $P(12,4)$; (d) A DRDF of $P(15,5)$.

Lemma 1.

${\gamma }_{dR}\left(P(3,1)\right)=6$, ${\gamma }_{dR}\left(P(6,2)\right)=11$, ${\gamma }_{dR}\left(P(9,3)\right)=15$, ${\gamma }_{dR}\left(P(12,4)\right)=21$, and ${\gamma }_{dR}\left(P(15,5)\right)=25$.

In general, the upper bounds are given by

Proposition 2.

For any integer $k>4$ it holds     ${\gamma }_{dR}\left(P(3k,k)\right)\le \left\{\begin{array}{cc}5k+1,\hfill & \mathit{if}k\in \{1,2,4\},\hfill \\ 5k,\hfill & \mathit{otherwise}\hfill \end{array}\right.$.

Proof. 

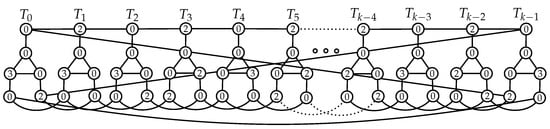
By Lemma 1, the statement holds for $k\le 5$. For $k>5$ we provide different constructions depending on $kmod6$. We use a pattern with 6 rows and k columns to represent a DRDF as follows.

$$\begin{array}{ccc}\hfill f\left(V\right(P(3k,k)\left)\right)& =& \left(\begin{array}{cccccc}f\left(u_0\right)\hfill & f\left(u_1\right)\hfill & \cdots \hfill & f\left(u_i\right)\hfill & \cdots \hfill & f\left(u_{k-1}\right)\hfill \\ f\left(v_0\right)\hfill & f\left(v_1\right)\hfill & \cdots \hfill & f\left(v_i\right)\hfill & \cdots \hfill & f\left(v_{k-1}\right)\hfill \\ f\left(v_{2k}\right)\hfill & f\left(v_{2k+1}\right)\hfill & \cdots \hfill & f\left(v_{2k+i}\right)\hfill & \cdots \hfill & f\left(v_{3k-1}\right)\hfill \\ f\left(v_k\right)\hfill & f\left(v_{k+1}\right)\hfill & \cdots \hfill & f\left(v_{k+i}\right)\hfill & \cdots \hfill & f\left(v_{2k-1}\right)\hfill \\ f\left(u_{2k}\right)\hfill & f\left(u_{2k+1}\right)\hfill & \cdots \hfill & f\left(u_{2k+i}\right)\hfill & \cdots \hfill & f\left(u_{3k-1}\right)\hfill \\ f\left(u_k\right)\hfill & f\left(u_{k+1}\right)\hfill & \cdots \hfill & f\left(u_{k+i}\right)\hfill & \cdots \hfill & f\left(u_{2k-1}\right)\hfill \end{array}\right)\hfill \end{array}$$

All the constructions below have a part with a repeated pattern and a fixed part at the end. The symbol “−” means that we repeat the leftmost six (or, in one case three) columns of the corresponding pattern $\ell -1$ times. Hence, we have ℓ repetitions of the pattern plus the rightmost part.

For $k=6\ell +4$ with $\ell \ge 1$, let

$$f\left(V\left(P(3k,k)\right)\right)=\left(\begin{array}{ccccccccccc}& 0\hfill & 2\hfill & 0\hfill & 2\hfill & 0\hfill & 2\hfill & 2\hfill & 0\hfill & 2\hfill & 0\hfill \\ & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ -\hfill & 3\hfill & 3\hfill & 3\hfill & 0\hfill & 0\hfill & 0\hfill & 2\hfill & 3\hfill & 2\hfill & 0\hfill \\ & 0\hfill & 0\hfill & 0\hfill & 2\hfill & 3\hfill & 2\hfill & 0\hfill & 0\hfill & 0\hfill & 3\hfill \\ & 0\hfill & 0\hfill & 0\hfill & 2\hfill & 0\hfill & 2\hfill & 0\hfill & 0\hfill & 0\hfill & 2\hfill \\ & 2\hfill & 0\hfill & 2\hfill & 0\hfill & 0\hfill & 0\hfill & 2\hfill & 0\hfill & 2\hfill & 0\hfill \end{array}\right).$$

It is straightforward to see that f is a DRDF of $P(3k,k)$ (see Figure 3).

Figure 3. A DRDF of $P(3k,k)$ with $k=6\ell +4$

For $k=3\ell$ with $\ell \ge 1$, let

$$f\left(V\left(P(3k,k)\right)\right)=\left(-\left|\begin{array}{ccc}0\hfill & 3\hfill & 0\hfill \\ 3\hfill & 0\hfill & 3\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 3\hfill & 0\hfill \\ 0\hfill & 3\hfill & 0\hfill \end{array}\right|\right).$$

Then f is a DRDF of $P(3k,k)$.

For $k=6\ell +1$ with $\ell \ge 1$, let

$$f\left(V\left(P(3k,k)\right)\right)=\left(\begin{array}{cccccccc}& 0\hfill & 2\hfill & 0\hfill & 2\hfill & 0\hfill & 2\hfill & 0\hfill \\ & 3\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ -\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 3\hfill \\ & 0\hfill & 2\hfill & 3\hfill & 3\hfill & 3\hfill & 2\hfill & 0\hfill \\ & 0\hfill & 2\hfill & 0\hfill & 2\hfill & 0\hfill & 2\hfill & 0\hfill \\ & 2\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 2\hfill \end{array}\right).$$

Then f is a DRDF of $P(3k,k)$.

For $k=6\ell +2$ with $\ell \ge 1$, let

$$f\left(V\left(P(3k,k)\right)\right)=\left(\begin{array}{ccccccccc}& 0\hfill & 0\hfill & 0\hfill & 2\hfill & 0\hfill & 2\hfill & 0\hfill & 0\hfill \\ & 2\hfill & 3\hfill & 2\hfill & 0\hfill & 0\hfill & 0\hfill & 3\hfill & 3\hfill \\ -\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ & 0\hfill & 0\hfill & 0\hfill & 2\hfill & 3\hfill & 2\hfill & 0\hfill & 0\hfill \\ & 2\hfill & 0\hfill & 2\hfill & 2\hfill & 0\hfill & 2\hfill & 0\hfill & 2\hfill \\ & 2\hfill & 0\hfill & 2\hfill & 0\hfill & 0\hfill & 0\hfill & 2\hfill & 0\hfill \end{array}\right).$$

Then f is a DRDF of $P(3k,k)$.

For $k=6\ell +5$ with $\ell \ge 1$, let

$$f\left(V\left(P(3k,k)\right)\right)=\left(\begin{array}{cccccccccccc}& 2\hfill & 0\hfill & 2\hfill & 2\hfill & 0\hfill & 2\hfill & 0\hfill & 0\hfill & 2\hfill & 0\hfill & 2\hfill \\ & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 3\hfill & 3\hfill & 0\hfill & 0\hfill & 0\hfill \\ -\hfill & 0\hfill & 0\hfill & 0\hfill & 2\hfill & 3\hfill & 2\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ & 2\hfill & 3\hfill & 2\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 2\hfill & 3\hfill & 2\hfill \\ & 2\hfill & 0\hfill & 2\hfill & 0\hfill & 0\hfill & 0\hfill & 2\hfill & 0\hfill & 2\hfill & 0\hfill & 2\hfill \\ & 0\hfill & 0\hfill & 0\hfill & 2\hfill & 0\hfill & 2\hfill & 0\hfill & 2\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right).$$

Then f is a DRDF of $P(3k,k)$.    □

4. The Lower Bound

Proposition 3.

For any integer $k>4$ it holds     ${\gamma }_{dR}\left(P(3k,k)\right)\ge \left\{\begin{array}{cc}5k+1,\hfill & \mathit{if}k\in \{1,2,4\},\hfill \\ 5k,\hfill & \mathit{otherwise}\hfill \end{array}\right.$.

We start by some definitions that are used in the proof of the lower bound and in formulation of the results. Recall that we can restrict our attention to the ${\gamma }_{dR}$-functions with no vertex assigned the value 1, and in addition, consider only ${\gamma }_{dR}$-functions with minimal $|V_2|$.

For a DRDF f, let $w_i={\sum }_{x\in T_i}f\left(x\right)$ and $s_{\left(i\right)}=w_{i-1}+w_i+w_{i+1}$. Clearly, $w_{i+k}=w_i$ and $s_{(i+k)}=s_{\left(i\right)}$ as $T_{i+k}=T_i$. In other words, for the Petersen graph $P(3k,k)$ we have $\left|U\right|=\left|I\right|=3k$ and subscripts of vertices $u_i$ and $v_i$ are taken modulo $3k$, but there are exactly k distinct $T_i$, and therefore subscripts of $T_i$, $w_i$ and $s_{\left(i\right)}$ are taken modulo k. Note also that we have $w\left(f\right)={\sum }_{i=0}^{k-1}{w}_i$ and $3w\left(f\right)={\sum }_{i=0}^{k-1}{s}_{\left(i\right)}$.

As proof that the lower bound is long, we divide the section in several subsections. First, we provide algorithms that for $k^{\prime }\le k$ construct a $P(3k^{\prime },k^{\prime })$ from $P(3k,k)$. In the second subsection, some more definitions and facts are given. Third, fourth, and fifth subsections provide analyses of three special cases. Finally, the proof of Proposition 3 is given.

4.1. Constructions of $P(3k^{\prime },K^{\prime })$ from $P(3k,K)$ for $K^{\prime }\le K$

In this subsection, we describe Algorithms 1–3 that construct $P(3k^{\prime },k^{\prime })$ from $P(3k,k)$ for $k^{\prime }\le k$.

Algorithm 1: (Algorithm A).

Input: the graph $P(3k,k)$, $k\ge 3$, integers $j\in \left[k\right]$ and $t\in [1,k-2]$. Output: the graph $P^{\prime }$. Step 1: remove the set of vertices $T_j$, $T_{j+1}$, $\cdots ,T_{j+t-1}$ along with their incident edges, and denote the resulting graph by Q; Step 2: define the edge set $E^{\prime }=\{u_{j-1}{u}_{j+t}$, $u_{j-1+2k}{u}_{j+t+2k}$, $u_{j-1+k}{u}_{j+t+k}\}$ and define the graph $P^{\prime }$ to have the vertex set $V\left(P^{\prime }\right)=V\left(Q\right)$ and the edge set $E\left(P^{\prime }\right)=E\left(Q\right)\cup E^{\prime }$. return$P^{\prime }$

The following lemma is immediate (see Figure 4), and the proof is omitted.

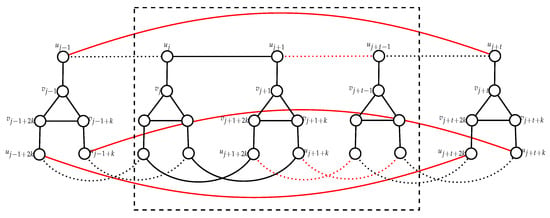
Figure 4. Illustrating Algorithm A for constructing $P^{\prime }$ from $P(3k,k)$.

Lemma 2.

The graph $P^{\prime }$ returned by Algorithm A is isomorphic to $P(3k-3t,k-t)$.

Algorithm 2: (Algorithm B).

Input: the graph $P(3k,k)$, $k\ge 3$, integers $j\in \left[k\right]$ and $t\in [k-1]$. Output: the graph $P^{\prime }$. Step 1: if $t>0$, remove the set of vertices $T_j$, $T_{j+1}$, $\cdots ,T_{j+t-1}$ along with their incident edges, and denote the resulting graph by Q; if $t=0$, remove the set of edges between $T_{j-1}$ and $T_j$ and let Q be a graf $V\left(Q\right)=V\left(P\right(3k,k\left)\right)$ and $E\left(Q\right)=E\left(P(3k,k)\right)\setminus \{u_{j-1}{u}_j$, $u_{j-1+k}{u}_{j+k}$, $u_{j-1+2k}{u}_{j+2k}\}$; Step 2: define the edge set $E^{\prime }=\{u_{j-1}{u}_{j+t+k}$, $u_{j+t}{u}_{j-1+2k}$, $u_{j-1+k}{u}_{j+t+2k}\}$ and define the graph $P^{\prime }$ to have the vertex set $V\left(P^{\prime }\right)=V\left(Q\right)$ and the edge set $E\left(P^{\prime }\right)=E\left(Q\right)\cup E^{\prime }$. return$P^{\prime }$

Lemma 3.

The graph $P^{\prime }$ returned by Algorithm B is isomorphic to $P(3k-3t,k-t)$.

Proof. 

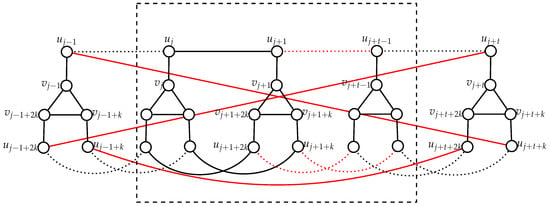
Consider the cycle $C^{\prime }=u_0{u}_1\cdots u_{j-1}$ $u_{j+t+k}$ $u_{j+t+k+1}$ $\cdots u_{k-1+k}$ $u_{2k}$ $u_{2k+1}\cdots$ $\cdots u_{j-1+2k}$ $u_{j+t}{u}_{j+t+1}\cdots$ $u_{k-1}$ $u_k$ $u_{k+1}\cdots$ $u_{j-1+k}{u}_{j+t+2k}$ $u_{j+t+2k+1}\cdots$ $u_{k-1+2k}{u}_0$ (see Figure 5). Now we relabel the vertices of $C^{\prime }$ as $C^{\prime }=u_{s_0}{u}_{s_1}\cdots u_{s_{3k-3t-1}}$ and consider a function $h:V\left(P^{\prime }\right)\to V\left(P(3k-3t,k-t)\right)$ with $h\left(u_{s_i}\right)=u_i$ and $h\left(v_{s_i}\right)=v_i$ for each $i\in [3k-3t]$. It can be verified that h is an isomorphism from $P^{\prime }$ to $P(3k-3t,k-t)$ and the proof is complete.    □

Figure 5. Illustrating Algorithm B for constructing $P^{\prime }$ from $P(3k,k)$.

Algorithm 3:(Algorithm C).

Input: the graph $P(3k,k)$, $k\ge 3$, integers $j_1,j_2\in \left[k\right]$ and $t_1+t_2\in [k-2]$, where: for $t_1=0$, $T_{j_1}\notin \{T_{j_2},T_{j_2+1},\dots ,T_{j_2+t_2}\}$, for $t_2=0$, $T_{j_2}\notin \{T_{j_1},T_{j_1+1},\dots ,T_{j_1+t_1}\}$, and for $t_1,t_2>0$, $\{T_{j_1-1},T_{j_1},\dots ,T_{j_1+t_1}\}\cap \{T_{j_2},T_{j_2+1},\dots ,T_{j_2+t_2-1}\}=\varnothing$ and $\{T_{j_1},T_{j_1+1},$$\dots ,$$T_{j_1+t_1-1}\}\cap \{T_{j_2-1},T_{j_2},\dots ,T_{j_2+t_2}\}=\varnothing$. Output: the graph $P^{\prime \prime }$. Step 1: let $i\in \{1,2\}$: for $t_i>0$, remove the set of vertices $T_{j_i}$, $T_{j_i+1}$, $\cdots ,T_{j_i+t_i-1}$ along with their incident edges, for $t_i=0$, remove the set of edges between $T_{j_i-1}$ and $T_{j_i}$, and denote the resulting graph by Q; Step 2: define the edge set $E^{\prime \prime }=\{u_{j_1-1}{u}_{j_1+t_1+k}$, $u_{j_1-1+k}{u}_{j_1+t_1+2k}$, $u_{j_1-1+2k}{u}_{j_1+t_1},u_{j_2-1}{u}_{j_2+t_2+2k}$, $u_{j_2-1+k}{u}_{j_2+t_2}$, $u_{j_2-1+2k}{u}_{j_2+t_2+k},\}$ and define the graph $P^{\prime \prime }$ to have the vertex set $V\left(P^{\prime \prime }\right)=V\left(Q\right)$ and the edge set $E\left(P^{\prime \prime }\right)=E\left(Q\right)\cup E^{\prime \prime }$. return $P^{\prime \prime }$

Lemma 4.

The graph $P^{\prime \prime }$ returned by Algorithm C is isomorphic to $P(3k-3t_1-3t_2,k-t_1-t_2)$.

Proof. 

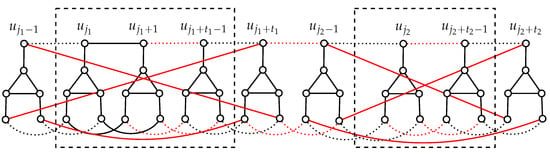
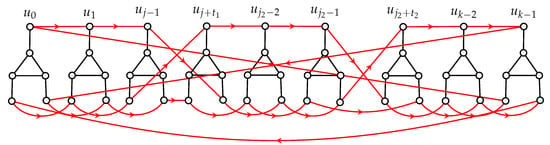
Result of Algorithm C is illustrated on Figure 6. Consider a cycle $C^{\prime }=u_0{u}_1\cdots u_{j-1}$ $u_{j+t_1+k}$ $\cdots u_{j_2-2+k}$ $u_{j_2-1+k}{u}_{j_2+t_2}$ $\cdots u_{k-2}$ $u_{k-1}$ $u_k{u}_{k+1}$ $\cdots u_{j-1+k}$ $u_{j+t_1+2k}$ $\cdots u_{j_2-2+2k}$$u_{j_2-1+2k}\cdots$ $u_{j_2+t_2+k}\cdots$ $u_{k-2+k}$ $u_{k-1+k}{u}_{2k}$ $u_{2k+1}\cdots u_{j-1+2k}$ $u_{j+t_1}\cdots$ $u_{j_2-2}{u}_{j_2-1}$ $u_{j_2+t_2+2k}\cdots$ $u_{k-2+2k}$ $u_{k-1+2k}{u}_0$ (see Figure 7 with red arrow lines). Now we relabel the vertices of $C^{\prime }$ as $C^{\prime }=u_{s_0}{u}_{s_1}\cdots u_{s_{3k-3t_1-3t_2-1}}$ and consider a function $h:V\left(P^{\prime \prime }\right)\to V\left(P(3k-3t_1-3t_2,k-t_1-t_2)\right)$ with $h\left(u_{s_i}\right)=u_i$ and $h\left(v_{s_i}\right)=v_i$ for each $i\in [3k-3t_1-3t_2]$. It can be verified that h is an isomorphism from $P^{\prime \prime }$ to $P(3k-3t_1-3t_2,k-t_1-t_2)$, and the proof is complete. □

Figure 6. Illustrating Algorithm C for constructing $P^{\prime \prime }$ from $P(3k,k)$.

Figure 7. A cycle containning all vertices of U in $P^{\prime \prime }$.

4.2. Useful Lemmas and Definitions

Lemma 5.

Let $k\ge 3$ and let f be ${\gamma }_{dR}$-function of $P(3k,k)$. Then $3\le w_i\le 9$ for each $i\in \left[k\right]$, and if $\left|V_2^f\right|$ is minimal then $w_i\ne 4$ for each $i\in \left[k\right]$.

Proof. 

Since vertices of $T_i\cap I$ can only be DR-dominated by vertices of $T_i$, we have $w_i\ge 3$. Assume that $w_i\ge 10$ for some $i\in \left[k\right]$. Then let $f^{\prime }\left(u_i\right)=f^{\prime }\left(u_{i+k}\right)=f^{\prime }\left(u_{i+2k}\right)=3$, $f^{\prime }\left(v_i\right)=f^{\prime }\left(v_{i+k}\right)=f^{\prime }\left(v_{i+2k}\right)=0$ and $f^{\prime }\left(x\right)=f\left(x\right)$ for $x\in V\left(P(3k,k)\right)\setminus T_i$. Clearly, $f^{\prime }$ is a DRDF with $w\left(f^{\prime }\right)<w\left(f\right)$; hence, f is not ${\gamma }_{dR}$-function, a contradiction. It follows that $w_i\le 9$ for each $i\in \left[k\right]$.

Let suppose now that $\left|V_2^f\right|$ is minimal and $w_i=4$ for some $i\in \left[k\right]$. Then we must have $|T_i\cap V_2\cap I|=2$, and by symmetry, we may assume $f\left(v_i\right)=f\left(v_{i+k}\right)=2$ and $f\left(x\right)=0$ for every $x\in T_i\setminus \{v_i,v_{i+k}\}$. To DR-dominate $u_i$, we must have $f\left(y\right)=2^{+}$ for some $y\in N\left(u_i\right)\setminus \left\{v_i\right\}$. Then we can construct a function $f^{\prime }$ with $f^{\prime }\left(y\right)=f^{\prime }\left(v_{i+k}\right)=3$, $f^{\prime }\left(v_i\right)=0$ and $f^{\prime }\left(x\right)=f\left(x\right)$ for each $x\in V\left(P(3k,k)\right)\setminus \{y,v_i,v_{i+k}\}$. Thus, we have $w\left(f^{\prime }\right)\le w\left(f\right)$ and $|V_2^{f^{\prime }}|<|V_2^f|$, contradicting with the assumption that $|V_2^f|$ is minimum. □

Lemma 6.

Let $k\ge 3$ and let f be a ${\gamma }_{dR}$-function of $P(3k,k)$, such that $\left|V_2^f\right|$ is minimal. If $w_i=8$ for some $i\in \left[k\right]$, then $|T_i\cap V_2|=1$.

Proof. 

First we will show that there exists ${\gamma }_{dR}$-function f such that at least one vertex of $T_i\cap U$ is DR-dominated by vertices in $T_i$ for each $i\in \left[k\right]$. Clearly, if $f\left(x\right)=2^{+}$ for some $x\in T_i\cap U$, or if $f\left(y\right)=3$ for some $y\in T_i\cap I$, the statement is true. By Lemma 5, we have $w_i\ne 4$; therefore, it remains to consider the case $f\left(u_i\right)=f\left(u_{i+k}\right)=f\left(u_{i+2k}\right)=0$ and $f\left(v_i\right)=f\left(v_{i+k}\right)=f\left(v_{i+2k}\right)=2$. We can construct a function $f^{\prime }$ with $f^{\prime }\left(u_i\right)=2$, $f^{\prime }\left(v_i\right)=0$ and $f^{\prime }\left(y\right)=f\left(y\right)$ for each $y\in V\left(P(3k,k)\right)\setminus \{u_i,v_i\}$. Then, $f^{\prime }$ is a DRDF with $w\left(f^{\prime }\right)=w\left(f\right)$, as desired. Note that $\left|V_2^{f^{\prime }}\right|=\left|V_2^f\right|$.

Let $k\ge 3$ and let f be ${\gamma }_{dR}$-function of $P(3k,k)$, such that $\left|V_2^f\right|$ is minimal. Assume that $w_i=8$ and $|T_i\cap V_2|\ne 1$ for some $i\in \left[k\right]$. Clearly, then we have $|T_i\cap V_2|=4$, and, without loss of generality, we may assume $f\left(u_i\right)=f\left(v_i\right)=2$. It is easy to see that if $f\left(v_{i+k}\right)=2$ or $f\left(v_{i+2k}\right)=2$ then f is not minimal because we can define another function with $f^{\prime }\left(v_i\right)=0$, $f^{\prime }\left(v_{i+k}\right)=3$ (or $f^{\prime }\left(v_{i+2k}\right)=3$, respectively), and $f^{\prime }\left(y\right)=f\left(y\right)$ elsewhere. It remains to consider the case where $f\left(u_i\right)=f\left(u_{i+k}\right)=f\left(u_{i+2k}\right)=f\left(v_i\right)=2$ and $f\left(v_{i+k}\right)=f\left(v_{i+2k}\right)=0$, i.e., $|T_i\cap U\cap V_2|=3$ and $|T_i\cap I\cap V_2|=1$. Note that in the case $|T_i\cap U\cap V_2|=3$ and $|T_i\cap I\cap V_2|=1$ an arbitrary vertex of the set $T_i\cap I$ can be assigned 2 under f.

Let x be the vertex of $T_{i-1}$ that is DR-dominated by vertices in $T_{i-1}$. Without loss of generality, we may assume $x=u_{i-1}$, and $f\left(u_i\right)=f\left(v_i\right)=2$. Clearly, if vertex $u_{i+1}$ is DR-dominated by vertices in $T_{i+1}$, then f is not minimal because we can define another function with $f^{\prime }\left(v_i\right)=3$, $f^{\prime }\left(u_i\right)=0$ and $f^{\prime }\left(y\right)=f\left(y\right)$ elsewhere. It follows that $f\left(u_{i+1}\right)=0$, and $f\left(y\right)=2$, where either $y=v_{i+1}$ or $y=u_{i+2}$. Now we consider DRDF $f^{\prime }$ with $f^{\prime }\left(u_i\right)=0$, $f^{\prime }\left(v_i\right)=3$, $f^{\prime }\left(y\right)=3$ and $f^{\prime }\left(s\right)=f\left(s\right)$ for $s\in V\left(P(3k,k)\right)\setminus \{u_i,v_i,y\}$. Thus, we have $w\left(f^{\prime }\right)=w\left(f\right)$ and $|V_2^{f^{\prime }}|<|V_2^f|$, contradicting with the assumption that $|V_2^f|$ is minimum. □

From now on we will assume that all DRDFs have minimal $|V_2|$. Furthermore, on the basis of the just-proven Lemmas, it is easy to see that we can restrict attention to ${\gamma }_{dR}$-functions f of $P(3k,k)$ with no neighboring vertices in $T_i$ that are assigned values 2 or more. Formally, for each $i\in \left[k\right]$ there are no vertices $x,y$ with $x,y\in T_i$, $xy\in E\left(P\right(3k,k\left)\right)$ such that both $f\left(x\right)=2^{+}$ and $f\left(y\right)=2^{+}$. It follows, that in each $T_i$ at most one of vertices $v_i$ is assigned $2^{+}$ by f. Clearly, the case $f\left(v_i\right)=f\left(v_{i+k}\right)=f\left(v_{i+2k}\right)=0$ is possible only in $T_i$ with $w_i=9$. On the other hand, if $w_i=9$ then we can assume that $f\left(v_i\right)=f\left(v_{i+k}\right)=f\left(v_{i+2k}\right)=0$ and $f\left(u_i\right)=f\left(u_{i+k}\right)=f\left(u_{i+2k}\right)=3$. Thus, in $T_i$ with $w_i\ne 9$ exactly one of vertices $v_i$ is assigned $2^{+}$ and two of them are assigned 0. More precisely, for each $T_i$ we have exactly nine possible DRDFs listed below (in the first row are values of vertices of $T_i\cap U$, in the second row are values of vertices of $T_i\cap I$, and each column represents adjacent vertices):

${\displaystyle w_i=3:\left(\begin{array}{ccc}0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 3\hfill \end{array}\right);}$${\displaystyle w_i=5:\left(\begin{array}{ccc}2\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 3\hfill \end{array}\right);}$

${\displaystyle w_i=6:\left(\begin{array}{ccc}3\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 3\hfill \end{array}\right)=:6^{\left(3\right)},\left(\begin{array}{ccc}2\hfill & 2\hfill & 0\hfill \\ 0\hfill & 0\hfill & 2\hfill \end{array}\right)=:6^{\left(2\right)};}$

${\displaystyle w_i=7:\left(\begin{array}{ccc}2\hfill & 2\hfill & 0\hfill \\ 0\hfill & 0\hfill & 3\hfill \end{array}\right)=:7^{\left(3\right)},\left(\begin{array}{ccc}2\hfill & 3\hfill & 0\hfill \\ 0\hfill & 0\hfill & 2\hfill \end{array}\right)=:7^{\left(2\right)};}$

${\displaystyle w_i=8:\left(\begin{array}{ccc}2\hfill & 3\hfill & 0\hfill \\ 0\hfill & 0\hfill & 3\hfill \end{array}\right)=:8^{\left(3\right)},\left(\begin{array}{ccc}3\hfill & 3\hfill & 0\hfill \\ 0\hfill & 0\hfill & 2\hfill \end{array}\right)=:8^{\left(2\right)};}$${\displaystyle w_i=9:\left(\begin{array}{ccc}3\hfill & 3\hfill & 3\hfill \\ 0\hfill & 0\hfill & 0\hfill \end{array}\right);}$

Lemma 7.

Let $k\ge 3$ and let f be a DRDF of $P(3k,k)$. Then for any $i\in \left[k\right]$ it holds:

(a) if $w_i=w_{i+1}=3$, then $w_{i+2}\in \{8^{\left(2\right)},9\}$;

(b) if $w_i=3$ and $w_{i+1}\in \{5,6^{\left(3\right)}\}$, then $w_{i+2}\in \{6^{\left(3\right)},7^{\left(2\right)},8^{+}\}$;

(c) if $w_i=3$ and $w_{i+1}\in \{6^{\left(2\right)},7^{\left(2\right)},8^{\left(2\right)}\}$, then $w_{i+2}=5^{+}$;

(d) if $w_i=5$ and $w_{i+1}=3$, then $w_{i+2}\in \{7^{\left(2\right)},8^{+}\}$;

(e) if $w_i=6^{\left(3\right)}$ and $w_{i+1}=3$, then $w_{i+2}\in \{6^{\left(3\right)},7^{\left(2\right)},8^{+}\}$;

(f) if $w_i\in \{6^{\left(2\right)},7^{\left(3\right)}\}$ and $w_{i+1}=3$, then $w_{i+2}\in \{6^{\left(2\right)},7^{+}\}$;

(g) if $w_i\in \{7^{\left(2\right)},8^{\left(3\right)}\}$ and $w_{i+1}=3$, then $w_{i+2}=5^{+}$;

(h) if $w_i=5$ and $w_{i+1}\in \{5,6^{\left(3\right)}\}$, then $w_{i+2}=5^{+}$;

(i) if $w_i\in \{6^{\left(2\right)},7^{\left(3\right)}\}$ and $w_{i+1}=5$, then $w_{i+2}=5^{+}$;

(j) if $w_i=w_{i+2}=3$, then $w_{i+1}\in \{7^{\left(3\right)},8^{\left(3\right)},9\}$.

Proof. 

Let f be a DRDF of $P(3k,k)$, $k\ge 3$, and $i\in \left[k\right]$.

Cases (a,b,c,j). If $w_i=3$, then vertices of $T_{i+1}\cap U$ are DR-dominated by vertices in $T_{i+1}\cup (T_{i+2}\cap U)$. In the case (a), exactly one vertex of $T_{i+1}\cap U$ is dominated by vertices in $T_{i+1}$, and two of them are dominated by two corresponding vertices of $T_{i+2}\cap U$ which are assigned 3 under f. It follows $|T_{i+2}\cap U\cap V_3^f|\ge 2$ and thus $w_{i+2}\in \{8^{\left(2\right)},9\}$. In the case (b), two vertices of $T_{i+1}\cap U$ are dominated by vertices in $T_{i+1}$, and one of them is dominated by the corresponding vertex of $T_{i+2}\cap U$, which is assigned 3 under f. Thus, $|T_{i+2}\cap U\cap V_3^f|\ge 1$, and the result follows. Similarly, in the case (c), one vertex of $T_{i+1}\cap U$ is dominated by the corresponding vertex of $T_{i+2}\cap U$, which is assigned $2^{+}$ and the result follows. In the case (j), all vertices of $T_{i+1}\cap U$ are DR-dominated by vertices in $T_{i+1}$, for which we have three possibilities, i.e., $w_{i+1}\in \{7^{\left(3\right)},8^{\left(3\right)},9\}$.

Cases (d,e,f,g). If $w_{i+1}=3$, then one vertex of $T_{i+1}\cap U$ is DR-dominated by a vertex in $T_{i+1}$, and two of them are dominated by the corresponding vertices of $(T_i\cup T_{i+2})\cap U$. Consider the values of vertices of $T_i\cap U$, and the result easily follows.

Cases (h,i). In these cases, observe that one vertex of $T_{i+1}\cap U$ is dominated by a vertex in $T_{i+2}$, which is assigned $2^{+}$ under f. Hence, $w_{i+2}=5^{+}$ as needed. □

Clearly, by symmetry Lemma 7 holds also in the other direction, i.e., for $w_i$, $w_{i-1}$ and $w_{i-2}$, respectively. For example statement (a) can be read as if $w_i=3$ and $w_{i-1}=3$, then $w_{i-2}\in \{8^{\left(2\right)},9\}$.

4.3. DRDF with $(W_I,W_{I+1},W_{I+2},W_{I+3},W_{I+4})=(5,7,3,5,6)$

In Lemmas from 8–11 we will consider DRDF f of $P(3k,k)$ with given sequence $(w_i,w_{i+1},w_{i+2},w_{i+3},w_{i+4})=(5,7,3,5,6)$ for some $i\in \left[k\right]$. Without loss of generality, we can set $i=0$, and in addition we may assume that $f\left(v_2\right)=3$ and $f\left(u_{1+k}\right)=3$. It is easy to see that f is defined as ${\displaystyle \left(\begin{array}{ccc}2\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 3\hfill \end{array}\right)\left(\begin{array}{ccc}0\hfill & 3\hfill & 2\hfill \\ 2\hfill & 0\hfill & 0\hfill \end{array}\right)\left(\begin{array}{ccc}0\hfill & 0\hfill & 0\hfill \\ 3\hfill & 0\hfill & 0\hfill \end{array}\right)\left(\begin{array}{ccc}0\hfill & 0\hfill & 2\hfill \\ b\hfill & a\hfill & 0\hfill \end{array}\right)\left(\begin{array}{ccc}a\hfill & b\hfill & 0\hfill \\ & \end{array}\right),}$ where $(a,b)\in \left\{\right(0,3),(3,0\left)\right\}$, and exactly one of the vertices of $T_4\cap I$ is assigned 3. Note that we can assume that $f\left(v_k\right)=0$ and $f\left(v_{2k}\right)=3$ because the vertex $u_k$ is DR-dominated by $u_{1+k}$. Furthermore, by Lemma 7 statement (h) we see $w_5=5^{+}$. In particular, the sequence $(5,7,3,5,6)$ gives rise to the sequence $(w_i,w_{i+1},w_{i+2},w_{i+3},w_{i+4},w_{i+5})=(5,7^{\left(2\right)},3,5,6^{\left(3\right)},5^{+})$.

In Lemmas 8–10 we suppose that $w\left(f\right)<5k$. Clearly, for $k=5$ and $k=6$ we have $w\left(f\right)>5k$; thus, observations consider the Petersen graphs with $k\ge 7$.

Let f be a DRDF of $P(3k,k)$. For integer j taken modulo k we denote $A_3=\left\{j\right|w_j=3\}$ and $A^{\prime }=\{j\in A_3|(w_{j-1},w_j,w_{j+1})\in \{(6,3,6),(5,3,7^{\left(2\right)}),(7^{\left(2\right)},3,5)\}\}$.

Lemma 8.

Let $k\ge 7$ and let f be a DRDF of $P(3k,k)$ such that $(w_0,w_1,w_2,w_3,w_4)=(5,7,3,5,6)$. If $w\left(f\right)<5k$ then there exists $j\in A_3\setminus A^{\prime }$.

Proof. 

Let $k\ge 7$ and let f be a given DRDF of $P(3k,k)$. Suppose to the contrary, that $w\left(f\right)<5k$ and $j\notin A_3\setminus A^{\prime }$ for each $j\in \left[k\right]$. Then, either $j\notin A_3$ or $j\in A^{\prime }$. It follows that either $w_j=5^{+}$ or $s_{\left(j\right)}=15$ for each $j\in \left[k\right]$.

For a DRDF f we have $w\left(f\right)={\sum }_{\ell =0}^{k-1}{w}_{\ell }={\sum }_{\ell =1}^k{w}_{\ell }={\sum }_{\ell =1}^3{w}_{\ell }+{\sum }_{\ell =4}^k{w}_{\ell }=15+{\sum }_{\ell =4}^k{w}_{\ell }$. Since $w_4=6$ and $w_k=w_0=5$, we may assume ${\sum }_{\ell =4}^k{w}_{\ell }\ge 5(k-3)$. Hence, $w\left(f\right)\ge 15+5(k-3)=5k$, a contradiction with $w\left(f\right)<5k$. □

Lemma 9.

Let $k\ge 7$ and let f be a DRDF of $P(3k,k)$ such that $(w_0,w_1,w_2,w_3,w_4)=(5,7,3,5,6)$. Assume that $w\left(f\right)<5k$ and let $j\in A_3\setminus A^{\prime }$. If ${\gamma }_{dR}\left(P(3t,t)\right)\ge 5t$ for each $t<k$ then $w_{j+1}\ne 8^{+}$ and $w_{j-1}\ne 8^{+}$.

Proof. 

Let $k\ge 7$ and let f be a given DRDF of $P(3k,k)$ with $w\left(f\right)<5k$. Let $j\in A_3\setminus A^{\prime }$. Then we have $j\in [6,k-1]$ and $w_j=3$. Without loss of generality, let j be the minimal integer such that $j\in A_3\setminus A^{\prime }$, thus we may assume $\left[j\right]\cap A_3\subseteq A^{\prime }$.

(A) First we will prove that $w_{j+1}\ne 8^{+}$. Suppose to the contrary there exists $j\in [6,k-1]$ such that $(w_j,w_{j+1})=(3,8^{+})$ and $\left[j\right]\cap A_3\subseteq A^{\prime }$. Then $w_{j+1}\in \{8^{\left(3\right)},8^{\left(2\right)},9\}$ and $w_{j+1}\ne w_0$; therefore, $j\ne k-1$, thus we have $j\in [6,k-2]$.

We will consider the following two cases.

• Case 1: Suppose that $w_{j+1}\in \{8^{\left(2\right)},9\}$.
  We apply Algorithm C with $j_1=j+1$, $j_2=1$, $t_1=0$, $t_2=3$ on a graph $P(3k,k)$. For the resulting graph $P^{\prime \prime }$ we have $V\left(P^{\prime \prime }\right)=V\left(P(3k,k)\right)\setminus \{T_1,T_2,T_3\}$, and by Lemma 4 we have $P^{\prime \prime }\cong P(3k-9,k-3)$ (see Figure 8).
  

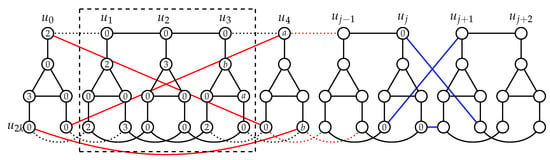  Figure 8. Constructing $P^{\prime \prime }$ in the proof of Lemma 9, Case 1.
  Now we let $f^{\prime }{=f|}_{P^{\prime \prime }}$, and furthermore we set $(a,b)=(3,0)$; hence, $f^{\prime }\left(u_4\right)=3$, $f^{\prime }\left(u_{4+k}\right)=0$, and all vertices of $T_0$ are DR-dominated in a graph $P^{\prime \prime }$. The neighbors of vertices $u_{4+k}$ and $u_{4+2k}$ are pairwise assigned the same values by $f^{\prime }$ and f in graph $P^{\prime \prime }$ and in graph $P(3k,k)$, respectively. Hence, all vertices of $T_4$ are DR-dominated in a graph $P^{\prime \prime }$. Clearly, if $w_{j+1}=9$ then all vertices of $T_j$ and $T_{j+1}$ are DR-dominated in graph $P^{\prime \prime }$. If $w_{j+1}=8$ then there are three different possibilities of assigned values under f of vertices of $T_{j+1}$ (see Figure 9). We can see that in all three cases the vertex in $T_{j+1}\cap U\cap V_0$ has a neighbor in $T_{j+2}$ with assigned value $2^{+}$ in graph $P(3k,k)$. Clearly, these vertices are also adjacent in $P^{\prime \prime }$; hence, all vertices of $T_{j+1}$ are DR-dominated in graph $P^{\prime \prime }$. Furthermore, in all three cases, all vertices of $T_j$ are DR-dominated in graph $P^{\prime \prime }$ (see Figure 9). Therefore, $f^{\prime }$ is a DRDF of graph $P^{\prime \prime }\cong P(3k-9,k-3)$.
  

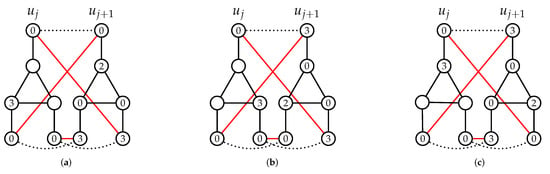  Figure 9. The DRDF’s for three subcases of Case 1 in Lemma 9.
  By assuming that ${\gamma }_{dR}\left(P(3t,t)\right)\ge 5t$ for each $t<k$, it follows $5(k-3)\le {\gamma }_{dR}\left(P(3k-9,k-3)\right)\le w\left(f^{\prime }\right)=w\left(f\right)-{\sum }_{\ell =1}^3{w}_{\ell }=w\left(f\right)-15,$ hence $w\left(f\right)\ge 5k$, contradicting the assumption $w\left(f\right)<5k$.
• Case 2: Assume that $w_{j+1}=8^{\left(3\right)}$.
  Note that in this case, by Lemma 7 statement (g), we have $w_{j-1}=5^{+}$. From $w_{j+1}=8^{\left(3\right)}$ it follows that exactly one of the vertices from $\{v_{j+1},v_{j+k+1},v_{j+2k+1}\}$ is assigned 3 by f. We consider each of these cases below.
  Case 2.1: Let $f\left(v_{j+1+k}\right)=3$. Then, $f\left(v_{j+1}\right)=f\left(v_{j+1+2k}\right)=f\left(u_{j+1+k}\right)=0$ and ($f\left(u_{j+1}\right),f\left(u_{j+1+2k}\right))\in \{(2,3),(3,2)\}$.
  We apply Algorithm B with $j^{\prime }=1$ and $t^{\prime }=j$ on a graph $P(3k,k)$, and by Lemma 3, for the resulting graph $P^{\prime }$ we have $P^{\prime }\cong P(3k-3j,k-j)$ (see Figure 10). Now we let $f^{\prime }{=f|}_{P^{\prime }}$, and in addition we set $f^{\prime }\left(u_{j+1}\right)=2$ and $f^{\prime }\left(u_{j+1+2k}\right)=3$; hence, all vertices of $T_0$ and $T_{j+1}$ are DR-dominated in a graph $P^{\prime }$. Even more, we can set $f^{\prime }\left(v_{j+1+k}\right)=2$, and all vertices remain DR-dominated in a graph $P^{\prime }$. Therefore, $f^{\prime }$ is a DRDF of $P^{\prime }$ with $w\left(f^{\prime }\right)=w\left(f{|}_{P^{\prime }}\right)-1=w\left(f\right)-1-{\sum }_{\ell =1}^j{w}_{\ell }=w\left(f\right)-1-({\sum }_{\ell =1}^4{w}_{\ell }+{\sum }_{\ell =5}^{j-1}{w}_{\ell }+w_j)=w\left(f\right)-25-{\sum }_{\ell =5}^{j-1}{w}_{\ell }$. Because of the condition $\left[j\right]\cap A_3\subseteq A^{\prime }$, and since $w_5=5^{+}$ and $w_{j-1}=5^{+}$, it follows that ${\sum }_{\ell =5}^{j-1}{w}_{\ell }\ge 5(j-5)$. By assumption, we have $5(k-j)\le {\gamma }_{dR}\left(P(3k-3j,k-j)\right)\le w\left(f^{\prime }\right)\le w\left(f\right)-25-5(j-5)=w\left(f\right)-5j,$ a contradiction.
  

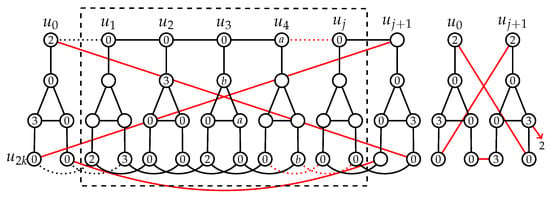  Figure 10. Case 2.1 of Lemma 9: $f\left(v_{j+1+k}\right)=3$.
  Case 2.2: Let $f\left(v_{j+1}\right)=3$. Then $f\left(v_{j+1+k}\right)=f\left(v_{j+1+2k}\right)=f\left(u_{j+1}\right)=0$ and ($f\left(u_{j+1+k}\right),f\left(u_{j+1+2k}\right))\in \{(2,3),(3,2)\}$.
  We apply Algorithm A with $j^{\prime }=1$ and $t^{\prime }=j$ on a graph $P(3k,k)$, and by Lemma 2, for the resulting graph $P^{\prime }$ we have $P^{\prime }\cong P(3k-3j,k-j)$ (see Figure 11). Now we let $f^{\prime }{=f|}_{P^{\prime }}$, and additional we set $f^{\prime }\left(u_{j+1+k}\right)=3$ and $f^{\prime }\left(u_{j+1+2k}\right)=2$; hence, all vertices of $T_0$ and $T_{j+1}$ are DR-dominated in a graph $P^{\prime }$. Similarly as in Case 2.1, we can see that there exists a DRDF $f^{\prime }$ of $P^{\prime }$ with $f^{\prime }\left(v_{j+1}\right)=2$ and $w\left(f^{\prime }\right)=w\left(f{|}_{P^{\prime }}\right)-1\le w\left(f\right)-5j$, a contradiction.
  

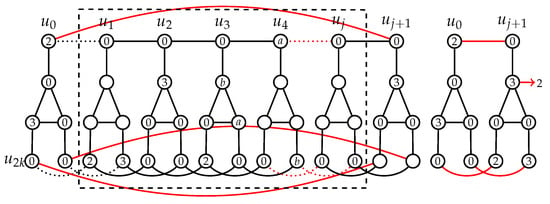  Figure 11. Case 2.2 of Lemma 9: $f\left(v_{j+1}\right)=3$.
  Case 2.3: Let $f\left(v_{j+1+2k}\right)=3$. Then $f\left(v_{j+1}\right)=f\left(v_{j+1+k}\right)=f\left(u_{j+1+2k}\right)=0$ and ($f\left(u_{j+1}\right),f\left(u_{j+1+k}\right))\in \{(2,3),(3,2)\}$.
  We apply Algorithm A with $j^{\prime }=4$ and $t^{\prime }=j-3$ on a graph $P(3k,k)$, and by Lemma 2, for the resulting graph $P^{\prime }$ we have $P^{\prime }\cong P(3k-3j+9,k-j+3)$ (see Figure 12). Now we let $f^{\prime }{=f|}_{P^{\prime }}$, additional we set either $(f^{\prime }\left(u_{j+1}\right),f^{\prime }\left(u_{j+1+k}\right))=(3,2)$ if $(a,b)=(3,0)$, or $(f^{\prime }\left(u_{j+1}\right),f^{\prime }\left(u_{j+1+k}\right))=(2,3)$ if $(a,b)=(0,3)$ (see Figure 12, cases a,b); hence, all vertices of $T_3$ and $T_{j+1}$ are DR-dominated in a graph $P^{\prime }$. Similarly as before, in both possibilities, there exists a DRDF $f^{\prime }$ of $P^{\prime }$ with $f^{\prime }\left(v_{j+1+2k}\right)=2$; hence, $w\left(f^{\prime }\right)=w\left(f{|}_{P^{\prime }}\right)-1=w\left(f\right)-1-{\sum }_{\ell =4}^j{w}_{\ell }=w\left(f\right)-1-(w_4+{\sum }_{\ell =5}^{j-1}{w}_{\ell }+w_j)=w\left(f\right)-10-{\sum }_{\ell =5}^{j-1}{w}_{\ell }\le w\left(f\right)-10-5(j-5)=w\left(f\right)+15-5j$. Recalling the assumption that ${\gamma }_{dR}\left(P(3t,t)\right)\ge 5t$ for each $t<k$, it follows $5(k-j+3)\le w\left(f^{\prime }\right)\le w\left(f\right)+15-5j,$ leading to contradiction.
  

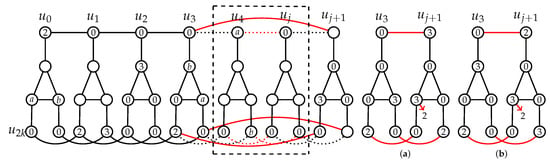  Figure 12. Case 2.3 of Lemma 9: $f\left(v_{j+1+2k}\right)=3$.

(B) Now assume that there exists $j\in [6,k-1]$ such that $(w_{j-1},w_j)=(8^{+},3)$ and $\left[j\right]\cap A_3\subseteq A^{\prime }$.

First assume that $j=k-1$. Then $w\left(f\right)={\sum }_{\ell =0}^j{w}_{\ell }={\sum }_{\ell =0}^4{w}_{\ell }+{\sum }_{\ell =5}^{j-2}{w}_{\ell }+w_{j-1}+w_j=37+{\sum }_{\ell =5}^{j-2}{w}_{\ell }$, where ${\sum }_{\ell =5}^{j-2}{w}_{\ell }=0$ if $j=6$.

Because of the condition $\left[j\right]\cap A_3\subseteq A^{\prime }$, it follows that $w_{j-2}=5^{+}$; therefore, we have ${\sum }_{\ell =5}^{j-2}{w}_{\ell }\ge 5(j-6)$. Hence, $w\left(f\right)\ge 7+5j=5k+2$, which is in contradiction with the assumption $w\left(f\right)<5k$. So, we can restrict attention to $j\in [6,k-2]$.

In continuation, the reasoning is analogous to the proof of Case (A). Instead of $T_{j+1}$ we consider $T_{j-1}$, and similarly, we apply algorithms on graph $P(3k,k)$; Algorithm C with $j_1=j$, $j_2=1$, $t_1=0$ and $t_2=3$ in Case 1, Algorithm B and Algorithm A with $j^{\prime }=1$ and $t^{\prime }=j-2$ in Cases 2.1 and 2.2, respectively; and Algorithm A with $j^{\prime }=4$ and $t^{\prime }=j-5$ in Case 2.3. □

Lemma 10.

Let $k\ge 7$ and let f be a DRDF of $P(3k,k)$ such that $(w_0,w_1,w_2,w_3,w_4)=(5,7,3,5,6)$. Suppose that $w\left(f\right)<5k$ and let $j\in A_3\setminus A^{\prime }$. If ${\gamma }_{dR}\left(P(3t,t)\right)\ge 5t$ for each $t<k$ then $w_{j+1}\ne 7^{\left(3\right)}$ and $w_{j-1}\ne 7^{\left(3\right)}$.

Proof. 

Let $k\ge 7$ and let f be a given DRDF of $P(3k,k)$ with $w\left(f\right)<5k$. Let $j\in A_3\setminus A^{\prime }$. Then we have $j\in [6,k-1]$ and $w_j=3$. Without loss of generality, let j be the minimal integer such that $j\in A_3\setminus A^{\prime }$; thus, we may assume $\left[j\right]\cap A_3\subseteq A^{\prime }$.

(A) Assume that $(w_j,w_{j+1})=(3,7^{\left(3\right)})$. Then $w_{j+1}\ne w_0$; therefore, $j\ne k-1$, and it follows that $j\in [6,k-2]$. By Lemma 7 statement (f), we have $w_{j-1}\in \{6^{\left(2\right)},7^{+}\}$, and thus $s_{\left(j\right)}={16}^{+}$. Note also that $w_{j-2}=5^{+}$. Namely, if $w_{j-1}\in \{6^{\left(2\right)},7^{\left(2\right)}\}$ then $w_{j-2}=5^{+}$ because of statement (c) of Lemma 7 and if $w_{j-1}\in \{7^{\left(3\right)},8^{+}\}$ then $w_{j-2}=5^{+}$ because of the condition $\left[j\right]\cap A_3\subseteq A^{\prime }$.

We first observe that we have to consider only $j\in [6,k-3]$. The argument is as follows. If $j=k-2$, then $w\left(f\right)={\sum }_{\ell =0}^{j+1}{w}_{\ell }={\sum }_{\ell =0}^3{w}_{\ell }+{\sum }_{\ell =4}^{j-1}{w}_{\ell }+w_j+w_{j+1}=30+{\sum }_{\ell =4}^{j-1}{w}_{\ell }$. Because of the condition $\left[j\right]\cap A_3\subseteq A^{\prime }$, and because of $w_4=6$ and $w_{j-1}=6^{+}$, it follows that ${\sum }_{\ell =4}^{j-1}{w}_{\ell }\ge 5(j-4)$. Thus, $w\left(f\right)\ge 30+5(j-4)=5j+10=5k$, but by assuming $w\left(f\right)<5k$, it is a contradiction. Therefore $j\in [6,k-3]$. We will consider the following two cases.

• Case 1: Suppose that $f\left(u_{j+1}\right)=2$. Then ($f\left(u_{j+1+k}\right),f\left(u_{j+1+2k}\right))\in \{(2,0),(0,2)\}$.
  We apply Algorithm A with $j^{\prime }=1$ and $t^{\prime }=j+1$ on graph $P(3k,k)$, and by Lemma 2, for the resulting graph $P^{\prime }$ we have $P^{\prime }\cong P(3k-3j-3,k-j-1)$.
  Now we let $f^{\prime }{=f|}_{P^{\prime }}$, and in addition we set either ($f^{\prime }\left(u_k\right)=2$ if $f\left(u_{j+1+k}\right)=2$), or ($f^{\prime }\left(u_{2k}\right)=2$, $f^{\prime }\left(v_{2k}\right)=0$ and $f^{\prime }\left(v_k\right)=3$ if $f\left(u_{j+1+2k}\right)=2$). Then, in both cases, all vertices of $T_0$ are DR-dominated in a graph $P^{\prime }$. The neighbors of vertices of $T_{j+2}\cap U$ have pairwise the same assigned values by $f^{\prime }$ and f in a graph $P^{\prime }$ and in a graph $P(3k,k)$, respectively. hence all vertices of $T_{j+2}$ are DR-dominated in graph $P^{\prime }$. Therefore $f^{\prime }$ is a DRDF of $P^{\prime }$ with $w\left(f^{\prime }\right)=w\left(f{|}_{P^{\prime }}\right)+2=w\left(f\right)+2-{\sum }_{\ell =1}^{j+1}{w}_{\ell }=w\left(f\right)+2-({\sum }_{\ell =1}^4{w}_{\ell }+{\sum }_{\ell =5}^{j-2}{w}_{\ell }+s_{\left(j\right)})\le w\left(f\right)-35-{\sum }_{\ell =5}^{j-2}{w}_{\ell }$, where ${\sum }_{\ell =5}^{j-2}{w}_{\ell }$ is equal to 0 if $j=6$.
  Because of the condition $\left[j\right]\cap A_3\subseteq A^{\prime }$, and because of $w_5=5^{+}$ and $w_{j-2}=5^{+}$, it follows, that ${\sum }_{\ell =5}^{j-2}{w}_{\ell }\ge 5(j-6)$.
  By assuming, ${\gamma }_{dR}\left(P(3t,t)\right)\ge 5t$ for each $t<k$, it follows $5(k-j-1)\le {\gamma }_{dR}\left(P(3k-3j-3,k-j-1)\right)\le w\left(f^{\prime }\right)\le w\left(f\right)-5j-5,$ but $w\left(f\right)<5k$, a contradiction.
• Case 2. It remains consider the case when $f\left(u_{j+1}\right)=0$. Then $f\left(u_{j+1+k}\right)=f\left(u_{j+1+2k}\right)=2$. We apply Algorithm A with $j^{\prime }=4$ and $t^{\prime }=j-2$ on graph $P(3k,k)$, and by Lemma 2, for the resulting graph $P^{\prime }$ we have $P^{\prime }\cong P(3k-3j+6,k-j+2)$. Now we let $f^{\prime }{=f|}_{P^{\prime }}$, and in addition we set $f^{\prime }\left(u_{3+k}\right)=2$, $f^{\prime }\left(v_3\right)=3$, and $f^{\prime }\left(v_{3+k}\right)=0$. Similarly as in Case 1, it follows, that $f^{\prime }$ is a DRDF of $P^{\prime }$ with $w\left(f^{\prime }\right)=w\left(f{|}_{P^{\prime }}\right)+2$, and thus, $5(k-j+2)\le w\left(f^{\prime }\right)=w\left(f\right)+2-{\sum }_{\ell =4}^{j+1}{w}_{\ell }\le w\left(f\right)+2-(22+5(j-6))=w\left(f\right)-5j+10$, a contradiction.

(B) Now assume $(w_{j-1},w_j)=(7^{\left(3\right)},3)$. We will consider the following two cases.

• Case 1. Suppose that $f\left(u_{j-1+k}\right)=2$. Then ($f\left(u_{j-1}\right),f\left(u_{j-1+2k}\right))\in \{(2,0),(0,2)\}$. We apply Algorithm A with $j^{\prime }=1$ and $t^{\prime }=j-2$ on a graph $P(3k,k)$, and by Lemma 2, for the resulting graph $P^{\prime }$ we have $P^{\prime }\cong P(3k-3j+6,k-j+2)$.
  Now we let $f^{\prime }{=f|}_{P^{\prime }}$, and in addition we set $f^{\prime }\left(u_{j-1+k}\right)=3$. Then, in both cases, all vertices of $T_0$ and $T_{j-1}$ are DR-dominated in a graph $P^{\prime }$. Therefore $f^{\prime }$ is a DRDF of $P^{\prime }$ with $w\left(f^{\prime }\right)=w\left(f{|}_{P^{\prime }}\right)+1=w\left(f\right)+1-{\sum }_{\ell =1}^{j-2}{w}_{\ell }$. Similarly as before, it follows $5(k-j+2)\le w\left(f^{\prime }\right)\le w\left(f\right)-20-5(j-6)=w\left(f\right)-5j+10$, but $w\left(f\right)<5k$, a contradiction.
• Case 2. It remains consider the case when $f\left(u_{j-1+k}\right)=0$. Then $f\left(u_{j-1}\right)=f\left(u_{j-1+2k}\right)=2$. We apply Algorithm B with $j^{\prime }=1$ and $t^{\prime }=j-2$ on a graph $P(3k,k)$, and by Lemma 3, for the resulting graph $P^{\prime }$ we have $P^{\prime }\cong P(3k-3j+6,k-j+2)$. Now we let $f^{\prime }{=f|}_{P^{\prime }}$, and in addition we set $f^{\prime }\left(u_{j-1+2k}\right)=3$. Similarly as in Case 1, it follows, that $f^{\prime }$ is a DRDF of $P^{\prime }$ with $w\left(f^{\prime }\right)=w\left(f{|}_{P^{\prime }}\right)+1\le w\left(f\right)-5j+10$, a contradiction.

□

Lemma 11.

Let $k\ge 6$ and let f be a DRDF of $P(3k,k)$ such that $(w_i,w_{i+1},w_{i+2},w_{i+3},w_{i+4})=(5,7,3,5,6)$ for any $i\in \left[k\right]$. If ${\gamma }_{dR}\left(P(3t,t)\right)\ge 5t$ for each $t<k$ then $w\left(f\right)\ge 5k$.

Proof. 

Let $k\ge 6$ and let f be a DRDF of $P(3k,k)$ as given. Observe that if $k=6$ then $w_{i+5}=5^{+}$ and $w\left(f\right)>5k=30$.

Let $k\ge 7$ and assume that $w\left(f\right)<5k$. By Lemma 8, there exists $j\in \left[k\right]$ such that $w_j=3$ and $(w_{j-1},w_j,w_{j+1})\notin \{(6,3,6),(5,3,7^{\left(2\right)}),(7^{\left(2\right)},3,5)\}$. By Lemmas 9 and 10 we have $\{w_{j-1},w_{j+1}\}\cap \{7^{\left(3\right)},8^{+}\}=\varnothing$. It follows that either $w_{j-1}=3$ or $w_{j+1}=3$, without loss of generality, say $w_{j-1}=3$. Then, using Lemma 7 statement (a), we have $w_{j+1}\in \{8^{\left(2\right)},9\}$, a contradiction. Thus $w\left(f\right)\ge 5k$. □

4.4. DRDF with $(W_{I-1},W_I,W_{I+1},W_{I+2},W_{I+3})=(3,8,3,5,6)$

Lemma 12.

Let $k\ge 6$ and let f be a DRDF of $P(3k,k)$ such that $(w_{i-1},w_i,w_{i+1},w_{i+2},w_{i+3})=(3,8,3,5,6)$ for some $i\in \left[k\right]$. If ${\gamma }_{dR}\left(P(3t,t)\right)\ge 5t$ for each $t<k$, then $w\left(f\right)\ge 5k$.

Proof. 

Let $k\ge 6$ and let f be a DRDF of $P(3k,k)$ such that $(w_{i-1},w_i,w_{i+1},w_{i+2},$ $w_{i+3})=(3,8,3,5,6)$ for some $i\in \left[k\right]$. By Lemma 7, statements (b) and (j), we have $w_i=8^{\left(3\right)}$ and $w_{i+3}=6^{\left(3\right)}$. Furthemore, by Lemma 7, statements (g) and (h), we have $w_{i-2}=5^{+}$ and $w_{i+4}=5^{+}$. Therefore, the given sequence gives rise to the sequence $(w_{i-2},w_{i-1},w_i,w_{i+1},w_{i+2},w_{i+3},w_{i+4})=(5^{+},3,8^{\left(3\right)},3,5,6^{\left(3\right)},5^{+})$.

If $k=6$ then $T_{i+4}=T_{i-2}$ and $w\left(f\right)\ge 30$.

Let $k>6$ and, without loss of generality, we set $i=0$. Then, $w_0=8^{\left(3\right)}$, and by symmetry we may assume that $f\left(u_0\right)=2$, $f\left(u_k\right)=f\left(v_{2k}\right)=3$ and $f\left(v_0\right)=f\left(v_k\right)=f\left(u_{2k}\right)=0$. It is easy to see that $f\left(v_{1+2k}\right)=3$ and $f\left(u_2\right)=2$, otherwise some vertices of $T_1$ are not DR-dominated. In particular, f of vertices of $T_0\cup T_1\cup T_2\cup T_3$ is given by ${\displaystyle \left(\begin{array}{ccc}2\hfill & 3\hfill & 0\hfill \\ 0\hfill & 0\hfill & 3\hfill \end{array}\right)\left(\begin{array}{ccc}0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 3\hfill \end{array}\right)\left(\begin{array}{ccc}2\hfill & 0\hfill & 0\hfill \\ 0\hfill & a\hfill & b\hfill \end{array}\right)\left(\begin{array}{ccc}0\hfill & b\hfill & a\hfill \\ ·\hfill & ·\hfill & ·\hfill \end{array}\right),}$ where $(a,b)\in \left\{\right(0,3),(3,0\left)\right\}$ and exactly one vertex of $T_3\cap I$ is assigned 3. Note that we have either ($f\left(v_3\right)=0$ and $f\left(u_4\right)=2^{+}$) or $f\left(v_3\right)=3$, otherwise vertex $u_3$ is not DR-dominated. We will consider the following two cases.

• Case 1. Assume that $f\left(u_4\right)=2^{+}$. Then $f\left(v_4\right)=0$. We apply Algorithm B with $j=1$ and $t=3$ on graph $P(3k,k)$. For the resulting graph $P^{\prime }$ we have $V\left(P^{\prime }\right)=V\left(P(3k,k)\right)\setminus \{T_1,T_2,T_3\}$, and by Lemma 3, we have $P^{\prime }\cong P(3k-9,k-3)$. Now we define $f^{\prime }$ as follows; we set $f^{\prime }\left(v_{2k}\right)=2$, $f^{\prime }\left(v_{4+k}\right)=3$, $f^{\prime }\left(v_{4+2k}\right)=0$, and $f^{\prime }\left(x\right)=f\left(x\right)$ for each $x\in V\left(P^{\prime }\right)\setminus \{v_{2k},v_{4+k},v_{4+2k}\}$. It is straightforward to check that in $P^{\prime }$, all vertices are DR-dominated by $f^{\prime }$, hence $f^{\prime }$ is a DRDF of $P^{\prime }$. As $f^{\prime }\left(v_{2k}\right)=f\left(v_{2k}\right)-1$, it follows that $w\left(f^{\prime }\right)=w\left(f{|}_{P^{\prime }}\right)-1=w\left(f\right)-1-s_{\left(2\right)}=w\left(f\right)-15$. Hence, assuming that ${\gamma }_{dR}\left(P(3t,t)\right)\ge 5t$ for each $t<k$, we have $w\left(f\right)\ge 5k$, as needed.
• Case 2. Assume now that $f\left(u_4\right)=0$. Then $f\left(v_3\right)=3$, otherwise vertex $u_3$ is not DR-dominated, and hence $f\left(v_{3+k}\right)=f\left(v_{3+2k}\right)=0$. Furthermore, if $b=0=f\left(u_{3+k}\right)$ then $f\left(u_{4+k}\right)=3$, and if $a=0=f\left(u_{3+2k}\right)$ then $f\left(u_{4+2k}\right)=3$, otherwise vertices $u_{3+k}$ and $u_{3+2k}$, respectively, are not DR-dominated. We apply Algorithm A with $j=3$ and $t=1$ on graph $P(3k,k)$. For the resulting graph $P^{\prime }$ we have $V\left(P^{\prime }\right)=V\left(P(3k,k)\right)\setminus T_3$, and by Lemma 2, we have $P^{\prime }\cong P(3k-3,k-1)$. Now we define $f^{\prime }$ as follows; $f^{\prime }\left(x\right)=f\left(x\right)$ for each $x\in V\left(P^{\prime }\right)\setminus \{T_2,T_4\}$. On $T_2$, we set $f^{\prime }\left(u_2\right)=3$, $f^{\prime }\left(v_{2+k}\right)=b$, $f\left(v_{2+2k}^{\prime }\right)=a$, and $f^{\prime }\left(y\right)=f\left(y\right)=0$ for each $y\in \{v_2,u_{2+k},u_{2+2k}\}$. On $T_4$, we set $f^{\prime }\left(v_4\right)=0$, $f^{\prime }\left(v_{4+k}\right)=b$, $f^{\prime }\left(v_{4+2k}\right)=a$, and $f^{\prime }\left(y\right)=f\left(y\right)$ for each $y\in T_4\cap U$. It is straightforward to check that in $P^{\prime }$, all vertices are DR-dominated by $f^{\prime }$, hence $f^{\prime }$ is a DRDF of $P^{\prime }$. As $f^{\prime }\left(u_2\right)=f\left(u_2\right)+1$, it follows that $w\left(f^{\prime }\right)=w\left(f{|}_{P^{\prime }}\right)+1=w\left(f\right)+1-w_3=w\left(f\right)-5$. Hence, assuming that ${\gamma }_{dR}\left(P(3t,t)\right)\ge 5t$ for each $t<k$, we have $w\left(f\right)\ge 5k$, as needed.

□

4.5. DRDF with $(W_{I-1},W_I,W_{I+1})=(3,7,3)$

Lemma 13.

Let $k\ge 6$ and f be a DRDF of $P(3k,k)$ such that $(w_{i-1},w_i,w_{i+1})=(3,7,3)$ for some $i\in \left[k\right]$. If ${\gamma }_{dR}\left(P(3t,t)\right)\ge 5t$ for each $t<k$, then $w\left(f\right)\ge 5k$.

Proof. 

Let $k\ge 6$ and let f be a DRDF of $P(3k,k)$ such that $(w_{i-1},w_i,w_{i+1})$=$(3,7,3)$ for some $i\in \left[k\right]$. By Lemma 7, statements (f,j), we have $w_i=7^{\left(3\right)}$, $w_{i-2}\in \{6^{\left(2\right)},7^{+}\}$, and $w_{i+2}\in \{6^{\left(2\right)},7^{+}\}$.

Without loss of generality, we set $i=2$. Then $w_2=7^{\left(3\right)}$ and by symmetry we may assume that $f\left(u_2\right)=f\left(u_{2+k}\right)=2$, $f\left(v_{2+2k}\right)=3$, and $f\left(v_2\right)=f\left(v_{2+k}\right)=f\left(u_{2+2k}\right)=0$. Furthermore, we have $w_1=w_3=3$; therefore, exactly one vertex of $T_1\cap I$ and exactly one vertex of $T_3\cap I$ are assigned 3, and all other vertices of $T_1\cup T_3$ are assigned 0 by f.

Now we will observe values of vertices of $T_0\cap U$. If $f\left(v_{1+2k}\right)=3$ then $f\left(u_0\right)=2^{+}$ and $f\left(u_k\right)=2^{+}$, otherwise vertices $u_1$ and $u_{1+k}$ are not DR-dominated. If $f\left(v_{1+2k}\right)\ne 3$ then either $f\left(v_1\right)=3$ or $f\left(v_{1+k}\right)=3$, and in both cases $f\left(u_{2k}\right)=3$ otherwise vertex $u_{1+2k}$ is not DR-dominated. More precisely, if $f\left(v_{1+k}\right)=3$ then $f\left(u_0\right)=2^{+}$ and $f\left(u_{2k}\right)=3$, and if $f\left(v_1\right)=3$ then $f\left(u_k\right)=2^{+}$ and $f\left(u_{2k}\right)=3$.

Similarly, for vertices of $T_4\cap U$ we have the next two possibilities; if $f\left(v_{3+2k}\right)=3$, then $f\left(u_4\right)=2^{+}$ and $f\left(u_{4+k}\right)=2^{+}$ and if $f\left(v_{3+2k}\right)\ne 3$ then $f\left(u_{4+2k}\right)=3$ and either $f\left(u_4\right)=2^{+}$ or $f\left(u_{4+k}\right)=2^{+}$.

First we will consider the case where either $f\left(v_{1+2k}\right)=3$ or $f\left(v_{3+2k}\right)=3$. Then it only remains to consider the case where $f\left(u_{2k}\right)=f\left(u_{4+2k}\right)=3$.

• Case 1. Assume that $f\left(v_{1+2k}\right)=3$ or $f\left(v_{3+2k}\right)=3$. Without loss of generality, let $f\left(v_{1+2k}\right)=3$. Then $f\left(u_0\right)=2^{+}$ and $f\left(u_k\right)=2^{+}$. Furthermore, if $f\left(v_{3+2k}\right)=3$ then $f\left(u_4\right)=2^{+}$ and $f\left(u_{4+k}\right)=2^{+}$, if $f\left(v_{3+k}\right)=3$ then $f\left(u_4\right)=2^{+}$ and $f\left(u_{4+2k}\right)=3$, if $f\left(v_3\right)=3$ then $f\left(u_{4+k}\right)=2^{+}$ and $f\left(u_{4+2k}\right)=3$.
  We apply Algorithm A with $j=1$ and $t=2$ on graph $P(3k,k)$. For the resulting graph $P^{\prime }$ we have $V\left(P^{\prime }\right)=V\left(P(3k,k)\right)\setminus \{T_1,T_2\}$, and by Lemma 2, we have $P^{\prime }\cong P(3k-6,k-2)$. Let $f^{\prime }{=f|}_{P^{\prime }}$. It is straightforward to check that in $P^{\prime }$ (in all three cases), all vertices are DR-dominated by $f^{\prime }$, therefore $f^{\prime }$ is a DRDF of $P^{\prime }$, where $w\left(f^{\prime }\right)=w\left(f{|}_{P^{\prime }}\right)=w\left(f\right)-10$. Hence, assuming that ${\gamma }_{dR}\left(P(3t,t)\right)\ge 5t$ for each $t<k$, we have $w\left(f\right)\ge 5k$, as needed.
• Case 2. Assume now that $f\left(v_{1+2k}\right)=f\left(v_{3+2k}\right)=0$. Then $f\left(u_{2k}\right)=f\left(u_{4+2k}\right)=3$.
  We apply Algorithm B with $j=1$ and $t=2$ on graph $P(3k,k)$. For the resulting graph $P^{\prime }$ we have $V\left(P^{\prime }\right)=V\left(P(3k,k)\right)\setminus \{T_1,T_2\}$, and by Lemma 3, we have $P^{\prime }\cong P(3k-6,k-2)$. Now we define $f^{\prime }$ as follows; we set $f^{\prime }\left(v_3\right)=0$, $f^{\prime }\left(v_{3+k}\right)=3$, and $f^{\prime }\left(x\right)=f\left(x\right)$ for each $x\in V\left(P^{\prime }\right)\setminus \{v_3,v_{3+k}\}$. It is straightforward to check that in $P^{\prime }$, all vertices are DR-dominated by $f^{\prime }$, hence $f^{\prime }$ is a DRDF of $P^{\prime }$ where $w\left(f^{\prime }\right)=w\left(f{|}_{P^{\prime }}\right)=w\left(f\right)-10$. Hence, assuming that ${\gamma }_{dR}\left(P(3t,t)\right)\ge 5t$ for each $t<k$, we have $w\left(f\right)\ge 5k$, as needed.

□

4.6. Last Subcase in the Proof of Proposition 3

Lemma 14.

Let $k\ge 6$ and let f be a DRDF of Petersen graph $P(3k,k)$, such that, for each $i\in \left[k\right]$, $(w_{i-1},w_i,$$w_{i+1},)\ne (3,7,3)$ and $(w_{i-1},w_i,$$w_{i+1},$$w_{i+2},w_{i+3})\notin \{(5,7,3,5,6),(3,8,3,5,6)\}$. Then $w\left(f\right)\ge 5k$.

Proof. 

Let $k\ge 6$ and let f be a DRDF of Petersen graph $P(3k,k)$, such that for each $i\in \left[k\right]$, $(w_{i-1},w_i,$$w_{i+1},)\ne (3,7,3)$ and $(w_{i-1},w_i,$$w_{i+1},$$w_{i+2},w_{i+3})\notin \{(5,7,3,5,6),(3,8,3,5,6)\}$. We will prove that the average weight $w_i$ is at least 5, i.e., that $w\left(f\right)=\sum w_i\ge 5k$ or, equivalently, that $\sum s_i\ge 15k$.

Clearly, if $s_i={15}^{+}$ for each i, then $w\left(f\right)\ge 5k$. By Lemma 7, we know that there are exactly five possible sequences $(w_{i-1},w_i,w_{i+1})$ for which $s_i<15$, in particular: $(w_{i-1},w_i,w_{i+1})\in \{(3,3,8^{\left(2\right)}),$$(3,5,6^{\left(3\right)}),$$(3,6^{\left(2\right)},5),$$(3,7^{\left(3\right)},3),$$(3,8^{\left(3\right)},3)\}$. By assumption, there is no subsequence $(3,7^{\left(3\right)},3)$. Below we will show that for every $T_i$ with $s_i<15$ we can define a set of $T_j$ such that their average s is at least 15. More formally, for each i with $s_i<15$ we define a set of indices $H_i$ such that $i\in H_i$ and the average $s_i$ in $H_i$ is ${15}^{+}$. As it will be easy to see that by construction, the sets $H_i$ are pairwise disjoint, it will follow that the average s is at least 15, more precisely ${\displaystyle \frac{1}{|H_i|}\sum _{j\in H_i}{s}_j={15}^{+}}$.

• Case 1. Assume $(w_{i-1},w_i,w_{i+1})=(3,3,8^{\left(2\right)})$.
  In this case $s_i=14$. By Lemma 7, statement (c), we have $w_{i+2}=5^{+}$, hence $s_{i+1}={16}^{+}$ and $s_{i+2}={16}^{+}$. Furthermore, by Lemma 7, statement (a), it follows that $w_{i-2}\in \{8^{\left(2\right)},9\}$.
  If $w_{i-2}=9$ then $s_{i-1}=15$ and $s_{i-2}={15}^{+}$, which implies $s_i+s_{i+1}=14+{16}^{+}={30}^{+}$ and we define $H_i=\{i,i+1\}$.
  If $w_{i-2}=8^{\left(2\right)}$ then by Lemma 7, statement (c), $w_{i-3}=5^{+}$, thus $s_{i-1}=14$, $s_{i-2}={16}^{+}$ and $s_{i-3}={16}^{+}$. Hence $s_i+s_{i+1}=14+{16}^{+}={30}^{+}$ and $s_{i-1}+s_{i-2}=14+{16}^{+}={30}^{+}$, so we can define $H_i=\{i-2,i-1,i,i+1\}$ (and $H_{i-1}=H_i=\{i-2,i-1,i,i+1\}$).
• Case 2. Assume $(w_{i-1},w_i,w_{i+1})=(3,6^{\left(2\right)},5)$, thus $s_i=14$. By Lemma 7, statement (i), we have $w_{i+2}=5^{+}$, thus $s_{i+1}={16}^{+}$. By Lemma 7, statement (f), we have $w_{i-2}\in \{6^{\left(2\right)},7^{+}\}$, thus $s_{i-1}={15}^{+}$.
  If $s_{i+2}={15}^{+}$, then $s_i+s_{i+1}=14+{16}^{+}={30}^{+}$ and we can define $H_i=\{i,i+1\}$.
  Assume now that $s_{i+2}<15$. It is easy to see there is only one possible continuation of the sequence: $(w_{i-1},w_i,w_{i+1},w_{i+2},w_{i+3})=(3,6^{\left(2\right)},5,$$6^{\left(2\right)},3)$. Then $s_{i+1}=17$, $s_{i+2}=14$, and by Lemma 7, statement (f), we have $s_{i+3}={15}^{+}$, and we define $H_i=H_{i+2}=\{i,i+1,i+2\}$.
• Case 3. Assume $(w_{i-1},w_i,w_{i+1})=(3,5,6^{\left(3\right)})$,
  thus $s_i=14$. By Lemma 7, statement (h), we have $w_{i+2}=5^{+}$, hence $s_{i+1}={16}^{+}$. Furthermore, by Lemma 7, statement (d), $w_{i-2}\in \{7^{\left(2\right)},8^{+}\}$, thus $s_{i-1}={15}^{+}$.
  If $s_{i+2}={15}^{+}$, then let $H_i=\{i,i+1\}$.
  Assume now that $s_{i+2}<15$. It is easy to see that there exists only one case: $(w_{i-1},w_i,w_{i+1},w_{i+2},w_{i+3})=(3,5,6^{\left(3\right)},5,3)$. By Lemma 7, statement (d), we have $w_{i+4}\in \{7^{\left(2\right)},8^{+}\}$.
  If $k=6$, then $T_{i+4}=T_{i-2}$. Note that $w_{i-1}=w_{i+3}=3$ and because of Lemma 7, statement (j), we have $w_{i+4}\in \{8^{\left(3\right)},9\}$, and thus $w\left(f\right)\ge 30$.
  Let $k>6$. By symmetry, it is enough to consider $w_{i-2}$. There are three possibilities.

  (a)

  Assume first that $w_{i-2}=9$. Then we have $(s_{i-2},s_{i-1},s_i,s_{i+1},s_{i+2},s_{i+3})=({15}^{+},17,14,16,14,{15}^{+})$, and $H_i=H_{i+2}=\{i-1,i,i+1,i+2\}$.

  (b)

  Suppose now that $w_{i-2}=7^{\left(2\right)}$. Then, by Lemma 7, statement (c), we have $w_{i-3}=5^{+}$. If $w_{i-3}=5$, then we obtain the sequence $(5,7,3,5,6)$ which is not possible by assumption. Therefore $w_{i-3}=6^{+}$, and we have $(s_{i-3},s_{i-2},s_{i-1},s_i,s_{i+1},$$s_{i+2},$$s_{i+3})=({16}^{+},{16}^{+},15,14,16,14,{15}^{+})$, so we can define $H_i=H_{i+2}=\{i-2,i-1,i,i+1,i+2\}$.

  (c)

  It remains to consider the case when $w_{i-2}=8$. We can assume $w_{i-3}\ne 3$ because otherwise we have the sequence $(3,8,3,5,6)$, which is not possible. Therefore $w_{i-3}=5^{+}$, thus we have $(s_{i-3},s_{i-2},s_{i-1},s_i,s_{i+1},s_{i+2},s_{i+3})=({16}^{+},{16}^{+},16,14,16,14,{15}^{+})$. So we can define $H_i=H_{i+2}=\{i-1,i,i+1,i+2\}$.

• Case 4. Finally, let $(w_{i-1},w_i,w_{i+1})=(3,8^{\left(3\right)},3)$.
  In this case $s_i=14$. By Lemma 7, statement (g), we have $w_{i-2}=5^{+}$ and $w_{i+2}=5^{+}$, thus $s_{i-1}={16}^{+}$ and $s_{i+1}={16}^{+}$.
  If $s_{i-2}={15}^{+}$ or $s_{i+2}={15}^{+}$, then $H_i=\{i,i-1\}$ or $H_i=\{i,i+1\}$. Assume now that $s_{i-2}<15$ and $s_{i+2}<15$. It is easy to see that there is exactly one case with $s_{i+2}<15$ that is left to be considered: $(w_{i-1},w_i,w_{i+1},w_{i+2},w_{i+3})=(3,8^{\left(3\right)},3,6^{\left(2\right)},5)$. Hence, by Lemma 7, statement (i), we have $w_{i+4}=5^{+}$, implying $(s_{i-1},s_i,s_{i+1},s_{i+2},s_{i+3})=({16}^{+},14,17,14,{16}^{+})$, so we can define $H_i=H_{i+2}=\{i,i+1,i+2\}$.

To conclude the proof, recall that by definitions we know that for each $H_i$ and $H_j$ we have either $H_i\cap H_j=\varnothing$ or $H_i=H_j$. We omit the details. □

4.7. Section Summary

In all cases, elaborated in previous subsections it was proven that a DRDF must have weight at least $5k$ under various assumptions that cover all possible cases (recall Lemmas 11–14). Therefore, Proposition 3 follows.

5. Conclusions

We established the double Roman domination numbers of all Petersen graphs $P(3k,k)$. In addition, the double Roman graphs are characterized among them. In our future work, we plan to explore similar statements for some other families such as $P(ck,k)$ for $c\ge 4$.