Modeling and Simulation Techniques Used in High Strain Rate Projectile Impact
Abstract
1. Introduction
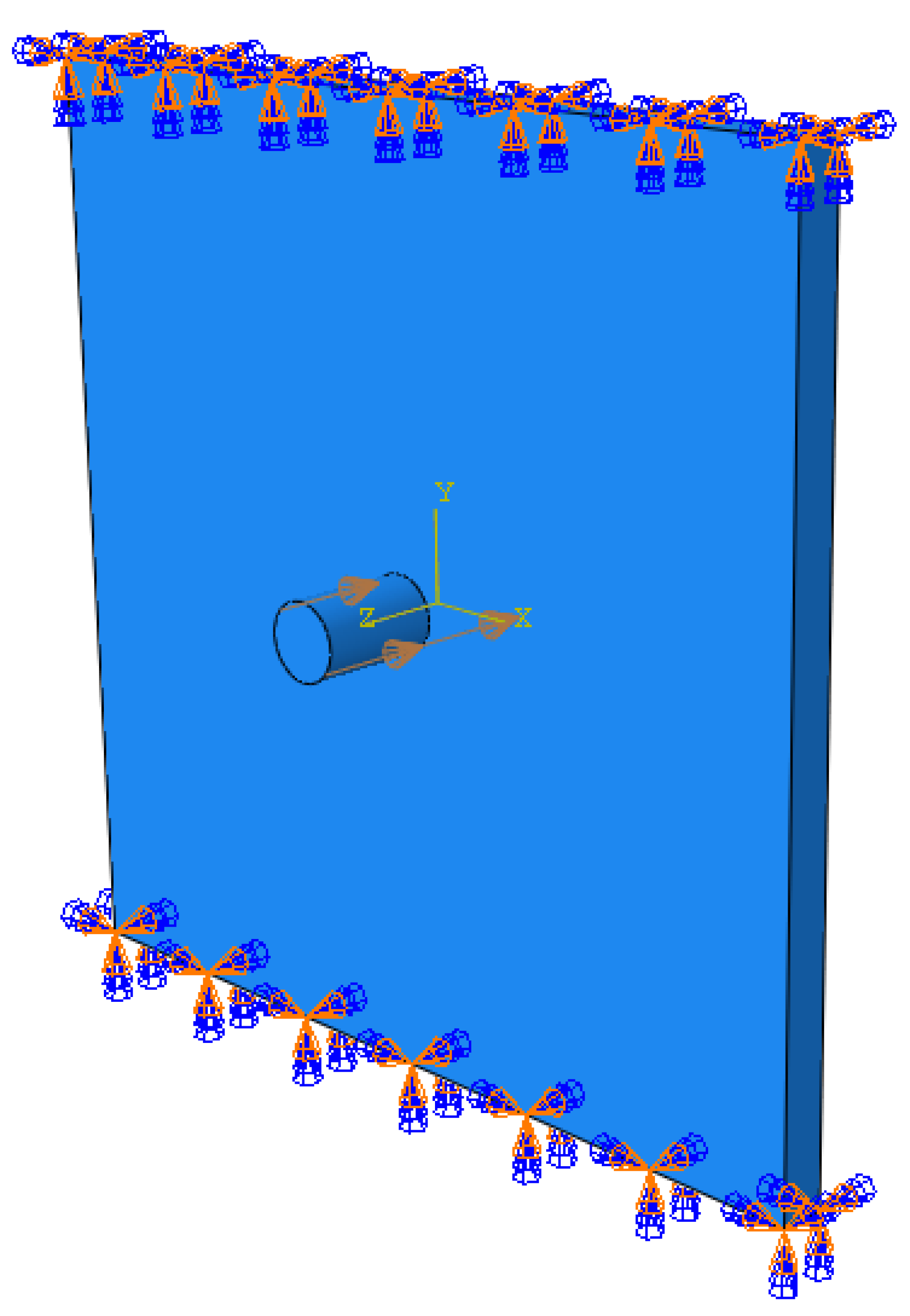
2. Methodology
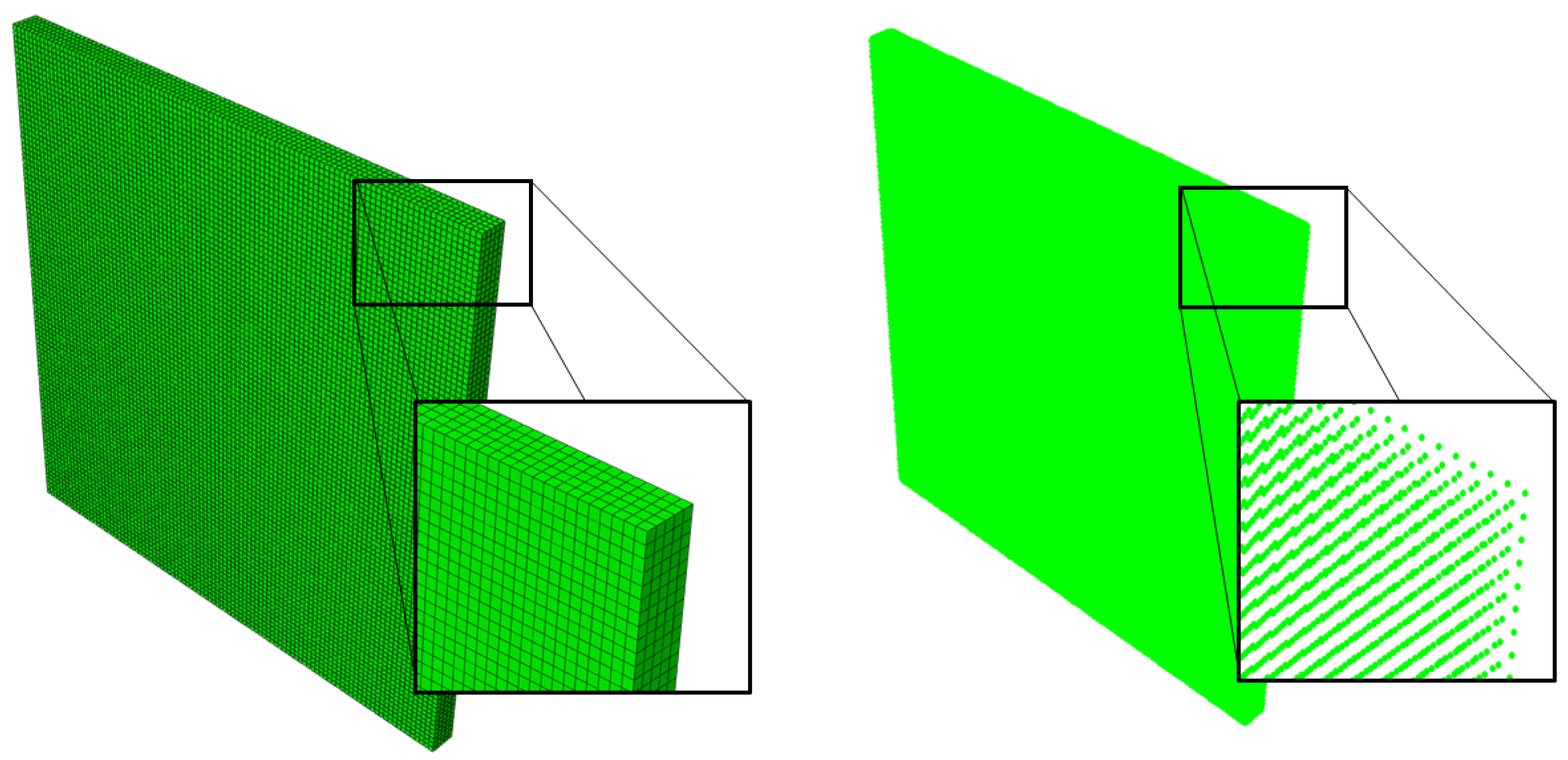
2.1. Lagrangian Finite Element Analysis
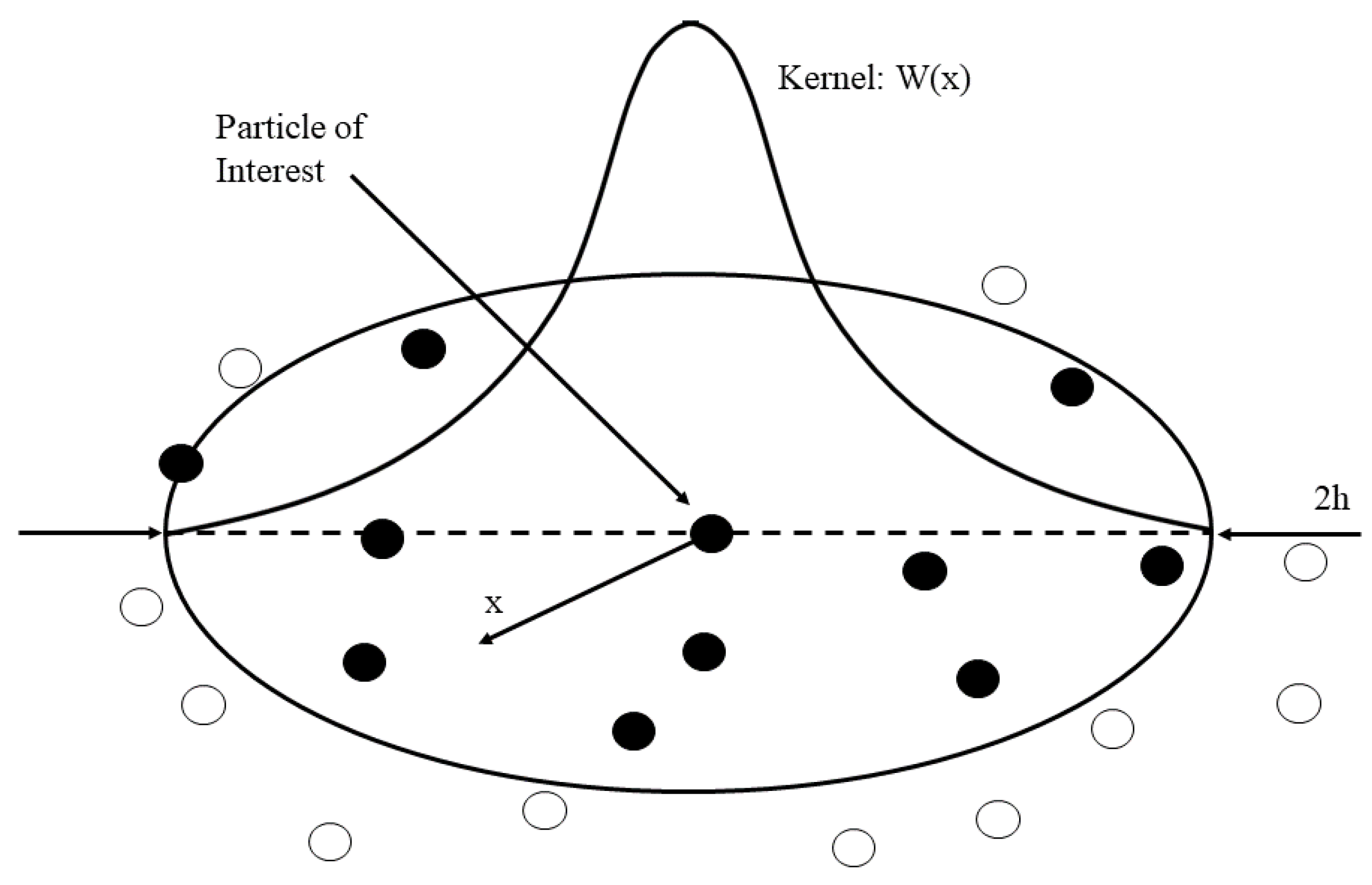
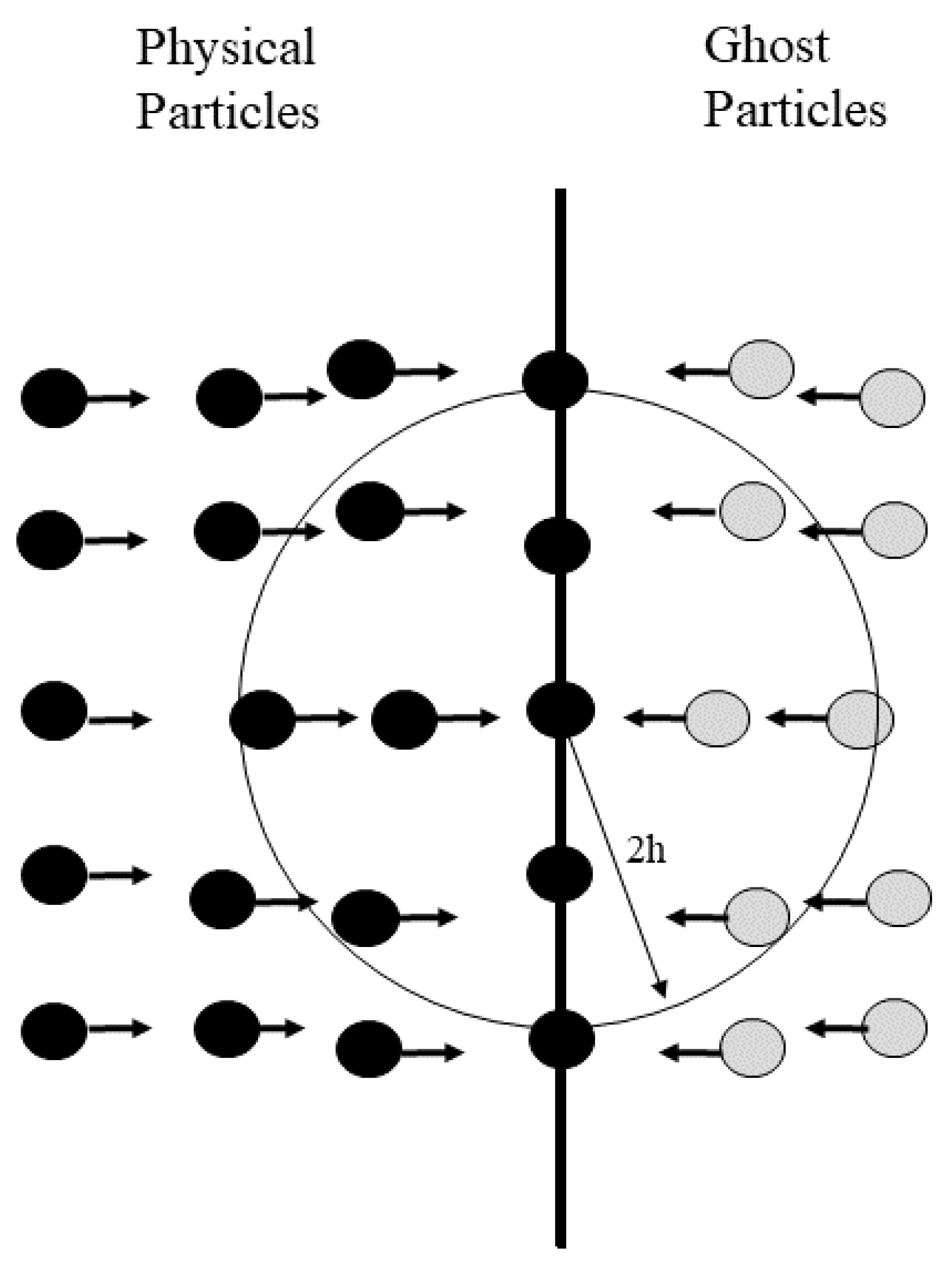
2.2. Smoothed Particle Hydrodynamics
2.3. Equation of State
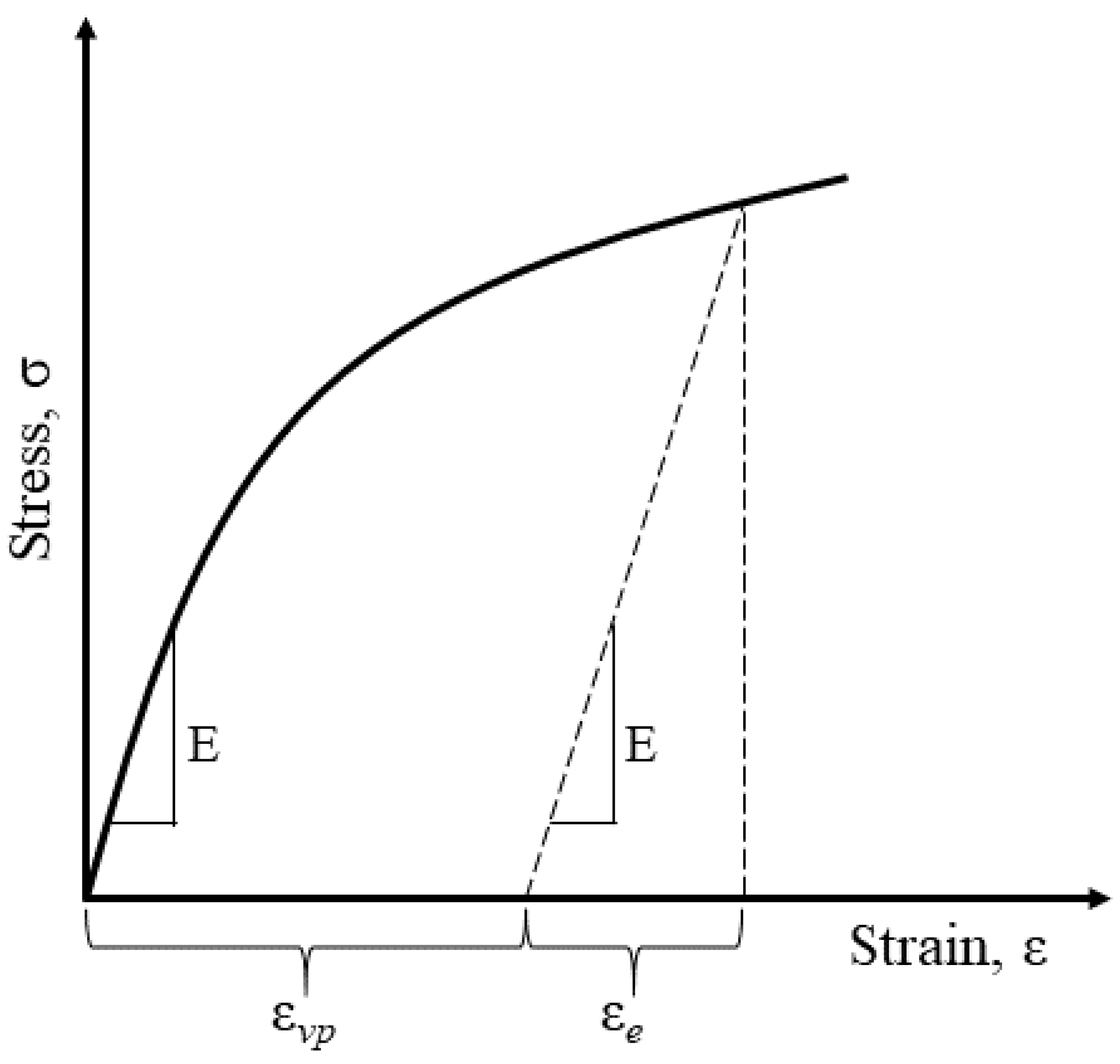
2.4. Damage Modeling
3. Results and Discussion
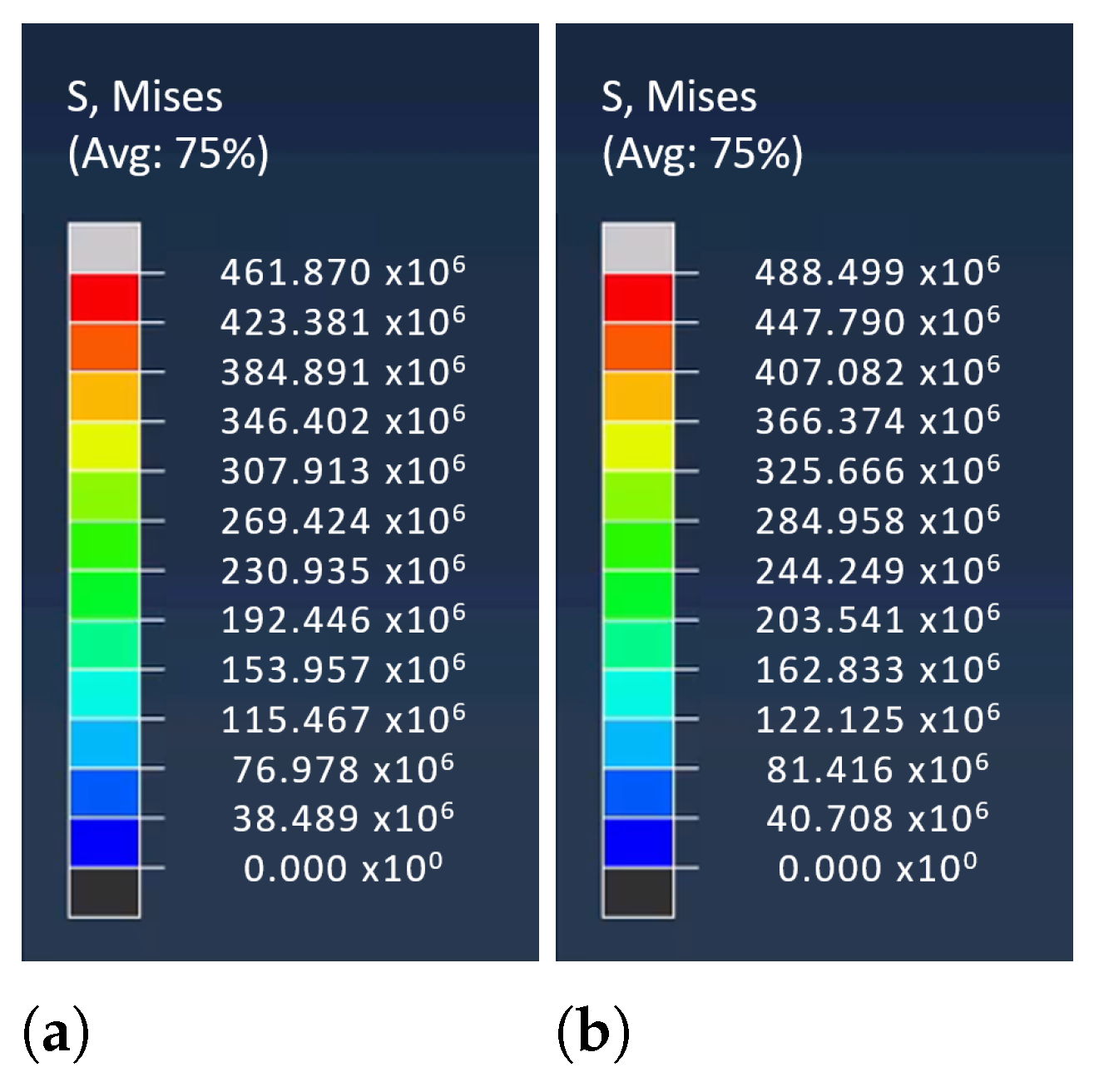
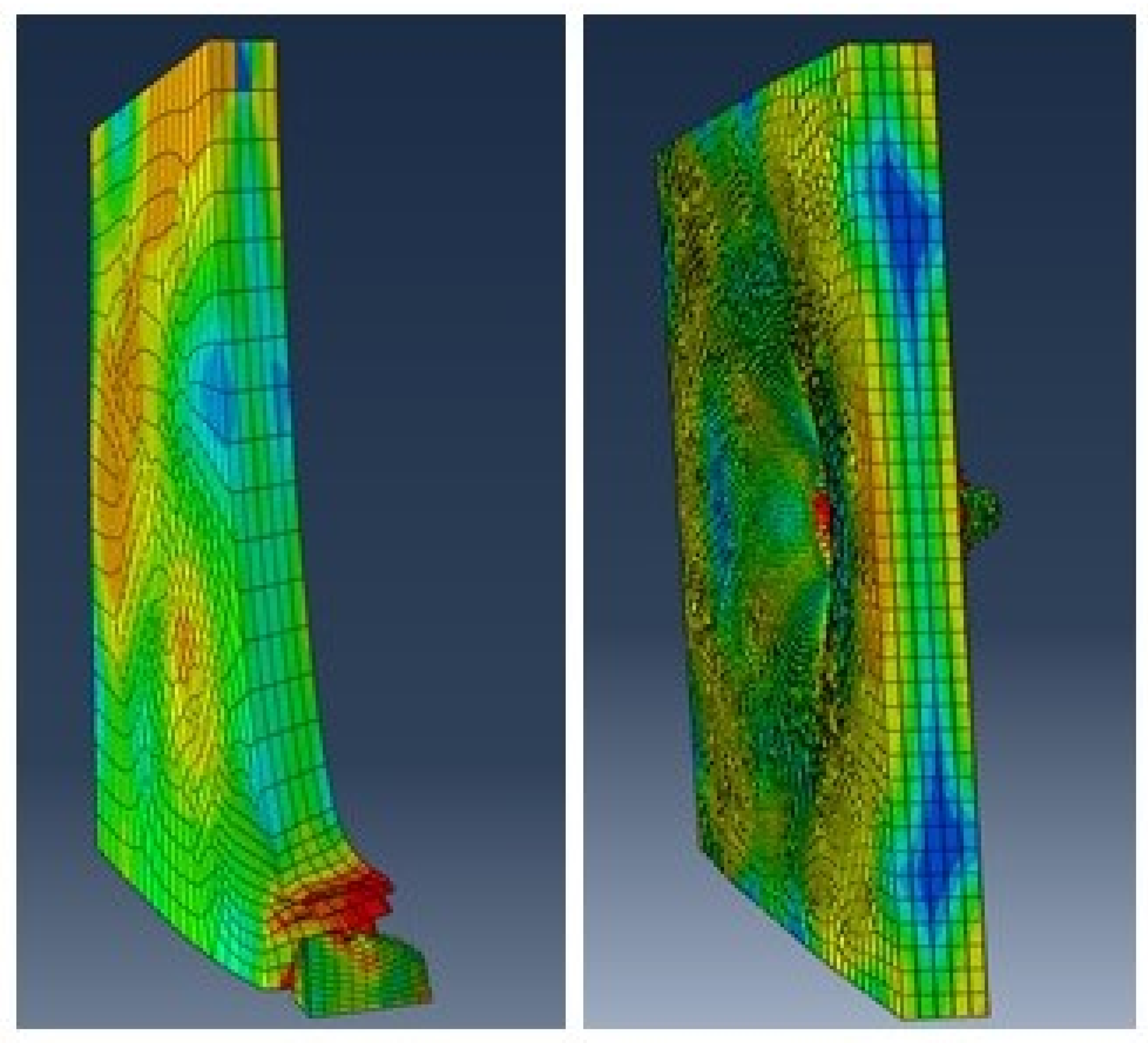
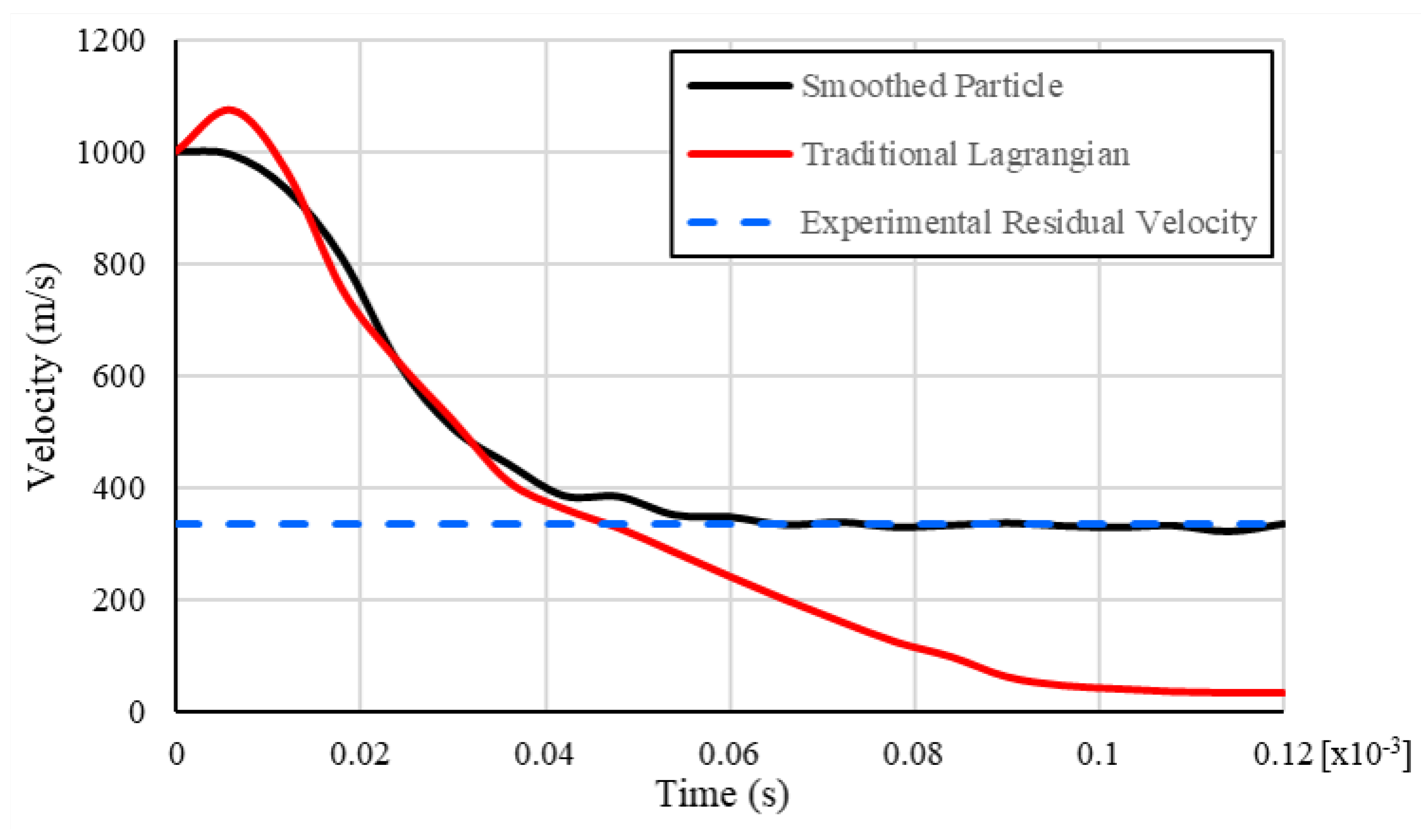
3.1. Lagrangian Models
3.2. Mixed SPH-Lagrangian Model
3.3. Further Comparison of Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CDTI | Central Difference Time Integration |
| EOS | Equation of State |
| FEA | Finite Element Analysis |
| FEM | Finite Element Method |
| KE | Kinetic Energy |
| SPH | Smoothed Particle Hydrodynamics |
References
- Ben-Dor, G.; Dubinsky, A.; Elperin, T. Ballistic impact: Recent advances in analytical modeling of plate penetration dynamics-a review. Appl. Mech. Rev. 2005, 58, 355–370. [Google Scholar] [CrossRef]
- Nair, R.P.; Rao, C.L. Simulation of depth of penetration during ballistic impact on thick targets using a one-dimensional discrete element model. Sadhana Acad. Proc. Eng. Sci. 2012, 37, 261–279. [Google Scholar] [CrossRef]
- Kurtaran, H.; Buyuk, M.; Eskandarian, A. Ballistic impact simulation of GT model vehicle door using finite element method. Theor. Appl. Fract. Mech. 2003, 40, 113–121. [Google Scholar] [CrossRef]
- Schwer, L.E. Aluminum Plate Perforation: A Comparative Case Study using Lagrange with Erosion, Multi-Material ALE, and Smooth Particle Hydrodynamics. In Proceedings of the 7th European LS-DYNA Conference, Salzburg, Austria, 14–15 May 2009; pp. 1–27. [Google Scholar]
- Resnyansky, A.; Katselis, G. Ballistic and Meterial Testing Procedures and Test Results for Composite Samples for the TIGER Helicopter Vulnerability Project, dsto-tr-16 ed.; Australian Government, Department of Defence: Canberra, Australia, 2004. [CrossRef]
- Johnson, G.R. High Velocity Impact Calculations in Three Dimensions. J. Appl. Mech. 1977, 44, 95–100. [Google Scholar] [CrossRef]
- Johnson, G.R. Closure to “Discussion of ‘High Velocity Impact Calculations in Three Dimensions’” (1977, ASME J. Appl. Mech., 44, pp. 793–794). J. Appl. Mech. 1977, 44, 794–795. [Google Scholar] [CrossRef]
- Gailly, B.A.; Espinosa, H.D. Modelling of failure mode transition in ballistic penetration with a continuum model describing microcracking and flow of pulverized media. Int. J. Numer. Methods Eng. 2002, 54, 365–398. [Google Scholar] [CrossRef]
- Grujicic, M.; Arakere, G.; He, T.; Bell, W.; Cheeseman, B.; Yen, C.F.; Scott, B. A ballistic material model for cross-plied unidirectional ultra-high molecular-weight polyethylene fiber-reinforced armor-grade composites. Mater. Sci. Eng. A 2008, 498, 231–241. [Google Scholar] [CrossRef]
- Grujicic, M.; Glomski, P.; He, T.; Arakere, G.; Bell, W.C.; Cheeseman, B. Material Modeling and Ballistic-Resistance Analysis of Armor-Grade Composites Reinforced with High-Performance Fibers. J. Mater. Eng. Perform. 2009, 18, 1169–1182. [Google Scholar] [CrossRef]
- Kantar, E.; Erdem, R.; Anıl, O. Nonlinear Finite Element Analysis of Impact Behavior of Concrete Beam. Math. Comput. Appl. 2011, 16, 183–193. [Google Scholar] [CrossRef]
- Hazell, P. Numerical simulations and experimental observations of the 5.56-MM L2A2 bullet perforating steel targets of two hardness values. J. Battlef. Technol. 2003, 6, 1–4. [Google Scholar]
- Borvik, T.; Dey, S.; Clausen, A. Perforation resistance of five different high-strength steel plates subjected to small-arms projectiles. Int. J. Impact Eng. 2009, 36, 948–964. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Libersky, L.D.; Petschek, A.G. Smooth particle hydrodynamics with strength of materials. In Advances in the Free-Lagrange Method Including Contributions on Adaptive Gridding and the Smooth Particle Hydrodynamics Method; Trease, H.E., Fritts, M.F., Crowley, W.P., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 248–257. [Google Scholar]
- Libersky, L.D.; Petschek, A.G.; Carney, T.C.; Hipp, J.R.; Allahdadi, F.A. High strain lagrangian hydrodynamics a three-dimensional SPH code for dynamic material response. J. Comput. Phys. 1993, 109, 67–75. [Google Scholar] [CrossRef]
- Randles, P.; Libersky, L. Smoothed Particle Hydrodynamics: Some recent improvements and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 375–408. [Google Scholar] [CrossRef]
- Johnson, G.; Petersen, E.H.; Stryk, R.A. Incorporation of an SPH option into the EPIC code for a wide range of high velocity impact computations. Int. J. Impact Eng. 1993, 14, 385–394. [Google Scholar] [CrossRef]
- Johnson, G.R.; Stryk, R.A.; Beissel, S.R. SPH for high velocity impact computations. Comput. Methods Appl. Mech. Eng. 1996, 139, 347–373. [Google Scholar] [CrossRef]
- O’Toole, B.; Trabia, M.; Hixson, R.; Roy, S.K.; Pena, M.; Becker, S.; Daykin, E.; Machorro, E.; Jennings, R.; Matthes, M. Modeling Plastic Deformation of Steel Plates in Hypervelocity Impact Experiments. Procedia Eng. 2015, 103, 458–465. [Google Scholar] [CrossRef][Green Version]
- Poniaev, S.; Kurakin, R.; Sedov, A.; Bobashev, S.; Zhukov, B.; Nechunaev, A. Hypervelocity impact of mm-size plastic projectile on thin aluminum plate. Acta Astronaut. 2017, 135, 26–33. [Google Scholar] [CrossRef]
- Taddei, L.; Awoukeng Goumtcha, A.; Roth, S. Smoothed particle hydrodynamics formulation for penetrating impacts on ballistic gelatine. Mech. Res. Commun. 2015, 70, 94–101. [Google Scholar] [CrossRef]
- Frissane, H.; Taddei, L.; Lebaal, N.; Roth, S. SPH modeling of high velocity impact into ballistic gelatin. Development of an axis-symmetrical formulation. Mech. Adv. Mater. Struct. 2019, 26, 1881–1888. [Google Scholar] [CrossRef]
- Xiao, Y.; Dong, H.; Zhou, J.; Wang, J. Studying normal perforation of monolithic and layered steel targets by conical projectiles with SPH simulation and analytical method. Eng. Anal. Bound. Elem. 2017, 75, 12–20. [Google Scholar] [CrossRef]
- Chaussonnet, G.; Bravo, L.; Flatau, A.; Koch, R.; Bauer, H.J. Smoothed Particle Hydrodynamics Simulation of High Velocity Impact Dynamics of Molten Sand Particles. Energies 2020, 13, 5134. [Google Scholar] [CrossRef]
- Soriano-Moranchel, F.A.; Sandoval-Pineda, J.M.; Gutiérrez-Paredes, G.J.; Silva-Rivera, U.S.; Flores-Herrera, L.A. Simulation of Bullet Fragmentation and Penetration in Granular Media. Materials 2020, 13, 5243. [Google Scholar] [CrossRef] [PubMed]
- Graves, W.T.; Liu, D.; Palazotto, A.N. Impact of an Additively Manufactured Projectile. J. Dyn. Behav. Mater. 2017, 3, 362–376. [Google Scholar] [CrossRef]
- Provchy, Z.A.; Palazotto, A.N.; Flater, P. Topology Optimization for Projectile Design. J. Dyn. Behav. Mater. 2018, 4, 129–137. [Google Scholar] [CrossRef]
- Patel, A.; Palazotto, A.N. Investigation of Hybrid Material Projectile Impact Against Concrete Targets. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Beard, A.; Palazotto, A.N. Composite Material for High-Speed Projectile Outer Casing. In Proceedings of the 2020 AIAA Science and Technology Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Spear, D.; Palazotto, A.N.; Kemnitz, R. Survivability and Damage Modeling of Advanced Materials. In Proceedings of the 2020 AIAA Science and Technology Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Spear, D.; Palazotto, A.N.; Kemnitz, R. First Cell Failure of Lattice Structure under Combined Axial and Buckling Load. In Proceedings of the AIAA Scitech 2021 Forum, Nashville, TN, USA, 11–15 January 2021; pp. 1–16. [Google Scholar] [CrossRef]
- Wilson, E.L. Structural analysis of axisymmetric solids. AIAA J. 1965, 3, 2269–2274. [Google Scholar] [CrossRef]
- Cook, R.D.; Malkus, D.S.; Plesha, M.E.; Witt, R.J. Concepts and Applications of Finite Element Analysis; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Dassault Systèmes. ABAQUS Version 6.12 Theory Manual; Dassault Systemes Simulia Corp: Johnston, RI, USA, 2016. [Google Scholar]
- KJ Bath. Finite Element Procedures, 2nd ed.; KJ Bathe: Watertown, MA, USA, 2014; p. 1037. [Google Scholar]
- Johnson, G.; Cook, W. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates, and High Temperatures. In Proceedings of the Seventh International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Leseur, D. Experimental Investigations of Material Models for Ti-6Al-4V Titanium and 2024-T3 Aluminum. DOT/FAA/AR-00/25. 2000, Volume 9, pp. 1–29. Available online: https://www.osti.gov/biblio/11977-experimental-investigationsmaterial-models-ti-t3 (accessed on 27 January 2021).
- Kay, G. Failure Modeling of Titanium-6Al-4V and 2024-T3 Aluminum with the Johnson-Cook Material Model. DOT/FAA/AR-03/57. 2003, Volume 9, pp. 1–17, doi:10.2172/15006359. Available online: https://www.osti.gov/biblio/15006359-failuremodeling-titanium-t3-aluminum-johnson-cook-material-model (accessed on 27 January 2021).
- Shames, I.; Cozzarelli, F. Elastic And Inelastic Stress Analysis; Taylor & Francis: Abingdon, UK, 1997. [Google Scholar]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013. [Google Scholar] [CrossRef]
- Wu, C.; Wu, Y.; Crawford, J.E.; Magallanes, J.M. Three-dimensional concrete impact and penetration simulations using the smoothed particle Galerkin method. Int. J. Impact Eng. 2017, 106, 1–17. [Google Scholar] [CrossRef]
- Islam, M.R.I.; Chakraborty, S.; Shaw, A. On consistency and energy conservation in smoothed particle hydrodynamics. Int. J. Numer. Methods Eng. 2018, 116, 601–632. [Google Scholar] [CrossRef]
- Chen, J.Y.; Peng, C.; Lien, F.S. Simulations for three-dimensional landmine detonation using the SPH method. Int. J. Impact Eng. 2019, 126, 40–49. [Google Scholar] [CrossRef]
- Monaghan, J.J. An introduction to SPH. Comput. Phys. Commun. 1988, 48, 89–96. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Liu, M.; Liu, G. Particle Methods for Multi-Scale and Multi-Physics; World Scientific: Singapore, 2016. [Google Scholar] [CrossRef]
- Zisis, I.; van der Linden, B.; Giannopapa, C. Towards a Smoothed Particle Hydrodynamics Algorithm for Shocks Through Layered Materials, Volume 4: Fluid-Structure Interaction. In Proceedings of the Pressure Vessels and Piping Conference, Paris, France, 14–18 July 2013; p. V004T04A005. [Google Scholar] [CrossRef]
- Stranex, T.; Wheaton, S. A new corrective scheme for SPH. Comput. Methods Appl. Mech. Eng. 2011, 200, 392–402. [Google Scholar] [CrossRef]
- Vignjevic, R.; Campbell, J.; Jaric, J.; Powell, S. Derivation of SPH equations in a moving referential coordinate system. Comput. Methods Appl. Mech. Eng. 2009, 198, 2403–2411. [Google Scholar] [CrossRef][Green Version]
- Batra, R.C.; Zhang, G.M. SSPH basis functions for meshless methods, and comparison of solutions with strong and weak formulations. Comput. Mech. 2008, 41, 527–545. [Google Scholar] [CrossRef]
- Zhang, G.M.; Batra, R.C. Symmetric smoothed particle hydrodynamics (SSPH) method and its application to elastic problems. Comput. Mech. 2009, 43, 321–340. [Google Scholar] [CrossRef]
- Cueto-Felgueroso, L.; Colominas, I.; Mosqueira, G.; Navarrina, F.; Casteleiro, M. On the Galerkin formulation of the smoothed particle hydrodynamics method. Int. J. Numer. Methods Eng. 2004, 60, 1475–1512. [Google Scholar] [CrossRef][Green Version]
- Dilts, G.A. Moving-Least-Squares-particle hydrodynamics—I. Consistency and stability. Int. J. Numer. Methods Eng. 1999, 44, 1115–1155. [Google Scholar] [CrossRef]
- Dilts, G.A. Moving least-squares particle hydrodynamics II: Conservation and boundaries. Int. J. Numer. Methods Eng. 2000, 48, 1503–1524. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Liu, G.; Liu, M. Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific: Singapore, 2003. [Google Scholar] [CrossRef]
- Danilewicz, A.; Sikora, Z. Numerical Simulation of Crater Creating Process in Dynamic Replacement Method by Smooth Particle Hydrodynamics. Stud. Geotech. Mech. 2015, 36, 3–8. [Google Scholar] [CrossRef]
- Barbosa, D.; Piccoli, F. Comparing the force due to the Lennard-Jones potential and the Coulomb force in the SPH Method. J. Ocean Eng. Sci. 2018, 3, 310–315. [Google Scholar] [CrossRef]
- Holzapfel, W.B. Equations of State and Thermophysical Properties of Solids Under Pressure. In High-Pressure Crystallography; Springer: Dordrecht, The Netherlands, 2004; pp. 217–236. [Google Scholar] [CrossRef]
- Meyers, M.A. Dynamic Behavior of Materials; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar] [CrossRef]
- Roy, S.K.; Trabia, M.; O’Toole, B.; Hixson, R.; Becker, S.; Pena, M.; Jennings, R.; Somasoundaram, D.; Matthes, M.; Daykin, E.; et al. Study of Hypervelocity Projectile Impact on Thick Metal Plates. Shock Vib. 2016, 2016, 1–11. [Google Scholar] [CrossRef]
- Zocher, M.; Maudlin, P.; Chen, S.; Flower-Maudlin, E. An Evaluation of Several Hardening Models using Taylor Cylinder Impact Data. In Proceedings of the European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2000), Barcelona, Spain, 11–14 September 2000; Volume 53, pp. 1–20. [Google Scholar] [CrossRef]
- Rice, M.H.; McQueen, R.G.; Walsh, J.M. Compression of Solids by Strong Shock Waves. Solid State Phys. Adv. Res. Appl. 1958, 6, 1–63. [Google Scholar] [CrossRef]
- Mandl, F. Statistical Physics, 2nd ed.; Wiley: Hoboken, NJ, USA, 1991. [Google Scholar]
- Marc, G.; McMillan, W.G. The Virial Theorem. In Advances in Chemical Physics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; Volume 63, pp. 209–361. [Google Scholar] [CrossRef]
- Heuzé, O. General form of the Mie-Grüneisen equation of state. Comptes Rendus-Mec. 2012, 340, 679–687. [Google Scholar] [CrossRef]
- Goldstein, H.; Poole, C.; Safko, J. Classical Mechanics; Addison Wesley: Boston, MA, USA, 2002. [Google Scholar]
- Grüneisen, E. Theorie des festen Zustandes einatomiger Elemente. Ann. Phys. 1912, 344, 257–306. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Cowan, R.; Winer, W. Frictional Heating Calculations. Frict. Lubr. Wear Technol. ASM Handb. 1992, 18, 39–44. [Google Scholar]
- Meyer, H.W.; Kleponis, D.S. Modeling the high strain rate behavior of titanium undergoing ballistic impact and penetration. Int. J. Impact Eng. 2001, 26, 509–521. [Google Scholar] [CrossRef]
- Wang, X.; Shi, J. Validation of Johnson-Cook plasticity and damage model using impact experiment. Int. J. Impact Eng. 2013, 60, 67–75. [Google Scholar] [CrossRef]
- Committee, A.H. Properties and Selection: Nonferrous Alloys and Special-Purpose Materials; ASM International: Almere, The Netherlands, 1990. [Google Scholar] [CrossRef]
- Johnson, G.R.; Holmquist, T.J. Test Data and Computational Strength and Fracture Model Constants for 23 Materials Subjected to Large Strains, High Strain Rates, and High Temperatures; Los Alamos National Laboratory: Los Alamos, NM, USA, 1989.




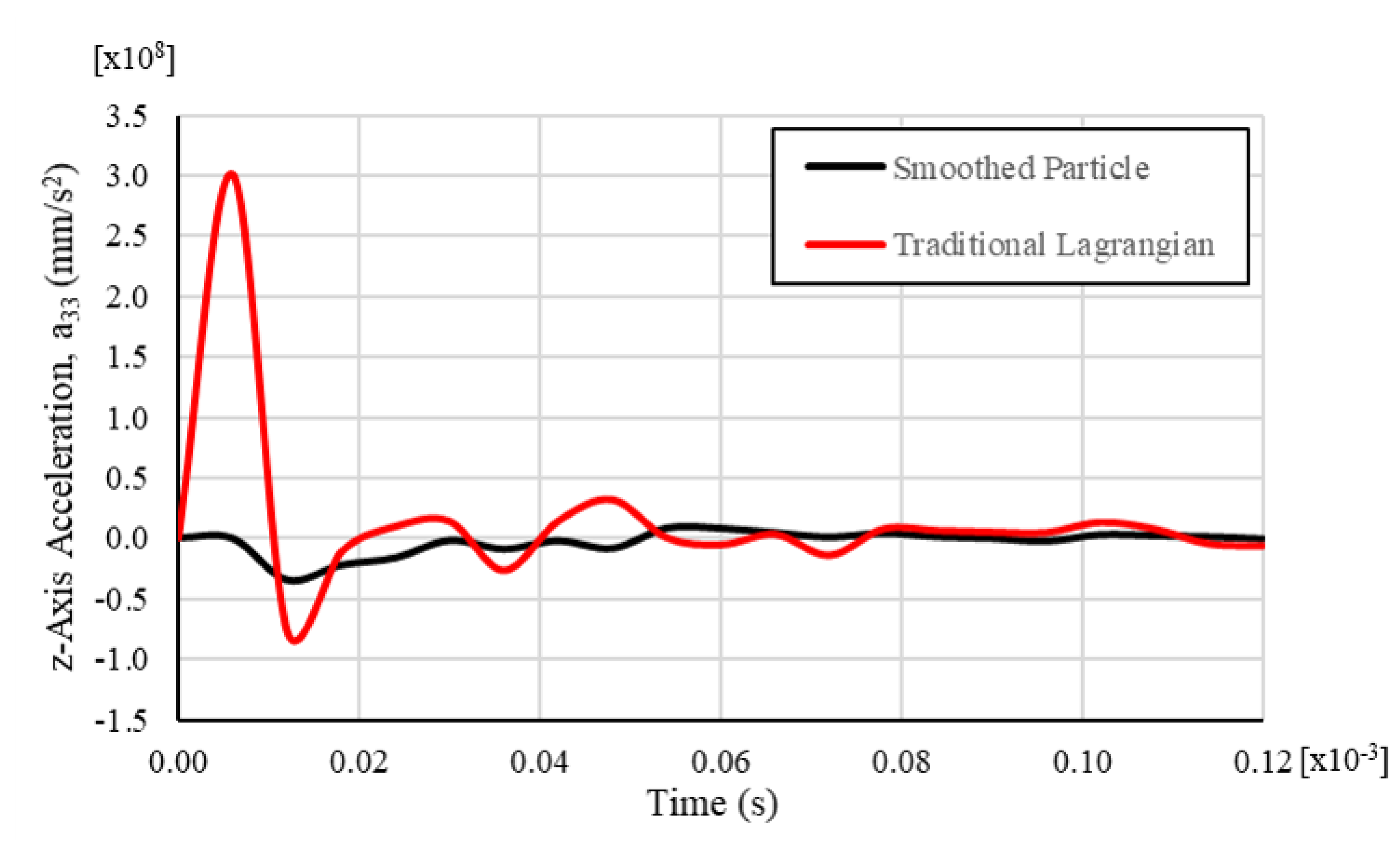
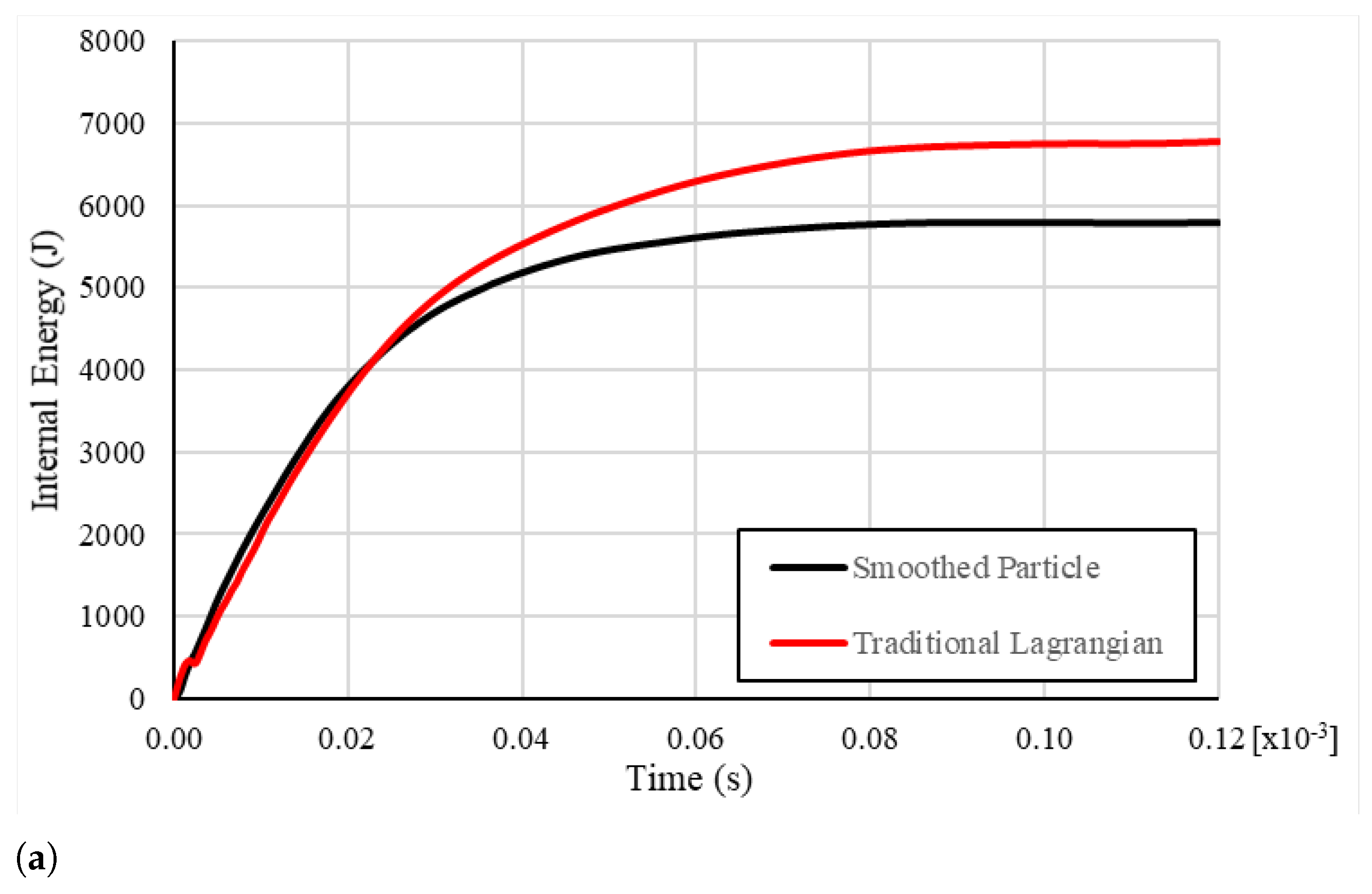
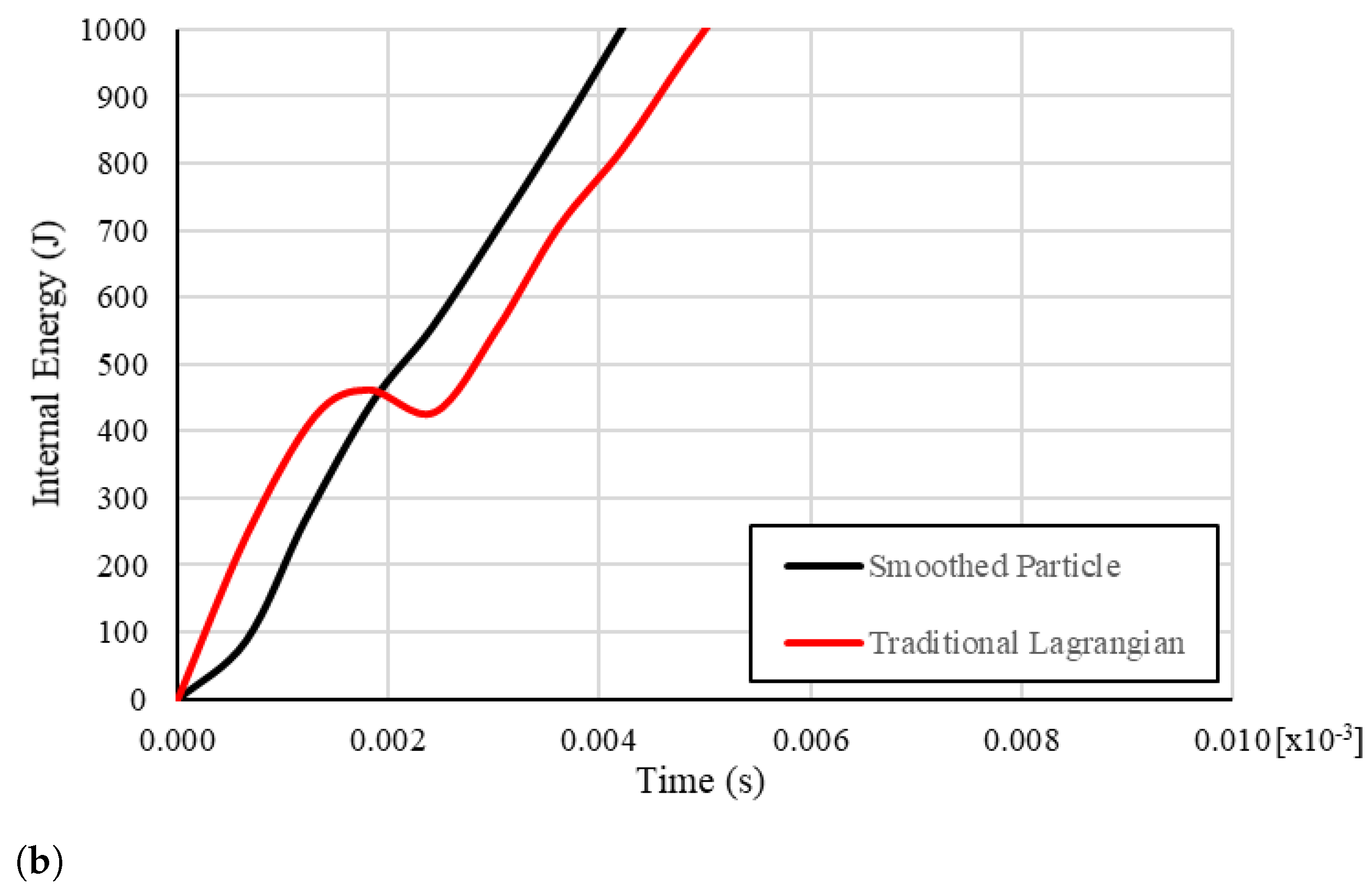
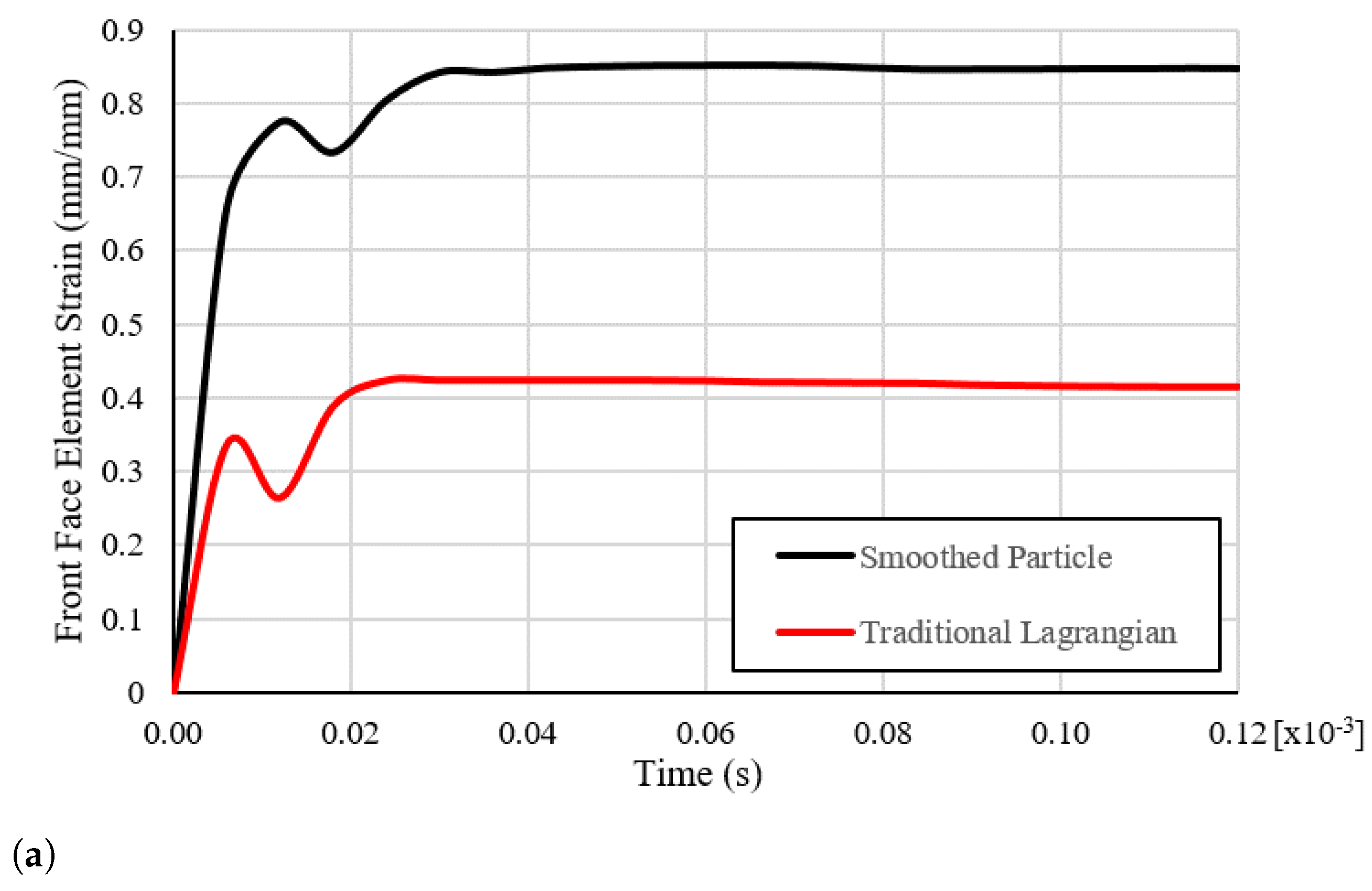
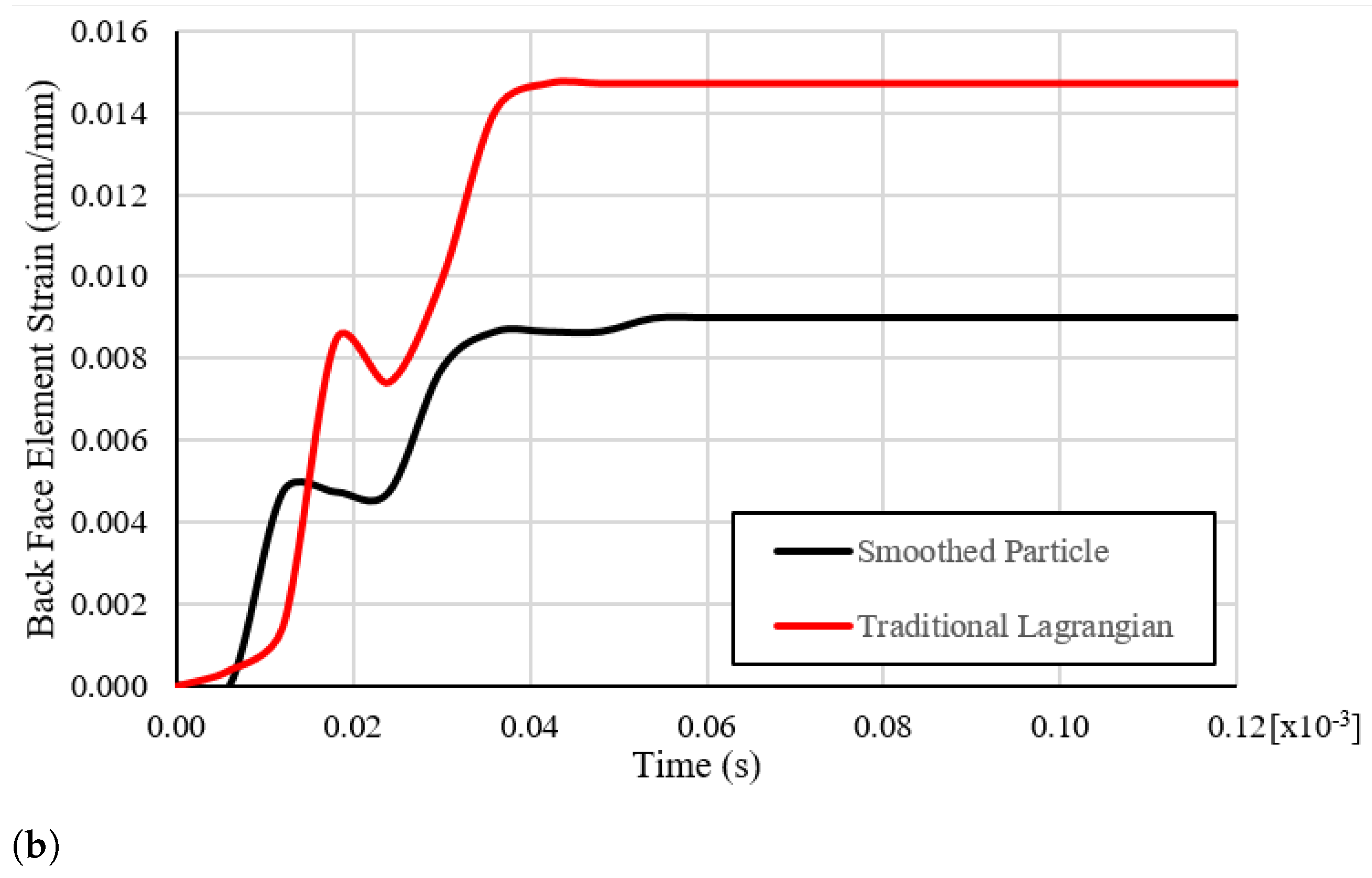
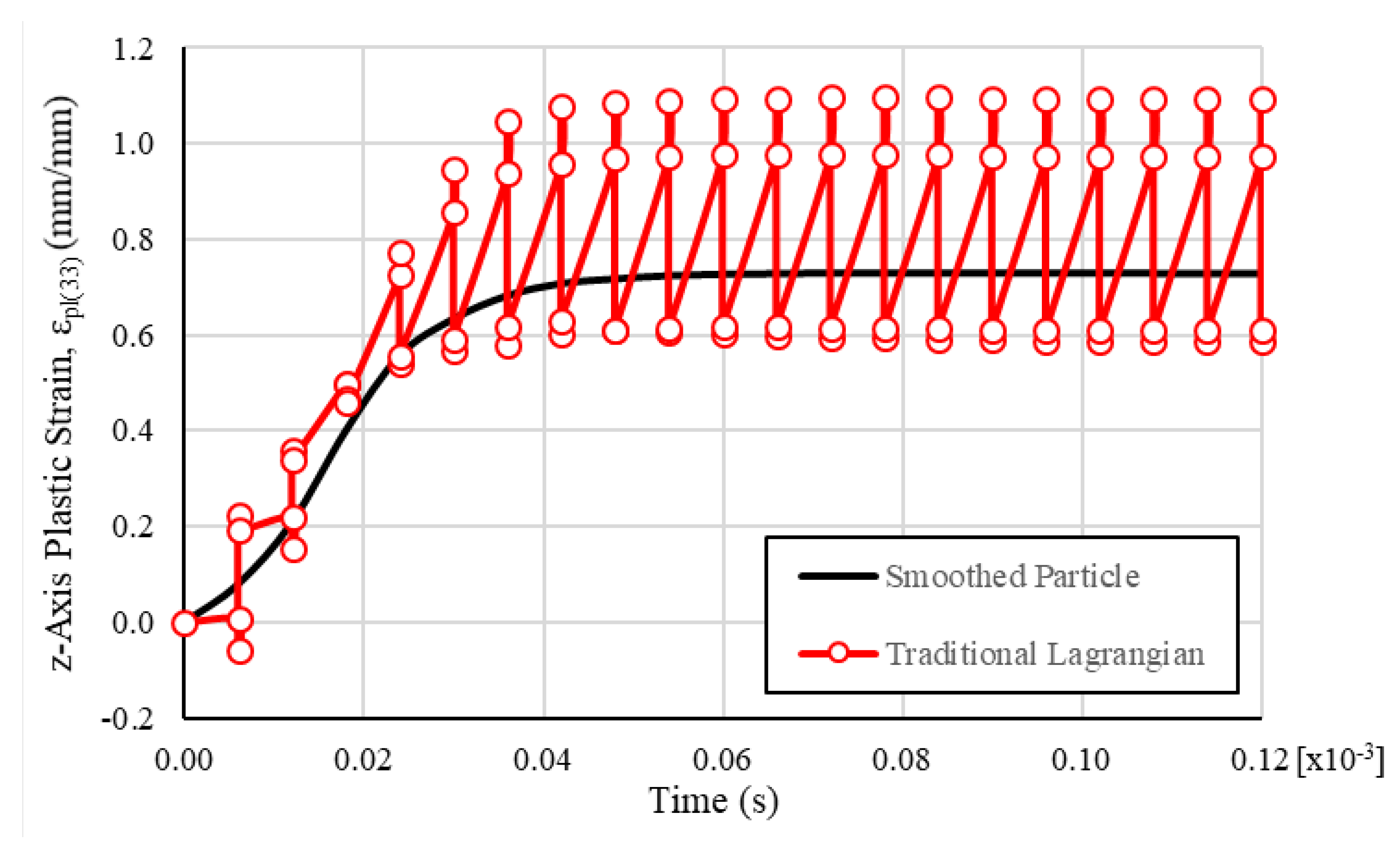
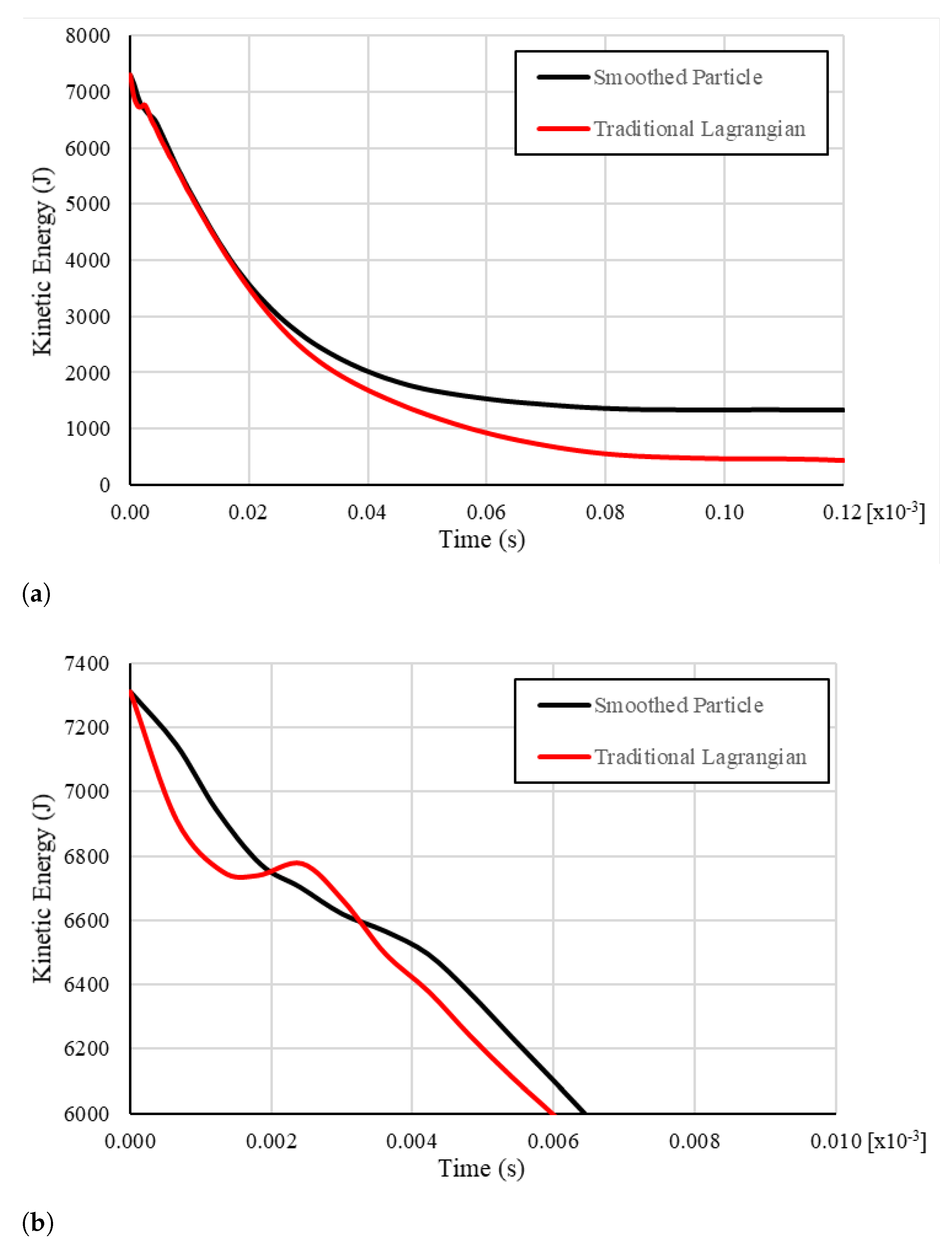
| Material Property | Value |
|---|---|
| Elastic Modulus, E | 69 GPa |
| Poisson’s Ratio, | 0.33 |
| Density, | 2700 g/m |
| Johnson-Cook Parameter | Value |
|---|---|
| Yield Stress, A | 324.1 MPa |
| Strain Hardening Parameter, B | 113.8 MPa |
| Strain Rate Parameter, C | 0.002 |
| Thermal Softening Exponent, m | 1.34 |
| Strain Hardening Exponent, n | 0.42 |
| Damage Constant, | −0.77 |
| Damage Constant, | 1.45 |
| Damage Constant, | −0.47 |
| Damage Constant, | 0.0 |
| Damage Constant, | 1.6 |
| Model | Residual Velocity (m/s) | Residual Velocity Error (%) | Processor Time (h) |
|---|---|---|---|
| Experimental | 336.194 | - | - |
| Traditional, Full | 30.186 | 91.021 | 1.0 |
| Traditional, Reduced | 30.189 | 91.020 | 0.3 |
| SPH | 335.406 | 0.234 | 5.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spear, D.G.; Palazotto, A.N.; Kemnitz, R.A. Modeling and Simulation Techniques Used in High Strain Rate Projectile Impact. Mathematics 2021, 9, 274. https://doi.org/10.3390/math9030274
Spear DG, Palazotto AN, Kemnitz RA. Modeling and Simulation Techniques Used in High Strain Rate Projectile Impact. Mathematics. 2021; 9(3):274. https://doi.org/10.3390/math9030274
Chicago/Turabian StyleSpear, Derek G., Anthony N. Palazotto, and Ryan A. Kemnitz. 2021. "Modeling and Simulation Techniques Used in High Strain Rate Projectile Impact" Mathematics 9, no. 3: 274. https://doi.org/10.3390/math9030274
APA StyleSpear, D. G., Palazotto, A. N., & Kemnitz, R. A. (2021). Modeling and Simulation Techniques Used in High Strain Rate Projectile Impact. Mathematics, 9(3), 274. https://doi.org/10.3390/math9030274





