Permanence for Nonautonomous Differential Systems with Delays in the Linear and Nonlinear Terms

Abstract

In this paper, we obtain sufficient conditions for the persistence and permanence of a family of nonautonomous systems of delay differential equations. This family includes structured models from mathematical biology, with either discrete or distributed delays in both the linear and nonlinear terms, and where typically the nonlinear terms are nonmonotone. Applications to systems inspired by mathematical biology models are given.

1. Introduction

In this paper, we investigate the persistence and permanence for a class of multidimensional nonautonomous delay differential equations (DDEs), which includes some structured models used in population dynamics, epidemiology, and other fields.

We start by setting the abstract framework for the DDEs which we deal with in the next sections. For $\tau \ge 0$, consider the Banach space $C:=C([-\tau ,0];{\mathbb{R}}^n)$ with the norm ${\displaystyle \parallel \varphi \parallel =\underset{\theta \in [-\tau ,0]}{max}\left|\varphi \left(\theta \right)\right|}$, where $|·|$ is a fixed norm in ${\mathbb{R}}^n$. We shall consider DDEs written in the abstract form:

$$x^{\prime }\left(t\right)=\mathcal{L}\left(t\right)x_t+f(t,x_t),t\ge t_0,$$

(1)

where $x_t\in C$ denotes the segment of a solution $x\left(t\right)$ given by $x_t\left(\theta \right)=x(t+\theta ),-\tau \le \theta \le 0$, the operator $\mathcal{L}\left(t\right):C\to {\mathbb{R}}^n$ is linear bounded, for $t\ge t_0$, and the nonlinearities are given by a continuous function $f:[t_0,\infty )\times C\to {[0,\infty )}^n$. For simplicity, we set $t_0=0$.

Recently, there has been a renewed interest in questions of persistence and permanence for DDEs. A number of methods has been proposed to tackle different situations, depending on whether the equations are autonomous or not, scalar or multi-dimensional, monotone or nonmonotone. See [1,2,3,4,5,6,7,8,9,10,11] and references therein for an explanation of the models and motivation from real world applications.

Here, the investigation concerning permanence in [5,6] is pursued. In [5] only cooperative systems were considered, whereas in [6], sufficient conditions for the permanence of systems:

$$\begin{array}{c}\hfill x_i^{\prime }\left(t\right)=-d_i\left(t\right)x_i\left(t\right)+\sum _{j=1}^n{a}_{ij}\left(t\right)x_j\left(t\right)+\sum _{k=1}^{m_i}{\beta }_{ik}\left(t\right)h_{ik}(t,x_i(t-{\tau }_{ik}\left(t\right))),i=1,\cdots ,n,t\ge 0,\end{array}$$

(2)

were established. Clearly, family (2) is a particular case of (1). In this paper, the more general framework of systems (1) with distributed delays in both $\mathcal{L}$ and f is considered. Although many works only consider constant or time-varying discrete delays, it is apparent that in many contexts distributed delays are more appropriate, for instance, the maturation delay for a species is not exactly the same for all individuals, or the incubation time for a disease is within a time frame (e.g., between 3 and 14 days for Covid-19), rather than a fixed value. These situations are better portrayed by distributed delays. In fact, the use of integro-differential equations with distributed (possibly infinite) delays in predator-prey models goes back to the works of Volterra in population dynamics [12], where typically the “memory functions” appear as $L^1$ integral kernels. PDEs (partial differential equations) models with discrete or distributed delays have also been largely analyzed. More recently, mathematicians have proposed fractional calculus to account for memory effects, in epidemic models as well as other fields – moreover, both time-delays and fractional-order derivatives have been used simultaneously, for different types of memory [13,14].

The criteria for permanence in [2,4,6] and other works demand that all coefficients are bounded. More recently, some authors have relaxed this restriction [8,9,15,16], though they still imposed some boundedness requirements. Here, the boundedness of all coefficients in (1) will not be a priori assumed. We also emphasize that typically the nonlinearites $f_i(t,\varphi )$ in (1) are not monotone in the second variable – which is the case of Nicholson-type systems, for example. Our results extend and improve some recent conclusions in the literature [2,3,9,16,17,18], which mostly deal with scalar DDEs and/or cooperative n-dimensional models. Special attention will be given to the case where each component $f_i$ of $f=(f_1,\cdots ,f_n)$ in (1) depends only on t and on the component i of the solution,

$$f(t,\varphi )=(f_1(t,{\varphi }_1),\cdots ,f_n(t,{\varphi }_n))\mathrm{for}t\ge 0,\varphi =({\varphi }_1,\cdots ,{\varphi }_n)\in C,$$

(3)

since sharper results will be obtained for such models.

We now introduce some standard notation. In what follows, ${\mathbb{R}}^{+}=[0,\infty )$, the matrix $I_n$, or simply I, denotes the $n\times n$ identity matrix and $\overrightarrow{1}=(1,\cdots ,1)\in {\mathbb{R}}^n.$ For $\tau >0$, the set $C^{+}=C([-\tau ,0];{\left({\mathbb{R}}^{+}\right)}^n)$ is the cone of nonnegative functions in C and ≤ the usual partial order generated by $C^{+}$: $\varphi \le \psi$ if and only if $\psi -\varphi \in C^{+}$. A vector $v\in {\mathbb{R}}^n$ is identified in C with the constant function $\psi \left(\theta \right)=v$ for $-\tau \le \theta \le 0$. In this way, for $u,v\in {\mathbb{R}}^n$ with $u\le v$, the interval $I=[u,v]$ in C is the set $\{\varphi \in C:u\le \varphi \le v\}$. For $\tau =0$, we take $C={\mathbb{R}}^n,C^{+}={\left({\mathbb{R}}^{+}\right)}^n$; a vector $v\in {\mathbb{R}}^n$ is positive if all its components are positive, and we write $v>0$. We write $\varphi <\psi$ if $\psi \left(\theta \right)<\varphi \left(\theta \right)$ for $\theta \in [-\tau ,0]$; the relations ≥ and > are also defined in the usual way.

For nonlinear DDEs (1) under conditions of existence and uniqueness of solutions, $x(t,\sigma ,\varphi )$ denotes the solution of (1) with initial condition $x_{\sigma }=\varphi$, for $(\sigma ,\varphi )\in {\mathbb{R}}^{+}\times C$. For models inspired by real world applications, we shall consider:

$$C_0^{+}=\{\varphi \in C^{+}:\varphi \left(0\right)>0\}$$

as the set of admissible initial conditions. Without loss of generality, we shall restrict the analysis to solutions $x(t,0,\varphi )$ with $\varphi \in C_0^{+}$, and assume that f is sufficiently regular so that such solutions are defined on ${\mathbb{R}}^{+}$. If the set $C_0^{+}$ is (positively) invariant for (1), the notions of (uniform) persistence, permanence, and stability always refer to solutions with initial conditions in $C_0^{+}$. In this way, we say that the system is uniformly persistent (in $C_0^{+}$) if there exists a positive uniform lower bound for all solutions with initial conditions in $C_0^{+}$, i.e., there is $m>0$ such that all solutions $x\left(t\right)=x(t,0,\varphi )$ with $\varphi \in C_0^{+}$ defined on ${\mathbb{R}}^{+}$ and satisfy $x_i(t,0,\varphi )\ge m$ for $t\gg 1$ and $i=1,\cdots ,n$. The system (1) is said to be permanent if there exist positive constants $m,M$ such that all solutions $x\left(t\right)=x(t,0,\varphi )$ with $\varphi \in C_0^{+}$ are defined on ${\mathbb{R}}^{+}$ and satisfy $m\le x_i\left(t\right)\le M$ for $t\gg 1$ and $i=1,\cdots ,n$. As usual, the expression $t\gg 1$ means “for $t>0$ sufficiently large". In some contexts, it will be apparent that it is more convenient to consider a proper and invariant subset S of $C_0^{+}$ as the set of admissible initial conditions for (1) (see e.g., Section 3.3). Here, a DDE $x^{\prime }\left(t\right)=F(t,x_t)$ is said to be cooperative if $F=(F_1,\cdots ,F_n)$ satisfies the quasi-monotone condition (Q) in [19] (p. 78): if $\varphi ,\psi \in C^{+}$ and $\varphi \ge \psi$, then $F_i(t,\varphi )\ge F_i(t,\psi )$ for $t\ge 0$, whenever ${\varphi }_i\left(0\right)={\psi }_i\left(0\right)$ for some i.

The remainder of this paper is divided into three sections. In Section 2, we establish sufficient conditions for uniform persistence and permanence for a large family of nonlinear system (1). To illustrate the results, several applications are given in Section 3, such as to generalized Nicholson systems, Mackey–Glass systems, and a competitive chemostat model. Some examples and counter-examples, showing the necessity of some hypotheses, will also be presented in Section 3. The paper ends with a short section of conclusions and open problems.

2. Persistence and Permanence for a Class of Nonautomous DDEs

In this section, we establish explicit and easily verifiable criteria for both the persistence and permanence of systems (1).

Let $C:=C([-\tau ,0];{\mathbb{R}}^n)$ with the supremum norm be the phase space. We start with a general nonutonomous linear differential equation in C,

$$x^{\prime }\left(t\right)=\mathcal{L}\left(t\right)x_t,$$

(4)

where $\mathcal{L}:{\mathbb{R}}^{+}\to L(C;{\mathbb{R}}^n)$, $L(C;{\mathbb{R}}^n)$ is the usual space of bounded linear operators from C to ${\mathbb{R}}^n$ equipped with the operator norm, and $t\mapsto \mathcal{L}\left(t\right)\varphi$ is the Borel measurable for each $\varphi$, with $\parallel \mathcal{L}\left(t\right)\parallel$ bounded on ${\mathbb{R}}^{+}$ by a function $m\left(t\right)$ in $L_{\mathrm{loc}}^1({\mathbb{R}}^{+};\mathbb{R})$.

Assuming the exponential asymptotic stability of (4), the next theorem provides conditions for the dissipativeness and extinction of perturbed nonlinear systems. Its proof is easily deduced from the variation of constant formula [20] and arguments similar to the ones for ODEs (ordinary differential equations), thus it is omitted.

Theorem 1.

Assume that (4) is exponentially asymptotically stable, and consider the perturbed equation:

$$x^{\prime }\left(t\right)=\mathcal{L}\left(t\right)x_t+f(t,x_t),t\ge 0,$$

(5)

where $f:{\mathbb{R}}^{+}\times S\to {\mathbb{R}}^n$ is continuous and S is a (positively) invariant set for (5).

(i)

If f is bounded, then (5) is dissipative i.e., all solutions of (5) are defined on ${\mathbb{R}}^{+}$ and there exists $M>0$ such that any solution $x\left(t\right)$ of (5) satisfies ${lim\; sup}_{t\to \infty }\left|x\left(t\right)\right|\le M$;

(ii)

If there exists $\beta :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ measurable with ${\int }^{\infty }\beta \left(s\right)ds<\infty$ such that $\left|f\right(t,\varphi \left)\right|\le \beta \left(t\right)\parallel \varphi \parallel ,t\gg 1,$ then all solutions $x\left(t\right)$ of (5) satisfy ${lim\; sup}_{t\to \infty }x\left(t\right)=0.$

For (4), we now suppose that $\mathcal{L}=({\mathcal{L}}_1,\cdots ,{\mathcal{L}}_n)$ is given by:

$${\mathcal{L}}_i\left(t\right)\varphi =-d_i\left(t\right){\varphi }_i\left(0\right)+\sum _{j=1}^n{L}_{ij}\left(t\right){\varphi }_j,t\ge 0,\varphi =({\varphi }_1,\cdots ,{\varphi }_n)\in C,i=1,\cdots ,n,$$

(6)

with $d_i\left(t\right)$ continuous and $L_{ij}\left(t\right)$ bounded linear functionals. Although it is not relevant for our results, we may assume that $L_{ii}\left(t\right)$ is non-atomic at zero (see [20] for a definition). For (4), define the $n\times n$ matrix-valued functions:

$$D\left(t\right)=diag(d_1\left(t\right),\cdots ,d_n\left(t\right)),A\left(t\right)=\left[a_{ij}\left(t\right)\right],$$

(7)

where

$$a_{ij}\left(t\right)=\parallel L_{ij}\left(t\right)\parallel ,t\ge 0,i,j\in \{1,\cdots ,n\}.$$

For (4), the general hypotheses below will be considered:

(H1)

The functions $d_i:{\mathbb{R}}^{+}\to \mathbb{R},L_{ij}:{\mathbb{R}}^{+}\to L(C([-\tau ,0];\mathbb{R});\mathbb{R})$ are continuous (for some $\tau \ge 0$), $i,j=1,\cdots ,n$;

(H2)

There exist a vector $v>0$ and a constant $\delta >0$ such that $\left[D\left(t\right)-A\left(t\right)-\delta I_n\right]v\ge 0$ for $t\gg 1$.

Instead of (H2), one may assume:

(H2*)

There exist a vector $v>0$ and a constant $\alpha >1$ such that $D\left(t\right)v\ge \alpha A\left(t\right)v$ for $t\gg 1$.

Note that the sign of the function $d_i\left(t\right)$ is not prescribed in (H1), however, if (H2) is fulfilled, then $d_i\left(t\right)>0$ for $t>0$ large. With the notation in (7), e.g., assumption (H2) above translates as: There exist a vector $v=(v_1,\cdots ,v_n)>0$ and $T\ge 0,\delta >0$ such that $d_i\left(t\right)v_i-{\sum }_{j=1}^n{a}_{ij}\left(t\right)v_j\ge \delta v_i$ for all $t\ge T,i=1,\cdots ,n$.

Next theorem gives some stability results selected from [21].

Theorem 2.

Consider the system (4) under (H1), and assume one of the following sets of conditions:

(i)

(H2) is satisfied and $a_{ij}\left(t\right)$ are bounded functions on ${\mathbb{R}}^{+}$ for all $i,j=1,\cdots ,n$;

(ii)

(H2*) is satisfied and ${lim\; inf}_{t\to \infty }{d}_i\left(t\right)>0$ for $i=1,\cdots ,n$;

(iii)

(4) is the ODE system $x_i^{\prime }\left(t\right)=-d_i\left(t\right)x_i\left(t\right)+{\sum }_{j\ne i}{d}_{ij}\left(t\right)x_j\left(t\right),1\le i\le n$, and (H2) is satisfied with $a_{ij}\left(t\right)=\left|d_{ij}\left(t\right)\right|$. Then, (4) is exponentially asymptotically stable, in other words, there exist $k,\alpha >0$ such that:

$$|x(t,t_0,\phi )|\le k{e}^{-\alpha (t-t_0)}\parallel \phi \parallel \mathrm{for}\mathrm{all}t\ge t_0\ge 0,\phi \in C.$$

Proof. 

The result follows from the criteria in [21] (Theorem 3.1). □

Henceforth, we consider delay differential systems written as:

$$x_i^{\prime }\left(t\right)=-d_i\left(t\right)x_i\left(t\right)+\sum _{j=1}^n{L}_{ij}\left(t\right)x_{j,t}+f_i(t,x_t),t\ge 0,i=1,\cdots ,n,$$

(8)

with the linear functionals $L_{ij}\left(t\right)$ nonnegative (i.e., $L_{ij}\left(t\right){\varphi }_j\ge 0$ for ${\varphi }_j\ge 0$) and $f_i(t,\varphi )$ continuous and satisfying same requirements formulated below. In general $\varphi \mapsto f_i(t,\varphi )$ is not monotone for the order ≤ associated with $C^{+}$, and therefore (8) is not cooperative. Recall that, by the Riesz representation theorem, the nonnegative bounded functionals $L_{ij}\left(t\right)$ have a representation:

$$L_{ij}\left(t\right){\varphi }_j=a_{ij}\left(t\right){\int }_{-\tau }^0{\varphi }_j\left(s\right)d_s{\nu }_{ij}(t,s),$$

(9)

where $a_{ij}\left(t\right)=\parallel L_{ij}\left(t\right)\parallel$, the functions ${\nu }_{ij}(t,s)$ are defined for $(t,s)\in {\mathbb{R}}^{+}\times [-\tau ,\infty )$, are continuous in t, left-continuous and nondecreasing in s, and normalized so that ${\int }_{-\tau }^0{d}_s{\nu }_{ij}(t,s)=1,t\ge 0.$ In the case of no delays in (9), then $L_{ij}\left(t\right)x_{j,t}=a_{ij}\left(t\right)x_j\left(t\right)$ with $a_{ij}\left(t\right)\ge 0$. Clearly, this framework includes the particular case of DDEs with multiple time discrete delays in both the linear and nonlinear terms.

Systems (8) are sufficiently general to encompass many relevant models from mathematical biology and other fields. In some contexts, they are interpreted as structured models for populations distributed over n different classes or patches, with migration among the patches, where $x_i\left(t\right)$ is the density of the species on class i, $a_{ij}\left(t\right)$ ($j\ne i)$ is the migration coefficient from class j to class i, $d_i\left(t\right)$ the coefficient of instantaneous loss for class i, and $f_i(t,\varphi )$ is the growth function for class i. DDEs where the delays intervene in the linear terms have deserved the attention of a number of researchers, e.g. as patch structured population or SIS (susceptible-infective-susceptible) multi-strain epidemic models with time delays for the dispersal among patches [9,11,17]. We also refer the reader to [1,2,3,15,19], for real interpretation of the DDEs under consideration and more applications.

In what follows, for $\varphi =({\varphi }_1,\cdots ,{\varphi }_n)\in C^{+}$ we use the notations:

$$\underline{{\varphi }_i}=\underset{s\in [-\tau ,0]}{min}{\varphi }_i\left(s\right),\underline{\varphi }=\underset{1\le i\le n}{min}\underline{{\varphi }_i}.$$

To obtain the uniform persistence of (8), we need to prescribe the behavior of $f(t,\varphi )$ when $\varphi \to 0^{+}$. We shall impose that the nonlinearities satisfy the following conditions:

(H3)

The functions $f_i:{\mathbb{R}}^{+}\times C^{+}\to {\mathbb{R}}^{+}$ are completely continuous and locally Lipschitzian in the second variable, $i\in \{1,\cdots ,n\};$

(H4)

There exist $r>0$, and continuous functions ${\beta }_i:{\mathbb{R}}^{+}\to (0,\infty ),h_i^{-}:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$, such that, for $i\in \{1,\cdots ,n\}$:

(i)

$h_i^{-}\left(0\right)=0,h_i^{-}\left(x\right)>0$ for $0<x\le r$ and there exists ${\left(h_i^{-}\right)}^{\prime }(0+)=1$;

(ii)

For any positive solution $x\left(t\right)$ of (8),

$$f_i(t,x_t)\ge {\beta }_i\left(t\right)h_i^{-}\left({\underline{x}}_t\right)\mathrm{if}\underline{x_t}\le r,\mathrm{for}t\gg 1;$$

(10)

(H5)

There exists a constant $\delta >0$ such that $[M\left(t\right)-\delta I_n]\overrightarrow{1}\ge 0,t\gg 1$, where $M\left(t\right)$ is the matrix-valued function defined by:

$$\begin{array}{cc}\hfill M\left(t\right)& =B\left(t\right)+A\left(t\right)-D\left(t\right),\mathrm{where}\hfill \\ \hfill B\left(t\right)& =diag({\beta }_1\left(t\right),\cdots ,{\beta }_n\left(t\right)),t\ge 0,\hfill \end{array}$$

(11)

with $D\left(t\right),A\left(t\right)$ as above and ${\beta }_i\left(t\right)$ as in (H4).

Instead of or together with (H5), and with the some notations, we shall often assume:

(H5*)

There exists a constant $\alpha >1$ such that $B\left(t\right)\overrightarrow{1}\ge \alpha \left[D\left(t\right)-A\left(t\right)\right]\overrightarrow{1}$ for $t\gg 1$.

Some comments about these assumptions are given in the remarks below.

Remark 1.

If the coefficients ${\beta }_i\left(t\right)$ are bounded, then (H5) implies (H5*). Indeed, if (H5) holds and there exists $M={max}_{1\le i\le n}{sup}_{t\ge 0}{\beta }_i\left(t\right)$ (as a matter of fact, it suffices that $d_i\left(t\right)-{\sum }_j{a}_{ij}\left(t\right)\le M$ for some M), then (H5*) is satisfied with any constant $\alpha \in (0,1+\delta /M]$. The converse is also true if ${\beta }_i\left(t\right)$ are all bounded from below by a positive constant, since in this case (H5*) implies that (H5) is satisfied with $\delta \in (0,(1-{\alpha }^{-1})c]$ for $c>0$ such that $c={min}_{1\le i\le n}{inf}_{t\ge 0}{\beta }_i\left(t\right)$. Similarly, one easily verifies (conf. [21]) that when the coefficients $d_i\left(t\right)$ are bounded from below by a positive constant, then (H2*) implies (H2) and that, if $a_{ij}\left(t\right)$ are all bounded, (H2) implies (H2*).

In the study of stability for nonautonous DDEs, a condition as (H2*) with $v=\overrightarrow{1}$ has been often presented (see e.g., [5,9]) in the equivalent form (for a positive denominator) ${lim\; inf}_{t\to \infty }\frac{d_i\left(t\right)}{{\sum }_{j=1}^n{a}_{ij}\left(t\right)}>1.$ Analogously, (H5*) can be written as ${lim\; inf}_{t\to \infty }\frac{{\beta }_i\left(t\right)}{d_i\left(t\right)-{\sum }_{j=1}^n{a}_{ij}\left(t\right)}>1,$ if $d_i\left(t\right)-{\sum }_{j=1}^n{a}_{ij}\left(t\right)>0$ for $t\gg 1$.

Remark 2.

If (10) holds with a function $h_i^{-}$ satisfying $h_i^{-}\left(0\right)=0$, $h_i^{-}\left(x\right)>0$ on $(0,\infty )$ and ${\left(h_i^{-}\right)}^{\prime }(0+)=c_i>0$, by replacing $h_i^{-}\left(x\right),{\beta }_i\left(t\right)$ by ${\overline{h}}_i^{-}\left(x\right)=c_i^{-1}{h}_i^{-}\left(x\right),{\overline{\beta }}_i\left(t\right)=c_i{\beta }_i\left(t\right)$, respectively, we may always assume that ${\left(h_i^{-}\right)}^{\prime }(0+)=1$.

The main criterion for the uniform persistence and permanence of (8) is now established. Although its proof follows along the main ideas in [6] (Theorem 3.3), new arguments are used to take into account the more general form of (8): Namely, delays are allowed in the linear part, the nonlinearity $f=(f_1,\cdots ,f_n)$ need not have the form (3), the coefficients $d_i\left(t\right),{\beta }_i\left(t\right)$ are not required to be bounded below or above by positive constants, nor $a_{ij}\left(t\right)$ if there are no delays in $L_{ij}\left(t\right)$, and $d_i\left(t\right)$ may actually change sign.

Moreover, we should mention that there was an incomplete argument in [6], finished here, since the case of a solution $x\left(t\right)$ with ${min}_{1\le j\le n}{lim\; inf}_{t\to \infty }{x}_j\left(t\right)={lim}_{t\to \infty }{x}_i\left(t\right)$ for some i with $x_i\left(t\right)$ strictly increasing for large $t>0$, was not addressed in [6]. See Step 4 of the proof below and Corollary 1, for the treatment of this situation.

Theorem 3.

For (8), assume (H1), (H3), and (H4). Furthermore, let the following conditions hold:

(i)

Either $L_{ij}\left(t\right){\varphi }_j=a_{ij}\left(t\right){\varphi }_j\left(0\right)$ with $a_{ij}\left(t\right)\ge 0$, for all $i,j=1,\cdots ,n$ and $t\ge 0$ (in other words, there are no delays in (4)), or $L_{ij}\left(t\right)$ are nonnegative and $a_{ij}\left(t\right)=\parallel L_{ij}\left(t\right)\parallel$ are bounded on ${\mathbb{R}}^{+}$, $i,j=1,\cdots ,n$;

(ii)

(H5) and (H5*) are both satisfied.

Then (8) is persistent (in $C_0^{+}$). If in addition (H2) holds and $f(t,\varphi )$ is bounded, the system is permanent.

Proof. 

The proof follows in several steps.

Step 1. Write (8) as $x^{\prime }\left(t\right)=F(t,x_t)$, where $F=(F_1,\cdots ,F_n)$,

$$F_i(t,\varphi )=-d_i\left(t\right){\varphi }_i\left(0\right)+\sum _{j=1}^n{L}_{ij}\left(t\right){\varphi }_j+f_i(t,\varphi )(1\le i\le n).$$

(12)

It is clear that F is continuous, locally Lipschitzian in the second variable and bounded on bounded sets of ${\mathbb{R}}^{+}\times C^{+}$. Observe that the solutions of (8) satisfy the ordinary differential inequalities $x_i^{\prime }\left(t\right)\ge -d_i\left(t\right)x_i\left(t\right)(1\le i\le n)$, thus the solutions $x(t,0,\varphi )$ with $\varphi \in C_0^{+}$ are positive for $t\ge 0$.

From (ii), there are ${\delta }_0>0$, ${\alpha }_0>1$ and $T_0>0$ such that:

$$\begin{array}{cc}\hfill {\beta }_i\left(t\right)& \ge d_i\left(t\right)-\sum _j{a}_{ij}\left(t\right)+{\delta }_0,\hfill \\ \hfill {\beta }_i\left(t\right)& \ge {\alpha }_0\left(d_i\left(t\right)-\sum _j{a}_{ij}\left(t\right)\right),t\ge T_0,i=1,\cdots ,n.\hfill \end{array}$$

(13)

Summing up these inequalities, we obtain:

$$\begin{array}{c}\hfill {\alpha }^{-1}{\beta }_i\left(t\right)\ge \left(d_i\left(t\right)-\sum _j{a}_{ij}\left(t\right)\right)+\delta t\ge T_0,i=1,\cdots ,n,\end{array}$$

(14)

for $\alpha =(1+{\alpha }_0)/2>1,{\delta }_0=\delta /2$.

Consider a positive solution $x\left(t\right)=x(t,0,\varphi )$ of (8). For $r>0$ as in (H4) choose $m\in (0,r]$ such that $h_i^{-}\left(x\right)$ is strictly increasing with ${\alpha }^{-1}x<h_i^{-}\left(x\right)$ on the interval $(0,m]$. In this way, $f_i(t,x_t)\ge {\beta }_i\left(t\right)h_i^{-}\left(\underline{x_t}\right)\ge {\alpha }^{-1}{\beta }_i\left(t\right)\underline{x_t}$ if $\underline{x_t}\le m$. Replacing $h_i^{-}\left(x\right)$ by the function $min\{h_i^{-}\left(x\right),x\}$, we may also assume that $h_i^{-}\left(x\right)\le x$ for all $x\ge 0$.

We now derive the uniform persistence of (8) by showing in the next steps that, for any solution $x\left(t\right)=x(t,T_0,\varphi )$, there exists $T\ge T_0$ such that:

$$x_i\left(t\right)\ge m\mathrm{for}\mathrm{all}t\ge T,1\le i\le n.$$

(15)

Step 2. We first prove that the ordered interval ${[m,\infty )}^n:=\{\varphi \in C:{\varphi }_i\ge m,i=1,\cdots ,n\}\subset C$ is invariant for (8) for $t\in [T_0,\infty )$.

Note that the operators $L_{ij}\left(t\right)$ are nondecreasing and $h_i^{-}\left(x\right)>{\alpha }^{-1}x$ on $(0,m]$. If $\varphi \in {[m,\infty )}^n$ and ${\varphi }_i\left(0\right)=m$ for some i, from (13) we therefore obtain, for $t\ge T_0$,

$$F_i(t,\varphi )\ge m\left[-d_i\left(t\right)+\sum _j{a}_{ij}\left(t\right)\right]+{\beta }_i\left(t\right)h_i^{-}\left(m\right)>m\left[-d_i\left(t\right)+\sum _j{a}_{ij}\left(t\right)+{\alpha }^{-1}{\beta }_i\left(t\right)\right]\ge 0.$$

From [19] (Remark 5.2.1), it follows that the set ${[m,\infty )}^n\subset C$ is positively invariant for (8).

Step 3. For $T_0$ as before, define:

$$s_0=\underset{j}{min}\underset{t\in [T_0,T_0+\tau ]}{min}{x}_j\left(t\right),s_1=\underset{j}{min}\underset{t\in [T_0+\tau ,T_0+2\tau ]}{min}{x}_j\left(t\right).$$

Let $s_1=x_i\left(t_0\right)$, for some $t_0\in [T_0+\tau ,T_0+2\tau ]$ and $i\in \{1,\cdots ,n\}$.

We first show that $s_1<m$ implies that $s_1>s_0$.

If $s_1\le s_0$, then:

$$s_1=x_i\left(t_0\right)=\underset{j}{min}\underset{t\in [T_0,T_0+2\tau ]}{min}{x}_j\left(t\right)$$

and $x_i^{\prime }\left(t_0\right)\le 0$. Assuming that $s_1\le s_0$ and $x_i\left(t_0\right)<m$, since $x_{j,t}\ge x_i\left(t_0\right)(1\le j\le n)$ for $t\in [t_0-\tau ,t_0]$, we get:

$$\begin{array}{cc}\hfill 0\ge x_i^{\prime }\left(t_0\right)\ge & -d_i\left(t_0\right)x_i\left(t_0\right)+\sum _j{a}_{ij}\left(t_0\right)\underline{x_{j,t_0}}+f_i(t_0,x_{t_0})\hfill \\ \hfill \ge & \left(-d_i\left(t_0\right)+\sum _j{a}_{ij}\left(t_0\right)\right)x_i\left(t_0\right)+{\beta }_i\left(t_0\right)h_i^{-}\left(x_i\left(t_0\right)\right)\hfill \\ \hfill >& \left(-d_i\left(t_0\right)+\sum _j{a}_{ij}\left(t_0\right)+{\alpha }^{-1}{\beta }_i\left(t_0\right)\right)x_i\left(t_0\right)\ge 0,\hfill \end{array}$$

which is a contradiction. This shows that $s_1>s_0$ whenever $s_1<m$.

Step 4. Define the sequence:

$$s_k=\underset{j}{min}\underset{t\in [T_0+k\tau ,T_0+(k+1)\tau ]}{min}{x}_j\left(t\right),k\in {\mathbb{N}}_0.$$

For the sake of contradiction, assume that $s_k<m$ for all $k\in {\mathbb{N}}_0$. Thus, reasoning as in Step 3, $\left(s_k\right)$ is strictly increasing. Let $t_k\in I_k:=[T_0+k\tau ,T_0+(k+1)\tau ]$ be such that $s_k=x_{i_k}\left(t_k\right)$, for some $i_k\in \{1,\cdots ,n\}.$ By jumping some of the intervals $I_k$ and considering a subsequence of $\left(t_k\right)$, still denoted by $\left(t_k\right)$, we may consider a unique $i\in \{1,\cdots ,n\}$ such that $s_k=x_i\left(t_k\right)$. Denote $\ell ={lim}_k{s}_k={sup}_k{s}_k>0$. Clearly, $\ell ={lim\; inf}_{t\to \infty }{x}_i\left(t\right)={min}_{1\le j\le n}{lim\; inf}_{t\to \infty }{x}_j\left(t\right)$.

If $\ell ={lim}_{t\to \infty }{x}_i\left(t\right)$, then $x_i\left(t\right)$ is bounded and from the fluctuation lemma (taking a subsequence if necessary) we have $x_i^{\prime }\left(t_k\right)\to 0$ as $k\to \infty$. If $x_i\left(t\right)$ does not converge to ℓ, $x_i\left(t_k\right)$ are local minima for k large, therefore $x_i^{\prime }\left(t_k\right)=0$. In both cases, we have $x_i^{\prime }\left(t_k\right)\to 0$ as $k\to \infty$.

Let $\alpha >1$ and $\delta >0$ be as in (14). We now claim that:

$$s_{k+1}\ge \alpha \underset{j}{min}{h}_j^{-}\left(s_k\right),k\in {\mathbb{N}}_0.$$

(16)

Otherwise, suppose that there is k such that $s_{k+1}<\alpha {min}_j{h}_j^{-}\left(s_k\right)$.

We distinguish two situations: Either there are no delays in (4), or $a_{ij}\left(t\right)$ are all bounded in ${\mathbb{R}}^{+}$ – in which case we suppose that $\alpha$ is chosen so that it also satisfies $1<\alpha <\frac{M_1}{M_1-\delta },$ where ${max}_{1\le j\le n}{sup}_{t\ge 0}\left({\sum }_j{a}_{ij}\left(t\right)\right)\le M_1$.

First, we treat the case of no delays in the linear part $\mathcal{L}$ of (4). In this situation, $L_{ij}\left(t\right)x_{j,t}=a_{ij}{x}_j\left(t\right)\ge a_{ij}\left(t\right)s_k$ for $t\in I_k(k\in {\mathbb{N}}_0)$. Estimate (14) leads to:

$$\begin{array}{cc}\hfill x_i^{\prime }\left(t_{k+1}\right)\ge & -d_i\left(t_{k+1}\right)s_{k+1}+\sum _j{a}_{ij}\left(t_{k+1}\right)s_{k+1}+{\beta }_i\left(t_{k+1}\right)h_i^{-}\left(s_k\right)\hfill \\ \hfill >& \left(-d_i\left(t_{k+1}\right)+\sum _j{a}_{ij}\left(t_{k+1}\right)+{\alpha }^{-1}{\beta }_i\left(t_{k+1}\right)\right)s_{k+1}\ge \delta s_{k+1}\to \delta \ell >0,\hfill \end{array}$$

(17)

which is not possible. Thus, (16) holds.

When delays are allowed in the linear part, we can write $L_{ij}{x}_{j,t}\ge a_{ij}\left(t\right)s_k$ for $t\in I_{k+1}$, and $s_k\ge h_i^{-}\left(s_k\right)>{\alpha }^{-1}{s}_{k+1}$, thus we have:

$$\begin{array}{cc}\hfill x_i^{\prime }\left(t_{k+1}\right)\ge & -d_i\left(t_{k+1}\right)s_{k+1}+\sum _j{a}_{ij}\left(t_{k+1}\right)s_k+{\beta }_i\left(t_{k+1}\right)h_i^{-}\left(s_k\right)\hfill \\ \hfill >& \left({\alpha }^{-1}{\beta }_i\left(t_{k+1}\right)+\sum _j{a}_{ij}\left(t_{k+1}\right)-d_i\left(t_{k+1}\right)\right)s_{k+1}+(s_k-s_{k+1})\sum _j{a}_{ij}\left(t_{k+1}\right)\hfill \\ \hfill \ge & \delta s_{k+1}+s_{k+1}({\alpha }^{-1}-1)M_1\hfill \\ \hfill =& [\delta +({\alpha }^{-1}-1)M_1]s_{k+1}\to [\delta +({\alpha }^{-1}-1)M_1]\ell >0,\hfill \end{array}$$

which is a contradiction. Thus, claim (16) is proven.

From (16), we obtain $m\ge \ell \ge \alpha {min}_j{h}_j^{-}\left(\ell \right)>\ell$, which is not possible. Therefore, $s_k\ge m$ for some k, and the result follows by Step 2.

If in addition (H2) is satisfied, from Theorem 2 the linear system (4) is exponentially asymptotically stable (for the case of no delays in the linear functionals $L_{ij}\left(t\right)$, recall that the boundedness of $a_{ij}\left(t\right)$ is not required). With f bounded, Theorem 1 implies now that (8) is dissipative, and therefore permanent. □

When $f=(f_1,\cdots ,f_n)$ has the form in (3), not only may one take $\underline{x_{i,t}}$ instead of $\underline{x_t}$ in (H4)(ii), but a slightly stronger version of the above theorem holds.

Theorem 4.

For

$$x_i^{\prime }\left(t\right)=-d_i\left(t\right)x_i\left(t\right)+\sum _{j=1}^n{L}_{ij}\left(t\right)x_{j,t}+f_i(t,x_{i,t}),t\ge 0,i=1,\cdots ,n,$$

(18)

the assertions in Theorem 3 are valid with (H4)(ii) replaced by:

$$f_i(t,x_{i,t})\ge {\beta }_i\left(t\right)h_i^{-}\left(\underline{x_{i,t}}\right)\mathrm{if}\underline{x_{i,t}}\le r,\mathrm{for}t\gg 1.$$

(19)

and (H5), (H5*) replaced by: There exist a positive vector v and:

(h5)

A constant $\delta >0$ such that $[M\left(t\right)-\delta I_n]v\ge 0,t\gg 1$;

(h5*)

A constant $\alpha >1$ such that $B\left(t\right)v\ge \alpha \left[D\left(t\right)-A\left(t\right)\right]v$ for $t\gg 1$.

Proof. 

For (18) under the above hypotheses, rescaling the variables by ${\widehat{x}}_i\left(t\right)=v_i^{-1}{x}_i\left(t\right)$$(1\le i\le n)$, where $v=(v_1,\cdots ,v_n)>0$ is a vector satisfying simultaneously (h5) and (h5*), we obtain a new system:

$${\widehat{x}}_i^{\prime }\left(t\right)=-d_i\left(t\right){\widehat{x}}_i\left(t\right)+\sum _{j=1}^n{\widehat{L}}_{ij}\left(t\right){\widehat{x}}_{j,t}+{\widehat{f}}_i(t,{\widehat{x}}_{i,t}),i=1,\cdots ,n,t\ge 0,$$

(20)

where ${\widehat{a}}_{ij}\left(t\right):=\parallel {\widehat{L}}_{ij}\left(t\right)\parallel =v_i^{-1}{a}_{ij}\left(t\right)v_j$ and ${\widehat{f}}_i(t,{\varphi }_i):=v_i^{-1}{f}_i(t,v_i{\varphi }_i)$. Hence, (H4) is satisfied with $h_i^{-}\left(x\right)$ in (19) replaced by ${\widehat{h}}_i^{-}\left(x\right)=v_i^{-1}{h}_i^{-}\left(v_{i}x\right)$. In this way, and after dropping the hats for simplicity, we may consider an original system (8) and take $v=\overrightarrow{1}$ in (h5), (h5*). The result follows by the proof of Theorem 3. □

In the case of bounded nonlinearities, Theorem 1 shows that the permanence in Theorem 3 is still obtained if one replaces (H2) by the requirement of (4) being exponentially asymptotically stable.

Remark 3.

When the linearities do not have delays, the proof of Theorem 3 requires the use of assumptions (H5*) and (H5) in (17), but not the boundedness of the coefficients $a_{ij}\left(t\right)$. Moreover, as explained below, (H5) is not needed at all, unless the solution has an eventually increasing component.

These observations and Theorem 2 (iii) allow us to conclude the following:

Corollary 1.

For

$$x_i^{\prime }\left(t\right)=-d_i\left(t\right)x_i\left(t\right)+\sum _{j=1}^n{a}_{ij}\left(t\right)x_j\left(t\right)+f_i(t,x_t),i=1,\cdots ,n,$$

(21)

with $d_i:{\mathbb{R}}^{+}\to (0,\infty ),a_{ij}:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ continuous for all $i,j$, assume (H3), (H4). If

$$\underset{t\to \infty }{lim\; inf}\left(d_i\left(t\right)-\sum _{j=1}^n{a}_{ij}\left(t\right)\right)>0,\underset{t\to \infty }{lim\; inf}\frac{{\beta }_i\left(t\right)}{d_i\left(t\right)-{\sum }_{j=1}^n{a}_{ij}\left(t\right)}>1\mathrm{for}i=1,\cdots ,n,$$

(22)

then (21) is persistent. If in addition $f=(f_1,\cdots ,f_n)$ is bounded, then (21) is permanent.

Proof. 

Condition (22) implies that (H5*) is satisfied, as well as (H2) with $v=\overrightarrow{1}$, hence we follow up the proof of Theorem 3.

Let ${\alpha }_0>1$ be such that $B\left(t\right)\overrightarrow{1}\ge {\alpha }_0\left[D\left(t\right)-A\left(t\right)\right]\overrightarrow{1}$ for $t>0$ large. Take some $\alpha \in (0,{\alpha }_0)$ in Step 4 of the aforementioned proof. From [11] (Lemma A6), for $x_i\left(t\right)$, $I_k$, and $\left(t_k\right)$ as in Step 4 of this proof, either $x_i^{\prime }\left(t_k\right)\le 0$ or $x_i\left(t\right)$ is eventually increasing. Observe that when there are no delays in the linear terms, assumption (H5) was just used in (17), to rule out the situation of $x_i\left(t\right)$ eventually increasing, since in this case, the minima $s_k=x\left(t_k\right)$ are attained at $t_k=min{I}_k$ and $x_i^{\prime }\left(t_k\right)\ge 0$.

In fact, if $x_i^{\prime }\left(t_k\right)\le 0$, from (17) we get:

$$x_i^{\prime }\left(t_{k+1}\right)>\left(-d_i\left(t_{k+1}\right)+\sum _j{a}_{ij}\left(t_{k+1}\right)+{\alpha }^{-1}{\beta }_i\left(t_{k+1}\right)\right)s_{k+1}\ge 0,$$

thus a contradiction. Now, suppose that $x_i\left(t\right)$ is eventually increasing. We just have to reach a contradiction without using (H5). Recall that, in this situation, $\ell ={lim}_{t\to \infty }{x}_i\left(t\right)={sup}_k{x}_i\left(t_k\right)>0$ and $x_i^{\prime }\left(t_k\right)\to 0^{+}$. For k large, as in (17) we have:

$$\begin{array}{cc}\hfill x_i^{\prime }\left(t_k\right)>& \left(-d_i\left(t_k\right)+\sum _j{a}_{ij}\left(t_k\right)+{\alpha }^{-1}{\beta }_i\left(t_k\right)\right)x_i\left(t_k\right)\hfill \\ \hfill =& \left(-d_i\left(t_k\right)+\sum _j{a}_{ij}\left(t_k\right)+{\alpha }_0^{-1}{\beta }_i\left(t_k\right)\right)x_i\left(t_k\right)+({\alpha }^{-1}-{\alpha }_0^{-1}){\beta }_i\left(t_k\right)x_i\left(t_k\right)\hfill \\ \hfill \ge & ({\alpha }^{-1}-{\alpha }_0^{-1}){\beta }_i\left(t_k\right)x_i\left(t_k\right)>0.\hfill \end{array}$$

(23)

If ${lim\; inf}_k{\beta }_i\left(t_k\right)=:b>0$, we obtain $0>b({\alpha }^{-1}-{\alpha }_0^{-1})\ell$, a contradiction. Otherwise, for a subsequence of ${\beta }_i\left(t_k\right)$ (still denoted by ${\beta }_i\left(t_k\right)$) such that ${\beta }_i\left(t_k\right)\to 0$, by taking limits in the above inequalities we obtain:

$$0=\underset{k}{lim}\left(-d_i\left(t_k\right)+\sum _j{a}_{ij}\left(t_k\right)+{\alpha }^{-1}{\beta }_i\left(t_k\right)\right)=\underset{k}{lim}\left(-d_i\left(t_k\right)+\sum _j{a}_{ij}\left(t_k\right)\right).$$

Again, this is not possible, since $d_i\left(t\right)-{\sum }_j{a}_{ij}\left(t\right)\ge \delta$ for $t\gg 1$ and some $\delta >0$.

Therefore, we conclude that (21) is uniformly persistent. If f is bounded, the permanence follows from Theorems 1 and 2 (iii). □

It is apparent that a scaling, as affected in Theorem 4, allows us to consider a general positive vector v in (22) if each component $f_i$ of $f(t,x_t)$ depends only on t and $x_{i,t}$.

Corollary 2.

Consider the DDE:

$$x_i^{\prime }\left(t\right)=-d_i\left(t\right)x_i\left(t\right)+\sum _{j=1}^n{a}_{ij}\left(t\right)x_j\left(t\right)+f_i(t,x_{i,t}),i=1,\cdots ,n,$$

(24)

where $d_i:{\mathbb{R}}^{+}\to (0,\infty ),a_{ij}:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ are continuous for all $i,j$ and $f=(f_1,\cdots ,f_n)$ satisfies (H3). Suppose that (H4) is satisfied with (19) instead of (10) and that there exists a positive vector $v=(v_1,\cdots ,v_n)$ such that:

$$\underset{t\to \infty }{lim\; inf}\left(d_i\left(t\right)v_i-\sum _{j=1}^n{a}_{ij}\left(t\right)v_j\right)>0,\underset{t\to \infty }{lim\; inf}\frac{{\beta }_i\left(t\right)v_i}{d_i\left(t\right)v_i-{\sum }_{j=1}^n{a}_{ij}\left(t\right)v_j}>1\mathrm{for}i=1,\cdots ,n.$$

(25)

Then (24) is persistent. Moreover, if f is bounded, then (24) is permanent.

If the nonlinear terms $f_i$ in (8) are not bounded but are sublinear at infinity, a condition stronger than (H2) still gives the dissipativeness of the system.

Theorem 5.

Consider (8), under (H1), (H3). Suppose that there exist functions ${\beta }_i^{+},h_i^{+}:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ and a constant $R_0>0$ such that, for $\varphi \in C_0^{+}$ and $i=1,\cdots ,n$:

(i)

$0\le f_i(t,\varphi )\le {\beta }_i^{+}\left(t\right)h_i^{+}(\parallel \varphi \parallel )$ for $t\gg 1$ and $\parallel \varphi \parallel \ge R_0$;

(ii)

$h_i^{+}\left(x\right)\le x$ for $x\ge R$;

(iii)

$N\left(t\right)\overrightarrow{1}\ge 0$ for $t\gg 1$, where $N\left(t\right)=diag(d_1\left(t\right)-{\beta }_1^{+}\left(t\right),\cdots ,d_n\left(t\right)-{\beta }_n^{+}\left(t\right))-A\left(t\right)$.Then all positive solutions are bounded. Moreover, if:

(iv)

${lim\; inf}_{t\to \infty }{\beta }_i^{+}\left(t\right)>0$ and $h_i^{+}\left(x\right)<x$ for $x\ge R_0$, then (8) is dissipative.

Proof. 

From (i) and (iii), take $T_0\ge \tau$ such that $0\le f_i(t,\varphi )\le {\beta }_i^{+}\left(t\right)h_i^{+}(\parallel \varphi \parallel )$ and $d_i\left(t\right)-{\sum }_j{a}_{ij}\left(t\right)-{\beta }_i^{+}\left(t\right)\ge 0$, for $\varphi \in C_0^{+}$ with $\parallel \varphi \parallel \ge R_0$ and $t\ge T_0,i=1,\cdots ,n$.

Consider any ordered interval ${[0,R]}^n$ in $C^{+}$, with $R\ge R_0$. For $F_i$ defined in (12), if $t\ge T_0$ and $\varphi \in {[0,R]}^n$ with ${\varphi }_i\left(0\right)=R$, we have

$$F_i(t,\varphi )=-d_i\left(t\right)R+\sum _j{L}_{ij}\left(t\right){\varphi }_j+f_i(t,\varphi )\le -\left(d_i\left(t\right)-\sum _j{a}_{ij}\left(t\right)-{\beta }_i^{+}\left(t\right)\right)R\le 0.$$

Hence, from [19] (Remark 5.2.1) the interval ${[0,R]}^n$ is positively invariant for $t\ge T_0$. In particular, all solutions are bounded.

Next, suppose that (iv) holds. Let $x\left(t\right)$ be a solution with initial condition in $C_0^{+}$. We claim that ${lim\; sup}_{t\to \infty }\left|x\left(t\right)\right|\le R_0$. Otherwise, there is i and a sequence $t_k\to \infty$ such that $\parallel x_{t_k}\parallel =x_i\left(t_k\right)>R_0$ and $x_i^{\prime }\left(t_k\right)\to 0$. This implies:

$$\begin{array}{cc}\hfill x_i^{\prime }\left(t_k\right)\le & -d_i\left(t_k\right)x_i\left(t_k\right)+\sum _j{a}_{ij}\left(t_k\right)\parallel x_{j,t_k}\parallel +{\beta }_i^{+}\left(t_k\right)h_i^{+}(\parallel x_{t_k}\parallel )\hfill \\ \hfill <& -d_i\left(t_k\right)x_i\left(t_k\right)+\sum _j{a}_{ij}\left(t_k\right)x_i\left(t_k\right)+{\beta }_i^{+}\left(t_k\right)h_i^{+}\left(x_i\left(t_k\right)\right)\hfill \\ \hfill =& -[d_i\left(t_k\right)-\sum _j{a}_{ij}\left(t_k\right)-{\beta }_i^{+}\left(t_k\right)]x_i\left(t_k\right)+{\beta }_i^{+}\left(t_k\right)\left[h_i^{+}\left(x_i\left(t_k\right)\right)-x_i\left(t_k\right)\right]\hfill \\ \hfill \le & {\beta }_i^{+}\left(t_k\right)\left[h_i^{+}\left(x_i\left(t_k\right)\right)-x_i\left(t_k\right)\right].\hfill \end{array}$$

As $x_i^{\prime }\left(t_k\right)\to 0$, taking a subsequence of $\left(x_i\left(t_k\right)\right)$ if necessary, we obtain $0\le {lim\; inf}_{t\to \infty }{\beta }_i^{+}\left(t\right)\left[h_i^{+}\left(M\right)-M\right]<0,$ where $M={lim}_k{x}_i\left(t_k\right)$, a contradiction. □

Remark 4.

Once again, in the case of (18), after a scaling one can replace the unit vector $\overrightarrow{1}$ in (iii) of the above theorem by some vector $u>0$. On the other hand, the above proof shows that Theorem 5 is still true with the assumption $[N\left(t\right)-\delta I_n]\overrightarrow{1}\ge 0$ for some $\delta >0$ and $t\gg 1$, instead of (iv).

We end this section with two remarks, leading to more precise and general results.

Remark 5.

More explicitly, we could have written the linear DDE (4) as:

$$\begin{array}{cc}\hfill x_i^{\prime }\left(t\right)& =-d_i\left(t\right)x_i\left(t\right)+\sum _{j\ne i}{d}_{ij}\left(t\right)x_j\left(t\right)+\sum _{j=1}^n{a}_{ij}\left(t\right){\int }_{-\tau }^0{x}_j(t+s)d_s{\nu }_{ij}(t,s),1\le i\le n,\hfill \end{array}$$

with $d_{ij}\left(t\right)$ continuous $(j\ne i)$ and $d_i\left(t\right),a_{ij}\left(t\right),{\nu }_{ij}(t,s)$ as above, with $s\mapsto {\nu }_{ij}(t,s)$ non atomic at zero, and apply more precise criteria for its exponential asymptotic stability, see [21]. Namely, the criteria in Theorem 2 hold with the matrix $D\left(t\right)=diag(d_1\left(t\right),\cdots ,d_n\left(t\right))$ replaced by $\tilde{D}\left(t\right)=\left[{\tilde{d}}_{ij}\left(t\right)\right]$, where ${\tilde{d}}_i\left(t\right)=d_i\left(t\right)$ and ${\tilde{d}}_{ij}\left(t\right)=-\left|d_{ij}\left(t\right)\right|$ for $j\ne i$. Naturally, in this case, the condition ${lim\; inf}_{t\to \infty }{d}_i\left(t\right)>0$ in (ii) of Theorem 2 should be replaced by ${lim\; inf}_{t\to \infty }(d_i\left(t\right)v_i-{\sum }_j|d_{ij}\left(t\right)\left|v_j\right)>0$, for all i. This means that the criterion for permanence in Theorem 3 remains valid with these changes.

Remark 6.

Consider nonlinearites which also incorporate a strictly sublinear negative feedback term of the form $-K_i(t,x_i\left(t\right))$, so that (8) reads as:

$$\begin{array}{cc}\hfill x_i^{\prime }\left(t\right)& =-d_i\left(t\right)x_i\left(t\right)+\sum _{j=1}^n{L}_{ij}\left(t\right)x_{j,t}+f_i(t,x_t)-K_i(t,x_i\left(t\right)),t\ge 0,i=1,\cdots ,n,\hfill \end{array}$$

(26)

where $K_i(t,x)\ge 0$ are continuous and $K_i(t,x)\le {\kappa }_i\left(t\right)g_i\left(x\right)$ for some continuous functions ${\kappa }_i,g_i:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ with ${\kappa }_i\left(t\right)$ bounded, $g_i\left(0\right)=0$ and with right-hand derivative ${\left(g_i\right)}^{\prime }(0+)=0$, and (H1), (H3) hold. With $f_i$ bounded functions, solutions of (26) satisfy the inequalities $-d_i\left(t\right)x_i\left(t\right)-K_i(t,x_i\left(t\right))\le x_i^{\prime }\left(t\right)\le -d_i\left(t\right)x_i\left(t\right)+{\sum }_{j=1}^n{L}_{ij}\left(t\right)x_{j,t}+C(1\le i\le n)$, where $C>0$ is such that $f_i(t,\varphi )\le C$ on ${\mathbb{R}}^{+}\times C^{+}$ for all i. By comparing below and above the solutions of (26) with solutions of cooperative systems [19] and from Theorem 1, it follows that (26) is dissipative and that $C_0^{+}$ is forward invariant for (26). On the other hand, for any fixed $\epsilon >0$ small, there is $m_0>0$ such that $0\le K_i(t,x)\le \epsilon x$ for $x\in [0,m_0]$. A careful analysis shows that the arguments in the proof of Theorem 3 carry over to (26) if one chooses $\epsilon \in (0,\delta )$, for $\delta >0$ as in (H5), so that (14) is satisfied with $d_i\left(t\right)$ replaced by $d_i\left(t\right)+\epsilon$. In this way, one may conclude that the permanence results stated in Theorems 3, 4 and Corollaries 1, 2 are still valid for (26). This more general framework allows in particular to consider structured models with harvesting.

3. Applications

We now apply the above results of persistence and permanence to some selected models.

3.1. Nicholson and Mackey–Glass-Type Systems

We first apply our results to generalized Nicholson and Mackey–Glass systems. The literature is recent, though extensive, and here we mention a few selected references dealing with the persistence and permanence for multidimensional Nicholson equations [3,6,7,10,18] and Mackey–Glass equations [2,6,15], and references therein. Meaningful applications were given in the early work of Berezansky et al. [3], where planar Nicholson systems were proposed as a compartment model for leukemia (with a delay representing the time required for the response of leukemia cells to growth) and a marine model with fishing and protected areas (with a maturation delay for the species).

Consider systems given by:

$$\begin{array}{cc}\hfill x_i^{\prime }\left(t\right)& =-d_i\left(t\right)x_i\left(t\right)+\sum _{j=1}^n{L}_{ij}\left(t\right)x_{j,t}\hfill \\ \hfill & +\sum _{k=1}^{m_i}{b}_{ik}\left(t\right){\int }_{t-{\tau }_{ik}\left(t\right)}^t{\lambda }_{ik}\left(s\right)g_{ik}(s,x_i\left(s\right))ds,i=1,\cdots ,n,\hfill \end{array}$$

(27)

where $L_{ij}\left(t\right)x_{j,t}=a_{ij}\left(t\right){\int }_{-{\sigma }_{ij}\left(t\right)}^0{x}_j(t+s)d_s{\nu }_{ij}(t,s)$ are as in (9) with ${\int }_{-{\sigma }_{ij}\left(t\right)}^0{d}_s{\nu }_{ij}(t,s)=1$ and either:

$$g_{ik}(t,x)=x{e}^{-c_{ik}\left(t\right)x}$$

(28)

or

$$g_{ik}(t,x)=\frac{x}{1+c_{ik}\left(t\right)x^{{\alpha }_i}}({\alpha }_i\ge 1).$$

(29)

The functions $d_i\left(t\right),a_{ij}\left(t\right),b_{ik}\left(t\right),{\sigma }_{ij}\left(t\right),{\tau }_{ik}\left(t\right),{\lambda }_{ik}\left(t\right),c_{ik}\left(t\right)$ are assumed to be continuous and nonnegative, with ${\sigma }_{ij}\left(t\right),{\tau }_{ik}\left(t\right)\in [0,\tau ]$ (for some $\tau >0$), and $d_i\left(t\right)>0,c_{ik}\left(t\right)\ge c_0>0$, for all $i,j,k$, and $t\ge 0$. For $g_{ik}$ as in (28) a modified Nicholson-type system is obtained, whereas the choice (29) provides a Mackey–Glass-type system. We suppose that the linear operators $L_{ij}\left(t\right)$ are nonnegative, thus $a_{ij}\left(t\right)=\parallel L_{ij}\left(t\right)\parallel$ as before, and define:

$${\beta }_i\left(t\right):=\sum _{k=1}^{m_i}{b}_{ik}\left(t\right){\int }_{t-{\tau }_{ik}\left(t\right)}^t{\lambda }_{ik}\left(s\right)ds>0,t\ge 0i=1,\cdots ,n.$$

From Theorem 4, we derive sufficient conditions for the permanence of (27).

Theorem 6.

For (27) under the general conditions above, let the matrices $D\left(t\right),A\left(t\right),M\left(t\right)$ be as in (7) and (11), and assume that:

(i)

The functions $a_{ij}\left(t\right),c_{ik}\left(t\right),{\beta }_i\left(t\right)$ are bounded on ${\mathbb{R}}^{+}$ for all $i,j=1,\cdots ,n,k=1,\cdots ,m_i$;

(ii)

There are positive vectors $u,v$, and $\delta >0$ such that $\left[D\right(t)-A(t)-\delta I]u\ge 0,\left[M\right(t)-\delta I]v\ge 0.$

Then system (27) is permanent.

Proof. 

Clearly, system (27) has the form (18), with $f_i(t,{\varphi }_i)={\sum }_{k=1}^{m_i}{b}_{ik}\left(t\right){\int }_{-{\tau }_{ik}\left(t\right)}^0{\lambda }_{ik}(t+s)g_{ik}(t+s,{\varphi }_i\left(s\right))ds$, for which (H1), (H3) hold. Condition (ii) expresses that (H2), (h5) are also satisfied. Since $g_{ik}$ and ${\beta }_i\left(t\right)$ are bounded, from Theorem 1 the system is dissipative. Note also that (h5) implies (h5*) (conf. Remark 1).

Choose $M>0$ such that $0<x_i\left(t\right)\le M,t\in {\mathbb{R}}^{+},i=1,\cdots ,n$, for any solution $x\left(t\right)$ with an initial condition in $C_0^{+}$. Let $0<c_0\le c_{ik}\left(t\right)\le \overline{c_i}$ for $t\ge 0$ and all $i,k$. Define $h_i\left(x\right):=x{e}^{-\overline{c_i}x}$, respectively $h_i\left(x\right):=\frac{x}{1+\overline{c_i}{x}^{{\alpha }_i}}$, for Nicholson, and respectively Machey–Glass systems. We always have $h_i^{\prime }\left(0\right)=1$. Moreover, the functions $h_i$ are unimodal with $h_i(\infty )=0$, with the exception of the increasing and bounded function $\frac{x}{1+\overline{c_i}x}$ (when ${\alpha }_i=1$ in (29)). Now, choose $m>0$ such that all the functions $h_i\left(x\right)$ are increasing in $[0,m]$ and: $h_i\left(m\right)\le h_i\left(M\right)$, and define $h_i^{-}\left(x\right):=\left\{\begin{array}{c}{h}_i\left(x\right),0\le x\le m\hfill \\ h_i\left(m\right),x>m\hfill \end{array}\right.$. Thus, (19) is satisfied with ${\beta }_i\left(t\right)$ as above and these choices of $h_i^{-}\left(x\right)$. The result follows from Theorem 4. □

Remark 7.

As mentioned previously, Theorems 3, 4, and 6 are still valid if one replaces (H2) by the assumptions (H2*) and ${lim\; inf}_{t\to \infty }{d}_i\left(t\right)>0$, for all i.

For the situation without delays in the linear part, the boundedness of $a_{ij}\left(t\right)$ is not required:

Corollary 3.

For $g_{ik}$ as in (28) or (29), consider the system:

$$\begin{array}{cc}\hfill x_i^{\prime }\left(t\right)& =-d_i\left(t\right)x_i\left(t\right)+\sum _{j=1}^n{a}_{ij}\left(t\right)x_j\left(t\right)+\sum _{k=1}^{m_i}{b}_{ik}\left(t\right){\int }_{t-{\tau }_{ik}\left(t\right)}^t{\lambda }_{ik}\left(s\right)g_{ik}(s,x_i\left(s\right))ds,i=1,\cdots ,n,\hfill \end{array}$$

(30)

under the above conditions on the coefficients and delays, and assume that:

(i)

The functions $c_{ik}\left(t\right),{\beta }_i\left(t\right)$ are bounded on ${\mathbb{R}}^{+}$ for all $i=1,\cdots ,n,k=1,\cdots ,m_i$;

(ii)

There are positive vectors $u,v$, and $\delta >0$ such that $\left[D\right(t)-A(t)-\delta I]u\ge 0,\left[M\right(t)-\delta I]v\ge 0.$

Then (30) is permanent.

We emphasize that this corollary gives a sharper criterion for permanence than the one in [6], and moreover applies to a much larger family of delayed structured models.

When ${\beta }_i\left(t\right)$ are not bounded, the results in the previous section allow us to derive criteria for persistence. This is illustrated in the example below.

Example 1.

Consider the Mackey–Glass-type system:

$$\begin{array}{cc}\hfill x_i^{\prime }\left(t\right)& =-d_{ii}{t}^{\eta }{x}_i\left(t\right)+\sum _{j=1,j\ne i}^n{d}_{ij}{t}^{\eta }{x}_j\left(t\right)+\sum _{j=1}^n{b}_{ij}{t}^{\eta }{\int }_{-{\tau }_{ij}\left(t\right)}^0{x}_j(t+s)ds\hfill \\ \hfill & +{\beta }_i\left(t\right){\int }_{-{\sigma }_i\left(t\right)}^0{k}_i\left(s\right)\frac{x_i(t+s)}{1+c_i\left(t\right)x_i{(t+s)}^{{\nu }_i}}ds,1\le i\le n,\hfill \end{array}$$

(31)

where $\eta >0,0<{\nu }_i\le 1,b_{ij},d_{ij}\in {\mathbb{R}}^{+}$ with $d_i:=d_{ii}>0$ for all i, and the delays ${\tau }_{ij}\left(t\right),{\sigma }_i\left(t\right)$ are continuous with $0\le {\tau }_{ij}\left(t\right)\le r_{ij},0<{\sigma }_i\left(t\right)\le R_i$ for some constants $r_{ij},R_i>0$, ${\beta }_i,c_i:{\mathbb{R}}^{+}\to (0,\infty )$ are continuous with $c_i\left(t\right)$ bounded below and above by positive constants, and $k_i:[-R_i,0]\to {\mathbb{R}}^{+}$ are integrable with ${\int }_{-{\sigma }_i\left(t\right)}^0{k}_i\left(s\right)ds=1$, $t\ge 0,i,j=1,\cdots ,n$. Choose $h_i^{-}\left(x\right)=\frac{x}{x+{\overline{c}}_i{x}^{{\nu }_i}}$ for x in some vicinity $[0,m]$ of 0 and ${\overline{c}}_i>0$ such that $c_i\left(t\right)\le {\overline{c}}_i(1\le i\le n)$.

With the previous notation, we have $d_i\left(t\right)=d_i{t}^{\eta },a_{ij}\left(t\right)=((1-{\delta }_{ij})d_{ij}+b_{ij}{\tau }_{ij}\left(t\right))t^{\eta }\le [(1-{\delta }_{ij})d_{ij}+b_{ij}{r}_{ij}]t^{\eta }$, where ${\delta }_{ij}=1$ if $i=j$ and ${\delta }_{ij}=0$ if $i\ne j$. Define the $n\times n$ matrices $D=diag(d_1,\cdots ,d_n),A=\left[(1-{\delta }_{ij})d_{ij}+b_{ij}{r}_{ij}\right]$, so that $D\left(t\right)=t^{\eta }D,A\left(t\right)=t^{\eta }A$. Assume that $N:=D-A$ is a non-singular M-matrix, or, in other words, that there exists a positive vector v such that $u:=Nv>0$. For $\delta >0$ small such that $\delta Av\le u$, we have $Dv\ge (1+\delta )Av$, hence (H2*) is satisfied. From Theorem 2 (ii) we deduce that the linear system:

$$x_i^{\prime }\left(t\right)=-d_{ii}{t}^{\eta }{x}_i\left(t\right)+\sum _{j=1,j\ne i}^n{d}_{ij}{t}^{\eta }{x}_j\left(t\right)+\sum _{j=1}^n{b}_{ij}{t}^{\eta }{\int }_{-{\tau }_{ij}\left(t\right)}^0{x}_j(t+s)ds,i=1,\cdots ,n,$$

is exponentially asymptotically stable.

Next, suppose that $b_{ij}=0$ for all $i,j$. If $\alpha >1$ such that ${\beta }_i\left(t\right)v_i\ge \alpha t^{\eta }{u}_i$ for $t\gg 1$, then also ${\beta }_i\left(t\right)v_i\ge t^{\eta }{u}_i+\delta$, for some $\delta >0$ and for $t\gg 1$, $1\le i\le n$. Under this condition, both (h5) and (h5*) hold. From Theorem 4 we conclude that (31) is uniformly persistent. Observe however that none of the coefficients $d_i\left(t\right),a_{ij}\left(t\right),{\beta }_i\left(t\right)$ is bounded.

3.2. A Structured Population Model

In [22], Arino et al. proposed an alternative model to the usual delayed logistic equation, given by:

$$x^{\prime }\left(t\right)=\frac{\gamma \mu e^{-\mu \tau }x(t-\tau )}{\mu +\kappa (1-e^{-\mu \tau })x(t-\tau )}-\mu x\left(t\right)-\kappa x^2\left(t\right),$$

(32)

where $\gamma ,\mu ,\kappa ,\tau >0$, and addressed the existence and stability of a positive carrying capacity. In this model, the growth rate at time t depends on the number of individuals over the time interval $[t-\tau ,t]$ that have survived until time t and the growth delay $\tau$ is consistent with the decay rate. It was assumed in [22] that $\tau <{\tau }_H$, where ${\tau }_H:=\frac{1}{\mu }log\frac{\gamma }{\mu }>0$ is a threshold time for survival: If $\tau <{\tau }_H$, $x\left(t\right)$ approaches the carrying capacity as $t\to \infty$, otherwise the species dies out. Recently, Lin et al. [23] argued that a distributed delay should be considered to account for different delays for different individuals of the population, and derived a generalization of the modified logistic law (32) as follows:

$$x^{\prime }\left(t\right)=\gamma {\int }_0^{\infty }\frac{\mu e^{-\mu s}x(t-s)k\left(s\right)}{\mu +\kappa (1-e^{-\mu s})x(t-s)}ds-\mu x\left(t\right)-\kappa x^2\left(t\right),$$

(33)

where $\gamma ,\mu ,\kappa >0$, the distribution kernel $k\left(s\right)\ge 0$ is normalized so that ${\int }_0^{\infty }k\left(s\right)ds=1$ and satisfies $\tau :={\int }_0^{\infty }sk\left(s\right)ds<\infty$, where $\tau$ is called the mean delay. See also in [Section 4] of [23], for a two species competition model. Meanwhile, a general nonautonomous n-dimensional version of the model in (32), which can be interpreted as a structured population model, was considered and studied in [5,9]:

$$\begin{array}{cc}\hfill x_i^{\prime }\left(t\right)=& \sum _{k=1}^{m_i}\frac{{\alpha }_{ik}\left(t\right)x_i(t-{\tau }_{ik}\left(t\right))}{1+c_{ik}\left(t\right)x_i(t-{\tau }_{ik}\left(t\right))}+\sum _{j=1}^n{a}_{ij}\left(t\right)x_j(t-{\sigma }_{ij}\left(t\right))\hfill \\ \hfill & -d_i\left(t\right)x_i\left(t\right)-{\kappa }_i\left(t\right)x_i^2\left(t\right),t\ge 0,i=1,\cdots ,n\hfill \end{array}$$

(34)

where all the coefficients ${\alpha }_{ik}\left(t\right),c_{ik}\left(t\right),a_{ij}\left(t\right),{\mu }_i\left(t\right),{\kappa }_i\left(t\right)$, and the delays ${\tau }_{ik}\left(t\right),{\sigma }_{ij}\left(t\right)$ are nonnegative and continuous, $0<\underline{c_{ik}}\le c_{ik}\left(t\right)\le \overline{c_{ik}}$ for $t\ge 0$, $k=1,\cdots ,m_i,i,j=1,\cdots ,n$. Contrarily to the setting in [9], the delays ${\tau }_{ik}\left(t\right),{\sigma }_{ij}\left(t\right)$ are not assumed to be bounded in [5]. See [9,22,23] and references therein, for a derivation of the models and further biological explanations.

Motivated by the aforementioned works, consider now a system with bounded distributed delays:

$$\begin{array}{cc}\hfill x_i^{\prime }\left(t\right)=& \sum _{k=1}^{m_i}{\alpha }_{ik}^0\left(t\right){\int }_{t-{\tau }_{ik}\left(t\right)}^t\frac{x_i\left(s\right)K_{ik}(t-s)}{1+c_{ik}(t-s)x_i\left(s\right)}ds+\sum _{j=1}^n{a}_{ij}^0\left(t\right){\int }_{t-{\sigma }_{ij}\left(t\right)}^t{x}_j\left(s\right)G_{ij}(t-s)ds\hfill \\ \hfill & -d_i\left(t\right)x_i\left(t\right)-{\kappa }_i\left(t\right)x_i^2\left(t\right),t\ge 0,i=1,\cdots ,n,\hfill \end{array}$$

(35)

where ${\alpha }_{ik}^0,c_{ik},a_{ij}^0:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+},{\tau }_{ik},{\sigma }_{ij}:{\mathbb{R}}^{+}\to [0,\tau ](\tau >0)$ are continuous, $c_{ik}\left(t\right)$ are bounded below and above by positive constants, the kernels $K_{ik},G_{ij}:[0,\tau ]\to {\mathbb{R}}^{+}$ are integrable, with:

$${\alpha }_{ik}\left(t\right):={\alpha }_{ik}^0\left(t\right){\int }_0^{{\tau }_{ik}\left(t\right)}{K}_{ik}\left(s\right)ds,a_{ij}\left(t\right):=a_{ij}^0\left(t\right){\int }_0^{{\sigma }_{ij}\left(t\right)}{G}_{ij}\left(s\right)ds$$

continuous, for all $i,j,k$. Denote also ${\beta }_i\left(t\right):={\sum }_{k=1}^{m_i}{\alpha }_{ik}\left(t\right),i=1,\cdots ,n.$

System (35) has the form (26), with $L_{ij}\left(t\right)$ nonnegative linear operators, $a_{ij}\left(t\right)=\parallel L_{ij}\left(t\right)\parallel$, $K_i(t,x)={\kappa }_i\left(t\right)x^2$ and:

$$f_i(t,x_{i,t})=\sum _{k=1}^{m_i}{\alpha }_{ik}^0\left(t\right){\int }_{t-{\tau }_{ik}\left(t\right)}^t\frac{x_i\left(s\right)K_{ik}(t-s)}{1+c_{ik}(t-s)x_i\left(s\right)}ds.$$

Proceeding as for (27), we derive that $f_i(t,x_{i,t})\ge {\beta }_i\left(t\right)h_i^{-}\left(x\right)$, with $h_i^{-}\left(x\right)=\frac{x}{1+\overline{c_i}x}$, where $\overline{c_i}={max}_k{sup}_{t\ge 0}{c}_{ik}\left(t\right)$. In fact, when ${\kappa }_i\equiv 0$, (35) is a particular case of (27), with nonlinearities of the form (29) and ${\alpha }_i=1$. Thus (see also Remark 6), when ${\kappa }_i\left(t\right)$ are bounded, Theorem 4 applies to (35). Namely, if ${lim\; inf}_{t\to \infty }{\beta }_i\left(t\right)>0$ and ${lim\; inf}_{t\to \infty }\frac{{\beta }_i\left(t\right)v_i}{d_i\left(t\right)v_i-{\sum }_{j=1}^n{a}_{ij}\left(t\right)v_j}>1$ for some $v_i>0$ and $1\le i\le n$, then both (h5), (h5*) are satisfied, and (35) is persistent. Since (35) is a cooperative system, the theory of monotone systems for DDEs [19] can be used to derive that the system is dissipative if in addition ${\beta }_i\left(t\right),a_{ij}\left(t\right)$ are all bounded (see [5] for details).

For systems (34), assuming that all the coefficients are bounded (and ${\kappa }_i\left(t\right)\ge {\kappa }_0>0$), its permanence was shown in [5] (Theorem 5.3), provided that there exists a vector $v>0$ such that:

$$Mv>0,\mathrm{where}M=diag({\underline{\beta }}_1-{\overline{d}}_1,\cdots ,{\underline{\beta }}_n-{\overline{d}}_n)+\left[{\underline{a}}_{ij}\right]$$

and the notations $\overline{f}={sup}_{t\ge 0}f\left(t\right),\underline{f}={inf}_{t\ge 0}f\left(t\right)$ for $f:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ bounded were used, a much stronger hypothesis. On the other hand, a criterion for the permanence of (34) was obtained by Győri et al. [9] (Corollary 3.7) under some different assumptions and not assuming the a priori boundedness of all coefficients: Instead of ${lim\; inf}_{t\to \infty }{d}_i\left(t\right)>0$, it was imposed that $d_i\left(t\right)>0$ with ${\int }_0^{\infty }{d}_i\left(t\right)dt=\infty$, and that there are uniform bounds $1<{\alpha }_i\le {\beta }_i\left(t\right)/d_i\left(t\right)\le C_i,a_{ij}/d_i\left(t\right)\le M_{ij},{\kappa }_i\left(t\right)/d_i\left(t\right)\le C_i$ for all $i,j$, and $t\ge 0$; nevertheless, the assumptions in [9] are much more restrictive when ${lim\; inf}_{t\to \infty }{d}_i\left(t\right)>0$.

In particular, our results allow to conclude that the scalar model:

$$x_i\left(t\right)=\sum _{k=1}^m{\alpha }_k^0\left(t\right){\int }_{t-{\tau }_k\left(t\right)}^t\frac{x\left(s\right)K_k(t-s)}{1+c_k(t-s)x\left(s\right)}ds-d\left(t\right)x\left(t\right)-\kappa \left(t\right)x^2\left(t\right),$$

(36)

is permanent if $\beta \left(t\right):={\sum }_{k=1}^m{\alpha }_k^0\left(t\right){\int }_0^{{\tau }_k\left(t\right)}{K}_k\left(s\right)ds\ge \underline{\beta }>0$ and $\beta \left(t\right)/d\left(t\right)\ge \alpha >1$ for t large. As expected, in the case of the autonomous Equation (33) with finite delay $\tau$, this requirement translates as $\gamma {\int }_0^{\tau }{e}^{-\mu s}k\left(s\right)ds>\mu$, shown in [23] to be a sharp condition for the existence and global stability of a positive equilibrium. Of course, it would be interesting to extend our results for (35) and (36) to the case of infinite delay.

3.3. A Chemostat Model

We consider a delayed nonautonomous version of the chemostat model with two microorganisms in competition studied by Ellermeyer [24]:

$$\begin{array}{cc}\hfill S^{\prime }\left(t\right)& =d\left(t\right)(S_0-S\left(t\right))-b_1\left(t\right)p_1\left(S\left(t\right)\right)x_1\left(t\right)-b_2\left(t\right)p_2\left(S\left(t\right)\right)x_2\left(t\right)\hfill \\ \hfill x_i^{\prime }\left(t\right)& =-d\left(t\right)x_i\left(t\right)+e^{-{\int }_{t-{\tau }_i\left(t\right)}^{t}d\left(s\right)ds}{b}_i\left(t\right)p_i\left(S(t-{\tau }_i\left(t\right))\right)x_i(t-{\tau }_i\left(t\right)),i=1,2,\hfill \end{array}$$

(37)

where $S_0>0,$ the functions $d,b_i:{\mathbb{R}}^{+}\to (0,\infty ),{\tau }_i,p_i:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ are continuous, ${\tau }_i\left(t\right)$ are bounded, and $p_i\left(0\right)=0,p_i\left(x\right)>0$ for $x>0,i=1,2$. Here, $S_0$ is the initial concentration of the nutrient in the chemostat vessel free of microorganisms, $S\left(t\right)$ is the concentration of the nutrient, $x_i\left(t\right)$ is the biomass of the species i in the growth vessel, and ${\tau }_i\left(t\right)$ is the time for the conversation of nutrient into its biomass ($i=1,2$), at time t. Typically, models with Michaelis–Menton functional responses $p_i\left(x\right)=\frac{m_{i}x}{1+k_{i}x}$ or other strictly increasing, smooth functions have been considered. See [24,25,26,27] and references therein, for further explanations of the model.

One easily sees that the ordered interval $S:=[0,S_0]\times {\mathbb{R}}^{+}\times {\mathbb{R}}^{+}\subset C^{+}$ is positively invariant for (37). After the change of variable $u\left(t\right)=S_0-S\left(t\right)$, (37) reads as:

$$\begin{array}{cc}\hfill u^{\prime }\left(t\right)& =-d\left(t\right)u\left(t\right)+b_1\left(t\right)p_1(S_0-u\left(t\right))x_1\left(t\right)+b_2\left(t\right)p_2(S_0-u\left(t\right))x_2\left(t\right)\hfill \\ \hfill x_i^{\prime }\left(t\right)& =-d\left(t\right)x_i\left(t\right)+e^{-{\int }_{t-{\tau }_i\left(t\right)}^{t}d\left(s\right)ds}{b}_i\left(t\right)p_i(S_0-u(t-{\tau }_i\left(t\right)))x_i(t-{\tau }_i\left(t\right)),i=1,2.\hfill \end{array}$$

(38)

For the latter system, the nonlinearites are given by:

$$\begin{array}{cc}\hfill f_1(t,\varphi )& =b_1\left(t\right)p_1(S_0-{\varphi }_1\left(0\right)){\varphi }_2\left(0\right)+b_2\left(t\right)p_2(S_0-{\varphi }_1\left(0\right)){\varphi }_3\left(0\right)\hfill \\ \hfill f_{i+1}(t,\varphi )=& e^{-{\int }_{t-{\tau }_i\left(t\right)}^{t}d\left(s\right)ds}{b}_i\left(t\right)p_i(S_0-{\varphi }_1(-{\tau }_i\left(t\right))){\varphi }_{i+1}(-{\tau }_i\left(t\right)),i=1,2,\hfill \end{array}$$

for $t\ge 0,\varphi =({\varphi }_1,{\varphi }_2,{\varphi }_3)\in S$. If ${lim\; inf}_{t\infty }d\left(t\right)=:\underline{d}>0$ and $b_1\left(t\right),b_2\left(t\right)$ are bounded, Theorem 1 implies that (38) is dissipative (in $S$). Moreover, for any solution $(S\left(t\right),x_1\left(t\right),x_2\left(t\right))$ in $S$ of (37), if there is a sequence $t_k\to \infty$ such that $S\left(t_k\right)\to 0,S^{\prime }\left(t_k\right)\to 0$, we get:

$$S^{\prime }\left(t_k\right)=d\left(t_k\right)(S_0-S\left(t_k\right))-b_1\left(t_k\right)p_1\left(S\left(t_k\right)\right)x_1\left(t_k\right)-b_2\left(t_k\right)p_2\left(S\left(t_k\right)\right)x_2\left(t_k\right)\to 0\ge S_0\underline{d}>0,$$

a contradiction. Thus $S\left(t\right)$ persists, i.e., ${lim\; inf}_{t\to \infty }S\left(t\right)>0$. Assuming in addition the uniform persistence of $S\left(t\right)$, the uniform persistence of the microorganisms is also obtained:

Theorem 7.

For (37) under the above conditions, assume that $S\left(t\right)$ uniformly persists, with ${lim\; inf}_{t\to \infty }S\left(t\right)\ge s_0>0$ for any solution $(S\left(t\right),x_1\left(t\right),x_2\left(t\right))$ with initial condition in $S$. If $b_1\left(t\right),b_2\left(t\right)$ are bounded and:

$$\underset{t\to \infty }{lim\; inf}\left({\pi }_i{e}^{-{\int }_{t-{\tau }_i\left(t\right)}^{t}d\left(s\right)ds}{b}_i\left(t\right)-d\left(t\right)\right)>0,i=1,2,$$

where ${\pi }_i={min}_{x\in [s_0,S_0]}{p}_i\left(x\right)$, then both species $x_1\left(t\right),x_2\left(t\right)$ uniformly persist.

Proof. 

Let $\delta >0$ be such ${\pi }_i{e}^{-{\int }_{t-{\tau }_i\left(t\right)}^{t}d\left(s\right)ds}{b}_i\left(t\right)-d\left(t\right)>\delta$ for $t\gg 1,i=1,2$. Fix $\epsilon >0$, and define ${\pi }_i\left(\epsilon \right)={min}_{x\in [s_0-\epsilon ,S_0]}{p}_i\left(x\right)(i=1,2)$. For solutions $X\left(t\right)=(u\left(t\right),x_1\left(t\right),x_2\left(t\right))$ of (38) with initial condition in $S$, for t sufficiently large we obtain the estimates $f_i(t,X_t)\ge {\beta }_i\left(t\right)h_i^{-}\left(\underline{X_t}\right)$, where:

$${\beta }_1\left(t\right)={\pi }_1\left(\epsilon \right)b_1\left(t\right)+{\pi }_2\left(\epsilon \right)b_2\left(t\right),{\beta }_{i+1}\left(t\right)={\pi }_i\left(\epsilon \right)e^{-{\int }_{t-{\tau }_i\left(t\right)}^{t}d\left(s\right)ds}{b}_i\left(t\right),i=1,2,$$

and $h_i^{-}\left(x\right)=x,i=1,2,3.$ With the notation in Section 2, $D\left(t\right)=diag\left(d\right(t),d(t),d(t\left)\right),A\left(t\right)\equiv 0$ and $M\left(t\right)=diag({\beta }_1\left(t\right)-d\left(t\right),{\beta }_2\left(t\right)-d\left(t\right),{\beta }_3\left(t\right)-d\left(t\right))$. For $\epsilon >0$ sufficiently small and t large, we obtain ${\beta }_i\left(t\right)-d\left(t\right)\ge \delta ,i=2,3$, and thus ${\beta }_1\left(t\right)-d\left(t\right)\ge \delta$ also holds. In this way, (H5) is satisfied, as well (H5*) (conf. Remark 1). From Theorem 3, (38) is uniformly persistent. □

For the autonomous environment model in [24], it was shown that the co-existence of two different competing species is not possible: Either the washout equilibrium $(S_0,0,0)$ is globally attractive, or only one species persists. For the nonautonomous version (38), the above result leads to the persistence of both microorganisms, provied that ${\pi }_i{b}_i\left(t\right)/d\left(t\right)\ge \alpha >1$ and the time-delays are small enough, $t\gg 1$.

3.4. A Planar System with Distributed Delays

We consider the planar system studied in [28]:

$$\begin{array}{cc}\hfill x^{\prime }\left(t\right)& =d_1\left(t\right)\left[{\int }_{t-{\tau }_1\left(t\right)}^t{f}_1\left(y\left(s\right)\right)d_s{\nu }_1(t,s)-x\left(t\right)\right]\hfill \\ \hfill y^{\prime }\left(t\right)& =d_2\left(t\right)\left[{\int }_{t-{\tau }_2\left(t\right)}^t{f}_2\left(x\left(s\right)\right)d_s{\nu }_2(t,s)-y\left(t\right)\right],\hfill \end{array}$$

(39)

where:

(a1)

$d_i,f_i,{\tau }_i:{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ are continuous, $f_i\left(x\right)>0$ for $x>0$, ${\tau }_i\left(t\right)\in [0,\tau ]$ for some $\tau >0$, ${\nu }_i(t,s)$ are defined for $(t,s)\in {\mathbb{R}}^{+}\times [-\tau ,\infty )$, continuous in t, left-continuous and nondecreasing in s, and such that ${\int }_{t-{\tau }_i\left(t\right)}^t{d}_s{\nu }_i(t,s)=1$, for $i=1,2,t\ge 0;$

(a2)

$f_i\left(x\right)$ is nondecreasing on $[0,r]$ for some $r>0$ and ${lim\; inf}_{x\to \infty }{f}_i\left(x\right)>0$, $i=1,2$;

(a3)

For each $i=1,2$, either $f_i\left(0\right)>0$ or $f_i\left(0\right)=0$ and there exists $f_i^{\prime }\left(0\right)>1$;

(a4)

${lim\; inf}_{t\to \infty }{d}_i\left(t\right)>0,i=1,2$.

For several real applications of this model, such as neuron networks and Lotka–Volterra cooperative systems, see [28] and references therein.

Theorem 8.

If (a1), (a4) hold, (39) is uniformly persistent. If in addition $d_i\left(t\right),f_i\left(x\right)$ are bounded, then the system is permanent.

Proof. 

If $l_i:={lim\; inf}_{x\to \infty }{f}_i\left(x\right)\le f_i\left(0\right)$, replace $f_i\left(x\right)$ by a continuous function ${\widehat{f}}_i\left(x\right)$ such that ${\widehat{f}}_i\left(x\right)=\alpha x$ on $[0,\epsilon )$ (for a small $\epsilon >0$ and $\alpha >1$), and ${\widehat{f}}_i\left(x\right)\le f_i\left(x\right)$ on ${\mathbb{R}}^{+}$. In this way, we may assume that $r>0$ in (a2) is such that ${\widehat{f}}_i\left(r\right)<{lim\; inf}_{x\to \infty }{\widehat{f}}_i\left(x\right)$, $i=1,2$. With the previous notations, where $L_{ij}\left(t\right)\equiv 0(i,j=1,2)$, (H1), (H3) are satisfied and $d_i\left(t\right){\int }_{t-{\tau }_i\left(t\right)}^t{f}_i\left(u\left(s\right)\right)d_s{\nu }_i(t,s)\ge d_i\left(t\right){\widehat{f}}_i\left(\underline{u}\right)$, for a positive function $u\left(t\right)$ with $\underline{u}:={inf}_{t}u\left(t\right)\le r$. Choosing a smaller positive $r>0$ if necessary, from (a3) there is $\alpha >1$ such that (H4) holds with ${\beta }_i\left(t\right)=\alpha d_i\left(t\right)$ and $h_i^{-}\left(x\right)=x$. Hence (H5), (H5*) are satisfied, and Theorem 3 gives the result. □

In fact, an interesting method was developed in [28] to study the global behavior of (39), under some other strong assumptions: Instead of (a2) and (a3), it was assumed that

(a2*)

$f_i\left(x\right)$ are strictly increasing on ${\mathbb{R}}^{+}$, with $f\left(x\right)>0$ for $x>0$, $i=1,2$;

(a3*)

The equation $f_1^{-1}\left(x\right)=f_2\left(x\right)$ has a unique positive solution $K>0$, with $\left(f_2\left(x\right)-f_1^{-1}\left(x\right)\right)(x-K)<0$ for $x>f_1\left(0\right),x\ne K$;

(a4*)

${\int }_0^{\infty }{d}_i\left(t\right)=\infty ,i=1,2$.

Note that (a2*), (a3*) imply that (39) is cooperative and that there exists a unique positive equilibrium, given by $(K,f_2\left(K\right))$. Under (a1), (a2*)–(a4*), the global attractivity of such an equilibrium was established in [28] [Theorem 3.1]. We stress however that our result on persistence and permanence does not a priori assume the existence of a positive equilibrium, nor that $f_i$ are increasing on ${\mathbb{R}}^{+}$.

3.5. On the Necessity of Some Assumptions

Some illustrative examples showing the necessity of our assumptions are now presented.

Example 2.

Consider the planar system:

$$\begin{array}{cc}\hfill x_1^{\prime }\left(t\right)& =-t^{\eta }{x}_1\left(t\right)+(t^{\eta }-1)x_2(t-{\tau }_1\left(t\right))+\beta h_1(t,x_1(t-{\sigma }_1\left(t\right))\hfill \\ \hfill x_2^{\prime }\left(t\right)& =-t^{\eta }{x}_2\left(t\right)+(t^{\eta }-1)x_1(t-{\tau }_2\left(t\right))+\beta h_2(t,x_2(t-{\sigma }_2\left(t\right))\hfill \end{array},t\ge 1,$$

(40)

with nonlinearities of either the Mackey–Glass or Nicholson type,

$$h_i(t,x)=\frac{x}{1+c_i\left(t\right)x^{{\nu }_i}}\mathrm{with}{\nu }_i\ge 1,\mathrm{or}{h}_i(t,x)=x{e}^{-c_i\left(t\right)x},$$

and $\eta >0,\beta >1$, where the delays ${\tau }_i\left(t\right),{\sigma }_i\left(t\right)$ are nonnegative, continuous, and bounded, $c_i\left(t\right)$ are positive, continuous, and $0<c_i\left(t\right)\le {\overline{c}}_i$ for some constants ${\overline{c}}_i,i=1,2$. With the previous notation, $d_i\left(t\right)=t^{\eta },a_{ii}\left(t\right)=0,{\beta }_i\left(t\right)\equiv \beta >1,i=1,2$, and $a_{12}\left(t\right)=a_{21}\left(t\right)=t^{\eta }-1$, thus:

$$D\left(t\right)=diag(t^{\eta },t^{\eta }),A\left(t\right)=\left[\begin{array}{cc}0& t^{\eta }-1\\ t^{\eta }-1& 0\end{array}\right],M\left(t\right)=\left[\begin{array}{cc}\beta -t^{\eta }& t^{\eta }-1\\ t^{\eta }-1& \beta -t^{\eta }\end{array}\right].$$

As,

$$[D\left(t\right)-A\left(t\right)]\left[\begin{array}{c}1\\ 1\end{array}\right]=\left[\begin{array}{c}1\\ 1\end{array}\right],M\left(t\right)\left[\begin{array}{c}1\\ 1\end{array}\right]=\left[\begin{array}{c}\beta -1\\ \beta -1\end{array}\right],$$

(H2), (h5) (and thus also (h5*)) hold with the common vector $\overrightarrow{1}=(1,1)$. Since $a_{12}\left(t\right),a_{21}\left(t\right)$ are not bounded, we cannot deduce that (40) is permanent (nor that (H2*) is satisfied). Nevertheless, if there are no delays in the linear part, i.e., ${\tau }_i\left(t\right)={\tau }_2\left(t\right)\equiv 0$, Corollary 2 yields the permanence of (40).

Example 3.

Consider the scalar equation:

$$x^{\prime }\left(t\right)=-d\left(t\right)x\left(t\right)+a\left(t\right)x(t-\tau \left(t\right))+\beta \left(t\right)h\left(x\left(t\right)\right),t\ge 0,$$

(41)

where $\tau \left(t\right)$ is continuous with $0\le \tau \left(t\right)\le \tau$, $h\left(x\right)=\left\{\begin{array}{c}{x}^2\mathrm{if}0\le x\le 1\hfill \\ 1\mathrm{if}x\ge 1\hfill \end{array}\right.$ and

$$a\left(t\right)=\mu \frac{t+C-\tau \left(t\right)}{\tau \left(t\right)},\beta \left(t\right)={\mu }_1\frac{t+C}{t+C-1},d\left(t\right)=a\left(t\right)+(\beta \left(t\right)+1)\frac{1}{t+C}+\mu .$$

for some constants $C>max(\tau ,1),\mu >0,{\mu }_1>\mu +1/C$. One easily sees that this equation has the solution $\phi \left(t\right)=\frac{1}{t+C}$, thus (41) is not persistent. Note that $\beta \left(t\right)$ is bounded and $d\left(t\right)-a\left(t\right)>\mu ,\beta \left(t\right)-d\left(t\right)+a\left(t\right)={\mu }_1-\mu -\frac{1}{t+C}\ge {\mu }_1-\mu -\frac{1}{C}>0$, therefore (H2), (H5), and (H5*) are satisfied. However, hypothesis (H4) is not fulfilled, because $h^{\prime }\left(0\right)=0$ (conf. Remark 2).

Example 4.

Consider the system:

$$\begin{array}{cc}\hfill x_1^{\prime }\left(t\right)& =-(a\left(t\right)+d_1\left(t\right))x_1\left(t\right)+a\left(t\right)x_2\left(t\right)+\beta \left(t\right)h\left(x_1(t-\tau )\right),\hfill \\ \hfill x_2^{\prime }\left(t\right)& =-(a\left(t\right)+d_1\left(t\right))x_2\left(t\right)+a\left(t\right)x_1\left(t\right)+\beta \left(t\right)h\left(x_2(t-\tau )\right),t\ge 0,\hfill \end{array}$$

(42)

where $\tau >0$, $a\left(t\right)$ is continuous, nonnegative and bounded, $h\left(x\right)=\frac{x}{1+x}$ and

$$d_1\left(t\right)=\mu \frac{t+C}{1-\tau },\beta \left(t\right)=\frac{t+C+1-\tau }{t+C}\left(d_1\left(t\right)-\frac{1}{t+C}\right),$$

for some $\tau \in (0,1)$ and $C>\tau$. It is easy to verify that $x\left(t\right)=\left(\frac{1}{t+C},\frac{1}{t+C}\right)$ is a solution of (42), thus this system is not permanent. Note that $d_1\left(t\right)\ge \mu \frac{C}{1-\tau },\beta \left(t\right)-d_1\left(t\right)=\mu -\frac{t+C+1-\tau }{{(t+C)}^2}\ge \mu /2$ for $t\gg 1$, hence (H2) and (H5) are satisfied. However Theorem 3 does not apply, because (H5*) does not hold.

3.6. A Numerical Example

A concrete numerical simulation is now included. For simplicity, a scalar model is chosen.

In their celebrated paper [29], Mackey and Glass proposed appropriate models to describe the hematopoiesis (the process of production, multiplication, and specialization of blood cells in bone marrow). Here, we consider a 1-periodic hematopoiesis model with monotone production rate:

$$y^{\prime }\left(t\right)=-\left(1+\frac{1}{2}cos\left(2\pi t\right)\right)y\left(t\right)+\frac{{\eta }_1\left(1+\frac{1}{2}cos\left(2\pi t\right)\right)}{1+y{(t-1-cos\left(2\pi t\right))}^n}+\frac{{\eta }_2\left(1+\frac{1}{2}sin\left(2\pi t\right)\right)}{1+y{(t-2)}^n},t\ge 0,$$

(43)

with $n>1$ and ${\eta }_1,{\eta }_2>0$. The model possesses two discrete delays, ${\tau }_1\left(t\right)=1+cos\left(2\pi t\right)$ and ${\tau }_2\left(t\right)\equiv 2$. Define $d\left(t\right)=1+\frac{1}{2}cos\left(2\pi t\right),b_1\left(t\right)={\eta }_1(1+\frac{1}{2}cos\left(2\pi t\right)),b_2\left(t\right)={\eta }_2(1+\frac{1}{2}sin\left(2\pi t\right)),b\left(t\right)=b_1\left(t\right)+b_2\left(t\right)$. Since all the coefficients are bounded, there is some $M>0$ such that all solutions of (43) satisfy ${lim\; sup}_{t\to \infty }y\left(t\right)<M$. Write (43) as $y^{\prime }\left(t\right)=-d\left(t\right)y\left(t\right)+f(t,y_t)$. Let $\eta ={\eta }_1+\frac{1}{3}{\eta }_2$, fix any $\alpha >1$ and $r\in (0,M)$ such that $\alpha r=\frac{\eta }{1+M^n}$. With $\beta \left(t\right)=\alpha b\left(t\right)$, $h^{-}\left(x\right)=x$ on $[0,r]$, $h^{-}\left(x\right)=\frac{\eta }{\alpha (1+M^n)}$ on $[r,\infty )$, one has $f(t,\varphi )\ge \beta \left(t\right)h\left(\underline{\varphi }\right)$ whenever $\varphi \in C_0^{+}$, and $\beta \left(t\right)/d\left(t\right)\ge \alpha$ for all t. Hence, (H4), (H5) are satisfied. From Theorem 3, (43) is permanent.

Take e.g., ${\eta }_1=0.2$, ${\eta }_2=0.3$, and $n=3$. From [2], (43) has a positive 1-periodic solution. The simulations below suggest that the positive solutions of (43) approach such a periodic solution as $t\to \infty$ (see Figure 1).

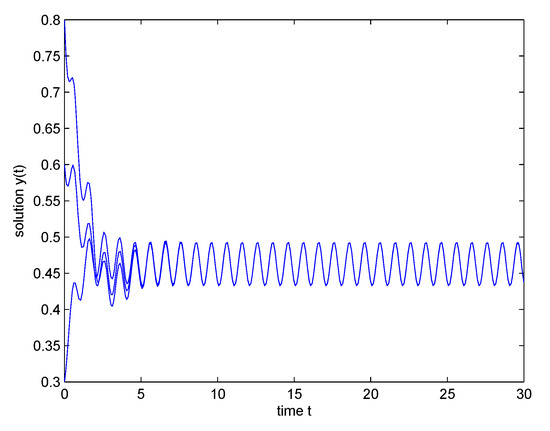
Figure 1. Numerical simulation of three solutions of (43) where ${\eta }_1=0.2$, ${\eta }_2=0.3$ and $n=3$, with initial condition $\phi \left(\theta \right)=0.3(cos(\theta )+1)$, $\phi \left(\theta \right)=0.8e^{\theta }$, and $\phi \left(\theta \right)=0.3(sin(\theta )+1)$, for $\theta \in [-2,0]$.

4. Discussion and Open Problems

In this paper, we have proven the persistence and permanence of delayed differential systems (8) which incorporate distributed delays in both the linear and nonlinear parts and are in general noncooperative. Moreover, not all the coefficients are required to be bounded. The main theorem, Theorem 3, extends known results in recent literature [2,3,6,7,9,16,18], as it applies to a broad family of nonautonomous delay differential systems.

Once the permanence of (8) is guaranteed, several open questions arise and should be addressed. First, it would be interesting to have explicit lower and upper uniform bounds for all positive solutions, as investigated in [3,4,5,8,9,16] for cooperative scalar or n-dimensional DDEs and in [7,18] for noncooperative systems. Secondly, the global stability of DDEs is a matter of crucial importance in applications, therefore a relevant task is to propose sufficient conditions forcing $x\left(t\right)-y\left(t\right)\to 0$ as $t\to \infty$, for any two positive solutions $x\left(t\right),y\left(t\right)$ of (8). In the case of nonautonomous noncooperative models, it is however clear that the response to these two questions depends on the specific nonlinearities. In a forthcoming paper, these topics will be addressed for generalized Nicholson systems. For periodic n-dimensional DDEs, it has been proven [30] that in some settings the permanence implies the existence of a positive periodic solution. In this context, a stability result will show that such a periodic solution is a global attractor of all positive solutions.

It is worthwhile mentioning that, in the last few years, the stability of nonautonomous linear DDEs has received a great deal of attention, and several methods have been used to obtain explicit sufficient conditions for the asymptotic and exponential asymptotic stability of a general linear system (4), see e.g., [21,31] and references therein. Actually, both delay independent and delay-dependent criteria for the stability of linear DDEs were given in e.g., [21,31], the latter also with possible infinite delays. Since the exponential stability of (4) is a key ingredient to show the permanence of (8), this leads us to two natural lines of future research, explained below.

The first one is to replace assumption (H2) or (H2*) – which forces (4) to possess diagonal terms without delay which dominate the effect of the delayed terms – by a condition depending on the size of delays, in such a way that (4) maintains the exponential asymptotic stability, and further analyze how such a condition interplays with the assumption (H5).

Another open problem is to study the persistence and permanence of systems of the form (8) with unbounded delays. DDEs with infinite delay are surely more challenging: Not only an admissible phase space satisfying some fundamental set of axioms should be chosen, but most techniques for finite delays do not apply for such equations. There has been some recent work on the permanence for scalar nonautonomous DDEs with infinite delay, see e.g., [23]. In the case of multidimensional DDEs with infinite delay, the work in [5] only contemplates situations of cooperative systems, namely of the form $x_i^{\prime }\left(t\right)=F_i(t,x_t)-x_i\left(t\right)G_i\left(x_t\right)(1\le i\le n)$ with $F_i,G_i$ cooperative and $F_i(t,x)$ sublinear in $x\in {\mathbb{R}}^{+}$. For the case of possible unbounded coefficients and nonmonotone nonlinearities in (8), it is clear that the technique developed in the proof of Theorem 3 does not apply to systems with infinite delay, since it relies on a step-wise iterative argument on intervals of lenght $\tau$, where $\tau$ is the supremum of all delays. Thus, new tools and arguments to tackle the difficulty must be proposed. This open problem is a strong motivation for future investigation.

The treatment of mixed monotonicity models, in what concerns questions of permanence, is another topic deserving attention, since they appear naturally in real-world applications. In fact, there has been an increasing interest in DDEs with mixed monotonicity, where the nonlinear terms involve one or more functions with different delays e.g., of the form $f(t,x(t-\tau \left(t\right)),x(t-\sigma \left(t\right)\left)\right)$, with $f(t,x,y)$ monotone increasing in the variable x and monotone decreasing in y. As illustrated by Berezansky and Braveman [15], though small delays are in general harmless, the presence of two or more delays in the same nonlinear function may change drastically the global properties of the solutions. The permanence and stability of DDEs with nonlinearities of mixed monotonicity have been analyzed in [1,8,15,16,32]. As far as the author knows, only the case of discrete delays has been dealt with. New tools are required to handle the case of systems with mixed monotonicity in the nonlinear terms.