Abstract
In 1639, the treatise Prodromi catoptricorum et dioptricorum sive Conicorum operis ad abdita radii reflexi et refracti mysteria praevij et facem praeferentis. Libri quatuor priores by Claude Mydorge was printed in Paris. This volume, which followed the printing of his first two books in 1631, has resonance especially in the writings of those who, after him, addressed the conics. This fact raises the question of who Mydorge was and what his knowledge of the “doctrine” of the conics was, what is the most appropriate cultural context in which to properly read this writing, and finally, what is the place of its content in the development of thought placed between the Veteres and the Recentiores. In this paper, I attempt to elaborate an answer to these different questions, with the aim of emphasizing how the author reads and interprets the first books of Apollonius’ Conics. Neither the treatise, nor the figure of Mydorge, have received much attention in the current literature, although he was estimated as a savant in Paris and he was believed by Descartes to be one of the greatest mathematicians of his time.
1. Introduction
In this work, I attempt to provide essential information on the life, interests and cultural activities of Claude Mydorge, on his knowledge of the “doctrine” of conics and on the cultural context in which his treatise on conics, from 1639, Prodromi catoptricorum et dioptricorum sive Conicorum operis ad abdita radii reflexi et refracti mysteria praevij et facem praeferentis. Libri quatuor priores [1], can be read.
I also attempt to highlight how the contents of this writing are placed within the development of thought between Veteres and Recentiores, that is, between ancient authors and those who expressed at least new elaborations in the first sixty years of the 17th century.
Before doing so, it is important to note that contemporary mathematicians and post-Mydorge mathematicians, such as M. Mersenne, Fr. van Schooten, Grégoire de Saint-Vincent, and Wallis, do not ignore his writing, although, either implicitly or explicitly, they want to go beyond its contents.
Mydorge’s writing of 1639 in four books (the 1631 edition in two books was almost unfindable; the later authors who referred to his writing had the 1639 edition on hand) was a novelty at a time when the attention to conics was relevant; for example, on the analytical method front there was Descartes’ Géométrie of 1637 [2], the first comments to this book and the preparation of its Latin translation, and Fermat’s Ad locos planos et solidos isagoge [3], composed in 1636, which began to circulate as a manuscript. There was also the publication of the Brouillon project… [4] by Desargues in 1639, and that of the Essai pour les coniques et generation des sectionis coniques [5] by Blaise Pascal of 1640. These and other writings spread above all in the Circle that was formed around Fr. Marin Mersenne in Paris, where the savants (i.e., those who were deemed capable of expressing and elaborating their own ideas) and perhaps the amateurs de science (i.e., those who were able to make them their own) converged. In this Circle Mydorge enjoyed great esteem.
Mydorge’s work, in relation to his treatise, consisted in documenting himself around the conics and in thinking of a writing useful for those who wanted to solve problems of catoptrics and dioptrics. It is advisable to keep in mind this purpose by considering, at the same time, that in those decades the scholars of the conics had few writings on the subject, such as, for example, the translation of the first four books of the Greek tradition by Commandino of 1566, very widespread, and of many new works scattered here and there, such as those concerning the study of burning mirrors, the hourly lines, the “marvellous problem”, and the construction of the parabola (an example are the Nonnullae propositiones de parabola [6] by Marino Ghetaldi of 1603). The appearance of Mydorge’s writing was seen and interpreted as a novelty on the front of geometry expressed according to the method of synthesis of the ancients, and not according to the analytical method. This novelty can be synthetized as follows: summarize the first four books of Apollonius on essential lines in a single book through a clear and linear language, by concentrating the attention on the pointwise construction of the conics in the plane (the ones that are needed when you want to solve problems); collect as many methods as possible to construct conics by points in the plane; show how to build up equal and similar conics, carefully reading Commandino’s writing and probably also a few pages of Pappus’s Mathematical Collections. His contemporaries realized this novelty. For example, Mersenne took up almost entirely the monitum of Mydorge in the Universae geometriae, mixtaeque mathematicae Sinopsis… of 1644 [7]. In this work Mersenne offered readers a presentation of some writings of mathematicians in the essential lines and, as regards the conics, presented the Conics of Apollonius, the treatise of Serenus of Antissa on the sections of the cylinder and the cone, and the treatise of Mydorge. In the praefatio he made explicit reference to Apollonius, Mydorge, Desargues and Pascal. Furthermore, it is interesting to note the attention paid by Franz van Schooten to Mydorge’s writing in De organica conicarum sectionum in plano descriptione tractatus… of 1646 [8], in which in the Praefatio ad Lectorem he referred to Descartes, de Beaune, Mydorge, and Desargues. Regarding the construction of the conics in the plane, van Schooten preferred to emphasize the construction with tools, while acknowledging that Mydorge had written a volume in which he taught to describe conics by points, without the use of tools. Mydorge is explicitly mentioned by Wallis in De sectionibus conicis, nova methodo expositis, Tractatus of 1655 [9].
The importance given to Mydorge’s writings by his contemporaries seems to indicate quite clearly that his contributions can be considered much more than mere popularizing works. The very fact that an edition of his writing of 1660 was issued, after his death in 1647, when conics were studied in many places in Europe, confirms this hypothesis. In any case, evidently, his writing was considered very useful and has gone through decades of keen attention to conics.
At the same time, we observe that little information about Mydorge has been passed on to subsequent generations, although he was a well-known figure in the cultural and scientific Paris of 1625–1645, particularly for his presence and for his recognized skills within the Circle that, in the same years, gathered the most culturally evolved people around Father Marin Mersenne at the Convent of the Friars Minor, located in Place Royale.
The letters of Mersenne and Descartes document Mydorge’s cultural role and his scientific interests [10,11].
Mydorge’s treatise can be considered one of the first moments in geometry in which attention to conics is focused on their construction as plane curves. When passing from the first to the second book of his treatise, Mydorge points out the fact that the properties of conics as sections of a cone are the same when considering them as plane curves, thus opening up the route to the treatment of conics inside the analytic geometry. Mydorge’s knowledge and competence in the solutions of problems in optics and in the construction of parabolic, hyperbolic and elliptic lenses will be subsequently very useful for Descartes.
What I will try to point out in this work is the importance of Mydorge’s elaborations and scientific accomplishments in view of the subsequent development of analytic geometry, as well as in the construction of optical tools for observational astronomy and, in general, for the study of the trajectories of planets and comets that was developed afterwards by the theoretical astrophysicists. Finally, the topics treated by Mydorge can be important for the teaching of conics.
The article is organized as follows: in the next section, I will try to focus on the main events of Mydorge’s life, along with his scientific interests and cultural activities; then I will outline the status of the “doctrine” of conics in the first 60 years of 17th century. Afterwards, I will try to explain how to frame the treatise of Mydorge among ancient and modern authors, and I will specify the structure of the first book and, subsequently, a direct comparison of it with the treatise by Apollonius. Finally, I draw some conclusions on the topic.
2. Essential Information about Claude Mydorge’s Life, Interests and Cultural Activities
Mydorge’s person and activity have generally been ignored in the current literature, though he was reputed a savant in Paris at his time. A primary source that reports news about his life and scientific activity is the first part of the book La vie de Monsieur Descartes by Adrien Baillet [12], the biographer of René Descartes (1596–1650), while some letters of the correspondence between Mersenne and Descartes put into light his cultural role. Baillet’s writing is an indispensable source of information about Mydorge due to the strict relationships between the latter and Descartes from 1625 on.
We find a brief mention of Mydorge’s treatise Prodromi cataptricorum et dioptricorum sive Conicorum operis… libri quatuor in J. F. Montucla’s writing Histoire des mathématiques in the late 18th century [13]. An analysis of this treatise was performed by Michel Chasles in 1837 [14], while the presentation of one of his manuscripts on practical geometry was published by C. Henry in 1881 [15]. In 2009, L. Maierù attempted to reconstruct the author’s biography and his cultural interests [16,17].
Claude Mydorge (1585–1647) was born, lived and died in Paris in one of the most illustrious and wealthy families of France, occupying important roles in public administration (Conseiller au Châtelet, Trésorier de France en la Généralité de Amiens). Instead of occupying his time with those activities, he preferred to devote himself to the study of mathematics and other related disciplines, such as astronomy and optics.
In 1625, he published anonymously a writing on the use of the astrolabe [18], revealing that he was the author of it in a later writing [19] (p. 192).
Likely in the same year, he met R. Descartes (1596–1650) in Paris, with whom he quickly established a solid relationship that lasted for the rest of his life [20]. As Baillet attests, Mydorge was considered by Descartes a “prudent and faithful friend”, and was judged by him to be the “first mathematician of France in his time”, [12] (pp. 36–37, 149), [11] (Volume 1, p. 5). At least in two moments, Mydorge’s knowledge and skills regarding optical problems and the construction of parabolic, hyperbolic and elliptical lenses were very useful to Descartes.
The first moment occurred in 1627 and 1628, when Descartes, who lived in Holland, needed a competent person to follow the lens manufacturer, Jean Ferrier, from whom he commissioned some useful lenses to perform experiments on refraction. He begged Mydorge, therefore, to follow Ferrier at every step, being recognized for “his sure hand” and for being “as delicate as the subtle spirit” in tracing with his own hand the hyperbolas, parabolas, and ellipses. Soon, the relationship between Mydorge and Ferrier degenerated. This happened when Mydorge, after having traced the hyperbola that was used to create the lenses for the study of the refraction of “the crystal of Venice on a large sheet of polished copper”, followed assiduously and closely the work of Ferrier. Thus Descartes had a problem to solve, because Ferrier demanded that Mydorge be removed from his shop [12] (pp. 149–151, 185–186, 215, 219), [11] (Volume 1, pp. 38–52, 128–135, 170–176, 177–182, 189–191, 192–196), [10] (Volume 2, pp. 413–419, 542–548, 559–564, 570–580, 594–598).
The second moment was in 1630, a year in which several events happened. Mydorge and Mersenne (1588–1648) urged Descartes to publish the Dioptrique, being convinced that the writing was ready to be printed. Descartes, for his part, wanted to delay the publication of this book, to provide a more careful and more comprehensive explanation of the nature of colors and light [11] (Volume 1, pp. 177–182), [10] (Volume 2, pp. 559–564). In the early months of this year, Mydorge proposed problems of a geometric and mechanical nature to Descartes, the solutions of which were sent by Descartes to Mersenne in his letter of 4 March 1630 [11] (Volume 1, pp. 124–127), [10] (Volume 2, pp. 406–408, 505). Descartes, in turn, proposed to Mydorge to solve the problems of the duplication of the cube and trisection of the angle, which were subjects of discussion among the savants. Mydorge only solved the first of the two problems [11] (vol.1, p. 175, 252, 256), [10] (Volume 2, p. 546,), [15] (p. 218). Finally, Mydorge published the Examen du livre des Récréations mathématiques du P. Levrechon, writing much studied by his contemporaries [19]. Descartes believed that the author of the mechanical and optical problems was Mydorge himself [11] (Volume 1, p. 287).
Important (and recognized by his contemporaries even before 1625) was Mydorge’s knowledge of many problems having the conics as their object, the relationships between them and problems on the nature of vision, on the dioptrics and on the catoptrics [10] (Volume 1, pp. 260–264, 331). This was expressed in a letter written to Mersenne [10] (Volume 1, pp. 404–414), in which he demonstrated the following propositions:
- Given the inclination and refraction of any ray on the surface of any transparent body, determine the refraction of all of the other rays inclined on the same surface;
- Given any type of transparent body, find the refraction of the ray that, coming from the air, penetrates the aforementioned transparent body;
- In all the hyperbolas, if from any point from the section two straight lines are drawn, one for the external focus and the other parallel to the axis, and if from the same point a third straight line perpendicular to the tangent to the section is drawn, then the sine of the angle formed by the parallel to the axis and by the perpendicular line is to the sine of the angle formed by the straight line passing through the focus and by the perpendicular itself as the axis crossing the section is to the distance between the foci;
- In all the ellipses, if from any point not on the section, two straight lines are drawn, one to the furthest focus and the other parallel to the axis, and a third straight line perpendicular to the tangent is drawn again from the same point, the sine of the angle formed by the parallel to the axis with the perpendicular is to the sine of the angle between the straight line drawn through the focus and the perpendicular as the major axis of the section is to the distance of the foci;
- Given the refraction of any inclined ray on the surface of any transparent body, describe the figure of this surface in such a way that all of the rays that it receives that are parallel meet at a given point or are diffused. These rays are called convergent or divergent.
The proofs of these propositions are organized in an elegant form and, at the same time, highlight the author’s culture. In particular, the last proposition, related to solids generated by the rotation of a hyperbola and an ellipse, is a vivid testimony of this fact.
Problems of the same type were recalled by Mersenne in the Quaestiones celeberrimae in Genesim [21] (p. 500, 506, 525, 530, 531, 764) and in Harmonie universelle [22] (p. 28), t. II, Nouvelles observations, and by Descartes in the Regulae ad directionem ingenii, likely composed during the winter of 1627–1628 [11] (Volume 10, pp. 393–395), and more widely in the Dioptrique [11] (Volume 6, pp. 181–186).
At the same time, news circulated between France and Holland that Jacob Golius (1596–1667), an Arabic language and mathematics lover in Leiden, returned from the Middle East, bringing with him a manuscript containing all the books of Apollonius’ Conics in Arabic. This news, awaited by many lovers of Conics and of the “doctrine” of conics, spread in France. In this regard, Mersenne wrote to André Rivet (1572–1650), who was in Leiden, to request information directly from Golius, after a request from Mydorge [10] (Volume 2, pp. 269–271).
By answering to Mersenne, Golius writes of the manuscript and transcript the initial and final propositions of the books V–VI–VII of the Conics, attempting a comparison between this edition and the one of the treatise of Apollonius that was known at that time [10] (Volume 2, pp. 383–388). Golius did not mention the first four books of Apollonius’ writing because, in the West, a Latin translation by Federico Commandino (1566) of a manuscript in Greek was widespread. Moreover, from his answer, we learn that the eighth book of Apollonius’ Conics was unobtainable till that moment.
Mydorge, after reading this letter, added some marginal notes in which he established a correlation between the transcribed propositions and some propositions of a treatise on conics that he was preparing during those years. Since the references to his manuscript were very accurate and precise, one can hypothesize that the treatise, at least in the parts related to the properties of conics, was likely ready for printing in 1630.
The treatise was printed in 1631 with the title Prodromi catoptricorum et dioptricorum sive conicorum operis … Libri primus et secundus [23]. This title contains the meaning to give to the writing, which aims to present the necessary knowledge on the conics and the main problems connected to them, which are indispensable for studying the phenomena of “catoptrics” and “dioptrics”, that is, of reflection and refraction, respectively.
The esteem for Mydorge went beyond the borders of France. A testimony of this esteem was given by Golius’ proposal to resolve the “problem of Pappus”, addressed to him and Descartes. Descartes provided a solution to the problem (January 1632); we do not know whether Mydorge gave one too [11] (vol.1, pp. 232–236, 254–257), [10] (vol.3, pp. 314–319). As it is well known, the study of the “problem of Pappus” is the main example of Descartes in book I of Géométrie (1637).
Mydorge enjoyed a great reputation among his contemporaries for his knowledge of the problems of cyclometria, i.e., problems of the squaring and rectification of the circle, and of meteorology [10] (Volume 2, pp. 7–8, 28, 34–35, 89, 90). For this reason, on 30 March 1634, he was appointed commissioner to evaluate, together with Étienne Pascal (1588–1651), Jean Boulanger, Jean de Beaugrand (1590–1640), and Pierre Herigone (1580–1643), the calculation of the Longitudes by Jean Baptiste Morin (1583–1656), professor of mathematics at the College de France [24], [10] (Volume 2, pp. 7–8), [11] (Volume 1, pp. 284–291).
Mydorge was interested in Descartes’ scientific works, mainly in the composition and publication of the Dioptrique [11] (vol.1, pp. 463–474, 481–486, 500–504), [10] (Volume 6, pp. 321–332; Volume 7, pp. 9–12, 37–42), placed among the appendices to the Discours de la Méthode of 1637 [2]. He criticized Dioptrique on several points, as Pierre de Fermat (1601–1665) did. While Mydorge’s criticisms were accepted by the author, Fermat’s criticisms were not. Regarding Mydorge’s criticisms, Descartes wrote to Mersenne [11] (Volume 1, p. 501):
I don’t find it strange that M. Mydorge disagrees with me in more things than what I wrote about vision because this is a subject that he has previously studied a lot, and not having followed the same principles as mine, he should be of a different opinion. However, I hope that the more he examines my reasons, the more they will satisfy him, and he has too good a spirit not to put himself on the side of Truth.
The controversy between Descartes and Fermat was rather acrid, starting from Fermat’s criticisms of several points of the Dioptrique, to which were added Descartes’ criticisms of Fermat’s method of determining the tangent to a parabola and his writing De maximis & minimis.
Descartes begged Mydorge to be a judge in this querelle, specifying the different points of the diatribe [11] (Volume 2, pp. 15–23).
In the same year, 1638, Mydorge asked Descartes to make known to him his Algébre. The answer appears in a letter from Descartes to Mersenne [11] (Volume 1, pp. 501–502), [10] (Volume 7, pp. 37–38), in which it is said that “his” Algèbre is book III of Géométrie. Descartes himself, speaking of Géométrie, states that, in France, those who are “very capable of understanding it” are Bachet de Méziriac, Mydorge, Hardy, Fermat and De Beaune [12] (pp. 292–294).
In 1639, Mydorge published his Prodromi catoptricorum et dioptricorum sive Conicorum operis… libri quatuor, judged by some of his contemporaries to be superior to other books on conics [12] (p. 43).
In 1640, Sir Charles Cavendish (1594–1654), William’s younger brother, first Marquis of Newcastle, attempted to have Descartes and Mydorge moved to England, but the latter opposed it. This obstacle did not stop Cavendish’s zeal, who spoke of it to King Charles I, who wanted to bring together great geniuses “to experience physics”. This project, however, was interrupted by the war in Great Britain [12] (pp. 67–68), [25] (p. 32, 51, 80–85).
In the same year, Mydorge, being judged “a wise and discreet person”, [12] (pp. 76–78), held a central position as an intermediary in the querelle between Descartes and the Jesuits about the interpretation that they gave of the Dioptrique.
Between 1640 and 1647, the year of his death, Mydorge’s life turned to the end, sustained “by the reputation for great integrity of life”.
He left a few of his manuscripts, including the second set of four books of the Coniques, which are believed to have been transported to England from Cavendish or Southampton, while the others (such as De la lumière, De l’ombre, and De la sciotérique) were dispersed in the troubles des guerres de Paris [12] (pp. 325–326).
3. The Context of the “Doctrine” of the Conics in the First Sixty Years of the 17th Century
From the information presented above, one realizes Mydorge’s excellent knowledge of the “doctrine” of conics and their application. Additionally, for this reason, he enjoyed the esteem of Descartes and other savants who frequented the circle of M. Mersenne in Paris, esteem that, going beyond the borders of France, reached as far as Holland and England.
We have glimpsed that his treatise on conics, indicated using the term Coniques by his successors, is composed of two parts, each consisting in turn of four books. The first part was published in 1639, while the second part remained handwritten until his death, and its traces were subsequently lost.
In this work, I limit myself to considering the published part, which was preceded and followed by publications on the same topic of writings by other lovers of mathematics.
To give an adequate place to this writing, I think it useful to trace briefly the history of the “doctrine” of conics between the end of the 16th century and 1660.
At the end of the 16th century, three lines can be identified along which much of the knowledge about the conics was transmitted [26].
The first concerns the transmission and knowledge of Apollonius’ Conics in the West. The second concerns the presence of conics in the treatises on burning mirrors and perspective. The third concerns the usefulness of the conic sections for determining hourly lines. In the same period other contexts in which conics began to be applied are identified, as for instance in architecture and gardening [27,28,29].
Apollonius’ Conics does not have a parallel history to that of the Elements of Euclid. At the beginning of the 16th century, there was growing interest in the Conics of Apollonius in the West, which passed from the first collections of propositions (Giorgio Valla 1501, Johann Werner 1521) to the translations of the first four books transmitted in Greek (Giovanni Battista Memo in 1537, Francesco Maurolico in 1547 and Federico Commandino in 1566). The translation of Memo was considered incorrect, and for this reason, it was not widespread; that of Maurolico (with the divination of books V and VI) was composed in 1547 and was published only in 1654. The translation of Commandino [30], written such that the tradition of Conics is borne in mind, remains available to scholars, inserting in the text the headwords presented by Pappus of Alexandria in book VII of the Mathematical Collections, the commentary of Eutocius of Ascalona in the first four books and the commentary of Commandino himself. In this translation, the best of the cultural tradition on conics is certainly recovered.
A further chapter concerns the attempt to retrieve the other four books of the Conics, which achieved positive results in the 17th and the first decade of the 18th century [16,31,32]. From the three different Arabic manuscripts that arrived in the West, it is concluded that the eighth book is completely lost. The translations of these manuscripts came into light in 1661 via A. Borelli, in 1669 via Chr. Ravius and in 1710 via E. Halley.
As I said, the second line concerns the presence of conics in the treatises on burning mirrors and perspective (geometric optics), in which the names of Alhazen and Witelo play central roles, and with which those of Oronce Finé, Antoine Gogava and John Dee are associated. Important is the edition edited by Risner of the treatises of Alhazen and Witelo in 1572 [33].
Collaterally, there is an interest in the “marvellous” problem, which addresses the relationship between a hyperbola and an asymptote of it (a situation formalized by Apollonius in his prop. II 14 of Conics), particularly during the 16th century. The history of this problem is marked by the names of Mosé of Narbonne, A. Gogava, O. Finé, G. Cardano, and J. Peletier, reaching its peak with F. Barozzi, who chose this problem to show what it means to demonstrate through analysis and synthesis in a volume from 1586 [34].
The third line concerns the “hourly” lines, the determination of which is possible by means of conics, as F. Maurolico showed in his 1575 treatise De Lineis Horariis libri tres [35], which is the most significant one on this subject. Some references also appeared in the writings of G. B. Benedetto and Chr. Clavius.
This “state of the art” at the end of the 16th century is the indispensable substratum for realizing how several scholars oriented themselves in the early 60 years of 17th century. Their writings circulated in Europe, so they must be considered to give a proper place to any treatise published during this period.
The Perspectivae libri sex by Guidobaldo del Monte from 1600 provided an updated and more complete reinterpretation of the doctrine of conics within the problems of geometric optics.
Marino Ghetaldi’s Nonnullae propositiones de parabola from 1603 provided a cultural connotation of the construction of “equal” parabolas, which are the prerequisites for the burning mirrors.
The Ad Vitellionem paralipomena by Johann Kepler from 1604 showed which part of optics (catoptrics and dioptrics) is found within astronomical problems, and how it is possible to study the eclipses of the sun and moon by observation.
A central place is occupied by Lo specchio ustorio overo trattato delle settioni coniche, et alcuni loro mirabili effetti intorno al lume, caldo, freddo, suono, et moto ancor by Bonaventura Cavalieri from 1632, a year after the publication of the first two books of the Prodromi… by Mydorge.
In the years between 1630 and 1645 in France, different readings were offered of the doctrine of conics and its applicability to the resolution of problems of various types.
From 1636 onwards, Pierre de Fermat’s Ad locos planos et solidos isagoge began to circulate, in which the “loci”, which solve plane and solid geometric problems, are expressed by means of equations. Thus, if the “loci” are conic sections, they are associated with easily solved equations with knowledge of elementary algebra.
Book II of Géométrie by René Descartes from 1637 presented the construction of conics by means of tools and the identification of the equation that specifies them.
As stated above, in 1639, Mydorge’s treatise was published in four books, in which significant problems were expressed ranging from knowledge of different methods for the construction of conics on a plane to the specification of equal and similar conics.
In the same year, Gerard Desargues published another work, Traité des coniques ayant pour titre: Brouillon project d’une atteinte aux evenements des rencontres du cone avec un plan…, in which conics are presented in a cultural context that finds their origin in the perspectives of painters. The method introduced is therefore totally different from that of Fermat, Descartes and Mydorge, and represents the first step in what would become projective geometry.
In 1640, the young Blaise Pascal published a leaflet, Essai pour les coniques, in which he attempted to generalize conics, after reading the treatise of Desargues. In this writing, we find what went down in history as “Pascal’s theorem”. The Traité des coniques, which Pascal subsequently wrote, remained in manuscript form during his life, and after events not easy to unravel, there is no information about it.
In 1644, Mersenne published the Universae geometriae mixtaeque mathematicae synopsis, et bini refractionum demonstratarum tractatus in Paris, in which the writings of ancient and recent authors on conics and on the phenomenon of refraction can be read.
Other writings later appeared in Europe.
In 1646, Franz van Schooten, professor of mathematics at Leiden, published De organica conicorum sectionum, in plano descriptione, tractatus, geometricis, opticis; praesertim vera gnonomicis & mechanicis utilis, in which he expanded the instrumental construction of conics presented by Descartes in book II of Gèométrie. For the composition of this treatise, Mydorge’s treatise of 1639, specifically book II dedicated to the construction of conics on the plane, was greatly considered. This writing by van Schooten is also an essential prerequisite for studying his commentary on Géométrie from 1649 and 1659–1661.
In 1647, Grégoire de Saint-Vincent published the volume Opus quadraturae Circuli, a significant part of which was occupied by the presentation of conics. It is appropriate to link his other posthumous work to the writing… ad Mesolabium per rationum proportionalium novas proprietates… from 1668.
John Wallis in 1655 printed De sectionibus conicis, nova methodo exposito, Tractatus in two parts. The first part presented the fundamental results of the doctrine of the conics by Apollonius, read in the context of Cavalieri’s method of indivisibles. In the second part, there is the presentation of conics on a plane in the language of algebra, showing initially that conics as plane curves are the same curves as those obtained as sections of a cone.
In this same year, the Jesuit Claude Richard presented Apollonii Pergaei Conicorum libri IV, containing extensive comments. This writing gave the impression of wanting to re-propose Conics as they come from tradition.
Finally, among the texts into which, directly or indirectly, the conics intervene, I refer to two volumes that contain writings inspired by Descartes’ Géométrie. The two volumes are the result of an editorial project directed by Fr. van Schooten, who however did not see its complete publication since he died in 1660. Within them, there are the writings of several mathematicians closely related to van Schooten. Among these writings and in relation to conics are the two books of Jan de Witt’s Elementa curvarum linearum, in which the language introduced by Desargues in the 1639 writing was used for the geometric presentation of conics and algebraic language (equations) for their identification. Conics, in this manner, are the “loci of points” of the plane that resolve solid problems.
To conclude this excursus on the writings that in the first sixty years of the 17th century saw light, we note that Apollonius’ Conics, while remaining a secure cultural reference point, did not engage the mathematicians around it. Instead, once they had appropriated the doctrine of the conics, as tradition gives it, they were committed to studying these curves, especially considering them as the loci of points on a plane and as solutions to solid problems, according to the classification of the ancients. At the same time, many of them emphasized their use in solving problems concerning reflection and refraction, the determination of time lines, and the study of eclipses.
4. The General Characters of the Script in 1639 and the Reading of Conics between Ancients and Moderns
What has been presented so far constitutes the necessary premise to begin reading the Prodromi catoptricorum et dioptricorum sive conicorum operis ad abdita radii reflexi et refracti mysteria… libri quatuor priores from 1639. The title proposes the volume as an essential prerequisite for studying the phenomena of refraction and reflection. In Mydorge’s project, there were four more books, prepared by the author and lost after his death, in which we would read how, using conics, we would be able to solve the problems regarding these phenomena.
The reference points for evaluating Mydorge’s work on the “doctrine” of conics are, on the one hand, Apollonius’ Conics, and, on the other hand, the treatises on the burning mirrors, the perspective, the study of reflection and refraction, and the determination of time lines. These treatises, while referring at many points to Apollonius’ writing, did not use it for comparison, as is the case of Mydorge’s writing, the four printed books of which present the passage from Conics in the attempt to study conics in a plane (book I), considering a set of methods of the construction of plane conics (book II), the construction of “equal” conics (book III) and the construction of “similar” conics (book IV).
This treatise certainly represented a novelty both in relation to the editions of the Conics and in relation to the treatises in which the conics are used to solve problems of a different nature. Mydorge’s volume represents the attempt, certainly not negligible, to give the presentation of conics, in view of their use, a solid cultural substrate, which can only be found in Apollonius’ Conics and in their tradition. This fact raises the question of which edition of Apollonius’ Conics Mydorge knew. A single answer emerges from the reading of his writing: the edition that he had was that of Commandino of 1566, every single part of which he studied, as emerges above all from reading books III and IV, in which the name of Commandino appears several times. In contrast, we cannot put forward other hypotheses since this volume was the only printed Latin-language text in circulation in Europe.
My intent is to present book I in its essential aspects and to emphasize how Mydorge saw and evaluated his relationship with the first four books of Conics.
For this reason, it would be misleading to compare his references to Apollonius’ propositions considering a more modern edition, such as that of Heiberg from 1890 [36], or as influenced by the recent study of Conics of Fried and Unguru from 2001 [37], in which the reading of Apollonius’ writing was provided in a philological and interpretative context.
My belief is that Mydorge intended to treat conics on a plane (books II, III and IV confirm this intention), considering them “loci of points”, useful to solve problems, as he affirms in the title, as done by Descartes and Fermat, in the same period, but in a different way. At the same time, following the propositions that follow one another, Mydorge intended to also highlight the treatment by Apollonius and determine how to reconcile, if possible, conics as “sections” with conics as “plane curves”.
To give proper weight to his language, it is appropriate to refer to the cultural categories through which the mathematical events (although not only these events) of this historical period are sometimes read.
In the premises to many mathematical writings of this period, the authors attempted to give a place to their writing, specifying that their work was far from those of Veteres or Antiqui, that is, of the ancients, and was therefore to be placed between those of the Recentiores, that is, of the moderns. With these terms, which generally do not provide a temporal collocation, we are to understand, on the one hand, the classical authors and those who re-proposed their methods in the solution of ancient and recent problems (the ancients and the subsequently formed tradition), and, on the other hand, those who, consolidated in the methods and contents transmitted by the classics, engaged in the search for new methods to address with them old and new problems (the moderns) [16] (pp. 11–20).
The clearest example of how the ancients were read by the moderns is expressed in Regula IV. Necessaria est methodus ad rerum veritatem invenstigandam of the Regulae ad directionem ingenii by Descartes, likely composed in 1627–1630 [11] (Volume 10, pp. 359–469), [38,39]. During the presentation of this rule, the author emphasized his experience in approaching the study of mathematical disciplines [11] (Volume 10, pp. 375–377). He affirmed that the ancient authors did not bother at all about teaching the way in which they achieved results, preferring instead to hide it: “it did not seem to me [that] they showed to the mind well enough why such things were like this and how they were found”.
Therefore, his commitment was to look for that “mathesis”, sought after by many since ancient times (his witnesses of the ancient world were Pappus and Diophantus), which he believed
was later suppressed by the authors themselves for some pernicious cunning: in fact, in the way in which many authors—it is now proved—have perhaps feared that, simple and very easy as it was, it would degrade once it was divulged and preferred to show us in its place so that we could admire them, certain sterile truths acutely demonstrated by way of consequences, as effects of their art, rather than teaching the art itself, which would have made the wonder stop.
In this way and in these terms, the ancients are considered. And the moderns?
Descartes went on to say:
Finally, there have been particularly ingenious men who in our century have tried to awaken this art.
His intention was to make everyone aware that a new era had begun, in which the same past was built and reread on new bases and with a different language.
Descartes’ judgement reveals a profound contrast between the ancients and the moderns. In fact, one has the impression that the gap is less deep or non-existent, it being possible to read, in the work of the moderns, a real continuity between the past and the present, since the advancements of the moderns in scientific knowledge and new elaborations presupposed their solid training in the writings of the ancients.
Mydorge was a living testimony of this assumption.
He had at his disposal the treatises in which the problems around natural phenomena solved by conics are presented. This availability is indicated in his treatise on optics and astronomy, in which reflection, refraction, conical lenses, hourly lines, the determination of the height of the horizon, etc., were studied. Moreover, having in mind the edition of Commandino from 1566, he could understand how the first four books of Conics are structured.
Thus, on the one hand, the conics and their properties are presented in a simple and essential language (the authors of the treatises limited themselves to giving the indispensable elements without letting themselves go on into discussions deemed useless or superfluous); on the other hand, the conics were studied in a general form with patience and completeness, in theorems and problems, from their generation as intersections on a cone to the specification of their elements (diameter, axis, ordinate, tangent, etc.).
Mydorge cultivated the project of drawing up a treatise in which the refraction and reflection problems were central, to which he intended to preface the presentation of the conics drawn up following the model proposed by Apollonius. In this way, the study of these phenomena was introduced by that of conics seen in their generality.
This introduction could not be a re-proposition of all of the contents of Apollonius’ books, nor could it give space to Pappus’s lemmas and comments in the wake of Commandino’s text if it were to be effective for the study of phenomena.
Mydorge had no choice but to have Apollonius’ writing in front of him, while the propositions on conics, presented in a simple and essential form, unfolded on his sheets.
He realized that there is no writing in which conics are presented in this way. His work, therefore, appeared as an operation not carried out by others before him. This conviction caused him to perform an action not dared before against a classic text, such as Conics, muffled with sacredness in the same way as Euclid’s Elements. His work, therefore, was a totally new operation upon a classic text, which only moderns could perform, with their being in the psychological and cultural conditions to be able to “dare” it. The Cartesian Regulae taught about this ability. Thus, if the action of Mydorge is to be considered proper to the moderns, it is evident that Conics and its tradition, in whatever way it is treated (including the edition of Commandino), is a work of the ancients.
With these words, I have attempted to summarize part of what Mydorge wrote in Monitum (Warning), with which he opened the treatise on conics. Of this Monitum, I will attempt to highlight the essential points, to which Mydorge drew the attention of his “friend reader”, to be reassured when he intended to follow him in his cultural adventure around conics and their applications.
First point. The author intends, first, to inform the reader of the contents of his treatise and the tools that he uses to demonstrate theorems and solve problems.
His writing on conics was “built”, based on Euclid’s Elements and not on Apollonius’ Conics, since he decided to make extensive use of the ”norm” alone, the “geometric proportion [as it is] contained in the Elements”. Therefore, those who undertake a little practice with it “easily walk the whole construction [of the writing] without stumbling”. This process allows him to present the content of Conics “in a simpler form”, believing that the “sources” from which they come are the same as those from which Apollonius “deduced the main and capital streams with hidden artifice”. Therefore, in book I, which is the “main” text from a cultural point of view, “it is demonstrated in direct form what most of the times is proved by Apollonius himself in an indirect or absurd form”. As can be verified, Apollonius in the proofs/solutions of his own propositions follows either the methods of analysis and synthesis or a “reductio ad absurdum”, whilst Mydorge limits himself to the direct form, which is proper in the method of classic synthesis. Consequently, Mydorge wrote:
Our purpose is very different from Apollonius’ purpose since he only pursued that his Conics [be] arranged at every point in a pure and abstract form for the determination and composition of solid problems. We search in Conics for physical [phenomena] and compose them for physical [phenomena].
From this we infer that Mydorge presents the essential elements of the conics in such a way as to solve with these curves the “solid problems”, according to the ancient classification, more specifically those concerning the physical phenomena. As such, he concluded:
what Apollonius dispersed in the first four books of Conics, the same for the most part but nevertheless more than enough, we have collected in our single [book].
These statements specify the project that Mydorge intended to pursue, that is, to give a reading of Conics, translating what concerns conics and is useful to study natural phenomena, so that there are demonstrations/solutions in a direct form. He realizes that, in order to pursue this aim, he does not need all the traditional mathematical tools, but only those of geometric proportion, much used in Euclid’s Elements, which he called with emphasis his “norm”. What he pursued cannot be categorized as a “paraphrase”, that is, a “leveling down” so that everyone understands (we find models of this idea in translations of Conics and Elements, as well as other writings, of the golden age of Arabic mathematics of the 9th–13th centuries). Mydorge reads in a careful and prudent way both the propositions by Apollonius and those of the tradition, and formulates “new” propositions (theorems and problems) by proving them in a direct form. All of this material constitutes the specificity of book I of his writing, even if we observe the same style in other books, especially books III and IV.
A coeval attempt with that of Mydorge is found in Lo specchio ustorio overo trattato delle sezioni coniche et al.cuni loro mirabili effetti intorno al lume, caldo, freddo, suono, e moto ancora by B. Cavalieri from 1632 [40]. In this writing, we perceive the same cultural passage while observing a different distribution of the contents, since the elements around the conics sections are presented in a very synthetic form in the first 60 pages. One may hypothesize that Cavalieri also had the 1566 edition of Commandino at hand.
Second Point. Mydorge presented the complete structure of his project by explaining the content of all of the books that would make up the writing. Having explained the contents of book I, he went on to say that:
- book II deals with the geometric construction of conics by points on the plane;
- book III speaks of the “equal” conics on the surface of the cone and on the plane;
- book IV presents “similar” conics on the surface of the cone and on the plane;
- book V, more addressed to the study of physical phenomena, presents “things worthy of being noticed” regarding portions of conic sections and sections of portions of the cone;
- book VI, useful for physical experiments, contains conics and the problems they cause;
- book VII deals with inscribed and circumscribed conics or “the maxima and minima concerning mirrors and dioptrics”;
- book VIII compares the conical lines and surfaces of cones and conoids, specifying the proper and special nature of each in relation to the radius in opaque and transparent materials.
This approach allows us to reveal “important mysteries” around reflected and refracted rays, not known by the “vulgo”, “in a new light”, “with a right and proper method” and “with constant work”, so as to be ready and to proceed safely in the construction of any mirror, or of the “desired” transparent lens.
As stated above, the second set of the four books did not reach the next generations.
One can observe that what Mydorge stated about book I can be generally extended to the evaluation of books III and IV, the compositions of which follow the same criteria as book I. At the same time, one can notice that each of these books has characteristics of its own, and by studying it one can clearly distinguish what comes from the tradition and what is not present in that.
Third point. Mydorge focused his attention on the definitions, some inserted at the beginning of the writing and others inserted when necessary. All are presented “simply, without any paraphrases and not accompanied by figures”. Furthermore, Mydorge invited the reader to neglect those issues that would not initially be clear, convinced that the demonstration/solution of the propositions with the added figures would illuminate what was defined. By following this method, one arrives at a “happy outcome”, acting patiently and returning repeatedly to things, and it finally “shows the much desired way”, through which it becomes easier to enter “the mathematical field”, where “first from chosen ears, then from the seed prepared by them and thrown [into the field], one finally comes to collect more bundles”. Then, he concluded:
[From] the cultivation of the field of the catoptrics and dioptrics we have collected the harvest around the conics, which we have decided to communicate willingly in the meantime, waiting for the integrated harvest of the catoptric and dioptric [phenomena] to be ripe.
Reading the Monitum causes us to realize how difficult it was for Mydorge to read and interpret Conics and, at the same time, how necessary it was for him to read this writing up to the end in order to offer his reader a “lighter” reading.
On the one hand, he wrote of “occult artifice”, of indirect and reductio ad absurdum proofs and of the presentation of conics and their properties in abstract form, for the sole purpose of enabling the reader to be able to solve a “solid” problem when the opportunity arises (which makes it clear why the study of conics as “sections” on a cone, right or scalene, is essential for Apollonius); on the other hand, perhaps in the face of the difficulties posed by some specific reflection or refraction problem or by the construction of some parabolic, hyperbolic or elliptical mirror, Mydorge realized that it is not important if the conic that we use is a “section” of some cone; rather, what is important is to be able to trace the conic on a sheet of paper so as to then pass it on to a more consistent material, and, finally, to consider the rotation that can be obtained from it as solid. Only after doing so will it be possible to think of “constructing” a specific mirror in opaque or transparent material.
All of this discussion suggests that the lovers of these phenomena are only interested in the conics being built on a plane, so that, on “this” plane, their properties can be understood; it further seems that Mydorge, with his “reading” of Conics, causes them to feel the cultural need to approach Apollonius’ text, recognizing in it the theoretical “foundation” indispensable for being able to trace a conic on a plane, whether equal or similar.
In conclusion, Mydorge’s aim was to create an edition, having Apollonius’ text as a reference point, and in which catoptrics and dioptrics lovers do not encounter difficulties of any type when reading it, can enrich their knowledge about conics by deepening their study, and can proceed with linearity in problem solving.
In an attempt to explain to the reader what the characteristics are of the reading of Conics proposed in his writing, Mydorge accentuated the expressions mentioned above to bear in mind that Apollonius was a spearhead of ancient mathematicians, and he was among them the “great geometer”. As such, following Descartes’ expressions, he “has hidden” (“occult artifice”) rather than revealed, or made it easy to read, his writing. This statement helps us to understand why Commandino in his edition gave so much preliminary space to the lemmas drawn up by Pappus in book VII of the Collection, to Eutocius of Ascalona’s comment, and to making his own comment. Mydorge’s operation, then, is one of disclosure and reassurance, remembering that, in demonstrations/solutions, the main operation consists of proportion, and expressing the definitions in simple and fully understandable language. It is surely an exaggeration to argue that Mydorge believed that his writing could replace Apollonius’ tout court, representing his attempt as a way to bring the readers closer to Apollonius’ writing. I now turn my attention to the first book, because in it a possible comparison with Apollonius’ writing is focused.
5. The Structure and Content of Book I of the ‘Prodromi…’
Reading book I, we realize how close and far, at the same time, Mydorge was to Apollonius’ writing, and how great his respect for it was, so much so as to give the impression of taking Apollonius’ book I as a model for his book, dividing the definitions into three groups and inserting them in different moments of the writing.
He included “all” doctrines of conics in 59 propositions (49 theorems, 8 problems and 2 lemmas), and in a certain number of corollaries.
He noted how much difficulty one encounters in attempting to summarize Apollonius’ four books. From time to time, therefore, he inserted other monita (3) and some consectaria generalia or general consequences (2) with which to help the reader understand the problems that have involved many mathematicians in the succession of history.
It is thus useful to focus the attention on such monita.
In the first monitum, he presented the historical path of the conics and the term with which each of them is indicated [30] (pp. 9–11). Initially, the parabola is a “section” of a rectangular cone, the hyperbola is a “section” of an obtuse cone, and the ellipse is a “section” of an acute-angled cone, following the Euclidean–Archimedean tradition. With Apollonius, Mydorge wrote, the conics are considered on the same cone, and they are called “parabola”, “hyperbola” and “ellipse”, specifying their construction in props. I 11, 12 and 13 of Conics.
Mydorge then asked himself why Apollonius did not consider the circumference to be conic, limiting himself to indicating only three, identified by the square of an ordinate at the diameter and by the rectangle applied to the right side or “parameter”: in the hyperbola, the square of the ordinate is greater than the figure formed by the parameter and the transverse diameter, and in the ellipse, the square of the ordinate is smaller than the figure formed by the parameter and by the transverse diameter.
We observe that the “right side” of tradition is constantly called “parameter” by Mydorge, as we read in the props. I 11, 12 and 13 [30] (pp. 13–15).
Apollonius himself presented the circumference in the right cone and in the scalene cone, after obtaining the triangle for the axis, intersecting the cone with a parallel plane (in the right cone) or placing it in a subcontrary way (in the scalene cone) at the base of this triangle (props. I 4 and 5) [30] (pp. 9–10).
While respecting the cataloguing given by Apollonius, Mydorge stated that nothing prevents us from considering the circumference as the fourth conic, that is, as a particular case of the ellipse. Such a problem was present in the tradition.
In the drafting of book I, he chose to follow Apollonius, considering only three conics. This position was overcome in a monitum of book III [1] (pp. 178–179), dedicated to “equal” conics, in which he presented how many ways a cone can be intersected by a plane and which conics are generated. Let us summarize this observation in these terms: if a cone is intersected first by a plane passing through the axis and then by a plane that intersects the triangle by the axis without passing through the vertex, this second plane can assume the following positions:
- Parallel to one of the sides of the triangle for the axis. In this case, the section on the surface of the cone is a parabola;
- Intersecting one side of the triangle and the extension of the other above the vertex. Then, the section is a hyperbola;
- Intersecting both sides of the triangle below the vertex and parallel to the base. Then, the section is a circumference;
- Intersecting both sides of the triangle below the vertex, remaining positioned in a subcontrary way at the base. Again, the section is a circumference;
- Intersecting both sides of the triangle without being parallel or subcontrarially positioned at the base. Then, the section is an ellipse.
This classification, slowly identified in tradition, found noteworthy expression in the 17th century in Philippe La Hire’s treatise, Sectiones conicae in novem libros distributae,… from 1685 [41].
In the second monitum, Mydorge caused the reader to reflect on the sections obtained on the right cone and on the scalene cone, the diameters of which in both cases do not enjoy the same property, that is, to be parallel to each other, creating a distinction between the axis of the cone and the diameter of the conic [1] (pp. 9–11). This fact is overcome by considering the conics on a plane since, in this case, in a parabola, all of the diameters are parallel to the main one, while in the ellipse, in the circumference and in the hyperbola, they are all inclined in the same way and intersect in the center of the section.
In the third monitum, Mydorge specified that what has been shown to be true for a branch of a hyperbola is also true for the other branch, and that it is possible to consider the opposite branches of a hyperbola starting from two cones in opposition [1] (p. 59). This is made explicit in props. I 42–46 [1] (pp. 59–64), in which the propositions present in the four books of Apollonius are gathered in a simpler form.
In book I, we also find two consectaria generalia, in which Mydorge collected the results achieved in the propositions. In the first, he showed how to construct a straight-line tangent to a parabola at one point, and how to distinguish it from other straight lines that cut the same parabola [1] (p. 32); in the second, he showed how to construct a tangent to a hyperbola, an ellipse and a circle [1] (p. 38).
Book I closes with some classical style problems [1] (pp. 69–80) that should allow the reader to verify their understanding of the proposed topics.
Let us focus our attention on the last problem (prop. I 49), in which one is asked to “exhibit” the parameter in relation to the cone on which any conic is obtained. This problem, like the whole approach of book I, highlights that Mydorge was following the same path proposed by Apollonius, which goes from the cone to the conical sections.
Reading books II, III and IV, one has the impression that the author did not want to detach himself from considering conics as “curves” on the plane. This observation is motivated above all by the second book, in which the reader is offered various possibilities of constructing conics on the plane using the simplest tools of geometry, such as drawing one or more straight lines, parallel or intersecting, and drawing a circle, once the center has been identified and the radius given (see Refs. [42,43] for similar examples in different contexts). With these operations, we do not deviate from the geometry of Euclid. Through these operations, we identify a certain number of points, all of which satisfy the same property.
What can be achieved by combining these points with a single curve? With what tool should we “do” this?
Mydorge stated, “si eadem curva aequabili manu ductu iungantur linea”; that is, “if with a single curve, drawn with a uniform hand, the points found are joined”, then we are faced with a specific conic. Thus, tracing “with a uniform hand” becomes a geometric operation, and the conics obtained are “curves” in the plane. Therefore, conics are the “loci of points” on the plane. This conclusion is indisputable in book II and is endorsed in books III and IV.
It is also the case with the treatises on burning mirrors, on perspective and on the phenomena of catoptrics and dioptrics.
Cavalieri in his 1632 writing introduced the construction of conics with a paragraph entitled Dei modi particolari di descrivere le settioni coniche, che s’aspettano all’invenzione piana vera, to therefore move on to the description of the specific conics on the plane [40] (pp. 179–223).
With book I, Mydorge remained bound to the construction of “these” conics as those obtained as “sections” on a conic surface. How can we link the two treatises?
Book I states that each conic is a “section” of the cone. Therefore, the following problem/theorem can be formulated: given any cone, draw on its surface a conic section (parabola, hyperbola, ellipse).
Can we justify the following problem: “Given a conic section on a plane, build the cone of which it is a section”? The solution of this problem causes us to affirm that conics as plane “curves” and as “sections” on a cone have the same properties: they are the “same”, as the mathematicians of the beginning of the 17th century would say.
The first problem is a natural consequence of the knowledge of Conics and of the treatments related to them; the second, however, requires some time to solve.
In the same years in which Descartes and Fermat built conics in the plane with or without tools, identifying them as the loci of points and indicating them with equations, and while Desargues was preparing with his writing a new path to the geometry of conics, Mydorge stopped at a lower level, offering the lovers of optical phenomena a wide-ranging cultural context in which to place conics. He realized that everyone worked on and with conics, considering them from different points of view. Mydorge did not stray from looking for a solution to the second problem, which he might have been thinking about for a long time.
We have seen (and will see later) that, in book I, he follows the example of Apollonius in a slavish manner, taking him from the cone to its sections. When composing books III and IV, he sketches a solution, albeit partial, of the problem. His reflection is testified to by props. III 34 and 35 [1] (pp. 181–184), the statements of which are as follows:
Proposition III 34.Given an ellipse, show the cone of which it is singular section;
Proposition III 35.Given an ellipse, show the cone which becomes one of the two subcontrary sections.
Mydorge could not go beyond the ellipse considered in two particular situations.
The problem did not leave other mathematicians indifferent. A solution to this problem appeared in the first part of J. Wallis’ treatise on conics of 1655. Within prop. 12, in which he showed how to determine the right side of the parabola, Wallis solved the problem that “each parabola can be built on a cone” with methods of analysis and synthesis [9]. Subsequently, in the treatises on conics, this proposition will be generalized for each conic.
6. A direct Comparison between the Treatise of Mydorge and That of Apollonius
A direct comparison between the treatise of Mydorge and that of Apollonius is possible only for specific parts of them. Let us focus our attention on three moments in the two writings.
6.1. Definitions
Both book I of Mydorge’s treatise on conics and book I of Apollonius’ Conics open with a group of 19 definitions [1] (pp. 1–3).
A second group, located in places different from Mydorge and Apollonius, consists of two definitions in Mydorge’s treatise and four definitions in Apollonius’ treatise [1] (p. 5).
The comparison between the lists of one and the other, shown in Table 1 and Table 2, urges the reader to evaluate, above all, the different linguistic expressions with which the geometric objects are presented.

Table 1.
Comparison between the first group of definitions by Mydorge and Apollonius.

Table 2.
Comparison between the second group of definitions by Mydorge and Apollonius.
Mydorge subsequently proposed (see Table 3) a third group of 13 definitions [1] (pp. 7–9), which do not have correspondents in Apollonius’ definitions.

Table 3.
The third group of definitions by Mydorge.
We note that Mydorge’s definition groups included Apollonius’ definitions and specified further elements.
6.2. Triangles and “Subcontrary" Sections
Particularly important is Mydorge’s second group of definitions, which do not correspond to Apollonius’. They specify what the subcontrary position and the subcontrary section of a cone are.
In def. II 1, two triangles are defined as subcontraries that (1) are similar, (2) have a common angle, and (3) have opposite sides to the common angle that are not parallel, as we see in Figure 1.
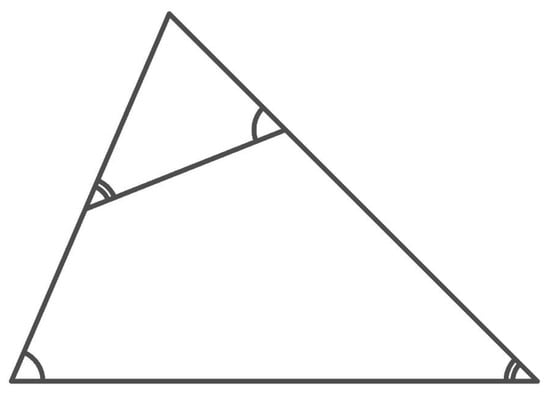
Figure 1.
Example of triangles subcontraries, namely two triangles that are similar, have a common angle and have opposite sides to the common angle that are not parallel.
In def. II 2, two conics are defined as subcontraries such that (1) the planes on which they lie are both perpendicular to the same plane passing through the axis of the cone and perpendicular to the base, and (2) the planes on which they lie detach from the triangle by the axis (intersection of the cone and plane ), starting from the vertex of the cone to two subcontraries triangles, as we see in Figure 2.
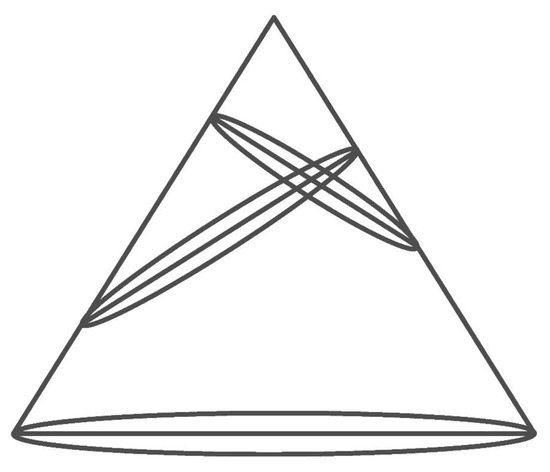
Figure 2.
Example of conic subcontraries, namely two conics such that the planes on which they lie are both perpendicular to the same plane passing through the axis of the cone and perpendicular to the base, and detach from the triangle by the axis, starting from the vertex of the cone to two subcontraries triangles.
In this way, Mydorge preferred to provide two separate definitions for the sections and for the subcontrary triangles.
Apollonius did not provide definitions of these “objects”, preferring to introduce the “subcontrary triangle” and the “subcontrary section” in two distinct propositions [30] (pp. 10, 12–13).
Proposition I 5.If a scalene cone is secated for the axis perpendicularly to the base and is secated with another plane perpendicular to the triangle for the axis, so that from the vertex side it detaches a triangle similar to that which is placed subcontrarily to the axis, the section will be a circle, also called a subcontrary section.
In prop. I 5, we find both the triangle and the subcontrary section specified. During the demonstration, it is specified which conditions they must both satisfy. We find this proposition in prop. I 3 of Mydorge, which thus reads [1] (p. 6):
Proposition I 3.If a scalene cone is subcontrarily secated from a plane at the base, a section [which is] the circumference of the circle is drawn on the surface of the cone.
In Apollonius’ treatise, the term “subcontrary” returns in prop. I 9 [30] (pp. 12–13).
Proposition I 9.If a cone is secated by a plane that cuts two sides of the triangle for the axis, which is neither parallel to the base nor placed in a subcontrary way, the section will not be a circle.
This proposition was used by Mydorge in the formulation and demonstration of prop. I 6. Most likely, Mydorge extrapolated the two definitions of the triangle and of the subcontrary section from the demonstration of these propositions in Apollonius.
6.3. The Presentation of the Conics
Another element of comparison is related to the introduction, specification and construction of the individual conics, presented by Apollonius in props. I 11, 12 and 13 [30] (pp. 13–15). He did not include these conics among his definitions, which are instead presented in three propositions in which it is also indicated how to build them on a cone, and what metric relationship with the points of each conic must be satisfied. Therefore, attention should be paid to the formulation of the three propositions of Apollonius.
Proposition I 11.If a cone is cut by a plane through its axis and also cut by another plane cutting the base of the cone in a straight line perpendicular to the base of the axial triangle, and if further, the diameter of the section is parallel to one [lateral] side of the axial triangle, and if any straight line is drawn from the section of the cone to its diameter such that this straight line is parallel to the common section of the cutting plane and of the cone’s base, then this straight line dropped to the diameter will be equal in square to [the rectangular plane] under the straight line from the section’s vertex to [the point] where the straight line dropped to the diameter cuts it off and under another straight line to the straight line between the angle of the cone and the vertex of the section as the square on the base of the axial triangle to [the rectangular plane] under the remaining two sides of the triangle. I call such a section a parabola.
Proposition I 12.If a cone is cut by a plane through its axis and also cut by another plane cutting the base of the cone in a straight line perpendicular to the base of the axial triangle, and if the diameter of the section continued to meet [continued] one [lateral] side of the axial triangle beyond the vertex of the cone, and if any straight line is drawn from the section to its diameter such that this straight line is parallel to the common section of the cutting plane and of the cone’s base, then this straight line to the diameter will be equal in square to some [rectangular] plane, which is applied to a straight line increased by the segment added along the diameter of the section such that this added segment subtends the exterior angle of the [vertex of the axial] triangle, and as the added segment is to the aforementioned straight line, so the square on the straight line drawn parallel to the section’s diameter from the cone’s vertex to the [axial] triangle’s base is to the [rectangular] plane under the segments of the triangle’s base divided by the straight line drawn from the vertex [of the cone], and the applied plane has as its breadth the straight line on the diameter from the section’s vertex to [the point] where the diameter is cut off by the straight line drawn from the section to the diameter, and this plane is [the rectangular plane under two mentioned straight lines] and increased by a figure that is similar and similarly situated on the plane under the mentioned straight line and the diameter. I will call such a section a hyperbola.
Proposition I 13.If a cone is cut by a plane through its axis and is also cut by another plane, which on the one hand meets both [lateral] sides of the axial triangle and on the other hand, when continued, is neither parallel to the base [of the cone] nor antiparallel to it, and if the plane of the base of the cone and the cutting plane meet in a straight line perpendicular either to the base of the axial triangle or to it continued, then any [straight] line drawn parallel to the common section of the [base and cutting] planes from the section of the cone to the diameter of the section will be equal in square to some [rectangular] plane applied to a straight line to which the diameter of the section is as the square on the straight line drawn parallel to the section’s diameter from the cone’s vertex to the [axial] triangle’s base to the [rectangular] plane under the straight lines cut [on the axial triangle’s base] by this straight line in the direction of the sides of the [axial] triangle, and the applied plane has as breadth of the straight line on the diameter from the section’s vertex to [the point] where the diameter is cut off by the straight line drawn from the section to the diameter, and this plane is [the rectangular plane under two mentioned straight lines] and is decreased by a figure similar and similarly situated on the plane under the aforementioned straight line and the diameter. I will call such a section an ellipse.
The proof of each of these propositions is very complex for today’s reader. Perhaps it would have been less difficult for a reader of Mydorge’s time, being more used to working with proportions.
Faced with difficulties deemed perhaps insurmountable for a simple lover of optical phenomena, Mydorge articulated Apollonius’ speech in three successive steps, first giving the definitions of the conic sections, then presenting their construction on the cone and finally indicating their metric relationship.
The Definition of Conics
Mydorge characterized the conics in the definitions of the third group [1] (p. 7):
Definition 1.We call a parabola any section of the cone whose diameter is parallel to one or the other side of the triangle for the axis;
Definition 2.We call any section of the cone a hyperbola, the prolonged diameter of which intersects the extension of one or the other side of the triangle by the axis beyond the vertex;
Definition 3.We call any section of the cone an ellipse, whose diameter intersects both sides of the triangle for the axis below the vertex and is neither parallel to the base nor placed in a subcontrary way;
Definition 4.We call opposite sections the two hyperbolas obtained on opposite surfaces intersected by a single and same plane not passing through the vertex.
The first three definitions can be extrapolated from the demonstration of props. I 11, 12 and 13 of Apollonius, while the fourth is likely extrapolated from prop. I 14 [30] (p. 16).
The construction of conics
The construction of the conics was presented by Mydorge in props. I 4–5–6, of which the statement and demonstration, in a very stringent form, are presented below [1] (pp. 12–15).
Proposition I 4 (Theorem I 4).If a cone is secated with a plane for the axis and if it is secated with a second plane that intersects the base of the cone along a straight line perpendicular to the base of the triangle for the axis, but the common section of the secant plane and the triangle for the axis is parallel to one or the other side of this same triangle, then the section formed on the surface of the cone is a parabola, the diameter of which is the common section of the secant plane and the diameter for the axis.
Cone , of vertex , of the base of the circle , is intersected with a plane for the axis forming triangle .
Then, let it intersect another plane, not passing through the vertex, along line perpendicular to , forming section on the surface of the cone.
The section common to this plane and to the triangle is , parallel to .
The section is a parabola having diameter .
Proposition I 5 (Theorem I 5).If a cone is secated with a plane for the axis and if it is secated with a second plane that intersects the base of the cone along a straight line perpendicular to the base of the triangle for the axis, but the common section of the secant plane and the triangle for the axis intersects the extension of one or the other side of the triangle for the axis above the vertex, then the section formed on the surface of the cone is a hyperbola, whose diameter is the common section of the secant plane and of the diameter for the axis.
Cone , of vertex , of the base of circle , is intersected with a plane for the axis forming triangle .
It is then intersected with another plane according to line perpendicular to and forming section on the conic surface.
The common section of this plane and of the triangle for the axis is the straight line , whose extension intersects the extension of above vertex in .
Section is a -diameter hyperbola.
Proposition I 6 (Theorem I 6).If a cone is secated with a plane for the axis and if it is secated with a second plane that intersects the base of the cone or its extension along a straight line perpendicular to the base of the triangle for the axis or its extension, but the section common to the secant plane and to the triangle for the axis intersects both sides of the triangle for the axis below the vertex, but it is not parallel to the base nor is it placed in a subcontrary way, also prolonging the cone if necessary, then the section formed on the surface of the cone is a hyperbola, the diameter of which is the common section of the secant plane and the diameter for the axis.
Let cone , of vertex , of the base of circle , intersect with a plane for the axis forming triangle .
Let it then intersect with another plane that intersects the base of the cone or a plane that is its extension along line or , perpendicular to or , forming section on the conic surface.
The section common to this secant plane and to the triangle for the axis is or , which intersects in and in , and is neither parallel nor subcontrarily placed at base .
Section is an ellipse having diameter or .
The metric relationship that specifies each conic
Mydorge pointed out that the names “parabola”, “hyperbola” and “ellipse”, relating to the “sections” of a cone, were given by Apollonius. His props. I 11, 12 and 13 reflected what was traditionally specified around the “classic” application of the areas (parabolic, hyperbolic and elliptical), which we indicate here with “metric relationship”. It is essential and concludes the sense of Apollonius’ propositions. Mydorge dedicated props. I 10 (for the parabola) [1] (pp. 17–18) and I 13 (for the hyperbola and the ellipse) [1] (pp. 20–21) to this relationship:
Proposition 1 10.Letbe a parabola of vertexand diameter. Letbe an ordinate applied to the diameter. Let parallelbe drawn to appliedfrom vertexso that it is. Letbe another applied to the diameter. Then,. SeeFigure 3.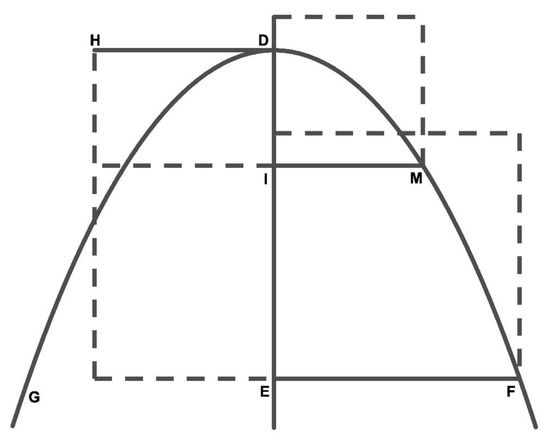 Figure 3. Parabola of vertex and diameter , as defined in prop. 1.10 in the text.
Figure 3. Parabola of vertex and diameter , as defined in prop. 1.10 in the text.
Proposition I 13.Letbe a hyperbola or an ellipse, such as a circumference, of vertexand transverse diameter. Letbe applied to the diameter () and conductparallel toso that we have. Joinwith. From any other pointof, draw the applied, parallel to, which intersectsat point. Then,. SeeFigure 4andFigure 5.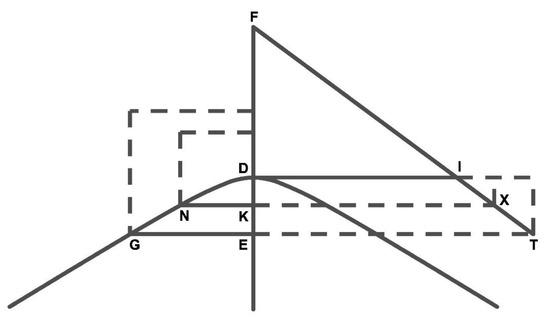 Figure 4. Hyperbola of vertex and transverse diameter as defined in prop. 1.13 in the text.
Figure 4. Hyperbola of vertex and transverse diameter as defined in prop. 1.13 in the text.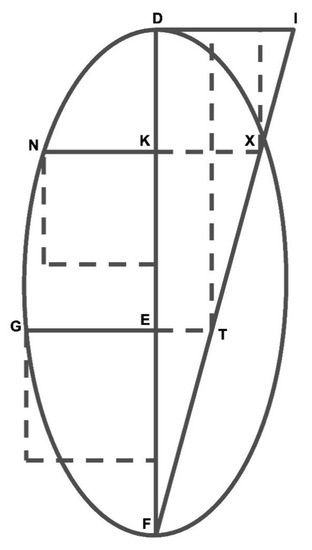 Figure 5. Ellipse of vertex and transverse diameter as defined in prop. 1.13 in the text.
Figure 5. Ellipse of vertex and transverse diameter as defined in prop. 1.13 in the text.
These examples highlight how and with what freedom Mydorge moved towards the Conics. Continuing in the comparison between the two texts, one has the impression that Mydorge wanted to offer his reader the greatest amount of knowledge drawn from Apollonius’ writing, not failing in his commitment to present everything in simple language, and structuring the knowledge while maintaining the sensibility of the mathematicians of the time about the need for definitions, the organization of demonstrations/solutions, etc.
7. Concluding Remarks on Mydorge’s Treatise
Mydorge’s writing certainly represents a novelty compared to the historical context since, during these years, no mathematician of the period had thought of editing a translation of Apollonius’ writing or of committing his professional activity to the recovery of the missing books.
Additionally, during the second half of 17th century, conics sections were an object of study and constituted the first step towards the general study of curves. At the same time, the diffusion of the analytic method was brought into the study of conics by starting from their equations (the Mathematical Papers by Newton are an example of this [44]). As such, we realize that, when the missing books of Conics were published in 1661 by G. A. Borelli, in 1669 by Chr. Ravius and in 1710 by E. Halley, their diffusion seemed to add nothing to the research that, meanwhile, had been done about conics. This recovering of the other of Apollonius’ books is a fact of a merely cultural nature.
The novelties of Mydorge’s treatise are not to be found in the demonstrations of the propositions, articulated following the direct argument well known by the ancients. The novelties can instead be grasped through a comparison with the treatise of Apollonius or with other mathematicians who translated or commented on it.
Considering conics built on a plane and showing that they have the same properties as conics built on a cone are certainly innovative maneuvers, and accentuate the interest in the construction of conics by points, leading one to ask how many points are needed to build them.
As mentioned above, Conics and Prodromi cataptricorum et dioptricorum… pursue different purposes.
Apollonius’ treatise is the prototype of the treatises on conics, after Euclid and Archimedes and for all future generations, because this treatise provided the basis for the knowledge of conics, whatever use is made of them, particularly as an indispensable tool for the solution of solid problems.
For his part, Mydorge elaborated the knowledge transmitted about the conics (for which Conics is a fundamental reference) in light of their use in the resolution of refractive and reflection problems. His text, written in a simple and usable language, becomes for the reader a “manual” for the construction of conics and, at the same time, a “guideline” for the passage from conics considered as sections on a cone to conics considered as plane curves.
The historical path that leads from the problem of areas to conics as flat curves, which we can represent in a temporal sequence, should not be overlooked, going from the problems of areas to conics on particular cones, to conics on any cone, to conics on a plane, and the understanding of which is essential for anyone who intends to address conics (research, teaching, etc.).
If there is an identification between conics on a cone and conics on a plane, it is necessary to explain how the passage from the first to the second occurs and whether it is possible to also conduct the passage in the opposite direction. The answer to the possibility of doing so in the opposite direction will be given definitively after Mydorge, specifically with the treatise on conics by John Wallis.
In the eyes of contemporary and later mathematicians, Mydorge’s treatise was “new” and contained “all” of the useful doctrines of conics, even though their treatment was done on an elementary level. Therefore, the name of its author has occurred in many later writings. For example, the writing of Br. Van Schooten from 1646, De organica conicarum sectionum in plano descriptione tractatus, constituted the natural continuation of Mydorge’s book II because, with this writing, emphasis was placed on (and the opportunity was offered for) studying building conics with tools; furthermore, the treatment of conics presented by Grégoire de Saint-Vincent in his 1647 writing Opus quadraturae Circuli is not negligible either. These references are only two non-secondary references showing how we might focus on the study of conics during the 17th century, which is fundamental for starting the history of curves in a modern sense.
These reflections on Mydorge’s book I are intended to constitute a necessary premise for the presentation of the contents of his other books, which, with the construction of conics and the knowledge of the many “geometric” methods used to create them, have enriched the cultural background of many generations.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The study did not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mydorge, C. Prodromi Catoptricorum et Dioptricorum sive Conicorum Operis ad Abdita Radii Reflexi et Refracti Mysteria Praevii et Facem Praferentis. Libri Quatuor Priores; Isaac Dedin: Paris, France, 1639. [Google Scholar]
- Descartes, R. Discours de la Méthode Pour Bien Conduire sa Raison, & Chercher la Vérité Dans les Sciences; Ian Maire: Leiden, The Netherlands, 1637. [Google Scholar]
- Fermat, P. Varia Opera Matematica D. Petri de Fermat, Senatoris Tolosani. Accesserunt Selectae Quaedam Ejusdem Epistolae, vel ad Ipsum a Plerisque Doctissimis Viris Gallice, Latine, vel Italice, de rebus ad Mathematicas Disciplinas, aut Physicam Pertinentibus Scriptae; Johannem Perch, Comitiorum Fuxensium Typographum, juxta Collegium PP. Societatis Jesu: Toulouse, France, 1679. [Google Scholar]
- Desargues, G.; Poudra, M. Oeuvres de Desargues; Leiber: Paris, France, 1864. [Google Scholar]
- Pascal, B.; Chevalier, J. Oeuvres Completes; Gallimard: Paris, France, 1954. [Google Scholar]
- Ghetaldi, M. Nonnullae Propositiones de Parabola. Nunc Primum Inventae & in Lucem Editae; Aloysium Zannettum: Roma, Italy, 1603. [Google Scholar]
- Mersenne, M. Universae Geometriae, Mixtaeque Mathematicae Synopsis, et Bini Refractionum Demonstratarum Tractatus; Antonium Bertier: Paris, France, 1644. [Google Scholar]
- Van Schooten, F. De Organica Conicarum Sectionum in Plano Descriptione Tractatus, Geometricis, Opticis; Præsertim vero Gnomonicis & Mechanicis Utilis. Cui Subnexa est Appendix, de Cubicarum Aequationum Resolutione; Officina Elzeviriorum: Leiden, The Netherlands, 1646. [Google Scholar]
- Wallis, J. De Sectionibus Conicis, Nova Methodo Expositis, Tractatus; Leon. Lichfield Academiae Typographi: Oxford, UK, 1655. [Google Scholar]
- Mersenne, M.; Tannery, P.; de Waard, C.; Pintard, R. Correspondance du P. Marin Mersenne: Religieux Minime; PUF: Paris, France, 1932–1988; ISBN 2222020557. [Google Scholar]
- Descartes, R.; Adam, C.; Tannery, P.; Beaude, J. Œuvres; Vrin: Paris, France, 1964–1974; ISBN 2-7116-1267-8. [Google Scholar]
- Baillet, A. La vie de Monsieur Descartes; repr. Georg Olms Verlag: Hildesheim, Germany, 1972; ISBN 978-1232559887. [Google Scholar]
- Montucla, J.E. Histoire des Mathématiques; Librairie Scientifique et Technique A. Blanchard: Paris, France, 1968; Volume 2, p. 74. ISBN 9782013385039. [Google Scholar]
- Chasles, M. Aperçu Historique sur L’origine et le Développement des Méthodes en Géométrie; repr. Éditions Jacques Gabay: Sceaux, France, 1989; pp. 88–90. ISBN 9782876470576. [Google Scholar]
- Henry, C. Notice sur un manuscrit inédit de Claude Mydorge. Problèmes de géométrie pratique de Mydorge. Boll. Bibliogr. Stor. Delle Sci. Mat. Fis. 1881, 14, 271–350. [Google Scholar]
- Maierù, L. Le Sezioni Coniche nel Seicento; Rubbettino: Soveria Mannelli, Italy, 2009; pp. 105–142. ISBN 9788849824612. [Google Scholar]
- Maierù, L. Le traité des coniques de Claude Mydorge, entre lecture des classique et nouvelles élaborations. In Les Courbes. Études sur L’histoire d’un Concept; Rashed, R., Crozet, P., Eds.; Librairie Scientifique et Technique Albert Blanchard: Paris, France, 2013; pp. 39–85. ISBN 978-2-85367-259-7. [Google Scholar]
- Mydorge, C. L’usage de L’une e de L’autre Astrolabe Particulier et Universel. Expliqué tant en la Declaration de Leurs Parties, Qu’exposition Fidelle & Facile de leur Practique en Astronomie & Géométrie; Jean Moreau: Paris, France, 1625. [Google Scholar]
- Mydorge, C. Examen du Livre des Récréations Mathématiques, et de ses Problèmes en Géométrie, Méchanique, Optique, & Catoptrique; J. Dedin: Paris, France, 1630. [Google Scholar]
- Dijksterhuis, J.F. Moving around the ellipse: Conic sections in Leiden, 1620–1660. In Silent Messengers the Circulation of Material Objects of Knowledge in the Early Modern Low Countries; Dupré, S., Lüthy, C., Eds.; LIT: Berlin, Germany, 2011; pp. 89–124. ISBN 9783825816353. [Google Scholar]
- Mersenne, M. Quaestiones Celeberrimae in Genesim, cum Accurata Textus Explicatione; Sebastien Cramoisy: Paris, France, 1623. [Google Scholar]
- Mersenne, M. Harmonie Universelle, Contenant la Théorie et la Pratique de la Musique; Sebastien Cramoisy: Paris, France, 1636. [Google Scholar]
- Mydorge, C. Prodromi Catoptricorum et Dioptricorum Sive Conicorum Operis ad Abdita Radii Reflexi et Refracti Mysteria Praevii et Facem Praferentis. Libri Primus et Secundus; Isaac Dedin: Paris, France, 1631. [Google Scholar]
- Morin, J.B. Longitudinum Terrestrium Necnon Caelestium, Nova et Hactenus Optata Scientia Duae Contradictoriae Sententiae; Jean Libert: Paris, France, 1634. [Google Scholar]
- Hobbes, T.; Malcolm, N. The Correspondance; Clarendon Press: Oxford, UK, 1997; Volume 1622–1659, ISBN 9780198237471. [Google Scholar]
- Maierù, L. La Teoria e l’uso Delle Coniche nel Cinquecento. Studi dell’Istituto Gramsci Siciliano, XVII; Salvatore Sciascia Editore: Roma, Italy, 1996. [Google Scholar]
- Gessner, S. Savoir manier les instruments: La géométrie dans les écrits italiens d’architecture (1545–1570). Rev. Hist. Math. 2010, 16, 1–62. [Google Scholar]
- Remmert, V.R. The Art of Garden and Landscape Design and the Mathematical Sciences in the Early Modern Period. In Gardens, Knowledge and the Sciences in the Early Modern Period; Fischer, H., Remmert, V.R., Wolschke-Bulmahn, J., Eds.; Springer: Cham, Switzerland, 2016; pp. 9–28. ISBN 978-3-319-26340-3. [Google Scholar]
- Raynaud, D. Le tracé continu des sections coniques à la Renaissance: Applications optico-perspectives, héritage de la tradition mathématique arabe. Arab. Sci. Philos. 2007, 17, 299–345. [Google Scholar] [CrossRef][Green Version]
- Commandino, F. Apollonii Pergaei Conicorum Libri Quattuor; Alexandri Benatii: Bologna, Italy, 1566. [Google Scholar]
- Toomer, G.J. Apollonius: Conics Books V to VII. The Arabic Translation of the Lost Greek Original in the Version of the Banū Mūsā; Springer: New York, NY, USA, 1990; ISBN 978-0-387-97216-9. [Google Scholar]
- Rashed, R. Apollonius de Perge, Coniques; Walter de Gruyter: Berlin, Germany, 2008–2010; ISBN 9783110217155. [Google Scholar]
- Witelo, E.C. Opticae Thesaurus. Alhazeni Arabis Libri Septem, nunc Primum editi. Eiusdem Liber de Crepusculis et Nubium Ascensionibus. Item Vitellionis Thuringopoloni Libri X. Omnes Instaurati, Figuris Illustrati & Aucti, Adiectis etiam in Alhazenum Commentarijs, a Federico Risnero; an. repr. Johnson Reprint Corporation: New York, NY, USA, 1972. [Google Scholar]
- Maierù, L. Francesco Barozzi, Admirandum Illud Geometricum Problema Tredecim Modis Demonstrandum; Clueb: Bologna, Italy, 1993. [Google Scholar]
- Maurolyci, D.F. Opuscula Mathematica; Nunc Primum in Lucem Aedita, cum Rerum Omnium Notatu Dignarum. Indice Locupletissimo. Pagella huic Proxime Contigua, Eorum Catalogus est…; Franciscum Franciscium Senensem: Venetijs, Italy, 1575. [Google Scholar]
- Pergaeus, A.; Heiberg, I.L. Apollonii Pergaei quæ Græce Exstant cum Commentariis Antiquis; B. G. Teubneri: Stuttgart, Germany, 1974; ISBN 978-1108061841. [Google Scholar]
- Fried, M.N.; Unguru, S. Apollonius of Perga’s Conica. Text, Context, Subtext; E. J. Brill: Leiden, The Netherlands, 2001; ISBN 978-9004119772. [Google Scholar]
- Robinet, A. Aux Sources de l’esprit Cartésien. L’axe La Tamée-Descartes de La Dialectique de 1555 aux Regulae; Vrin: Paris, France, 1996; ISBN 978-2711612635. [Google Scholar]
- Weber, J.P. La constitution du Texte des Regulae; Sedes: Paris, France, 1964. [Google Scholar]
- Cavalieri, B. Lo Specchio Ustorio Overo Trattato Delle Settioni Coniche, et Alcuni loro Mirabili Effetti Intorno al Lume, Caldo, Freddo, Suono, et Moto Ancora; Clemente Ferroni: Bologna, Italy, 1632. [Google Scholar]
- De La Hire, P. Sectiones Conicae in Novem Libros Distributae; S. Michallet: Paris, France, 1685. [Google Scholar]
- Florio, E. A Synergy between History of Mathematics and Mathematics Education: A Possible Path from Geometry to Symbolic Algebra. Educ. Sci. 2020, 10, 243. [Google Scholar] [CrossRef]
- Florio, E.; Maierù, L.; Fenaroli, G. The construction of regular polygons between geometry and algebra: A didactic-historical example. Learn. Math. 2020, 40, 23–24. [Google Scholar]
- Newton, I.; Whiteside, D.T. The Mathematical Papers of Isaac Newton; Cambridge University Press: Cambridge, UK, 1967–1981; Volume I–VIII, ISBN 978-0521201032. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).