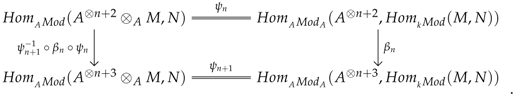Lower-Estimates on the Hochschild (Co)Homological Dimension of Commutative Algebras and Applications to Smooth Affine Schemes and Quasi-Free Algebras

Anastasis Kratsios

doi:10.3390/math9030251

Department of Mathematics, ETH Zürich, Rämistrasse 101, 8092 Zurich, Switzerland

Mathematics2021, 9(3), 251;https://doi.org/10.3390/math9030251

This article belongs to the Special Issue New Trends in Algebraic Geometry and Its Applications

Version Notes

Order Reprints

Abstract

The Hochschild cohomological dimension of any commutative k-algebra is lower-bounded by the least-upper bound of the flat-dimension difference and its global dimension. Our result is used to show that for a smooth affine scheme X satisfying Pointcaré duality, there must exist a vector bundle with section M and suitable n which the module of algebraic differential n-forms

Ω^{n} (X, M)

. Further restricting the notion of smoothness, we use our result to show that most k-algebras fail to be smooth in the quasi-free sense. This consequence, extends the currently known results, which are restricted to the case where

k = C

.

Keywords:

hochschild cohomology; homological dimension theory; non-commutative geometry; quasi-free algebras; pointcaré duality; higher differential forms

1. Introduction

Non-commutative geometry is a rapidly developing area of contemporary mathematical research that studies non-commutative algebras using formal geometric tools. The field traces its most evident origins back to the results of [1], which show that any compact Hausdorff space can be fully reconstructed, and largely understood, from its associated

C^{⋆}

-algebra of functions

C (X)

. However, the trend of understanding geometric properties via algebraic dual theories is echoed throughout mathematics; with notable examples coming from the duality between finitely generated algebras and affine schemes (see [2]), the description of any smooth manifold M through its commutative algebra

C^{\infty} (M)

, and ultimately culminating with the work of [3,4] describing the duality relationship between algebra and geometry in full generality.

Though a large portion of the interest in non-commutative geometry stems from its connections with physics, see [5,6,7]. A. Connes largely made these connections through the cyclic cohomology theory of [8], a generalized de Rham cohomology theory for non-commutative spaces, which closely tied through the Connes complex to one of the central tools of non-commutative geometry and the central object of study of this paper, namely Hochschild (co)homology.

Hochschild (co)homology, originally introduced in [9], is a cohomology theory for non-commutative k-algebras. Since its introduction, it has become a key tool and object of study in non-commutative geometry since the results of [10] (and more recently generalized in [11] to characteristic p fields); which identifies the Hochschild homology of commutative k-algebras over a characteristic 0 field k, to the module of Khäler differentials over their associated affine scheme. Likewise, the result identifies Hochschild’s cohomology theory with the modules of derivations and, therefore, with the tangential structure over the commutative algebra’s associated affine scheme. Likewise, in these cases, Pointcaré duality-like results can also be entirely formulated between these structures and the Hochschild (co)homology theories as shown in [12].

This article focuses on a fundamental non-commutative geometric invariant derived from the Hochschild (co)homology, namely its (co)homological dimension. We focus on the interplay between this (co)homological invariant of commutative k-algebras over general commutative rings k, and its implications on various notions of smoothness of its associated dual non-commutative space; such as the quasi-freeness (or formal smoothness) of [13,14], or more generally, the vanishing of their higher modules of differential forms as seen in [12].

The relationship between the Hochschild (co)homology theory and smoothness has seen study in the case where k is a field in [15,16]. However, the general case is still far from understood and this is likely due to it requiring a more subtle treatment offered by the less-standard tools of relative homological-algebraic (see [17,18] for example). Indeed, this paper proposes a set of lower-estimates of this invariant, which can be easily computed from local data of any commutative k-algebra over a commutative ring k with unity.

The paper’s main results are used to show that for any smooth affine scheme X there must exist a vector bundle on X with section M and a suitably small natural number n for which the module of algebraic differential n-forms with values in M, denoted by

Ω^{n} (X, M)

is non-trivial. Our results are also used to derive simple tests for a k-algebras’ quasi-freeness. This latter application extends known results of [14] in the special case where

k = C

. Using this result, we conclude that typical k-algebras are not quasi-free. Concrete applications are considered within the scope of arithmetic geometry.

Organization of the Paper

The paper is organized as follows. Section 2 contains the paper’s main theorems as well as its non-commutative geometric questions consequences. Each result is followed by examples which unpack the general implications in the context of algebraic geometry. Appendix A contains detailed background material in the relative homological algebraic tools required for the paper’s proofs is included after the paper’s conclusion. Likewise, the paper’s proofs and any auxiliary technical lemma is also relegated to Appendix B, Appendix C and Appendix D.

2. Main Result

From here on out, A will always be a commutative k-algebra. The remainder of this paper will focus on establishing the following result. An analogous statement was made in [14] that all affine algebraic varieties over

C

of dimension at greater than 1 fail to have a quasi-free

C

-algebra of functions. Once, the assumption that

k = C

is relaxed, we find an analogous claim is true; however, the analysis is more delicate. Our principle result is the following.

Theorem 1

(Lower-Bound on Hochschild Cohomological Dimension). Let A be a commutative k-algebra and

m

be a non-zero maximal ideal in A such that

A_{m}

is has finite

k_{i^{- 1} [m]}

-flat dimension and

D (k_{i^{- 1} [m]})

is finite. Then:

\begin{matrix} f d_{A_{m}} (M_{m}) - D (k_{i^{- 1} [m]}) - f d_{k_{m}} (A_{m}) \leq & H C d i m (A | k) \end{matrix}

Theorem 1 allows for an easily computable lower-bound on the Hochschild cohomological dimension of nearly any commutative k-algebra A, granted that it is smooth in the classical sense at-least at one point. The next result, obtains an even simpler criterion under the additional assumption that A is k-flat.

Theorem 2.

Let k be of finite global dimension, A be a k-algebra which is flat as a k-module. Then M:

f d_{A} (M) - D (k) \leq H C d i m (A | k) .

(1)

Example 1.

Let A be a commutative k-algebra and

m

be a non-zero maximal ideal in A such that

A_{m}

is has finite

k_{i^{- 1} [m]}

-flat dimension,

D (k_{i^{- 1} [m]})

, and A is Cohen-Macaulay at some maximal ideal

m

. Then

K r u l l (A_{m}) - D (k_{i^{- 1} [m]}) - f d_{m} (A_{m}) \leq H C d i m (A | k) .

Example 2.

Let k be of finite global dimension, A be a k-algebra which is flat as a k-module. Then, for every A-module M, if

x_{1}, .., x_{n}

is a regular sequence in A then:

n - D (k) \leq H C d i m (A | k) .

(2)

Furthermore if A is commutative and Cohen-Macaulay at a maximal ideal

m

then:

K r u l l (A_{m}) - D (k) \leq H C d i m (A | k) .

(3)

Next, we consider the implications of our dimension-theoretic formulas within the scope of algebraic geometry from the non-commutative geometric vantage-point.

2.1. Non-Triviality of Higher Differential Forms

The paper’s provides a homological argument showing that a smooth affine scheme must have some non-trivial module of higher-differential forms. These begin with the non-triviality of the Hochschild homology modules.

To show our result, we begin by recalling the terminology introduced in [12]. Recall that a k-algebra is satisfies Pointcaré duality in dimension d if the dualising module

ω_{A} ≜ E x t_{E_{A}^{k}}^{d} (A, A)

satisfies

E x t_{E_{A}^{k}}^{i} (A, k) = 0

for every

i \neq d

and if in addition

p d_{E_{A}^{k}} (ω_{A}) < \infty

. We also recall that an A-bimodule M is invertible if and only if there exits another A-bimodule, which we denote by

M^{- 1}

, for which

M \otimes_{A} M^{- 1} ≅ M^{- 1} \otimes_{A} M ≅ A

in

_{A} M o d_{A}

.

Corollary 1

(Non-Triviality of Hochschild Homology Modules). Let k be a commutative ring and X be a d-dimensional smooth affine scheme over k whose coordinate ring satisfies Pointcaré duality in dimension d and is invertible. Then, there is an A-bimodule M and some

0 \leq n \leq d - f d_{A} (M) + D (k)

satisfying

H H_{n} (A, M) ≇ 0 .

On applying the Hochschild-Kostant-Rosenberg Theorem to Corollary 1, we immediately obtain the claimed result. Recall that

Ω^{n} (X, M)

denotes the algebraic differential n-forms on the affine scheme X with coefficients in the vector bundle whose section is the

k [A]

-bimodule M.

Corollary 2.

Let k be a commutative ring and X be a d-dimensional smooth affine scheme over k whose coordinate ring satisfies Pointcaré duality in dimension d and is invertible. Then, there exists a some

0 \leq n \leq d - f d_{A} (M) + D (k)

and a vector bundle whose section is the

k [A]

-module M for which the algebraic differential n-forms for which

Ω^{n} (X, M) ≇ 0 .

Next, we use Theorem 1 to demonstrate the rarity of commutative quasi-free k-algebras.

2.2. Quasi-Free Algebras are Uncommon

Corollary 3

(Krull Dimension-Theoretic Criterion for Quasi-Freeness). Let A be a commutative k-algebra and

m

be a non-zero maximal ideal in A such that

A_{m}

is has finite

k_{i^{- 1} [m]}

-flat dimension,

D (k_{i^{- 1} [m]})

, and A is Cohen-Macaulay at some maximal ideal

m

. Then, A is not Quasi-free if

K r u l l (A_{m}) \leq 2 + D (k_{i^{- 1} [m]}) - f d_{m} (A_{m}) .

Let us also consider the simpler form implied by Theorem 2.

Corollary 4.

If k is of finite global dimension, A is a k-algebra which is flat as a k-module, and if

A_{m}

’s Krull dimension is at least

2 + D (k)

then A is not Quasi-free.

We unpack Theorem 2 in the context of classical algebraic and arithmetic geometry.

Examples

To build intuition before proceeding, we consider a counter-intuitive consequence. Namely, that most examples of smooth commutative algebras fail to be quasi-free, even when

k \neq C

. This makes smoothness, in the sense of [14], very rare in the non-commutative category. The following example from arithmetic geometry is of interest.

Let be an affine algebraic

C

-variety

V (A)

. For any point x in

V (A)

the ideal generated by the collection of regular functions on

V (A)

vanishing at the point x is denoted by

I (x)

; in fact

I (x)

is a maximal ideal in A [19]. Moreover, for any affine-algebraic variety

V (A)

there exists a point x such that

A_{I (x)}

is regular. Since every regular local

C

-algebra is Cohen Macaulay at its maximal ideal, then A is Cohen-Macaulay at

I (x)

. Since

C

is a field it is a regular local ring of Krull dimension 0; the Auslander-Buchsbaum-Serre theorem thus implies

D (k) = K r u l l (k) = 0

, moreover

A_{I (x)}

is a

C

-vector space whence it is a

C

-free and so is a

C

-flat module. Therefore Theorem 2 applies if

K r u l l (A) \geq 2

. We summarize this finding as follows.

Corollary 5.

If X is an affine

C

-variety and

k [A]

’s Krull dimension is greater than 1 then the

C

-algebra A is not quasi-free

Remark 1.

Corollary 5 implies that any affine algebraic

C

-variety which is not a disjoint union of curves or points has a coordinate ring which fails to be quasi-free over

C

.

Example 3.

The

C

-algebra

C {[x_{1, 1}, x_{1, 2}, x_{2, 1}, x_{2, 2}]}_{(d e t)}

is not quasi-free.

Proof.

C {[x_{1, 1}, x_{1, 2}, x_{2, 1}, x_{2, 2}]}_{(d e t)}

is of Krull dimension

4 > 1

[20] therefore Theorem 2 applies. □

Corollary 6

(Arithmetic Polynomial-Algebras). The

Z

-algebra

Z [x_{1}, .., x_{n}]

fails to be quasi-free for values of

n > 1

.

Proof.

Since

Z [x_{1}, \dots x_{n}]

is Cohen-Macaulay at the maximal ideal

(x_{1}, \dots x_{n}, p)

and is of Krull dimension

n + 1 = K r u l l (Z [x_{1}, \dots x_{n}])

. Moreover, one computes that

D (Z) = 1

. Whence by point 2 of Theorem 2:

Z [x_{1}, .., x_{n}]

fails to be Quasi-free if

2 \leq K r u l l (Z [x_{1}, \dots x_{n}]) - D (Z) = (n + 1) - 1 = n

. □

The contributions of the paper are now summarized.

3. Conclusions

This paper’s main result derived a general lower bound on the Hochschild cohomological dimension of an arbitrary commutative k-algebra A over a general commutative ring k. Theorem 1 derived, the lower-bound for this (co)homological invariant was expressed in terms of other (co)homological dimension-theoretic invariants, namely the flat dimension over A, the global dimension of A, and the flat dimension of A over k; where each quantity was appropriately localized. Examples 1 and 2, built on these results to lower-bound the Hochschild cohomological dimension purely in terms of easily computable quantities, such as the Krull dimension, when A was Cohen-Macaulay. Theorem 2 then expresses a non-localized analog of Theorem 1 wherein no commutativity of A was required.

The paper’s results have then been applied the results to purely geometric questions. First, the dimension-theoretic formula was used in Corollary 2 to show infer the non-triviality of certain higher algebraic differential forms of any smooth affine scheme with values in a vector bundle with a non-trivial section. The dual result was also considered in Corollary 1 where dimension-theoretic conditions were obtained for the non-vanishing of some of the Hochschild homology modules under Pointcaré duality in the sense of [12].

Next, using the general (co)homological dimension-theoretic estimates, a result of [14], which showed that most commutative affine k-algebras fail to be smooth in the non-commutative sense formalized by quasi-freeness, was extended from the simple case where k was a field to the general case where k is simply a commutative ring. Specifically, in Corollaries 3 and 4, easily applicable dimension-theoretic tests for the non-quasi-freeness (non-formal smoothness) of a commutative k-algebra over a general ring k were derived. The tools are simple and only require a simple computation involving the Krull dimension of A, the flat-dimension of k at one point, and the base ring’s global dimension to identify if A’s associated non-commutative space is quasi-free or not.

Author Contributions

All relevant work was carried out by the author. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the ETH Zürich Foundation.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not Applicable.

Acknowledgments

I would like to thank Abraham Broer for the numerous helpful and insightful conversations.

Conflicts of Interest

The author declares no conflict of interest.

Appendix A. Background

This appendix contains the necessary background material for the formulation of this paper’s main results. We refer the reader in further reading to the notes of [21].

Appendix A.1. Relative Homological Algebra

The results in this paper are formulated using the relative homological algebra, see [17] for example. The theory is analogous to standard homological algebra; see [22] for example, but in this case, one builds the entire theory relative to a suitable subclass of epi(resp. mono)-morphisms. In our case, these are defined as follows.

Definition A1

(

E_{A}^{k}

-Epimorphism). For any k-algebra A, an epimorphism ϵ in

_{A} M o d

is an

E_{A}^{k}

-epimorphism if and only if ϵ’s underlying morphism of k-modules is a k-split epimorphism in

_{k} M o d

. The class of these epimorphisms is denoted

E_{A}^{k}

.

Definition A2

(

E_{A}^{k}

-Exact sequence). An exact sequence of A-modules:

\dots \overset{ϕ_{i - 1}}{\to} M_{i} \overset{ϕ_{i}}{\to} M_{i + 1} \overset{ϕ_{i + 1}}{\to} M_{i + 2} \overset{ϕ_{i + 2}}{\to} \dots

(A1)

is said to be $E_{A}^{k}$ -exact if and only if for every integer i the there exists a morphism of k-modules

ψ_{i} : M_{i + 1} \to M_{i}

such that:

ϕ_{i} = ϕ_{i} \circ ψ_{i} \circ ϕ_{i} .

(A2)

In particular, a short exact sequence of A-modules which is

E_{A}^{k}

-exact is called an

E_{A}^{k}

-short exact sequence.

Remark A1.

Property (A2) is called

E_{A^{e}}^{k}

-admissibility [18]. Alternatively, it is called

E_{A^{e}}^{k}

-allowable [23].

Example A1.

The augmented bar complex

{\hat{C B}}_{⋆} (A)

of a k-algebra A is

E_{A^{e}}^{k}

-exact.

Definition A3

(

E_{A}^{k}

-Projective module). If A is a k-algebra and P is an A-module, then P is said to be

E_{A}^{k}

-projective if and only if for every

E_{A}^{k}

-short exact sequence:

0 \overset{}{\to} M \overset{η}{\to} N \overset{ϵ}{\to} N^{'} \overset{}{\to} 0

(A3)

the sequence of k-modules:

0 \overset{}{\to} H o m_{A} (P, M) \overset{η^{⋆}}{\to} H o m_{A} (P, N) \overset{ϵ^{⋆}}{\to} H o m_{A} (P, N^{'}) \overset{}{\to} 0

(A4)

is exact.

Remark A2.

This definition is equivalent to requiring that P verify the universal property of projective modules only on

E_{A}^{k}

-epimorphisms [23].

Example A2.

A^{\otimes n + 2}

is

E_{A^{e}}^{k}

-projective for all

n \in N

.

E_{A}^{k}

-projective A-modules have analogous properties to projective A-modules. For example,

E_{A}^{k}

-projective A-modules admit the following characterization.

Proposition A1.

For any A-module P the following are equivalent:

$E_{A}^{k}$ -Short exact sequence preservation property P is $E_{A}^{k}$ -projective.
$E_{A}^{k}$ -lifting property For every $E_{A}^{k}$ -epimorphism $f : N \to M$ if there exists an A-module morphism $g : P \to M$ then there exists an A-module map $\tilde{f} : P \to N$ such that $f \circ \tilde{f} = g$ .
$E_{A}^{k}$ -splitting property Every short $E_{A}^{k}$ -exact sequence of the form:

$E_{π} : 0 \overset{}{\to} M \overset{}{\to} N \overset{}{\to} P \overset{}{\to} 0$

(A5)

is A-split-exact.
$E_{A}^{k}$ -free direct summand property There exists a k-module F, an A-module Q and an isomorphism of A-modules $ϕ : P \oplus Q \overset{≅}{\to} A \otimes_{k} F$ .

Remark A3.

If F is a free k-module, some authors call

A \otimes_{k} F

an

E_{A}^{k}

-free module. In fact this gives an alternative proof that

A^{e} \otimes_{k} A^{\otimes n} ≅ A^{\otimes n + 2}

is

E_{A^{e}}^{k}

-free for every

n \in N

.)

Proof.

See [23] pages 261 for the equivalence of 1, 2 and 3 and page 277 for the equivalence of 1 and 4. □

For a homological algebraic theory to be possible, one needs enough projective (resp. injective) objects. The next result shows that there are indeed enough

E_{A}^{k}

-projectives in

_{A} M o d

.

Proposition A2

(Enough

E_{A}^{k}

-projectives). If A is a k-algebra and M is an A-module then there exists an

E_{A}^{k}

-epimorphism

ϵ : P \to M

where P is an

E_{A}^{k}

-projective.

Proof.

By Proposition A1

A \otimes_{k} M

is

E_{A}^{k}

-projective. Moreover, the A-map

ζ : A \otimes_{k} M \to M

described on elementary tensors as

(\forall a \otimes_{k} m \in A \otimes_{k} M) ζ (a \otimes_{k} m) : = a \cdot m

is epi and is k-split by the section

m \mapsto 1 \otimes_{k} m

. □

Since there are enough projective objects, then one can build a resolution of any A-module by

E_{A}^{k}

-projective modules.

Definition A4

(

E_{A}^{k}

-projective resolution). If M is an

A^{e}

-module then a resolution

P_{⋆}

of M is called an

E_{A}^{k}

-projective resolution of M if and only if each

P_{i}

is an

E_{A}^{k}

-projective module and

P_{⋆}

is an

E_{A}^{k}

-exact sequence.

Example A3.

The augmented bar complex

{\hat{C B}}_{⋆} (A)

of A is an

E_{A^{e}}^{k}

-projective resolution of A.

Remark A4.

A nearly completely analogous argument to Example A3 shows that for any

(A, A)

-bimodule M,

M \otimes_{A} {\hat{C B}}_{⋆} (A)

is an

E_{A^{e}}^{k}

-projective resolution of M, see for details [24].

Following [18], the

E_{A}^{k}

-relative derived functors of the tensor product and the

H o m_{A}

-functors are introduced, as follows.

Definition A5.

$E_{A}^{k}$ -relative Tor

If N is a right A-module, M is an A-module and

P_{⋆}

is an

E_{A}^{k}

-projective resolution of N then the k-modules

H_{⋆} (P_{⋆}

\otimes_{A} M)

are called the

E_{A}^{k}

-relative Tor k-modules of N with coefficients in the A-module M and are denoted by

T o r_{E_{A}^{k}}^{n} (N, M)

.

Let

H_{⋆}

(resp.

H^{⋆}

) denote the (co)homology functor from the category of chain (co)complexes on an A-module to the category of A-modules. The

E_{A}^{k}

-relative Tor functors are defined as follows.

Example A4.

The

E_{A}^{k}

-relative Tor functors may differ from the usual (or "absolute") Tor functors. For example consider all the

Z

-algebra

Z

, any

Z

-modules N and M are

E_{Z}^{Z}

-projective. In particular, this is true for the

Z

-modules

Z

and

Z / 2 Z

. Therefore

T o r_{E_{Z}^{Z}}^{n} (Z, Z / 2 Z)

vanish for every positive n, however

T o r_{Z}^{n} (Z, Z / 2 Z)

does not. For example,

T o r_{Z}^{1} (Z, Z / 2 Z) ≅ Z / 2 Z

[22].

Similarly there are

E_{A}^{k}

-relative Ext functors.

Definition A6

(

E_{A}^{k}

-relative Ext). If N is and M are A-modules and

P_{⋆}

is an

E_{A}^{k}

-projective resolution of N then the k-modules

H^{⋆} (H o m_{A} (P_{⋆}, M))

are called the

E_{A}^{k}

-relative Ext k-modules of N with coefficients in the A-module M and are denoted by

E x t_{E_{A}^{k}}^{n} (N, M)

.

The

E_{A}^{k}

-relative homological algebra is indeed well defined, since both the definitions of

E_{A}^{k}

-relative Ext and

E_{A}^{k}

-relative Tor are independent of the choice of

E_{A}^{k}

-projective resolution.

Theorem A1

(

E_{A}^{k}

-Comparison theorem). If

P_{⋆}

and

P_{⋆}^{'}

are

E_{A}^{k}

-projective resolutions of an A-module N then for any A-module M there are natural isomorphisms:

H^{⋆} (H o m_{E_{A}^{k}} (P_{⋆}, N)) \overset{≅}{\to} H^{⋆} (H o m_{E_{A}^{k}} (P_{⋆}^{'}, N))

(A6)

and if

P_{⋆}

and

P_{⋆}^{'}

are

E_{A}^{k}

-projective resolutions of a right A-module N then:

H_{⋆} (P_{⋆} \otimes_{A} N) \overset{≅}{\to} H_{⋆} (P_{⋆}^{'} \otimes_{A} N)

(A7)

Proof.

Nearly identical to the usual comparison theorem, see [23]. □

Example A5.

The

E x t_{Z}

and

E_{Z}^{Z}

-relative Ext may differ. For example, one easily computes

E x t_{Z}^{1} (Z, Z / 2 Z) ≅ Z / 2 Z

. However,

E x t_{E_{Z}^{Z}}^{1} (Z, Z / 2 Z) ≅ 0

.

Analogous to the fact that for any A-module P, P is projective if and only if

E x t_{A}^{1} (P, N) ≅ 0

for every A-module N there is the following result, which can be found in ([18], Chapter IX).

Proposition A3.

P is an

E_{A}^{k}

-projective module if and only if for every A-module N:

E x t_{E_{A}^{k}}^{1} (P, N) ≅ 0

(A8)

Using the theory of relative (co)homology, we are now in-place to review the Hochschild cohomology theory over general k-algebras.

Appendix A.2. Hochschild (Co)homological Dimension

Since

C B_{⋆} (A)

is an

E_{A^{e}}^{k}

-projective resolution of A then Theorem A1 and the definition of the

E x t_{E_{A^{e}}^{k}}^{⋆} (A, -)

functors imply that the Hochschild cohomology of A with coefficients in of [9], denoted by

H H^{⋆} (A, N)

, can be expressed using the

E x t_{E_{A^{e}}^{k}}^{⋆}

. We maintain this perspective throughout this entire article.

Proposition A4.

For every

A^{e}

module N there are k-module isomorphisms, natural in N:

H H^{⋆} (A, N) \overset{≅}{\to} E x t_{E_{A^{e}}^{k}}^{⋆} (A, N)

(A9)

Taking short

E_{A^{e}}^{k}

-exact sequences to isomorphic long exact sequences.

Definition A7

(Hochschild Homology). The Hochschild homology

H H_{⋆} (A, N)

of a k-algebra A with coefficient in the

(A, A)

-bimodule N is defined as:

H H_{⋆} (A, N) : = H_{⋆} (P_{⋆} \otimes_{A} N)

(A10)

where

P_{⋆}

is an

E_{A^{e}}^{k}

-projective resolution of A.

Following the results of [10], the Hochschild cohomology has become the central tool for obtaining non-commutative algebraic geometric analogues of classical commutative algebraic geometric notions. The one of central focus in this paper, is the Hochschild cohomological dimension,

Definition A8

(Hochschild cohomological dimension). The Hochschild cohomological dimension of a k-algebra A is defined as:

H C d i m (A | k) : = \underset{M \in_{A^{e}} M o d}{s u p} (s u p {n \in N^{#} | H H^{n} (A, M) ≇ 0}) .

(A11)

where

N^{#}

is the ordered set of extended natural numbers.

The Hochschild cohomological dimension may be related to the following cohomological dimension.

Definition A9

(

E_{A}^{k}

-projective dimension). If n is a natural number and M is an A-module then M is said to be of

E_{A}^{k}

-projective dimension at most n if and only if there exists a deleted

E_{A}^{k}

-projective resolution of M of length n. If no such

E_{A}^{k}

-projective resolution of M exists then M is said to be of

E_{A}^{k}

-projective dimension ∞. The

E_{A}^{k}

-projective dimension of M is denoted $p d_{E_{A}^{k}} (M)$ .

The following is a translation of a classical homological algebraic result into the setting of

E_{A^{e}}^{k}

-projective dimension,

Ω^{n} (A / k)

and Hochschild cohomology. Here,

Ω^{n} (A / k) ≜ K e r (b_{n - 1}^{'})

and

b_{n - 1}^{'}

is the

{(n - 1)}^{t h}

differential in the augmented Bar resolution of A; see [24] for details on the augmenter Bar complex.

Theorem A2.

For every natural number n, the following are equivalent:

$H C d i m (A | k) \leq n$
A is of $E_{A^{e}}^{k}$ -projective dimension at most n
$Ω^{n} (A / k)$ is an $E_{A^{e}}^{k}$ -projective module.
$H H^{n + 1} (A, M)$ vanishes for every $(A, A)$ -bimodule M.
$E x t_{E_{A^{e}}^{k}}^{n + 1} (A, M)$ vanishes for every $A^{e}$ -module M.

Proof. (1 ⇒ 4)

By definition of the Hochschild cohomological dimension. (4 ⇔ 5) By Proposition A4. (3 ⇒ 2) Since

Ω^{n} (A / k)

is

E_{A^{e}}^{k}

-projective:

0 \to Ω^{n} (A / k) \to C B_{n - 1} (A) \overset{b_{n - 1}^{'}}{\to} . . . . \overset{b_{0}^{'}}{\to} A \to 0

is a

E_{A^{e}}^{k}

-projective resolution of A of length n. Therefore

p d_{E_{A^{e}}^{k}} (A) \leq n

.

(3 ⇔ 4) By Proposition A9 there are isomorphism natural in M:

(\forall M \in_{A^{e}} M o d) H H^{1 + n} (A, M) ≅ E x t_{E_{A^{e}}^{k}}^{1 + n} (A, M) ≅ E x t_{E_{A^{e}}^{k}}^{1} (Ω^{n} (A / k), M) .

Therefore for every

A^{e}

-module M:

E x t_{E_{A^{e}}^{k}}^{1} (Ω^{n} (A / k), M) ≅ 0 i f a n d o n l y i f H H^{1 + n} (A, M) ≅ 0 .

By Proposition A3

Ω^{n} (A / k)

is

E_{A}^{k}

-projective if and only if

E x t_{E_{A^{e}}^{k}}^{1} (Ω^{n} (A / k), M) ≅ 0 .

(2 ⇒ 1) If A admits an

E_{A^{e}}^{k}

-projective resolution

P_{⋆}

of length n then Theorem A1 implies there are natural isomorphisms of

A^{e}

-modules:

(\forall M \in_{A^{e}} M o d) E x t_{E_{A^{e}}^{k}}^{⋆} (A, M) ≅ H^{⋆} (H o m_{A^{e}} (P_{⋆}, M)) .

(A12)

Since

P_{⋆}

is of length n all the maps

p_{j} : P_{j + 1} \to P_{j}

are the zero maps therefore so are the maps

p_{j}^{⋆} : H o m_{A^{e}} (P_{j}) \to H o m_{A^{e}} (P_{j + 1})

. Whence (A12) entails that for all

j > n + 1

E x t_{E_{A^{e}}^{k}}^{⋆} (A, M)

vanishes. By Proposition A4 this is equivalent to

H H^{j} (A, M)

vanishing for all

j > n + 1

for all

M \in_{A^{e}} M o d

. Hence A is of Hochschild cohomological dimension at most n. □

Next, the non-commutative geometric object focused on in this paper is reviewed.

Appendix A.3. Quasi-Free Algebras

Many of the properties of an algebra are summarized by its Hochschild cohomological dimension, see [10,17] for example. However, this article focuses on the following non-commutative analogue of smoothness of [13], introduced by [14].

Remark A5.

Due to their lifting property, the quasi-free k-algebras are considered a non-commutative analogue to smooth k-algebras; that is k-algebras for which

Ω_{A | k}

is a projective A-module.

This notion of smoothness has played a key role in a number of places in non-commutative algebraic geometry, especially in the cyclic (co)homology of [25].

Definition A10

(Quasi-free k-algebra). A k-algebra for which all k-Hochschild extensions of A by an

(A, A)

-bimodule lift is called a quasi-free k-algebra.

Corollary A1.

For a k-algebra A, the following are equivalent:

A is $H C d i m (A | k) \leq 1$ .
$Ω^{1} (A / k)$ is a $E_{A^{e}}^{k}$ -projective $A^{e}$ -module.
A is quasi-free.

One typically construct quasi-free algebras using Morita equivalences. However, the next proposition, which extends a result of [14] to the case where k need not be a field, may also be used without any such restrictions on k.

Proposition A5.

If A is a quasi-free k-algebra and P is an

E_{A^{e}}^{k}

-projective

(A, A)

-bimodule then

T_{A} (P)

is a quasi-free A-algebra.

Proof.

Differed until the appendix. □

Example A6.

Let

n \in N

. The

Z

-algebra

T_{Z} (⨁_{i = 0}^{n} Z)

is quasi-free.

Proof.

Since all free

Z

-modules are projective

Z

-modules and all projective

Z

-modules are

E_{Z}^{Z}

-projective modules, the free

Z

-module

⨁_{i = 0}^{n} Z

is

E_{Z}^{Z}

-projective. Whence Proposition A5 implies

T_{Z} (⨁_{i = 0}^{n} Z)

is a quasi-free

Z

-algebra. □

Example A7.

If A is a quasi-free k-algebra then

T_{A} (Ω^{1} (A / k))

is a quasi-free A-algebra.

Proof.

By Corollary A1 if A is quasi-free

Ω^{1} (A / k)

must be an

E_{A^{e}}^{k}

-projective

(A, A)

-bimodule; whence Proposition A5 applies. □

Next, we overview some relevant dimension-theoretic notions and terminology.

Appendix A.4. Classical Cohomological Dimensions

We remind the reader of a few important algebraic invariants which we will require. The reader unfamiliar with certain of these notions from commutative algebra and algebraic geometry is referred to [2,26] or to [19].

Definition A11

(A-Flat Dimension). If A is a commutative ring then the A-flat dimension

f d_{A} (M)

of an A-module M is the extended natural number n, defined as the shortest length of a resolution of M by A-flat A-modules. If no such finite n exists n is taken to be ∞.

We will require the following result, whose proof can be found in [24].

Proposition A6.

If n is a positive integer and if there exists a regular sequence

x_{1}, .., x_{n}

in A of length n then:

n = f d_{A} (A / (x_{1}, .., x_{n})) .

(A13)

One more ingredient related to the flat dimension will soon be needed.

Proposition A7.

If A is a commutative ring and

m

is a maximal ideal of A then for any A-module M

f d_{A_{m}} (M_{m})

is a lower-bound for

f d_{A} (M)

.

Definition A12.

A-Projective Dimension

If A is a commutative ring and M is an A-module then the A-projective dimension

p d_{A} (M)

of M is the extended natural number n, defined as the shortest length of a deleted A-projective resolution of M. If no such finite n exists n is taken to be ∞.

Lemma A1.

If A is a commutative ring and M is an A-module then

f d_{A} (M) \leq p d_{A} (M)

.

Proof.

Since all A-projective A-modules are A-flat, then any A-projective resolution is a A-flat resolution. □

Lemma A2.

If A is a commutative ring then for any A-module M the following are equivalent:

The A-projective dimension of M is at most n.
For every A-module N, the A-module $E x t_{n + 1}^{A} (M, N)$ is trivial.
For every A-module N and every integer $m \geq n + 1$ : $E x t_{m}^{A} (M, N) ≅ 0$ .

Proof.

Nearly identical to the proof of Theorem A2, see page 456 of [22] for details. □

Definition A13

(Cohen-Macaulay at an Ideal). A commutative ring A is said to be Cohen-Macaulay at a maximal ideal

m

if and only if either:

$K r u l l (A_{m})$ is finite and there is an $A_{m}$ -regular sequence $x_{1}, \dots, x_{d}$ in $A_{m}$ of maximal length $d = K r u l l (A_{m})$ such that ${x_{1}, .., x_{d}} \subseteq m$ .
$K r u l l (A_{m})$ is infinite and for every positive integer d there is an $A_{m}$ -regular sequence $x_{1}, .., x_{d}$ in $m$ on A of length d.

Proposition A8

([24]). If A is a commutative ring which is Cohen Macaulay at the maximal ideal

m

and

K r u l l (A_{m})

is finite then:

K r u l l (A_{m}) = f d_{A_{m}} (A_{m} / (x_{1}, .., x_{n})) \leq p d_{A} (A_{m} / (x_{1}, .., x_{n}))

(A14)

Definition A14.

Global Dimension

The global dimension

D (A)

of a ring A, is defined as the supremum of all the A-projective dimensions of its A-modules. That is:

D (A) : = \underset{M \in_{A} M o d}{s u p} p d_{A} (M) .

(A15)

The following modification of the global dimension of a k-algebra, does not ignore the influence of k on a k-algebra A, as will be observed in the next section of this paper.

Definition A15.

$E^{k}$ -Global dimension

The

E^{k}

-global Dimension

D_{E^{k}} (A)

of a k-algebra A is defined as the supremum of all the

E_{A}^{k}

-projective dimensions of its A-modules. That is:

D_{E^{k}} (A) : = \underset{M \in_{A} M o d}{s u p} p d_{E_{A}^{k}} (M) .

(A16)

Appendix B. Proofs

This appendix contains certain technical lemmas or auxiliary results that otherwise detracted from the overall flow of the paper.

Appendix C. Technical Lemmas

We make use of the following result appearing in a technical note of Hochschild circa 1958, see [27].

Theorem A3

([27]). If k is of finite global dimension, A is a k-algebra which is flat as a k-module and M is an A-module then:

p d_{A} (M) - D (k) \leq p d_{E_{A}^{k}} (M)

(A17)

Proposition A9

(Dimension Shifting). If

\dots \overset{d_{n + 1}}{\to} P_{n + j} P_{n} \overset{d_{n}}{\to} \dots \overset{d_{2}}{\to} P_{1} \overset{d_{1}}{\to} P_{0} \overset{}{\to} 0

(A18)

is a deleted

E_{A}^{k}

-projective resolution of an A-module M then for every A-module N and for every positive integer n there are isomorphisms natural in N:

E x t_{E_{A}^{k}}^{1} (K e r (d_{n}), N) ≅ E x t_{E_{A}^{k}}^{n + 1} (A, N)

(A19)

Proof.

By definition the truncated sequence is exact:

\dots \overset{d_{n + j}}{\to} P_{n + j} \overset{d_{n + j - 1}}{\to} \dots \overset{d_{n + 1}}{\to} P_{n + 1} \overset{η}{\to} K e r (d_{n}) \overset{}{\to} 0,,

(A20)

where

η

is the canonical map satisfying

d_{n} = k e r (d_{n}) \circ η

(arising from the universal property of

k e r (d_{n})

). Moreover, since (A30) is

E_{A}^{k}

-exact,

d_{n}

is k-split; whence

η

must be k-split. Moreover, for every

j \geq n + 1

,

d_{j}

was by assumption k-split therefore (A20) is

E_{A}^{k}

-exact and since for every natural number

m > n

P_{m}

is by hypothesis

E_{A}^{k}

-projective then (A20) is an augmented

E_{A}^{k}

-projective resolution of the A-module

K e r (d_{n})

.

For every natural number m, relabel:

Q_{m} : = P_{m + n} a n d p_{m} : = d_{n + m} .

(A21)

By Theorem A1, for all

N \in_{A} M o d

and all

m \in N

, we have that:

\begin{matrix} E x t_{E_{A}^{k}}^{m} (K e r (d_{n}), N) ≅ & H^{m} (H o m_{A} (Q_{⋆}, N)) \\ = & K e r (H o m_{A} (p_{n}, N)) / I m (H o m_{A} (p_{n + 1}, N)) \\ = & K e r (H o m_{A} (d_{n + m}, N)) / I m (H o m_{A} (d_{n + m + 1}, N)) \\ = & H^{m + n} (H o m_{A} (P_{⋆}, N)) \\ ≅ & E x t_{E_{A}^{k}}^{m} (A, N) . \end{matrix}

(A22)

Therefore, the result follows. □

Appendix D. Auxiliary Results

Proof of Proposition A5.

Let

0 \to M \to B \overset{π}{\to} T_{A} (P) \to 0

(A23)

be a k-Hochschild extension of

T_{A} (P)

by M. We use the universal property of

T_{A} (P)

to show that there must exist a lift l of (A23).

Let

p : T_{A} (P) \to A

be the projection k-algebra homomorphism of

T_{A} (P)

onto A. p is k-split since the k-module inclusion

i : A \to T_{A} (P)

is a section of p; therefore p is an

E_{A^{e}}^{k}

-epimorphism and

0 \to K e r (p \circ π) \to B \to A \to 0

(A24)

is a k-Hochschild extension of A by the

(A, A)

-bimodule

K e r (p \circ π)

. Since A is a quasi-free k-algebra there exists a k-algebra homomorphism

l_{1} : A \to B

lifting

p \circ π

. Hence B inherits the structure of an

(A, A)

-bimodule and

π

may be viewed as an

(A, A)

-bimodule homomorphism. Moreover,

l_{1}

induces an A-algebra structure on B.

Let

f : P \to T_{A} (P)

be the

(A, A)

-bimodule homomorphism satisfying the universal property of the tensor algebra on the

(A, A)

-bimodule P. Since

π : B \to A

is an

E_{A^{e}}^{k}

-epimorphism and since P is an

E_{A^{e}}^{k}

-projective

(A, A)

-bimodule, Proposition A1 implies that that there exists an

(A, A)

-bimodule homomorphism

l_{2} : P \to B

satisfying

π \circ l_{2} = f

.

Since

l_{2} : P \to B

is an

(A, A)

-bimodule homomorphism to a A-algebra the universal property of the tensor algebra

T_{A} (P)

on the

(A, A)

-bimodule P, see [28], implies there is an A-algebra homomorphism

l : T_{A} (P) \to B

whose underlying function satisfies:

l \circ f = l_{2}

.

Therefore

l \circ π \circ l_{2} = l_{2}

; whence

l \circ π = 1_{T_{A} (P)}

; that is l is a A-algebra homomorphism which is a section of

π

, that is l lifts

π

. □

Appendix D.1. Proof of Theorem 1

Our first lemma is a generalization of the central theorem of [27]; which does not rely on the assumption that A is k-flat.

Lemma A3.

If k is of finite global dimension and A is a k-algebra which is of finite flat dimension as a k-module, then for every A-module M:

p d_{A} (M) - D (k) - f d_{k} (A) \leq p d_{E_{A}^{k}} (M)

(A25)

The proof of Lemma A3 relies on the following lemma.

Lemma A4.

If A is a k-algebra such that

f d_{k} (A) < \infty

then:

(\forall M \in_{k} M o d) p d_{A} (A \otimes_{k} M) - f d_{k} (A) \leq p d_{k} (M)

(A26)

Proof.

For every k-module M and every A-module N there is a convergent third quadrant spectral sequence (see [22], page 667):

E x t_{A}^{p} (T o r_{q}^{k} (A, M), N) \underset{p}{\Rightarrow} E x t_{k}^{p + q} (M, H o m_{A} (A, N)) .

(A27)

Moreover, the adjunction

- \otimes_{k} A ⊣ H o m_{A} (A, -)

extends to a natural isomorphism:

(\forall p, q \in N) E x t_{k}^{p + q} (M, H o m_{A} (A, N)) ≅ E x t_{A}^{p + q} (M \otimes_{k} A, N) .

(A28)

Therefore there is a convergent third-quadrant spectral sequence:

E x t_{A}^{p} (T o r_{q}^{k} (A, M), N) \underset{p}{\Rightarrow} E x t_{A}^{p + q} (M \otimes_{k} A, N) .

(A29)

If

p d_{A} (N) < \infty

, then the result is immediate. Therefore assume that:

p d_{A} (N) < \infty

. If

p + q > f d_{k} (A) + p d_{A} (N)

then either

p > p d_{A} (N)

or

q > f d_{k} (A)

. In the case of th

0 ≅ E_{2}^{p, q} ≅ E_{\infty}^{p, q} ≅ E x t_{A}^{p + q} (M \otimes_{k} A, N)

and in the latter case

0 ≅ E_{2}^{p, q} ≅ E_{\infty}^{p, q} ≅ E x t_{A}^{p + q} (M \otimes_{k} A, N)

also. Therefore

(\forall N \in A_{M} o d) 0 ≅ E x t_{A}^{n} (M \otimes_{k} A, N) i f n > f d_{k} (A) + p d_{A} (N);

hence:

p d_{A} (M \otimes_{k} A) \leq f d_{k} (A) + p d_{A} (M)

.

Finally, the result follows since

f d_{k} (A)

is finite and, therefore, can be subtracted unambiguously. □

Lemma A5.

If A is a k-algebra then for any k-module M there is an

E_{A}^{k}

-exact sequence:

0 \overset{}{\to} K e r (a) \overset{}{\to} A \otimes_{k} M \overset{α}{\to} M \overset{}{\to} 0

(A30)

where α be the map defined on elementary tensors

(a \otimes_{k} m)

in

A \otimes_{k} M

as

a \otimes_{k} m \mapsto a \cdot m

.

Proof.

α

is k-split by the map

β : M \to A \otimes_{k} M

defined on elements

m \in M

as

m \mapsto 1 \otimes_{k} m

. Indeed if

m \in M

then:

α \circ β (m) = α (1 \otimes_{k} m) = 1 \cdot m = m .

(A31)

□

Lemma A6.

If M and N are A-modules then:

p d_{A} (M) \leq p d_{A} (M \oplus N) .

(A32)

Proof.

(\forall n \in N) (\forall X \in_{A} M o d) E x t_{A}^{n} (M, X) \oplus E x t_{A}^{n} (N, X) ≅ E x t_{A}^{n} (M \oplus N, X) .

(A33)

Therefore

E x t_{A}^{n} (M \oplus N, X)

vanishes only if both

E x t_{A}^{n} (M, X)

and

E x t_{A}^{n} (N, X)

vanish. Lemma then implies:

p d_{A} (M) \leq p d (M \oplus N)

. □

Proof of Lemma A3

Proof.

Case 1:

p d_{E_{A}^{k}} (M) = \infty

By definition

p d_{A} (M) \leq \infty

therefore trivially if

p d_{E_{A}^{k}} (M) = \infty

then:

p d_{A} (M) \leq p d_{E_{A}^{k}} (M) + D (k) .

(A34)

Since k’s global dimension is finite hence (A34) implies:

p d_{A} (M) - D (k) \leq \infty = p d_{E_{A}^{k}} (M) .

(A35)

Case 2:

p d_{E_{A}^{k}} (M) < \infty

Let $d : = p d_{E_{A}^{k}} (M) + D (k) + f d_{k} (A)$ . The proof will proceed by induction on d.

Base: $d = 0$
Suppose $p d_{E_{A}^{k}} (M) = 0$ .
By Theorem A2 M is $E_{A}^{k}$ -projective. Lemma A5 implies there is an $E_{A}^{k}$ -exact sequence:

$0 \overset{}{\to} K e r (a) \overset{}{\to} A \otimes_{k} M \overset{α}{\to} M \overset{}{\to} 0 .$

(A36)

Proposition A1 implies that (A36) is A-split therefore M is a direct summand of the A-module $A \otimes_{k} M$ . Hence Lemma A6 implies:

$p d_{A} (M) \leq p d_{A} (M \otimes_{k} A) .$

(A37)

Lemma A4 together with (A37) imply:

$p d_{A} (M) \leq p d_{A} (M \otimes_{k} A) \leq p d_{k} (M) .$

(A38)

Definition A15 and (A38) together with the assumption that $p d_{E_{A}^{k}} (M) = 0$ imply:

$\begin{matrix} p d_{A} (M) \leq p d_{k} (M) \leq D (k) = D (k) + 0 + 0 = D (k) + p d_{E_{A}^{k}} (M) + f d_{k} (A) . \end{matrix}$

(A39)

Since k’s global dimension and $f d_{k} (A)$ are finite then (A39) implies:

$p d_{A} (M) - D (k) - f d_{k} (A) \leq p d_{E_{A}^{k}} (M) .$

(A40)
Inductive Step: $d > 0$
Suppose the result holds for all A-modules K such that $p d_{E_{A}^{k}} (K) + D (k) + f d_{k} (A) = d$ for some integer $d > 0$ . Again appealing to Lemma A5, there is an $E_{A}^{k}$ -exact sequence:

$0 \overset{}{\to} K e r (a) \overset{}{\to} A \otimes_{k} M \overset{α}{\to} M \overset{}{\to} 0 .$

(A41)

Proposition A1 implies $A \otimes_{k} M$ is $E_{A}^{k}$ -projective; whence (A41) implies:

$p d_{E_{A}^{k}} (K e r (α)) + 1 = p d_{E_{A}^{k}} (M) .$

(A42)

Since $K e r (α)$ is an A-module of strictly smaller $E_{A}^{k}$ -projective dimension than M the induction hypothesis applies to $K e r (α)$ whence: -4.6cm0cm

$\begin{matrix} p d_{A} (K e r (α)) + 1 \leq & p d_{E_{A}^{k}} (K e r (α)) + 1 + D (k) + f d_{k} (A) \\ \leq & p d_{E_{A}^{k}} (M) + D (k) + f d_{k} (A) . \end{matrix}$

(A43)

The proof will be completed by demonstrating that: $p d_{A} (M) \leq p d_{A} (K e r (α)) + 1$ .
For any $N \in_{A} M o d$ $E x t_{A}^{⋆} (-, N)$ applied to (A41) gives way to the long exact sequence in homology, particularly the following of its segments are exact:

$E x t_{A}^{n - 1} (A \otimes_{k} M, N) \to E x t_{A}^{n - 1} (K e r (a), N) \overset{\partial^{n}}{\to} E x t_{A}^{n} (M, N) \to E x t_{A}^{n} (A \otimes_{k} M, N)$

(A44)

Since $A \otimes_{k} M$ is $E_{A}^{k}$ -projective $p d_{E_{A}^{k}} (A \otimes_{k} M) = 0$ , therefore by the base case of the induction hypothesis $p d_{A} (A \otimes_{k} M) \leq p d_{E_{A}^{k}} + D (k) + f d_{k} (A) = D (k) + f d_{k} (A)$ ; thus for every positive integer $n \geq D (k)$ (in particular d is at least n):

$(\forall N \in_{A} M o d) E x t_{A}^{n - 1} (A \otimes_{k} M, N) ≅ 0 ≅ E x t_{A}^{n} (A \otimes_{k} M, N);$

(A45)

whence $\partial^{n}$ must be an isomorphism. Therefore Lemma A2 implies $p d_{A} (M)$ is at most equal to $p d_{A} (K e r (α)) + 1$ .
Therefore:

$\begin{matrix} p d_{A} (M) \leq p d_{A} (K e r (α)) + 1 \end{matrix}$

(46)

$\begin{matrix} \leq p d_{E_{A}^{k}} (K e r (α)) + 1 + D (k) + f d_{k} (A) \end{matrix}$

(47)

$\begin{matrix} \leq p d_{E_{A}^{k}} (M) + D (k) + f d_{k} (A) . \end{matrix}$

(48)

Finally since k is of finite global dimension and A is of finite k-flat dimension then (A48) implies:

$p d_{A} (M) - D (k) - f d_{k} (A) \leq p d_{E_{A}^{k}} (M);$

(A49)

thus concluding the induction.

□

We will also require the following result.

Remark A6.

Let A be a k-algebra,

i : k \to A

the morphism defining the k-algebra A and

m

a maximal ideal in A. For legibility the

E_{A_{m}}^{k_{i^{- 1} [m]}}

-projective dimension of an

A_{m}

-module N will be abbreviated by

p d_{E_{m, k}} (N)

(instead of writing

p d_{E_{A_{m}}^{k_{i^{- 1} [m]}}} (N)

).

Lemma A7.

If A is a commutative k-algebra and

m

is a non-zero maximal ideal in A then for every A-module M:

p d_{E_{m, k}} (M_{m}) \leq p d_{E_{A}^{k}} (M),

(A50)

where

i : k \to A

is the inclusion of k into A.

Proof.

Since

m

is a prime ideal in A,

i^{- 1} [m]

is a maximal ideal in

k_{i^{- 1} [m]}

, whence the localized ring

k_{i^{- 1} [m]}

is a well-defined sub-ring of

A_{m}

. Let

\dots \overset{d_{n + 1}}{\to} P_{n} \overset{d_{n}}{\to} \dots \overset{d_{2}}{\to} P_{1} \overset{d_{1}}{\to} P_{0} \overset{d_{0}}{\to} M \overset{}{\to} 0

(A51)

be an

E_{A}^{k}

-projective resolution of an A-module M. The exactness of localization [26] implies: -4.6cm0cm

\dots . \overset{d_{n + 1}}{\to} P_{n} \otimes_{A} A_{m} \overset{d_{n} \otimes_{A} A_{m}}{\to} \dots \overset{d_{2} \otimes_{A} A_{m}}{\to} P_{1} \otimes_{A} A_{m} \overset{d_{1} \otimes_{A} A_{m}}{\to} P_{0} \otimes_{A} A_{m} \overset{d_{0} \otimes_{A} A_{m}}{\to} M \otimes_{A} A_{m} \to 0

(A52)

is exact. It will now be verified that (A52) is a

E_{m, k}

-projective resolution of the

A_{m}

-module

M_{m}

.

The $d_{n} \otimes_{A} A_{m}$ are $k_{i^{- 1} [m]}$ -split
Since (A51) was k-split then for every $i \in N$ there existed a k-module homomorphism $s_{i} : P_{n - 1} \to P_{n}$ (where for convenience write $P_{- 1} : = M$ ) satisfying $d_{i} = d_{i} \circ s_{i} \circ d_{i}$ . Since $A_{m}$ is a $k_{i^{- 1} [m]}$ -algebra $A_{m}$ may be viewed as a $k_{i^{- 1} [m]}$ -module therefore the maps: $s_{i} \otimes_{A} 1_{A_{m}}$ are $k_{i^{- 1} [m]}$ -module homomorphisms; moreover they must satisfy:

$d_{i} \otimes_{A} 1_{A_{m}} = d_{i} \otimes_{A} 1_{A_{m}} \circ s_{i} \otimes_{A} 1_{A_{m}} \circ d_{i} \otimes_{A} 1_{A_{m}} .$

(A53)

Therefore (A52) is $k_{i^{- 1} [m]}$ -split-exact.
The $P_{i} \otimes_{A} A_{m}$ are $E_{m, k}$ -projective
For each $i \in N$ if $P_{i}$ is $E_{A}^{k}$ -projective therefore Proposition A1 implies there exists some A-module Q and some k-module X satisfying:

$P_{i} \oplus Q ≅ A \otimes_{k} X .$

(A54)

Therefore we have that:

$\begin{matrix} (P_{i} \otimes_{A} A_{m}) \oplus (Q \otimes_{A} A_{m}) ≅ & (P_{i} \otimes_{A} Q) \otimes_{A} A_{m} \\ ≅ & (A \otimes_{k} X) \otimes_{A} A_{m} \\ ≅ & (A \otimes_{k} X) \otimes_{A} (A_{m} \otimes_{k_{i^{- 1} [m]}} k_{i^{- 1} [m]}) \end{matrix}$

(A55)

Since $A, k$ and $k_{i^{- 1} [m]}$ are commutative rings the tensor products $- \otimes_{A} -$ , $- \otimes_{k} -$ and $- \otimes_{k_{i^{- 1} [m]}} -$ are symmetric [22], hence (A55) implies:

$\begin{matrix} (P_{i} \otimes_{A} A_{m}) \oplus (Q \otimes_{A} A_{m}) ≅ & (A \otimes_{k} X) \otimes_{A} (A_{m} \otimes_{k_{i^{- 1} [m]}} k_{i^{- 1} [m]}) \\ ≅ & (A_{m} \otimes_{A} A) \otimes_{k_{i^{- 1} [m]}} (k_{i^{- 1} [m]} \otimes_{k} X) \end{matrix}$

(A56)

Since A is a subring of $A_{m}$ then (A56) implies:

$(P_{i} \otimes_{A} A_{m}) \oplus (Q \otimes_{A} A_{m}) ≅ A_{m} \otimes_{k_{i^{- 1} [m]}} (k_{i^{- 1} [m]} \otimes_{k} X) .$

(A57)

$(k_{i^{- 1} [m]} \otimes_{k} X)$ may be viewed as a $k_{i^{- 1} [m]}$ -module with action $\hat{\cdot}$ defined as:

$(\forall c \in k) (\forall (c^{'} \otimes_{k} x) \in k_{i^{- 1} [m]} \otimes_{k} X) c \hat{\cdot} (c^{'} \otimes_{k} x) : = c \cdot c^{'} \otimes x .$

(A58)

Since $(k_{i^{- 1} [m]} \otimes_{k} X)$ is a $k_{i^{- 1} [m]}$ -module then for each $i \in N$ $(P_{i} \otimes_{A} A_{m})$ is a direct summand of an $A_{m}$ -module of the form $A_{m} \otimes_{k_{i^{- 1} [m]}} X^{'}$ where $X^{'}$ is a $k_{i^{- 1} [m]}$ -module, thus Proposition A1 implies that $P_{i} \otimes_{A} A_{m}$ is $A_{m}$ -projective.

Hence (A52) is an

E_{m, k}

-projective resolution of

M \otimes_{A} A_{m} ≅ M_{m}

; whence:

p d_{E_{m, k}} (M_{m}) \leq p d_{E_{A}^{k}} (M) .

(A59)

□

All the homological dimensions discussed to date are related as follows:

Proposition A10.

If A is a commutative k-algebra and

m

be a non-zero maximal ideal in A such that

A_{m}

has finite

k_{i^{- 1} [m]}

-flat dimension and

D (k_{i^{- 1} [m]})

is finite then there is a string of inequalities:

\begin{matrix} f d_{A_{m}} (M_{m}) - D (k_{i^{- 1} [m]}) - f d_{k} (A) \leq & p d_{A_{m}} (M_{m}) - D (k_{i^{- 1} [m]}) - f d_{k} (A) \\ \leq & p d_{E_{m, k}} (M_{m}) \\ \leq & p d_{E_{A}^{k}} (M) \\ \leq & D_{E^{k}} (A) . \end{matrix}

Proof.

By definition: $p d_{E_{A}^{k}} (M) \leq D_{E^{k}} (A)$ .
By Lemma A7: $p d_{E_{m, k}} (M_{m}) \leq p d_{E_{A}^{k}} (M)$
Since $A_{m}$ is flat as a $k_{i^{- 1} [m]}$ -module and $D (k_{i^{- 1} [m]})$ is finite Lemma A3 entails:
$p d_{A_{m}} (M_{m}) - D (k_{i^{- 1} [m]}) - f d_{k} (A) \leq p d_{E_{m, k}} (M_{m})$
Lemma A1 implies:

$f d_{A_{m}} (M_{m}) \leq p d_{A_{m}} (M_{m}) .$

(A60)

Since the global dimension of $k_{i^{- 1} [m]}$ was assumed to be finite (A60) implies:

$f d_{A_{m}} (M_{m}) - D (k_{i^{- 1} [m]}) \leq p d_{A_{m}} (M_{m}) - D (k_{i^{- 1} [m]}) .$

(A61)

□

Lemma A8.

If A is a commutative k-algebra and M and N be A-modules, then there are natural isomorphisms:

E x t_{E_{A}^{k}}^{n} (M, N) ≅ H H^{n} (A, H o m_{k} (M, N)) ≅ E x t_{E_{A^{e}}^{k}}^{n} (A, H o m_{k} (M, N)) .

(A62)

Proof.

For any $(A, A)$ -bimodule X, $X \otimes_{A} M$ is an $(A, A)$ -bimodule [22] [Cor. 2.53].
Moreover, there are natural isomorphisms [22]:

$H o m_{_{A} M o d} (X \otimes_{A} M, N) \overset{≅}{\to} H o m_{_{A} M o d_{A}} (X, H o m_{_{k} M o d} (M, N)) [Thrm . 2.75] .$

(A63)

In particular (A63) implies that for every n in $N$ there is an isomorphism which is natural in the first input:

$H o m_{_{A} M o d} (A^{\otimes n} \otimes_{A} M, N) \overset{ψ_{n}}{\to} H o m_{_{A} M o d_{A}} (A^{\otimes n}, H o m_{_{k} M o d} (M, N)) .$

(A64)

whence if $b_{n + 1}^{'} : A^{\otimes n + 3} \to A^{\otimes n + 2}$ is the $n^{t h}$ map in the Bar complex (recall Example A3) and for legibility denote $H o m_{_{A} M o d_{A}} (b_{n}^{'}, H o m_{k} (M, N))$ by $β_{n}$ . The naturality of the maps $ψ_{n}$ imply the following diagram of k-modules commutes:

(A65)
Therefore for every n in $N$ :

$\begin{matrix} (ψ_{n + 2}^{- 1} \circ β_{n + 1} \circ ψ_{n + 1}) \circ (ψ_{n + 1}^{- 1} \circ β_{n} \circ ψ_{n}) = & β_{n + 1} \circ β_{n} \\ = & 0 . \end{matrix}$

(A66)

Whence $< H o m_{_{A} M o d} (A^{\otimes ⋆ + 2} \otimes_{A} M, N), (ψ_{⋆ + 1}^{- 1} \circ β_{⋆} \circ ψ_{⋆}) >$ is a chain complex. Moreover, the commutativity of (A65) implies that:

$\begin{matrix} (\forall n \in N) H^{n} (H o m_{_{A} M o d} (A^{\otimes ⋆ + 2} \otimes_{A} M, N)) & = K e r (ψ_{⋆ + 1}^{- 1} \circ β_{⋆} \circ ψ_{⋆}) / I m (ψ_{n + 2}^{- 1} \circ β_{n + 1} \circ ψ_{n + 1}) \\ ≅ & K e r (β_{n}) / I m (β_{n + 1}) \\ = & H^{n} (H o m_{_{A} M o d_{A}} (A^{\otimes ⋆ + 2}, H o m_{_{k} M o d} (M, N))) \\ = & H H^{n} (A, H o m_{k} (M, N)) . \end{matrix}$

(A67)

Furthermore Proposition A4 implies there are natural isomorphisms:

$H H^{n} (A, H o m_{k} (M, N)) ≅ E x t_{E_{A^{e}}^{k}}^{n} (A, H o m_{k} (M, N));$

(A68)

Whence for all n in $N$ there are natural isomorphisms:

$H^{n} (H o m_{_{A} M o d} (A^{\otimes ⋆ + 2} \otimes_{A} M, N)) ≅ H H^{n} (A, H o m_{k} (M, N)) ≅ E x t_{E_{A^{e}}^{k}}^{n} (A, H o m_{k} (M, N)) .$

(A69)
Finally if M is an A-module then $< H o m_{_{A} M o d} (A^{\otimes ⋆ + 2} \otimes_{A} M, N), (ψ_{⋆ + 1}^{- 1} \circ β_{⋆} \circ ψ_{⋆}) >$ calculates the $E_{A}^{k}$ -relative Ext groups of M with coefficients in N; therefore, by ([24], pg. 289), there are natural isomorphisms:

$H^{n} (H o m_{_{A} M o d} (A^{\otimes ⋆ + 2} \otimes_{A} M, N)) ≅ E x t_{E_{A}^{k}}^{n} (M, N) .$

(A70)
Putting it all together, for every n in $N$ there are natural isomorphisms:

$E x t_{E_{A^{e}}^{k}}^{n} (A, H o m_{k} (M, N)) ≅ H H^{n} (A, H o m_{k} (M, N)) ≅ E x t_{E_{A^{e}}^{k}}^{n} (A, H o m_{k} (M, N)) .$

(A71)

□

We may now prove Theorem 1.

Proof of Theorem 1.

For any A-modules M and N Lemma A8 implied:

$E x t_{E_{A}^{k}}^{⋆} (N, M) ≅ H H^{⋆} (A, H o m_{k} (N, M)) .$

(A72)

Therefore taking supremums over all the A-modules $M, N$ , of the integers n for which (A85) is non-trivial implies:

$D_{E^{k}} (A) = \underset{M, N \in_{A} M o d}{s u p} (s u p ({n \in N^{#} | E x t^{n} (M, N) \neq 0}))$

(A73)

$= \underset{M, N \in_{A} M o d}{s u p} (s u p ({n \in N^{#} | H H^{n} (A, H o m_{k} (N, M)) \neq 0})) .$

(A74)

$H o m_{k} (N, M)$ is only a particular case of an $A^{e}$ -module; therefore taking supremums over all A-modules bounds (A87) above as follows:

$D_{E^{k}} (A) = \underset{M, N \in_{A} M o d}{s u p} (s u p ({n \in N^{#} | H H^{⋆} (A, H o m_{k} (N, M)) \neq 0}))$

(A75)

$\leq \underset{\tilde{M} \in_{A^{e}} M o d}{s u p} (s u p ({n \in N^{#} | H H^{n} (A, \tilde{M}) \neq 0})) .$

(A76)

The right hand side of (A89) is precisely the definition of the Hochschild cohomological dimension. Therefore

$D_{E^{k}} (A) \leq H C d i m (A | k)$

(A77)

Proposition A10 applied to (A90), which draws out the conclusion.
- Case 1: $K r u l l (A_{m})$ is finite
  Since A is Cohen-Macaulay at $m$ there is an $A_{m}$ -regular sequence $x_{1}, .., x_{d}$ in $m$ of length $d : = K r u l l (A_{m})$ in $A_{m}$ . Therefore Proposition A6 implies:
  
  $K r u l l (A_{m}) = f d_{A_{m}} (A_{m} / (x_{1}, .., x_{n})) .$
  
  (A78)
  
  Part 1 of Theorem 1 applied to (A78) implies: -4.6cm0cm
  
  $K r u l l (A_{m}) - D (k_{i^{- 1} [m]}) - f d_{m} (A_{m}) = f d_{A_{m}} (A_{m}) - D (k_{i^{- 1} [m]}) - f d_{m} (A_{m}) \leq H C d i m (A | k) .$
  
  (A79)
  
  Moreover, the characterization of quasi-freeness given in Corollary A1 implies that A cannot be quasi-free if:
  
  $2 + D (k_{i^{- 1} [m]}) - f d_{m} (A_{m}) \leq K r u l l (A_{m}) .$
  
  (A80)
- Case 2: $K r u l l (A_{m})$ is infinite
  For every positive integer d there exists an $A_{m}$ -regular sequence $x_{1}^{d}, .., x_{d}^{d}$ in $m$ of length d. Therefore Proposition A6 implies:
  
  $(\forall d \in Z^{+}) d = f d_{A_{m}} (A_{m} / (x_{1}^{d}, .., x_{d}^{d})) .$
  
  (A81)
  
  Therefore part one of Theorem 1 implies:
  
  $(\forall d \in Z^{+}) d - D (k_{i^{- 1} [m]}) - f d_{m} (A_{m}) = f d_{A_{m}} (A_{m} / (x_{1}^{d}, .., x_{d}^{d})) - D (k_{i^{- 1} [m]}) - f d_{m} (A_{m}) \leq H C d i m (A | k) .$
  
  (A82)
  
  Since $D (k)$ and $f d_{m} (A_{m})$ are finite:
  
  $\infty - D (k_{i^{- 1} [m]}) - f d_{m} (A_{m}) = \infty \leq H C d i m (A | k) .$
  
  (A83)
  
  Since $K r u l l (A_{m})$ is infinite (A83) implies:
  
  $K r u l l (A_{m}) - D (k_{i^{- 1} [m]}) - f d_{m} (A_{m}) = \infty = H C d i m (A | k) .$
  
  (A84)
  
  In this case Corollary A1 implies that A is not quasi-free.

□

Appendix D.2. Proof of Theorem 2

Proof of Theorem 2.

For any A-modules M and N Lemma A8 implied:

E x t_{E_{A}^{k}}^{⋆} (N, M) ≅ H H^{⋆} (A, H o m_{k} (N, M)) .

(A85)

Therefore taking supremums over all the A-modules

M, N

, of the integers n for which (A85) is non-trivial implies:

D_{E^{k}} (A) = \underset{M, N \in_{A} M o d}{s u p} (s u p ({n \in N^{#} | E x t^{n} (M, N) \neq 0}))

(A86)

= \underset{M, N \in_{A} M o d}{s u p} (s u p ({n \in N^{#} | H H^{n} (A, H o m_{k} (N, M)) \neq 0})) .

(A87)

H o m_{k} (N, M)

is only a particular case of an

A^{e}

-module; therefore taking supremums over all A-modules bounds (A87) above as follows:

D_{E^{k}} (A) = \underset{M, N \in_{A} M o d}{s u p} (s u p ({n \in N^{#} | H H^{⋆} (A, H o m_{k} (N, M)) \neq 0}))

(A88)

\leq \underset{\tilde{M} \in_{A^{e}} M o d}{s u p} (s u p ({n \in N^{#} | H H^{n} (A, \tilde{M}) \neq 0})) .

(A89)

The right hand side of (A89) is precisely the definition of the Hochschild cohomological dimension. Therefore

D_{E^{k}} (A) \leq H C d i m (A | k)

(A90)

Proposition A10 applied to (A90) then draws out the conclusion.

Proposition A6 implies that:

n = f d_{A} (A / (x_{1}, .., x_{n})) .

(A91)

Therefore (1) applied to the A-module

A / (x_{1}, .., x_{n}

together with (A91) imply:

n - D (k) = f d_{A} (A / (x_{1}, .., x_{n}) \leq D_{E^{k}} \leq H C D i m (A / k) .

(A92)

If

Ω^{1} (A / k)

is generated by a regular sequence

x_{1}, .., x_{n}

then Proposition A6 implies:

n = f d_{A^{e}} (A \otimes_{k} A / Ω^{1} (A / k))

(A93)

However by definition of

Ω^{1} (A / k)

as the kernel of

μ_{A}

:

A \otimes_{k} A / Ω^{1} (A / k) ≅ A

. Therefore:

n = f d_{A^{e}} (A) .

(A94)

Lemma A1 together with Lemma A3 imply:

n = f d_{A^{e}} (A) \leq p d_{A^{e}} (A) \leq p d_{E_{A^{e}}^{k}} (A) + D (k) .

(A95)

Since

D (k)

is finite then (A95) entails:

n - D (k) \leq p d_{E_{A^{e}}^{k}} (A) .

(A96)

By Theorem A2 (A96) is equivalent to:

n - D (k) \leq H C D i m (A) .

(A97)

If A is Cohen-Macaulay at one of its maximal ideals

m

then there exists a maximal regular

x_{1}, . ., x_{d}

in

A_{m}

with

d = K r u l l (A_{m})

. Therefore (2) implies:

K r u l l (A_{m}) - D (k) = d - D (k) \leq D (A_{m}) - D (k) .

(A98)

Since

D (A_{m}) \leq D (A)

, then

K r u l l (A_{m}) - D (k) \leq D (A_{m}) - D (k) \leq D (A) - D (k) .

(A99)

Finally (1) applied to (A99) implies:

K r u l l (A_{m}) - D (k) \leq D (A) - D (k) \leq H C D i m (A) .

(A100)

□

Appendix D.3. Proofs of Consequences

Proof of Corollary 1.

Since X is a smooth affine scheme its coordinate ring satisfies Pointcaré duality in dimension d then Van den Bergh’s Theorem ([12]) applied. Hence, we have that for every

M \in_{A^{e}} M o d

H H^{n} (A, M) ≅ H H_{d - n} (A, H_{d - n} (A, ω_{A}^{- 1} \otimes_{A} M) .

(A101)

Since

k [X]

is flat as a k-module then we may apply Theorem 2 to the left-hand side of (A101) to conclude that

0 ≇ H H^{n} (A, M) ≅ H H_{d - n} (A, ω_{A}^{- 1} \otimes_{A} M),

(A102)

for some A-bimodule M and some

n \geq f d_{A} (M) - D (k)

. Again by Van den Bergh’s theorem we conclude that

H H_{m} (A, ω_{A}^{- 1} \otimes_{A} M) ≅ 0

for any

m > d

. Hence, (A102) must hold for some A-bimodule M and some

f d_{A} (M) - D (k) \leq n \leq d .

Thus, there exists an A-bimodule

M^{'}

and some non-negative integer

n^{'}

for which

0 \leq n^{'} \leq d - f d_{A} (M) + D (k),

and

H H_{n^{'}} (A, M^{'}) ≇ 0

; where

M^{'} ≜ ω_{A}^{- 1} \otimes_{A} M

. Relabeling the index we obtain the conclusion. □

Proof of Corollary 2.

By the Hochschild-Kostant-Rosenberg ([10]) there are isomorphisms of A-bimodules

H H_{n} (A, M) ≅ Ω^{n} (A, M) ≜ Ω^{n} (A) \otimes_{A} M,

(A103)

for every A-bimodule M. In particular, (A103) holds for the A-bimodule M of Corollary 1. □

References

Gel’and, I.; Neumark, M. On the imbedding of normed rings into the ring of operators in Hilbert space. C*-algebras 1943–1993 (San Antonio TX 1993) 1994, 167, 2–19, Corrected reprint of the 1943 original [MR 5, 147]. [Google Scholar] [CrossRef]
Hartshorne, R. Algebraic Geometry; Graduate Texts in Mathematics, No. 52; Springer: New York, NY, USA, 1977; p. xvi+496. [Google Scholar]
Isbell, J.R. Structure of categories. Bull. Am. Math. Soc. 1966, 72, 619–655. [Google Scholar] [CrossRef]
Isbell, J.R. Normal completions of categories. In Reports of the Midwest Category Seminar; Springer: Berlin, Germany, 1967; pp. 110–155. [Google Scholar]
Seiberg, N.; Witten, E. String theory and noncommutative geometry. J. High Energy Phys. 1999, 1999, 032. [Google Scholar] [CrossRef]
Lurie, J. On the classification of topological field theories. In Current Developments in Mathematics, 2008; International Press: Somerville, MA, USA, 2009; pp. 129–280. [Google Scholar]
Hawkins, E. A cohomological perspective on algebraic quantum field theory. Commun. Math. Phys. 2018, 360, 439–479. [Google Scholar] [CrossRef]
Connes, A. Noncommutative differential geometry. Inst. Hautes Études Sci. Publ. Math. 1985, 62, 141–144. [Google Scholar] [CrossRef]
Hochschild, G. On the cohomology groups of an associative algebra. Ann. Math. 1945, 46, 58–67. [Google Scholar] [CrossRef]
Hochschild, G.; Kostant, B.; Rosenberg, A. Differential forms on regular affine algebras. Trans. Am. Math. Soc. 1962, 102, 383–408. [Google Scholar] [CrossRef]
Antieau, B.; Vezzosi, G. A remark on the Hochschild-Kostant-Rosenberg theorem in characteristic p. Ann. Sc. Norm. Super. Pisa Cl. Sci. 2020, 20, 1135–1145. [Google Scholar] [CrossRef]
Van den Bergh, M. A relation between Hochschild homology and cohomology for Gorenstein rings. Proc. Am. Math. Soc. 1998, 126, 1345–1348. [Google Scholar] [CrossRef]
Grothendieck, A.; Raynaud, M. Revêtements étales et groupe fondamental (SGA 1). arXiv 2002, arXiv:math/0206203. [Google Scholar]
Cuntz, J.; Quillen, D. Algebra extensions and nonsingularity. J. Am. Math. Soc. 1995, 8, 251–289. [Google Scholar] [CrossRef]
Avramov, L.L.; Vigué-Poirrier, M. Hochschild homology criteria for smoothness. Int. Math. Res. Not. 1992, 1992, 17–25. [Google Scholar] [CrossRef]
Avramov, L.L.; Iyengar, S. Gaps in Hochschild cohomology imply smoothness for commutative algebras. Math. Res. Lett. 2005, 12, 789–804. [Google Scholar] [CrossRef]
Beck, J.M. Triples, Algebras and Cohomology. Reprints in Theory and Applications of Categories. 2003, pp. 1–59. Available online: http://www.tac.mta.ca/tac/reprints/articles/2/tr2abs.html (accessed on 20 November 2020).
Hilton, P.J.; Stammbach, U. A Course in Homological Algebra. In Graduate Texts in Mathematics, 2nd ed.; Springer: New York, NY, USA, 1997; Volume 4, p. xii+364. [Google Scholar]
De Jong, A.J. The Stacks Project. Algebr. Stacks. 2013. Available online: https://stacks.math.columbia.edu/ (accessed on 20 November 2020).
Springer, T.A. Linear Algebraic Groups, 2nd ed.; Modern Birkhäuser Classics; Birkhäuser Boston, Inc.: Boston, MA, USA, 2009; p. xvi+334. [Google Scholar]
Keller, B. Introduction to Kontsevich’s Quantization Theorem. Preprint. 2004. Available online: https://webusers.imj-prg.fr/bernhard.keller/publ/emalca.pdf (accessed on 20 November 2020).
Rotman, J.J. An Introduction to Homological Algebra, 2nd ed.; Universitext; Springer: New York, NY, USA, 2009; p. xiv+709. [Google Scholar]
MacLane, S. Homology, 1st ed.; Springer: Berlin, Germany; New York, NY, USA, 1967; p. x+422. [Google Scholar]
Weibel, C.A. An Introduction to Homological Algebra; Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, UK, 1994; Volume 38, p. xiv+450. [Google Scholar]
Connes, A.; Cuntz, J.; Guentner, E.; Higson, N.; Kaminker, J.; Roberts, J.E. Noncommutative Geometry. In Lectures Given at the C.I.M.E. Summer School Held in Martina Franca, 3–9 September 2000; Doplicher, S., Longo, R., Eds.; Fondazione CIME/CIME Foundation Subseries; Springer: Berlin, Germamy, 2004; Volume 1831, p. xiv+343. [Google Scholar] [CrossRef]
Eisenbud, D. Commutative Algebra; Graduate Texts in Mathematics; Springer: New York, NY, USA, 1995; Volume 150, p. xvi+785. [Google Scholar]
Hochschild, G. Note on relative homological dimension. Nagoya Math. J. 1958, 13, 89–94. [Google Scholar] [CrossRef][Green Version]
Bourbaki, N. Commutative Algebra; Elements of Mathematics (Berlin); Springer: Berlin, Germany, 1998; Chapters 1–7; p. xxiv+625. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Lower-Estimates on the Hochschild (Co)Homological Dimension of Commutative Algebras and Applications to Smooth Affine Schemes and Quasi-Free Algebras

Abstract

1. Introduction

Organization of the Paper

2. Main Result

2.1. Non-Triviality of Higher Differential Forms

2.2. Quasi-Free Algebras are Uncommon

Examples

3. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A. Background

Appendix A.1. Relative Homological Algebra

Appendix A.2. Hochschild (Co)homological Dimension

Appendix A.3. Quasi-Free Algebras

Appendix A.4. Classical Cohomological Dimensions

Appendix B. Proofs

Appendix C. Technical Lemmas

Appendix D. Auxiliary Results

Appendix D.1. Proof of Theorem 1

Proof of Lemma A3

Appendix D.2. Proof of Theorem 2

Appendix D.3. Proofs of Consequences

References

Article Metrics

Citations

Article Access Statistics