Abstract
The purpose of this paper is to develop a data augmentation technique for statistical inference concerning stochastic cusp catastrophe model subject to missing data and partially observed observations. We propose a Bayesian inference solution that naturally treats missing observations as parameters and we validate this novel approach by conducting a series of Monte Carlo simulation studies assuming the cusp catastrophe model as the underlying model. We demonstrate that this Bayesian data augmentation technique can recover and estimate the underlying parameters from the stochastic cusp catastrophe model.
1. Introduction
In real-world system dynamics, a bifurcation is defined when a small change to a system’s parameter values generates a sudden change in its system behavior. Catastrophe theorists are then to study the mathematical characteristics of bifurcation phenomena in order to solve real-life applications associated with these catastrophe changes.
Catastrophe theory, a branch of dynamic systems in mathematics was initially proposed by Thom [1,2,3] in the 1970s. Cobb [4,5,6,7] along with other researchers [8,9,10] popularized catastrophe in the following decades in statistics and statistical modeling.
Cusp catastrophe model is one of the elementary catastrophe models under catastrophe theory. The deterministic catastrophe model is often expressed as
where is some potential function. When V is specified as
it this the cusp catastrophe model,
where model parameters and are referred to as the asymmetry and bifurcation parameters, respectively. Additionally, the system’s equilibria can be obtained by finding the roots of the cubic function in Equation (2).
Associated with the roots in this cubic function, an important concept in cusp catastrophe model is the Cardan’s discriminant, which is defined as and often used to classify the solutions. Specifically,
- (1)
- If , for example , Equation (2) has three distinct real roots;
- (2)
- If , for example , Equation (2) has two distinct real roots with one of the two being a double root;
- (3)
- If , for example , Equation (2) has only one real root.
The stochastic cusp catastrophe model is further developed to incorporate measurement errors in real-world applications with the stochastic differential equation as follows:
where is a Wiener process with dispersion parameter .
Generally, time-series data, such as financial time-series data and health bio-marker time-series data in this big data era, are often collected sequentially in time. Stochastic differential equations, such as the stochastic cusp catastrophe models, are used to model the underlying data generating process. Developing rigorous statistical methods to calibrate the underlying model of the measured observations becomes important.
In our recent work, we proposed a Bayesian approach inference method that combines Hamiltonian Monte Carlo with two different transition density approximation methods, namely Euler method and Hermite expansion [11]. By extensive simulation studies and empirical example, we showed that the proposed methods achieved satisfactory results in statistical inference to stochastic cusp catastrophe models with different model parameter settings.
To better illustrate the contributions of this paper, including how this paper addresses a different problem from our recent work [11], Figure 1 shows a sample trajectory of stochastic cusp catastrophe model with parameters . The upper plot is a sample trajectory assuming no missing values, and our recent work [11] has addressed the statistical inference problem under this so-called “complete” observations settings. The lower plot is the same sample trajectory assuming missing values. In this paper, we focus on tackling the inference problem assuming missing values. Our solution is a Bayesian approach that naturally incorporates the missing values as parameters to be estimated, which is a one data augmented approach. Our simulation results implemented the Bayesian approach to cusp catastrophe model shows feasible solution by using only the observed observations.
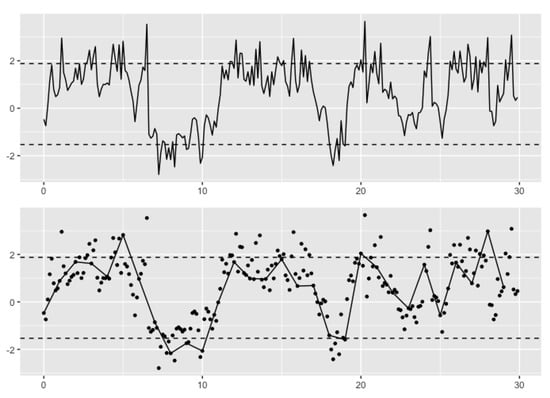
Figure 1.
A sample trajectory of stochastic cusp catastrophe model with parameters . (top) Inference with complete observations; (bottom) inference with partial observations.
2. Inference from Partial Observations
In reality, complete observations may not be possible or not be available all the time due to different missing mechanisms, resulting in partial observation scenario; therefore, a fundamental question is how valid the statistical inference developed for the scenario of complete observations is for the scenario of partially observed data.
One apparent situation is when two consecutive observations in time series can be considerably sparse with partial observations where time interval (denoted by ) between these two consecutive observations are large. As increases, the discrepancy between models with the complete data and partially observed data can be substantial and should not be neglected since it could lead to inconsistent estimators as pointed out in [12,13,14].
In this paper, we propose a Bayesian data augmentation technique to tackle the statistical inference problem with partially observed data for stochastic cusp catastrophe model by a series of Monte Carlo simulation studies.
2.1. Bayesian Data Augmentation
Under the partial observations scenario, data points are assumed to be observed more sparsely in time than the complete observations scenario studied by the work of [11]. Figure 1 is a simulated sample trajectory of stochastic cusp catastrophe model with parameters .
One approach to tackle the problem is to formulate this partial observations scenario as a missing value problem and attempt to improve the estimation accuracy with Bayesian data augmentation. Simply saying, this Bayesian data augmentation treats those unobserved or missing data points between two consecutive observed as unknown parameters in addition to the unknown parameters in the stochastic cusp catastrophe model (i.e., and ) so that we can estimate them simultaneously.
That being said, Bayesian inference treats unknowns as random variables and naturally associates them to probability distributions. In notation,
where is the actual observed data points, is latent or unobserved data points.
By doing so, the unknown model parameters ( and in our stochastic cusp catastrophe model) are to be estimated along with the incorporation , potentially a very high dimensional estimation problem; therefore, the complexity, as well as the computational cost, can increase substantially due to the introduction of high dimensional missing values; however, the approximated transition density would have a much smaller discretization , which would lead to a less biased approximation—we hope that a more “accurate” estimation result could be attained.
To better illustrate how data augmentation works, particularly how the latent variable are incorporated into the parameter estimation algorithm, we will now look at a concrete example: as depicted in Figure 2.

Figure 2.
Illustration of Bayesian data augmentation.
In the above plot, two endpoints in blue, namely and denote two consecutive observed data points. Further, there are three points in red, namely , and , representing unobserved data points. They are “synthetic” data in the sense that we do not have the actual observation, either because we were not able to do so, or we just simply did not do so, but these three data points have been generated at those time points.
By incorporating those unobserved data points into our model, (1) the dimension of parameters increased substantially. To see this, let us suppose we have n observed data points. Now for each time interval between two consecutive observed data points, we introduced three unobserved data points. Consequently, we introduced new unknowns to be estimated in addition to the two unknown model parameters and . (2) The time difference two the combined data points (i.e., both the actual observed and the synthetic data points) is becoming smaller. To see this, without introducing synthetic data, consider that the time difference between the measurement of two consecutive data points is , then by introducing additional three synthetic data points and inserting them into one observation interval, the difference becomes . Hence, a better approximation to the true transition density since has been reduced to . From this perspective, we would expect an improvement in the accuracy of the approximation due to a better-approximated transition density, hence, likelihood function.
2.2. General Case
The above example showed how data augmentation works by giving a simple illustration with three synthetic observations inserted between two consecutive observed data points. Of course the number of synthetic observation can be generalized to for each consecutive observed data points.
Let be ( is a non-negative integer) unobserved hence synthetic observations between two consecutive observed data points and . Furthermore, let us assume and let be the time difference between two observed data points, and let .
Without assuming any synthetic data points between observed data points, the log-likelihood function given only the observed ones is:
where the log-likelihood function given both observed and synthetic data points is
where .
2.3. Hamiltonian Monte Carlo
Theoretically, Bayesian inference is a natural choice for providing an accurate estimation of cusp model parameters, this is because the Bayesian approach explores the entire distribution region rather than searching for the optimal of a given function, such as likelihood function, which is achieved by associating model parameters to probability distributions. Consequently, a natural and direct estimation for the uncertainty over the range of model parameter values can be obtained. Besides providing an accurate estimation to model parameters and for the cusp catastrophe model, Bayesian inference naturally incorporates the missing observations as additional parameters—see Section 2.1.
The Hamiltonian Monte Carlo (HMC) has been developed under the framework of Markov Chain Monte Carlo (MCMC). By adopting and utilizing a Hamiltonian dynamic between states, samples obtained by using HMC have a much reduced autocorrelation than those obtained using Metropolis–Hastings algorithm. This is because HMC utilizes the gradient information in addition to the probability distribution, so that HMC is able to explore the target distribution more efficiently, which results in reduced autocorrelation and faster convergence [15,16,16].
The implementation of this Hamiltonian Monte Carlo is illustrated in six steps as illustrated in Algorithm 1 as follows:
| Algorithm 1: Implementation of Hamiltonian Monte Carlo. |
Start with a collection of samples with being the latest draw; Let be ; Sample a new initial momentum variable from ; Run the Leap Frog algorithm Algorithm 2 starting at for L steps with step-size to obtain proposed states and : Compute the acceptance ratio: Accept with following acceptance–rejection criterion: |
| Algorithm 2: Leap Frog algorithm. |
Take a half step forward in time to update the momentum variable while fixing position variable at t: Take a full step forward in time to update the position variable while fixing momentum variable computed at time from the previous step: Take the remaining half step in time to finish updating the momentum variable while fixing position variable at time : |
Samples generated from Hamiltonian Monte Carlo are the empirical posterior distributions to unknown parameters which include both model parameters and missing observations .
3. Simulation Study
To validate the proposed Bayesian data augmentation, we make use of simulation studies. The most common and intuitive method of the simulation study is to generate data with known model parameter values and then use these simulated data to estimate the model parameters using the developed parameter estimation algorithm to see whether or not the model can recover these parameters from the simulated data.
3.1. Simulation Design
The simulation experiment is designed to test the parameter estimation algorithms for different number of augmented points under different parameter settings.
To do so, we first choose a combination of and values as seen in Table 1. We fix to be 3 and select to be 1, 2, and 3, which correspond to the three cases of Cardan’s discriminant to be less than zero, equal to zero, and great than zero. We also choose the number of augmented points to be 0, 1, 3, and 7 in this simulation study.

Table 1.
Simulation settings.
We then perform trajectory simulation for 30 units of time with discretization step-size being using Euler–Maruyama method [17,18] to obtain 240 (i.e., 30/0.125) data points, which is considered a nearly “continuous" sample trajectory. We then take observations for every m points (m = 8), and discard the rest. We pretend that we were only able to observe 1 observation per unit time, which leads us to a total number of 30 observed data points.
The goal is to use this 30 data points as observations to perform parameter estimations. We repeat this sample trajectory generating process times. So eventually we will have sample trajectories and 30 observation points per sample trajectory.
Model parameters are estimated based on the empirical posterior distributions that are sampled using HMC, as described in Section 2.3. A non-informative flat prior was used as the choice of prior distribution. Furthermore, to ensure the retained posterior samples obtained by HMC are fine empirical representations of the true posterior distribution, the HMC hyper-parameters, including burn-in and the total number of HMC runs, have been fine-tuned following the standard MCMC convergence diagnostic criteria [19]. Table 2 computes and records the following statistics for both and estimates.

Table 2.
Major statistics used for posterior analysis.
3.2. Results
Table 3 summarizes the simulation study. The simulation was designed in a way that to first generate a large number of sample trajectories with each pre-selected model parameter pair and , and then only keep one observation for every eight generated points on the trajectory. The goal is to use only the observed data points (hide all remaining generated points) to perform an inference by using the proposed Bayesian inference method. Moreover, in Table 3, for each pre-selected parameter pair, we compare across a different number of augmented points in the Bayesian approach. For example, zero augmented points assume no missing values between two observations; similarly, seven augmented points assume seven missing values between two observations—which is the actual number of data points being generated at the sample trajectory generation process but assumed to be not observed.

Table 3.
Summary of simulations.
The Bayesian inference method estimates model parameters and and naturally incorporates the missing observations as additional parameters. As seen from Table 3, the “Mean” estimate for both and approach their true values as the number of augmented data points being inserted increases from 0 to 1 to 3 to 7. Further, the “SE” and “ESE” are moving closer, resulting in the increase in the coverage probability (CP) for both and .
Additionally, we are providing the distributions of posterior MAP estimators as shown in Figure 3, Figure 4 and Figure 5. The results in Table 3 can be further graphically illustrated in Figure 3 for parameters and , Figure 4 for parameters and , and Figure 5 for parameters and . The distributions in each figure are generated from M = 500 simulations for their posterior mode used in Table 3. As seen from these figures, we observe that as the number of augmented points increase (to 7), the distribution of the estimated and are less biased to the true values (as shown in the vertical dashed lines).
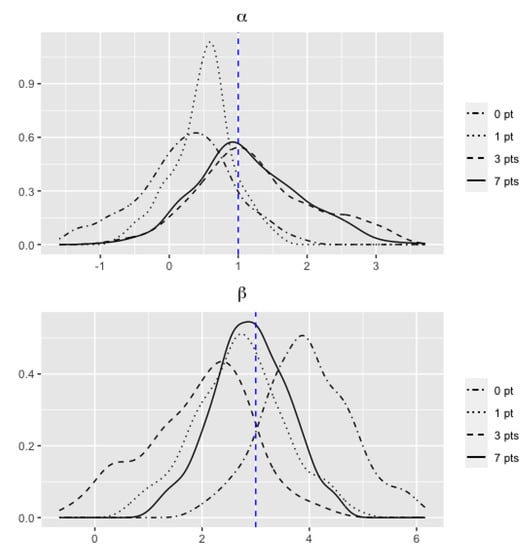
Figure 3.
Distribution of estimated parameters when .
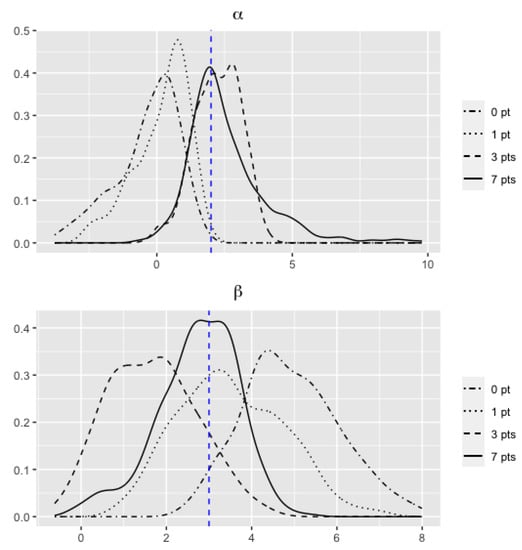
Figure 4.
Distribution of estimated parameters when .
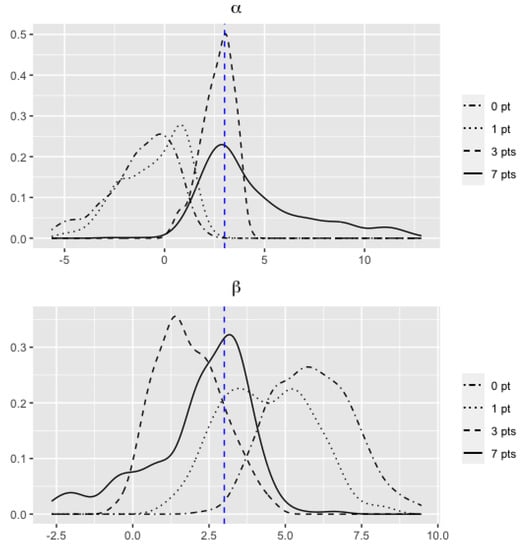
Figure 5.
Distribution of estimated parameters when .
The simulation is based on this simulation study; by increasing the number of augmented data points per unit time interval, we have gained the increasing coverage probabilities as well as unbiased estimates for both and under all three different parameter pair settings—this might be more practically desirable in reality.
4. Conclusions
In this paper we present a Bayesian solution for statistical inference concerning stochastic cusp catastrophe model subject to partially observed observations. Theoretically, the Bayesian inference solution naturally treats missing observations as parameters. We validated this approach using a series of simulation studies, and the simulation studies demonstrated that the Bayesian data augmentation can satisfactorily recover the parameter estimation and statistical inference for the stochastic cusp catastrophe models subject to missing values.
Author Contributions
Conceptualization, D.-G.C., H.G. and C.J.; methodology, D.-G.C. and H.G.; software, H.G.; validation, D.-G.C. and H.G.; writing, D.-G.C. and H.G.; supervision, C.J. All authors have read and agreed to the published version of the manuscript.
Funding
South Africa DST-NRF-SAMRC SARChI Research Chair in Biostatistics, grant number 114613.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work is partially based on research supported by the South Africa National Research Foun-dation (NRF) and the South Africa Medical Research Council (SAMRC). The opinions expressed and conclusions arrived at are those of the authors, and are not necessarily to be attributed to the NRF and/or SAMRC.
Conflicts of Interest
The authors declare that they have no competing interest.
References
- Thom, R.; Zeeman, E. Catastrophe theory: Its present state and future perspectives. In Dynamical Systems-Warwick; Springer: Berlin/Heidelberg, Germany, 1974; p. 366. [Google Scholar]
- Thom, R. Structural Stability and Morphogenesis; Benjamin-Addison-Wesley: New York, NY, USA, 1975. [Google Scholar]
- Thom, R.; Fowler, D.H. Structural Stability and Morphogenesis: An Outline of a General Theory of Models; W. A. Benjamin: New York, NY, USA, 1975. [Google Scholar]
- Cobb, L.; Ragade, R.K. Applications of Catastrophe Theory in the Behavioral and Life Sciences; Behavioral Science: New York, NY, USA, 1978; Volume 23, p. i. [Google Scholar]
- Cobb, L. Estimation Theory for the Cusp Catastrophe Model. In Proceedings of the American Statistical Association, Section on Survey Research Methods (March 1981); 1980; pp. 772–776. Available online: http://www.asasrms.org/Proceedings/papers/1980_162.pdf (accessed on 12 December 2021).
- Cobb, L.; Watson, B. Statistical catastrophe theory: An overview. Math. Model. 1980, 1, 311–317. [Google Scholar] [CrossRef] [Green Version]
- Cobb, L.; Zacks, S. Applications of catastrophe theory for statistical modeling in the biosciences. J. Am. Stat. Assoc. 1985, 80, 793–802. [Google Scholar] [CrossRef]
- Honerkamp, J. Stochastic Dynamical System: Concepts, Numerical Methods, Data Analysis; VCH Publishers: New York, NY, USA, 1994. [Google Scholar]
- Hartelman, A.I. Stochastic Catastrophe Theory; University of Amsterdam: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Grasman, R.P.; van der Mass, H.L.; Wagenmakers, E. Fitting the cusp catastrophe in R: A cusp package primer. J. Stat. Softw. 2009, 32, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.G.; Gao, H.; Ji, C.; Chen, X. Stochastic cusp catastrophe model and its Bayesian computations. J. Appl. Stat. 2021, 1–20. [Google Scholar] [CrossRef]
- Melino, A. Estimation of continuous-time models in finance. In Advances in Econometrics Sixth World Congress; Sims, C.A., Ed.; Cambridge University Press: Cambridge, UK, 1996; Volume 2, pp. 313–351. [Google Scholar]
- Jones, C.S. Bayesian Estimation of Continuous-Time Finance Models; University of Rochester: New York, NY, USA, 1998. [Google Scholar]
- Ait-Sahalia, Y. Closed-form likelihood expansions for multivariate diffusions. Ann. Stat. 2008, 36, 906–937. [Google Scholar] [CrossRef]
- Neal, R.M. MCMC using Hamiltonian dynamics. Handb. Markov Chain. Monte Carlo 2011, 2, 2. [Google Scholar]
- Betancourt, M. A conceptual introduction to Hamiltonian Monte Carlo. arXiv 2017, arXiv:1701.02434. [Google Scholar]
- Iacus, S.M. Simulation and Inference for Stochastic Differential Equations: With R Examples; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Platen, E. An introduction to numerical methods for stochastic differential equations. Acta Numer. 1999, 8, 197–246. [Google Scholar] [CrossRef] [Green Version]
- Gelman, A.; Stern, H.S.; Carlin, J.B.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall: London, UK; CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).