Scalability of k-Tridiagonal Matrix Singular Value Decomposition
Abstract
1. Introduction
2. Background
3. Parallel Singular Value Decomposition for -Tridiagonal Matrices
| Algorithm 1 Parallel conventional SVD for k-tridiagonal matrices |
|
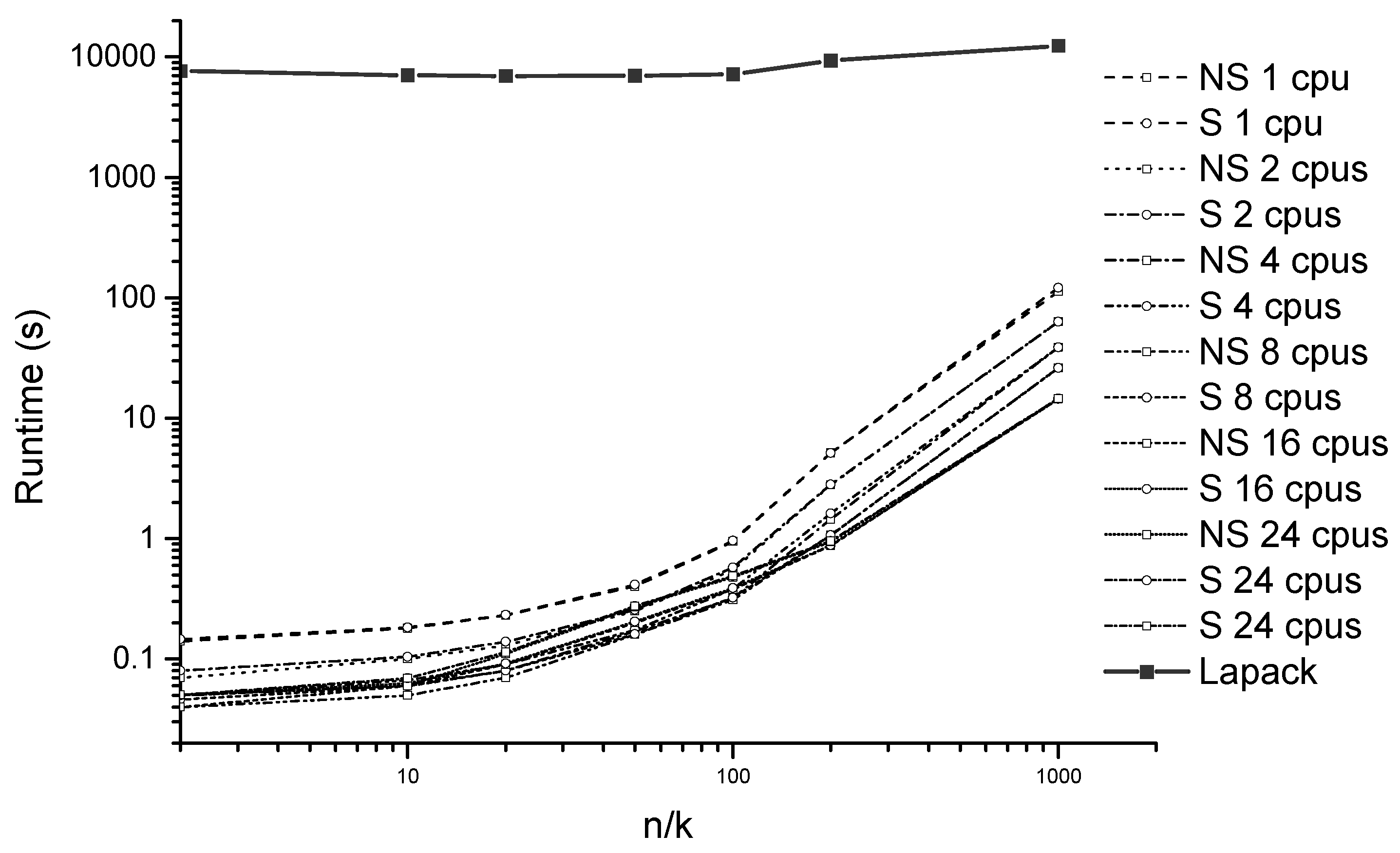
4. Numerical Examples
5. Evaluation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SVD | Singular value decomposition |
| PCA | Principal component analysis |
| NFS | Network file system |
| RSD | Relative standard deviation |
References
- Horn, R.A.; Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer Science+ Business Media: New York, NY, USA, 2006. [Google Scholar]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef] [PubMed]
- Luo, W.H.; Huang, T.Z.; Gu, X.M.; Liu, Y. Barycentric rational collocation methods for a class of nonlinear parabolic partial differential equations. Appl. Math. Lett. 2017, 68, 13–19. [Google Scholar] [CrossRef]
- McMillen, T.; Bourget, A.; Agnew, A. On the zeros of complex Van Vleck polynomials. J. Comput. Appl. Math. 2009, 223, 862–871. [Google Scholar] [CrossRef][Green Version]
- Gu, X.M.; Sun, H.W.; Zhao, Y.L.; Zheng, X. An implicit difference scheme for time-fractional diffusion equations with a time-invariant type variable order. Appl. Math. Lett. 2021, 120, 107270. [Google Scholar] [CrossRef]
- Luo, W.H.; Gu, X.M.; Yang, L.; Meng, J. A Lagrange-quadratic spline optimal collocation method for the time tempered fractional diffusion equation. Math. Comput. Simul. 2021, 182, 1–24. [Google Scholar] [CrossRef]
- Peng, W.; Xin, B. An integrated autoencoder-based filter for sparse big data. J. Control. Decis. 2020, 8, 260–268. [Google Scholar] [CrossRef]
- Ruble, M.; Güvenç, İ. Multilinear Singular Value Decomposition for Millimeter Wave Channel Parameter Estimation. IEEE Access 2020, 8, 75592–75606. [Google Scholar] [CrossRef]
- He, Y.L.; Tian, Y.; Xu, Y.; Zhu, Q.X. Novel soft sensor development using echo state network integrated with singular value decomposition: Application to complex chemical processes. Chemom. Intell. Lab. Syst. 2020, 200, 103981. [Google Scholar] [CrossRef]
- Han, S.; Ng, W.K.; Philip, S.Y. Privacy-preserving singular value decomposition. In Proceedings of the 2009 IEEE 25th International Conference on Data Engineering, Shanghai, China, 29 March–2 April 2009; pp. 1267–1270. [Google Scholar]
- Chan, T.F. An improved algorithm for computing the singular value decomposition. ACM Trans. Math. Softw. (TOMS) 1982, 8, 72–83. [Google Scholar] [CrossRef]
- Gu, M.; Eisenstat, S.C. A divide-and-conquer algorithm for the bidiagonal SVD. SIAM J. Matrix Anal. Appl. 1995, 16, 79–92. [Google Scholar] [CrossRef]
- Nakatsukasa, Y.; Higham, N.J. Stable and efficient spectral divide and conquer algorithms for the symmetric eigenvalue decomposition and the SVD. SIAM J. Sci. Comput. 2013, 35, A1325–A1349. [Google Scholar] [CrossRef]
- de Rijk, P. A one-sided Jacobi algorithm for computing the singular value decomposition on a vector computer. SIAM J. Sci. Stat. Comput. 1989, 10, 359–371. [Google Scholar] [CrossRef]
- Konda, T.; Nakamura, Y. A new algorithm for singular value decomposition and its parallelization. Parallel Comput. 2009, 35, 331–344. [Google Scholar] [CrossRef]
- Musco, C.; Musco, C. Randomized block Krylov methods for stronger and faster approximate singular value decomposition. In Proceedings of the Annual Conference on Neural Information Processing Systems 2015, Montreal, QC, Canada, 7–12 December 2015; pp. 1396–1404. [Google Scholar]
- Kokiopoulou, E.; Bekas, C.; Gallopoulos, E. Computing smallest singular triplets with implicitly restarted Lanczos bidiagonalization. Appl. Numer. Math. 2004, 49, 39–61. [Google Scholar] [CrossRef]
- Niu, D.; Yuan, X. An implicitly restarted Lanczos bidiagonalization method with refined harmonic shifts for computing smallest singular triplets. J. Comput. Appl. Math. 2014, 260, 208–217. [Google Scholar] [CrossRef]
- Ishida, Y.; Takata, M.; Kimura, K.; Nakamura, Y. An Improvement of Augmented Implicitly Restarted Lanczos Bidiagonalization Method. In Proceedings of the International Conference on Parallel and Distributed Processing Techniques and Applications (PDPTA). The Steering Committee of The World Congress in Computer Science, Computer Engineering and Applied Computing (WorldComp), Las Vegas, NV, USA, 17–20 July 2017; pp. 281–287. [Google Scholar]
- Sogabe, T.; El-Mikkawy, M. Fast block diagonalization of k-tridiagonal matrices. Appl. Math. Comput. 2011, 218, 2740–2743. [Google Scholar] [CrossRef]
- El-Mikkawy, M.; Atlan, F. A novel algorithm for inverting a general k-tridiagonal matrix. Appl. Math. Lett. 2014, 32, 41–47. [Google Scholar] [CrossRef]
- El-Mikkawy, M.; Atlan, F. A new recursive algorithm for inverting general k-tridiagonal matrices. Appl. Math. Lett. 2015, 44, 34–39. [Google Scholar] [CrossRef]
- Sogabe, T.; Yılmaz, F. A note on a fast breakdown-free algorithm for computing the determinants and the permanents of k-tridiagonal matrices. Appl. Math. Comput. 2014, 249, 98–102. [Google Scholar] [CrossRef]
- Kirklar, E.; Yilmaz, F. A Note on k-Tridiagonal k-Toeplitz Matrices. Ala. J. Math. 2015, 3, 39. [Google Scholar]
- Jia, J.; Li, S. Symbolic algorithms for the inverses of general k-tridiagonal matrices. Comput. Math. Appl. 2015, 70, 3032–3042. [Google Scholar] [CrossRef]
- Ohashi, A.; Usuda, T.; Sogabe, T. On Tensor product decomposition of k-tridiagonal toeplitz matrices. Int. J. Pure Appl. Math. 2015, 103, 537–545. [Google Scholar] [CrossRef]
- Takahira, S.; Sogabe, T.; Usuda, T. Bidiagonalization of (k, k+ 1)-tridiagonal matrices. Spec. Matrices 2019, 7, 20–26. [Google Scholar] [CrossRef]
- Küçük, A.Z.; Özen, M.; İnce, H. Recursive and Combinational Formulas for Permanents of General k-tridiagonal Toeplitz Matrices. Filomat 2019, 33, 307–317. [Google Scholar]
- Tănăsescu, A.; Popescu, P.G. A fast singular value decomposition algorithm of general k-tridiagonal matrices. J. Comput. Sci. 2019, 31, 1–5. [Google Scholar] [CrossRef]
- Marques, O.; Demmel, J.; Vasconcelos, P.B. Bidiagonal SVD Computation via an Associated Tridiagonal Eigenproblem. ACM Trans. Math. Softw. (TOMS) 2020, 46, 1–25. [Google Scholar] [CrossRef]
- Liao, X.; Li, S.; Cheng, L.; Gu, M. An improved divide-and-conquer algorithm for the banded matrices with narrow bandwidths. Comput. Math. Appl. 2016, 71, 1933–1943. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tănăsescu, A.; Carabaş, M.; Pop, F.; Popescu, P.G. Scalability of k-Tridiagonal Matrix Singular Value Decomposition. Mathematics 2021, 9, 3123. https://doi.org/10.3390/math9233123
Tănăsescu A, Carabaş M, Pop F, Popescu PG. Scalability of k-Tridiagonal Matrix Singular Value Decomposition. Mathematics. 2021; 9(23):3123. https://doi.org/10.3390/math9233123
Chicago/Turabian StyleTănăsescu, Andrei, Mihai Carabaş, Florin Pop, and Pantelimon George Popescu. 2021. "Scalability of k-Tridiagonal Matrix Singular Value Decomposition" Mathematics 9, no. 23: 3123. https://doi.org/10.3390/math9233123
APA StyleTănăsescu, A., Carabaş, M., Pop, F., & Popescu, P. G. (2021). Scalability of k-Tridiagonal Matrix Singular Value Decomposition. Mathematics, 9(23), 3123. https://doi.org/10.3390/math9233123






