A New Modified Fixed-Point Iteration Process
Abstract
:1. Introduction
2. Preliminaries
3. Convergence Results
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Brouwer, L. Uber Abbildungen von Mannigfaltigkeiten. Math. Ann. 1912, 70, 97–115. [Google Scholar]
- Yao, Y.; Leng, L.; Postolache, M.; Zheng, X. Mann-type iteration method for solving the split common fixed point problem. J. Nonlinear Convex Anal. 2017, 18, 875–882. [Google Scholar]
- Yao, Y.; Qin, X.; Yao, J.C. Projection methods for firmly type nonexpansive operators. J. Nonlinear Convex Anal. 2018, 19, 407–415. [Google Scholar]
- Garodia, C.; Uddin, I. Approximating common fixed points of non-expansive mappings in CAT(0) spaces. U.P.B. Sci. Bull. Ser. A 2019, 81, 85–96. [Google Scholar]
- Garodia, C.; Uddin, I. A new iterative method for solving split feasibility problem. J. Appl. Anal. Comput. 2020, 10, 986–1004. [Google Scholar] [CrossRef]
- Garodia, C.; Uddin, I. A new fixed-point algorithm for finding the solution of a delay differential equation. Aims Math. 2020, 5, 3182–3200. [Google Scholar] [CrossRef]
- Banach, S. Sur les operations dans les ensembles abstraits et leurs applications. Fundam. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Browder, F.E. Nonexpansive nonlinear operators in a Banach space. Proc. Natl. Acad. Sci. USA 1965, 54, 1041–1044. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Göhde, D. Zum Prinzip der kontraktiven abbildung. Math. Nachr. 1965, 30, 251–258. [Google Scholar] [CrossRef]
- Kirk, W.A. A fixed point theorem for mappings which do not increase distances. Am. Math. Mon. 1965, 72, 1004–1006. [Google Scholar] [CrossRef] [Green Version]
- Mann, W.R. Mean value methods in iteration. Proc. Am. Math. Soc. 1953, 4, 506–510. [Google Scholar] [CrossRef]
- Ishikawa, S. Fixed points by a new iteration method. Proc. Am. Math. Soc. 1974, 44, 147–150. [Google Scholar] [CrossRef]
- Halpern, B. Fixed points of nonexpanding maps. Bull. Am. Math. Soc. 1967, 73, 957–961. [Google Scholar] [CrossRef] [Green Version]
- Noor, M.A. New approximation schemes for general variational inequalities. J. Math. Anal. Appl. 2000, 251, 217–229. [Google Scholar] [CrossRef] [Green Version]
- Regan, R.P.A.D.Ó.; Sahu, D.R. Iterative construction of fixed points of nearly asymptotically nonexpansive mappings. J. Nonlinear Convex Anal. 2007, 8, 61–79. [Google Scholar]
- Abbas, M.; Nazir, T. A new faster iteration process applied to constrained minimization and feasibility problems. Mat. Vesn. 2014, 66, 223–234. [Google Scholar]
- Thakur, B.S.; Thakur, D.; Postolache, M. A New iteration scheme for approximating fixed points of nonexpansive mappings. Filomat 2016, 30, 2711–2720. [Google Scholar] [CrossRef] [Green Version]
- Schu, J. Weak and strong convergence to fixed points of asymptotically nonexpansive mappings. Bull. Aust. Math. Soc. 1991, 43, 153–159. [Google Scholar] [CrossRef] [Green Version]
- Senter, H.F.; Dotson, W.G. Approximating fixed points of nonexpansive mappings. Proc. Am. Math. Soc. 1974, 44, 375–380. [Google Scholar] [CrossRef]
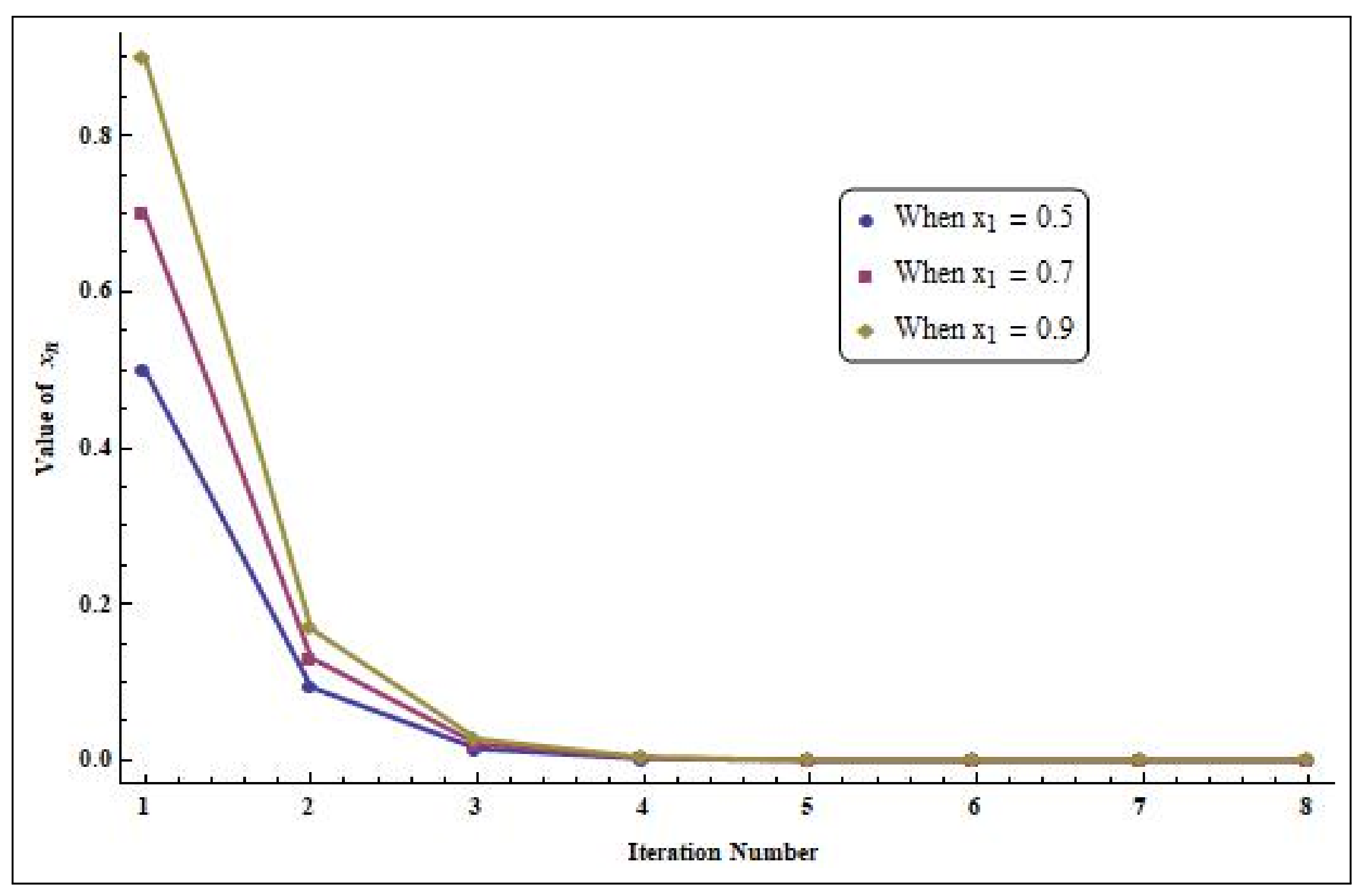

| Step | When | When | When |
|---|---|---|---|
| 1 | 0.5 | 0.7 | 0.9 |
| 2 | 0.09361111 | 0.1310556 | 0.1685 |
| 3 | 0.01512179 | 0.02117051 | 0.02721923 |
| 4 | 0.002209895 | 0.003093853 | 0.00397781 |
| 5 | 0.0003001744 | 0.0004202442 | 0.000540314 |
| 6 | 0.00003855415 | 0.00005397581 | 0.00006939747 |
| 7 | |||
| 8 |
| Step | When | When | When |
|---|---|---|---|
| 1 | 10 | 100 | 1000 |
| 2 | 1.872222 | 18.72222 | 187.2222 |
| 3 | 0.3024359 | 3.024359 | 30.24359 |
| 4 | 0.04419789 | 0.44197897 | 4.419789 |
| 5 | 0.006003488 | 0.06003488 | 0.6003488 |
| 6 | 0.000771083 | 0.00771083 | 70.0771083 |
| 7 | 0.00009474682 | 0.0009474682 | 0.009474682 |
| 8 | 0.00001123078 | 0.0001123078 | 0.001123078 |
| 9 | 0.00001292143 | 0.0001292143 | |
| 10 | 0.00001449783 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garodia, C.; Abdou, A.A.N.; Uddin, I. A New Modified Fixed-Point Iteration Process. Mathematics 2021, 9, 3109. https://doi.org/10.3390/math9233109
Garodia C, Abdou AAN, Uddin I. A New Modified Fixed-Point Iteration Process. Mathematics. 2021; 9(23):3109. https://doi.org/10.3390/math9233109
Chicago/Turabian StyleGarodia, Chanchal, Afrah A. N. Abdou, and Izhar Uddin. 2021. "A New Modified Fixed-Point Iteration Process" Mathematics 9, no. 23: 3109. https://doi.org/10.3390/math9233109
APA StyleGarodia, C., Abdou, A. A. N., & Uddin, I. (2021). A New Modified Fixed-Point Iteration Process. Mathematics, 9(23), 3109. https://doi.org/10.3390/math9233109






