Iterative Algorithm for Parameterization of Two-Region Piecewise Uniform Quantizer for the Laplacian Source

Abstract

Motivated by the fact that uniform quantization is not suitable for signals having non-uniform probability density functions (pdfs), as the Laplacian pdf is, in this paper we have divided the support region of the quantizer into two disjunctive regions and utilized the simplest uniform quantization with equal bit-rates within both regions. In particular, we assumed a narrow central granular region (CGR) covering the peak of the Laplacian pdf and a wider peripheral granular region (PGR) where the pdf is predominantly tailed. We performed optimization of the widths of CGR and PGR via distortion optimization per border–clipping threshold scaling ratio which resulted in an iterative formula enabling the parametrization of our piecewise uniform quantizer (PWUQ). For medium and high bit-rates, we demonstrated the convenience of our PWUQ over the uniform quantizer, paying special attention to the case where 99.99% of the signal amplitudes belong to the support region or clipping region. We believe that the resulting formulas for PWUQ design and performance assessment are greatly beneficial in neural networks where weights and activations are typically modelled by the Laplacian distribution, and where uniform quantization is commonly used to decrease memory footprint.

1. Introduction

One of the growing interests in neural networks (NNs) is directed towards the efficient representation of weights and activations by means of quantization [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. Quantization, as a bit-width compression method, is a desirable mechanism that can dictate the entire NN performance [10,12]. In other words, the overall network complexity reduction, provided by the quantization process, can lead to commensurately reduced overall accuracy if the pathway toward this reduction is not chosen prudently. Quantization is significantly beneficial for NN implementation on resource-limited devices since it is capable of fitting the whole NN model into the on-chip memory of edge devices such that the high overhead that occurs by off-chip memory access can be mitigated [9]. Namely, standard implementation of NNs supposes 32-bits full-precision (FP32) representation of NN parameters, requiring complex and expensive hardware. By quantizing FP32 weights and activations with low-bits, that is, by thoughtfully choosing a quantizer model for NN parameters, one can significantly reduce the required bit-width for the digital representation of NN parameters, greatly reducing the overall complexity of the NN while degrading the network accuracy to some extent [2,3,5,6,8,9]. For that reason, a few of new quantizer models and quantization methodologies have been proposed, for instance in [4,5,11,13], with a main objective—to enable quantized NNs to have the slightly degraded or almost the same accuracy level as their full-precision counterparts.

In general, to optimize a quantizer model, one has to know the statistical distribution of the input signal, allowing for the quantizer to be adapted as best as possible to the statistical characteristics of the signal itself. The symmetric Laplacian probability density functions (pdf) with the pronounced peak and heavy tails has been successfully used for modelling signals in many practical applications [8,10,13,15,16,17]. Furthermore, it is arguably the most suitable pdf form for speech and audio signals because it fits many distinctive attributes of these signals [15,16,17,18,19]. In addition, transformed signals and other quantities that are derived from original signals often follow the Laplacian pdf [16]. As it is commonly encountered in many applications, in this paper we favor signal modelling by the Laplacian pdf.

It is well known that a nonuniform quantizer model, well accommodated to the signal’s amplitude dynamic and a nonuniform pdf, has lower quantization error compared to the uniform quantizer (UQ) model with an equal number of quantization levels or equal bit-rates [2,11,13,18,20,21,22,23,24,25,26,27]. However, due to the fact that UQ is the simplest quantizer model, it has been intensively studied, for instance in [23,24,28,29,30,31,32]. Moreover, the high complexity of nonuniform quantizers can outweigh the potential performance advantages over uniform quantizers [21]. Substantial progress in this direction might go towards the usage of one well-designed PWUQ, composed of the optimized pair of UQs with equal bit-rates, capable of accommodating the statistical characteristics of the assumed Laplacian pdf in the predefined amplitude regions. For that reason, in this paper we address the parameterization of a PWUQ with the goal to provide beneficial performance improvements over the existing UQ solutions.

By following [24,25], we accept quantizer’s support region definition as a region separating the signal amplitudes into a granular region and an overload region, or alternatively, into an inner and an outer region. For the symmetric quantizer, such as the one we propose in this paper, these regions are separated by the support region thresholds or clipping thresholds, as denoted by ±x_clip (see Figure 1). These thresholds have particular real values that define a quantizer’s support region [−x_clip, x_clip], where distortion due to quantization and clipping is bounded. The problem of determining the value of x_clip of the binary scalar quantizer for the assumed Laplacian pdf has been recently addressed in [33]. Since the Laplacian pdf is a long-tailed pdf, a fair percentage of the samples are concentrated around the mean value, whereas a small percentage of the samples are in the granular region, near to the support region threshold, or out of the granular region. Observe that the shrinkage of the support region for a fixed number of quantization levels results in a reduction of the granular distortion, while at the same time causing an unwanted increase of the overload distortion [22]. On the other hand, for the given number of quantization levels, with the increase of the support region width, the overload region, and hence the overload distortion, is reduced at the expense of the granular distortion increase. In that regard, the main trade-off in quantizer design is making the support region width large enough to accommodate the signal’s amplitude dynamic while keeping this support region width small enough to minimize quantizer distortion.

By inspecting the specific features of the Laplacian pdf, we propose a novel PWUQ whose granular region is wide enough so that the overload distortion can be nullified, whereas the granular region is divided properly into two non-overlapping regions (the central granular region (CGR) and the peripheral granular region (PGR)) and to utilize the simplest uniform quantization within each of the regions. In particular, we assume a narrow region around the mean for the CGR covering the peak of the Laplacian pdf, while for the PGR we specify a wider region, that is the rest of the granular region where the pdf is tailed. These two regions are separated by the granular region border thresholds, denoted by ±x_b, that are symmetrically placed around the mean. Since our goal is to minimize the overall distortion, especially the granular distortion, the parameterization of our PWUQ so that most of the samples (99.99%) from the assumed Laplacian pdf belong to the granular region, can indeed be considered as a ubiquitous optimization task. Nevertheless, the authors of this paper have found an iterative manner to solve this task in a convenient way, explained in detail below.

In brief, the novelty of this paper in the field of quantization is reflected in the following:

-

by a studious inspection of the shape of the Laplacian pdf, a novel idea with the partition of the amplitude range of the quantizer into two regions, CGR and PGR, is proposed;

-

for given x_clip values, the widths of these two regions are optimized using our iterative algorithm so that the distortion of PWUQ is minimal;

-

the simplest model of a uniform quantizer is exploited, for equal bit-rates it is applied in each of the two regions, which makes the design of our model much simpler compared to many non-uniform quantizer models that are available in the literature (for instance, see [21,22,27]);

-

a significant gain is achieved in SQNR in relation to the uniform quantizer, which justifies the meaningfulness of our idea.

The paper is organized as follows: Section 2 describes the iterative algorithm for the parameterization of our novel PWUQ that is optimized for the given support region threshold and the assumed Laplacian pdf. Section 3 provides the discussion on the gain in performance that is achieved with the proposed quantizer when compared to UQ. Section 4 summarizes and concludes our research results.

2. Iterative Parameterization of PWUQ

At the beginning of this section, we briefly recall the basic theory of quantization. An Nlevel quantizer Q_N is defined by mapping Q_N: ℝ → Y [25], where ℝ is a set of the real numbers, Y = {y₋−_N/2, …, y₋₁, y₁, …, y_N/2} ⸦ ℝ is the code book of size N containing representation levels y_i, where N = 2^r and r is a bit-rate. With the N-level quantizer Q_N, ℝ is partitioned into N bounded in-width granular cells ℜ_i and two unbounded overload cells. The i-th granular cell is given by ℜ_i = {x|x ∈ [−x_clip, x_clip], Q_N(x) = y_i}, where it holds ℜ_i∩ℜ_j = ∅, for i ≠ j. In other words, y_i specifies the i-th codeword and is the only representative for all real values x from ℜ_i.

Let us define our novel symmetrical PWUQ that consisted of two UQs of the same number of quantization levels N/2 = K. One quantizer is utilized for quantization of amplitudes belonging to the CGR [−x_b, x_b] and the second one is used for PGR [−x_clip, x_b) ∪ (x_b, x_clip] (see Figure 1). Let us also assume that the amplitudes belonging to the two overload cells, that is, to (−∞, −x_clip) ∪ (x_clip, +∞), are clipped. Further, define CGR and PGR as:

$${\Re }^{\mathrm{CGR}}={\displaystyle \underset{i=-K/2}{\overset{-1}{\cup }}{\Re }_i}\cup {\displaystyle \underset{i=1}{\overset{K/2}{\cup }}{\Re }_i=\left[x_{-K/2},x_{K/2}\right]},{\Re }^{\mathrm{PGR}}={\displaystyle \underset{i=-K}{\overset{-K/2-1}{\cup }}{\Re }_i}\cup {\displaystyle \underset{i=K/2+1}{\overset{K}{\cup }}{\Re }_i=}\left[x_{-K},x_{-K/2}\right)\cup \left(x_{K/2},x_K\right],$$

(1)

which are separated by the border thresholds as denoted by ±x_b, for which it holds ±x_b = ±x_K/2. Due to the symmetry of the Laplacian pdf of zero mean and variance σ² = 1, for which we design our PWUQ:

$$p\left(x\right)={\frac{\exp \left\{-\sqrt{2}\left|x\right|/\sigma \right\}}{\sqrt{2}\sigma }|}_{{\sigma }^2=1}=\frac{\exp \left\{-\sqrt{2}\left|x\right|\right\}}{\sqrt{2}},$$

(2)

decision thresholds and representation levels of our quantizer are symmetrically placed about the mean value. Without loss of generality, we restrict our attention to the K positive counterparts, whereas the negative counterparts trivially follow from the symmetry

$$x_{-i}=-x_i,i=1,2,\dots ,K.$$

(3)

In particular, non-negative decision thresholds of our PWUQ consisted of two UQs of the same number of quantization levels N/2 = K, for a given K, x_clip and x_b calculates from:

$$x_i=\{\begin{array}{l}i\cdot \frac{2\hspace{0.17em}{x}_{\mathrm{b}}}{K},i=0,1\dots ,\frac{K}{2}\\ x_{\mathrm{b}}+\frac{2\left(x_{\mathrm{clip}}-x_{\mathrm{b}}\right)}{K}\left(i-\frac{K}{2}\right),\hspace{0.17em}i=\frac{K}{2}+1,\frac{K}{2}+2,\dots ,K\end{array}.$$

(4)

In other words, both regions, CGR covering [−x_b, x_b] and PGR covering [−x_clip, −x_b) ∪ (x_b, x_clip] are symmetrically partitioned into K uniform cells (see Figure 2 where transfer characteristic of PWUQ is shown for N = 16). Due to symmetry, this equally means that each of the regions [0, x_b] and (x_b, x_clip] is partitioned into K/2 uniform cells. Since these two UQs compose our PWUQ the notation of the decision thresholds in the CGR ends with index K/2, whereas the index of the decision thresholds in the PGR increases up to K.

In what follows, we describe other parameters of our PWUQ, provide derivation of the distortion, and perform its optimization per ψ = x_b/x_clip, for a given x_clip value by using the iterative algorithm. In other words, for a given x_clip value, we perform optimization of the widths of CGR and PGR via distortion optimization per border–clipping threshold scaling ratio ψ and we end up with an iterative formula enabling the concrete design of our PWUQ.

Let us define the quantization step sizes Δ^CGR and Δ^PGR as a uniform width of cells ℜ_i from ℜ^CGR and ℜ^PGR, respectively

$${\Delta }^{\mathrm{CGR}}=\frac{2x_{\mathrm{b}}}{K}=\frac{2\psi x_{\mathrm{clip}}}{K},$$

(5)

$${\Delta }^{\mathrm{PGR}}=\frac{2\left(x_{\mathrm{clip}}-x_{\mathrm{b}}\right)}{K}=\frac{2\left(1-\psi \right)x_{\mathrm{clip}}}{K}.$$

(6)

We introduce parameter ψ, that is border–clipping threshold scaling ratio, specified as ψ = x_b/x_clip, for which, in accordance with our PWUQ model definition (see Figure 1), it holds ψ < 1, or more precisely ψ < 0.5. Observing the area under the Laplacian pdf, we opt to increase quantization step size in ℜ^PGR since it is counterbalanced by a corresponding diminution of the step size in ℜ^CGR. Our symmetrical PWUQ maps a real value x ∈ ℝ to one of the representation levels y_i, where it holds:

$$y_{-i}=-y_i,i=1,2,\dots ,K,$$

(7)

and y_i is determined as the midpoint of the corresponding quantization cells ℜ_i ∈ ℜ^CGR for i = 1, …, K/2 and ℜ_i ∈ ℜ^PGR for i = K/2+1, …, K

$$y_i=\{\begin{array}{l}\left(i-\frac{1}{2}\right){\Delta }^{\mathrm{CGR}},\hspace{0.17em}i=1,\dots ,\frac{K}{2}\\ x_{\mathrm{b}}+\left(i-\frac{K+1}{2}\right){\Delta }^{\mathrm{PGR}},\hspace{0.17em}i=\frac{K}{2}+1,\frac{K}{2}+2,\dots ,K\end{array}.$$

(8)

Determining the decision thresholds and representation levels of the quantizer specifies its entire performance. If they are chosen more suitably, the overall distortion is smaller which translates to a reduction in the number of bits that are required from the quantizer for achieving certain distortion. The main idea behind our PWUQ design is to improve the overall quantization performance by the prudent application of the simplest uniform quantization. To assess the performance of our PWUQ for a given bit-rate, r (r = log₂N), and a given support region threshold we have to specify its distortion. Specifically, in accordance with our PWUQ model, we have to determine the sum of the granular distortions originating from quantization in ℜ^CGR and ℜ^PGR, that is to determine D_g^CGR and D_g^PGR

$$D_{\mathrm{g}}{}^{\mathrm{PWUQ}}=D_{\mathrm{g}}^{\mathrm{CGR}}+D_{\mathrm{g}}^{\mathrm{PGR}},$$

(9)

$$D_{\mathrm{g}}{}^{\mathrm{PWUQ}}=\frac{1}{12}\left({\left({\Delta }^{\mathrm{CGR}}\right)}^2{P}^{\mathrm{CGR}}+{\left({\Delta }^{\mathrm{P}GR}\right)}^2{P}^{\mathrm{PGR}}\right).$$

(10)

P^CGR and P^PGR denote the probability of belonging the input sample x to ℜ^CGR and ℜ^PGR, respectively

$$P^{\mathrm{CGR}}=2{\displaystyle \underset{0}{\overset{x_{\mathrm{b}}}{\int }}p\left(x\right)dx},$$

(11)

$$P^{\mathrm{PGR}}=2{\displaystyle \underset{x_{\mathrm{b}}}{\overset{x_{\mathrm{clip}}}{\int }}p\left(x\right)dx}.$$

(12)

Let us recall that the mean is a measure of central tendency and that it specifies where the values of x tend to cluster, whereas the standard deviation σ, indicates how the data are spread out from the selected mean to form the measure of dispersion [25]. Also, let us recall that on an unbounded amplitude domain, the cumulative distribution function (CDF), denoted as F_CDF, is given by

$$F_{\mathrm{CDF}}\left(b\right)={\displaystyle \underset{-\infty }{\overset{b}{\int }}p\left(x\right)}dx,$$

(13)

where CDF satisfies F_CDF(∞) = 1. For a symmetric pdf, such as the pdf that is given in (2), it holds:

$$\Phi \left(-b,b\right)=F_{\mathrm{CDF}}\left(b\right)-F_{\mathrm{CDF}}\left(-b\right)=2{\displaystyle \underset{0}{\overset{b}{\int }}p\left(x\right)dx},$$

(14)

where Φ(−b, b) is the probability that the value of the input sample x having pdf p(x) belongs to the given interval [−b, b]. By invoking (2), (13), and (14) for P^CGR and P^PGR, we have:

$$P^{\mathrm{CGR}}=\Phi \left(-x_{\mathrm{b}},x_{\mathrm{b}}\right)=2{\displaystyle \underset{0}{\overset{x_{\mathrm{b}}}{\int }}p\left(x\right)dx}=1-\exp \left\{-\sqrt{2}{x}_{\mathrm{b}}\right\},$$

(15)

$$P^{\mathrm{PGR}}=\Phi \left(-x_{\mathrm{clip}},x_{\mathrm{clip}}\right)-\Phi \left(-x_{\mathrm{b}},x_{\mathrm{b}}\right)=2{\displaystyle \underset{x_{\mathrm{b}}}{\overset{x_{\mathrm{clip}}}{\int }}p\left(x\right)dx}=\exp \left\{-\sqrt{2}{x}_{\mathrm{b}}\right\}-\exp \left\{-\sqrt{2}{x}_{\mathrm{clip}}\right\}.$$

(16)

Substituting (5), (6), (15) and (16) in (10) yields

$$D_g{}^{\mathrm{PWUQ}}=C\left[{\psi }^2\left(1-\exp \left\{-\sqrt{2}\psi \hspace{0.17em}{x}_{\mathrm{clip}}\right\}\right)+{\left(1-\psi \right)}^2\left(\exp \left\{-\sqrt{2}\psi \hspace{0.17em}{x}_{\mathrm{clip}}\right\}-\exp \left\{-\sqrt{2}{x}_{\mathrm{clip}}\right\}\right)\right],$$

(17)

where C = 4 x_clip²/(3N²). By further setting the first derivate of D_g^PWUQ with respect to ψ equal to zero

$$\frac{\partial D_{\mathrm{g}}{}^{\mathrm{PWUQ}}}{\partial \psi }=0,$$

(18)

we obtain:

$$x_{\mathrm{b}}=\psi \hspace{0.17em}{x}_{\mathrm{clip}}=\frac{1}{\sqrt{2}}\ln \left[\frac{1+\frac{x_{\mathrm{clip}}}{\sqrt{2}}-\sqrt{2}\psi \hspace{0.17em}{x}_{\mathrm{clip}}}{\psi +\left(1-\psi \right)\exp \left\{-\sqrt{2}{x}_{\mathrm{clip}}\right\}}\right].$$

(19)

From (19) and discussions about x_b or ψ determining, the application of an iterative numerical method is required:

$${\psi }^{\left(i\right)}=\frac{1}{\sqrt{2}{x}_{\mathrm{clip}}}\ln \hspace{0.17em}\left(\frac{1+\frac{x_{\mathrm{clip}}}{\sqrt{2}}\left(1-2{\psi }^{\left(i-1\right)}\right)}{{\psi }^{\left(i-1\right)}+\left(1-{\psi }^{(i-1)}\right)\exp \left\{-\sqrt{2}{x}_{\mathrm{clip}}\right\}}\right).$$

(20)

Taking the second derivative of (17) with respect to ψ yields:

$$\frac{{\partial }^2{D}_g{}^{\mathrm{PWUQ}}}{\partial {\psi }^2}=1-\exp \left\{-\sqrt{2}{x}_{\mathrm{clip}}\right\}+x_{clip}\hspace{0.17em}\exp \left\{-\sqrt{2}\psi \hspace{0.17em}{x}_{\mathrm{clip}}\right\}\hspace{0.17em}\left[2\sqrt{2}+x_{\mathrm{clip}}\left(1-2\psi \right)\right].$$

(21)

As it holds x_b ≤ x_clip/2, $2\sqrt{2}+x_{\mathrm{clip}}\left(1-2\psi \right)>2\sqrt{2}$, we can conclude that D_g^PWUQ is a convex function of ψ, and subsequently of the border threshold x_b, where x_b ∈ (0, x_clip/2]. In other words, as it holds ∂²D_g^PWUQ/∂ψ² > 0, D_g^PWUQ is also a convex function of the border threshold x_b so that for the given x_clip, one unique optimal value of x_b and one unique optimal value of ψ exists that minimizes D_g^PWUQ.

Pseudo-code (see Algorithm 1) that is shown here summarizes our iterative algorithm for the concreate designing and parameterization of PWUQ for a given bit-rate and a clipping threshold. PWUQ parameterization implies specifying the clipping thresholds, x_clip, and iteratively determining: border thresholds x_b*, and border–clipping threshold scaling ratio ψ* = x_b*/x_clip, Δ^CGR, Δ^PGR—uniform step sizes in ℜ^CGR and ℜ^PGR; {y_−i, y_i}, i = 1, 2, …, K—symmetrical representation levels; {x_−i, x_i}, i = 1, 2, …, K—symmetrical decision thresholds.

We initialize our PWUQ model with the UQ model, that is with x_b(0) = x_clip/2, to follow performance improvement that is achieved by the iterative algorithm. In other words, we assume that it holds ψ(0) = 0.5 as for this ψ value and the same number of levels N, PWUQ and UQ model are matched. We define that the iterative algorithm stopping criterion is satisfied when the absolute error

$${\epsilon }^{\left(i\right)}=\left|{\psi }^{*}-{\psi }^{\left(i-1\right)}\right|$$

(22)

is less than ε_min = 10⁻⁴.

Recalling (11)–(13) we can calculate λ, as the probability that an input sample x, with unrestricted pdf p(x), belongs to the granular region:

$$\lambda =\frac{P^{\mathrm{CGR}}+P^{\mathrm{PGR}}}{F_{\mathrm{CDF}}(\infty )}=P^{\mathrm{CGR}}+P^{\mathrm{PGR}}.$$

(23)

We should also highlight here that x_clip, x_b, and N have a direct effect on the distortion. If the clipping threshold x_clip has a very small value, the quantization accuracy may be decreased because too many samples will be clipped [24]. Note that the clipping effect nullifies the overload distortion where it can indeed degrade the granular distortion if the clipping threshold is not appropriately specified. Accordingly, setting a suitable clipping threshold value is crucial for achieving the best possible performance of the given quantization task. We can anticipate that for the given clipping threshold, the border threshold x_b has a large impact on the granular distortion because the CGR and PGR distortion, which compose the total granular distortion, behave opposite in relation to the border threshold x_b. In particular, for the fixed and an equal number of quantization levels that are assumed in ℜ^CGR and ℜ^PGR, with the decrease of the border threshold value, the CGR distortion is reduced at the expense of the increase in PGR distortion. Namely, the shrinkage of ℜ^CGR can cause a significant distortion reduction in CGR, while at the same time, can result in an unwanted but expected increase of the distortion in the pdf tailed PGR. Therefore, we can conclude that tuning the values of the border thresholds ± x_b and the clipping thresholds ± x_clip, is one of the key challenges when heavy-tailed Laplacian pdf are taken into consideration. In what follows, we will show that, for the Laplacian pdf given in (2), our PWUQ that is composed of only two UQs provides significantly better performance than one UQ. That is, it provides a higher signal–quantization-noise-ratio (SQNR)

$${\mathrm{SQNR}}^{\mathrm{PWUQ}}\hspace{0.17em}[\mathrm{dB}]=-10\cdot {\log }_{10}\left(D_g{}^{\mathrm{PWUQ}}\right),$$

(24)

compared to UQ for the same bit-rate

$${\mathrm{SQNR}}^{\mathrm{UQ}}\hspace{0.17em}[\mathrm{dB}]=-10\cdot {\log }_{10}\left(D_g{}^{\mathrm{UQ}}\right),$$

(25)

$$D_g{}^{\mathrm{UQ}}=\frac{x_{\mathrm{UQ}}{}^2}{3N^2}.$$

(26)

It is interesting to notice that if we assume equal values of the support region thresholds, or clipping thresholds of PWUQ and UQ, x_clip = x_UQ, we can end up with the simple closed-form formula providing a detailed insight in performance gain. That is, SQNR gain achievable with our PWUQ over UQ can be calculated from:

$$\delta =-10{\log }_{10}\left(\frac{D_g{}^{\mathrm{PWUQ}}}{D_g{}^{\mathrm{UQ}}}\right)=-10{\log }_{10}\left(4\hspace{0.17em}\left[{\psi }^2\hspace{0.17em}\left(P^{\mathrm{CGR}}+P^{\mathrm{PGR}}\right)+\left(1-2\psi \right)P^{\mathrm{PGR}}\right]\right).$$

(27)

Obviously, for ψ = 0.5 and the same number of levels N, the PWUQ and UQ models are matched so that SQNR^PWUQ is equal to SQNR^UQ.

Algorithm 1. PWUQ Laplacian (N, xclip, εmin)—iterative parameterization of PWUQ for the Laplacian pdf and the given xclip—determining ψ* and Φ (−xb*, xb*)

Input: Total number of quantization levels N, predefined clipping threshold xclip, εmin << 1

1st Output:ψ*, Φ(−xb*, xb*)

2nd Output: ΔCGR, ΔPGR, {y−i, yi}, {x−i, xi}, i = 1, 2, …, K

1:  Initialize i ← 0,

2:  ψ* ← 0.5,

3:  ε(0) ← 0.5

4:  while ε (i) > εmin do

5:   i ← i + 1

6:   ψ(i − 1) ← ψ*

7:   compute ψ(i) using (20)

8:   ψ* ← ψ(i)

9:   compute ε(i) using (22)

10: end while

11: xb* ← ψ* × xclip

12: compute Φ(−xb*, xb*) by using (15)

13: return ψ*, Φ(−xb*, xb*)

14: calculate ΔCGR, ΔPGR, {y−i, yi}, {x−i, xi}, i = 1, 2, …, K

Let us highlight that we have performed our analysis for the Laplacian source; similar analyses can be derived for some other source. That is, for some other pdf that we can first specify in (2) and then substitute in (11) and (12), which will further affect the derivation of the formulas starting from (15). However, not every pdf will allow the derivation of the expressions in closed form. Moreover, to provide a similar iterative algorithm, as in this paper, the distortion should be a convex function of ψ, so this should be taken into consideration as well. In brief, as the Laplacian source is one of the widely used sources, it can be concluded that the analysis that is presented in this paper is indeed significant.

Let us also highlight that our piecewise uniform quantizer, with the border threshold between two segments as determined iteratively, can be considered a piecewise linear quantizer if we consider its realization from the standpoint of a companding technique. Taking this fact into account, our novel model can be related to adaptive rejection sampling, as used in [34,35,36,37,38,39] for the generation of samples from a given pdf where piecewise linearization is performed with linear segments as tangents on log pdf and with iteratively calculated nodes specifying the linear segments. This approach with piecewise linear approximation is especially useful for pdfs such as Gaussian. As with the Gaussian pdf, one cannot solve the integrals provided in our analysis in a closed form. Due to the widespread utilization of both the Laplacian and Gaussian pdf, our future work will be focused on designing a quantizer that is based on the piecewise linear approximation of the Gaussian pdf by using a similar technique to the one proposed in [34,35,36,37,38,39].

3. Numerical Results

The most important step in designing our PWUQ is determining the value of its key parameter ψ. For a given x_clip, we can calculate ψ* using the above algorithm. Then we can calculate x_b* = ψ*·x_clip and other parameters of PWUQ, as well as its performance (SQNR^PWUQ). Since the Laplacian pdf is long-tailed and accordingly persistently unbounded, we can assume that most of the pdf’s samples are in the granular region for λ^GR = P^CGR + P^PGR = 0.9999. We can analyse the case where the values of the clipping and border thresholds x_clip^GR and x_b^GR, as well as of ψ^GR, are determined from λ^GR = 0.9999, where the GR notation indicates the granular region. By invoking (15) and (16) for λ^GR = 0.9999, we have:

$$x_{\mathrm{clip}}{}^{\mathrm{GR}}=-\frac{1}{\sqrt{2}}\ln \left(1-{\lambda }^{\mathrm{GR}}\right)=2\sqrt{2}\ln \left(10\right).$$

(28)

For medium and high bit-rates, where r amounts from 5 bit/sample to 8 bit/sample, we have calculated ψ*, x_b* = ψ*·x_clip, Φ(−x_b*, x_b*), λ*, SQNR^UQ, SQNR^PWUQ, and δ for different x_clip values (see

Table 1. Competitive presentation of key design parameters and performances of UQ and PWUQ.

r [bit/Sample]		xclip	ψ*	xb*	Φ(−xb*, xb*)	λ*	SQNRUQ	SQNRPWUQ	δ
5	[J]	4.4800	0.3100	1.38880	0.8597	0.9982	21.8487	24.1089	2.2602
	[H]	4.9013	0.2996	1.46843	0.8747	0.9990	21.0680	23.6010	2.5330
	GR	6.5127	0.2674	1.74150	0.9148	0.9999	18.5990	22.1220	3.5230
6	[J]	5.3024	0.2903	1.53929	0.8866	0.9994	26.4054	29.1938	2.7884
	[H]	5.8815	0.2789	1.64035	0.9017	0.9998	25.5050	28.6522	3.1472
	GR	6.5127	0.2674	1.74150	0.9148	0.9999	24.6196	28.1426	3.5230
7	[J]	6.1504	0.2740	1.6852	0.9077	0.9998	31.1373	34.4466	3.3093
	[H]	6.8618	0.2616	1.79505	0.9210	0.9999	30.1866	33.9106	3.7240
	GR	6.5127	0.2674	1.74150	0.9148	0.9999	30.6402	34.1632	3.5230
8	[J]	7.0272	0.2589	1.81934	0.9237	0.9999	36.0004	39.8178	3.8174
	[H]	7.8421	0.2467	1.83465	0.9552	0.9999	35.0474	39.3096	4.2622
	GR	6.5127	0.2674	1.74150	0.9148	0.9999	36.6608	40.1838	3.5230

). In particular, along with x_clip^GR, as determined from (28), we assume x_clip values as determined in [24,25], by Hui and Jayant, respectively. To distinguish between these three different cases, we use notation [J], [H], and [GR] (or just GR) in the line or in the superscript. As we can see from Figure 2, we can simply calculate from (5) and (6) (Δ^CGR/Δ^PGR = ψ*/(1 − ψ*)), it holds Δ^PGR ≈ 2Δ^CGR, so that from K×(Δ^PGR + Δ^CGR) = 2K × Δ^UQ it implies Δ^UQ ≈ 1.5 Δ^CGR and Δ^UQ ≈ 0.75 Δ^PGR. Accordingly, we show that in comparison to UQ, more precise quantization is enabled in ℜ^CGR to which most of samples from the assumed Laplace pdf belong, while in ℜ^PGR, where pdf is predominantly tailed, UQ provides slightly better performances since Δ^UQ < Δ^PGR. In other words, keeping in mind the shape of the Laplacian pdf, we show that it makes sense to favor the more meticulous quantization of the dominant number of samples that are concentrated around the mean belonging to ℜ^CGR. Since we assume ψ* < 0.5, from Δ^CGR/Δ^PGR = ψ*/(1 − ψ*) we can write Δ^CGR < Δ^PGR, proving that in the narrower ℜ^CGR to which most of samples from the assumed Laplacian pdf belong, smaller quantization errors indeed occur. In brief, by taking into account the shape of the assumed Laplacian pdf and the manner in which we perform parameterization of our PWUQ, the overall gain in SQNR that is achieved with PWUQ over UQ can be completely justified.

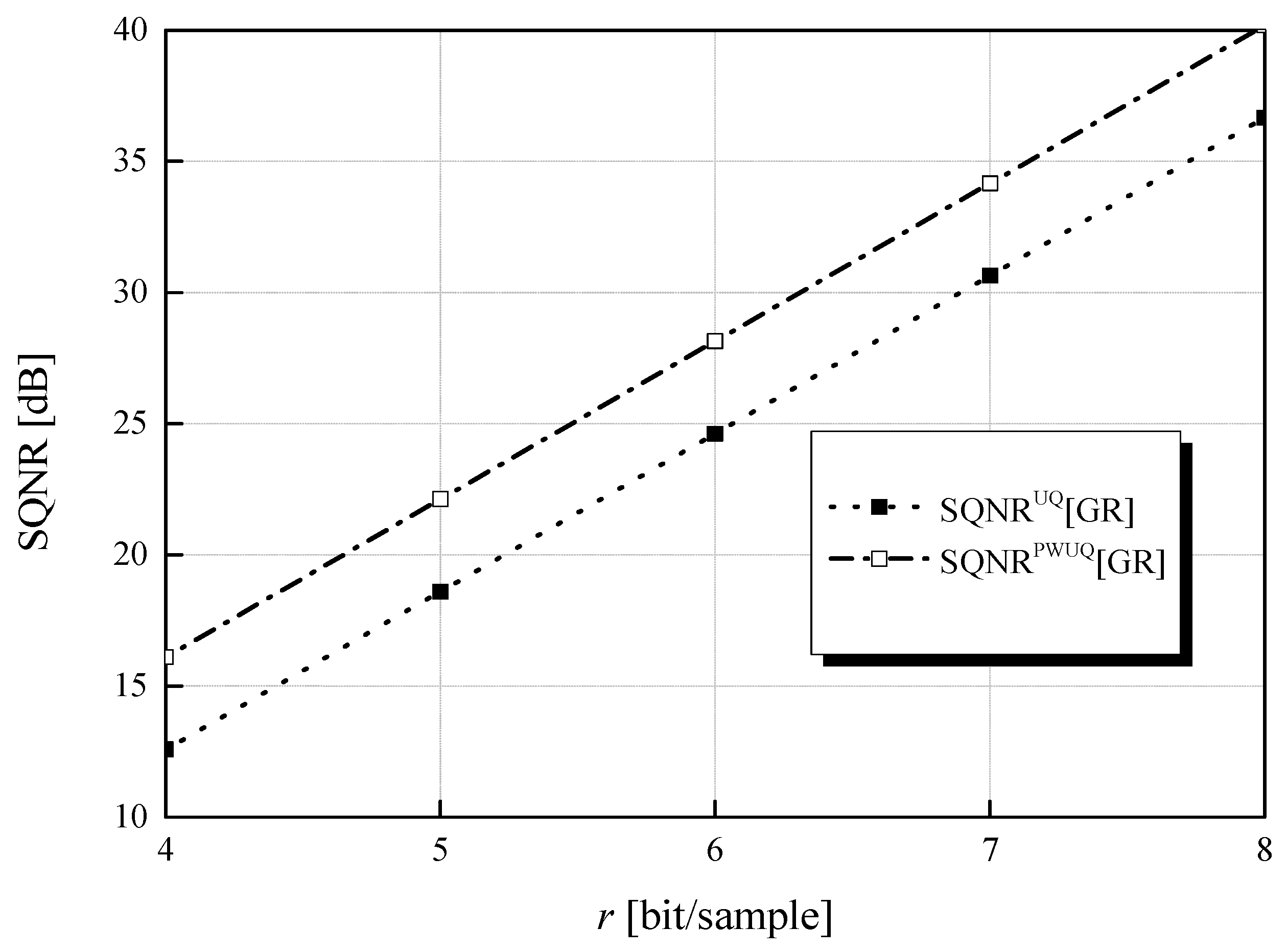
Let us observe that for x_clip, as calculated from (28) so that λ^GR = 0.9999 and for ε < 10⁻⁴, ψ^GR, amounts to 0.2674 and is not dependent on the bit-rate. Namely, we have calculated the following fixed values: x_clip = x_clip^GR = 6.5127, ψ^GR = 0.2674, x_b^GR = 1.74150, and Φ(−x_b^GR, x_b^GR) = 0.9148, whereas SQNR^PWUQ strictly depends on r. It is interesting to notice that although SQNR^PWUQ depends on r, the gain in SQNR that is achieved by PWUQ over UQ in the so-called GR case, is also constant and it amounts to 3.523 dB (see Figure 3 for GR case). To justify this constant gain in SQNR we can observe (27) from which it trivially follows our conclusion for given fixed ψ^GR, x_clip^GR and x_b^GR values. Eventually, we can notice that for r = 8 bit/sample, SQNR^PWUQ[GR], determined for x_clip = x_clip^GR = 6.5127, is higher than SQNR^PWUQ[H] [24] and SQNR^PWUQ[J] [25], which can be justified by the suitable clipping effect that was performed in the GR case in accordance with the assumption that it holds λ^GR = 0.9999 and also by the fact that in [24,25], the optimization of the support region threshold, here considered as a clipping threshold, have been performed without nullifying the overload distortion, i.e., by avoiding a clipping effect.

It is worthy to notice from Table 1 that the Laplacian pdf is expected to be in the defined granular regions with λ*[J] = 0.9982, λ*[H] = 0.9990 for r = 5 bit/sample, whereas for r = 8 bit/sample λ*[J] and λ*[H] are equal to λ^GR = 0.9999. By calculating λ* and Φ(−x_b*, x_b*) for our three different cases, we confirm that with a convenient choice of clipping values, only a few quantized samples are in the granular region near to the support or clipping threshold or out of the granular region. From Table 1, we can also conclude that the probability of belonging samples x to ℜ^CGR grows with the bit-rate since values of x_clip[J] and x_clip[H] increase with the bit-rate. Also, we can notice that Φ(−x_b^GR, x_b^GR) shows dominance compared to Φ(−x_b*[J], x_b*[J]) and Φ(−x_b*[H], x_b*[H]) for r equal to 5 bit/sample and 6 bit/sample, whereas Φ(−x_b^GR, x_b^GR) takes close values to Φ(−x_b*[J], x_b*[J]) and Φ(−x_b*[H], x_b*[H]) for r = 7 bit/sample and r = 8 bit/sample. Since the values of Φ(−x_b^GR, x_b^GR) and x_clip^GR are constant and for r = 7 bit/sample it holds x_clip^GR < x_clip[H], as a result we have SQNR^PWUQ[GR] > SQNR^PWUQ[H]. Similarly, for r = 8 bit/sample, from x_clip^GR < x_clip[J], it implies that SQNR^PWUQ[GR] > SQNR^PWUQ[J]. 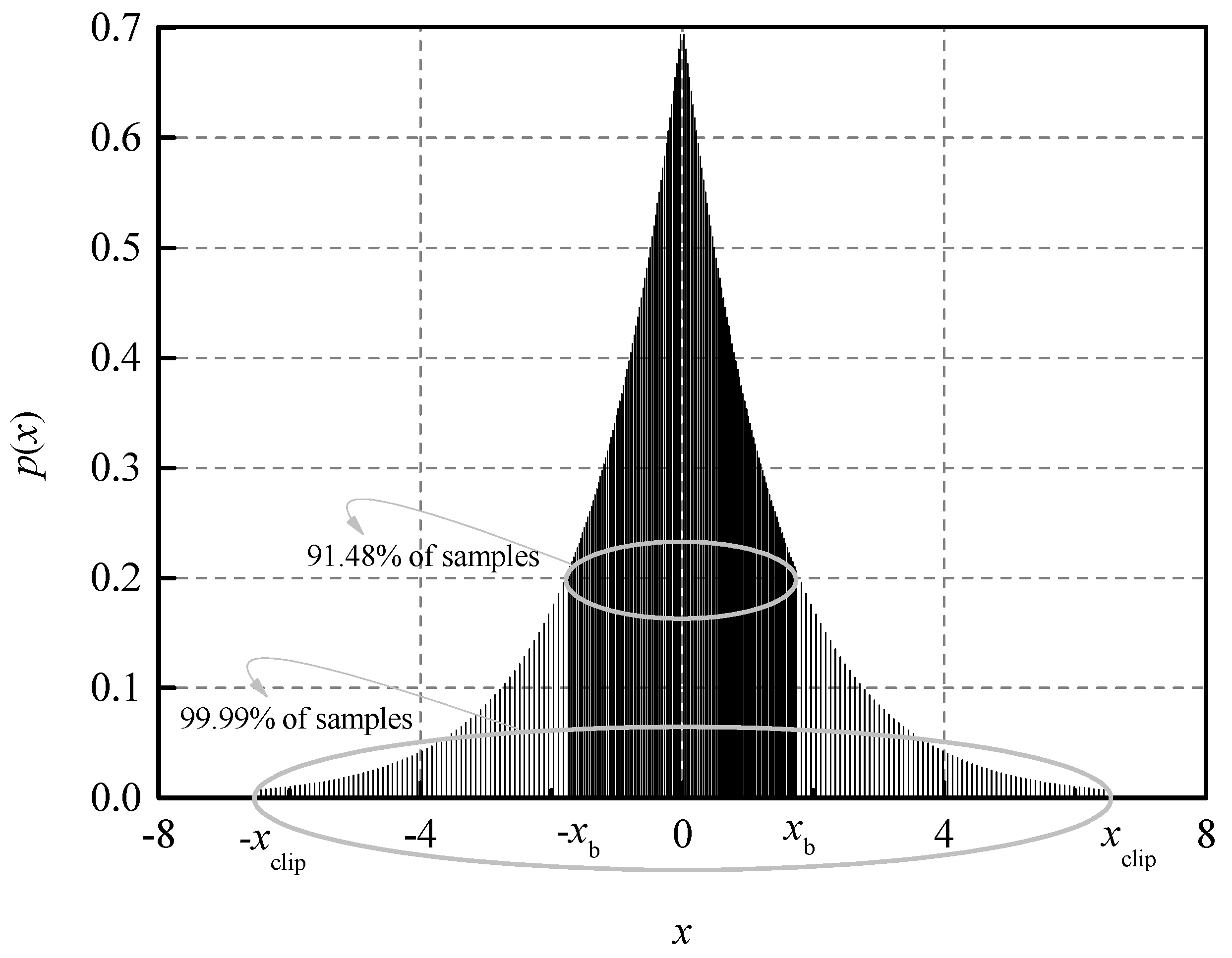For the highest observed bit-rate, r = 8 bit/sample, along with the values of the key design parameters and performances of UQ and PWUQ given in the last row of Table 1 for the GR case, we present additional descriptive information, given in Figure 4. From Figure 4, we can notice that 91.48% of the samples belonged to ℜ^CGR, whereas 99.99% of samples belonged to ℜ^CGR ∪ ℜ^PGR, meaning that we have determined the value of ψ = ψ^GR so that a huge percentage of the samples do belong to ℜ^CGR. In the case with r = 8 bit/sample we have determined the smallest values of ψ* in [J] and [H] cases. That is, we have determined the largest absolute differences from the initial value ψ(0) = 0.5. In these two cases, the number of iterations for determining ψ* ranges up to 25, where the values of ψ* matches with the results of the numerical distortion optimization per ψ, meaning that our algorithm converges fast.

To illustrate the importance of determining not only the optimized value of ψ, but also of the choice of x_clip values, Figure 5 shows the dependences of SQNR^PWUQ on ψ for r = 6 bit/sample for the three cases that were considered, where x_clip is equal to x_clip^GR, x_clip[H], x_clip[J]. Let us highlight that the values of the parameter ψ, which are the results of our iterative algorithm for the considered three cases, marked with asterisks in Figure 5, are indeed optimal and gives the corresponding maximum of SQNR of PWUQ for each of these three cases. To select one of the values for x_clip for a given bit-rate, r, we can choose the one giving the highest SQNR. Eventually, we can conclude that although the range of values for ψ is relatively narrow, its selection is very significant since the unfavorable choice of this parameter can significantly degrade the performance of our PWUQ. This observation additionally justifies the importance of our proposal, described in the paper.

4. Summary and Conclusions

To improve upon the uniform quantizer model in terms of SQNR and to utilize the benefits that are provided by the simplest UQ, in this paper we have proposed one PWUQ model. This model deliberately applies equal bit-rates uniform quantization in regions called CGR and PGR whose widths are optimized in an iterative manner so that for the assumed clipping thresholds and Laplacian pdf, the distortion is minimal. In other words, we have opted to perform parameterization of our PWUQ to achieve an increase of the quantization step size in PGR which is counterbalanced by a corresponding diminution of the step size in CGR to which most of samples from the assumed Laplacian pdf belong. We have proved that in comparison to UQ, smaller quantization errors have indeed occurred in the CGR, resulting in a significant SQNR gain achieved by PWUQ over UQ. Moreover, for the three different cases of specifying the clipping threshold values, we have shown and justified that this SQNR gain originates from the optimization of the border–clipping threshold scaling factor, performed in accordance with the proposed iterative algorithm. We have shown that although the range of values for border–clipping threshold scaling factor is relatively narrow, its choice is very significant since the unfavorable choice of this parameter, or unfavorable parameterization, can significantly degrade the performance of our PWUQ. Eventually, we found that with a convenient choice of clipping values, 99.99% of samples from the assumed Laplacian pdf do belong to the granular region. Accordingly, we can anticipate that our PWUQ model can be deployed as an outstanding replacement for the widely-used UQ, not only in traditional, but also in contemporary quantized neural network solutions where weights are typically modelled by the Laplacian distribution, as we assumed in this paper.