Abstract
Categorical functional data represented by paths of a stochastic jump process with continuous time and a finite set of states are considered. As an extension of the multiple correspondence analysis to an infinite set of variables, optimal encodings of states over time are approximated using an arbitrary finite basis of functions. This allows dimension reduction, optimal representation, and visualisation of data in lower dimensional spaces. The methodology is implemented in the cfda R package and is illustrated using a real data set in the clustering framework.
1. Introduction
Most literature devoted to functional data considers data as sample paths of a real-valued stochastic process, , , , where is some continuous set. Among a considerable number of papers on the subject, the monographs of [1,2] are still the main references presenting methodologies for visualisation, denoising, clustering, and regression when dealing with functional data represented by real-valued functions. The fda R package [3,4] implements these methodologies and tools for such functional data.
In this paper, we consider the case where the underlying stochastic model generating the data is a continuous-time stochastic process such that for all , is a categorical random variable rather than a real-valued one.
Let be a probability space, , , be a set of K states, and
be a family of categorical random variables indexed by . Thus, for some , a path of X, , is a sequence of states and time points of transitions from one state to another one:
where are the jump times in , and with , . This path is read as follows. At time , is in some state ; at time , , moves randomly from to the state ; then, at time it moves from the state to state , and so on. If is the interval of time for some , then the observation process stops when the time T is reached or some absorbing state is observed.
We call the sample paths of X given by sequences of type (2) categorical functional data generated by the process X.
Notice that there is no order assumption on the set of states. However, in some applications that order can be natural, all methodology developed in this paper being still valid. Figure 1 presents the graphical representation of one observation of a categorical functional random variable. The representation in (a) is appropriate when no natural order relationship exists on the set of states , whereas the representation in (b) supposes that there exists some order relationship (≺) on : .
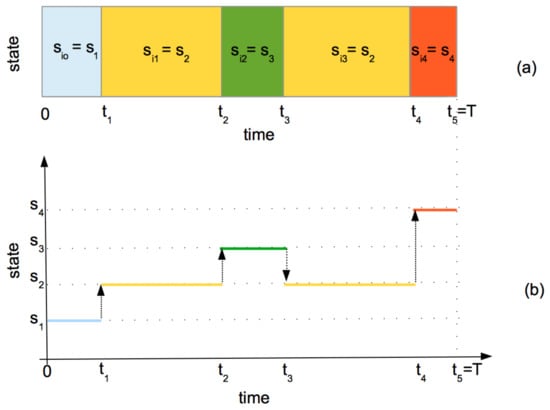
Figure 1.
Categorical functional data: graphical representation of a path with (a) not ordered states, (b) ordered states.
To the best of our knowledge, and quite surprisingly, there is no recent research devoted to categorical functional data despite its ability to model real situations in different fields of applications: health and medicine (status of a patient over time) [5], economy (status of the market) [6,7], sociology (evolution of social status) [8,9], and so on. As a starting point on this topic, we mention the works of [7,8,10,11]. These works are devoted to the extension of factorial techniques (canonical and multiple correspondence analysis) towards functional data. The authors call that methodology “harmonic analysis”. Applications of these techniques are presented in [9] for analysing career data and in [12] for studying the spectral properties of the transition probability matrix of a stationary Markovian jump process with continuous time. In [13], the authors cluster paths of semi-Markov processes using mixtures with application to sensory data. In [14], the authors present the harmonic analysis applied to the Brownian motion as an extension to an infinite (continuous) number of states.
In this article, we present categorical functional data analysis as an extension of the multiple correspondence analysis towards functional data and its implementation in the cfda R package. The theoretical foundations of this work are given in [8] and are based on the concept of optimal encoding of the states of the process X with respect to maximum variance criterion among all encodings. In Section 2, we present the theoretical background of the optimal encoding methodology defining the principal components of the process X throughout the optimal encodings. The approximation of the optimal encodings of the states into a basis of functions and optimal representation of categorical functional data in lower dimensional spaces are detailed. The implementation of the optimal encodings is presented throughout the cfda R package in Section 3, where an application on a real data set (care trajectories for patients diagnosed with severe infection) is performed in view of visualisation, descriptive statistics, and clustering.
2. Categorical Functional Data Analysis
Introduced in [8,11] under the name “analyse harmonique qualitative”, multiple correspondence analysis is extended to categorical functional data. There are several ways to complete this; we have chosen in this work to introduce it as a problem of finding the latent variables (principal components) that are the most related to the process . Therefore, the principal components will enable defining the optimal encoding of states .
Without loss of generality, let us suppose that , with . For , and , let us denote by:
- and
The general hypotheses considered in that framework are:
Hypothesis 1. (H1)
the process X is continuous in probability,
and
Hypothesis 2. (H2)
for each time (except possibly a finite discrete set of timepoints), any state has a strictly positive probability to occur:
2.1. The Principal Components
Let be the space of real random variables with finite second moment and, for some , be the linear space spanned by . Then, the conditional expectation operator associated to ,
is also the orthogonal projector on the space linearly spanned by the set of indicator random variables . Notice that is self-adjoint, idempotent, and of rank K.
For and , the coefficient
is a measure of the correlation between z and the variable . The empirical version of is known as Wilks’ Lambda statistics, well known in multivariate ANOVA [15].
Let us recall that if are p different time points in , then, the random variable z, which maximizes
defines the first principal component of the multiple correspondence analysis of the set of p categorical variables [16]. By an iterative procedure, the principal components of higher order are defined as maximizing (3) under orthogonality conditions with respect to the principal components of lower order.
In [8,11], the authors extend the multiple correspondence analysis to the process (seen as an infinite set of categorical random variables). More specifically, the principal components are defined as the random variable z that maximizes the criterion
They show that under the Hypotheses H and H, the variable z, which maximizes (4) is the variable associated with the largest eigenvalue of the following (stochastic) eigenvalue problem:
The operator is positive, hermitian, and compact. Therefore, Q has a countable set of positive eigenvalues and eigenvectors, such that and
The variables are called principal components of the process X. Notice that (constant) is an eigenvector of Q associated to the largest eigenvalue . It follows that the principal components form a set of zero-mean uncorrelated random variables.
Moreover, we have that
where K is the number of states. Thus, excluding the trivial eigenvalue , the contribution of the i-th principal component to (4) is
2.2. Optimal Encoding Functions
In order to solve (5), let denote by
Under the Hypotheses H and H, for each is -measurable, i.e., and is a -continuous stochastic process.
From (5) it follows that
Taking the conditional expectation with respect to in (5), one obtains that the stochastic process is eigenvector of the following (stochastic) eigenvalue problem posed in the space of -continuous stochastic processes:
with , for all . Recall that the spectral analysis of the kernel yields to the canonical analysis of and [17].
It can be shown ([11]) that the eigenvalue problems (5) and (8) are equivalent in that sense that they have the same set of eigenvalues and there is an one-to-one correspondence between the principal components and the process , . This correspondence is given by (6).
As in (5), the solution of (8) is unique up to a constant. To have unique eigenvectors, the usual constraint on is that of total variance equals to one,
The relation (9) implies
It follows from (6) that is -measurable for all , and one can write
where are deterministic functions on that we call optimal encoding functions. Introducing (11) into (8) one obtains the following eigenvalue equation,
where , and
The integral system (12) is a more “classic” one than (5) and (8). Under the Hypotheses H and H, it admits the sequence of eigenvalues associated with the optimal encoding eigen-functions .
Notice that the constraint conditions in (9) are expressed now in terms of optimal encoding functions,
According to (7), for , the i-th principal component is derived from the i-th optimal encoding functions as
2.3. Expansion Formulas and Dimension Reduction
As a summary of the previous section, the three equivalent eigen-problems stated in (5), (8), and (12) yield to the following elements of the analysis of X:
- the set of principal components are zero-mean and uncorrelated:
- –
- –
- the set of eigen-processes , which generates the principal components by (7),are zero-mean and of unit total variance.
- the optimal encoding functions, . They generate the eigen-processes by (11),They satisfy the normalization condition (13).
Expansion Formulas
As an analogy to the Karhunen-Loève expansion for the scalar processes [18], the following expansion formulas hold [11]:
- for the process throughout the indicators :
- for the bivariate joint probability function, : applying the Mercer theorem [19] to the integral Equation (12), one has the following expansion formula:In particular, for and , we obtain
Dimension Reduction
Using only the q first terms in the right-side part of (15), , one obtains the best approximation of order q of X (viewed as a vector process ) under the norm, among all the linear expansions of type
Thus, the q first principal components,
allow for
- –
- graphical representation of sample paths of X in (especially for , one obtains a 2-D representation of categorical functional data);
- –
- fit of clustering and regression models with X as explanatory variables;
- –
- outliers or unusual data detection: in the context of real-valued functional data, in [20], the authors propose transformations and algorithms based on the concept of depth function in order to detect outliers. Transforming a real-valued functional variable into a categorical functional one (interval discretisation) and then performing optimal encoding can be an alternative to that proposed in [20].
2.4. Approximation of Optimal Encoding Functions: A Basis Expansion Approach
The eigenvalue equation in (12) provides the optimal encoding functions. For a two-state process, [11] considers the birth-and-death process on ,
where is a random variable uniformly distributed on . The authors provide in this case explicit formulas for the eigenvalues , the optimal encoding functions , , and the principal components . In [12], the author considers the case of stationary Markovian continuous time processes with reversible distribution. In this case, the system in (12) reduces to a system of linear second-order differential equations with constant coefficients.
In general, the solution of (12) is obtained by approximation. In their seminal work [8], the authors propose to approximate the encoding functions , , into a basis of functions of dimension m, . As in the classical framework of functional data ([1]), the choice of m is a tradeoff between complexity computation and precision of the approximation. In our simulation study (Section 4), we show the influence of the choice of m on the approximation of optimal encodings.
Let , , , be a basis of functions (Fourier, B-splines, monomial, etc.), and for each consider the approximation:
where is the column vector of the expansion coefficients of into the basis .
Plugging (19) into (12) and (13), one obtains the following classical eigen-problem:
under the constraint
where is the column vector obtained by the concatenation of the vectors , and G and F are square matrices of size defined as follows:
- The matrix G is the covariance matrix of the random variables , defined as
- The matrix F is defined bywhere is the random variableThus, F is a block diagonal matrix, each block being a square matrix of size corresponding to each x in , .
Example 1.
Let us observe that if is a sequence of timepoints in , and for , one defines the basis (B-splines of order 1),
then, the random variable represents the time spent in the state x in the interval . Since , then F is a diagonal matrix with elements , , .
2.5. Estimation
Notice that the random variables and , , are computed from throughout the basis of functions .
Thus, if is a sample of n paths of X corresponding to a random sample , then the corresponding samples and , , provide two classical data sets, V and U, as:
- the V data set with n rows and columns for the V’s random variables,
- and the U dataset with n rows and Km columns for the U’s random variables, respectively:
Therefore, the matrices G and F are estimated from the sample by the matrices and , the covariance matrix estimator of the random variables V’s, and the mean estimator of the random variables U’s. For each i and j in and x and y in , one has:
and
An estimate of i-th eigen vector of (20), , is the i-th eigenvector of the eigen-Equation (26),
under the constraint
Notice that, from the construction of F and G matrices, the elements of are indexed by the couple (state and basis function) i.e., with and :
Then, for each , the i-th encoding eigen-function is estimated by
The estimates for the encoding functions enable computing the principal components for each unit in the sample , as
Bootstrapping from the V and U datasets, through (26), one obtains an estimate of the covariance matrix of denoted with . Therefore, for each , we have
where is the column vector , and is the covariance matrix of . Notice that is a submatrix of .
Then, for a confidence level , , a confidence interval for is obtained as
where is the quantile of order of the standard normal distribution.
Computational details
- The approximation of optimal encoding functions in a basis of functions is based on the computation of random variables and defined in (22) and (25), respectively. The computation of integrals involved in the definition of these random variables uses the inprod function of the fda R package which, at its turn, calls the function eval.fd. For n and K fixed, this step is the most computational in terms of time resources, and it depends on the number of basis functions, m, considered for the approximation (19). As the computation is performed for every in , parallel computation is performed.
- The F matrix (24) can be singular in some specific situations, namely when there exists an interval and some state x such that . In this case, the hypothesis is not satisfied. For , the operator is degenerated; however, the eigenvalue Equation (5) is still valid. From (12), the optimal encoding function is not defined for . From a computational point of view, if is some element of the basis functions with support in I, then the random variables and are zero-constant and therefore, the row and column corresponding to in the F and G matrices are zero vectors. Thus, the element of the expansion coefficients vector is not defined. Dropping the rows and columns from F and G corresponding to enables solving the eigen-problem in (26). Notice that the constraints (27) are fulfilled.
3. The cfda Package through Examples
The cfda R package (available online: https://cran.r-project.org/package=cfda, accessed on 28 November 2021) provides functions to analyze categorical functional data enabling computation of basic statistics (such as transition tables or visualisation) and the optimal encoding functions. It uses the ggplot2 [21] package to display graphics and the parallel [4] and pbapply [22] packages for code parallelization.
Many other R packages analyzing categorical data indexed by time exist, but they do not take into account the functional feature of data (continuous-time) or do not provide optimal representation of data for statistical learning purposes. The TraMineR [23] R package provides functions to perform descriptive analysis, and distance functions between sequences are defined to perform clustering analysis. The WeightedCluster [24] package relies on TraMineR and implements an associated clustering method. The msm [5] package estimates from categorical functional data and covariates a continuous-time (hidden) Markov multi-state model. The R packages ClickClust [25] and clickstream [26] deal with categorical functional data as discrete Markov chains and propose clustering methods based on mixture models.
3.1. Data
3.1.1. An Example of Real Dataset: Paths of Patients with Severe Infection
The cfda package is illustrated with the care dataset [27]. It contains 2929 care trajectories for patients diagnosed with a severe infection. Each month from the diagnosis of the infection, the followup of each patient is recorded using one of the following four states:
- –
- “D”: the patient has not a medical followup,
- –
- “C”: the patient has a medical followup but no treatment,
- –
- “T”: the patient has a medical followup with a treatment, but the infection is not suppressed,
- –
- “S”: the patient has a medical followup with a treatment, and the infection is suppressed.
The dataset is loaded running:
R> data(care)
R> head(care, 10)
id time state 3 0 D 3 5 D 9 0 D 9 1 D 13 0 D 13 7 D 15 0 D 15 4 T 15 7 C 15 8 D
The dataset is in a specific format required by every function in this package. Data must be provided as a data.frame with three columns named id, time, and state. The id column contains the identifiers of the statistical units (e.g., patient IDs), the time column contains the different timepoints of state changes, and the state column contains the state that occurs at the corresponding time. For example, in the dataset above, four patients with IDs 3, 9, 13, and 15 are shown. The patient with ID 15 has an initial state (D) at time , he stays in this state until months, at which time he moves in a new state (T), and so on.
Note that within each trajectory, the time values must be ordered. Concerning id and state, the used format is quite versatile: character, factor, or integer can be used.
3.1.2. Visualize a Dataset
The summary_cfd function gives an overview of the dataset by printing information such as the number of paths, the time range, or the number of states, etc. All this information is returned in a list.
R> summary_cfd(care)
Number of rows: 10017 Number of individuals: 2929 Time Range: 0--50 Same time start value for all ids: TRUE Same time end value for all ids: FALSE Number of states: 4 States: D, T, C, S Number of individuals visiting each state: D C T S 2905 1154 1014 1063
Notice that all paths have the same start time value but not the same end time value. This does not meet the constraints for performing a functional data analysis. A subsample of paths observed until some specified time must be considered in order to perform optimal encoding computation.
A sample of paths from the care dataset is plotted using the plotData function (see Figure 2). Each line corresponds to a patient path in the dataset, the successive changes of states are represented by different colors.
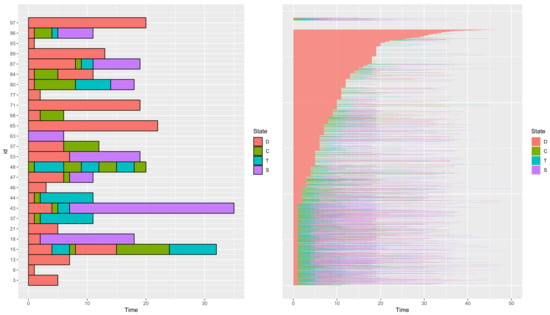
Figure 2.
A sample (left) and all paths (right) from the care dataset plotted using the plotData function.
plotData(data, col, addId, addBorder, sort)
The plotData function takes in argument a formatted data.frame (data) and additional aesthetic parameters:
- group
- a vector of the length of the number of paths of data containing a variable describing a group structure (if any) of data. Paths from different groups are displayed on different subplots. Paths whose group is coded asNA are ignored.
- addId
- a boolean to add the id of paths on the y-axis.
- addBorder
- a boolean to add the black border around each state.
- sort
- a boolean to sort paths according to the duration of their first state.
- col
- allows users to customize state colors by providing a vector of the same length as the number of state. col is a character (named) vector containing defined color names from R (e.g., c(“red”, “blue”, “darkgreen”)) or RGB colors (e.g., c(“#E41A1C”, “#377EB8”, “#4DAF4A”)).
- nCol
- only when group is used, the number of columns used to display different groups.
R> plotData(care[care$id <= 100, ])
R> plotData(care, addBorder = FALSE, addId = FALSE, sort = TRUE)
3.1.3. Paths of Same Length T
To compute the encoding functions, all paths must have the same start and end time. This is not the case in the care dataset. So, we need to select patients followed on a time interval of the same length, say .
First, we compute the length (duration of followup) of each patient path using the compute_duration function. It returns a named vector, with the id as names, containing the duration. The results can be plotted using the hist function with the output of compute_duration as argument; it returns a ggplot object that can be modified.
R> duration <- compute_duration(care)
R> head(duration)
3 9 13 15 18 21 5 1 7 32 18 5
R> hist(duration)
The resulting plot is displayed in Figure 3. Most paths last less than 40 months with a mode value around 20 months. We decide to keep in the analysis a followup on the common interval .
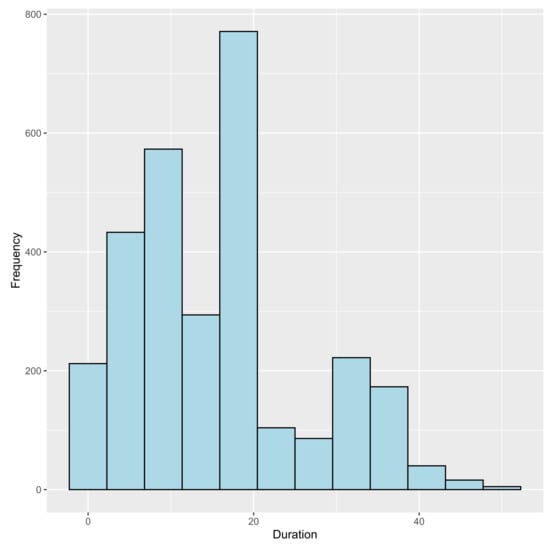
Figure 3.
Distribution of the duration of trajectories.
To restrict paths to the interval , we use the cut_data function that has two parameters: data and Tmax, the maximal time value. After applying this function, the result contains all paths observed on .
R> idToKeep <- names(duration[duration >= 18])
R> care2 <- cut_data(care[care$id %in% idToKeep, ], 18)
R> head(care2)
id time state 1 15 0 D 2 15 4 T 3 15 7 C 4 15 8 D 5 15 15 C 6 15 18 C 7 18 0 D 8 18 2 S 9 18 18 S 10 43 0 D
3.2. Basic Statistics for Categorical Functional Data
3.2.1. Time Spent in Each State
An interesting statistic is the time spent in each state per patient that can be computed with compute_time_spent function. It returns a matrix with n rows (number of patients) and K columns (number of states) with the computed time. A plot function is provided to plot the distribution for each state. Figure 4 displays the graphic for the care dataset. We note that patients tend to stay longer without medical followup (D) than in the other states.
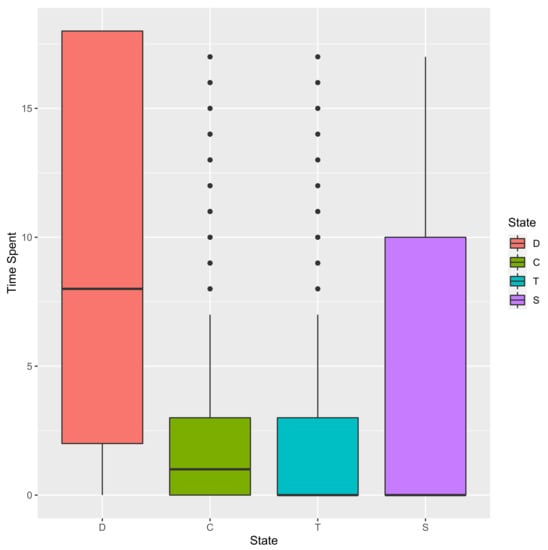
Figure 4.
Distribution of time spent per state.
R> timeSpent <- compute_time_spent(care2)
R> head(timeSpent)
D C T S 15 11 4 3 0 18 2 0 0 16 43 4 1 2 11 48 0 7 11 0 53 7 0 0 11 65 18 0 0 0
R> boxplot(timeSpent)
3.2.2. Number of Jumps
The compute_number_jumps function counts the number of transitions within paths. It has two arguments: data, the dataset in the right format and countDuplicated, a binary value indicating if jumps in the same state must be ignored (FALSE) or not, the default is FALSE. A hist function is provided to plot the distribution of the number of jumps. For the care dataset, the number of jumps varies between 0 and 8 (cf. Figure 5), with most patients with less than 6 jumps.
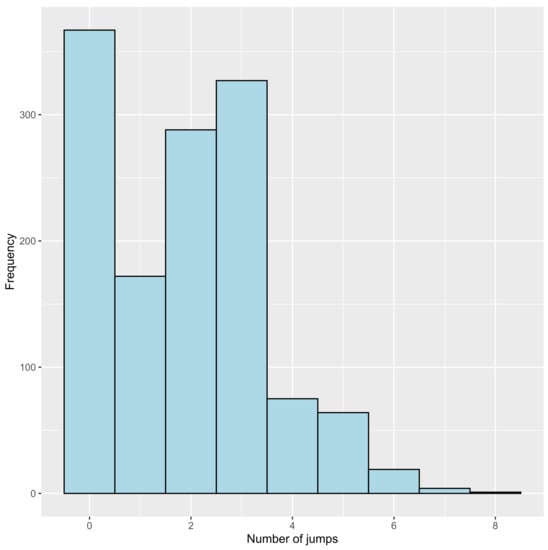
Figure 5.
Distribution of number of jumps per individual.
R> nJump <- compute_number_jumps(care2, countDuplicated = FALSE)
R> head(nJump)
15 18 43 48 53 65 4 1 3 6 1 0
R> hist(nJump)
The transitions are visible using the statetable function that counts the number of transitions between each pair of states. Transitions between identical states can be removed from the output table using removeDiagonal = TRUE.
R> statetable(care2, removeDiagonal = TRUE)
to from D C T S D 0 697 253 146 C 271 0 346 97 T 16 74 0 461 S 16 91 31 0
Notice that the state S (infection suppressed) is not an absorbing state, indicating some patients have relapsed.
3.2.3. States Distribution over Time
The last interesting statistic is the probability to be in some state at a given time. It is computed using the estimate_pt function. It has two arguments: data, the dataset in the right format and NAafterTmax. If NAafterTmax = FALSE, it considers that the last entry of an individual corresponds to its last change of state, i.e., the individual stays in the last recorded state for any time greater than the last time entry; if TRUE, it considers that for any time greater than the last time entry, the records are missing; the default is FALSE. This is an important parameter when paths have different ending times. This function returns a list of two elements: t, a vector containing the time values, and pt, a matrix (with the states in rows and the time values in columns) containing the computed probabilities. A plot function is provided to display the results; the first parameter is the output of estimate_pt function, the second is ribbon. If ribbon = FALSE, the probability for a state is displayed with a line, if TRUE, with a ribbon (cf. Figure 6). In this figure, we note that the probability of not having a followup (D) decreases over time, whereas the probability to be cured (S) has an opposite trend.
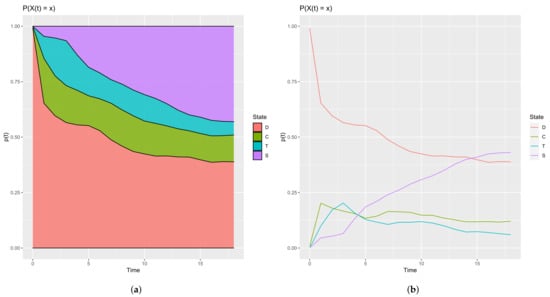
Figure 6.
Probabilities to be in each state with regards to the time. (a) ribbon = TRUE; (b) ribbon = FALSE.
R> proba <- estimate_pt(care2)
R> proba
$pt 0 1 2 3 4 5 ... D 0.991 0.653 0.596 0.566 0.555 0.552 ... C 0.008 0.202 0.180 0.166 0.156 0.134 ... T 0.000 0.099 0.171 0.203 0.159 0.128 ... S 0.001 0.046 0.053 0.065 0.131 0.185 ... $t [1] 0 1 2 3 4 5 6 ...
R> plot(proba, ribbon = TRUE)
3.2.4. Continuous-Time Markov Chain
Let us assume data come from a continuous-time Markov process with a set of states , . Then for and , the probability that the process will be in state j at time , given it is in state i at time s, and the whole history until s is given by:
A continuous-time Markov chain is completely described by its transition matrix and , the parameters of the exponentially distributed sojourn time in each state. See for more details [5].
The estimate_Markov function estimates the transition matrix () and the parameter (lambda) associated with the mean sojourn time spent in each state.
R> mark <- estimate_Markov(care2)
R> mark
$P to from D C T S D 0.00000000 0.63594891 0.23083942 0.13321168 C 0.37955182 0.00000000 0.48459384 0.13585434 T 0.02903811 0.13430127 0.00000000 0.83666062 S 0.11594203 0.65942029 0.22463768~0.00000000 $lambda D C T S 0.1328033 0.2538578 0.2438443 0.1149503 attr(,“class”) [1] “Markov”
The estimated process can be plotted as a diagram with the plot function displayed in Figure 7. Each node represents a state with its mean sojourn time. An arrow between two nodes defines a possible transition with its probability.
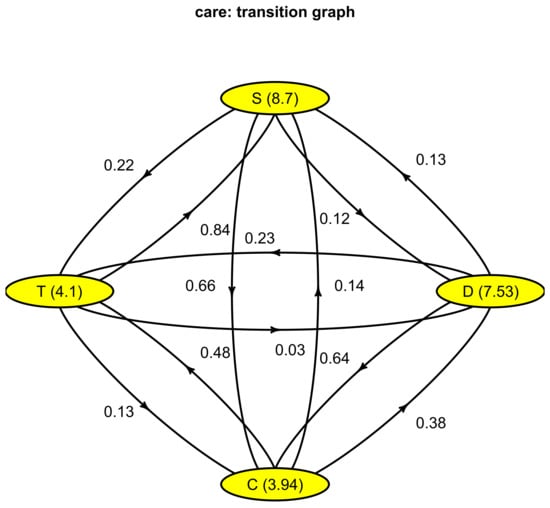
Figure 7.
Transition graph displayed using plot.Markov.
R> plot(mark, main = “care: transition graph”)
3.3. Optimal Encoding
The main contribution of cfda is the computation of an optimal encoding for categorical functional data performed by the compute_optimal_encoding function. The two main parameters are data, the dataset in the cfda format, and basisobj, a basisfd object created using the different create.*.basis functions from the fda package. It also performs bootstrapping for computing confidence intervals of the computed encoding functions; associated parameters are computeCI, a logical indicating whether bootstrap must be performed, nBootstrap, the number of bootstrap samples, and propBootstrap, the proportion of individuals used for each bootstrap sample. Other parameters are nCores the number of cores to use, verbose, if TRUE, some information is printed during the process. The compute_optimal_encoding function uses integrate [4] to compute integrals, parameters for this function can be passed through ... in particular subdivisions, the number of subdivisions to estimate the integral.
R> set.seed(42)
R> basis <- create.bspline.basis(c(0, 18), nbasis = 10, norder = 4)
R> fmca <- compute_optimal_encoding(care2, basis, nCores = 7)
######### Compute encoding ######### Number of individuals: 1317 Number of states: 4 Basis type: bspline Number of basis functions: 10 Number of cores: 7 ---- Compute V matrix: |==================================================| 100% elapsed=21 s DONE in 21.78 s ---- Compute U matrix: |==================================================| 100% elapsed=122 s DONE in 122.42 s ---- Compute encoding: DONE in 0.13 s ---- Compute Bootstrap Encoding: ************************************************** DONE in 1.3 s Run Time: 149.84 s
The main part of the computational time comes from the computation of V and U matrices using parallel computation. Once these matrices are computed, a bootstrap estimation is performed for a low computational cost. The output object of compute_optimal_encoding is a list containing:
- eigenvalues
- eigenvalues of the problem (26)
- alpha
- coefficients of the different encoding for each eigenvector (a list of matrices) (26)
- pc
- principal components for each eigenvector
- F
- F matrix (see Equation (24))
- V
- V matrix (see Equation (22))
- G
- covariance matrix of V (see Equation (23))
- basisobj
- basisobj parameter
- bootstrap
- encoding for each bootstrap sample
- varAlpha
- a list containing, covariance matrix of
This object has its own summary and print functions.
3.3.1. Plot Functions
Three plot functions are associated with the compute_optimal_encoding function; the first argument of these functions is the output of compute_optimal_encoding.
The first one, the plot function plots the encodings associated with a given eigenvector (harm parameter, by default, the encodings associated with the first eigenvector are plotted). If compute_optimal_encoding was run with parameter computeCI = TRUE, then the confidence interval can be added on the plot using the parameter addCI = TRUE. A subset of states can be plotted by providing a vector with the state names to the states parameter.
The plotEigenvalues function plots the computed eigenvalues. It has two extra boolean parameters: cumulative, if TRUE, the cumulative sum of the eigenvalues is plotted and normalize, if TRUE, eigenvalues are normalized such that their sum is equal to 1.
The third one is the plotComponent function that plots paths coordinates using the principal components (comp parameter, a vector of length 2 containing the components number). The other arguments are addNames that adds the path’s names on the plot and some parameters to adjust the position and size of these names (nudge_x, nudge_y and size).
The plots for the care dataset are shown in Figure 8 and Figure 9 and are produced by the following code:
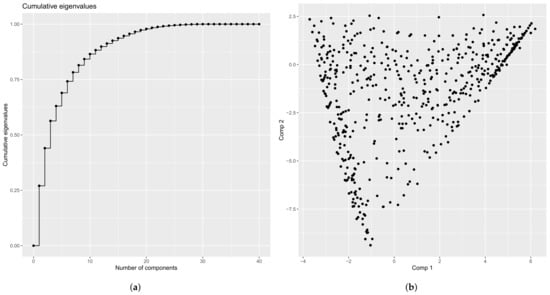
Figure 8.
Plots generated by different graphical functions on the output of the compute_optimal_encoding function. (a) plotEigenvalues; (b) plotComponent.
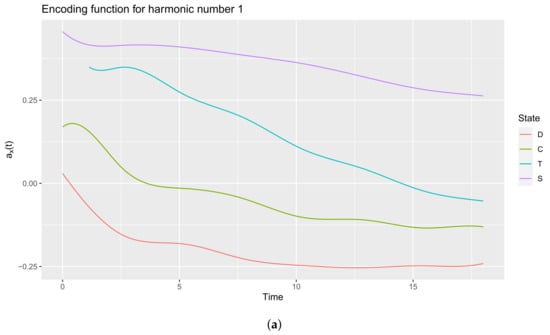
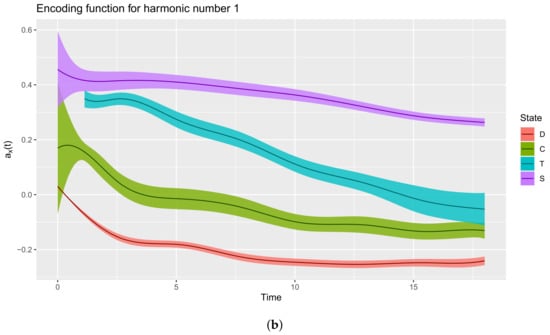
Figure 9.
Plots generated by the plot function on the output of the compute_optimal_encoding function. (a) plot(fmca); (b) plot(fmca, addCI = TRUE).
R> plotEigenvalues(fmca, cumulative = TRUE, normalize = TRUE)
R> plotComponent(fmca, comp = c(1, 2), addNames = FALSE)
R> plot(fmca)
R> plot(fmca, addCI = TRUE)
3.3.2. Extract the Encoding Functions
The computed encoding functions can be extracted using the get_encoding function as an object of class fd (functional object from fda) using fdObject = TRUE or as a matrix using fdObject = FALSE. In the latter case, an extra parameter nx specifies the number of time points to extract.
R> encodingFd <- get_encoding(fmca, fdObject = TRUE)
R> str(encodingFd)
List of 3 $ coefs : num [1:10, 1:4] 0.0299 -0.0543 -0.1965 -0.1645 -0.2371 ... ..- attr(*, “dimnames”)=List of 2 .. ..$ : NULL .. ..$ : chr [1:4] “D” “C” “T” “S” $ basis :List of 10 ..$ call : language basisfd(type = type, | __truncated__ ..$ type : chr “bspline” ..$ rangeval : num [1:2] 0 18 ..$ nbasis : num 10 ..$ params : num [1:6] 2.57 5.14 7.71 10.29 12.86 ... ..$ dropind : NULL ..$ quadvals : NULL ..$ values : list() ..$ basisvalues: list() ..$ names: chr [1:10] “bspl4.1” “bspl4.2” “bspl4.3” “bspl4.4” ... ..- attr(*, “class”)= chr “basisfd” $ fdnames:List of 3 ..$ args: chr “time” ..$ reps: chr [1:4] “reps 1” “reps 2” “reps 3” “reps 4” ..$ funs: chr “values” - attr(*, “class”)= chr “fd”
R> encodingMat <- get_encoding(fmca, fdObject = FALSE, nx = 19)
R> encodingMat
$x [1] 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17~18 $y D C T S [1,] 0.02986969 0.169492601 0.50380590 0.4559043 [2,] -0.06073672 0.163315622 0.35643506 0.4180230 [3,] -0.12970105 0.088328506 0.34225746 0.4126089 [4,] -0.16758420 0.020411074 0.34651825 0.4159033 [5,] -0.17812958 -0.007566828 0.31652186 0.4149973 [6,] -0.18096760 -0.014569119 0.27436391 0.4100582 [7,] -0.19348217 -0.020533054 0.24249695 0.4020949 [8,] -0.21335627 -0.032358522 0.21809774 0.3925044 [9,] -0.23081796 -0.051930578 0.18880144 0.3828197 [10,] -0.24069960 -0.077085840 0.15014660 0.3734934 [11,] -0.24597159 -0.098545473 0.11162958 0.3630747 [12,] -0.25009513 -0.107580629 0.08297660 0.3500902 [13,] -0.25321503 -0.107980977 0.06221397 0.3347482 [14,] -0.25359641 -0.110631333 0.04073503 0.3182122 [15,] -0.25084388 -0.121299335 0.01379572 0.3018281 [16,] -0.24813344 -0.132111070 -0.01301242 0.2873926 [17,] -0.24881502 -0.133707940 -0.03278505 0.2766485 [18,] -0.24943891 -0.128922501 -0.04469775 0.2692082 [19,] -0.24091335 -0.130703127 -0.05297104 0.2629170
3.3.3. Interpreting the Encoding Functions
First, look at the plot of the encoding functions associated with the first principal component (harmonic 1, cf. Figure 9).
R> plot(fmca, harm = 1)
At each time, the curve corresponding to state “D” is the lowest one, this indicates that paths with a “large” negative value for principal component number 1 tend to spend more time in this state, whereas those with large positive values will visit less this state. Similarly, individuals with a large positive value tend to spend more time in the state “S”. To check these statements, individuals with extreme values on the first component are plotted using the plotData function with the group parameter. A group variable is created with two different values: “min” for the individuals with the 5% lowest value and “max” for the individuals with 5% highest value.
R> minpc1 <- names(which(fmca$pc[,1] <= quantile(fmca$pc[,1], 0.05)))
R> maxpc1 <- names(which(fmca$pc[,1] >= quantile(fmca$pc[,1], 0.95)))
R> ids <- unique(care2$id)
R> group <- factor(rep(NA, length(ids)), levels = c(“min”, “max”))
R> group[ids %in% minpc1] = “min”
R> group[ids %in% maxpc1] = "max"
R> plotData(care2, group = group, addId = FALSE, addBorder = FALSE,
+ sort = TRUE) +
+ ggplot2::labs(title = “Extreme individuals on component 1”)
The result is visible in Figure 10 and confirms our interpretation. Clearly, patients in the “min” group spend 18 months in the “D” state (without medical followup), whereas patients in the “max” group spend most of their time in the state “S” (infection suppressed).
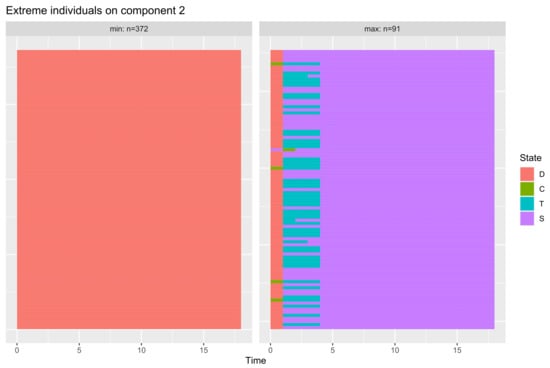
Figure 10.
Individuals with extreme negative value (min) and extreme positive value (max) on the component 1.
3.3.4. Application to Clustering
The proposed method produces numerical encoding for categorical functional data. This encoding can be used for statistical learning purposes such as regression or clustering. In the following, we perform a hierarchical clustering to find hidden patterns (structure) in the care dataset.
The clustering is performed with the first principal components explaining at least 90% of the variance. The associated tree is displayed in Figure 11.
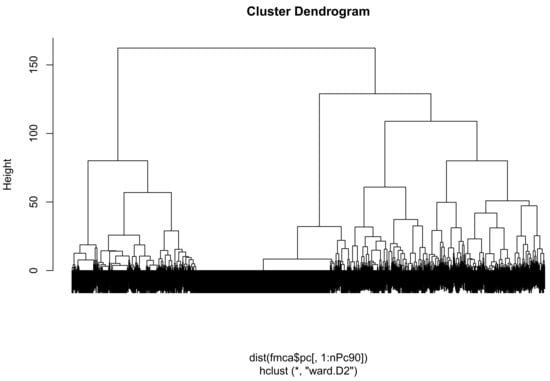
Figure 11.
Hierarchical tree obtained using the principal components.
R> nPc90 <- which(cumsum(prop.table(fmca$eigenvalues)) > 0.9)[1]
R> hc <- hclust(dist(fmca$pc[, 1:nPc90]), method = “ward.D2”)
R> plot(hc, labels = FALSE)
We decided to keep four clusters regarding the heights of the tree. The resulting clusters can be displayed using the plotData function with the group argument.
R> class <- cutree(hc, k = 4)
R> plotData(care2, group = class, addId = FALSE, addBorder = FALSE, +
+ sort = TRUE)
The different clusters are associated with the time spent in the different states after leaving the state “D” (cf. Figure 12). For example, the cluster number 1 corresponds to patients that have spent most of their time (after “D”) in the “C” state.
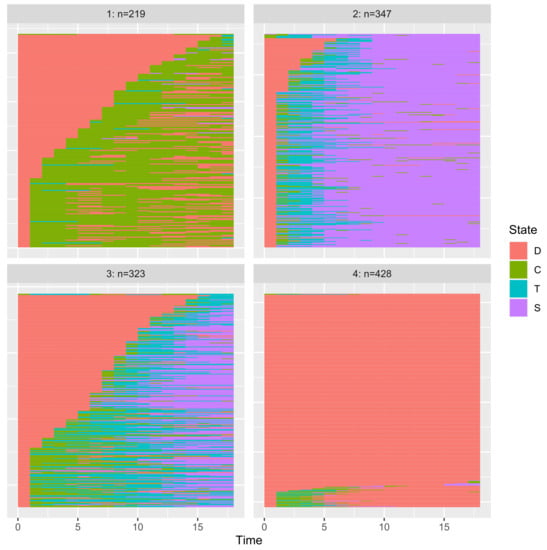
Figure 12.
Content of the different clusters.
A ready-to-run R code implementing optimal encoding for the care dataset towards clustering is presented in Appendix A.
4. Simulation Study
4.1. Birth-and-Death Process
Data are simulated under the simple model of the birth-and-death process presented in [11]. The process is defined on the interval time by
where is a random variable uniformly distributed on .
In this case, , , and
For , we have
and for ,
From (12) and (14), the authors in [11] provide explicit formulas for the eigenvalues , the optimal encoding functions , , and the principal components , as follows:
- the eigenvalues are given by:
- if is the Legendre polynomials of order n, then the principal components corresponding to , are given, up to a constant, by:In particular, for ,is uniformly distributed on , andObserve that and are linearly uncorrelated but related byshowing some regularity of the 2-D representation of data throughout the plot .
- for , the optimal encoding functions are given by:and
4.2. Results
We simulate data from the above process with different numbers of trajectories (individuals), , and a B-spline basis function of order 4 with different numbers of basis functions (equidistant knots). Simulation results are compared to the theoretical results presented in Section 4.1 to ensure the good behaviour of the implemented method.
4.2.1. Eigenvalues
The first five eigenvalues for the different settings are compared to the eigenvalues from (32) in Table 1. The estimations are presented together with the associated standard errors in order to measure the impact of the choice of the sample size (n) and the dimension of the basis (m).

Table 1.
True and estimated eigenvalues for the birth-and-death process. The estimated values are the mean over 100 samples. In brackets, the standard error is displayed.
4.2.2. Encoding Functions
Figure 13 shows the mean over 100 samples of the first and second encoding functions for the state 0 for . The true encoding functions (34) and (35) are displayed in solid black line. As for the eigenvalues, the best estimates are achieved with and . The same conclusion holds for and , but the number of basis functions does not seem to influence the accuracy.
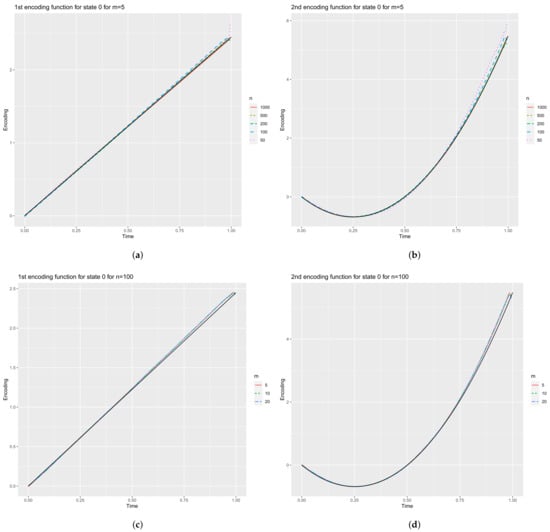
Figure 13.
True (solid black) and estimated encoding functions for state 0 of the birth-and-death process. The estimated encoding functions are the mean of 100 samples. (a) First encoding function for state 0 (); (b) Second encoding function for state 0 (); (c) First encoding function for state 0 (); (d) Second encoding function for state 0 ().
4.2.3. Principal Components
In Figure 14, we check the relation between the first and second principal component (33). The theoretical equation is displayed in black, whereas the computed principal components for a sample with and are in red. We note the closeness of the computed components with the theoretical equation.
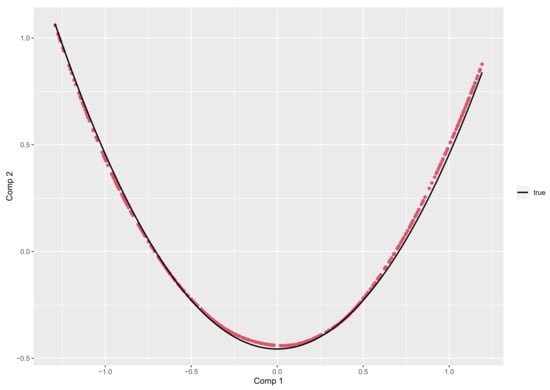
Figure 14.
In red, first and second principal components for every observation of the birth-and-death process for and . In solid black, the theoretical relation between these two components.
In Figure 15, the cumulative distribution functions (cdf) for the two first principal components are displayed as well as their empiric equivalent for and . As described above, follows a uniform distribution between and , the empirical cdf (in red) is close to the theoretical one. The same representation is made for .
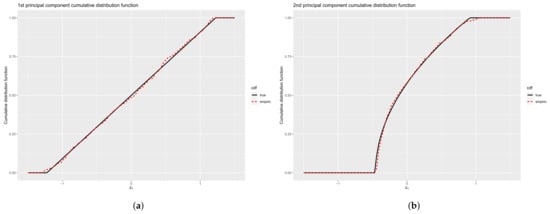
Figure 15.
Empirical (resp. theoretical) cumulative distribution function for the first () and second () principal components of the birth-and-death process for and . (a) Cumulative distribution function for ; (b) Cumulative distribution function for .
The results in this paper were obtained using R 4.0.3 with the cfda 0.9.9 package. R itself and all packages used are available from the Comprehensive R Archive Network (CRAN) [4].
5. Summary and Discussion
Categorical functional data are represented by paths of a continuous-time stochastic process with values in a finite set of states. This is less popular than the real-valued functional data, which are yet another kind of infinite dimensional object. The analysis of categorical functional data is presented in this paper as an extension of the multiple correspondence analysis for the finite dimensional setting. Principal components, optimal encoding functions, and optimal representations are presented. A simulation study and a real data application illustrate the methodology implemented in the cfda R package.
In future work, we propose to address the problem of missing and noisy data. More specifically, timepoints are observed with noise or/and are missing.
Author Contributions
Conceptualization, C.P.; methodology, C.P., Q.G. and V.V.; software, Q.G. and C.P.; validation, C.P., Q.G. and V.V.; formal analysis, C.P.; investigation, C.P., Q.G. and V.V.; resources, Q.G., C.P. and V.V.; writing–original draft preparation, C.P., Q.G. and V.V.; writing–review and editing, C.P., Q.G. and V.V.; supervision, C.P.; project administration, C.P. and Q.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
R Code: Care Application
R> library(cfda)
R> # load the dataset
R> data(care)
R> summary_cfd(care)
R> # visualize the dataset
R> plotData(care[care$id <= 100, ])
R> plotData(care, addId = FALSE, addBorder = FALSE, sort = TRUE)
R> duration <- compute_duration(care)
R> head(duration)
R> hist(duration)
R> ####### Select individuals for encoding
R> ## We keep individuals with at least 18 months of follow-up and works on the first 18 months
R> length(duration[duration >= 18])
R> idToKeep <- as.numeric(names(duration[duration >= 18]))
R> care2 <- cut_data(care[care$id %in% idToKeep, ], 18)
R> head(care2, 10)
R> summary_cfd(care2)
R> plotData(care2, addId = FALSE, addBorder = FALSE, sort = TRUE)
R> ####### Basic statistics
R> timeSpent <- compute_time_spent(care2)
R> boxplot(timeSpent)
R> nJump <- compute_number_jumps(care2, countDuplicated = FALSE)
R> head(nJump)
R> hist(nJump)
R> statetable(care2, removeDiagonal = TRUE)
R> # individuals have not the same length and the last state is not necessarily an absorbing state,
so we use NAafterTmax = TRUE
R> proba <- estimate_pt(care2, NAafterTmax = TRUE)
R> plot(proba, ribbon = TRUE)
R> plot(proba)
R> mark <- estimate_Markov(care2)
R> plot(mark, main = “care: transition graph”)
R> ####### Encoding
R> set.seed(42)
R> basis <- create.bspline.basis(c(0, 18), nbasis = 10, norder = 4)
R> fmca <- compute_optimal_encoding(care2, basis, nCores = 7)
R> plotEigenvalues(fmca, cumulative = TRUE, normalize = TRUE)
R> plot(fmca)
R> plot(fmca, addCI = TRUE)
R> plotComponent(fmca, addNames = FALSE)
R> encodingFd <- get_encoding(fmca, fdObject = TRUE)
R> encodingMat <- get_encoding(fmca, fdObject = FALSE, nx = 19)
R> ## interpreting the results
R> plot(fmca, harm = 1)
R> minpc1 <- names(which(fmca$pc[,1] <= quantile(fmca$pc[,1], 0.05)))
R> maxpc1 <- names(which(fmca$pc[,1] >= quantile(fmca$pc[,1], 0.95)))
R> group <- rep(NA, length(unique(care2$id)))
R> group[unique(care2$id) %in% minpc1] = "min"
R> group[unique(care2$id) %in% maxpc1] = "max"
R> plotData(care2, group = group, addId = FALSE, addBorder = FALSE, sort = TRUE) +
R> ggplot2::labs(title = “Extreme individuals on component 1”)
R> plot(fmca, harm = 2)
R> minpc2 <- names(which(fmca$pc[,2] <= quantile(fmca$pc[,2], 0.05)))
R> maxpc2 <- names(which(fmca$pc[,2] >= quantile(fmca$pc[,2], 0.95)))
R> group <- rep(NA, length(unique(care2$id)))
R> group[unique(care2$id) %in% minpc1] = "min"
R> group[unique(care2$id) %in% maxpc1] = "max"
R> plotData(care2, group = group, addId = FALSE, addBorder = FALSE, sort = FALSE) +
R> ggplot2::labs(title = “Extreme individuals on component 2”)
R> ####### Clustering
R> nPc90 <- which(cumsum(prop.table(fmca$eigenvalues)) > 0.9)[1]
R> hc <- hclust(dist(fmca$pc[, 1:nPc90]), method = “ward.D2”)
R> plot(hc, labels = FALSE)
R> barplot(rev(hc$height)[1:20])
R> cluster <- cutree(hc, k = 4)
R> plotData(care2, group = cluster, addId = FALSE, addBorder = FALSE, sort = TRUE)
References
- Ramsay, J.; Silverman, B. Functional Data Analysis; Wiley Series in Probability and Statistics; Springer: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Ferraty, F.; Vieu, P. Nonparameric Functional Data Analysis. Theory and Practice; Springer: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Wickham, H.; Graves, S.; Hooker, G. fda: Functional Data Analysis, R Package Version 5.5.1; 2021. Available online: https://cran.r-project.org/package=fda (accessed on 28 November 2021).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Jackson, C.H. Multi-State Models for Panel Data: The msm Package for R. J. Stat. Softw. 2011, 38, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Idrovo-Aguirre, B.J.; Lozano, F.J.; Contreras-Reyes, J.E. Prosperity or Real Estate Bubble? Exuberance Probability Index of Real Housing Prices in Chile. Int. J. Financ. Stud. 2021, 9, 51. [Google Scholar] [CrossRef]
- Deville, J.C.; Saporta, G. Correspondence Analysis with an Extension towards Nominal Time Series. J. Econom. 1983, 22, 169–189. [Google Scholar] [CrossRef] [Green Version]
- Deville, J.C. Analyse de Données Chronologiques Qualitatives: Comment Analyser des Calendriers? Ann. De L’INSEE 1982, 45, 45–104. [Google Scholar] [CrossRef]
- Heijden, P.; Teunissen, J.; van Orlé, C. Multiple Correspondence Analysis as a Tool for Quantification or Classification of Career Data. J. Educ. Behav. Stat. 1997, 22, 447–477. [Google Scholar] [CrossRef]
- Boumaza, R. Contribution à l’Étude Descriptive d’une Fonction Aléatoire Qualitative. Ph.D. Thesis, Université Paul Sabatier, Toulouse, France, 1980. [Google Scholar]
- Saporta, G. Méthodes Exploratoires d’Analyse de Données Temporelles; Université Pierre et Marie Curie: Paris, France, 1981. [Google Scholar]
- Preda, C. Analyse Harmonique Qualitative des Processus Markoviens des Sauts Stationnaires. Sci. Ann. Comput. Sci. 1998, 7, 5–18. [Google Scholar]
- Cardot, H.; Lecuelle, G.; Schlich, P.; Visalli, M. Estimating Finite Mixtures of Semi-Markov Chains: An Application to the Segmentation of Temporal Sensory Data. J. R. Stat. Soc. C 2019, 68, 1281–1303. [Google Scholar] [CrossRef]
- Deville, J. Qualitative Harmonic Analysis: An Application to Brownian Motion, Alternative Approach to Time Series Analysis; Publications des Facultés Universitaires Saint-Louis; Universitaires Saint-Louis: Brussels, Belgium, 1984; pp. 1–10. [Google Scholar]
- Nath, R.; Pavur, R. A New Statistic in the One Way Multivariate Analysis of Variance. Comput. Stat. Data Anal. 1985, 2, 297–315. [Google Scholar] [CrossRef]
- Escofier, B. Analyse Factorielle et Distances Répondant au Principe d’Équivalence Distributionnelle. Rev. De Stat. Appliquées 1978, 26, 29–37. [Google Scholar]
- Hotelling, H. Relations Between Two Sets of Variates. Biometrika 1936, 28, 321–377. [Google Scholar] [CrossRef]
- Deville, J.C. Méthodes Statistiques et Numériques de l’Analyse Harmonique. Ann. L’INSEE 1974, 15, 5–101. [Google Scholar] [CrossRef]
- Mercer, J. Functions of Positive and Negative Type and their Connection with the Theory of Integral Equations. Philos. Trans. R. Soc. A 1909, 209, 441–458. [Google Scholar] [CrossRef]
- Dai, W.; Mrkvička, T.; Sun, Y.; Genton, M.G. Functional outlier detection and taxonomy by sequential transformations. Comput. Stat. Data Anal. 2020, 149, 106960. [Google Scholar] [CrossRef] [Green Version]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016. [Google Scholar]
- Solymos, P.; Zawadzki, Z. pbapply: Adding Progress Bar to ’*apply’ Functions, R Package Version 1.4-3; 2020. Available online: https://cran.r-project.org/package=pbapply (accessed on 28 November 2021).
- Gabadinho, A.; Studer, M.; Müller, N.; Bürgin, R.; Fonta, P.A.; Ritschard, G. TraMineR: Trajectory Miner: A Toolbox for Exploring and Rendering Sequences, R Package Version 2.0-13; 2019. Available online: https://cran.r-project.org/package=TraMineR (accessed on 28 November 2021).
- Studer, M. WeightedCluster Library Manual: A Practical Guide to Creating Typologies of Trajectories in the Social Sciences with R. Technical Report, LIVES Working Papers 24. 2013. Available online: https://cran.r-project.org/package=WeightedCluster (accessed on 28 November 2021). [CrossRef]
- Melnykov, V. ClickClust: An R Package for Model-Based Clustering of Categorical Sequences. J. Stat. Softw. 2016, 74, 1–34. [Google Scholar] [CrossRef] [Green Version]
- Scholz, M. R Package clickstream: Analyzing Clickstream Data with Markov Chains. J. Stat. Softw. 2016, 74, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Larmarange, J. Trajectoires de Soins. 2018. Available online: https://larmarange.github.io/analyse-R/trajectoires-de-soins.html (accessed on 28 November 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).