Implicit Solitary Waves for One of the Generalized Nonlinear Schrödinger Equations
Abstract
:1. Introduction
2. Method Applied
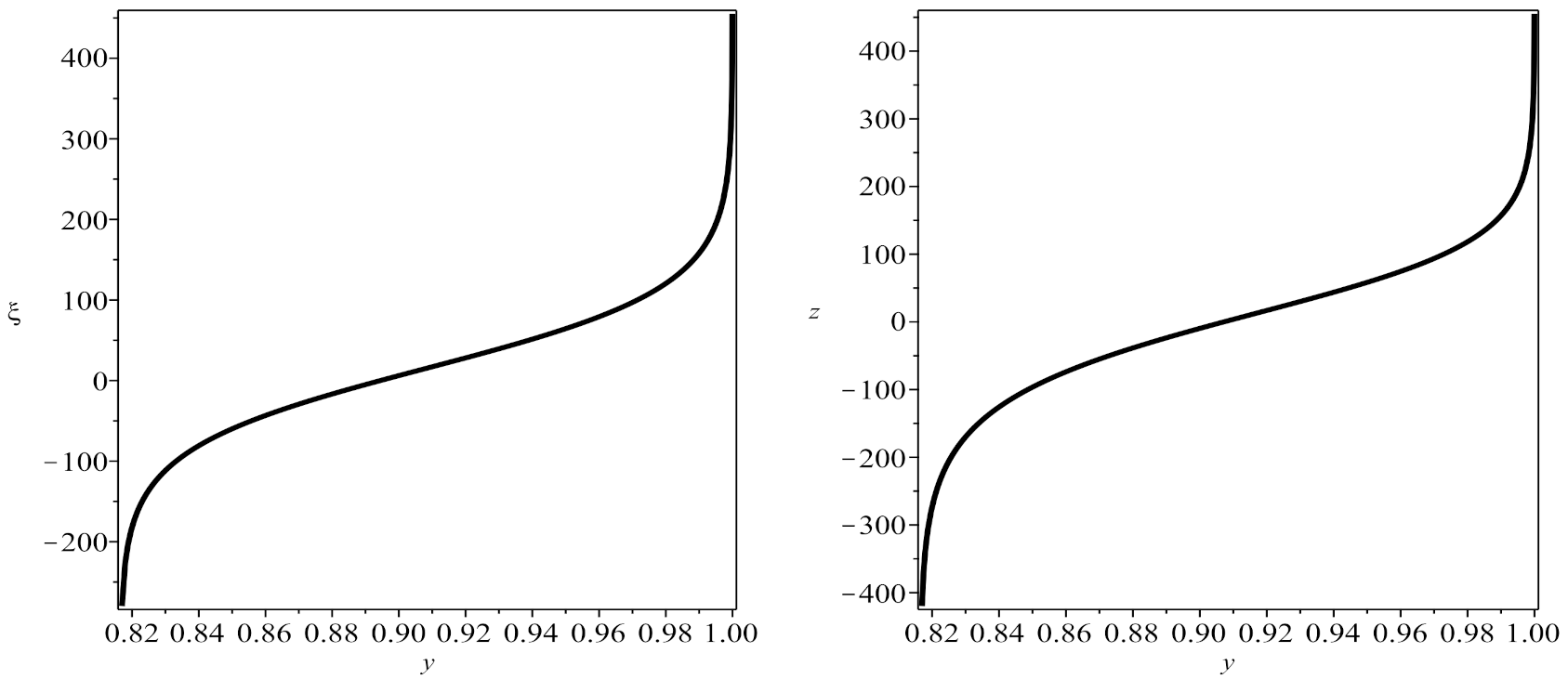
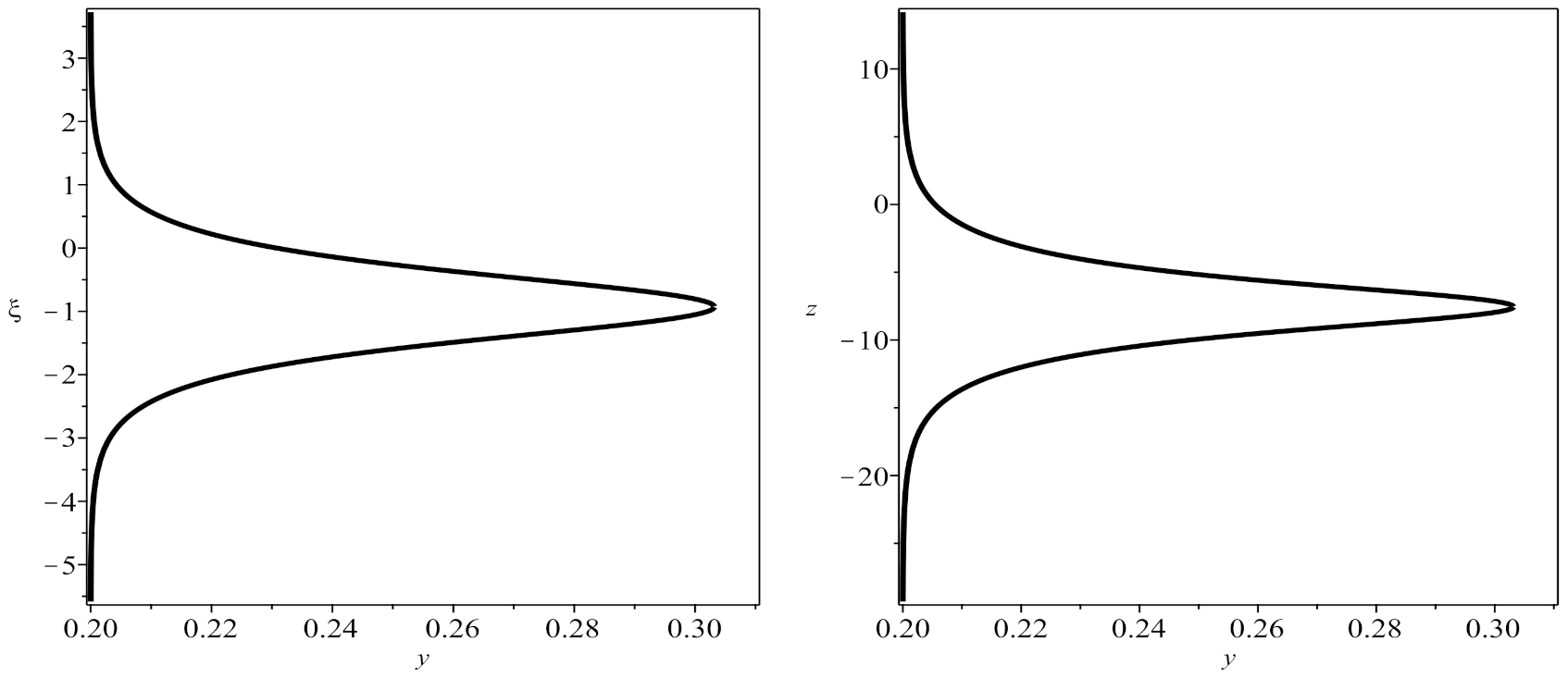
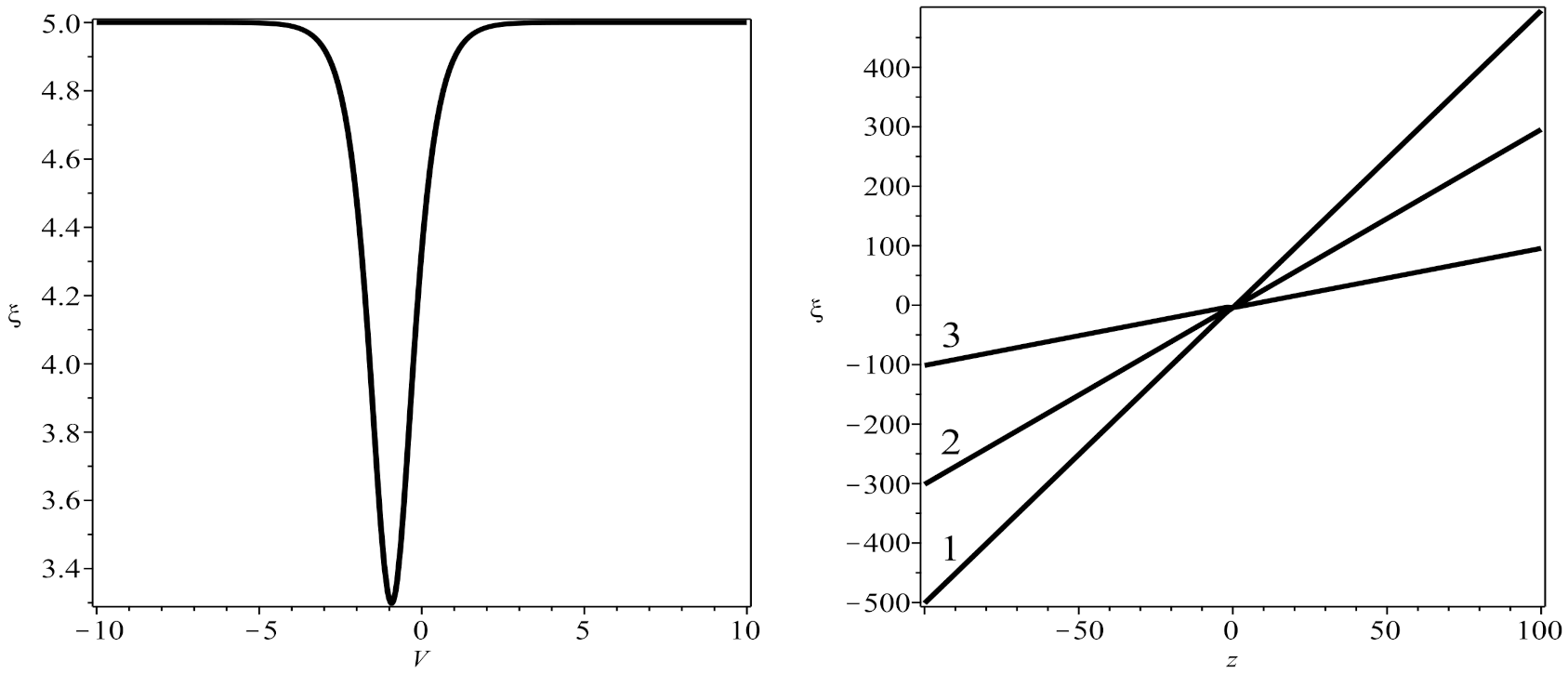
3. Implicit Solitary Wave Solutions of the Generalized Nonlinear Schrödinger Equation in Form Kink
4. Implicit Optical Solitons of the Generalized Nonlinear Schrödinger Equation
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kudryashov, N.A. Model of propagation pulses in an optical fiber with a new law of refractive indices. Optik 2021, 248, 168160. [Google Scholar] [CrossRef]
- Kudryashov, N.A. A generalized model for description of propagation pulses in optical fiber. Optik 2019, 189, 42–52. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Mathematical model of propagation pulse in optical fiber with power nonlinearities. Optik 2020, 212, 164750. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Solitary wave solutions of hierarchy with non-local nonlinearity. Appl. Math. Lett. 2020, 103, 106155. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Shohib, R.M.A.; Biswas, A.; Ekici, M.; Triki, H.; Alzahrani, A.K.; Belic, M.R. Optical solitons and other solutions to Kudryashov’s equation with three innovative integration norms. Optik 2020, 211, 164431. [Google Scholar] [CrossRef]
- Arshed, S.; Arif, A. Soliton solutions of higher-order nonlinear schrodinger equation (NLSE) and nonlinear kudryashov’s equation. Optik 2020, 209, 164588. [Google Scholar] [CrossRef]
- Kumar, S.; Malik, S.; Biswas, A.; Zhou, Q.; Moraru, L.; Alzahrani, A.K.; Belic, M.R. Optical Solitons with Kudryashov’s Equation by Lie Symmetry Analysis. Phys. Wave Phenom. 2020, 28, 299–304. [Google Scholar] [CrossRef]
- Yildirim, Y.; Biswas, A.; Ekici, M.; Gonzalez-Gaxiola, O.; Khan, S.; Triki, H.; Moraru, L.; Alzahrani, A.K.; Belic, M.R. Optical solitons with Kudryashov’s model by a range of integration norms. Chin. J. Phys. 2020, 66, 660–672. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Optical solitons of the resonant nonlinear Schrodinger equation with arbitrary index. Optik 2021, 235, 166626. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Shohib, R.M.A.; Biswas, A.; Ekici, M.; Moraru, L.; Alzahrani, A.K.; Belic, M.R. Optical solitons with differential group delay for Kudryashov’s model by the auxiliary equation mapping method. Chin. J. Phys. 2020, 67, 631–645. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alngar, M.E.M.; Biswas, A.; Asma, M.; Ekici, M.; Alzahrani, A.K.; Belic, M.R. Optical solitons and conservation laws with generalized Kudryashov’s law of refractive index. Chaos Solitons Fractals 2020, 139, 110284. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alngar, M.E.M.; Biswas, A.; Asma, M.; Ekici, M.; Alzahrani, A.K.; Belic, M.R. Solitons in magneto–optic waveguides with Kudryashov’s law of refractive index. Chaos Solitons Fractals 2020, 140, 110129. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Optical solitons of mathematical model with arbitrary refractive index. Optik 2021, 231, 166443. [Google Scholar] [CrossRef]
- Biswas, A.; Asma, M.; Guggilla, P.; Mullick, L.; Moraru, L.; Ekici, M.; Alzahrani, A.K.; Belic, M.R. Optical soliton perturbation with Kudryashov’s equation by semi–inverse variational principle. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2020, 384, 126830. [Google Scholar] [CrossRef]
- Biswas, A.; Sonmezoglu, A.; Ekici, M.; Alzahrani, A.K.; Belic, M.R. Cubic–Quartic Optical Solitons with Differential Group Delay for Kudryashov’s Model by Extended Trial Function. J. Commun. Technol. Electron. 2020, 65, 1384–1398. [Google Scholar] [CrossRef]
- Arnous, A.H.; Biswas, A.; Ekici, M.; Alzahrani, A.K.; Belic, M.R. Optical solitons and conservation laws of Kudryashov’s equation with improved modified extended tanh-function. Optik 2021, 225, 165406. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alngar, M.E.M. Optical soliton solutions for the generalized Kudryashov equation of propagation pulse in optical fiber with power nonlinearities by three integration algorithms. Math. Methods Appl. Sci. 2021, 44, 315–324. [Google Scholar] [CrossRef]
- Hyder, A.A.; Soliman, A.H. Exact solutions of space-time local fractal nonlinear evolution equations generalized comformable derivative approach. Resilts Phys. 2020, 17, 103135. [Google Scholar] [CrossRef]
- Hyder, A.A.; Soliman, A.H. An extended Kudryashov technique for solving stochastic nonlinear models with generalized comformable derivatives. Commun. Nonlinear Sci. Numer. Simul. 2021, 97, 105730. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Shohib, R.M.A.; Alngar, M.E.M.; Biswas, A.; Kara, A.H.; Dakova, A.; Khan, S.; Alshehri, H.M.; Belic, M.R. Solitons and conservation laws in magneto-optic waveguides with generalized Kudryashov’s equation by the unified auxiliary equation approach. Optik 2021, 245, 167694. [Google Scholar] [CrossRef]
- Ekici, M.; Sonmezoglu, A.; Biswas, A. Stationary optical solitons with Kudryashov’s laws of refractive index. Chaos Solitons Fractals 2021, 151, 111226. [Google Scholar] [CrossRef]
- Yildirim, Y.; Biswas, A.; Kara, A.H.; Ekici, M.; Alzahrani, A.K.; Belic, M.R. Cubic–quartic optical soliton perturbation and conservation laws with generalized Kudryashov’s form of refractive index. J. Opt. 2021, 50, 354–360. [Google Scholar] [CrossRef]
- Biswas, A.; Ekici, M.; Dakova, A.; Khan, S.; Moshokoa, S.P.; Alshehri, H.M.; Belic, M.R. Highly dispersive optical soliton perturbation with Kudryashov’s sextic-power law nonlinear refractive index by semi-inverse variation. Results Phys. 2021, 27, 104539. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Exact solutions of the equation for surface waves in a convecting fluid. Appl. Math. Comput. 2019, 344–345, 97–106. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Method for finding highly dispersive optical solitons of nonlinear differential equations. Optik 2019, 206, 163550. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Highly dispersive optical solitons of the generalized nonlinear eigth-order Scrödinger equation. Optik 2020, 206, 164335. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Exact solutions of the generalized Kuramoto-Sivashinsky equation. Phys. Lett. A 1990, 147, 287–291. [Google Scholar] [CrossRef]
- Parkes, E.J.; Duffy, B.R. An automated tanh-function method for finding solitary wave solutions to non-linear evolution equations. Comput. Phys. Commun. 1996, 98, 288–300. [Google Scholar] [CrossRef]
- Malfliet, W.; Hereman, W. The Tanh method: I Exact solutions of nonlinear evolution and wave equations. Phys. Scr. 1996, 54, 563–568. [Google Scholar] [CrossRef]
- Fan, E. Extended tanh-function method and its applications to nonlinear equations. Phys. Lett. A 2000, 227, 212–218. [Google Scholar] [CrossRef]
- Fu, Z.; Liu, S.; Liu, S.; Zhao, Q. New Jacobi elliptic function expansion and new periodic solutions of nonlinear wave equations. Phys. Lett. A 2001, 290, 72–76. [Google Scholar] [CrossRef]
- Liu, S.; Fu, Z.; Liu, S.; Zhao, Q. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 2001, 289, 69–74. [Google Scholar] [CrossRef]
- Biswas, A. 1-soliton solution of the generalized Radhakrishnan–Kundu–Laksmanan equation. Phys. Lett. A 2009, 373, 2546–2548. [Google Scholar] [CrossRef]
- Vitanov, N.K. Application of simplest equations of Bernoulli and Riccati kind for obtaining exact traveling-wave solutions for a class of PDEs with polynomial nonlinearity. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2050–2060. [Google Scholar] [CrossRef]
- Vitanov, N.K. Modified method of simplest equation: Powerful tool for obtaining exact and approximate traveling-wave solutions of nonlinear PDEs. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1176–1185. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Dimitrova, Z.I.; Kantz, H. Modified method of simplest equation and its application to nonlinear PDEs. Appl. Math. Comput. 2010, 216, 2587–2595. [Google Scholar] [CrossRef]
- Kudryashov, N.A. One method for finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2248–2253. [Google Scholar] [CrossRef] [Green Version]
- Yildirim, Y.; Biswas, A.; Kara, A.H.; Guggilla, P.; Khan, S.; Alzahrani, A.K.; Belic, M.R. Highly dispersive optical solitons and conservation laws with Kudryashov’s sextic power-law of nonlinear refractive index. Optik 2021, 240, 166915. [Google Scholar] [CrossRef]
- Elsherbeny, A.M.; El-Barkouky, R.; Ahmed, H.M.; Arnous, A.H.; El-Hassani, R.M.I.; Biswas, A.; Yildirim, Y.; Alshomrani, A.S. Optical soliton perturbation with Kudryashov’s generalized nonlinear refractive index. Optik 2021, 240, 166620. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alngar, M.E.M.; Biswas, A.; Kara, A.H.; Asma, M.; Ekici, M.; Khan, S.; Alzahrani, A.K.; Belic, M.R. Solitons and conservation laws in magneto–optic waveguides with generalized Kudryashov’s equation. Chin. J. Phys. 2021, 69, 186–205. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Shohib, R.M.A.; Alngar, M.E.M.; Biswas, A.; Ekici, M.; Khan, S.; Alzahrani, A.K.; Belic, M.R. Optical solitons and conservation laws associated with Kudryashov’s sextic power-law nonlinearity of refractive index. Ukr. J. Phys. Opt. 2021, 22, 38–49. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alngar, M.E.M.; Biswas, A.; Ekici, M.; Alzahrani, A.K.; Belic, M.R. Chirped and Chirp-Free Optical Solitons in Fiber Bragg Gratings with Kudryashov’s Model in Presence of Dispersive Reflectivity. J. Commun. Technol. Electron. 2020, 65, 1267–1287. [Google Scholar] [CrossRef]
- Arnous, A.H.; Zhou, Q.; Biswas, A.; Guggilla, P.; Khan, S.; Yildirim, Y.; Alshomrani, A.S.; Alshehri, H.M. Optical solitons in fiber Bragg gratings with cubic-quartic dispersive reflectivity by enhanced Kudryashov’s approach. Phys. Lett. A 2022, 422, 127797. [Google Scholar] [CrossRef]
- Gonzalez-Gaxiola, O. Optical soliton solutions for Triki-Biswas equation by Kudryashov’s R function method. Optik 2022, 249, 168230. [Google Scholar] [CrossRef]
- Arnous, A.H. Optical solitons with Biswas-Milovic equation in magneto-optic waveguide having Kudryashov’s aw of refractive index. Optik 2021, 247, 167987. [Google Scholar] [CrossRef]
- Alotaibi, H. Traveling wave solutions to the nonlinear evolution equation using expansion method and addendum to Kudryashov’s method. Symmetry 2021, 13, 2126. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Highly dispersive solitary wave solutions of perturbed nonlinear Schrödinger equations. Appl. Math. Comput. 2020, 371, 124972. [Google Scholar] [CrossRef]
- Raza, N.; Seadawy, A.R.; Kaplan, M.; Butt, A.R. Symbolic computation and sensitivity analysis of nonlinear Kudryashov’s dynamical equation with applications. Phys. Scr. 2021, 96, 105216. [Google Scholar] [CrossRef]
- Kaplan, M.; Akbulut, A. The analysis of the soliton-type solutions of conformable equations by using generalized Kudryashov method. Opt. Quantum Electron. 2021, 53, 498. [Google Scholar] [CrossRef]
- Malik, S.; Kumar, S.; Biswas, A.; Ekici, M.; Dakova, A.; Alzahrani, A.K.; Belic, M.R. Optical solitons and bifurcation analysis in fiber Bragg gratings with Lie symmetry and Kudryashov’s approach. Nonlinear Dyn. 2021, 105, 735–751. [Google Scholar] [CrossRef]
- Rahman, Z.; Ali, M.Z.; Roshid, H.-O. Closed form soliton solutions of three nonlinear fractional models through proposed improved Kudryashov method. Chin. Phys. B 2021, 30, 050202. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kudryashov, N.A. Implicit Solitary Waves for One of the Generalized Nonlinear Schrödinger Equations. Mathematics 2021, 9, 3024. https://doi.org/10.3390/math9233024
Kudryashov NA. Implicit Solitary Waves for One of the Generalized Nonlinear Schrödinger Equations. Mathematics. 2021; 9(23):3024. https://doi.org/10.3390/math9233024
Chicago/Turabian StyleKudryashov, Nikolay A. 2021. "Implicit Solitary Waves for One of the Generalized Nonlinear Schrödinger Equations" Mathematics 9, no. 23: 3024. https://doi.org/10.3390/math9233024
APA StyleKudryashov, N. A. (2021). Implicit Solitary Waves for One of the Generalized Nonlinear Schrödinger Equations. Mathematics, 9(23), 3024. https://doi.org/10.3390/math9233024