On Multilevel and Control Variate Monte Carlo Methods for Option Pricing under the Rough Heston Model
Abstract
:1. Introduction
1.1. Prerequisites
2. Discretization Methods
2.1. Euler–Maruyama Discretization Method
- (AA1)
- For , let when , and the following holds:for all .
- (AA2)
- For , and , the following holds:
- (AA3)
- For , and , the following holds:
- (AA4)
- For , the following holds:
- (AA5)
- For , the following holds:
- (AA6)
- For , the following holds:
- (AA7)
- For , the following holds:
- (BB1)
- For and , let hold. The following inequalities hold:
2.2. Second-Order Euler Discretization Method
3. Monte Carlo Methods
3.1. Control Variate Method
3.2. Multilevel Monte Carlo
3.3. Multilevel Control Variate Method
4. Numerical Experiments
- Pre-run the simulation of the methods with relatively small and store the intended result.
- Compute time-taken to run a single simulation.
- Compute as the number of simulations needed to achieve the specific run-time or cost C.
- With the previous simulations stored, conduct the rest of simulations.
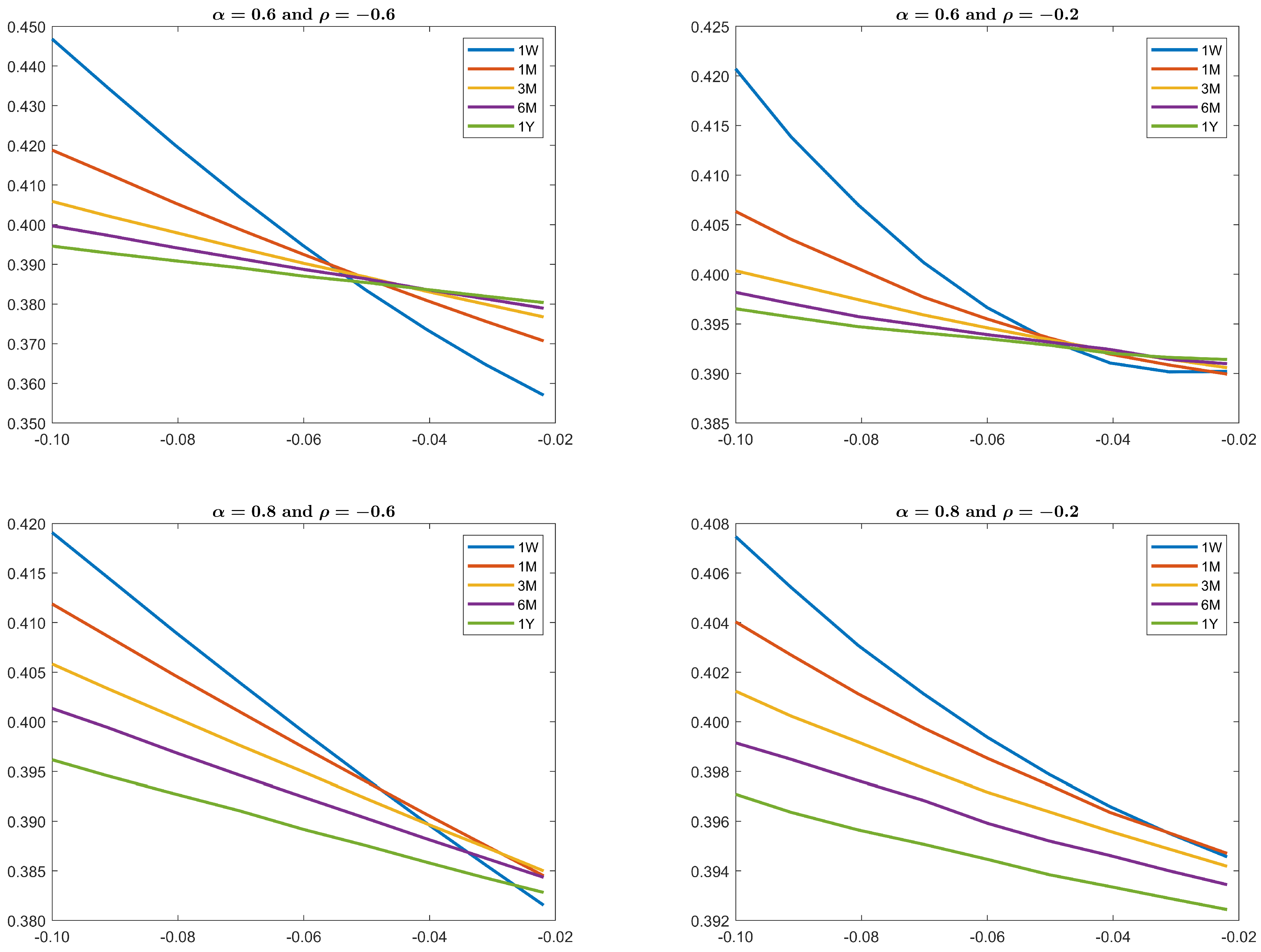
4.1. The and Change
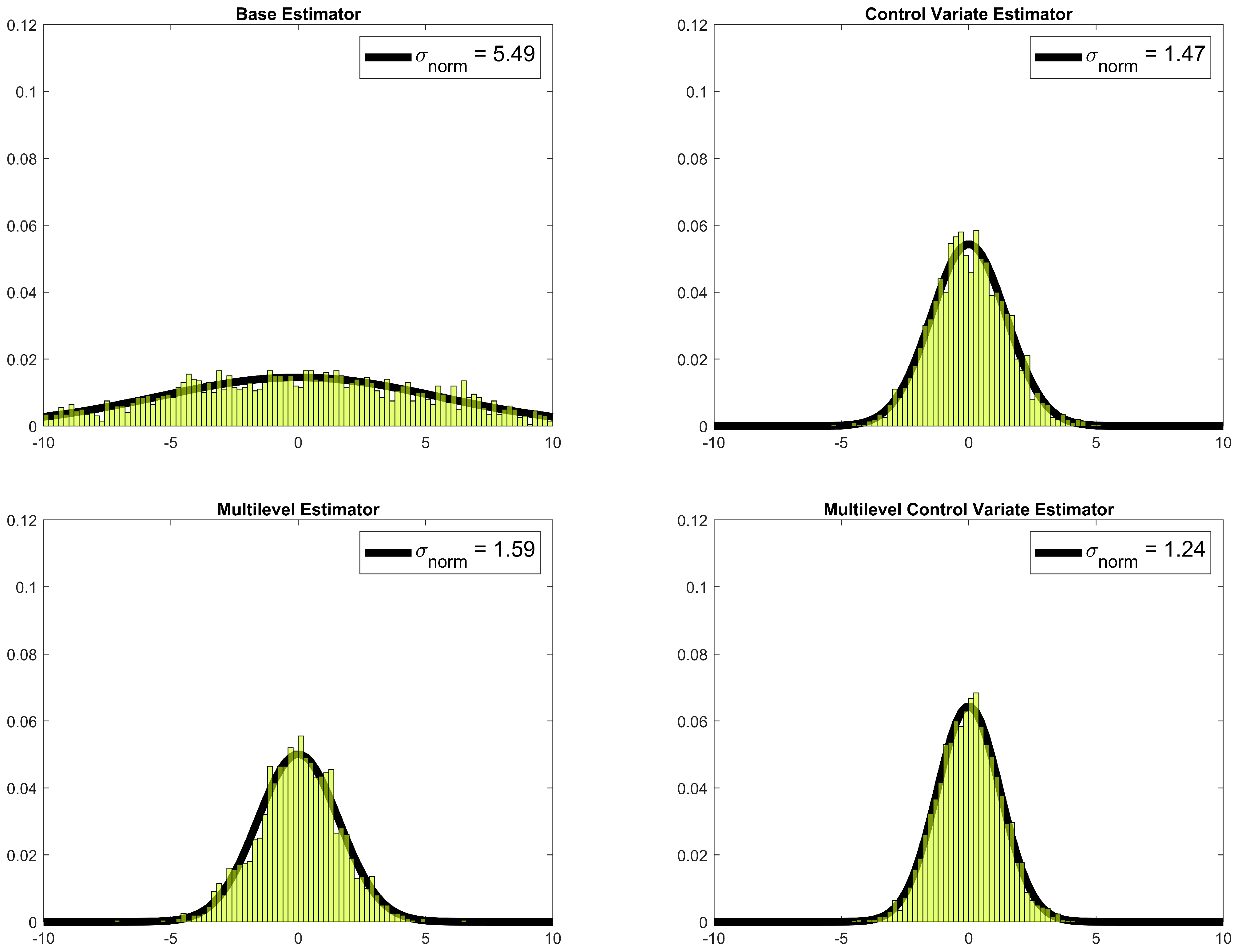
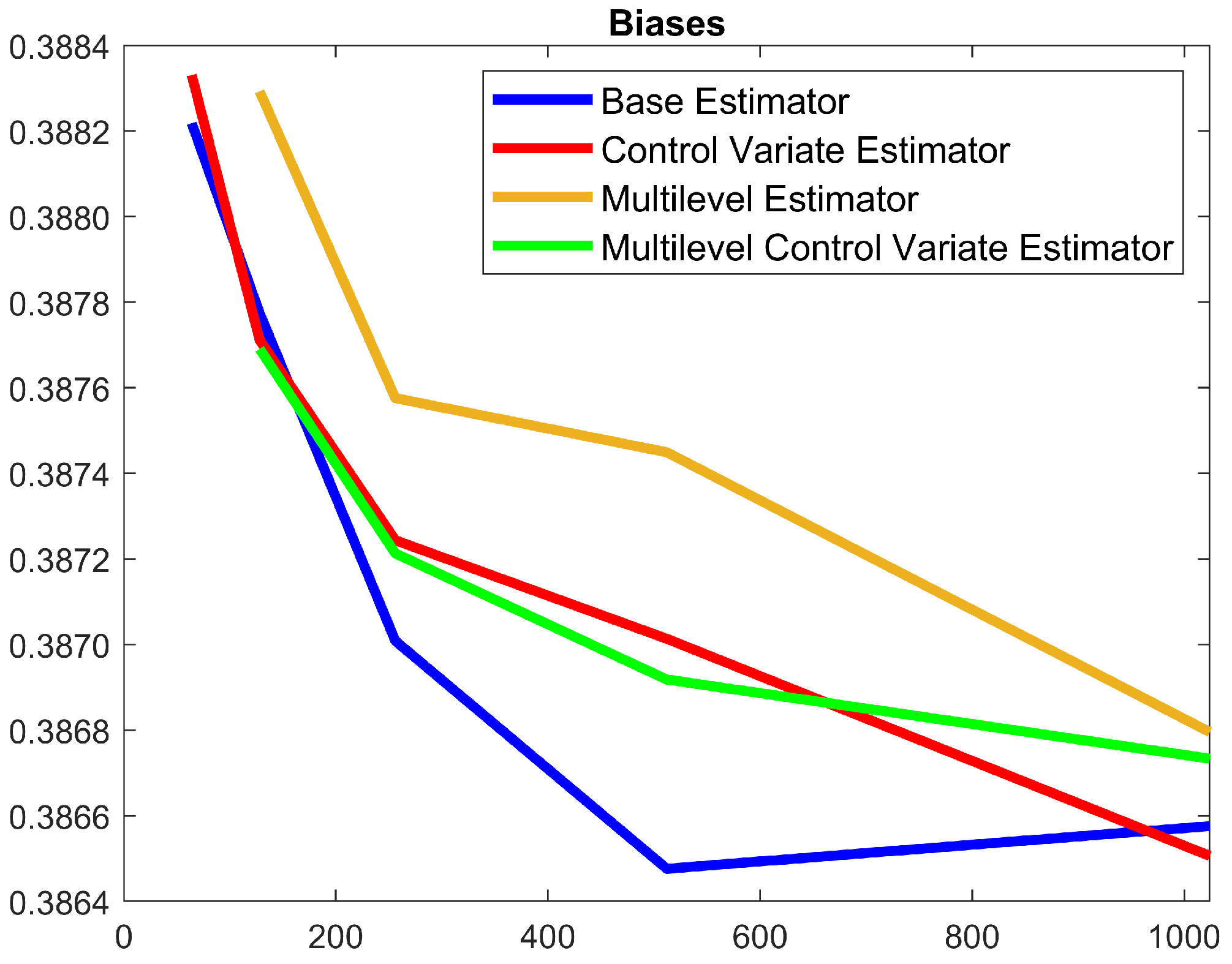
4.2. Cost-Adjusted Variation and Bias
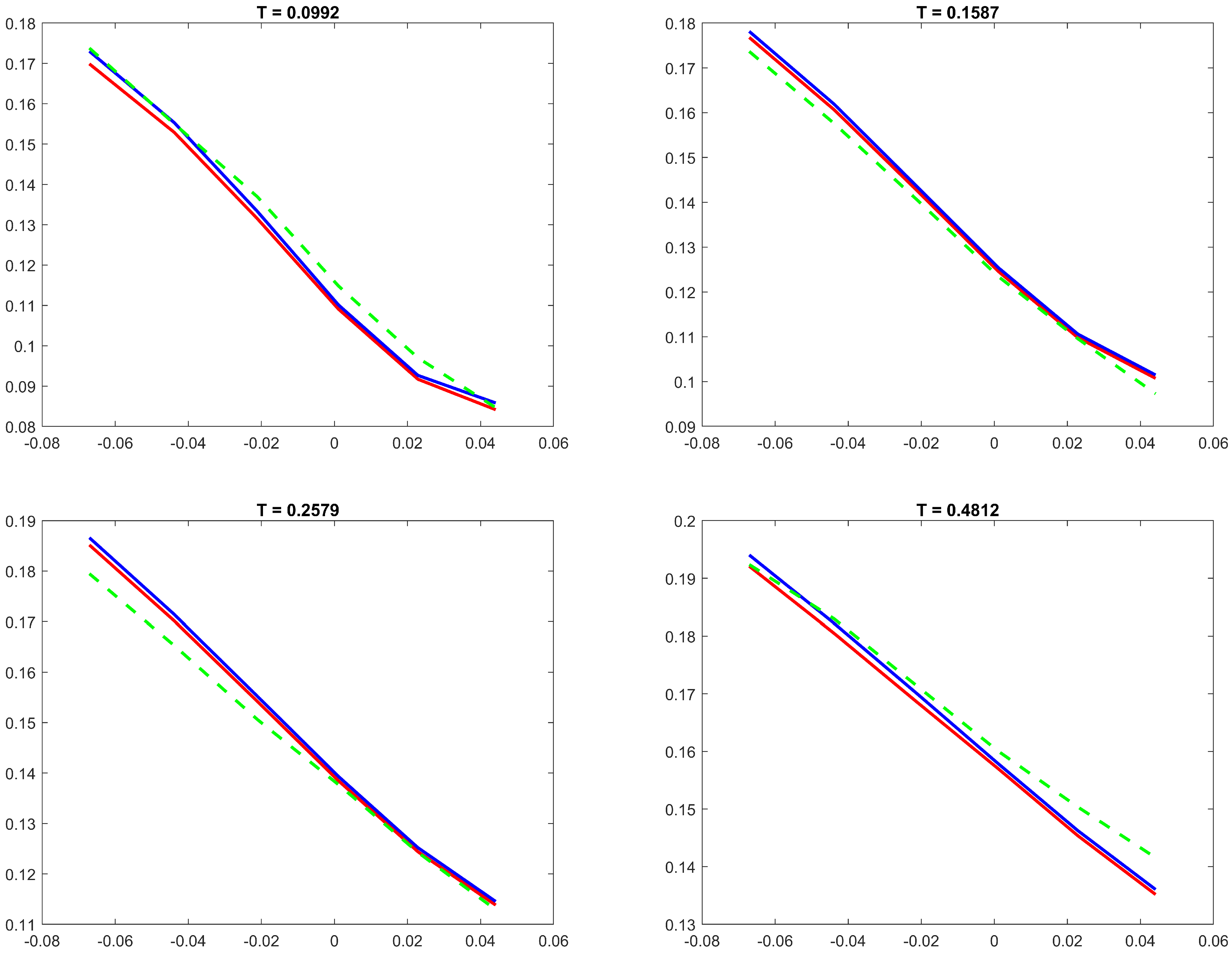
4.3. Calibration to SPX Options
5. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OTM | Out-of-the-money |
| ATM | At-the-money |
| ITM | In-the-money |
| BE | Base estimator |
| CV | Control variate estimator |
| ML | Multilevel estimator |
| MLCV | Multilevel control variate estimator |
Appendix A. Proof of Lemma 1
Appendix B. Proof of Theorem 1
Appendix C. Proof of Theorem 2
References
- Gatheral, J.; Jaisson, T.; Rosenbaum, M. Volatility is rough. Quant. Financ. 2018, 18, 933–949. [Google Scholar] [CrossRef]
- Comte, F.; Renault, E. Long memory in continuous-time stochastic volatility models. Math. Financ. 1998, 8, 291–323. [Google Scholar] [CrossRef]
- Cheridito, P. Mixed fractional Brownian motion. Bernoulli 2001, 7, 913–934. [Google Scholar] [CrossRef]
- Alòs, E.; León, J.A.; Vives, J. On the short-time behavior of the implied volatility for jump-diffusion models with stochastic volatility. Financ. Stoch. 2007, 11, 571–589. [Google Scholar] [CrossRef] [Green Version]
- Fukasawa, M. Asymptotic analysis for stochastic volatility: Martingale expansion. Financ. Stoch. 2011, 15, 635–654. [Google Scholar] [CrossRef] [Green Version]
- Bayer, C.; Friz, P.; Gatheral, J. Pricing under rough volatility. Quant. Financ. 2016, 16, 887–904. [Google Scholar] [CrossRef]
- Bergomi, L. Smile Dynamics II. SSRN 2005. Available online: http://dx.doi.org/10.2139/ssrn.1493302 (accessed on 3 May 2021).
- El Euch, O.; Fukasawa, M.; Rosenbaum, M. The microstructural foundations of leverage effect and rough volatility. Financ. Stoch. 2018, 22, 241–280. [Google Scholar] [CrossRef] [Green Version]
- El Euch, O.; Rosenbaum, M. The characteristic function of rough Heston models. Math. Financ. 2019, 29, 3–38. [Google Scholar] [CrossRef] [Green Version]
- El Euch, O.; Gatheral, J.; Radoicic, R.; Rosenbaum, M. The zumbach effect under rough heston. arXiv 2018, arXiv:1809.02098. Available online: https://arxiv.org/abs/1809.02098 (accessed on 2 April 2021). [CrossRef] [Green Version]
- Gatheral, J.; Radoicic, R. Rational approximation of the rough Heston solution. Int. J. Theor. Appl. Financ. 2019, 22, 1950010. [Google Scholar] [CrossRef]
- Jeng, S.W.; Kilicman, A. Approximation formula for option prices under rough heston model and short-time implied volatility behaviour. Symmetry 2020, 12, 1878. [Google Scholar] [CrossRef]
- Jeng, S.W.; Kilicman, A. Fractional Riccati Equation and Its Applications to Rough Heston Model Using Numerical Methods. Symmetry 2020, 12, 959. [Google Scholar] [CrossRef]
- Jeng, S.W.; Kilicman, A. Series Expansion and Fourth-Order Global Padé Approximation for a Rough Heston Solution. Mathematics 2020, 8, 1968. [Google Scholar] [CrossRef]
- Abi Jaber, E. Lifting the Heston model. Quant. Financ. 2019, 19, 1995–2013. [Google Scholar] [CrossRef]
- Giles, M.B. Multilevel monte carlo path simulation. Oper. Res. 2008, 56, 607–617. [Google Scholar] [CrossRef] [Green Version]
- Giles, M.B. Multilevel monte carlo methods. Acta Numer. 2015, 24, 259. [Google Scholar] [CrossRef] [Green Version]
- Glasserman, P. Monte Carlo Methods in Financial Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003; Volume 53. [Google Scholar]
- Liu, G.; Zhao, Q.; Gu, G. A simple control variate method for options pricing with stochastic volatility models. Int. J. Appl. Math. 2015, 8, 1968. [Google Scholar]
- McCrickerd, R.; Pakkanen, M.S. Turbocharging Monte Carlo pricing for the rough Bergomi model. Quant. Financ. 2018, 18, 1877–1886. [Google Scholar] [CrossRef] [Green Version]
- Richard, A.; Tan, X.; Yang, F. Discrete-time simulation of stochastic volterra equations. arXiv 2020, arXiv:2004.00340. Available online: https://arxiv.org/abs/2004.00340 (accessed on 3 May 2021). [CrossRef]
- El Euch, O.; Rosenbaum, M. Perfect hedging in rough Heston models. Ann. Appl. Probab. 2018, 28, 3813–3856. [Google Scholar] [CrossRef] [Green Version]
- Forde, M.; Gerhold, S.; Smith, B. Small-time and large-time smile behaviour for the Rough Heston model. arXiv 2019, arXiv:1906.09034. Available online: https://arxiv.org/abs/1906.09034 (accessed on 25 April 2021).
- Gatheral, J.; Keller-Ressel, M. Affine forward variance models. Financ. Stoch. 2018, 23, 501–533. [Google Scholar] [CrossRef] [Green Version]
- Maruyama, G. Continuous markov processes and stochastic equations. Rend. Del Circ. Mat. Di Palermo 1955, 4, 48. [Google Scholar] [CrossRef]
- Milstein, G. Approximate integration of stochastic differential equations. Theory Probab. Its Appl. 1975, 19, 557–562. [Google Scholar]
- Richard, A.; Tan, X.; Yang, F. On the discrete-time simulation of the rough Heston model. arXiv 2021, arXiv:2107.07835. Available online: https://arxiv.org/abs/2107.07835 (accessed on 3 May 2021).
- Milstein, G. A method of second-order accuracy integration of stochastic differential equations. Theory Probab. Its Appl. 1979, 23, 396–401. [Google Scholar] [CrossRef]
- Talay, D. Efficient numerical schemes for the approximation of expectations of functionals of the solution of a sde, and applications. In Filtering and Control of Random Processes; Springer: Berlin/Heidelberg, Germany, 1984; pp. 294–313. [Google Scholar]
- Shreve, S.E. Stochastic Calculus for Finance II: Continuous Time Models; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004; Volume 11. [Google Scholar]
- Fairbanks, H.R.; Doostan, A.; Ketelsen, C.; Iaccarino, G. A low-rank control variate for multilevel Monte Carlo simulation of high-dimensional uncertain systems. J. Comput. Phys. 2017, 341, 121–139. [Google Scholar] [CrossRef] [Green Version]
- Nobile, F.; Tesei, F. A Multi Level Monte Carlo method with control variate for elliptic PDEs with log-normal coefficients. Stoch. Partial Differ. Equ. Anal. Comput. 2015, 3, 398–444. [Google Scholar] [CrossRef]
- Rømer, S.E. The Hybrid-Exponential Scheme for Stochastic Volterra Equations. SSRN 2020, ssrn.3706253. Available online: http://dx.doi.org/10.2139/ssrn.3706253 (accessed on 23 April 2021).
- Bennedsen, M.; Lunde, A.; Pakkanen, M.S. Hybrid scheme for Brownian semistationary processes. Financ. Stoch. 2017, 21, 931–965. [Google Scholar] [CrossRef] [Green Version]
- Alfonsi, A. On the discretization schemes for the CIR (and Bessel squared) processes. De Gruyter 2005, 355–384. [Google Scholar] [CrossRef]
- Mitrinovic, D.S.; Pecaric, J.; Fink, A.M. Inequalities Involving Functions and Their Integrals and Derivatives; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 53. [Google Scholar]

| 0.00084 | 0.00084 | 0.00100 | 0.00123 | |
| 0.00025 | 0.00036 | 0.00045 | 0.00062 | |
| 0.00089 | 0.00107 | 0.00123 | 0.00156 | |
| 0.00033 | 0.00044 | 0.00062 | 0.00085 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeng, S.W.; Kiliçman, A. On Multilevel and Control Variate Monte Carlo Methods for Option Pricing under the Rough Heston Model. Mathematics 2021, 9, 2930. https://doi.org/10.3390/math9222930
Jeng SW, Kiliçman A. On Multilevel and Control Variate Monte Carlo Methods for Option Pricing under the Rough Heston Model. Mathematics. 2021; 9(22):2930. https://doi.org/10.3390/math9222930
Chicago/Turabian StyleJeng, Siow Woon, and Adem Kiliçman. 2021. "On Multilevel and Control Variate Monte Carlo Methods for Option Pricing under the Rough Heston Model" Mathematics 9, no. 22: 2930. https://doi.org/10.3390/math9222930
APA StyleJeng, S. W., & Kiliçman, A. (2021). On Multilevel and Control Variate Monte Carlo Methods for Option Pricing under the Rough Heston Model. Mathematics, 9(22), 2930. https://doi.org/10.3390/math9222930







