Mathematical Modelling of Climate Change and Variability in the Context of Outdoor Ergonomics
Abstract
:1. Introduction
2. Notes on Outdoor Environmental Ergonomics through the Prism of Climate Change
3. Climate Models as Dynamical Systems and Their Sensitivity Analysis
3.1. Climate as a Complex Dynamical System
- –
- As mentioned earlier, it is a five-element large-scale physical system with several global hydrological and biochemical cycles. Its elements, being heterogeneous thermo-dynamical systems, have significant differences in their structure, dynamics, physics and chemistry. Dynamical and physical processes that occur in the ECS subsystems differ in their scales, both spatial and temporal. Elements of the ECS link together through numerous physical coupling mechanisms, both weak and strong, including feedback mechanisms. In turn, each ECS subsystem can be viewed as complex, consisting of subsystems, which themselves are composed of low-order subsystems. The atmosphere, for instance, can be divided into several vertical layers depending on its thermal stratification: the troposphere, stratosphere, mesosphere and thermosphere. The troposphere, in turn, can also be subdivided into the surface layer, boundary layer and free atmosphere based on the effect of the surface friction.
- –
- Physical and dynamical processes in ECS span a wide range of time and space scales. Temporal scales range from seconds to decades, and spatial scales range from molecular to planetary scales. The dynamics of the ECS is nonlinear. ECS elements interact with each other nonlinearly, creating, under certain conditions, chaotic behaviour of subsystems and the climate system as a whole.
- –
- ECS has a large number of feedback mechanisms, both positive and negative, that strongly affect climate formation.
- –
- ECS components are non-insulated systems that act as cascade systems and interact with each other in various ways, including through the transfer of momentum, sensible and latent heat, gases and particulate matter. Collectively, ECS elements constitute a climate system, which is a unique large-scale natural object.
- –
- Each ECS component has a specific response time, which must be considered when building ECS models. For example, the atmosphere can be considered the only component of the ECS model for dynamical processes with timescales from days to weeks since the tropospheric response time is about one month, while oceans, land surface and ice cover can be used to specify boundary conditions and/or external forcing. To explore the dynamical processes with timescales ranging from months to years, the ECS model must include the atmosphere and ocean, along with sea ice. Thus, ECS models are built from a hierarchy of models that ultimately form a complex integrated model.
- –
- The ECS is an oscillating system that is characterized by fluctuations that are under the influence of internal factors (natural oscillations), as well as due to external perturbations (forced oscillations). Naturally occurring fluctuations result from internal instabilities (e.g., hydrodynamic instabilities, such as barotropic and baroclinic instabilities) and heat transport within the climate system that is caused by the interaction of its components [7]. Intentional and unintentional human impacts belong to the class of external forcings.
- –
- Since the ECS exchanges energy with the environment, in this sense, it is a thermodynamically open and non-isolated system. However, the ECS is a closed system with regard to the exchange of matter with the environment. The main energy source that drives the ECS is solar energy. Climate is affected by variations in external driving forces that imply natural causes, such as fluctuations in solar and volcanic activities, as well as changes in the gaseous and chemical composition of the atmosphere due to anthropogenic factors. The impact of the ECS on outer space is nonessential. At present, climate change is most influenced by variations in the composition of atmospheric particles and gases. Carbon dioxide (CO2), the concentration of which in the atmosphere has been continuously increasing since the Industrial Revolution, has the greatest impact on current climate change.
- –
- The ECS and its subsystems possess emergent properties, examples of which are atmospheric emerging phenomena, such as clouds, large-scale baroclinic and barotropic eddies (cyclones, hurricanes) and small-scale eddies (tornadoes). An example of an emerging climate event is the El Niño–Southern Oscillation, which is a sporadic quasi-periodic variation in ocean surface temperatures across the tropical Pacific Ocean that affects the global atmospheric circulation and ocean circulation patterns. Natural emergent phenomena occur suddenly under some favorable conditions.
- –
- These systems belong to the class of dissipative dynamical systems that possess (strange) attractors.
- –
- Trajectories of climate dynamical systems are generally unstable in the Lyapunov sense.
- –
- Some unstable trajectory, enclosed in an attractor, generates deterministic dynamical chaos.
3.2. Climate System Sensitivity to External Forcing
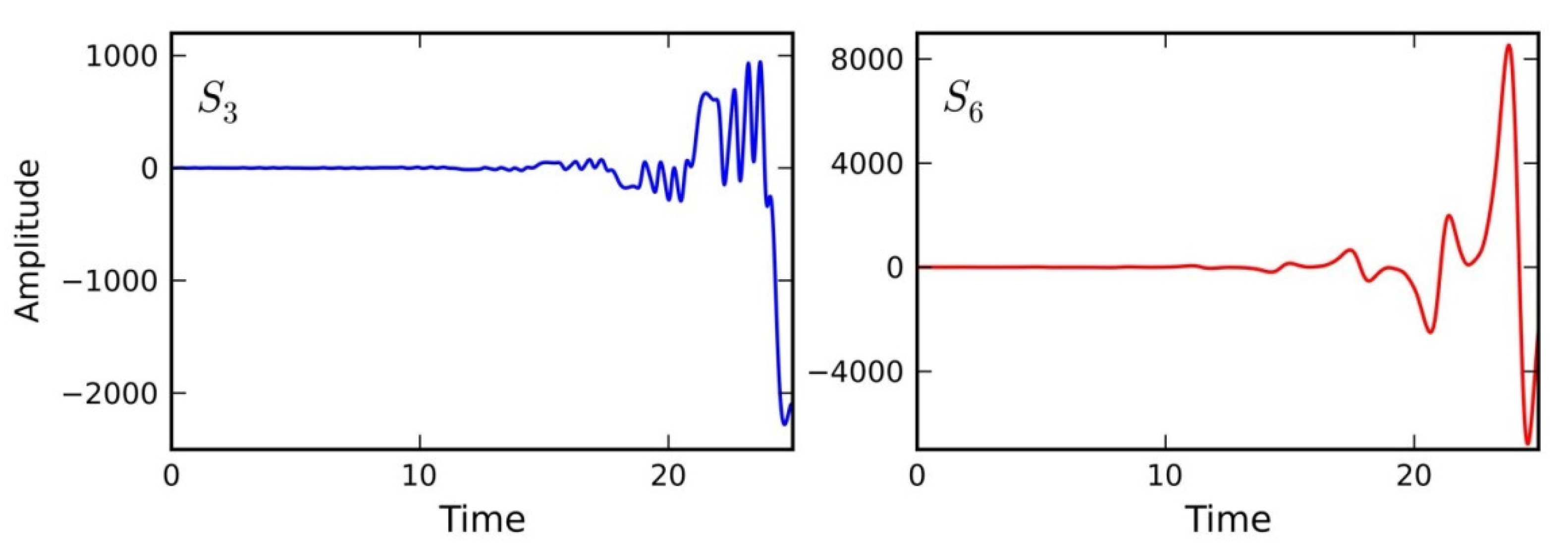
3.3. Sensitivity Analysis of a Chaotic Dynamical System
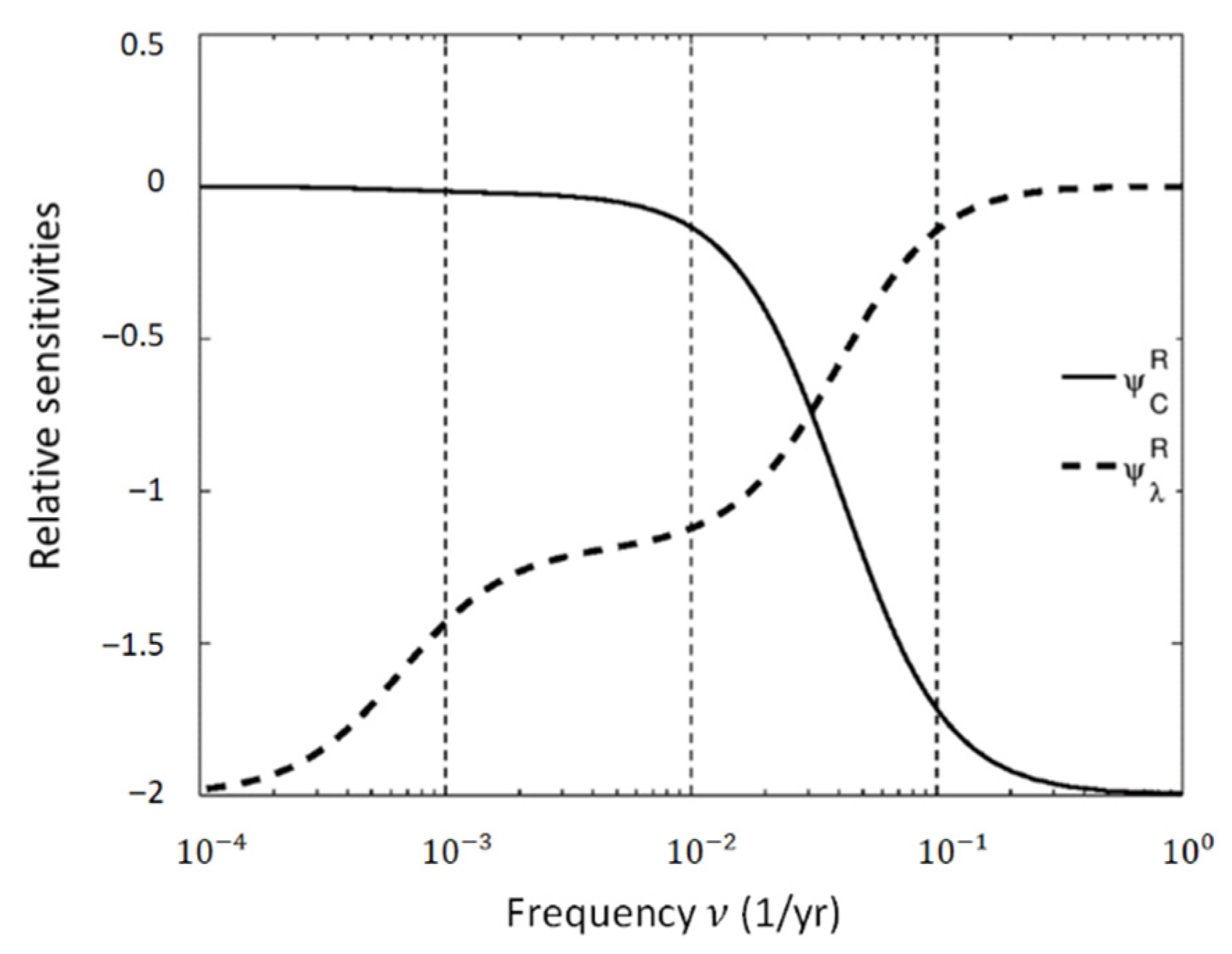
3.4. Climate System Response to Small External Forcing Based on the Fluctuation Dissipation Relation
4. Mathematical Models of Climate System
4.1. General Notes on Climate Modelling
- –
- The mathematical formulation of the problem, i.e., the translation of the real-world problem into the form of mathematical equations to be solved.
- –
- Consideration of the existence and uniqueness of a solution to the climate model equations.
- –
- The problem of the existence of attractor and estimating its dimension.
- –
- Study of the attractor’s fractal structure and invariant measure of the attracting set.
- –
- Finite-difference approximations and their convergence, stability and consistency.
- –
- Climate model sensitivity theory (theorems on linear approximation for various moments, linear response theory to small perturbations, algorithms for constructing the response operator).
- –
- Response operator approximation methods.
- –
- Numerical experiments and their analysis.
- –
- Atmospheric radiative transfer processes (transfer of shortwave (solar) and longwave (terrestrial) radiation through the atmosphere).
- –
- Hydrological cycle, including cloud formation and precipitation.
- –
- Convection.
- –
- Turbulence in the boundary and surface layers.
- –
- Small-scale orography.
- –
- The gravity wave drag.
- –
- Small-scale diffusion and dissipation.
- –
- Land surface processes.
- –
- Mixed ocean layer processes.
4.2. Governing Equations
- (a)
- Two momentum equations:
- (b)
- The thermodynamic equation:
- (c)
- The equation for specific humidity that describes the hydrological cycle:
- (d)
- The continuity equation:
- (e)
- Hydrostatic equation:
- (f)
- The equation of state:
- (a)
- Two momentum equations:
- (b)
- The thermodynamic equation:
- (c)
- The equation for the mass continuity of salinity:
- (d)
- The continuity equation:
- (e)
- Hydrostatic equation:
- (f)
- The equation of state:
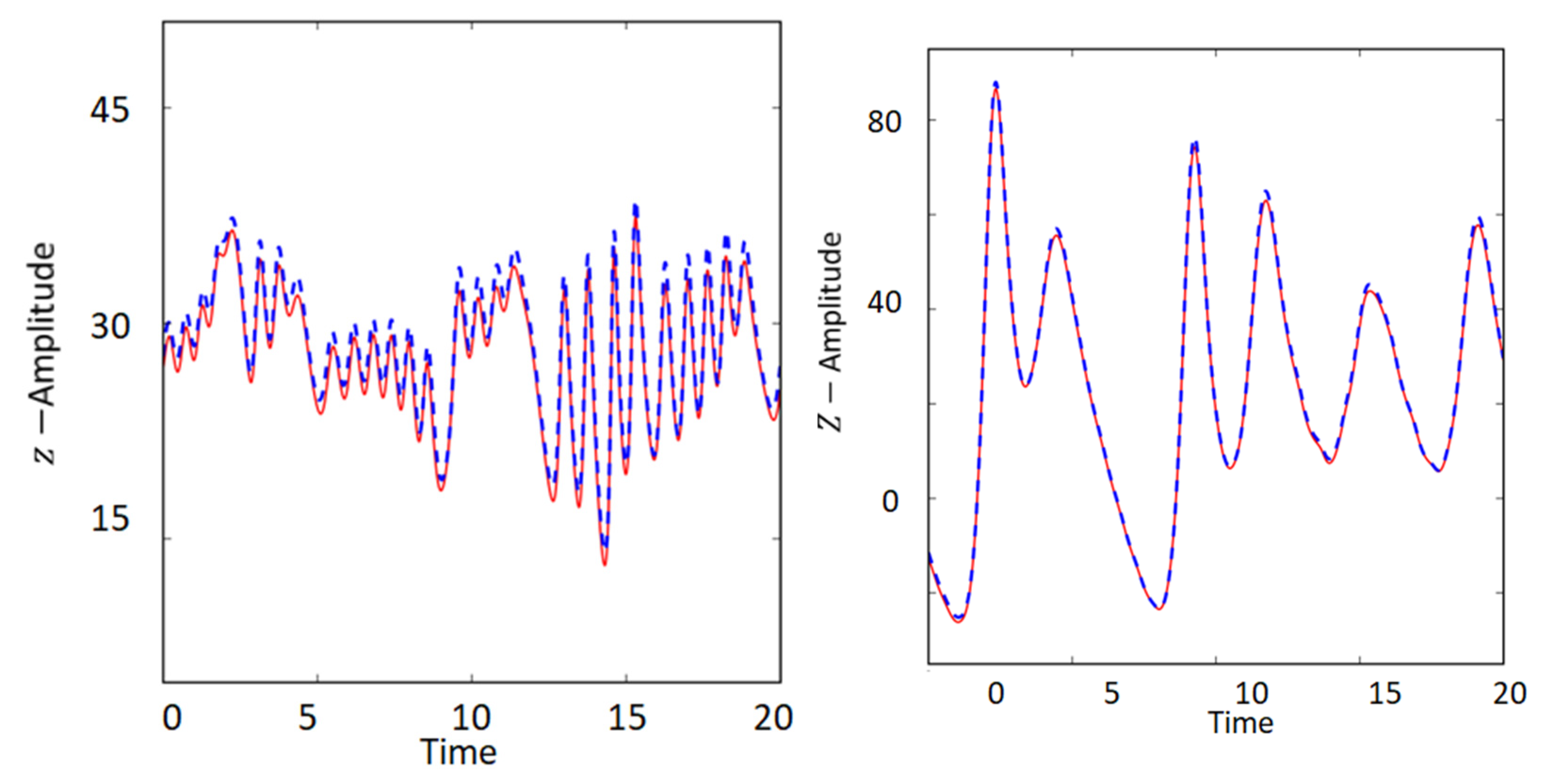
4.3. Using Low-Order Simple Models to Study Climate Variability
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stroud, K. Essential Mathematics for Science and Technology: A Self-Learning Guide; Industrial Press: South Norwalk, CT, USA, 2009; 728p. [Google Scholar]
- Riley, K.F.; Hobson, M.P. Student Solution Manual for Mathematical Methods for Physics and Engineering, 3rd ed.; Cambridge University Press: Cambridge, UK, 2019; 542p. [Google Scholar]
- Yevick, D.; Yevik, H. Fundamental Mathematics and Physics for Scientists and Engineers; John Wiley & Sons: New York, NY, USA, 2014; 464p. [Google Scholar]
- Reynolds, J.J.; Harshbarger, R.J. Mathematical Applications for the Management, Life, and Social Sciences. Cengage: Boston, MA, USA, 2012; 1104p. [Google Scholar]
- Yang, X.-S. Introductory Mathematics for Earth Scientists; Dunedin Academic Press: Edinburgh, UK, 2009; 228p. [Google Scholar]
- Brocker, J.; Calderhead, B.; Cheraghi, D.; Cotter, C.; Holm, D.; Kuna, T.; Pelloni, B.; Shepherd, T.; Weller, H. Mathematics of Planet. Earth. A Premier; World Scientific Publishing: London, UK, 2017; 372p. [Google Scholar]
- IPCC 2013. Contribution of working group I to the Fifth assessment report of the intergovernmental panel on climate change. In Climate Change 2013: The Physical Science Basis; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; 1535p. [Google Scholar]
- IPCC. 2021: Summary for Policymakers. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK, in press.
- NOAA National Centers for Environmental Information, State of the Climate. Global Climate Report. December 2018. Available online: www.ncdc.noaa.gov/sotc/global/201812 (accessed on 21 December 2020).
- Soldatenko, S.; Yusupov, R.; Colman, R. Cybernetic Approach to problem of interaction between nature and human society in the context of unprecedented climate change. SPIIRAS Proc. 2020, 19, 5–42. [Google Scholar] [CrossRef]
- Osipov, V.; Kuleshov, S.; Zaytseva, A.; Aksenov, A. Approach for the COVID-19 epidemic source localization in Russia based on mathematical modelling. Inform. Autom. 2021, 220, 1065–1089. [Google Scholar] [CrossRef]
- Simpson, N.P.; Mach, K.J.; Costable, A.; Hess, J.; Hogarth, R.; Howden, M.; Lawrence, J.; Lempert, R.J.; Muccione, V.; Mackey, B.; et al. A Framework for complex climate risk assessment. One Earth 2021, 4, 489–501. [Google Scholar] [CrossRef]
- Soldatenko, S.A.; Alekseev, G.V. Managing climate risks associated with socio-economic development of the Russian Arctic. Iop Conf. Ser. Earth Environ. Sci. 2020, 606, 12060. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Amer. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef] [Green Version]
- Meehl, G.A.; Stocker, T.F.; Collins, W.D.; Friedlingstein, P.; Thierno Gaye, A.T.; Gregory, J.M.; Kitoh, A.; Knutti, R.; Murphy, J.M.; Noda, A.; et al. Global Climate Projections/Climate Change 2007: The Physical Science Basis. In Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; pp. 747–845. [Google Scholar]
- Collins, M.; Knutti, R.; Arblaster, J.; Dufresne, J.L.; Fichefet, T.; Friedlingstein, P.; Gao, X.; Gutowski, W.J.; Johns, T.; Krinner, G.; et al. Long-term Climate Change: Projections, Commitments and Irreversibility/Climate Change 2013: The Physical Science Basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M.M.B., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 1029–1136. [Google Scholar]
- Flato, G.; Marotzke, J.; Abiodun, B.; Braconnot, P.; Chou, S.C.; Collins, W.; Cox, P.; Driouech, F.; Emori, S.; Eyring, V.; et al. Evaluation of Climate Models/Climate Change 2013: The Physical Science Basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 741–866. [Google Scholar]
- Grose, M.R.; Gregory, J.; Colman, R.A.; Andrews, T. What climate sensitivity measure is most useful for projections? Geophys Res. Lett. 2018, 45, 1559–1566. [Google Scholar] [CrossRef] [Green Version]
- Colman, R.; Soldatenko, S. Understanding the links between climate feedbacks, variability and change using a two-layer energy balance model. Clim. Dyn. 2020, 54, 3441–3459. [Google Scholar] [CrossRef]
- Karper, H.; Engler, H. Mathematics and Climate; SIAM: Philadelphia, PA, USA, 2013; 295p. [Google Scholar]
- Shen, S.S.P.; Somerville, R.C.J. Climate Mathematics: Theory and Applications; Cambridge University Press: Cambridge, UK, 2019; 391p. [Google Scholar]
- Soldatenko, S.A. Weather and climate manipulation as an optimal control for adaptive dynamical systems. Complexity 2017, 2017, 4615072. [Google Scholar] [CrossRef] [Green Version]
- Ergonomics. Available online: https://www.merriam-webster.com/dictionary/ergonomics (accessed on 9 September 2021).
- Moda, H.M.; Filho, W.L.; Minhas, A. Impacts of climate change on outdoor workers and their safety: Some research priorities. Int. J. Environ. Res. 2019, 16, 3458. [Google Scholar] [CrossRef] [Green Version]
- Kiefer, M.; Lincoln, J.; Schulte, P.; Jacklistch, B. Climate Change and Occupational Health and Safety. NIOSH Science Blog. Centre for Disease Control and Prevention. 2014. Available online: http://blogs.cdc.gov/nioshscience-blog/2014/09/22/climate-change (accessed on 10 September 2021).
- Parsons, K.C. Environmental ergonomics: A review of principles, methods and models. Appl. Ergon. 2000, 31, 581–594. [Google Scholar] [CrossRef]
- Giorgi, F, Uncertainties in climate change projections, from the global to the regional scale. EPJ Web Conf. 2010, 9, 115–129. [CrossRef]
- Carson, M.; Lyu, K.; Richter, K.; Becker, M.; Domingues, C.M.; Han, W.; Zanna, L. Climate model uncertainty and trend detection in regional sea level projections: A review. Surv. Geophys 2019, 40, 1632–1653. [Google Scholar] [CrossRef]
- Colman, R.A.; Power, S.B. What can decadal variability tell us about climate feedbacks and sensitivity? Clim. Dyn. 2018, 51, 3815–3828. [Google Scholar] [CrossRef]
- Meadows, D.; Write, D. Thinking in Systems: A Primer; Chelsea Green Publishing: London, UK, 2008; 235p. [Google Scholar]
- Daede, A.P.M.; Ahlonsou, R.; Ding, Y.; Schimel. The climate system: An overview. In IPCC, 2001: Climate Change 2001: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Houghton, J.T., Ding, Y., Grogs, D.J., Noguer, M., van der Linden, P.J., Dai, X., Maskell, K., Johnson, C.A., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001; pp. 85–98. [Google Scholar]
- Dymnikov, V.P.; Filatov, A.N. Mathematics of Climate Modelling; Birkhäuser: Boston, UK, 1997; 264p. [Google Scholar]
- Dijkstra, H.A. Nonlinear Climate Dynamics; Cambridge University Press: New York, NY, USA, 2013; 367p. [Google Scholar]
- Trenberth, K.E. Climate System Modelling; Cambridge University Press: Cambridge, UK, 2010; 820p. [Google Scholar]
- Mezinger, F.; Arakawa, A. Numerical Methods Used in Atmospheric Models; GARP Publications Series, No. 17; WMO: Geneva, Switzerland, 1976; Volume 2. [Google Scholar]
- Kaplan, J.L.; Yorke, J.A. Chaotic Behaviour of Multidimensional Difference Equations. In Functional Differential Equations and Approximations of Fixed Points. Lecture Notes in Mathematics; Peitgen, H.-O., Walter, H.-O., Eds.; Springer: Berlin, Germany, 1979; pp. 228–237. [Google Scholar]
- Hasselmann, K. Stochastic climate models part I. Theory. Tellus 1976, 28, 473–485. [Google Scholar] [CrossRef] [Green Version]
- Rosenwasser, E.; Yusupov, R. Sensitivity of Automatic Control Systems; CRC Press: Boca Raton, FL, USA, 2000; 456p. [Google Scholar]
- Cacuci, D.G. Sensitivity and Uncertainty Analysis. Volume I: Theory; CRC Press: Boca Raton, FL, USA, 2003; 285p. [Google Scholar]
- Cacuci, D.G.; Ionesku-Bujor, M.; Navon, I.M. Sensitivity and Uncertainty Analysis, Volume II: Applications to Large-Scale Systems; CRC Press: Boca Raton, FL, USA, 2005; 353p. [Google Scholar]
- Lea, D.; Allen, M.R.; Haine, T. Sensitivity analysis of the climate of a chaotic system. Tellus 2000, 52A, 523–532. [Google Scholar] [CrossRef]
- Wang, Q. Forward and adjoint sensitivity computation for chaotic dynamical systems. J. Comput. Phys. 2013, 235, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Soldatenko, S.; Steinle, P.; Tingwell, C.; Chichkine, D. Some aspects of sensitivity analysis in variational data assimilation for coupled dynamical systems. Adv. Meteorol. 2015, 753031, 22p. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Pilyugin, S.Y. Shadowing in Dynamical Systems, Lecture Notes in Mathematics; Springer: Berlin, Germany, 1999; 276p. [Google Scholar]
- Peña, M.; Kalnay, E. Separating fast and slow models in coupled chaotic systems. Nonlinear Process. Geophys. 2004, 11, 319–327. [Google Scholar] [CrossRef]
- Leith, C.E. Climate response and fluctuation dissipation. J. Atmos. Sci. 1975, 32, 2022–2026. [Google Scholar] [CrossRef] [Green Version]
- Myhre, G.; Highwood, E.J.; Shine, K.P.; Strodal, F. New estimates of radiative forcing due to well mixed greenhouse gases. Geophys. Res. Lett. 1998, 25, 2715–2718. [Google Scholar] [CrossRef]
- Ruelle, D. General linear response formula in statistical mechanics and the fluctuation-dissipation theorem far from equilibrium. Phys. Lett. A 1998, 245, 220–224. [Google Scholar] [CrossRef]
- Zeeman, E.C. Stability of dynamical systems. Nonlinearity 1998, 1, 115–135. [Google Scholar] [CrossRef]
- Majda, A.J.; Abramov, R.; Grote, M. Information Theory and Stochastics for Multiscale Nonlinear Systems; American Mathematical Society, Centre de Recherches Mathematiques: Montreal, QC, Canada, 2005; 133p. [Google Scholar]
- Gritsun, A.; Branstator, G. Climate response using a three dimensional operator based on the fluctuation–dissipation theorem. J. Atmos. Sci. 2007, 64, 2558–2575. [Google Scholar] [CrossRef] [Green Version]
- Jeevanjee, N.; Hassanzadeh, P.; Hill, S.; Sheshadri, A. A perspective on climate model hierarchies. J. Adv. Model. Earth Syst. 2017, 9, 1760–1771. [Google Scholar] [CrossRef] [Green Version]
- Maher, P.; Gerber, E.P.; Medeiros, B.; Merlis, T.M.; Sherwood, S.; Sheshadri, A.; Sobel, A.H.; Vallis, G.K.; Voigt, A.; Zurita-Gotor, P. Model hierarchies for understanding atmospheric circulation. Rev. Geophys. 2019, 57, 250–280. [Google Scholar] [CrossRef] [Green Version]
- Volodin, E.M.; Mortikov, E.V.; Kostrykin, S.V.; Galin, V.Y.; Lykossov, V.N.; Gritsun, A.; Diansky, N.A.; Gusev, A.V.; Iakovlev, N.; Shestakova, A.A.; et al. Simulation of the modern climate using the INM-CM48 climate model. Russ. J. Anal. Math. Model. 2018, 33, 367–374. [Google Scholar] [CrossRef]
- Volodin, E.; Vorobyova, V. Evaluation of the INM RAS climate model skill in climate indices and stratospheric anomalies on seasonal time scale. Tellus A: Dyn. Meteorol. Oceanogr. 2021, 73, 1–12. [Google Scholar]
- Zalesny, V.B. Mathematical model of sea dynamics in a σ-coordinate system. Russ. J. Anal. Math. Model. 2005, 20, 97–113. [Google Scholar] [CrossRef]
- Zalesny, V.; Agoshkov, V.; Shutyaev, V.; Parmuzin, E.; Zakharova, N. Numerical Modelling of Marine Circulation with 4D Variational Data Assimilation. J. Mar. Sci. Eng. 2020, 8, 503. [Google Scholar] [CrossRef]
- Cox, P.M.; Huntingford, C.; Williamson, M.S. Emergent constraint on equilibrium climate sensitivity from global temperature variability. Nature 2018, 553, 319–322. [Google Scholar] [CrossRef] [PubMed]
- Power, S.B.; Surral, R.; Chung, C.; Colman, R.; Kharin, V.; Boer, G.; Gergis, J.; Henley, B.; McGregor, S.; Arblaster, J.; et al. Towards the prediction of multi-year to decadal climate variability in the Southern Hemisphere. CLIVAR Exch. 2017, 72, 32–40. [Google Scholar] [CrossRef]
- Budyko, M.I. The effect of solar radiation variations on the climate of the Earth. Tellus 1969, 21, 611–619. [Google Scholar] [CrossRef] [Green Version]
- Sellers, W.D. A global climatic model based on the energy balance of the Earth atmosphere system. J. Appl. Meteorol. 1969, 21, 391–400. [Google Scholar] [CrossRef]
- North, G.R. Analytical solution of a simple climate model with diffusive heat transport. J. Atmos. Sci. 1975, 32, 1300–1307. [Google Scholar] [CrossRef] [Green Version]
- Ghil, M. Climate stability for a Sellers-type model. J. Atmos. Sci. 1976, 33, 3–20. [Google Scholar] [CrossRef]
- North, G.R.; Cahalan, R.F.; James, J.; Coakley, J.A. Energy balance climate models. Rev. Geophys. Space Phys. 1981, 19, 91–121. [Google Scholar] [CrossRef] [Green Version]
- Ghil, M.; Childress, S. Topics in Geophysical Fluid Dynamics: Atmospheric Dynamics, Dynamo Theory, and Climate Dynamics; Springer: New York, NY, USA, 1987; 512p. [Google Scholar]
- Stocker, T.F.; Wright, D.G.; Mysak, L. A zonally averaged, coupled ocean-atmosphere model for paleoclimate studies. J. Clim. 1992, 5, 773–797. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Gerdes, R.; Lohmann, G. A 1-D Atmospheric energy balance model developed for ocean modelling. Appl. Clim. 1995, 51, 25–38. [Google Scholar] [CrossRef]
- Shell, K.M.; Somerville, R.C. A generalized energy balance climate model with parameterized dynamics and diabatic heating. J. Clim. 2005, 18, 1753–1772. [Google Scholar] [CrossRef]
- Lucarini, V.; Fraedrich, K.; Lunkeit, F. Thermodynamic analysis of snowball Earth hysteresis experiment: Efficiency, entropy production and irreversibility. Quart. J. R. Met. Soc. 2010, 136, 2–11. [Google Scholar] [CrossRef] [Green Version]
- Lohmann, G. Temperatures from energy balance models: The effective heat capacity matters. Earth Syst. Dynam. 2020, 11, 1195–1208. [Google Scholar] [CrossRef]
- Fraedrich, K. Catastrophes and resilience of a zero-dimensional climate system with ice-albedo and greenhouse feedback. Quart. J. R. Met. Soc. 1979, 105, 147–167. [Google Scholar] [CrossRef]
- Roe, G. Feedbacks, timescales, and seeing red. Annu. Rev. Earth Planet. Sci. 2009, 37, 93–115. [Google Scholar] [CrossRef] [Green Version]
- Alberti, T.; Lepreti, F.; Vecchio, A.; Carbone, V. On the stability of a climate model for an Earth-like planet with land-ocean coverage. J. Phys. Commun. 2018, 2, 065018. [Google Scholar] [CrossRef]
- Rombouts, J.; Ghil, M. Oscillations in a simple climate–vegetation model. Nonlin. Process. Geophys. 2015, 22, 275–288. [Google Scholar] [CrossRef] [Green Version]
- Watson, A.J.; Lovelock, J.E. Biological homeostasis of the global environment: The parable of daisyworld. Tellus 1983, 35B, 284–289. [Google Scholar] [CrossRef]
- Adams, B.; Carr, J.; Lenton, T.M.; White, A. Onedimensional daisyworld: Spatial interactions and pattern formation. J. Biol. 2003, 223, 505–513. [Google Scholar]
- Lucarini, V.; Pascale, S.; Boschi, R.; Kirk, E.; Iro, N. Habitability and multistablility in Earth-like planets. Astron. Nachr. 2013, 334, 576–578. [Google Scholar] [CrossRef] [Green Version]
- Kilic, C.; Raible, C.C.; Stocker, T.F. Multiple climate states of habitable exoplanets: The role of obliquity and irradiance. Astrophys. J. 2017, 844, 147. [Google Scholar] [CrossRef]
- Gregory, J.M. Vertical heat transport in the ocean and their effect on time-dependent climate change. Clim. Dyn. 2010, 16, 501–515. [Google Scholar] [CrossRef]
- Held, I.M.; Winton, M.; Takahashi, K.; Delworth, T.; Zeng, F.; Vallis, G.K. Probing the fast and slow components of global warming by returning abruptly to preindustrial forcing. J. Clim. 2000, 16, 2418–2427. [Google Scholar] [CrossRef] [Green Version]
- Soldatenko, S. Estimating the effect of radiative feedback uncertainties on climate response to changes in the concentration of stratospheric aerosols. Atmosphere 2020, 11, 654. [Google Scholar] [CrossRef]
- Frankignoul, C.; Hasselmann, K. Stochastic climate models, part II. Application to sea surface temperature anomalies and thermocline variability. Tellus 1977, 29, 289–305. [Google Scholar] [CrossRef] [Green Version]
- Ghil, M. Climate sensitivity, energy balance models, and oscillatory climate models. J. Geophys. Res. 1984, 89, 1280–1284. [Google Scholar] [CrossRef]
- Saravanan, R.; McWilliams, J. Advective ocean–atmosphere interaction: An analytical stochastic model with implications for decadal variability. J. Clim. 1998, 11, 165–188. [Google Scholar] [CrossRef]
- Kleeman, R. Measuring dynamical prediction utility using relative entropy. J. Atmos. Sci. 2002, 59, 2057–2072. [Google Scholar] [CrossRef] [Green Version]
- Kleeman, R. Spectral analysis of multi-dimensional stochastic geophysical models with an application to decadal ENSO variability. J. Atmos. Sci. 2011, 68, 13–25. [Google Scholar] [CrossRef]
- Rogues, L.; Chekroun, M.D.; Cristofol, M.; Soubeyrand, S.; Ghil, M. Parameter estimation for energy balance models with memory. Proc. R. Soc. 2014, A 470, 20140349. [Google Scholar] [CrossRef] [Green Version]
- Proistosescu, C.; Donohoe, A.; Armour, K.C. at al. Radiative feedbacks from stochastic variability in surface temperature and radiative imbalance. Geophys. Res. Lett. 2018, 45, 5082–5094. [Google Scholar] [CrossRef] [Green Version]
- Cummins, D.P.; Stephenson, D.B.; Stott, P.A. Optimal estimation of stochastic energy balance model parameters. J. Clim. 2020, 33, 7909–7926. [Google Scholar] [CrossRef] [Green Version]
- Klyatskin, V.I. Lectures on Dynamics of Stochastic Systems; Elsevier: Amsterdam, The Netherlands, 2010; 410p. [Google Scholar]
- Gardiner, C. Stochastic Methods: A Handbook for the Natural and Social Sciences, 4th ed.; Springer: Berlin, Germany, 2009; 447p. [Google Scholar]
- Geoffroy, O.; Saint-Martin, D.; Olivie, D.J.L.; Voldoire, A.; Bellon, G.; Tytéca, S. Transient climate response in a two-layer energy-balance model. Part I: Analytical solution and parameter calibration using representation of the efficacy of deep-ocean heat uptake and validation for CMIP5 AOGCMs. J. Clim. 2013, 26, 1841–1857. [Google Scholar] [CrossRef]
- Soldatenko, S.; Colman, R. Climate variability from annual to multi-decadal timescales in a two-layer stochastic energy balance model: Analytic solutions and implications for general circulation models. Tellus A Dyn. Meteorol. Oceanogr. 2019, 71, 1554421. [Google Scholar] [CrossRef]
- Pelletier, J.D. The power spectral density of atmospheric temperature from time scales of 10−2 to 106 yr. Earth Planet. Sci. Lett. 1998, 158, 157–164. [Google Scholar] [CrossRef]
- Pelletier, J.D. Natural variability of atmospheric temperatures and geomagnetic intensity over a wide range of time scales. PNAS 2003, 99, 2546–2553. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fredriksen, H.-B.; Rypdal, K. Spectral characteristics of instrumental and climate model surface temperatures. J. Clim. 2016, 29, 1253–1268. [Google Scholar] [CrossRef]
- Zhu, F.; Emile-Geay, J.; McKay, N.P.; Hakim, G.J.; Khider, D.; Ault, T.R.; Steig, E.J.; Dee, S.; Kirchner, J.W. Climate models can correctly simulate the continuum of global temperature variability. PNAS 2019, 116, 8728–8733. [Google Scholar] [CrossRef] [PubMed] [Green Version]


| c | ||||||
|---|---|---|---|---|---|---|
| 0.8 | 0.07 | 0.07 | 1.02 | 0.03 | 0.08 | 0.69 |
| 0.15 | −0.01 | −0.01 | 1.01 | −0.09 | −0.09 | 0.91 |
| Uncertainty | Period of Oscillations (yr) | |||
|---|---|---|---|---|
| 2 | 10 | 30 | 100 | |
| ±8.66 × 10−8 | ±4.03 × 10−5 | ±7.14 × 10−4 | ±1.793 × 10−3 | |
| ±1.20 × 10−5 | ±2.23 × 10−4 | ±4.46 × 10−4 | ±1.17 × 10−4 | |
| ) | ±0.2 | ±4.7 | ±19.6 | ±30.9 |
| ) | ±29.8 | ±25.7 | ±12.2 | ±2.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soldatenko, S.; Bogomolov, A.; Ronzhin, A. Mathematical Modelling of Climate Change and Variability in the Context of Outdoor Ergonomics. Mathematics 2021, 9, 2920. https://doi.org/10.3390/math9222920
Soldatenko S, Bogomolov A, Ronzhin A. Mathematical Modelling of Climate Change and Variability in the Context of Outdoor Ergonomics. Mathematics. 2021; 9(22):2920. https://doi.org/10.3390/math9222920
Chicago/Turabian StyleSoldatenko, Sergei, Alexey Bogomolov, and Andrey Ronzhin. 2021. "Mathematical Modelling of Climate Change and Variability in the Context of Outdoor Ergonomics" Mathematics 9, no. 22: 2920. https://doi.org/10.3390/math9222920
APA StyleSoldatenko, S., Bogomolov, A., & Ronzhin, A. (2021). Mathematical Modelling of Climate Change and Variability in the Context of Outdoor Ergonomics. Mathematics, 9(22), 2920. https://doi.org/10.3390/math9222920







