Fuzzy Logical Algebra and Study of the Effectiveness of Medications for COVID-19

Abstract

A fuzzy logical algebra has diverse applications in various domains such as engineering, economics, environment, medicine, and so on. However, the existing techniques in algebra do not apply to delta-algebra. Therefore, the purpose of this paper was to investigate new types of cubic soft algebras and study their applications, the representation of cubic soft sets with $\delta$-algebras, and new types of cubic soft algebras, such as cubic soft $\delta$-subalgebra based on the parameter $\lambda$ (λ-CSδ-SA) and cubic soft $\delta$-subalgebra (CSδ-SA) over $\eta$. This study explains why the P-union is not really a soft cubic $\delta$-subalgebra of two soft cubic $\delta$-subalgebras. We also reveal that any R/P-cubic soft subsets of (CSδ-SA) is not necessarily (CSδ-SA). Furthermore, we present the required conditions to prove that the R-union of two members is (CSδ-SA) if each one of them is (CSδ-SA). To illustrate our assumptions, the proposed (CSδ-SA) is applied to study the effectiveness of medications for COVID-19 using the python program.

1. Introduction

Artificial Intelligence (AI) and logical algebra are studied in different non-classical sets like soft sets [1], fuzzy sets [2], and others, to solve various problems in our life. For example, in 2021, nano-sets have been used to study COVID-19 [3]. COVID-19 has also been studied by Arfan and others [4]. Zhong et al. [5] showed that the majority of inhabitants with an above-average socioeconomic status, particularly females, expressed optimism about COVID-19. A variety of AI and logic applications have been introduced in diverse domains including the medical field [6,7]. The concept of fuzzy set (FS) was introduced by Zadeh [8] in 1965 and has been then successfully applied in different domains [9,10]. The connotation of fuzzy algebra determined by G. Xi [9] is called fuzzy $BCK$-algebra. Several applications of fuzzy $BCK$-algebras were discussed by Y. B. Jun [10].

In [11], some concepts of fuzzy algebras such as fuzzy $\rho$-subalgebra $\left(F\rho \text{-}SA\right)$, fuzzy $\rho$-ideal $\left(F\rho \text{-}I\right)$, and fuzzy $\overline{\rho }$-ideal $\left(F\overline{\rho }\text{-}I\right)$ were introduced. The mathematical idea of soft sets is a fresh notion studied by D. Molodtsov [12]. This theory has been applied in various fields, as fuzzy sets theory [13]. The notion of fuzzy soft algebra was introduced by Jun and others [14], who called it fuzzy soft $BCK$-algebra.

The connotations of interval-valued fuzzy sets (IVFS) were investigated as an extension of FS [15]. Similar to BCK, IVFS has been applied to various domains and subgroups [2]. Moreover, the general ideas of algebraic fuzzy systems (AFS) are enriched by introducing the notion of fuzzy subsets. Jun et al. [16] presented some operations such as P/R-union and P/R-intersection on cubic sets. They described several different ways to find the solutions for intricate problems in engineering, economics, and environment.

While conventional methods have been successfully applied in diverse domains, these methods do not handle uncertainties. Sometimes traditional methods in logical algebra are not sufficient to solve some problems or to obtain good results because different uncertainties models are necessary for those problems. The majority of system algebras are not commutative for any non-fixed pair of their members. Therefore, some algebra structures that are commutative for any non-fixed pair of their members, such as $\rho$-algebra [11] and $\delta$-algebra [17], have been proposed. In this work, we used $\delta$-algebra to consider new types of cubic soft algebras, such as (λ-CSδ-SA) and (CSδ-SA). These classes in $\delta$-algebra are different from any other class, since any pair $\omega \ne \upsilon \in \eta -\{f\}$ in algebra $\left(\eta ,o,f\right)$, they satisfy the condition $\left(\upsilon o\left(\upsilon o\omega \right)\right)o\left(\omega o\upsilon \right)=f$. We also proved that P-union is not really a soft cubic subalgebra of two soft cubic $\delta$-subalgebras. We revealed that for any R/P-cubic soft subset of (CSδ-SA), it is not necessarily true to be (CSδ-SA). Furthermore, we present the required conditions to prove that the R-union of two members is (CSδ-SA) if each one of them is (CSδ-SA). To illustrate our notations, the applied (CSδ-SA) to study the effectiveness of medications for COVID-19.

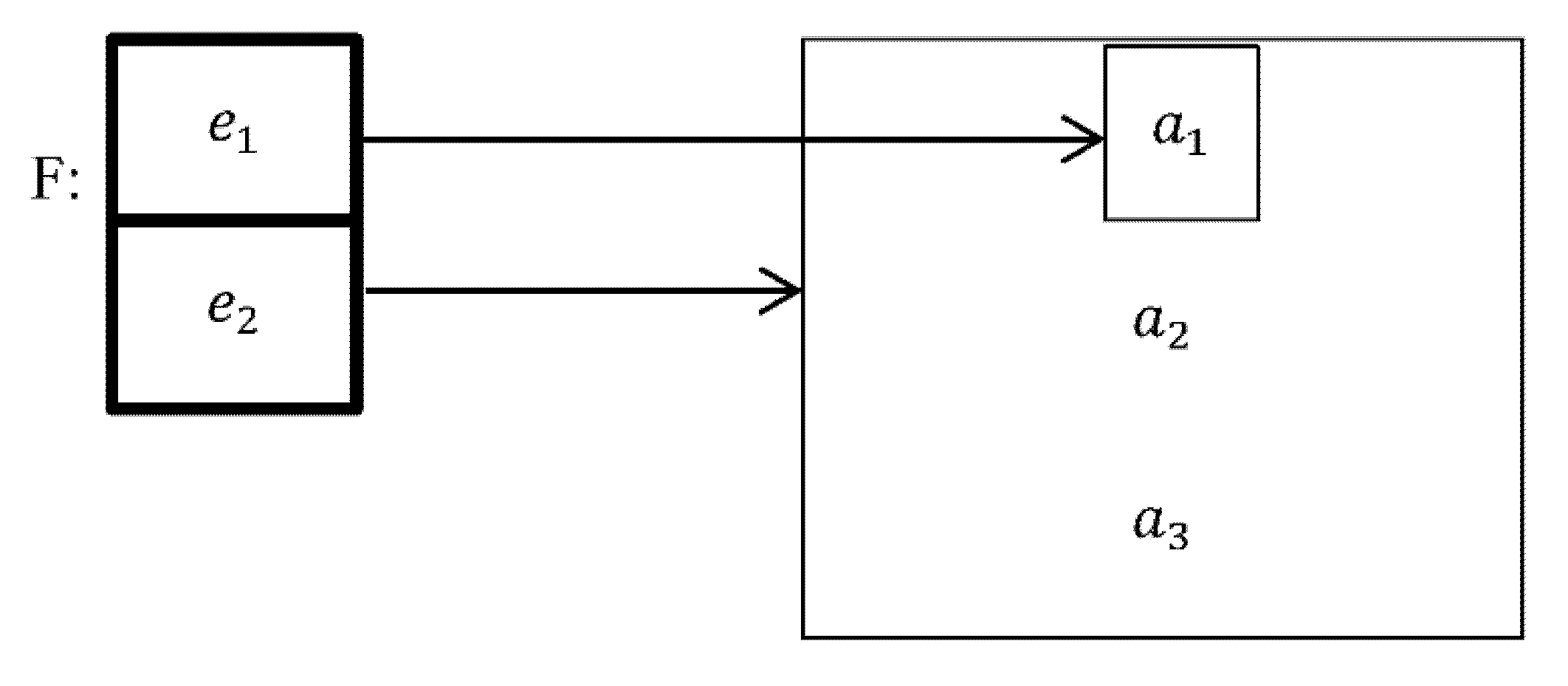
2. Preliminary

In this section, we will present some definitions that are necessary for our work.

Definition 1.

([17]) We denote $\left(\eta ,o,f\right)$ as $\delta$-algebra (briefly, $\left(\delta \text{-}A\right)$) if $f\in$, and the following assumptions are fulfilled:

(i)

$\upsilon o\upsilon =f$

(ii)

$fo\upsilon =f$

(iii)

$\upsilon o\omega =f$ and $\omega o\upsilon =f$ → $\upsilon =\omega$, for all $\omega ,\upsilon \in \eta$.

(iv)

For all $\omega \ne \upsilon \in \eta -\{f\}$ → $\upsilon o\omega =\omega o\upsilon \ne f$.

(v)

For all $\omega \ne \upsilon \in \eta -\{f\}$ → $\left(\upsilon o\left(\upsilon o\omega \right)\right)o\left(\omega o\upsilon \right)=f$.

Definition 2.

([8]) Let $\eta \ne \varnothing$. A mapping $\psi :\eta \to \left[0,1\right]$ is called fuzzy set (FS) of $\eta$. We denote the family of all (FSs) in $\eta$ by ${{\rm B}}^{\eta }$. Let ≤ be a relation on ${{\rm B}}^{\eta }$ specified by:

$$\left(\psi \le {\psi }^{\prime },\forall \psi ,{\psi }^{\prime }\in {{\rm B}}^{\eta }\right)\iff \left(\psi \left(\upsilon \right)\le {\psi }^{\prime }\left(\upsilon \right),\forall \upsilon \in \eta \right)$$

(1)

Let ($\vee$) and ($\wedge$) be operations on ${{\rm B}}^{\eta }$, specified by:

$$\left(\psi \vee {\psi }^{\prime }\right)\left(\upsilon \right)=\max \{\psi \left(\upsilon \right),{\psi }^{\prime }\left(\upsilon \right)\},$$

$$\left(\psi \wedge {\psi }^{\prime }\right)\left(\upsilon \right)=\min \{\psi \left(\upsilon \right),{\psi }^{\prime }\left(\upsilon \right)\},\forall \upsilon \in \eta$$

(2)

For each $\psi \in {{\rm B}}^{\eta }$, we denote its complement as ${\psi }^c$, specified by

$${\psi }^c\left(\upsilon \right)=1-\psi \left(\upsilon \right),\forall \upsilon \in \eta$$

(3)

Let $\{{\psi }_{\lambda }|\lambda \in \mathsf{\Delta }\}$ be a collection of (FSs), where $\mathsf{\Delta }$ is an index set. Therefore, ($\vee$) and ($\wedge$) are specified by:

$$(\underset{\lambda \in \mathsf{\Delta }}{\vee }\psi )(\upsilon )=\sup \{{\psi }_{\lambda }(\upsilon )|\lambda \in \mathsf{\Delta }\},$$

(4)

$$(\underset{\lambda \in \mathsf{\Delta }}{\wedge }\psi )(\upsilon )=\inf \{{\psi }_{\lambda }(\upsilon )|\lambda \in \mathsf{\Delta }\},\forall \upsilon \in \eta$$

Definition 3.

([18]) Let ${\rm Z}=\left[{\theta }_{}^{-},{\theta }_{}^{+}\right]$ be a closed subinterval of ${\rm B}=\left[0,1\right]$; Z is said to be an interval number (IN), where $0\le {\theta }^{-}\le {\theta }^{+}\le 1$. The family of all interval numbers (INs) is symbolized by $\left[B\right].$

Some operations on $\left[{\rm B}\right]$ like r min (refined minimum), r max (refined maximum), “$\tilde{\ge }$”, “$\tilde{\le }$” and “=”, are specified by:

$$r\min \{{\rm Z},{{\rm Z}}^{\prime }\}=[\min \{{\theta }_{}^{-},{{\theta }^{\prime }}_{}^{-}\},\min \{{\theta }_{}^{+},{{\theta }^{\prime }}_{}^{+}\}]$$

$$r\max \{{\rm Z},{{\rm Z}}^{\prime }\}=[\max \{{\theta }_{}^{-},{{\theta }^{\prime }}_{}^{-}\},\max \{{\theta }_{}^{+},{{\theta }^{\prime }}_{}^{+}\}]$$

(5)

${\rm Z}\tilde{\ge }{{\rm Z}}^{\prime }\iff {\theta }_{}^{-}\ge {{\theta }^{\prime }}_{}^{-}$ and ${\theta }_{}^{+}\ge {{\theta }^{\prime }}_{}^{+},$ Moreover, ${\rm Z}={{\rm Z}}^{\prime }\iff {\theta }^{-}={{\theta }^{\prime }}_{}^{-}$, ${\theta }_{}^{+}={{\theta }^{\prime }}_{}^{+}$, if $\underset{\lambda \in \mathsf{\Delta }}{{\displaystyle \psi }}\in \{[B]/\lambda \in \mathsf{\Delta }\}$, is a collection of INs. Then,

$$r{\inf }_{\lambda \in \mathsf{\Delta }}{{\rm Z}}_{\lambda }=\left[{\inf }_{\lambda \in \mathsf{\Delta }}{\theta }_{\lambda }^{-},{\inf }_{\lambda \in \mathsf{\Delta }}{\theta }_{\lambda }^{+}\right],$$

$$r{\sup }_{\lambda \in \mathsf{\Delta }}{{\rm Z}}_{\lambda }=\left[{\sup }_{\lambda \in \mathsf{\Delta }}{\theta }_{\lambda }^{-},{\sup }_{\lambda \in \mathsf{\Delta }}{\theta }_{\lambda }^{+}\right]$$

(6)

We refer to the complement of any ${\rm Z}\in \left[{\rm B}\right]$ by ${{\rm Z}}^c$, where

$${{\rm Z}}^c=\left[1-{\theta }_{}^{+},1-{\theta }_{}^{-}\right]$$

(7)

Let $\varnothing \ne \eta$. Then, $\zeta : \eta \to \left[{\rm B}\right]$ is called an interval-valued fuzzy set (IVFS) in $\eta$. We refer to the family of all interval-valued fuzzy sets (IVFSs) in $\eta$ by ${[{\rm B}]}^{\eta }$. On the other side, if $\xi \in {[{\rm B}]}^{\eta }$ and $\upsilon \in \eta$, we refer to the degree of membership of $\upsilon$ to $\eta$ by $\xi \left(\upsilon \right)=\left[{\xi }^{-}\left(\upsilon \right),{\xi }^{+}\left(\upsilon \right)\right]$ or $\xi =\left[{\xi }^{-},{\xi }^{+}\right]$, where ${\xi }^{-}:\eta \to {\rm B}$ is the lower fuzzy set (LFS), and ${\xi }^{+}:\eta \to {\rm B}$ is the upper fuzzy set (UFS) in $\eta$. The definitions of the symbols “$\subseteq$” and “=” on any ${\xi }_{},{\xi }_{}^{\text{'}}\in {[{\rm B}]}^{\eta }$ can be given as follows:

$${\xi }_{}\subseteq {\xi }^{\prime }\iff \xi \left(\upsilon \right)\tilde{\le }{\xi }^{\prime }\left(\upsilon \right),\forall \upsilon \in \eta$$

$${\xi }_{}={\xi }^{\prime }\iff \xi \left(\upsilon \right)={\xi }^{\prime }\left(\upsilon \right),\forall \upsilon \in \eta$$

(8)

We refer to the complement of any $\xi \in {[{\rm B}]}^{\eta }$ by ${\xi }^c$, where ${\xi }^c\left(\upsilon \right)=\xi {(\upsilon )}^c$, $\forall \upsilon \in \eta$. That means

$${\xi }^c\left(\upsilon \right)=\left[1-{\xi }^{+}\left(\upsilon \right),1-{\xi }^{-}\left(\upsilon \right)\right]\forall \upsilon \in \eta$$

(9)

If $\{{\xi }_{\lambda }\in {\left[{\rm B}\right]}^{\eta }|\lambda \in \mathsf{\Delta }\}$ is a family of (IVFSs), then “${{\displaystyle \cup }}^{}”$ and “${{\displaystyle \cap }}^{}$” are defined in ${[{\rm B}]}^{\eta }$ as follows:

$$\left({{{\displaystyle \cup }}^{}}_{\lambda \in \mathsf{\Delta }}{\xi }_{\lambda }\right)\left(\upsilon \right)=r{\sup }_{\lambda \in \mathsf{\Delta }}{\xi }_{\lambda }\left(\upsilon \right),\forall \upsilon \in \eta ,$$

$$\left({{{\displaystyle \cap }}^{}}_{\lambda \in \mathsf{\Delta }}{\xi }_{\lambda }\right)\left(\upsilon \right)=r{\inf }_{\lambda \in \mathsf{\Delta }}{\xi }_{\lambda }\left(\upsilon \right),\forall \upsilon \in \eta .$$

(10)

Definition 4.

([12]) Let $\eta$ be a universal set, with parameter set $\mathsf{\Delta }$; $\left(\epsilon ,\sigma \right)$ is said to be a soft set (over $\eta$), where $\epsilon :\sigma \to P\left(\eta \right)$, and $P\left(\eta \right)$ is the power set of $\eta$ with $\sigma \subseteq \mathsf{\Delta }$.

Definition 5.

([16]) We define a cubic set $\Phi$ (CS) in $\eta$ by

$$\Phi =\{\langle \upsilon ,\xi \left(\upsilon \right),\psi \left(\upsilon \right)\rangle /\upsilon \in \eta \}$$

(11)

We can also write it as $\Phi =\langle \xi ,\psi \rangle$, where $\xi$ is IVFS, and $\psi$ is FS.

Definition 6.

([16]) Let $\Phi =\langle \xi ,\psi \rangle$ and ${\Phi }^{\prime }=\langle {\xi }^{\prime },{\psi }^{\prime }\rangle$ be a pair of cubic sets (CSs) in $\eta$. We define “${\subseteq }_P$”, “${\subseteq }_R$”, and “=” by the following:

(i)

(P-order) $\Phi {\subseteq }_P{\Phi }^{\prime }\iff \xi \subseteq {\xi }^{\prime }$ and $\psi \le {\psi }^{\prime }$.

(ii)

(R-order) $\Phi {\subseteq }_R{\Phi }^{\prime }\iff \xi \subseteq {\xi }^{\prime }$ and $\psi \ge {\psi }^{\prime }$.

(iii)

(Equality) $\Phi ={\Phi }^{\prime }\iff \xi ={\xi }^{\prime }$ and $\psi ={\psi }^{\prime }$.

Definition 7.

([16]) Let ${\{{\Phi }_{\lambda }=\{\langle \upsilon ,{\xi }_{\lambda }\left(\upsilon \right),{\psi }_{\lambda }\left(\upsilon \right)\rangle /\upsilon \in \eta \}\}}_{\lambda \in \mathsf{\Delta }}$ be a collection of (CSs) in $\eta$. The symbol “${{{\displaystyle \cup }}^{}}_P$” (resp., “${{{\displaystyle \cap }}^{}}_P$”, “${{{\displaystyle \cup }}^{}}_R$” and “${{{\displaystyle \cap }}^{}}_R$”) is said to be (P-union) (resp., P-intersection, R-union, and R-intersection) and is obtained as follows:

(1)

${{{\displaystyle \cup }}^{}}_{p,\lambda \in \mathsf{\Delta }}{\Phi }_{\alpha }=\{\langle \upsilon ,\underset{\lambda \in \mathsf{\Delta }}{{{\displaystyle \cup }}^{}}{\xi }_{\lambda }\left(\upsilon \right),\underset{\lambda \in \mathsf{\Delta }}{\vee }{\psi }_{\lambda }\left(\upsilon \right)\rangle /\upsilon \in \eta \}$,

(2)

${{{\displaystyle \cap }}^{}}_{p,\lambda \in \mathsf{\Delta }}{\Phi }_{\lambda }=\{\langle \upsilon ,\underset{\lambda \in \mathsf{\Delta }}{{{\displaystyle \cap }}^{}}{\xi }_{\lambda }\left(\upsilon \right),\underset{\lambda \in \mathsf{\Delta }}{\wedge }\psi \lambda \left(\upsilon \right)\rangle /\upsilon \in \eta \}$,

(3)

${{{\displaystyle \cup }}^{}}_{R,\lambda \in \mathsf{\Delta }}{\Phi }_{\alpha }=\{\langle \upsilon ,\underset{\lambda \in \mathsf{\Delta }}{{{\displaystyle \cup }}^{}}{\xi }_{\lambda }\left(\upsilon \right),\underset{\lambda \in \mathsf{\Delta }}{\vee }{\psi }_{\lambda }\left(\upsilon \right)\rangle /\upsilon \in \eta \}$,

(4)

${{{\displaystyle \cap }}^{}}_{R,\lambda \in \mathsf{\Delta }}{\Phi }_{\lambda }=\{\langle \upsilon ,\underset{\lambda \in \mathsf{\Delta }}{{{\displaystyle \cap }}^{}}{\xi }_{\lambda }\left(\upsilon \right),\underset{\lambda \in \mathsf{\Delta }}{\wedge }\psi \lambda \left(\upsilon \right)\rangle /\upsilon \in \eta \}$,

Remark 1.

([19])

The complement of $\Phi =\langle \xi ,\psi \rangle$ is defined as:

$${\Phi }^c=\{\langle \upsilon ,\xi {(\upsilon )}^c,{\psi }^c\left(\upsilon \right)\rangle /\upsilon \in \eta \}$$

(12)

$$({\Phi }^c{)}^c=\Phi$$

(13)

If ${\{{\Phi }_{\lambda }=\{\langle \upsilon ,{\xi }_{\lambda }\left(\upsilon \right),{\psi }_{\alpha }\left(\upsilon \right)\rangle /\upsilon \in \eta \}\}}_{\lambda \in \mathsf{\Delta }}$ is a collection of (CSs) in $\eta$, then we have the followng;

$${({{{\displaystyle \cup }}^{}}_{p,\lambda \in \mathsf{\Delta }}{\Phi }_{\lambda })}^c={{{\displaystyle \cup }}^{}}_{p,\lambda \in \mathsf{\Delta }}{({\Phi }_{\lambda })}^c,{({{{\displaystyle \cap }}^{}}_{p,\lambda \in \mathsf{\Delta }}\Phi \lambda )}^c={{{\displaystyle \cap }}^{}}_{p,\lambda \in \mathsf{\Delta }}{({\Phi }_{\lambda })}^c,{({{{\displaystyle \cup }}^{}}_{R,\lambda \in \mathsf{\Delta }}{\Phi }_{\lambda })}^c={{{\displaystyle \cap }}^{}}_{R,\lambda \in \mathsf{\Delta }}{({\Phi }_{\lambda })}^c\mathrm{and}{({{{\displaystyle \cap }}^{}}_{R,\lambda \in \mathsf{\Delta }}{\Phi }_{\lambda })}^c={{{\displaystyle \cup }}^{}}_{R,\lambda \in \mathsf{\Delta }}{({\Phi }_{\lambda })}^c$$

(14)

Therefore, a (CS) $\Phi =\{\langle \upsilon ,{\xi }_{\Phi }\left(\upsilon \right),{\psi }_{\Phi }\left(\upsilon \right)\rangle /\upsilon \in \eta \}$ is denoted by $\Phi =\langle {\xi }_{\Phi },{\psi }_{\Phi }\rangle$. The family of all (CSs) in $\eta$ is referred to as ${{{\displaystyle \int }}^{}}^{\eta }$.

Definition 8.

([19]) Let $\eta$ be a universal set with the parameter set $\mathsf{\Delta }$; $\left(\Omega ,\Re \right)$ is said to be a cubic soft set (CSS) over $\eta$, where $\Re \subseteq \mathsf{\Delta }$, and $\Omega :\Re \to {{\int }^{}}^{\eta }$ is a mapping. We write $\left(\Omega ,\Re \right)$ as:

$$\left(\Omega ,\Re \right)=\{\Omega \left(\lambda \right)/\lambda \in \Re \},\mathrm{where} \Omega \left(\lambda \right)=\langle {\xi }_{\Omega \left(\lambda \right)},{\psi }_{\Omega \left(\lambda \right)}\rangle .$$

(15)

The set of all cubic soft sets (CSSs) is symbolized by ${ }_{\mathsf{\Delta }}{{\int }^{}}^{\eta }$.

Definition 9.

([19]) Let $\left(\Omega ,\Re \right)$, $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ ${\in }_{\mathsf{\Delta }}{{{\displaystyle \int }}^{}}^{\eta }$. The R-union of $\left(\Omega ,\Re \right)$ and $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ is a (CSS) $\left(D,W\right)$ symbolized by $\left(D,W\right)$ = $\left(\Omega ,\Re \right)$ ${\overline{\cup }}_R\left({\Omega }^{\prime },{\Re }^{\prime }\right)$, where $W=\Re {{\displaystyle \cup }}^{}{\Re }^{\prime }$ and

$$\left(\lambda \right)=\{\begin{array}{c}\Omega \left(\lambda \right),if\lambda \in \Re \backslash {\Re }^{\prime }\\ {\Omega }^{\prime }\left(\lambda \right),if\lambda \in {\Re }^{\prime }\backslash \Re \\ \Omega \left(\lambda \right){{{\displaystyle \cup }}^{}}_R{\Omega }^{\prime }\left(\lambda \right),if\lambda \in \Re {{\displaystyle \cap }}^{}{\Re }^{\prime }\end{array},\forall \lambda \in W$$

(16)

Definition 10.

([19]) Let $\left(\Omega ,\Re \right)$, $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ ${\in }_{\mathsf{\Delta }}{{{\displaystyle \int }}^{}}^{\eta }$. The p-union of $\left(\Omega ,\Re \right)$ and $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ is a (CSS) $\left(D,W\right)$ symbolized by $\left(D,W\right)=$ $(\Omega ,\Re )$${\overline{\cup }}_P\left({\Omega }^{\prime },{\Re }^{\prime }\right)$, where $W=\Re {{\displaystyle \cup }}^{}{\Re }^{\prime }$ and

$$\left(\lambda \right)=\{\begin{array}{c}\Omega \left(\lambda \right),if\lambda \in \Re \backslash {\Re }^{\prime }\\ {\Omega }^{\prime }\left(\lambda \right),if\lambda \in {\Re }^{\prime }\backslash \Re \\ \Omega \left(\lambda \right){{{\displaystyle \cup }}^{}}_P{\Omega }^{\prime }\left(\lambda \right),if\lambda \in \Re {{\displaystyle \cap }}^{}{\Re }^{\prime }\end{array},\forall \lambda \in W$$

(17)

Definition 11.

([19]) Let $\left(\Omega ,\Re \right)$, $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ ${\in }_{\mathsf{\Delta }}{{{\displaystyle \int }}^{}}^{\eta }$. The p-intersection of $\left(\Omega ,\Re \right)$ and $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ is a (CSS) $\left(D,W\right)$ symbolized by $\left(D,W\right)=$ $(\Omega ,\Re )$${\overline{{{\displaystyle \cap }}^{}}}_P\left({\Omega }^{\prime },{\Re }^{\prime }\right)$, where $W=\Re {{\displaystyle \cup }}^{}{\Re }^{\prime }$ and

$$D\left(\lambda \right)=\{\begin{array}{c}\Omega \left(\lambda \right),if\lambda \in \Re \backslash {\Re }^{\prime }\\ {\Omega }^{\prime }\left(\lambda \right),if\lambda \in {\Re }^{\prime }\backslash \Re \\ \Omega \left(\lambda \right){{{\displaystyle \cap }}^{}}_P{\Omega }^{\prime }\left(\lambda \right),if\lambda \in \Re {{\displaystyle \cap }}^{}{\Re }^{\prime }\end{array},\forall \lambda \in W$$

(18)

Definition 12.

([19]) Let $\left(\Omega ,\Re \right)$, $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ ${\in }_{\mathsf{\Delta }}{{{\displaystyle \int }}^{}}^{\eta }$. We say $\left(\Omega ,\Re \right)$ is an R-cubic soft subset of $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ if

$$\Re \subseteq {\Re }^{\prime },\Omega \left(\lambda \right){\subseteq }_R{\Omega }^{\prime }\left(\lambda \right),\forall \lambda \in \Re .$$

(19)

Definition 13.

([19]) Let $\left(\Omega ,\Re \right)$, $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ ${\in }_{\mathsf{\Delta }}{{{\displaystyle \int }}^{}}^{\eta }$. We say $\left(\Omega ,\Re \right)$ is a P-cubic soft subset of $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ if

$$\Re \subseteq {\Re }^{\prime },\Omega \left(\lambda \right){\subseteq }_P{\Omega }^{\prime }\left(\lambda \right),\forall \lambda \in \Re .$$

(20)

Example 1.

Let the set of students under consideration be $\eta =$ $\{a_1,a_2,a_3\}$. Let $E=$ {pleasing personality ($e_1$); conduct ($e_2$); good result ($e_3$); sincerity ($e_4$)} be the set of parameters used to choose the best student. Suppose that the soft set $(F,A)$ describing Mr. $X$’s opinion about the best student in an academic year is defined by

$$A=\{e_1,e_2\},F(e_1)=\{a_1\},F(e_2)=\{a_1,a_2,a_3\}$$

The description of Mr. $X$’s opinion is explained see Figure 1.

However, if we define $\left(\Omega ,A\right)=$ {{$\langle \left[0.5,0.7\right],0.8\rangle$, 〈[0.3, 0.5], 0.3〉, 〈[0.4, 0.6], 0.7〉}, {〈[0.4, 0.5], 0.8〉, 〈[0.3, 0.4], 0.8〉, 〈[0.2, 0.5], 0.6〉}}, then $\left(\Omega ,A\right)$ is a cubic soft set over $\eta =$ {$a_1,a_2$, $a_3$}, dependent on (FS) to describe the best student by the rates of some activities $A=\{e_1,e_2\}$ of $E$; each rate ranges between 0 and 1 and approaches 0 when an activity is low, while it approaches 1 when an activity is high).

3. Cubic Soft $\delta$-Subalgebras in $\delta$-Algebras and Its Application for COVID-19

In this section, we will consider several new forms of cubic soft algebras and see how they can be used to study the effectiveness of medications for COVID-19.

Definition 14.

Let $\left(\Omega ,\Re \right)$ be (CSS) over $\eta$; $\left(\eta ,o,f\right)$ is $\left(\delta \text{-}A\right)$, if there exists a parameter $\lambda \in \Im$ that satisfies the following:

$${\xi }_{\Omega \left(\lambda \right)}\left(\upsilon \circ \omega \right)\tilde{\ge }r\min \{{\xi }_{\Omega \left(\lambda \right)}\left(\upsilon \right),{\xi }_{\Omega \left(\lambda \right)}\left(\omega \right)\}\forall \upsilon ,\omega \in \eta$$

(21)

$${\psi }_{\Omega \left(\lambda \right)}\left(\upsilon \circ \omega \right)\tilde{\le }r\max \{{\psi }_{\Omega \left(\lambda \right)}\left(\upsilon \right),{\psi }_{\Omega \left(\lambda \right)}\left(\omega \right)\}\forall \upsilon ,\omega \in \eta$$

(22)

$\left(\Omega ,\Re \right)$ is said to be a cubic soft $\delta$-subalgebra over $\eta$ based on a parameter $\lambda$ (briefly, (λ-CSδ-SA) over $\eta$) and is called a cubic soft $\delta$-subalgebra (CSδ-SA) over $\eta$, if $it$ is an (λ-CSδ-SA) over $\eta ,\forall \lambda \in \Re$.

Theorem 1.

If $\left(\Omega ,\Re \right)$, $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ ${\in }_{\mathsf{\Delta }}{{\int }^{}}^{\eta }$ with $\Re$ and ${\Re }^{\prime }$ are disjoint, then their P-union is a (CSδ-SA) over $\eta$.

Proof. 

From Definition (10), we have $\left(D,W\right)=\left(\Omega ,\Re \right){\overline{\cup }}_P\left({\Omega }^{\prime },{\Re }^{\prime }\right)$, where $W=\Re {{\displaystyle \cup }}^{}{\Re }^{\prime }$ and

$$D\left(\lambda \right)=\{\begin{array}{c}\Omega \left(\lambda \right),if\lambda \in \Re \backslash {\Re }^{\prime }\\ {\Omega }^{\prime }\left(\lambda \right),if\lambda \in {\Re }^{\prime }\backslash \Re \\ \Omega \left(\lambda \right){{{\displaystyle \cup }}^{}}_P{\Omega }^{\prime }\left(\lambda \right),if\lambda \in \Re {{\displaystyle \cap }}^{}{\Re }^{\prime } \end{array},\forall \lambda \in W$$

(23)

Therefore, either $\lambda \in \Re \backslash {\Re }^{\prime }$ or $\lambda \in {\Re }^{\prime }\backslash \Re ,\forall \lambda \in W$ (since $\Re {{\displaystyle \cap }}^{}{\Re }^{\prime }=\phi$). If $\lambda \in \Re \backslash {\Re }^{\prime }$, then $D\left(\lambda \right)=\Omega \left(\lambda \right)$ is a $CS\delta$-subalgebra over $\eta$. In addition, if $\lambda \in {\Re }^{\prime }\backslash \Re$, then $D\left(\lambda \right)={\Omega }^{\prime }\left(\lambda \right)$ is a (CSδ-SA) over $\eta$. So, $\left(D,W\right)=(\Omega ,\Re )$ ${\overline{\cup }}_P\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ is a (CSδ-SA) over $\eta$.  □

Remark 2.

The above theorem is not true in general when $\Re$ and ${\Re }^{\prime }$ are not disjoint.

Example 2.

Let $\eta =\{f,\upsilon ,\omega ,\sigma ,\tau \}$ be a universal set of some medications for (COVID-19), as follows $f=$ Chloroquine, $\upsilon =$ Arbidol, $\omega$ = Tamiflu, $\sigma$ = Kaletra, $\tau$ = Remdesivir. These medications were chosen because they have been tried and discussed by researchers, for example, Chloroquine in [20], Arbidol in [21], Tamiflu in [22], Kaletra in [23], and Remdesivir in [24]. We used virtual reality to introduce a mathematical method where the composition of the members forms an $algebraic$ system; we determined how to find the cubic soft set over $\eta$, when it is dependent on (FS) to describe the best medication in the basis of its activity evaluated by rates, with each rate confined between 0 and 1. If a rate appr2oaches 0, then activity is low, whereas if the rate is closer to 1, the activity is high. Suppose that for any two members in $\eta$, their composition under operation is defined by the python program as follows:

from numpy import array

X = ['f','v','w','σ','τ']

i = 0

lst = array (range (25), dtype = str). reshape (5,5)

for a in X:

j = 0

for b in X:

# print (a, '    ', b)

if ((a == 'f') or (a == b) :

m = 'f'

elif ((b = 'f')):

m = a

elif ((a! = 'f') and (b! = 'f') ):

m = 'v'

lst [i,j] = m

j = j + 1

I = I + 1

print(lst)

Using this program, let us consider Figure 2, where rows are placed in a table.

This algorithm makes the members distributive for any set $\eta =\{r_1,r_2,\dots ,r_n\}$ that has $n$ members inside a matrix $M=\left(\begin{array}{ccc}{m}_{11}& \cdots & m_{1n}\\ ⋮& \ddots & ⋮\\ m_{n1}& \cdots & m_{nn}\end{array}\right)$ of degree ($n\times n$), where $m_{ij}=r_{i}o{r}_j=r_k\in \eta$ for some $\left(1\le k\le n\right)$ and all $\left(1\le i,j\le n\right)$. By this matrix, our table can have the structure of $\delta$-algebra.

Therefore, the binary operation $o$ is described in a

Table 1. (η,ο,f) is a δ-algebra.

$\tau$	$\sigma$	$\omega$	$\upsilon$	$f$	$o$
$f$	$f$	$f$	$f$	$f$	$f$
$\upsilon$	$\upsilon$	$\upsilon$	$f$	$\upsilon$	$\upsilon$
$\upsilon$	$\upsilon$	$f$	$\upsilon$	$\omega$	$\omega$
$\upsilon$	$f$	$\upsilon$	$\upsilon$	$\sigma$	$\sigma$
$f$	$\upsilon$	$\upsilon$	$\upsilon$	$\tau$	$\tau$

.

Then, $\left(\eta ,o,f\right)$ is a $\delta$-algebra. Figure 3 explains that the member $f$ does not change and retains more than 50% of its properties if $f$ is entered from pipe 1, and any member h in $\eta$ is entered from pipe 2.

Moreover, the same engineering device in Figure 4 explains that $f$ will lose more than 50% of its properties if it is entered from pipe 2 and any member h in $\eta$ is entered from pipe 1; the member $f$ will chang and get the same properties of the member h. In $\delta$-algebra, the member f is called the fixed member.

Now, let $\mathsf{\Delta }=\{$“body temperature” (${\lambda }_1$), “cough with chest congestion” (${\lambda }_2$), “body ache” (${\lambda }_3$), “cough with no chest congestion” (${\lambda }_4$), “breathing trouble”, (${\lambda }_5$)} be a parameter set. Here, $\mathsf{\Delta }$ give us the effectiveness for these medications that help somebody want to select one of them based on his opinion of what he prefers of these attributives. Take $\Re =\{{\lambda }_1$, ${\lambda }_3$, ${\lambda }_5\}$ and ${\Re }^{\prime }=\{{\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, ${\lambda }_4\}$, then from

Table 2. $\left(\Omega ,\Re \right)$ is (CSδ-SA).

	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_3$	${\mathit{\lambda }}_5$
$f$	〈[0.6, 0.8], 0.2〉	〈[0.5, 0.6], 0.1〉	〈[0.5, 0.8], 0.5〉
$\upsilon$	〈[0.6, 0.7], 0.5〉	〈[0.4, 0.6], 0.4〉	〈[0.5, 0.8], 0.7〉
$\omega$	〈[0.5, 0.7], 0.8〉	〈[0.4, 0.5], 0.8〉	〈[0.5, 0.7], 0.9〉
$\sigma$	〈[0.4, 0.6], 0.7〉	〈[0.2, 0.5], 0.6〉	〈[0.2, 0.4], 0.6〉
$\tau$	〈[0.3, 0.5], 0.3〉	〈[0.3, 0.4], 0.8〉	〈[0.5, 0.7], 0.5〉

and

Table 3. $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ is (CSδ-SA).

	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	${\mathit{\lambda }}_3$	${\mathit{\lambda }}_4$
$f$	〈[0.4, 0.7], 0.4〉	〈[0.6, 0.9], 0.6〉	〈[0.5, 0.6], 0.1〉	〈[0.4, 0.5], 0.3〉
$\upsilon$	〈[0.4, 0.6], 0.6〉	〈[0.4, 0.8], 0.8〉	〈[0.4, 0.5], 0.3〉	〈[0.4, 0.5], 0.5〉
$\omega$	〈[0.4, 0.6], 0.8〉	〈[0.6, 0.8], 0.7〉	〈[0.4, 0.5], 0.6〉	〈[0.3, 0.4], 0.4〉
$\sigma$	〈[0.1, 0.3], 0.5〉	〈[0.3, 0.5], 0.7〉	〈[0.3, 0.5], 0.8〉	〈[0.1, 0.4], 0.8〉
$\tau$	〈[0.4, 0.7], 0.4〉	〈[0.5, 0.8], 0.6〉	〈[0.2, 0.3], 0.8〉	〈[0.2, 0.3], 0.3〉

, we consider that $\left(\Omega ,\Re \right)$ and $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ are $CS\delta$-subalgebras over $\eta$.

Here, $\Re$ and ${\Re }^{\prime }$ are not disjoint. The R-union $\left(D,W\right)=$ $\left(\Omega ,\Re \right){\overline{\cup }}_p\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ is given in

Table 4. $\left(D,W\right)$ is (CSS).

	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_2$	${\mathit{\lambda }}_3$	${\mathit{\lambda }}_4$	${\mathit{\lambda }}_5$
$f$	〈[0.6, 0.7], 0.4〉	〈[0.6, 0.9], 0.6〉	〈[0.5, 0.6], 0.1〉	〈[0.4, 0.5], 0.3〉	〈[0.5, 0.8], 0.5〉
$\upsilon$	〈[0.6, 0.7], 0.6〉	〈[0.4, 0.8], 0.8〉	〈[0.4, 0.6], 0.4〉	〈[0.1, 0.3], 0.5〉	〈[0.3, 0.8], 0.7〉
$\omega$	〈[0.5, 0.7], 0.8〉	〈[0.6, 0.8], 0.7〉	〈[0.4, 0.5], 0.8〉	〈[0.3, 0.4], 0.4〉	〈[0.5, 0.7], 0.9〉
$\sigma$	〈[0.4, 0.6], 0.7〉	〈[0.3, 0.5], 0.7〉	〈[0.3, 0.5], 0.8〉	〈[0.1, 0.4], 0.8〉	〈[0.2, 0.4], 0.6〉
$\tau$	〈[0.4, 0.7], 0.4〉	〈[0.5, 0.8], 0.6〉	〈[0.3, 0.4], 0.8〉	〈[0.2, 0.3], 0.3〉	〈[0.5, 0.7], 0.5〉

.

We have

$${\xi }_{D\left({\lambda }_4\right)}\left(\omega o\tau \right)={\xi }_{D\left({\lambda }_4\right)}\left(\upsilon \right)=[0.1,0.3],[0.2,0.3]=r\min \{[0.3,0.4],[0.2,0.3]\}=r\min \{{\xi }_{D\left({\lambda }_4\right)}\left(\omega \right),{\xi }_{D\left({\lambda }_4\right)}\left(\tau \right)\}$$

(24)

and/or

$${\psi }_{D\left({\lambda }_4\right)}\left(\omega o\tau \right)={\psi }_{D\left({\lambda }_4\right)}\left(\upsilon \right)=0.5>0.3=\max \{0.4,0.3\}=\max \{{\psi }_{D\left({\lambda }_4\right)}\left(\omega \right),{\psi }_{D\left({\lambda }_4\right)}\left(\tau \right)\}$$

(25)

Remark 3.

(1)

For any R-cubic soft subset of (CSδ-SA), it is not necessary that each one is (CSδ-SA).

(2)

For any P-cubic soft subset of (CSδ-SA), it is not necessary that each one is (CSδ-SA) too.

Example 3.

In Example 2, let $\eta =\{f,\upsilon ,\omega ,\sigma ,\tau \}$ and $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ be an R-cubic soft subset of $\left(\Omega ,\Re \right)$ as shown in

Table 5. $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ R-cubic soft subset of $\left(\Omega ,\Re \right)$.

	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_5$
$f$	〈[0.3, 0.5], 0.8〉	〈[0.5, 0.8], 0.5〉
$\upsilon$	〈[0.3, 0.6], 0.6〉	〈[0.3, 0.8], 0.7〉
$\omega$	〈[0.4, 0.5], 0.8〉	〈[0.5, 0.7], 0.9〉
$\sigma$	〈[0.3, 0.4], 0.8〉	〈[0.2, 0.4], 0.6〉
$\tau$	〈[0.2, 0.4], 0.5〉	〈[0.5, 0.7], 0.5〉

.

Then, we have

${\xi }_{D\left({\lambda }_1\right)}\left(\sigma o\omega \right)$ $={\xi }_{D\left({\lambda }_1\right)}\left(\upsilon \right)=$ [0.2, 0.3] ≤ [0.3, 0.4] = r min {[0.3, 0.4], [0.4, 0.5]} = r min {${\xi }_{D\left({\lambda }_1\right)}\left(\sigma \right)$, ${\xi }_{D\left({\lambda }_1\right)}\left(\omega \right)$}. $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ is not a (CSδ-SA) over $\eta$.

Here, we consider that it is not necessary that any P-cubic soft subset of (CSδ-SA) is (CSδ-SA) too.

Example 4.

In Example 2, let $\eta =\{f,\upsilon ,\omega ,\sigma ,\tau \}$ and $\left(\Omega \prime ,{\Re }^{\prime }\right)$ be a P-cubic soft subset of $\left(\Omega ,\Re \right)$, as defined in

Table 6. $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ P-cubic soft subset of $\left(\Omega ,\Re \right)$.

	${\mathit{\lambda }}_1$	${\mathit{\lambda }}_5$
$f$	〈[0.3, 0.5], 0.1〉	〈[0.5, 0.8], 0.5〉
$\upsilon$	〈[0.2, 0.3], 0.4〉	〈[0.3, 0.8], 0.7〉
$\omega$	〈[0.4, 0.5], 0.7〉	〈[0.5, 0.7], 0.9〉
$\sigma$	〈[0.3, 0.4], 0.6〉	〈[0.2, 0.4], 0.6〉
$\tau$	〈[0.2, 0.4], 0.2〉	〈[0.5, 0.7], 0.5〉

:

${\xi }_{D\left({\lambda }_1\right)}\left(\sigma o\omega \right)$ = ${\xi }_{D\left({\lambda }_1\right)}\left(\upsilon \right)=$ [0.2, 0.3] $\widetilde{<}$ [0.3, 0.4] = r min {[0.3, 0.4], [0.4, 0.5]} = r min {${\xi }_{D\left({\lambda }_1\right)}\left(\sigma \right)$, ${\xi }_{D\left({\lambda }_1\right)}\left(\omega \right)$}. $\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ is not a (CSδ-SA) over $\eta$. Here, we consider that for any R-cubic soft subset of (CSδ-SA), it is not necessary to be (CSδ-SA) too.

Proposition 1.

Let $\left(\Omega ,\Re \right){\in }_{\mathsf{\Delta }}{{{\displaystyle \int }}^{}}^{\eta }$ with $\left(\eta ,o,f\right)$ is $\left(\delta \text{-}A\right)$ and $\lambda \in \mathsf{\Delta }$. Then, ${\xi }_{\Omega \left(\lambda \right)}\left(f\right)\tilde{\ge }$ ${\xi }_{\Omega \left(\lambda \right)}\left(\upsilon \right)$ and ${\psi }_{\Omega (\lambda )}(f)\tilde{\le }$ ${\psi }_{\Omega \left(\lambda \right)}\left(\upsilon \right)$, $\forall \upsilon \in \eta$, if $\left(\Omega ,\Re \right)$ is (λ-CSδ-SA) over $\eta$.

Proof. 

$\forall \upsilon \in \eta$, we consider that:

${\xi }_{\Omega \left(\lambda \right)}\left(f\right)$ = ${\xi }_{\Omega \left(\lambda \right)}\left(\upsilon o\upsilon \right)\tilde{\ge }$ r min {${\xi }_{\Omega \left(\lambda \right)}\left(\upsilon \right)$, ${\xi }_{\Omega \left(\lambda \right)}\left(\upsilon \right)$} = r min{[${\xi }_{\Omega \left(\lambda \right)}{(\upsilon )}^{-}$, ${\xi }_{\Omega \left(\lambda \right)}{(\upsilon )}^{+}$], [${\xi }_{\Omega \left(\lambda \right)}{(\upsilon )}^{-}$, ${\xi }_{\Omega \left(\lambda \right)}{(\upsilon )}^{+}$]} = [${\xi }_{\Omega \left(\lambda \right)}{(\upsilon )}^{-}$, ${\xi }_{\Omega \left(\lambda \right)}{(\upsilon )}^{+}$] = ${\xi }_{\Omega \left(\lambda \right)}\left(\upsilon \right)$ and ${\psi }_{\Omega \left(\lambda \right)}\left(f\right)$ = ${\psi }_{\Omega \left(\lambda \right)}\left(\upsilon o\upsilon \right)\tilde{\le }$ max {${\psi }_{\Omega \left(\lambda \right)}\left(\upsilon \right)$, ${\psi }_{\Omega \left(\lambda \right)}\left(\upsilon \right)$} = ${\psi }_{\Omega \left(\lambda \right)}\left(\upsilon \right)$.  □

Theorem 2.

Assume $\left(\Omega ,\Re \right){\in }_{\mathsf{\Delta }}{{{\displaystyle \int }}^{}}^{\eta }$ is (λ-CSδ-SA) over $\eta \mathrm{with}\left(\eta ,o,f\right)\mathrm{is}\left(\delta \text{-}A\right)$. Then, ${\xi }_{\Omega \left(\lambda \right)}\left({\upsilon }_n\right)$ = [1, 1] and ${\psi }_{\Omega \left(\lambda \right)}\left({\upsilon }_n\right)=0$, if $\langle {\upsilon }_n\rangle$ is a sequence in $\eta$ with $\underset{n\to \infty }{\lim }{\xi }_{\Omega \left(\lambda \right)}\left({\upsilon }_n\right)$ = [1, 1] and $\underset{n\to \infty }{\lim }{\psi }_{\Omega \left(\lambda \right)}\left({\upsilon }_n\right)=0$.

Proof. 

Since ${\xi }_{\Omega \left(\lambda \right)}\left(f\right)\tilde{\ge }$ ${\xi }_{\Omega \left(\lambda \right)}\left(\upsilon \right)$, ${\psi }_{\Omega (\lambda )}(f)\tilde{\le }$ ${\psi }_{\Omega \left(\lambda \right)}\left(\upsilon \right)$, $\forall \upsilon \in \eta$, we have

$${\xi }_{\Omega \left(\lambda \right)}\left(f\right)\tilde{\ge }{\xi }_{\Omega \left(\lambda \right)}\left({\upsilon }_n\right),\forall n\in N,$$

$${\psi }_{\Omega (\lambda )}(f)\tilde{\le }{\psi }_{\Omega \left(\lambda \right)}\left(\upsilon \right),\forall n\in N.$$

(26)

However, [1, 1] $\tilde{\ge }{\xi }_{\Omega \left(\lambda \right)}\left(f\right)\tilde{\ge }$ $\underset{n\to \infty }{\lim }{\xi }_{\Omega \left(\lambda \right)}\left({\upsilon }_n\right)$ = [1, 1]. Also, 0 $\tilde{\le }\underset{n\to \infty }{\lim }{\psi }_{\Omega (\lambda )}({\upsilon }_n)\tilde{\le }$ $\underset{n\to \infty }{\lim }{\psi }_{\Omega \left(\lambda \right)}\left({\upsilon }_n\right)=0$. Therefore ${\xi }_{\Omega \left(\lambda \right)}\left({\upsilon }_n\right)$ = [1, 1] and ${\psi }_{\Omega \left(\lambda \right)}\left({\upsilon }_n\right)=0$.  □

Theorem 3.

If each of $\left(\Omega ,\Re \right),\left(\Omega \prime ,{\Re }^{\prime }\right)$ ${\in }_{\mathsf{\Delta }}{{{\displaystyle \int }}^{}}^{\mathsf{\eta }}$ is a (CSδ-SA), then their R-intersection is also (CSδ-SA).

Proof. 

Let $\left(\Omega ,\Re \right)\mathrm{and}\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ are $\left(CS\delta \text{-}SA\right)$ and $\left(D,W\right)=$ $(\Omega ,\Re )$${\overline{{{\displaystyle \cap }}^{}}}_P\left({\Omega }^{\prime },{\Re }^{\prime }\right)$, where $W=\Re {{\displaystyle \cup }}^{}{\Re }^{\prime }$ and

$$D\left(\lambda \right)=\{\begin{array}{c}\Omega \left(\lambda \right),if\lambda \in \Re \backslash {\Re }^{\prime }\\ {\Omega }^{\prime }\left(\lambda \right),if\lambda \in {\Re }^{\prime }\backslash \Re \\ \Omega \left(\lambda \right){{{\displaystyle \cap }}^{}}_R{\Omega }^{\prime }\left(\lambda \right),if\lambda \in \Re {{\displaystyle \cap }}^{}{\Re }^{\prime }\end{array},\forall \lambda \in W$$

(27)

Now, $\forall \lambda \in W$, we consider three states: (i) $\lambda \in \Re /{\Re }^{\prime }$, (ii) $\lambda \in {\Re }^{\prime }/\Re$, (iii) $\lambda \in \Re {{\displaystyle \cap }}^{}{\Re }^{\prime }$.

In state (i), we obtain;

$${\xi }_{D\left(\lambda \right)}\left(\upsilon \circ \omega \right)={\xi }_{\Omega \left(\lambda \right)}\left(\upsilon \circ \omega \right)\tilde{\ge }r\min \{{\xi }_{\Omega \left(\lambda \right)}\left(\upsilon \right),{\xi }_{\Omega \left(\lambda \right)}\left(\omega \right)\}=r\min \{{\xi }_{D\left(\lambda \right)}\left(\upsilon \right),{\xi }_{D\left(\lambda \right)}\left(\omega \right)\},$$

(28)

$${\psi }_{D\left(\lambda \right)}\left(\upsilon \circ \omega \right)={\psi }_{\Omega \left(\lambda \right)}\left(\upsilon \circ \omega \right)\tilde{\le }\max \{{\psi }_{\Omega \left(\lambda \right)}\left(\upsilon \right),{\psi }_{\Omega \left(\lambda \right)}\left(\omega \right)\}=\max \{{\psi }_{D\left(\lambda \right)}\left(\upsilon \right),{\psi }_{D\left(\lambda \right)}\left(\omega \right)\},$$

In state (ii), we obtain;

$${\xi }_{D\left(\lambda \right)}\left(\upsilon \circ \omega \right)={\xi }_{{\Omega }^{\prime }\left(\lambda \right)}\left(\upsilon \circ \omega \right)\tilde{\ge }r\min \{{\xi }_{{\Omega }^{\prime }\left(\lambda \right)}\left(\upsilon \right),{\xi }_{\Omega \left(\lambda \right)}\left(\omega \right)\}=r\min \{{\xi }_{D\left(\lambda \right)}\left(\upsilon \right),{\xi }_{D\left(\lambda \right)}\left(\omega \right)\},$$

(29)

$${\psi }_{D\left(\lambda \right)}\left(\upsilon \circ \omega \right)={\psi }_{{\Omega }^{\prime }\left(\lambda \right)}\left(\upsilon \circ \omega \right)\tilde{\le }\max \{{\psi }_{{\Omega }^{\prime }\left(\lambda \right)}\left(\upsilon \right),{\psi }_{{\Omega }^{\prime }\left(\lambda \right)}\left(\omega \right)\}=\max \{{\psi }_{D\left(\lambda \right)}\left(\upsilon \right),{\psi }_{D\left(\lambda \right)}\left(\omega \right)\},$$

In state (iii), we obtain;

$$\begin{array}{l}{\xi }_{D\left(\lambda \right)}\left(\upsilon \circ \omega \right)=({\xi }_{\Omega \left(j\right)}{\overline{{{\displaystyle \cap }}^{}}}_R{\xi }_{{\Omega }^{\prime }\left(\lambda \right)})\left(\upsilon \circ \omega \right)=r\min \{{\xi }_{\Omega \left(\lambda \right)}\left(\upsilon \circ \omega \right),{\xi }_{{\Omega }^{\prime }\left(\lambda \right)}\left(\upsilon \circ \omega \right)\}\\ \tilde{\ge }r\min \{r\min \{{\xi }_{\Omega \left(\lambda \right)}\left(\upsilon \right),{\xi }_{\Omega \left(\lambda \right)}\left(\omega \right)\},r\min \{{\xi }_{{\Omega }^{\prime }\left(\lambda \right)}\left(\upsilon \right),{\xi }_{{\Omega }^{\prime }\left(\lambda \right)}\left(\omega \right)\}\}\\ =r\min \{r\min \{{\xi }_{\Omega \left(\lambda \right)}\left(\upsilon \right),{\xi }_{{\Omega }^{\prime }\left(\lambda \right)}\left(\upsilon \right)\},r\min \{{\xi }_{\Omega \left(\lambda \right)}\left(\upsilon \right),{\xi }_{{\Omega }^{\prime }\left(\lambda \right)}\left(\omega \right)\}\}\\ =r\min \{({\xi }_{\Omega \left(\lambda \right)}{\overline{{{\displaystyle \cap }}^{}}}_R{\xi }_{{\Omega }^{\prime }\left(\lambda \right)})\left(\upsilon \right),({\xi }_{\Omega \left(\lambda \right)}{\overline{{{\displaystyle \cap }}^{}}}_R{\xi }_{{\Omega }^{\prime }\left(\lambda \right)})\left(\omega \right)\}=r\min \{{\xi }_{D\left(\lambda \right)}\left(\upsilon \right),{\xi }_{D\left(\lambda \right)}\left(\omega \right)\}.\end{array}$$

(30)

Also,

$$\begin{array}{l}{\psi }_{D\left(\lambda \right)}\left(\upsilon \circ \omega \right)=\left({\psi }_{\Omega \left(j\right)}{\overline{{{\displaystyle \cap }}^{}}}_R{\psi }_{{\Omega }^{\prime }\left(\lambda \right)}\right)\left(\upsilon \circ \omega \right)=r\min \{{\psi }_{\Omega \left(\lambda \right)}\left(\upsilon \circ \omega \right),{\psi }_{{\Omega }^{\prime }\left(\lambda \right)}\left(\upsilon \circ \omega \right)\}\\ \tilde{\le }\max \{\max \{{\psi }_{\Omega \left(\lambda \right)}\left(\upsilon \right),{\psi }_{\Omega \left(\lambda \right)}\left(\omega \right)\},\max \{{\psi }_{{\Omega }^{\prime }\left(\lambda \right)}\left(\upsilon \right),{\psi }_{{\Omega }^{\prime }\left(\lambda \right)}\left(\omega \right)\}\}\\ =\max n\{\max \{{\psi }_{\Omega \left(\lambda \right)}\left(\upsilon \right),{\psi }_{{\Omega }^{\prime }\left(\lambda \right)}\left(\upsilon \right)\},\max \{{\psi }_{\Omega \left(\lambda \right)}\left(\upsilon \right),{\psi }_{{\Omega }^{\prime }\left(\lambda \right)}\left(\omega \right)\}\}\\ =\max \{\left({\psi }_{\Omega \left(\lambda \right)}{\overline{{{\displaystyle \cap }}^{}}}_R{\psi }_{{\Omega }^{\prime }\left(\lambda \right)}\right)\left(\upsilon \right),\left({\psi }_{\Omega \left(\lambda \right)}{\overline{{{\displaystyle \cap }}^{}}}_R{\psi }_{{\Omega }^{\prime }\left(\lambda \right)}\right)\left(\omega \right)\}=\max \{{\psi }_{D\left(\lambda \right)}\left(\upsilon \right),{\psi }_{D\left(\lambda \right)}\left(\omega \right)\}.\end{array}$$

(31)

Hence $\left(D,W\right)=$ $(\Omega ,\Re )$${\overline{{{\displaystyle \cap }}^{}}}_R\left({\Omega }^{\prime },{\Re }^{\prime }\right)$ is a (CSδ-SA) over $\eta$.  □

Corollary 1.

If $\Re =\{{(\Omega \prime ,{\Re }^{\prime })}_{\lambda }{\in }_{\Delta }{{{\displaystyle \int }}^{}}^{\eta }|\lambda \in \Delta \}$ is a family of cubic soft $\mathsf{\delta }$-subalgebras over $\mathsf{\eta }$, then the R-intersection $\overline{{{{\displaystyle \cap }}^{}}_R}{\{{(\Omega \prime ,{\Re }^{\prime })}_{\lambda }\}}_{\lambda \in {\Re }^{\prime }}$ is a (CSδ-SA) over $\mathsf{\eta }$.

Proof. 

From Definition (7) and Theorem (3), the proof is straightforward.  □

4. Comparative Study

In 2021 [8], a technique used nano-sets to study medications suitable for COVID-19 depending on the lower approximation, upper approximation, and boundary region for nano-topological space (NTS). However, a parameter set was not used, which means this work discussed the rate of health recovery for patients in general, without any other detail. Therefore, in our work, we used cubic soft $\delta$-algebras and parameters such as $\mathsf{\Delta }=\{$“body temperature” (${\lambda }_1$), “cough with chest congestion” (${\lambda }_2$), “body ache” (${\lambda }_3$), “cough with no chest congestion” (${\lambda }_4$), “breathing trouble” (${\lambda }_5$)} and hence we introduced more factors related to patients to study the activity of medications.

5. Conclusions

We showed that is not necessarily any R/P-cubic soft subset of (CSδ-SA) is (CSδ-SA). That means the P-union is not really a soft cubic $\delta$-subalgebra of two soft cubic $\delta$-subalgebras. We further provide the necessary criteria to demonstrate that the R-union of two members is (CSδ-SA) if each of them is (CSδ-SA). To demonstrate our notations, we use the used (CSδ-SA) to investigate the efficacy of medicines for COVID-19. In the future, more engineering device applications may express the composition of two or more members in engineering devices as a P/R-union, specifying the member that will be considered from the composition of known members. Moreover, there is a recent development in soft set theory, i.e., the idea of T-Bipolar soft set, as explained by Tahir [25]. Therefore, we can increase the application of T-Bipolar soft sets using new classes of operations.