Trochoidal Milling Path with Variable Feed. Application to the Machining of a Ti-6Al-4V Part
Abstract
:1. Introduction
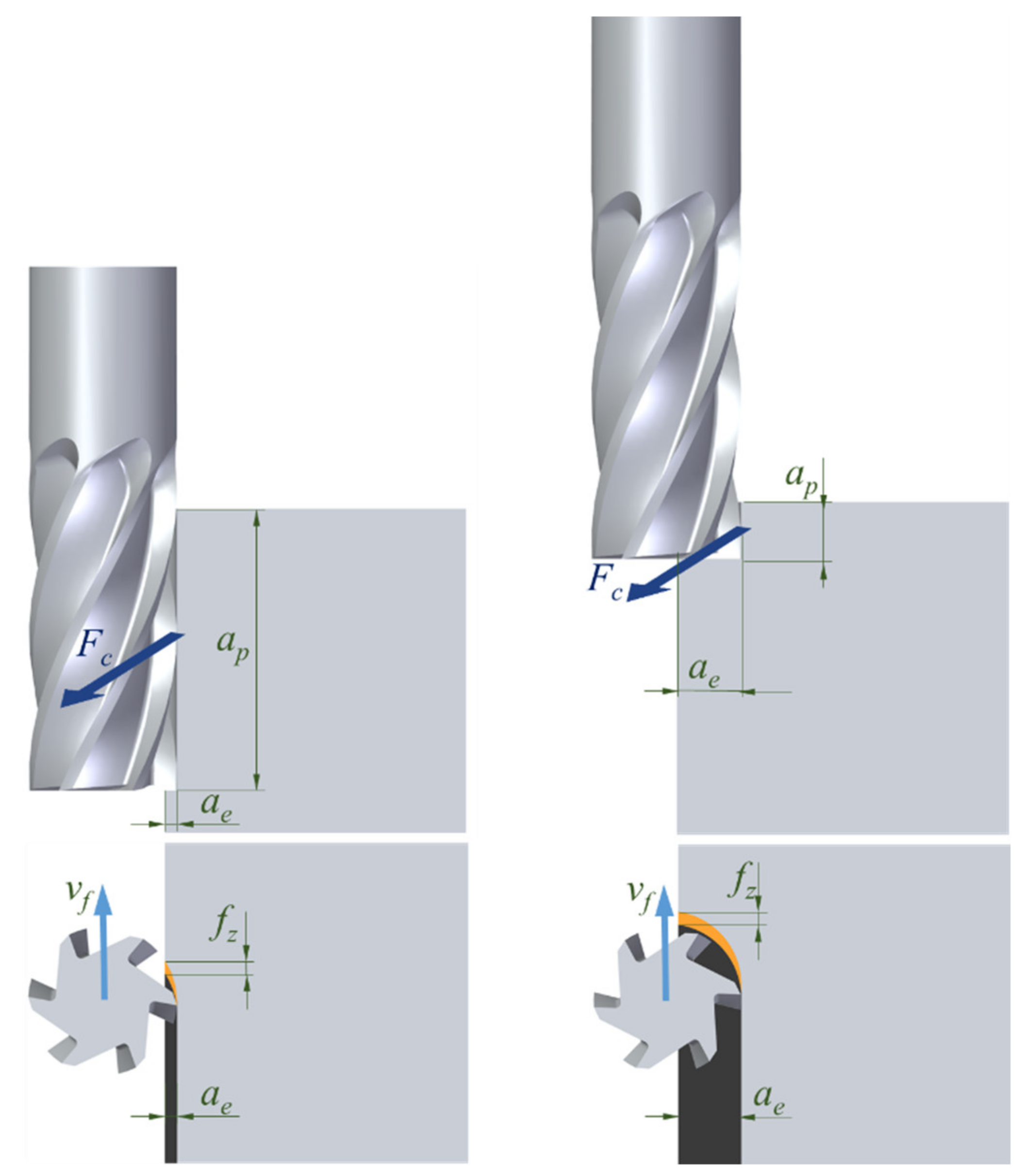
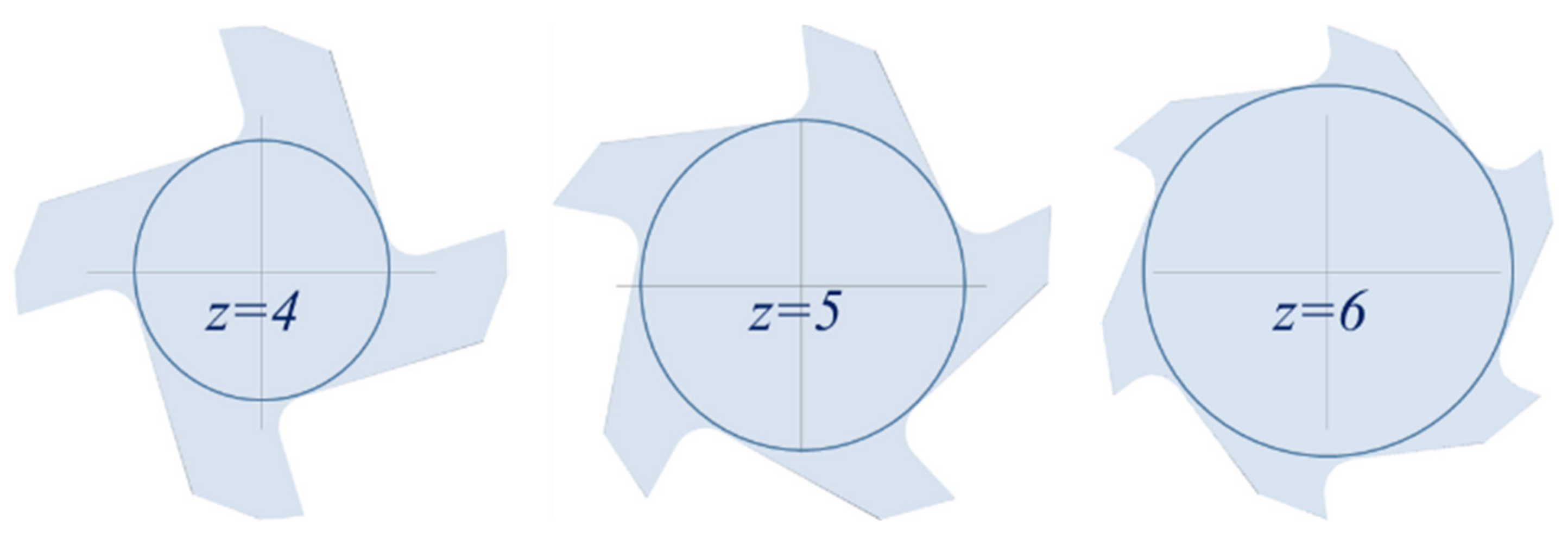
- The tooth gap can be smaller for the same feed (the chip width is reduced), so more teeth can be implemented and, for the same feed per tooth, the final feed rises and, as a result, the machining time decreases.
- As a consequence, the mill core has a wider section, being able to support bigger flection and torque forces, Figure 3. This bigger rigidity makes possible to decrease deformation and vibrations, being more suitable for materials with superior cutting requirements [4], such as titanium and nickel alloys.
2. Materials and Methods
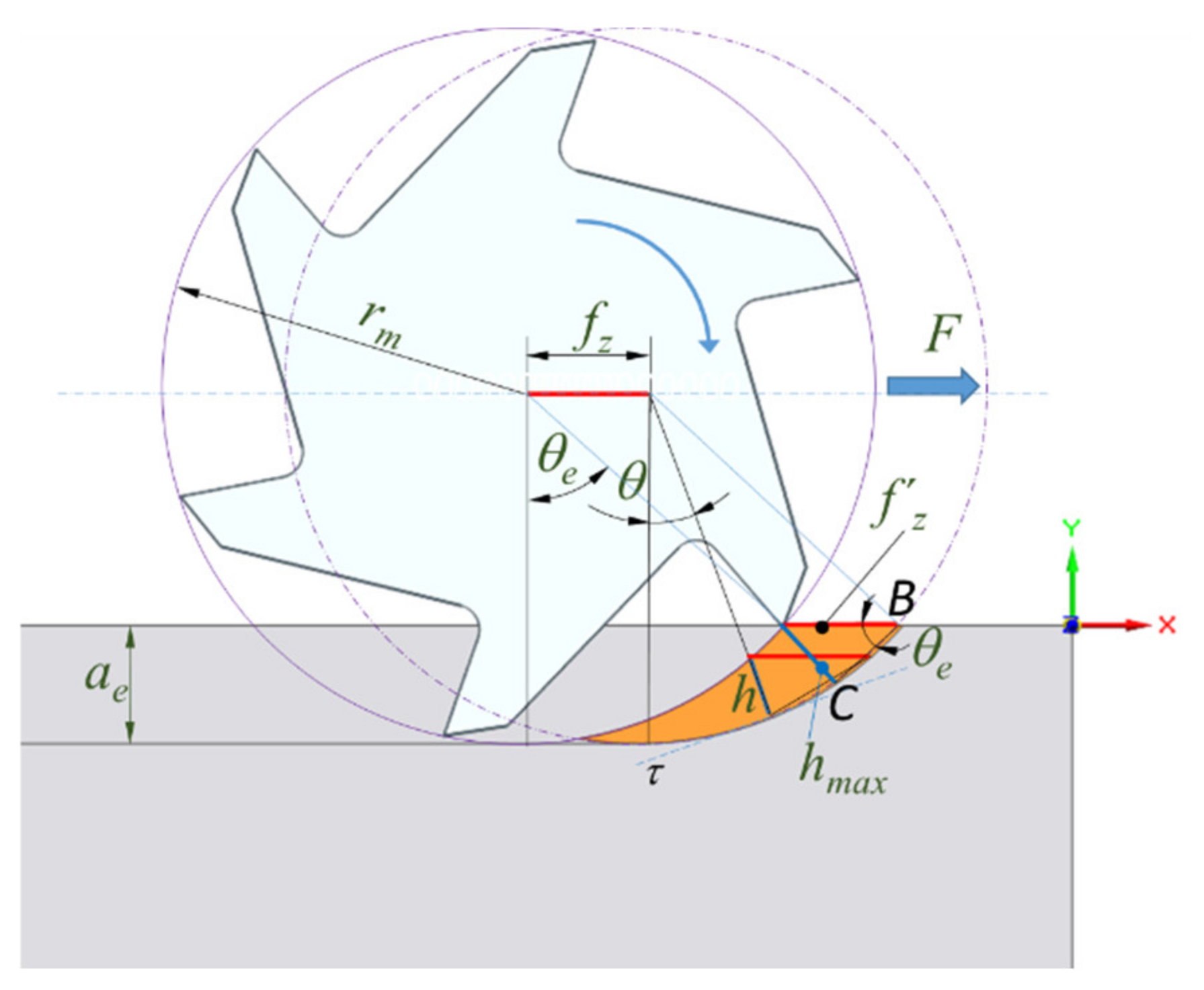
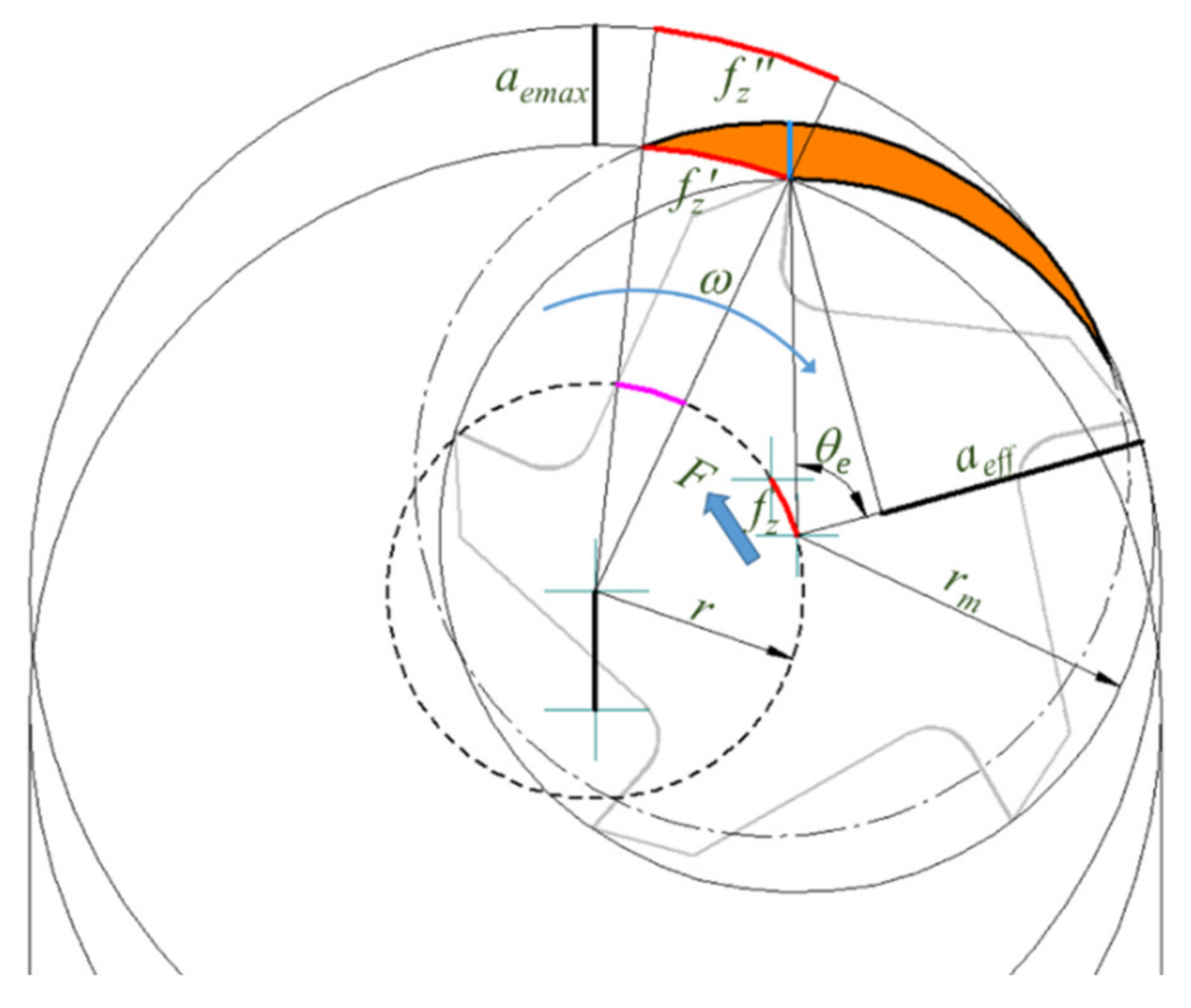
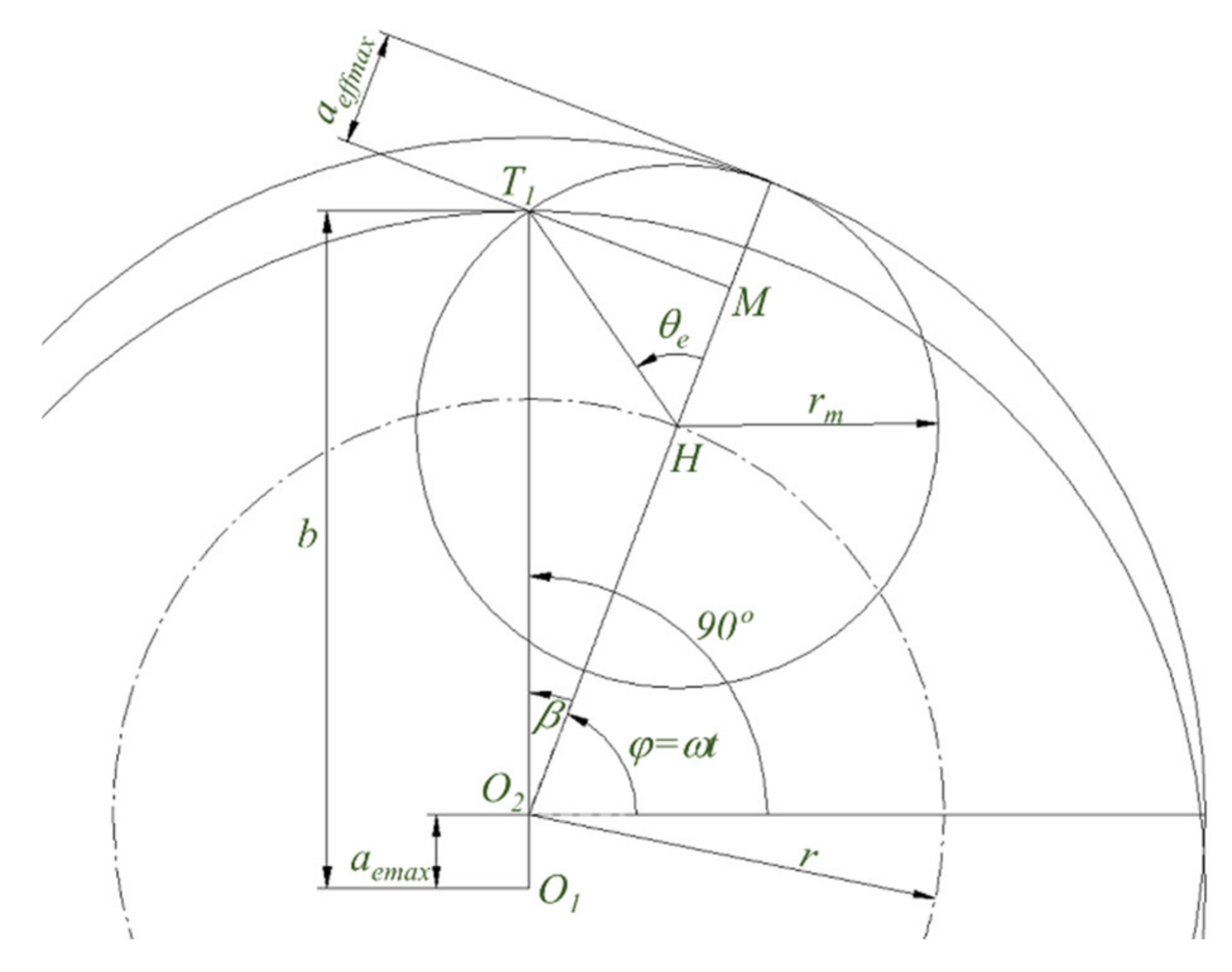
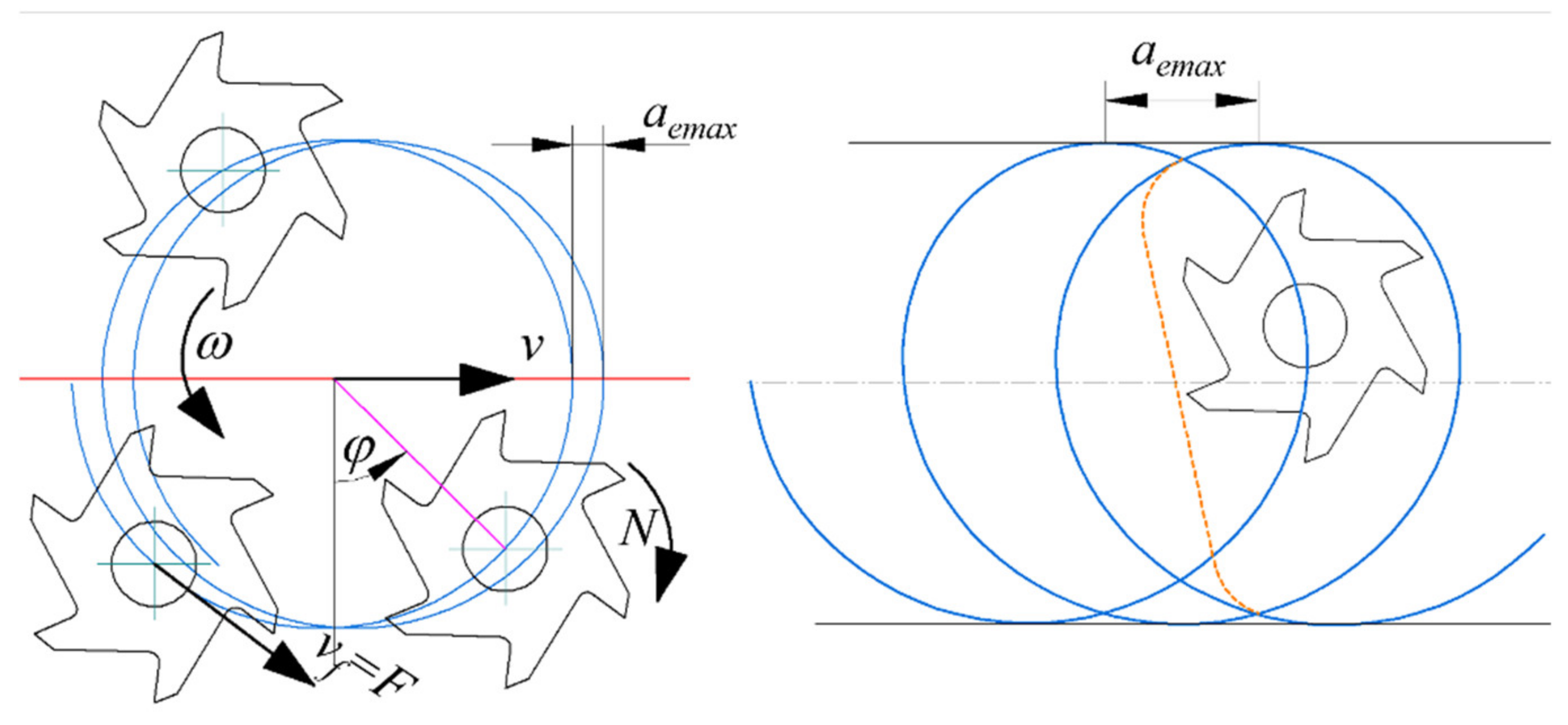
2.1. Selection of the Radial Cut Depth
- Considering that ae is small in comparison to the milling tool radius rm.
- Avoiding the use of the squared parenthesis. According to the previous aspect, it is not significant compared to the other equation terms.
- Using the milling tool diameter instead of the radius.
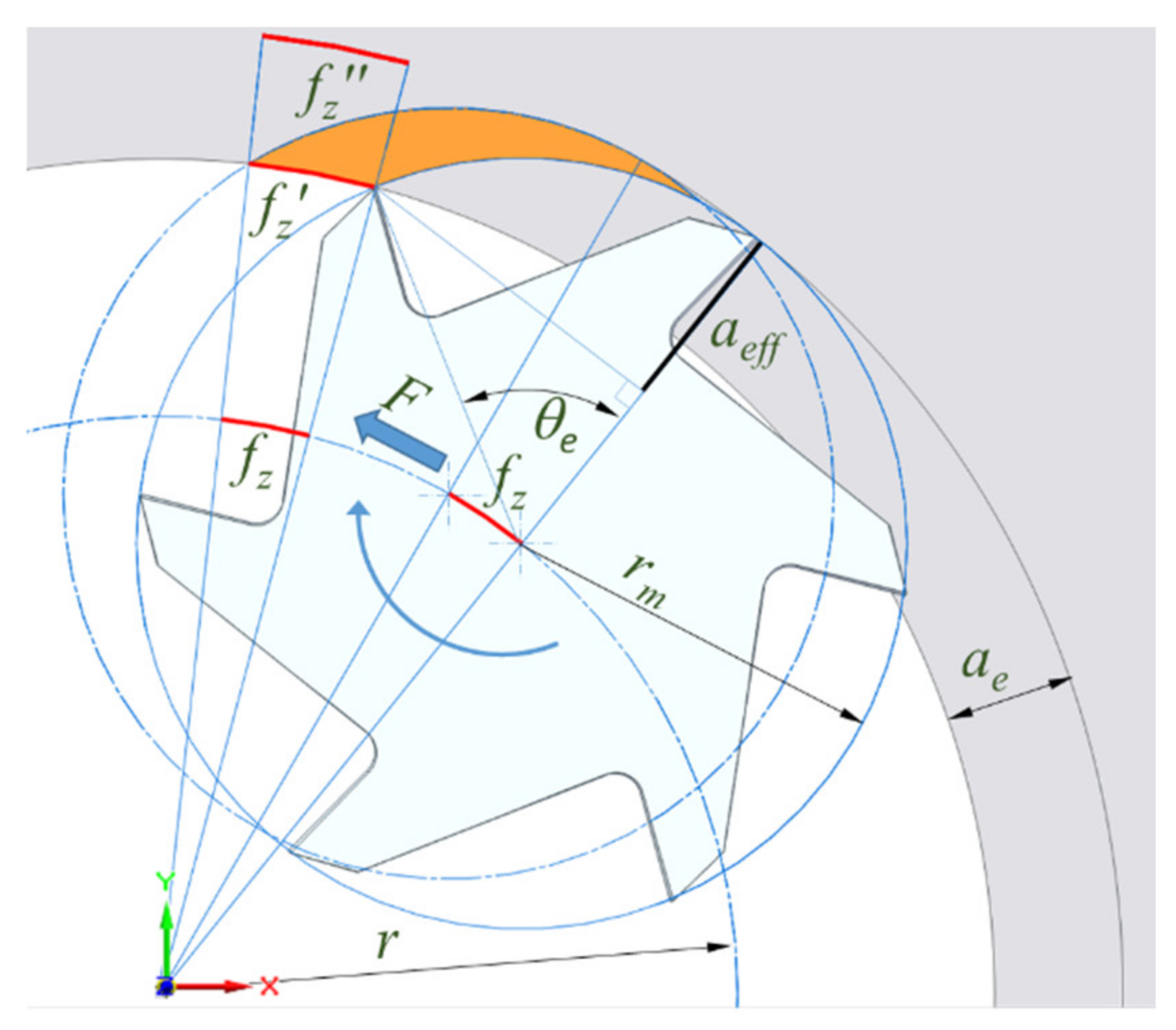
- For the same feed in the milled part, the programmed feed must be lower in the interior tool path.
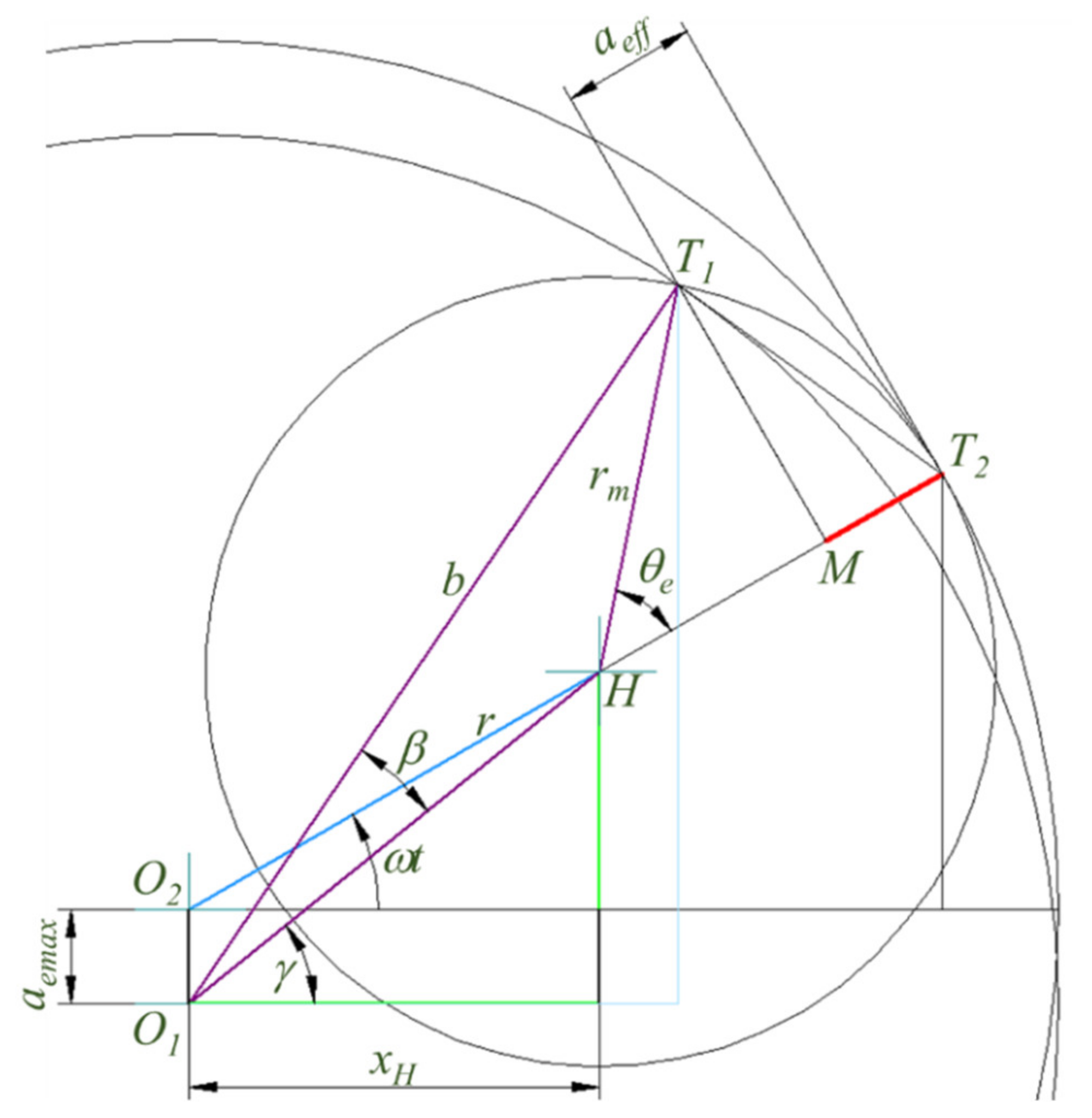
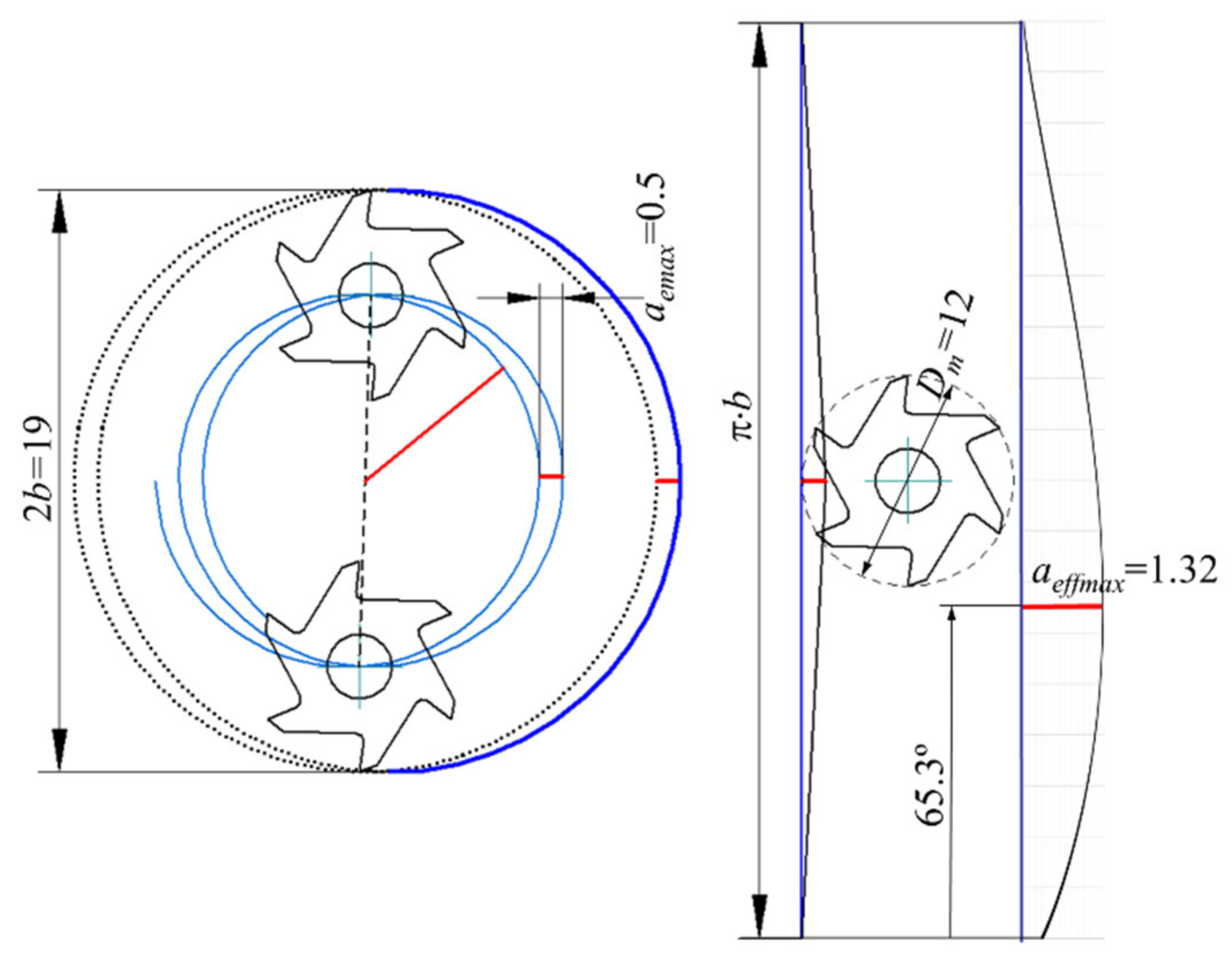
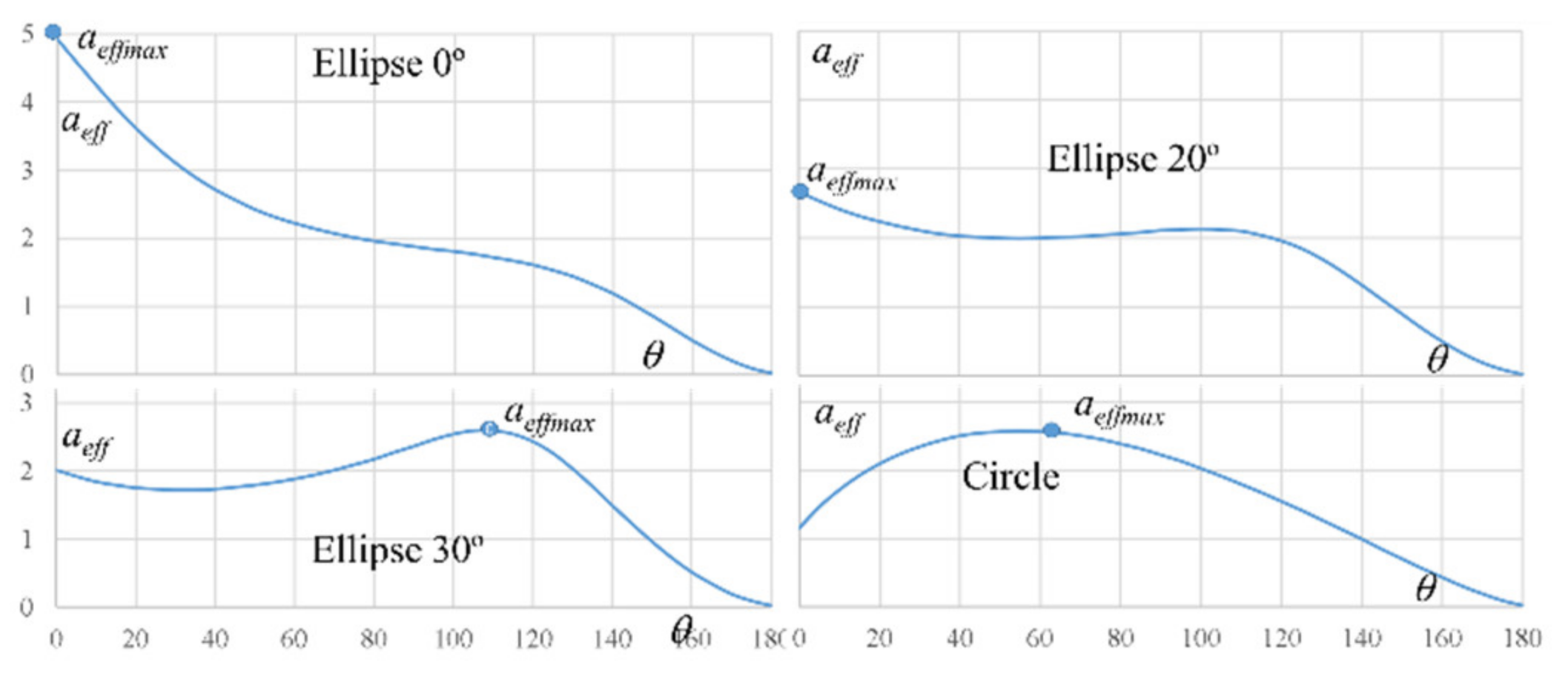
- According to Figure 5 and Equations (2) and (8), for the interior tool path, the engagement angle is higher for the same radial depth, ae, as aeff is larger than ae.
- As the value of the feed per tooth is low in comparison to the milling tool dimensions, the arch of fz′ is close to a straight line. Thus, the mean thickness can be approximated to the previous case, considering aeff instead of ae:
- As ae is constant, the values of the engagement angle and the effective axial depth are constant. However, they are not constant in trochoidal milling.
- The mean chip depth should not be decreased. For this reason, in this study, to let hm be constant when aeff varies, the feed per tooth fz′ will be continuously modified.
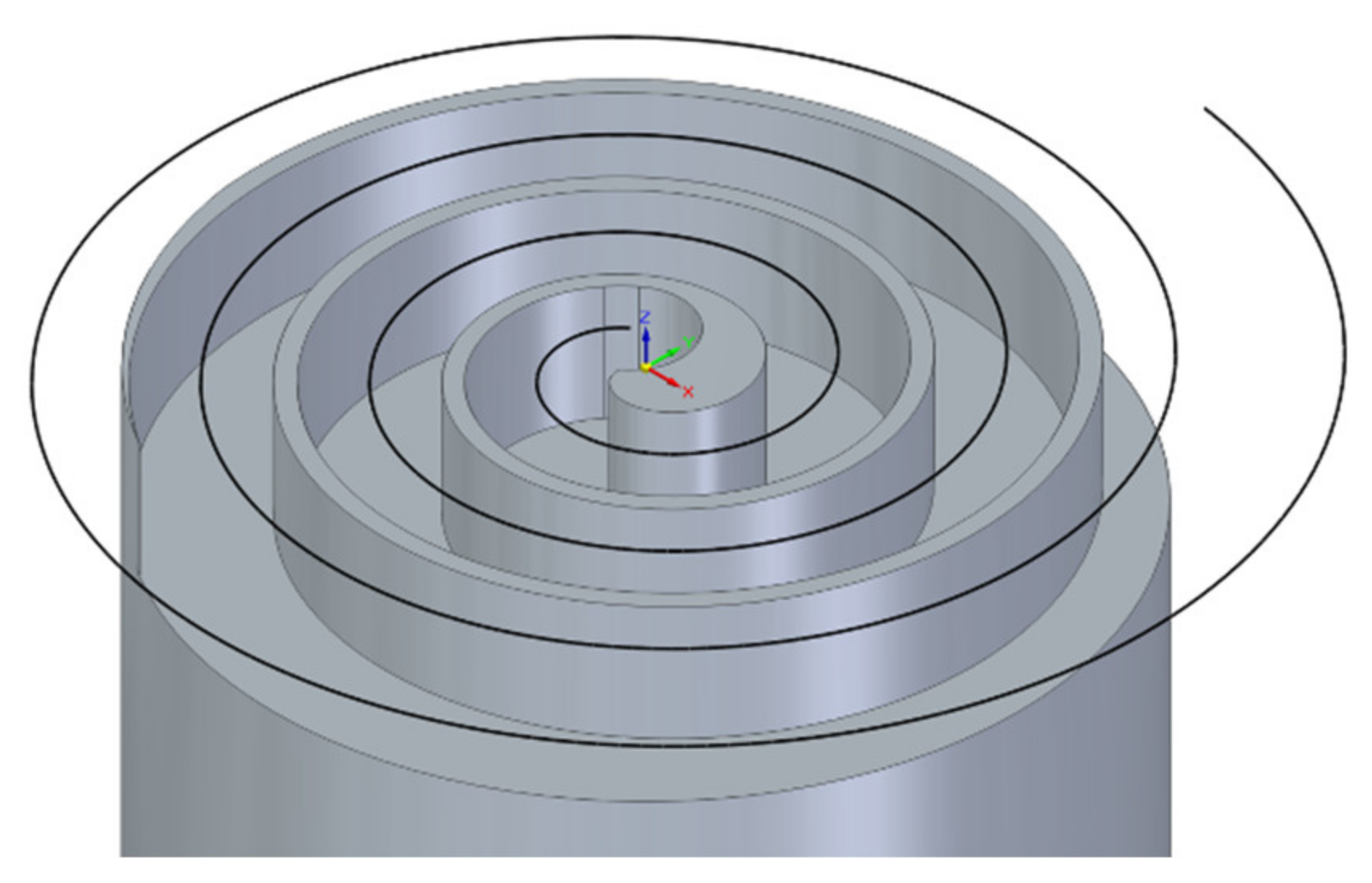
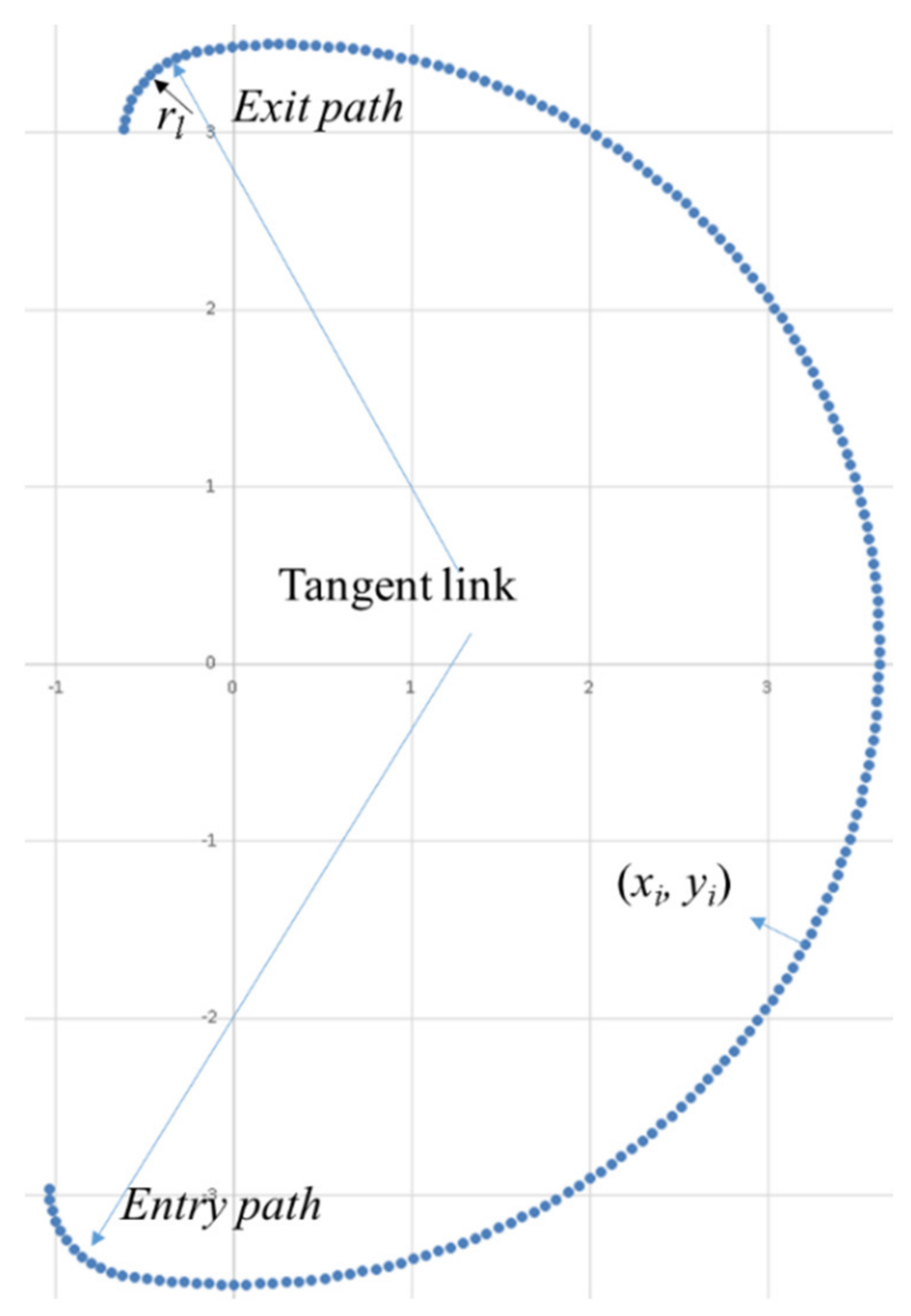
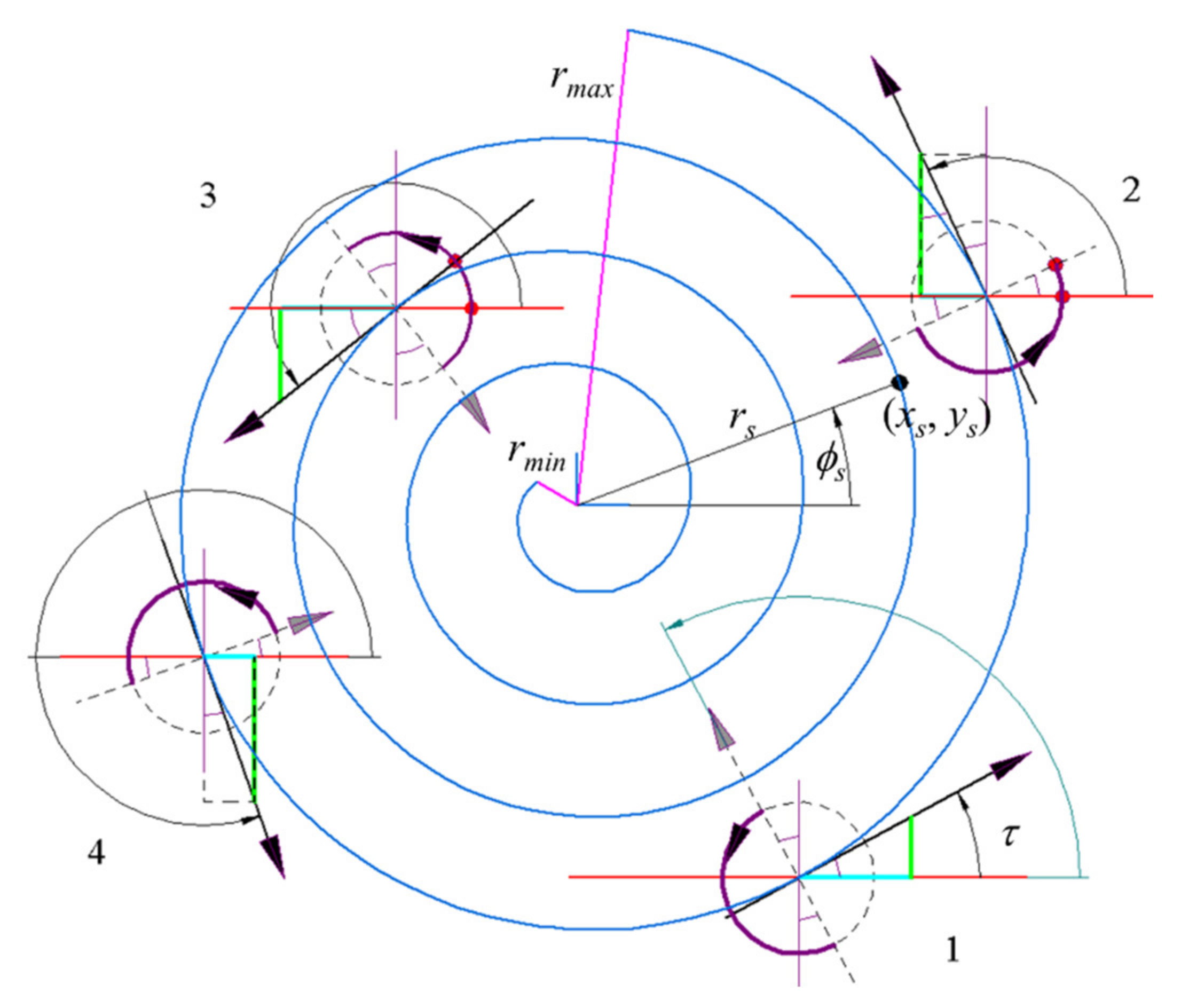
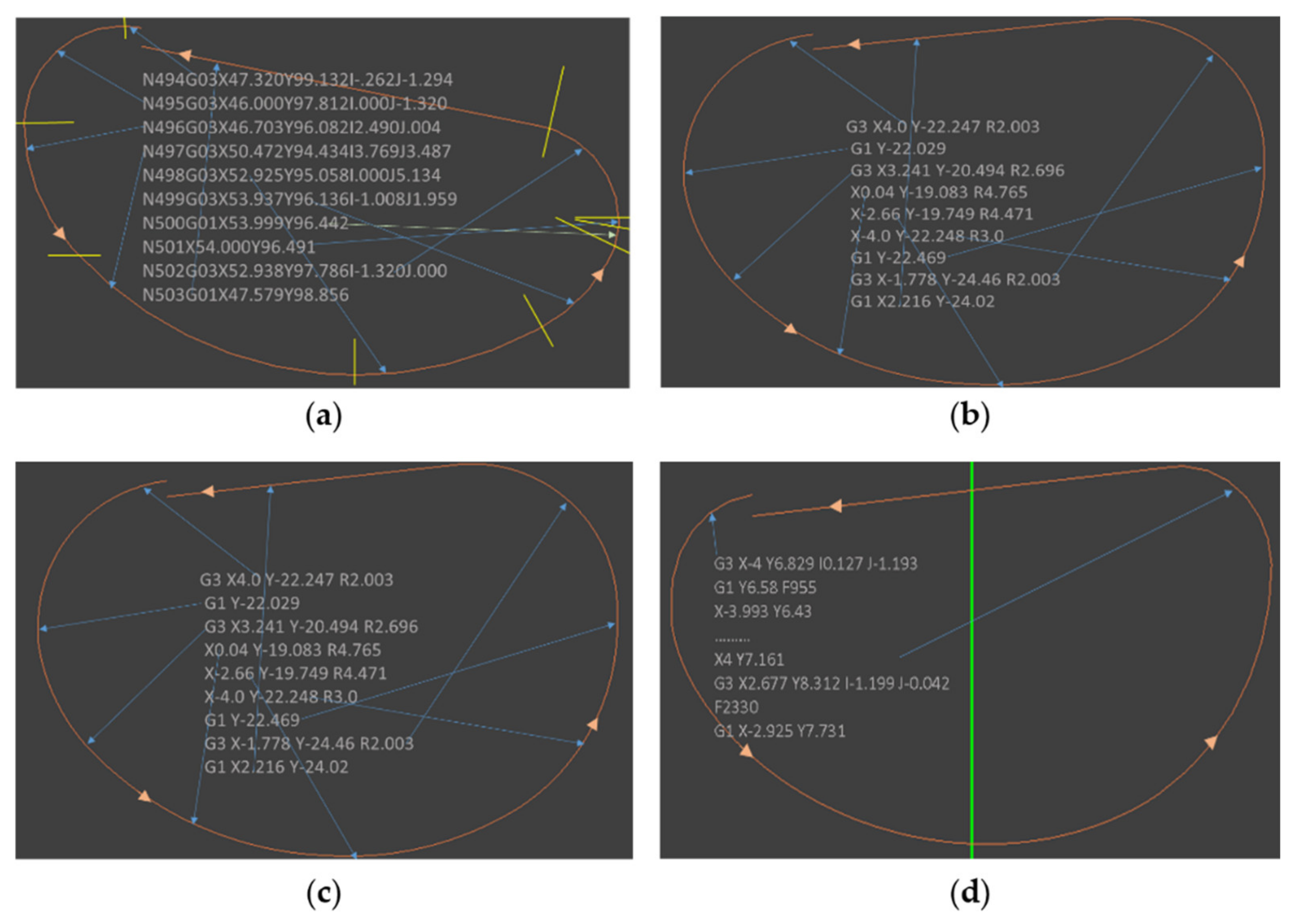
2.2. NC Program of a Trochoid with Adaptive Feed
- The points that define a step of the trochoidal path were obtained using (36).
- ω was obtained from (30), using the feed fz for peripheral milling.
- Introducing the previous values of Δφ and ω in (37), Δt is obtained.
- With (33), v is obtained.
- Using (34), the coordinates of the trochoidal arc (0 to π) were obtained, with Δφ.
- For each of the previous coordinates (x, y), the effective chip width was obtained (27).
- The mean value of chip width was obtained from (6), for the peripheral milling, with ae = aemax.
- With (10), the value of f’z can be found.
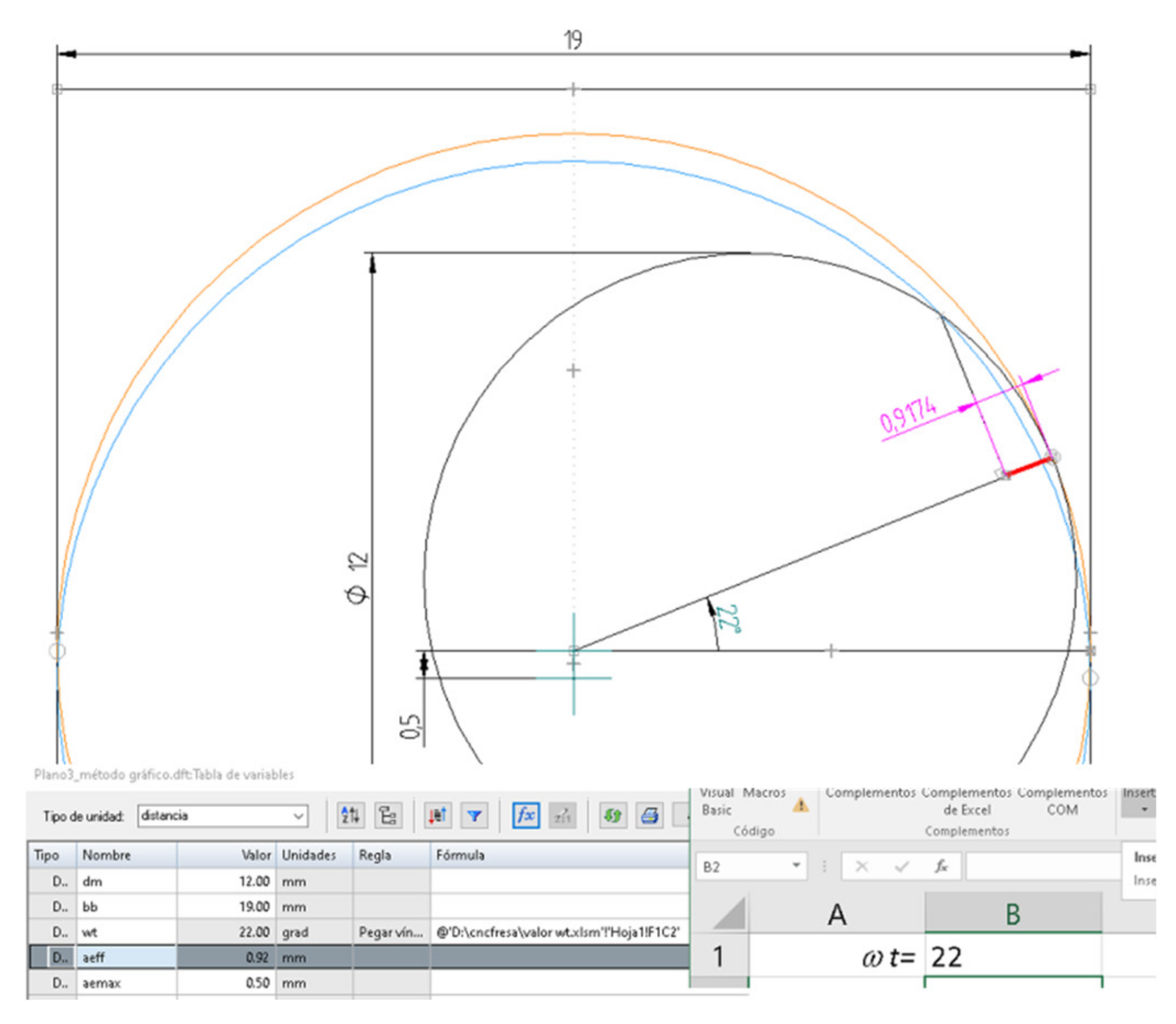
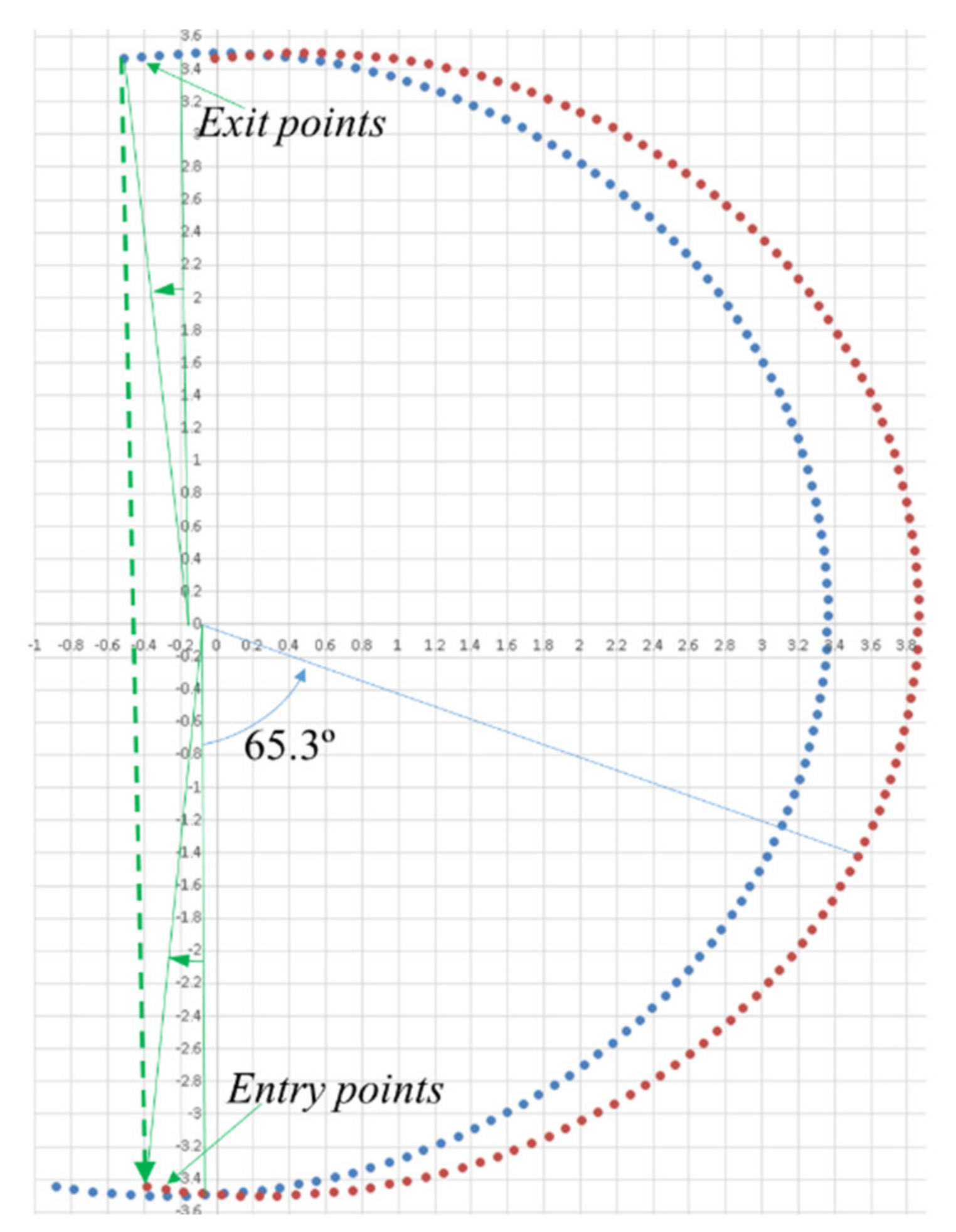
- As the cut is interior, Equation (11) makes it possible to find the corrected fz for each point. When aeffmax is reached, fz is at the minimum, being maximum in the trochoid limits (Figure 11).
- Finally, rotation (38) and translation are applied to the points obtained in the previous step. This step is described below.
- The cost of a cylinder (∅ = 183 mm) of Ti-6Al-4V was significantly lower than a rectangular plate. In fact, the local provider had a leftover, which made it more affordable.
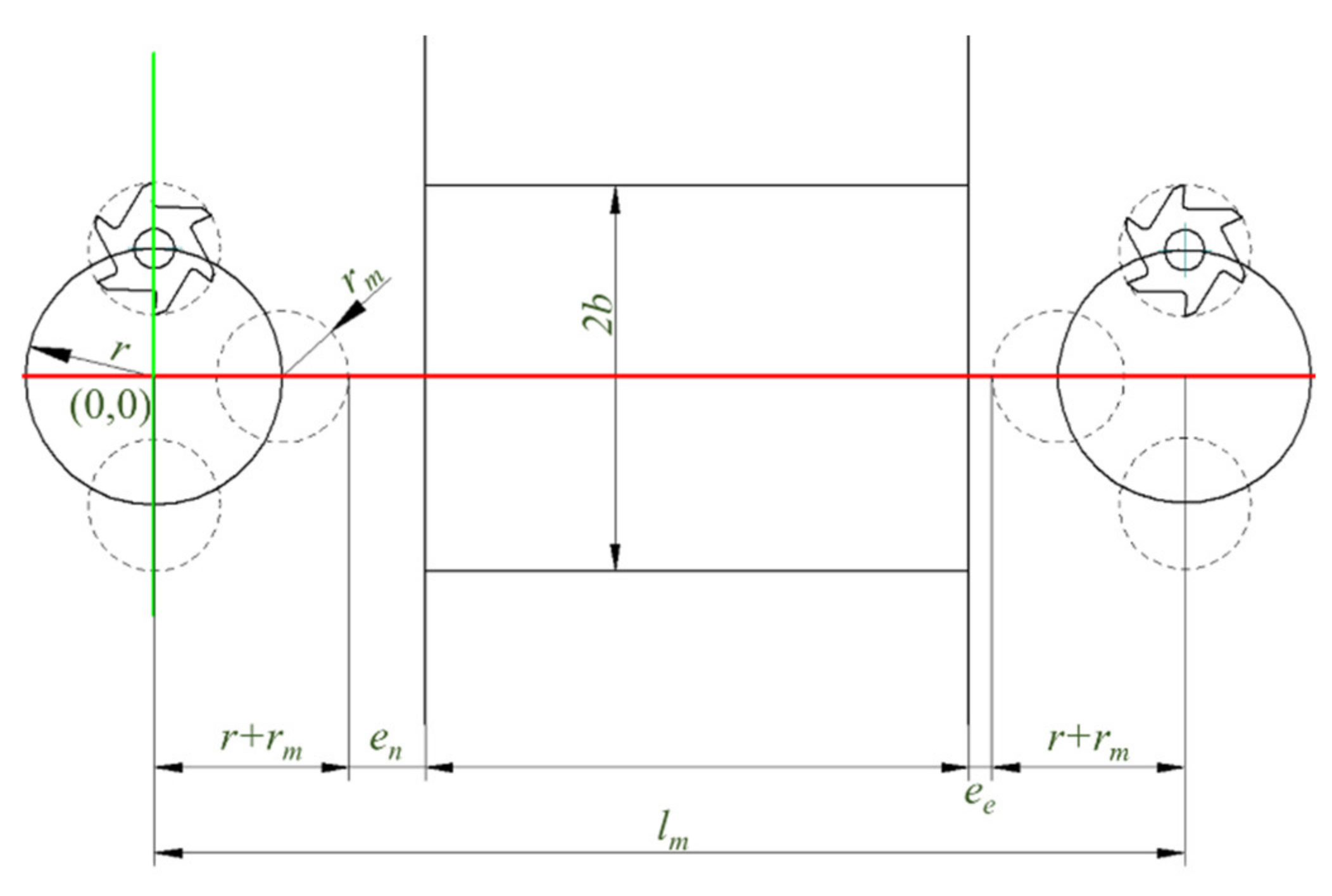
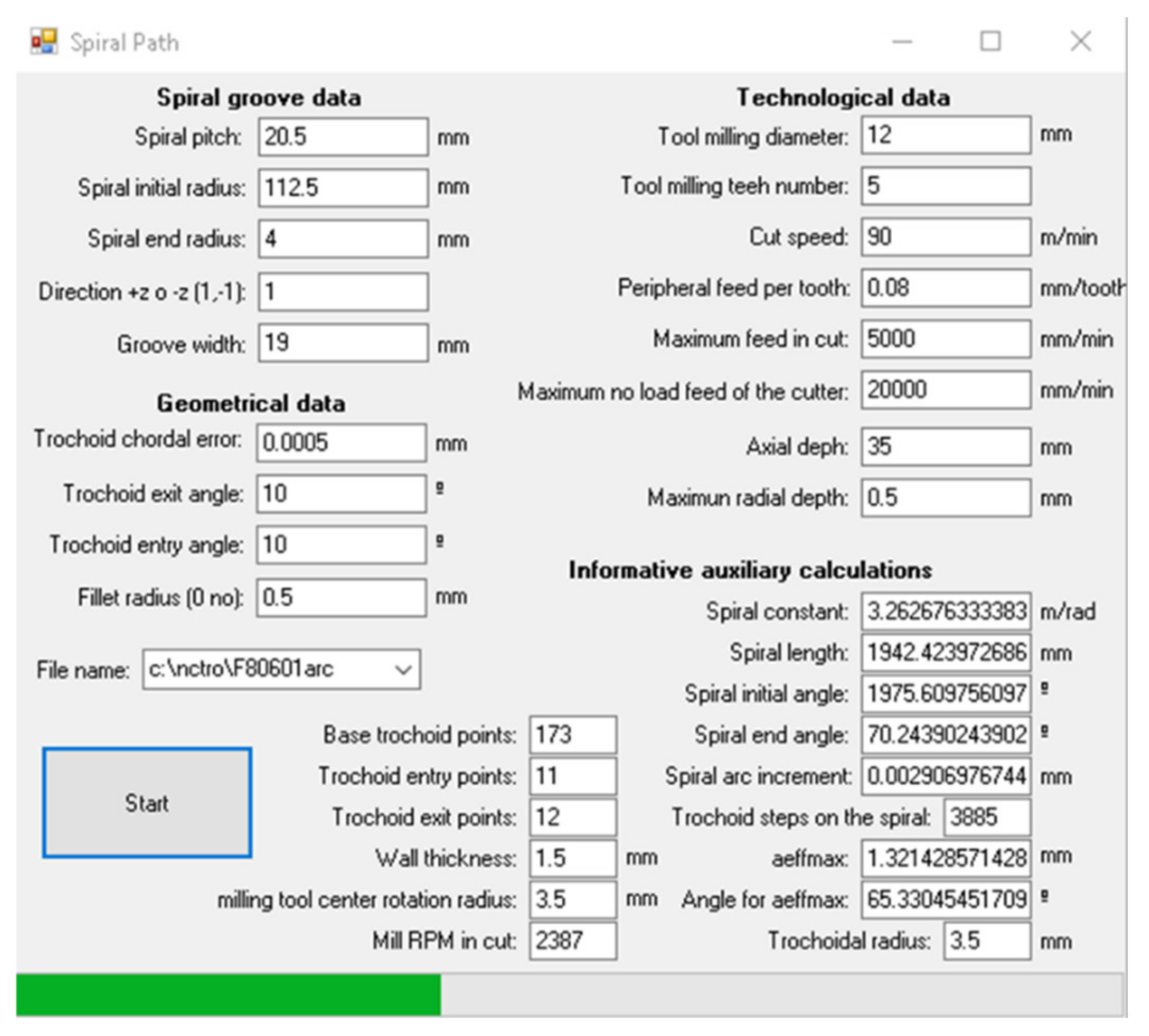
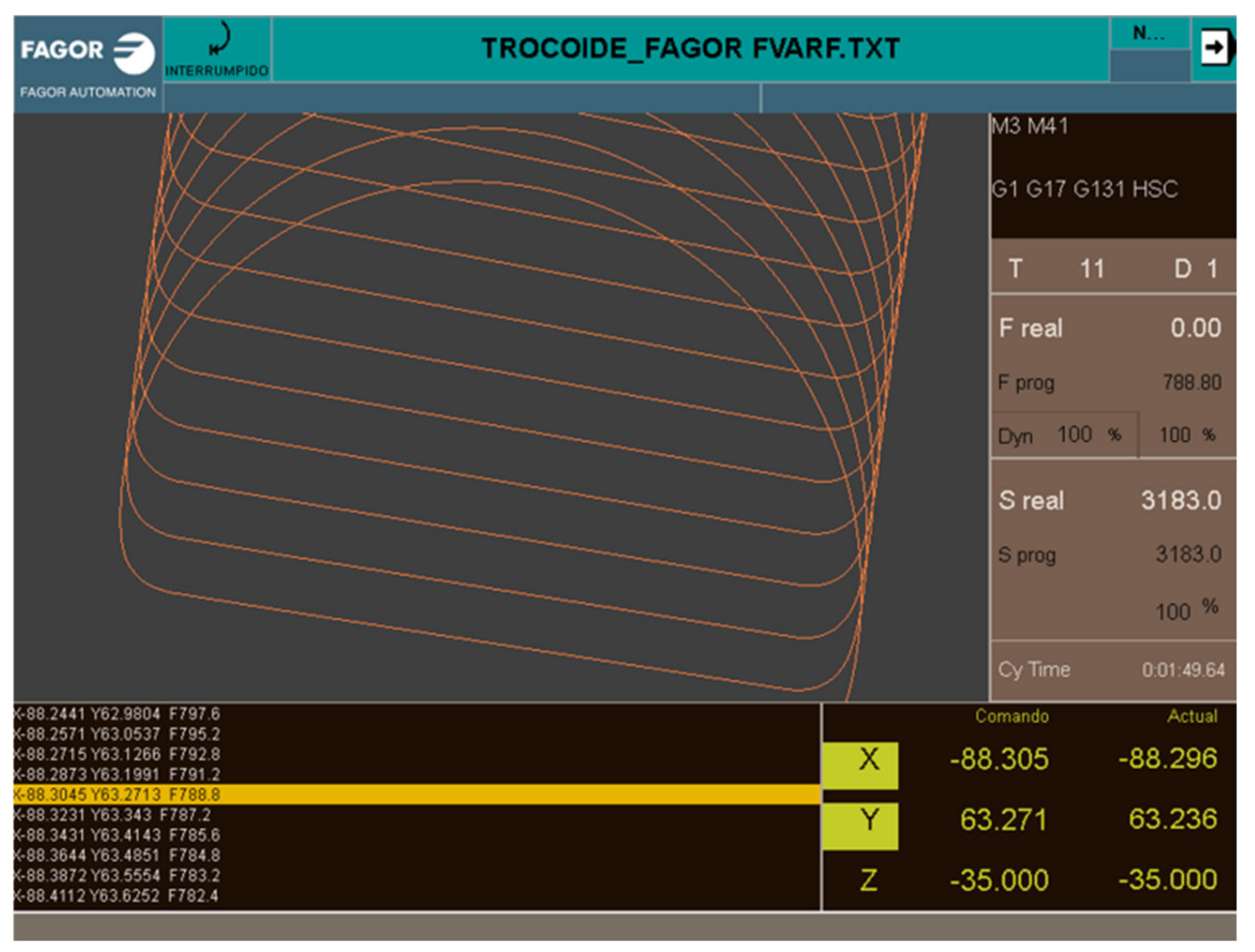
2.3. Practical Development
- The substitution of angle φe (46).
- The substitution of the length increment Δlm by the value of aemax divided by the value obtained from (48).
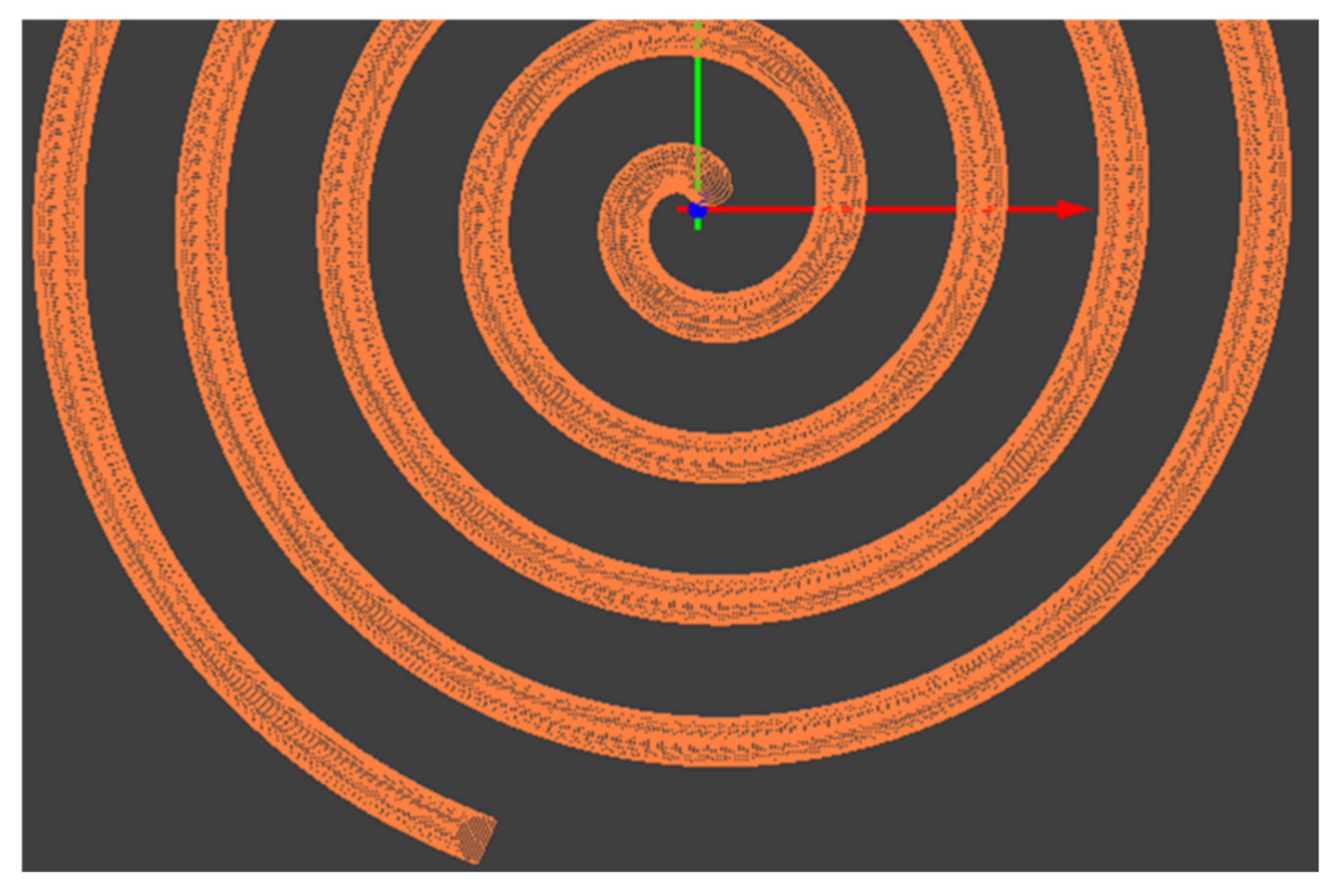
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harvey Tools. Hem Guidebook a Machinist’s Guide to Increasing Shop Productivity with High Efficiency Milling; Harvey Performance Company, LLC: Rowley, MA, USA, 2017; Volume 9, pp. 38–40. [Google Scholar]
- Pérez, J.; Llorente, J.I.; Sanchez, J.A. Advanced cutting conditions for the milling of aeronautical alloys. J. Mater. Process. Technol. 2000, 100, 1–11. [Google Scholar]
- Okokpujie, I.P.; Okonkwo, U.C. Effects of cutting parameters on surface roughness during end milling of aluminium under minimum quantity lubrication (MQL). Int. J. Sci. Res. 2015, 4, 2937–2942. [Google Scholar]
- Available online: https://www.harveyperformance.com/in-the-loupe/flute-count-matters/ (accessed on 7 May 2021).
- Jacso, A.; Matyasi, G.; Szalay, T. The fast constant engagement offsetting method for generating milling tool paths. Int. J. Adv. Manuf. Technol. 2019, 103, 4293–4305. [Google Scholar] [CrossRef] [Green Version]
- Choy, H.S.; Chan, K.W. A corner-looping based tool path for pocket milling. Comput. Aided Des. 2003, 35, 155–166. [Google Scholar] [CrossRef]
- Wu, S.; Zhao, Z.; Wang, C.Y.; Xie, Y.; Ma, W. Optimization of toolpath with circular cycle transition for sharp corners in pocket milling. Int. J. Adv. Manuf. Technol. 2016, 86, 2861–2871. [Google Scholar] [CrossRef]
- Masters in Solid Carbide Tooling. SCT Special Carbide Tooling. 2020, pp. 144–145. Available online: https://sct-tools.com/wp-content/uploads/2020/06/Catalog_2020_Downloads_SCT_Tools_.pdf (accessed on 7 May 2021).
- 2017 Master Cataloge. WIDIA. pp. 1266–1272. Available online: https://s7d2.scene7.com/skins/Kennametal/A-15-04580_Master17_Catalog_Metric_LRpdf (accessed on 7 May 2021).
- Trochoidal Shank End Mill with Variable Helix. S. v. Bassewitz GmbH & Co. KG (pp. 4 y 7). Available online: https://www.bassewitz.com/en/ (accessed on 7 May 2021).
- Solar, Z.C. Problemas de Tecnología de la Fresadora. Biblioteca Tecnológica de la Fabricación Mecánica; Biblioteca Tecnológica de la Fabricación Mecánica: Gijón, Spain, 1970; p. 49. [Google Scholar]
- Boothroyd, G. Fundamentos del corte de los metales y de las máquinas herramientas/. Geoffrey Boothroyd. Mcgraw Hill. Lat. SA. 1975, Book, 29–37. [Google Scholar]
- Micheletti, G.F.; Doménech, T.L. Mecanizado por arranque de viruta: Tecnología mecánica. Blume 1980, Book, 150–153. [Google Scholar]
- Peláez Vara, J. La Fresadora. Colección La Máquina Herramienta (TOMO II); Ediciones CEDEL: Barcelona, Spain, 1992; pp. 43–44. [Google Scholar]
- Richardson, D.J.; Keavey, M.A.; Dailami, F. Modelling of cutting induced workpiece temperatures for dry milling. Int. J. Mach. Tools Manuf. 2006, 46, 1139–1145. [Google Scholar] [CrossRef]
- Rao, B.; Shin, Y.C. Analysis on high-speed face-milling of 7075-T6 aluminum using carbide and diamond cutters. Int. J. Mach. Tools Manuf. 2001, 41, 1763–1781. [Google Scholar] [CrossRef]
- Perez, H.; Rios, J.; Diez, E.; Vizan, A. Increase of material removal rate in peripheral milling by varying feed rate. J. Mater. Process. Technol. 2008, 201, 486–490. [Google Scholar] [CrossRef]
- Fagor Automation. Manual de Programación CNC 8060 8065. Available online: https://www.fagorautomation.com (accessed on 14 May 2021).
- Otkur, M.; Lazoglu, I. Trochoidal milling. Int. J. Mach. Tools Manuf. 2007, 47, 1324–1332. [Google Scholar] [CrossRef]
- Pleta, A.; Mears, L. Cutting force investigation of trochoidal milling in nickel-based superalloy. Procedia Manuf. 2016, 5, 1348–1356. [Google Scholar] [CrossRef] [Green Version]
- Talón, J.L.H.; Boria, D.R.; Muro, L.B.; Gómez, C.L.; Zurdo, J.J.M.; Calvo, F.V.; Barace, J.J.G. Functional check test for high-speed milling centres of up to five axes. Int. J. Adv. Manuf. Technol. 2011, 55, 39–51. [Google Scholar] [CrossRef]
- Sanvik Coromant. Fresado (PDF Format). pp. 121–122. Available online: https://www.sandvik.coromant.com/es-es/knowledge/milling/milling-holes-cavities-pockets/pages/slicing-trochoidal-milling.aspx (accessed on 21 May 2021).
- Seco, Fresas Enterizas JABRO. (PDF Format), p. 420. Available online: https://usercontent.azureedge.net/Content/UserContent/Documents/027782.pdf (accessed on 21 May 2021).
- Gross, D.; Friedl, F.; Meier, T.; Hanenkamp, N. Comparison of linear and trochoidal milling for wear and vibration reduced machining. Procedia CIRP 2020, 90, 563–567. [Google Scholar] [CrossRef]
- Karkalos, N.E.; Karmiris-Obratański, P.; Kurpiel, S.; Zagórski, K.; Markopoulos, A.P. Investigation on the Surface Quality Obtained during Trochoidal Milling of 6082 Aluminum Alloy. Machines 2021, 9, 75. [Google Scholar] [CrossRef]
- Waszczuk, K.; Skowronek, H.; Karolczak, P.; Kowalski, M.; Kołodziej, M. Influence of the Trochoidal Tool Path on Quality Surface of Groove Walls. Adv. Sci. Technology. Res. J. 2019, 13, 38–42. [Google Scholar] [CrossRef]
- Santhakumar, J.; Iqbal, U.M. Role of trochoidal machining process parameter and chip morphology studies during end milling of AISI D3 steel. J. Intell. Manuf. 2021, 32, 649–665. [Google Scholar] [CrossRef]
- Garde-Barace, J.J.; Huertas-Talón, J.L.; Valdivia-Calvo FBueno-Pérez, J.A.; Cano-Álvarez, B.; Álcazar-Sánchez, M.A.; Ponz-Cuenca, R.; Tzotzis, A. Velocidad de corte constante en fresado. IMHE Ed. Técnicas IZARO 2021, 476, 80–98. [Google Scholar]
- Aguirre, N. La espiral de Arquímedes en un proyecto de modelación matemática. Rev. Educ. Matemática 2008, 23, 1–10. [Google Scholar]
- Huang, X.; Wu, S.; Liang, L.; Li, X.; Huang, N. Efficient trochoidal milling based on medial axis transformation and inscribed ellipse. Int. J. Adv. Manuf. Technol. 2020, 111, 1069–1076. [Google Scholar] [CrossRef]
- Klocke, F.; Bergs, T.; Busch, M.; Rohde, L.; Witty, M.; Cabral, G.F. Integrated approach for a knowledge-based process layout for simultaneous 5-axis milling of advanced materials. Adv. Tribol. 2011, 2011, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Käsemodel, R.B.; de Souza, A.F.; Voigt, R.; Basso, I.; Rodrigues, A.R. CAD/CAM interfaced algorithm reduces cutting force, roughness, and machining time in free-form milling. Int. J. Adv. Manuf. Technol. 2020, 107, 1883–1900. [Google Scholar] [CrossRef]
- Huertas, J.L.; Faci, E.; Ros, E. CO2, la mejor opción. IMHE 2006, 330, 59–78. [Google Scholar]
- Jamil, M.; Zhao, W.; He, N.; Gupta, M.K.; Sarikaya, M.; Khan, A.M.; Sanjay, M.R.; Siengchin, S.; Pimenov, D.Y. Sustainable milling of Ti–6Al–4V: A trade-off between energy efficiency, carbon emissions and machining characteristics under MQL and cryogenic environment. J. Clean. Prod. 2021, 281, 1–14. [Google Scholar] [CrossRef]
- Albertelli, P.; Mussi, V.; Strano, M.; Monno, M. Experimental investigation of the effects of cryogenic cooling on tool life in Ti6Al4V milling. Int. Adv. Manuf. Technol. 2021. Available online: https://link.springer.com/article/10.1007%2Fs00170-021-07161-9#citeas (accessed on 21 May 2021).
- Eltaggaz, A.; Nouzil, I.; Deiab, I. Machining Ti-6Al-4V Alloy Using Nano-Cutting Fluids: Investigation and Analysis. J. Manuf. Mater. Process 2021, 5, 42. [Google Scholar]
- Kim, D.-H.; Lee, C.-M. Experimental Investigation on Machinability of Titanium Alloy by Laser-Assisted End Milling. Metals 2021, 11, 1552. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Hernández, C.; Garde-Barace, J.-J.; Valdivia-Sánchez, J.-J.; Ubieto-Artur, P.; Bueno-Pérez, J.-A.; Cano-Álvarez, B.; Alcázar-Sánchez, M.-Á.; Valdivia-Calvo, F.; Ponz-Cuenca, R.; Huertas-Talón, J.-L.; et al. Trochoidal Milling Path with Variable Feed. Application to the Machining of a Ti-6Al-4V Part. Mathematics 2021, 9, 2701. https://doi.org/10.3390/math9212701
García-Hernández C, Garde-Barace J-J, Valdivia-Sánchez J-J, Ubieto-Artur P, Bueno-Pérez J-A, Cano-Álvarez B, Alcázar-Sánchez M-Á, Valdivia-Calvo F, Ponz-Cuenca R, Huertas-Talón J-L, et al. Trochoidal Milling Path with Variable Feed. Application to the Machining of a Ti-6Al-4V Part. Mathematics. 2021; 9(21):2701. https://doi.org/10.3390/math9212701
Chicago/Turabian StyleGarcía-Hernández, César, Juan-José Garde-Barace, Juan-Jesús Valdivia-Sánchez, Pedro Ubieto-Artur, José-Antonio Bueno-Pérez, Basilio Cano-Álvarez, Miguel-Ángel Alcázar-Sánchez, Francisco Valdivia-Calvo, Rubén Ponz-Cuenca, José-Luis Huertas-Talón, and et al. 2021. "Trochoidal Milling Path with Variable Feed. Application to the Machining of a Ti-6Al-4V Part" Mathematics 9, no. 21: 2701. https://doi.org/10.3390/math9212701
APA StyleGarcía-Hernández, C., Garde-Barace, J.-J., Valdivia-Sánchez, J.-J., Ubieto-Artur, P., Bueno-Pérez, J.-A., Cano-Álvarez, B., Alcázar-Sánchez, M.-Á., Valdivia-Calvo, F., Ponz-Cuenca, R., Huertas-Talón, J.-L., & Kyratsis, P. (2021). Trochoidal Milling Path with Variable Feed. Application to the Machining of a Ti-6Al-4V Part. Mathematics, 9(21), 2701. https://doi.org/10.3390/math9212701






