Controlling Effects of Astrocyte on Neuron Behavior in Tripartite Synapse Using VHDL–AMS
Abstract
:1. Introduction
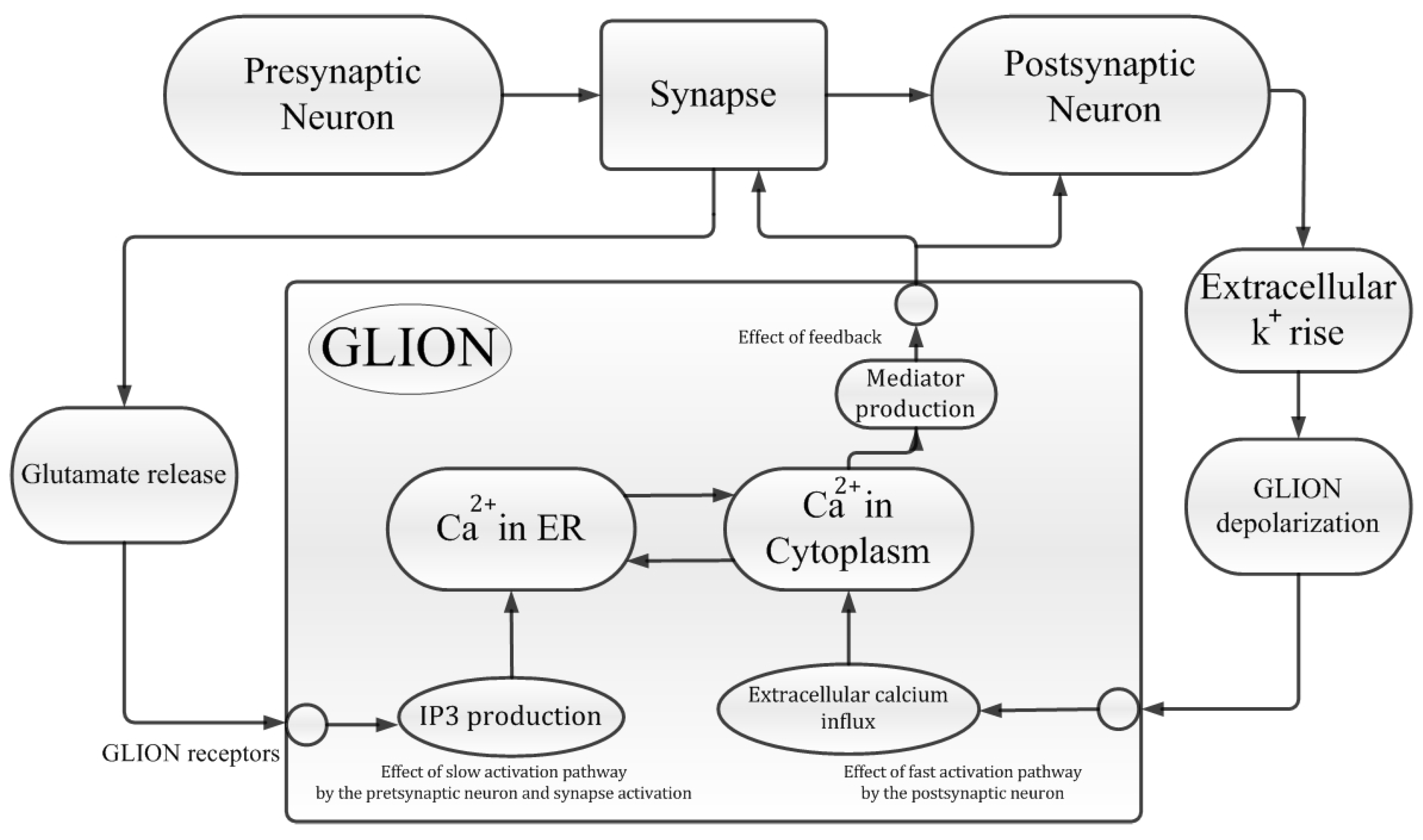
2. Neural–Glial Interaction
3. Tripartite Synapse
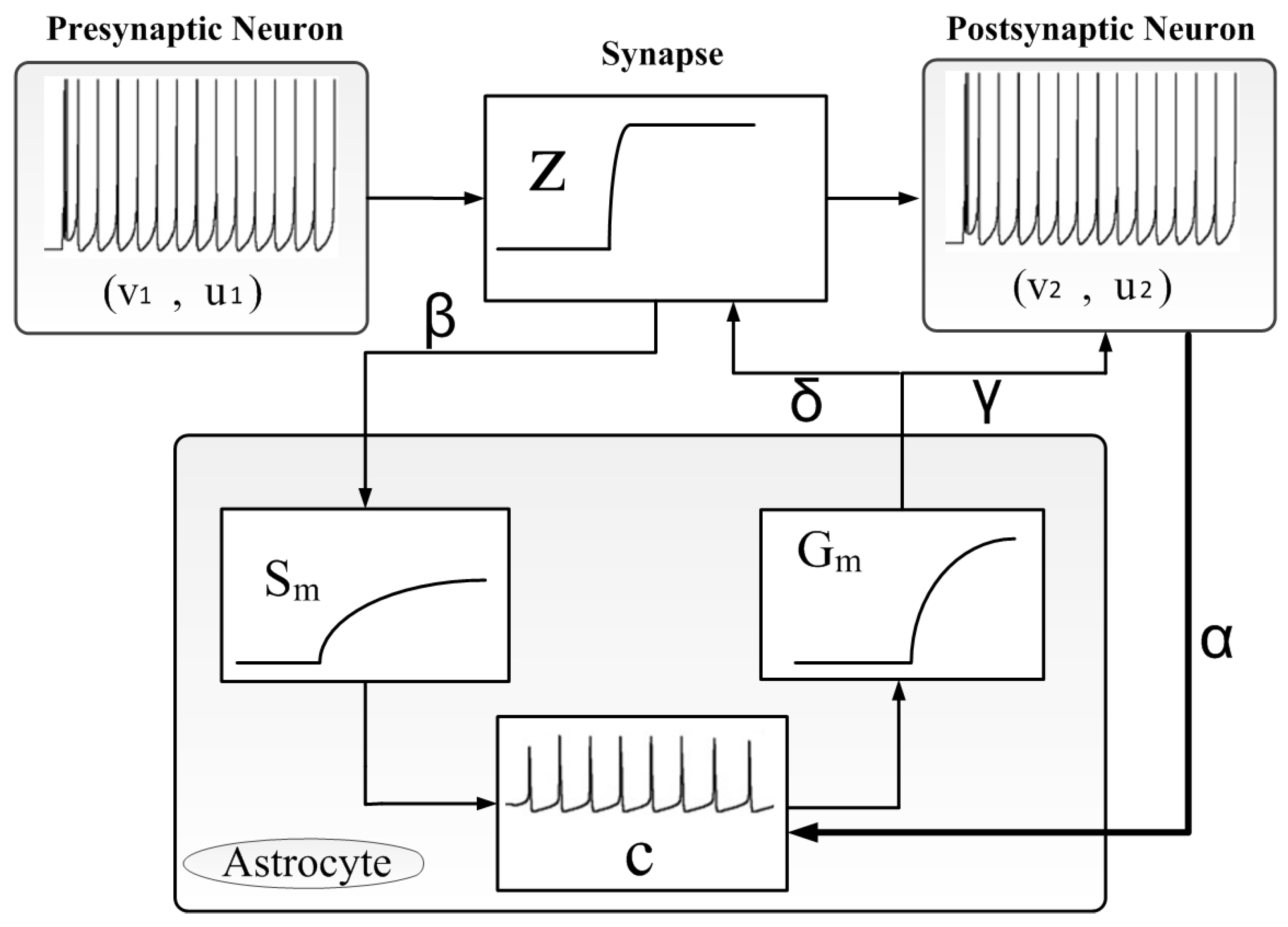
4. System Modeling Using VHDL–AMS
4.1. Neuron and Synapse Modeling
- : delay (s);
- : activation and relaxation of z;
- : Threshold parameter;
- : Synapse stimulus current;
- : Conductance;
- : Response for astrocyte;
- : Reference state of z.
4.2. Astrocytic Cell
5. Controlling Effects of Astrocyte Module
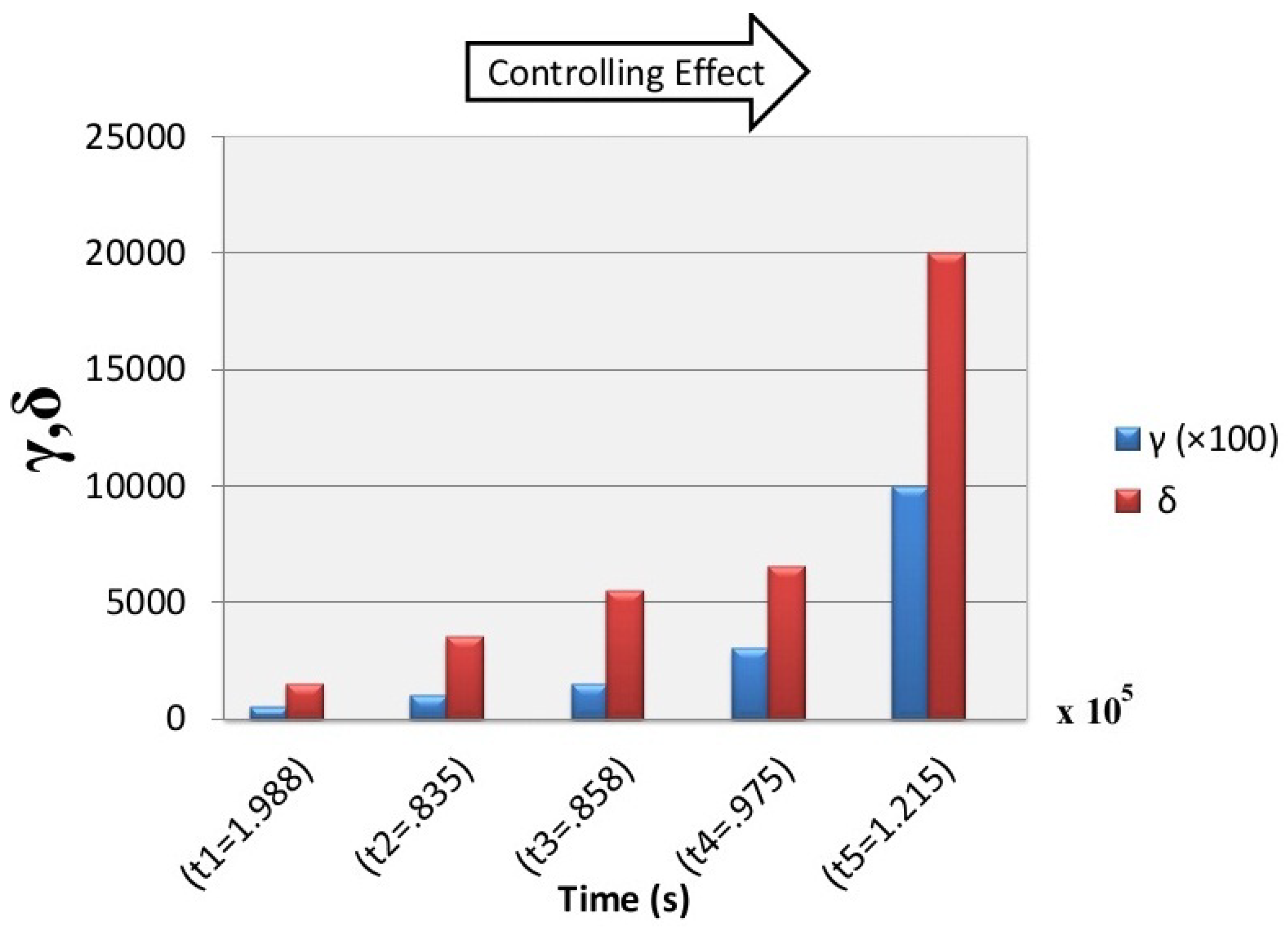
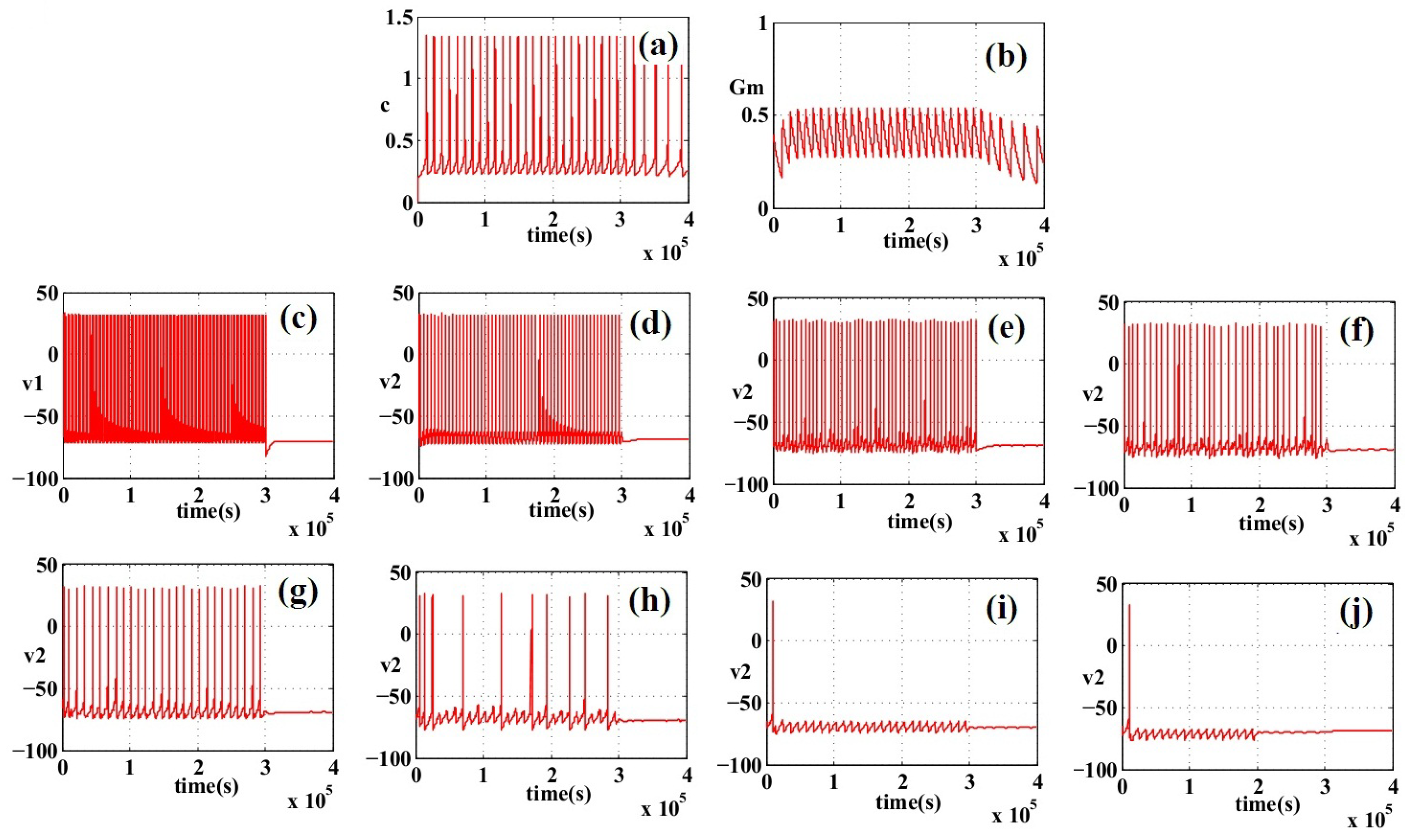
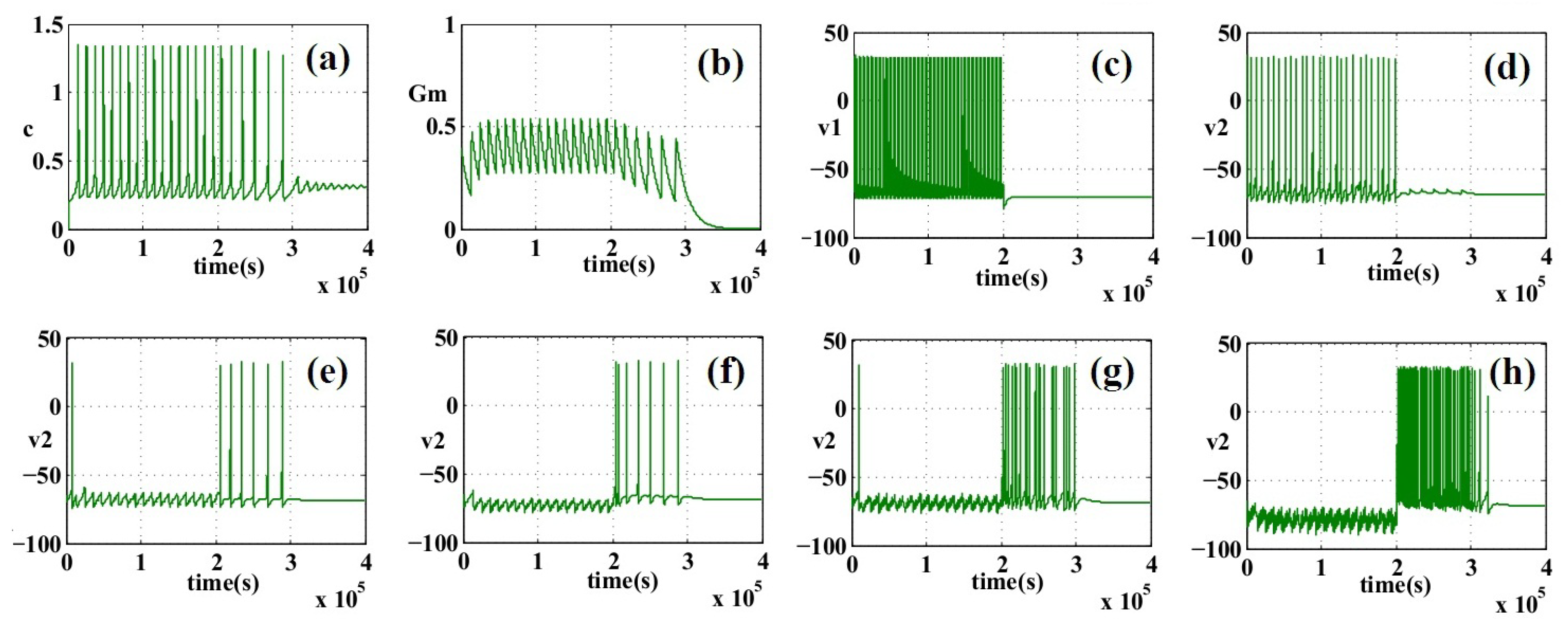
6. Simulation Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Roshani, G.; Nazemi, E.; Roshani, M. Usage of two transmitted detectors with optimized orientation in order to three phase flow metering. Measurement 2017, 100, 122–130. [Google Scholar] [CrossRef]
- Hosseinzadeh-Bandbafha, H.; Nazemi, F.; Khounani, Z.; Ghanavati, H.; Shafiei, M.; Karimi, K.; Lam, S.S.; Aghbashlo, M.; Tabatabaei, M. Safflower-based biorefinery producing a broad spectrum of biofuels and biochemicals: A life cycle assessment perspective. Sci. Total Environ. 2021, 802, 149842. [Google Scholar] [CrossRef]
- Roshani, G.; Nazemi, E.; Roshani, M. Intelligent recognition of gasoil-water three-phase flow regime and determination of volume fraction using radial basis function. Flow Meas. Instrum. 2017, 54, 39–45. [Google Scholar] [CrossRef]
- Karami, A.; Yousefi, T.; Harsini, I.; Maleki, E.; Mahmoudinezhad, S. Neuro-Fuzzy Modeling of the Free Convection Heat Transfer from a Wavy Surface. Heat Transf. Eng. 2015, 36, 847–855. [Google Scholar] [CrossRef]
- Alwan, S.; Al-Saeed, M.; Abid, H. Safety assessment and biochemical evaluation of biogenic silver nanoparticles (using bark extract of C. zeylanicum) in Rattus norvegicus rats. Baghdad J. Biochem. Appl. Biol. Sci. 2021, 2, 138–150. [Google Scholar] [CrossRef]
- Nazemi, F.; Karimi, K.; Denayer, J.F.; Shafiei, M. Techno-economic aspects of different process approaches based on brown macroalgae feedstock: A step toward commercialization of seaweed-based biorefineries. Algal. Res. 2021, 58, 102366. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, B.; Zhao, L.; Zhao, L.; Wang, Q.; Wang, C.; Xu, B. A dansyl-based fluorescent probe for sensing Cu2+ in aqueous solution. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 261, 120009. [Google Scholar] [CrossRef]
- Roshani, M.; Sattari, M.A.; Ali, P.J.M.; Roshani, G.H.; Nazemi, B.; Corniani, E.; Nazemi, E. Application of GMDH neural network technique to improve measuring precision of a simplified photon attenuation based two-phase flowmeter. Flow Meas. Instrum. 2020, 75, 101804. [Google Scholar] [CrossRef]
- Shalaby, M.N.; Sakoury, M.M.; Kholif, M.A.; Alsayed, N.I. The role of Amino Acids in improving immunity and growth factors of Volleyball players. J. Adv. Pharm. Educ. Res. 2020, 10, 141. [Google Scholar]
- Roshani, S.; Roshani, S. Design of a high efficiency class-F power amplifier with large signal and small signal measurements. Measurement 2020, 149, 106991. [Google Scholar] [CrossRef]
- Pourbemany, J.; Mirjalily, G.; Abouei, J.; Raouf, A.H.F. Load Balanced Ad-Hoc On-Demand Routing Basedon Weighted Mean Queue Length Metric. In Proceedings of the Electrical Engineering (ICEE), Iranian Conference on IEEE, Mashhad, Iran, 8–10 May 2018; pp. 470–475. [Google Scholar]
- Pirasteh, A.; Roshani, S.; Roshani, S. A modified class-F power amplifier with miniaturized harmonic control circuit. AEU Int. J. Electron. Commun. 2018, 97, 202–209. [Google Scholar] [CrossRef]
- Jamshidi, M.B.; Roshani, S.; Talla, J.; Roshani, S.; Peroutka, Z. Size reduction and performance improvement of a microstrip Wilkinson power divider using a hybrid design technique. Sci. Rep. 2021, 11, 7773. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wang, X.; Zhang, Z.; Cui, Y.; Ling, L.; Cai, G. An Adaptative Control Strategy for Interfacing Converter of Hybrid Microgrid Based on Improved Virtual Synchronous Generator. IET Renew. Power Gener. 2021, 15, 2674–2685. [Google Scholar] [CrossRef]
- Jamshidi, M.B.; Siahkamari, H.; Roshani, S.; Roshani, S. A compact Gysel power divider design using U-shaped and T-shaped resonators with harmonics suppression. Electromagnetics 2019, 39, 491–504. [Google Scholar] [CrossRef]
- Roshani, S.; Roshani, S.; Zarinitabar, A. A modified Wilkinson power divider with ultra harmonic suppression using open stubs and lowpass filters. Analog. Integr. Circuits Signal Process 2019, 98, 395–399. [Google Scholar] [CrossRef]
- Roshani, S.; Roshani, S. Design of a very compact and sharp bandpass diplexer with bended lines for GSM and LTE applications. AEU Int. J. Electron. Commun. 2019, 99, 354–360. [Google Scholar] [CrossRef]
- Roshani, S.; Roshani, S. A compact coupler design using meandered line compact microstrip resonant cell (MLCMRC) and bended lines. Wirel. Netw. 2021, 27, 677–684. [Google Scholar] [CrossRef]
- Pirasteh, A.; Roshani, S.; Roshani, S. Compact microstrip lowpass filter with ultrasharp response using a square-loaded modified T-shaped resonator. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 1736–1746. [Google Scholar] [CrossRef]
- Jha, A.K.; Ali, A.; Kumar, M.; Kumar, M.; Badhani, P.P.; Murthy, N.B.S.; Chandrakant, K. Outcome of routine histopathological examination of gallbladder specimen following elective laparoscopic cholecystectomy. J. Carcinog. 2021, 20, 19. [Google Scholar] [CrossRef]
- Leman, M.A.; Claramita, M.; Rahayu, G.R. Predicting Factors on Modeling Health Behavior: A Systematic Review. Am. J. Health Behav. 2021, 45, 268. [Google Scholar] [CrossRef]
- Anil, M.A.; Rebello, R.M.; Bhat, J.S. Speech-language profile of a child with fahrs disease: Case report of a rare neurodegenerative disorder. J. Nat. Sci. Biol. Med. 2020, 11, 206. [Google Scholar]
- Ghanbari, B. On the modeling of the interaction between tumor growth and the immune system using some new fractional and fractional-fractal operators. Adv. Differ. Equ. 2020, 2020, 585. [Google Scholar] [CrossRef]
- Zhao, H. Prediction and Evaluation of Athletes’ Positive Emotions Based on Emotional Intelligence Theory. Rev. Psicol. Deporte (J. Sport Psychol.) 2021, 30, 38–52. [Google Scholar]
- Ghanbari, B. Chaotic behaviors of the prevalence of an infectious disease in a prey and predator system using fractional derivatives. Math. Methods Appl. Sci. 2021, 44, 9998–10013. [Google Scholar] [CrossRef]
- Nabishah, B.M.; Merican, Z.; Morat, P.B.; Alias, A.K.; Khalid, B.A. Effects of steroid hormones pretreatment on isoprenaline-induced cyclic adenosine 3′,5′-monophosphate in rat lung. Gen. Pharmacol. 1990, 21, 935–938. [Google Scholar] [CrossRef]
- Das, S.; Selvaraji, K.; Dutta, M.; Isa, M.Z.A.; Moorthy, T.N. A pilot study on glaucoma and depth variation, A factor that affect the accuracy of eyewitness identification. Int. J. Med. Toxicol. Leg. Med. 2018, 21, 239–242. [Google Scholar] [CrossRef]
- Bahari, R.; Alwi, M.N.M.; Ahmad, M.R. Translation and validation of the Malay posttraumatic stress disorder checklist for DSM-5 (MPLC-5). Malays. J. Med. Health Sci. 2019, 15 (Suppl. S1), 15–20. [Google Scholar]
- Ghanbari, B. A new model for investigating the transmission of infectious diseases in a preypredator system using a nonsingular fractional derivative. Math. Methods Appl. Sci. 2021, 44, 9998–10013. [Google Scholar] [CrossRef]
- Yang, L.W.; Fattepur, S.; Nilugal, K.C.; Asmani, F.; Yusuf, E.; Ghani, M.N.A.; Abdullah, I. Neuroprotection of abelmoschus esculentus l. against diabetic neuropathy. Asian J. Pharm. Clin. Res. 2018, 11, 28–31. [Google Scholar] [CrossRef]
- Shalaby, M.N.; Sakoury, M.M.A.; Al-jameel, S.S.; Alghamdi, A. The Effect of Diving for Different Years on CD34+ Stem Cells and Some Physiological Variables for Commercial Divers. Int. J. Hum. Mov. Sport. Sci. 2021, 9, 1146–1156. [Google Scholar]
- Shalaby, M.N. The Effect of Whey Protein (Natural Nanoparticle) on Muscle Strength, GH, IGF, T. Protein and body composition. Int. J. Pharm. Res. Allied Sci. 2018, 7, 126–132. [Google Scholar]
- Shalaby, M.N.; Fadl, M.A. Relative Indicators and Predicative Ability of Some Biological Variables on Cardiac Neural Activity for Volleyball Players. Syst. Rev. Pharm. 2020, 11, 834–840. [Google Scholar]
- Djilali, S.; Ghanbari, B. The influence of an infectious disease on a prey-predator model equipped with a fractional-order derivative. Adv. Differ. Equ. 2021, 2021, 20. [Google Scholar] [CrossRef]
- Roshani, G.H.; Nazemi, E.; Feghhi, S.A.H.; Setayeshi, S. Flow regime identification and void fraction prediction in two-phase flows based on gamma ray attenuation. Measurement 2015, 62, 25–32. [Google Scholar] [CrossRef]
- Abolhasani, M.; Karami, A.; Rahimi, M. Numerical Modeling and Optimization of the Enhancement of the Cooling Rate in Concentric Tubes Under Ultrasound Field. Numer. Heat Transf. Part A Appl. 2015, 67, 1282–1309. [Google Scholar] [CrossRef]
- Roshani, G.H.; Feghhi, S.A.H.; Mahmoudi-Aznaveh, A.; Nazemi, E.; Adineh-Vand, A. Precise volume fraction prediction in oil–water–gas multiphase flows by means of gamma-ray attenuation and artificial neural networks using one detector. Measurement 2014, 51, 34–41. [Google Scholar] [CrossRef]
- Aghakhani, M.; Ghaderi, M.R.; Karami, A.; Derakhshan, A.A. Combined effect of TiO2 nanoparticles and input welding parameters on the weld bead penetration in submerged arc welding process using fuzzy logic. Int. J. Adv. Manuf. Technol 2014, 70, 63–72. [Google Scholar] [CrossRef]
- Nazemi, E.; Roshani, G.H.; Feghhi, S.A.H.; Setayeshi, S.; Zadeh, E.E.; Fatehi, A. Optimization of a method for identifying the flow regime and measuring void fraction in a broad beam gamma-ray attenuation technique. Int. J. Hydrogen Energy 2016, 41, 7438–7444. [Google Scholar] [CrossRef]
- Karami, A.; Veysi, F.; Mohebbi, S.; Ghashghaei, D. Optimization of Laminar Free Convection in a Horizontal Cavity Consisting of Flow Diverters Using ICA. Arab. J. Sci. Eng 2014, 39, 2295–2306. [Google Scholar] [CrossRef]
- Nazemi, E.; Feghhi, S.A.H.; Roshani, G.H.; Setayeshi, S.; Peyvandi, R.G. A radiation-based hydrocarbon two-phase flow meter for estimating of phase fraction independent of liquid phase density in stratified regime. Flow Meas. Instrum. 2015, 46, 25–32. [Google Scholar] [CrossRef]
- Jiang, B.; Liu, Y.; Zhao, L.; Zhao, L.; Wang, C.; Liu, C.; Xu, B. Construction of a pH-sensitive self-assembly in aqueous solutions based on a dansyl-modified cyclodextrin. Soft Matter 2021, 17, 7516–7523. [Google Scholar] [CrossRef]
- Nazemi, E.; Feghhi, S.A.H.; Roshani, G.H.; Peyvandi, R.G.; Setayeshi, S. Precise void fraction measurement in two-phase flows independent of the flow regime using gamma-ray attenuation. Nucl. Eng. Technol. 2016, 48, 64–71. [Google Scholar] [CrossRef] [Green Version]
- Roshani, G.H.; Nazemi, E.; Feghhi, S.A.H. Investigation of using 60Co source and one detector for determining the flow regime and void fraction in gas–liquid two-phase flows. Flow Meas. Instrum. 2016, 50, 73–79. [Google Scholar] [CrossRef]
- Sattari, M.A.; Roshani, G.H.; Hanus, R.; Nazemi, E. Applicability of time-domain feature extraction methods and artificial intelligence in two-phase flow meters based on gamma-ray absorption technique. Measurement 2021, 168, 108474. [Google Scholar] [CrossRef]
- Basahel, A.; Sattari, M.; Taylan, O.; Nazemi, E. Application of Feature Extraction and Artificial Intelligence Techniques for Increasing the Accuracy of X-ray Radiation Based Two Phase Flow Meter. Mathematics 2021, 9, 1227. [Google Scholar] [CrossRef]
- Moradi, M.J.; Hariri-Ardebili, M.A. Developing a Library of Shear Walls Database and the Neural Network Based Predictive Meta Model. Appl. Sci. 2019, 9, 2562. [Google Scholar] [CrossRef] [Green Version]
- Nazemi, B.; Rafiean, M. Forecasting house prices in Iran using GMDH. Int. J. Hous. Mark. Anal. 2021, 14, 555–568. [Google Scholar] [CrossRef]
- Moradi, M.J.; Roshani, M.M.; Shabani, A.; Kioumarsi, M. Prediction of the Load-Bearing Behavior of SPSW with Rectangular Opening by RBF Network. Appl. Sci. 2020, 10, 1185. [Google Scholar] [CrossRef] [Green Version]
- Moradi, M.; Daneshvar, K.; Ghazi-Nader, D.; Hajiloo, H. The prediction of fire performance of concrete-filled steel tubes (CFST) using artificial neural network. Thin Walled Struct. 2021, 161, 107499. [Google Scholar] [CrossRef]
- Zajmi, L.; Ahmed, F.Y.; Jaharadak, A.A. Concepts, methods, and performances of particle swarm optimization, backpropagation, and neural networks. Appl. Comput. Intell. Soft Comput. 2018, 2018, 9547212. [Google Scholar] [CrossRef]
- Amidi, Y.; Nazari, B.; Sadri, S.; Yousefi, A. Parameter Estimation in Multiple Dynamic Synaptic Coupling Model Using Bayesian Point Process State-Space Modeling Framework. Neural Comput. 2021, 33, 1269–1299. [Google Scholar] [CrossRef]
- Yousefi, A.; Amidi, Y.; Nazari, B.; Eden, U.T. Assessing Goodness-of-Fit in Marked Point Process Models of Neural Population Coding via Time and Rate Rescaling. Neural Comput. 2020, 32, 2145–2186. [Google Scholar] [CrossRef] [PubMed]
- Roshani, M.; Phan, G.; Roshani, G.H.; Hanus, R.; Nazemi, B.; Corniani, E.; Nazemi, E. Combination of X-ray tube and GMDH neural network as a nondestructive and potential technique for measuring characteristics of gas-oil–water three phase flows. Measurement 2021, 168, 108427. [Google Scholar] [CrossRef]
- Roshani, M.; Phan, G.; Faraj, R.H.; Phan, N.H.; Roshani, G.H.; Nazemi, B.; Corniani, E.; Nazemi, E. Proposing a gamma radiation based intelligent system for simultaneous analyzing and detecting type and amount of petroleum by-products. Nucl. Eng. Technol. 2021, 53, 1277–1283. [Google Scholar] [CrossRef]
- Roshani, G.; Nazemi, E. Intelligent densitometry of petroleum products in stratified regime of two phase flows using gamma ray and neural network. Flow Meas. Instrum. 2017, 58, 6–11. [Google Scholar] [CrossRef]
- Karami, A.; Roshani, G.H.; Khazaei, A.; Nazemi, E.; Fallahi, M. Investigation of different sources in order to optimize the nuclear metering system of gas–oil–water annular flows. Neural Comput. Appl. 2020, 32, 3619–3631. [Google Scholar] [CrossRef]
- Karami, A.; Roshani, G.H.; Nazemi, E.; Roshani, S. Enhancing the performance of a dual-energy gamma ray based three-phase flow meter with the help of grey wolf optimization algorithm. Flow Meas. Instrum. 2018, 64, 164–172. [Google Scholar] [CrossRef]
- Roshani, G.H.; Roshani, S.; Nazemi, E.; Roshani, S. Online measuring density of oil products in annular regime of gas-liquid two phase flows. Measurement 2018, 129, 296–301. [Google Scholar] [CrossRef]
- Alkabaa, A.S.; Nazemi, E.; Taylan, O.; Kalmoun, E.M. Application of Artificial Intelligence and Gamma Attenuation Tech-niques for Predicting Gas–Oil–Water Volume Fraction in Annular Regime of Three-Phase Flow Independent of Oil Pipeline’s Scale Layer. Mathematics 2021, 9, 1460. [Google Scholar] [CrossRef]
- Roshani, G.; Nazemi, E.; Roshani, M. Identification of flow regime and estimation of volume fraction independent of liquid phase density in gas-liquid two-phase flow. Prog. Nucl. Energy 2017, 98, 29–37. [Google Scholar] [CrossRef]
- Roshani, G.; Hanus, R.; Khazaei, A.; Zych, M.; Nazemi, E.; Mosorov, V. Density and velocity determination for single-phase flow based on radiotracer technique and neural networks. Flow Meas. Instrum. 2018, 61, 9–14. [Google Scholar] [CrossRef]
- Djilali, S.; Ghanbari, B. Dynamical behavior of two predators-one prey model with generalized functional response and time-fractional derivative. Adv. Differ. Equ. 2021, 2021, 235. [Google Scholar] [CrossRef]
- Ghanbari, B. Abundant exact solutions to a generalized nonlinear Schrödinger equation with local fractional derivative. Math. Methods Appl. Sci. 2021, 44, 8759–8774. [Google Scholar] [CrossRef]
- Ghanbari, B. On novel nondifferentiable exact solutions to local fractional Gardner’s equation using an effective technique. Math. Methods Appl. Sci. 2021, 44, 4673–4685. [Google Scholar] [CrossRef]
- Nabti, A.; Ghanbari, B. Global stability analysis of a fractional SVEIR epidemic model. Math. Methods Appl. Sci. 2021, 44, 8577–8597. [Google Scholar] [CrossRef]
- Ghanbari, B. On approximate solutions for a fractional prey-predator model involving the Atangana-Baleanu derivative. Adv. Differ. Equ. 2020, 2020, 679. [Google Scholar] [CrossRef]
- Ghanbari, B. A fractional system of delay differential equation with nonsingular kernels in modeling hand-foot-mouth disease. Adv. Differ. Equ. 2020, 2020, 536. [Google Scholar] [CrossRef]
- Ghanbari, B.; Atangana, A. Some new edge detecting techniques based on fractional derivatives with non-local and non-singular kernels. Adv. Differ. Equ. 2020, 2020, 435. [Google Scholar] [CrossRef]
- Ghanbari, B.; Nisar, K.S.; Aldhaifallah, M. Abundant solitary wave solutions to an extended nonlinear Schrödinger’s equation with conformable derivative using an efficient integration method. Adv. Differ. Equ. 2020, 2020, 328. [Google Scholar] [CrossRef]
- Ghanbari, B.; Yusuf, A.; Baleanu, D. The new exact solitary wave solutions and stability analysis for the (2 + 1)-dimensional Zakharov-Kuznetsov equation. Adv. Differ. Equ. 2019, 2019, 49. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, H.M.; Günerhan, H.; Ghanbari, B. Exact traveling wave solutions for resonance nonlinear Schrödinger equation with intermodal dispersions and the Kerr law nonlinearity. Math. Methods Appl. Sci. 2019, 42, 7210–7221. [Google Scholar] [CrossRef]
- Ghanbari, B.; Rada, L. Solitary wave solutions to the Tzitzeica type equations obtained by a new efficient approach. J. Appl. Anal. Comput. 2019, 9, 568–589. [Google Scholar] [CrossRef]
- Rahman, G.; Nisar, K.S.; Ghanbari, B.; Abdeljawad, T. On generalized fractional integral inequalities for the monotone weighted Chebyshev functionals. Adv. Differ. Equ. 2020, 2020, 368. [Google Scholar] [CrossRef]
- Haghiri, S.; Ahmadi, A.; Saif, M. VLSI implementable neuron-astrocyte control mechanism. Neurocomputing 2016, 214, 280–296. [Google Scholar] [CrossRef]
- Gomar, S.; Ahmadi, A. Digital multiplierless implementation of biological adaptive-exponential neuron model. IEEE Trans. Circuits Syst. I 2013, 61, 1206–1219. [Google Scholar] [CrossRef]
- Postnov, D.E.; Ryazanov, L.S.; Sosnovtsev, O.V. Functional modeling of neural-glial interaction. BioSystems 2007, 89, 8491. [Google Scholar] [CrossRef]
- Araque, A.; Parpura, V.; Sanzgiri, R.P.; Haydon, P.G. Tripartite synapses: Glia, the unacknowledged partner. Trends Neurosci. 1999, 22, 208–215. [Google Scholar] [CrossRef]
- Volman, V.; Ben-Jacob, E.; Levine, H. The astrocyte as a gatekeeper of synaptic information transfer. Neural Comput. 2007, 19, 303–326. [Google Scholar] [CrossRef]
- Valenza, G.; Pioggia, G.; Armato, A.; Ferro, M.; Scilingo, E.P.; de Rossi, D. A neuron–astrocyte transistor-like model for neuromorphic dressed neurons. Neural Netw. 2011, 24, 679–685. [Google Scholar] [CrossRef]
- Ghaderi, V.S.; Allam, S.L.; Ambert, N.; Bouteiller, J.-C.; Choma, J. Modeling Neuron-Glia Interactions: From Parametric Model to Neuromorphic Hardware. In Proceedings of the 33rd Annual International Conference of the IEEE EMBS, Boston, MA, USA, 30 August–3 September 2011. [Google Scholar]
- Postnov, D.E.; Koreshkov, R.N.; Brazhe, N.A.; Brazhe, A.R.; Sosnovtseva, O.V. Dynamical patterns of calcium signaling in a functional model of neuron–astrocyte networks. J. Biol. Phys. 2009, 35, 425–445. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soleimani, H.; Bavandpour, M.; Ahmadi, A.; Abbott, D. Digital implementation of a biological astrocyte model and its application. IEEE Trans. Neural Netw. 2014, 26, 127–139. [Google Scholar] [CrossRef] [PubMed]
- Soleimani, H.; Drakakis, E.M. An efficient and reconfigurable synchronous neuron model. IEEE Trans. Circuits Syst. II 2017, 6, 91–95. [Google Scholar] [CrossRef]
- Nazari, S.; Faez, K.; Karimi, E.; Amiri, M. A digital neurmorphic circuit for a simplified model of astrocyte dynamics. Neurosci. Lett. 2014, 582, 21–26. [Google Scholar] [CrossRef]
- Nazari, S.; Amiri, M.; Faez, K.; Amiri, M. Multiplierless digital implementation of neuron–astrocyte signalling on FPGA. Neurocomputing 2015, 164, 281–292. [Google Scholar] [CrossRef]
- Nazari, S.; Faez, K.; Amiri, M.; Karimi, E. A digital implementation of neuron–astrocyte interaction for neuromorphic applications. Neural Netw. 2015, 66, 79–90. [Google Scholar] [CrossRef] [PubMed]
- Haghiri, S.; Ahmadi, A.; Saif, M. Complete Neuron-Astrocyte Interaction Model: Digital Multiplierless Design and Networking Mechanism. IEEE Trans. Biomed. Circuits Syst. 2017, 11, 117–127. [Google Scholar] [CrossRef] [PubMed]
- Narayanan, R.; Abbasi, N.; Al Sammane, G.; Zaki, M.; Tahar, S. A Comparative Study of AMS Circuit Simulation in VHDL-AMS and SystemC-AMS. In Proceedings of the IEEE International Conference on Embedded Systems and Critical Applications, Tunis, Tunisia, 15–16 May 2008; Volume 5, pp. 23–28. [Google Scholar]
- Ashenden, P.J.; Peterson, G.D.; Teegarden, D.A. The System Designer’s Guide to VHDL-AMS; Morgan Kaufmann: San Francisco, CA, USA, 2002. [Google Scholar]
- de Pitta, M.; Volman, V.; Levine, G.; Pioggia, D.; de Rossi, D.; Ben-Jacob, E. Coexistence of amplitude and frequency modulations in intracellular calcium dynamics. Phys. Rev. E 2008, 77, 030903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nadkarni, S.; Jung, P. Dressed neurons: Modeling neural-glia interactions. Phys. Biol. 2004, 1, 35–41. [Google Scholar] [CrossRef] [PubMed]
- Parpura, V.; Haydon, P. Physiological astrocytic calcium levels stimulate glutamate release to modulate adjacent neurons. Proc. Natl. Acad. Sci. USA 2000, 97, 8629–8634. [Google Scholar] [CrossRef] [Green Version]
- Izhikevich, E.M. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. In Computational Neuroscience; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Kopell, N.; Ermentrout, G.B.; Whittington, M.A.; Traub, R.D. Gamma rhythms and beta rhythms have different synchronization properties. Proc. Natl. Acad. Sci. USA 2000, 97, 1867–1872. [Google Scholar] [CrossRef] [Green Version]
- Zobeiri, M.; Luijtelaar, G.V.; Budde, T.; Sysoev, I.V. The Brain Network in a Model of Thalamocortical Dysrhythmia. Brain Connect. 2019, 9, 273–284. [Google Scholar] [CrossRef] [PubMed]
- Medvedeva, T.M.; Sysoeva, M.V.; van Luijtelaar, G.; Sysoev, I.V. Modeling spike-wave discharges by a complex network of neuronal oscillators. Neural Netw. 2018, 98, 271–282. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vich, C.; Prohens, R.; Teruel, A.E.; Guillamon, A. Estimation of Synaptic Activity during Neuronal Oscillations. Mathematics 2020, 8, 2153. [Google Scholar] [CrossRef]
- Orcioni, S.; Paffi, A.; Apollonio, F.; Liberti, M. Revealing Spectrum Features of Stochastic Neuron Spike Trains. Mathematics 2020, 8, 1011. [Google Scholar] [CrossRef]
- Ascione, G.; Toaldo, B. A Semi-Markov Leaky Integrate-and-Fire Model. Mathematics 2019, 7, 1022. [Google Scholar] [CrossRef] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taylan, O.; Abusurrah, M.; Eftekhari-Zadeh, E.; Nazemi, E.; Bano, F.; Roshani, A. Controlling Effects of Astrocyte on Neuron Behavior in Tripartite Synapse Using VHDL–AMS. Mathematics 2021, 9, 2700. https://doi.org/10.3390/math9212700
Taylan O, Abusurrah M, Eftekhari-Zadeh E, Nazemi E, Bano F, Roshani A. Controlling Effects of Astrocyte on Neuron Behavior in Tripartite Synapse Using VHDL–AMS. Mathematics. 2021; 9(21):2700. https://doi.org/10.3390/math9212700
Chicago/Turabian StyleTaylan, Osman, Mona Abusurrah, Ehsan Eftekhari-Zadeh, Ehsan Nazemi, Farheen Bano, and Ali Roshani. 2021. "Controlling Effects of Astrocyte on Neuron Behavior in Tripartite Synapse Using VHDL–AMS" Mathematics 9, no. 21: 2700. https://doi.org/10.3390/math9212700
APA StyleTaylan, O., Abusurrah, M., Eftekhari-Zadeh, E., Nazemi, E., Bano, F., & Roshani, A. (2021). Controlling Effects of Astrocyte on Neuron Behavior in Tripartite Synapse Using VHDL–AMS. Mathematics, 9(21), 2700. https://doi.org/10.3390/math9212700







