Approximating Solutions of Matrix Equations via Fixed Point Techniques

Abstract

The principal goal of this work is to investigate new sufficient conditions for the existence and convergence of positive definite solutions to certain classes of matrix equations. Under specific assumptions, the basic tool in our study is a monotone mapping, which admits a unique fixed point in the setting of a partially ordered Banach space. To estimate solutions to these matrix equations, we use the Krasnosel’skiĭ iterative technique. We also discuss some useful examples to illustrate our results.

1. Introduction

Matrix equations are often used in the study of ladder networks, control theory, stochastic filtering, dynamic programming, statistics, and other fields, according to Anderson [1]. Consider the linear matrix equation below [2].

$$U-A_1^{*}U{A}_1+\cdots +A_m^{*}U{A}_m=Q$$

(1)

where $A_1,\cdots ,A_m$ are arbitrary matrices of order $n\times n,$ for each $i,$$A_i^{*}$ is adjoint of $A_i$ and Q is a positive definite matrix of order $n\times n$. Next, consider the following nonlinear matrix equation:

$$U=Q\pm \sum _{j=1}^m{A}_j^{*}F\left(U\right)A_j$$

(2)

where F is continuous mapping in the set of all positive definite matrices to itself, under certain assumptions on F (order-preserving or order reversing).

Ran and Reurings [2] obtained positive definite solutions of matrix Equations (1) and (2) using the aid of the Banach contraction principle in partially ordered sets. Nieto and Rodríguez-López [3] also used partially ordered spaces and fixed point theorems to find solutions of some differential equations [4]. The advantage of this strategy is that the mapping requirements only need to be satisfied for comparable elements, and the relevance of this viewpoint is to govern the essence of the solutions, whether they are negative or positive, which leads to a variety of interesting applications. For more details on the applications of fixed point theory in partially ordered spaces, one may refer to [5,6,7,8] and references therein.

Berinde [9], on the other hand, recently developed a new form of contraction mappings called as $(b,\theta )$-enriched contraction mappings, which generalize contraction and nonexpansive mappings.

The purpose of this work is to investigate the existence and convergence of solutions of matrix equations. To accomplish this, we use the idea of monotone enriched contraction mapping in partially ordered Banach spaces. More specifically, we extend the concept of $(b,\theta )$-enriched contraction mapping in the setting of partially ordered Banach spaces and establish some existence and convergence results. Thereafter, we use these findings to solve the matrix Equations (1) and (2). To approximate the solutions of these matrix equations, we use the Krasnosel’skiĭ iterative technique. Some useful examples discussed herein illustrate our results.

2. Preliminaries

Let $\mathcal{B}$ be a Banach space and ⪯ is a partial order on $\mathcal{B}$. We say that $\vartheta ,\nu \in \mathcal{B}$ are comparable whenever $\vartheta ⪯\nu$ or $\nu ⪯\vartheta .$ Let partial order ⪯ be compatible with the linear structure of $\mathcal{B}$, that is, for every $\vartheta ,\nu ,\zeta \in \mathcal{B}$ and $\lambda \ge 0$, we have

$$\begin{array}{ccc}\hfill \vartheta & ⪯& \nu \mathrm{implies}\vartheta +\zeta ⪯\nu +\zeta ,\hfill \\ \hfill \vartheta & ⪯& \nu \mathrm{implies}\lambda \vartheta ⪯\lambda \nu .\hfill \end{array}$$

This implies that all order intervals $[\vartheta ,\to ]=\{\zeta \in \mathcal{B}:\vartheta ⪯\zeta \}$ and $[\leftarrow ,\nu ]=\{\zeta \in \mathcal{B}:\zeta ⪯\nu \}$ are convex. Further, we suppose that each $[\vartheta ,\to ]$ and $[\leftarrow ,\nu ]$ is closed.

A sequence $\left\{{\vartheta }_n\right\}$ is monotone increasing if ${\vartheta }_n⪯{\vartheta }_{n+1}$ for all $n\in \mathbb{N}.$ We shall utilize the observation considered in [5] (Lemma 3.1). Assume that $\left\{{\vartheta }_n\right\}$ is a monotone sequence that has a cluster point, that is, there is a subsequence $\left\{{\vartheta }_{n_j}\right\}$ that converges to g. Since the order intervals are closed, it follows $g\in [{\vartheta }_n,\to )$ for each n, that is, g is an upper bound for $\left\{{\vartheta }_n\right\}.$ If $g_1$ is another upper bound for $\left\{{\vartheta }_n\right\}$, then ${\vartheta }_n\in (\leftarrow ,g_1]$ for each n, and hence $g⪯g_1.$ It implies that $\left\{{\vartheta }_n\right\}$ converges to $g=sup\left\{{\vartheta }_n\right\}.$ If $\left\{{\vartheta }_n\right\}$ is a monotone increasing (resp. monotone decreasing) sequence that converges to p, then ${\vartheta }_n⪯p$ (resp. $p⪯{\vartheta }_n$).

Definition 1

([10] (p. 27)). A mapping $\xi :\mathcal{B}\to \mathcal{B}$ is said to be nonexpansive if for all $\vartheta ,\nu \in \mathcal{B}$

$$\parallel \xi \left(\vartheta \right)-\xi \left(\nu \right)\parallel \le \parallel \vartheta -\nu \parallel .$$

Definition 2

([11]). A mapping $\xi :\mathcal{B}\to \mathcal{B}$ is said to be quasi-nonexpansive if for all $\vartheta \in \mathcal{B}$ and ${\vartheta }^{†}\in F\left(\xi \right)\ne \varnothing ,$

$$\parallel \xi \left(\vartheta \right)-{\vartheta }^{†}\parallel \le \parallel \vartheta -{\vartheta }^{†}\parallel .$$

where $F\left(\xi \right)$ is the set of all fixed points of $\xi .$

It is well-known that a nonexpansive mapping with a fixed point is quasi-nonexpansive. However, the converse need not be true.

Let $\mathcal{B}$ be a Banach space and $\xi :\mathcal{B}\to \mathcal{B}$ a mapping. The following iterative method is known as the Krasnosel’skiĭ method (see [12]):

$$\left\{\begin{array}{c}{\vartheta }_1\in \mathcal{B}\hfill \\ {\vartheta }_{n+1}=\alpha {\vartheta }_n+(1-\alpha )\xi \left({\vartheta }_n\right)\hfill \end{array}\right.$$

(3)

where $\alpha \in (0,1).$

Lemma 1

([13]). Let $\mathcal{B}$ be a Banach space and $\xi :\mathcal{B}\to \mathcal{B}$ a mapping, define $S:\mathcal{B}\to \mathcal{B}$ as follows:

$$S\left(\vartheta \right)=(1-\lambda )\vartheta +\lambda \xi \left(\vartheta \right)$$

for all $\vartheta \in \mathcal{B}$ and $\lambda \in (0,1).$ Then $F\left(S\right)=F\left(\xi \right).$

3. Main Results

Berinde [9] recently introduced a new type of contraction mapping, which is described below:

Definition 3.

Let$(\mathcal{B},\parallel .\parallel )$be a Banach space. A mapping$\xi :\mathcal{B}\to \mathcal{B}$is said to be$(b,\theta )$-enriched contraction mapping if there exist$b\in [0,\infty )$and$\theta \in [0,b+1)$such that for all$\vartheta ,\nu \in \mathcal{B}$

$$\parallel b(\vartheta -\nu )+\xi \left(\vartheta \right)-\xi \left(\nu \right)\parallel \le \theta \parallel \vartheta -\nu \parallel .$$

(4)

Remark 1.

•

It is shown in [9] that every contraction mapping ξ is a $(0,\theta )$-enriched mapping.

•

The class of nonexpansive mappings and the class of$(b,\theta )$-enriched contraction mappings are independent in nature.

Example 1

([9]). Let $\mathcal{C}=\left[0,1\right]\subset \mathbb{R}$ and $\xi :\mathcal{C}\to \mathcal{C}$ be a mapping defined as $\xi \left(\vartheta \right)=1-\vartheta$ Then $F\left(\xi \right)=\left\{\frac{1}{2}\right\}$. It is nonexpansive mapping and ξ is a $(b,1-b)$-enriched contraction mapping for any $b\in (0,1).$

Example 2

([13]). Let $\mathcal{C}=\left[\frac{1}{2},2\right]\subset \mathbb{R}$ and $\xi :\mathcal{C}\to \mathcal{C}$ be a mapping defined as $\xi \left(\vartheta \right)=\frac{1}{\vartheta }.$ Then $F\left(\xi \right)=\left\{1\right\}$. It can be seen that ξ is a $\left(2,\frac{5}{2}\right)$-enriched contraction mapping. Indeed, for all $\vartheta ,\nu \in \left[\frac{1}{2},2\right]$

$$\left|2-\frac{1}{\vartheta \nu }\right|\le \frac{5}{2}.$$

Thus, for all$\vartheta ,\nu \in \left[\frac{1}{2},2\right]$

$$\begin{array}{ccc}\hfill \left|2-\frac{1}{\vartheta \nu }\right||\vartheta -\nu |& \le & \frac{5}{2}|\vartheta -\nu |\hfill \\ \hfill \iff \left|2(\vartheta -\nu )+\frac{1}{\vartheta }-\frac{1}{\nu }\right|& \le & \frac{5}{2}|\vartheta -\nu |\hfill \\ \hfill \iff \left|2\right(\vartheta -\nu )+\xi (\vartheta )-\xi (\nu \left)\right|& \le & \frac{5}{2}|\vartheta -\nu |.\hfill \end{array}$$

On the other hand,$\vartheta =\frac{1}{2}$and$\nu =1$, we have

$$|\xi \left(\vartheta \right)-\xi \left(\nu \right)|=|2-1|=1>\frac{1}{2}=\left|\frac{1}{2}-1\right|.$$

Thus, ξ is not a nonexpansive mapping (or not even quasi-nonexpansive).

Example 3.

Let$\mathcal{B}=\mathbb{R}$ be the Banach space equipped with the usual norm and $\xi :\mathcal{B}\to \mathcal{B}$ be a mapping defined by $\xi \left(\vartheta \right)=\vartheta$ for all $\vartheta \in \mathcal{B}.$ Then $F\left(\xi \right)=\mathcal{B}$ and ξ is an isometry (or nonexpansive) mapping. On the other hand for all $\vartheta ,\nu \in \mathcal{B}$

$$\left|b\right(\vartheta -\nu )+\xi (\vartheta )-\xi (\nu \left)\right|=(b+1)|\vartheta -\nu |>\theta |\vartheta -\nu |$$

for all $b\in [0,\infty )$ and $\theta \in [0,b+1)$. Thus, ξ is not a $(b,\theta )$-enriched contraction.

Definition 4.

Let$(\mathcal{B},\parallel .\parallel ,⪯)$be a partially ordered Banach space and a mapping$\xi :\mathcal{B}\to \mathcal{B}$is said to be monotone if

$$\vartheta ⪯\nu \mathrm{implies} \xi \left(\vartheta \right)⪯\xi \left(\nu \right),$$

where$\vartheta ,\nu \in \mathcal{B}.$

Now, we extend Definition 3 in the setting of partially ordered Banach spaces as follows:

Definition 5.

Let$(\mathcal{B},\parallel .\parallel ,⪯)$be a partially ordered Banach space. A mapping$\xi :\mathcal{B}\to \mathcal{B}$is said to be monotone$(b,\theta )$-enriched contraction mapping if ξ is monotone and there exist$b\in [0,\infty ),$and$\theta \in [0,b+1)$such that

$$\parallel b(\vartheta -\nu )+\xi \left(\vartheta \right)-\xi \left(\nu \right)\parallel \le \theta \parallel \vartheta -\nu \parallel$$

(5)

for all$\vartheta ,\nu \in \mathcal{B}$with ϑ and ν are comparable.

It can be seen that every monotone contraction mapping with constant $\theta$ is a $(0,\theta )$-monotone enriched contraction mapping.

Example 4.

Let$\mathcal{B}=\{1,2,3\}$be the Banach space equipped with the usual norm and the order$⪯:=\left\{\right(1,1),(2,2),(3,3),(3,1\left)\right\}$. Let$\xi :\mathcal{B}\to \mathcal{B}$be a mapping defined by$\xi \left(1\right)=1,\xi \left(2\right)=3,\xi \left(3\right)=1.$It can be easily seen that ξ satisfies Definition 5 for all comparable elements, and 1 is a unique fixed point of$\xi .$On the other hand, if$\vartheta =1$and$\nu =2$, then

$$\begin{array}{ccc}\hfill \parallel b(\vartheta -\nu )+\xi \left(\vartheta \right)-\xi \left(\nu \right)\parallel & =& \parallel b(1-2)+\xi \left(1\right)-\xi \left(2\right)\parallel \hfill \\ & =& b+2>b+1=(b+1)\parallel 1-2\parallel =(b+1)\parallel \vartheta -\nu \parallel \hfill \end{array}$$

for any$b\in [0,\infty )$. Hence ξ is not a$(b,\theta )$-enriched contraction mapping.

Theorem 1.

Let$(\mathcal{B},\parallel .\parallel ,⪯)$be a partially ordered Banach space and$\xi :\mathcal{B}\to \mathcal{B}$a monotone$(b,\theta )$-enriched contraction mapping. Suppose that there exists a point${\vartheta }_1$in$\mathcal{B}$such that${\vartheta }_1$and$\xi \left({\vartheta }_1\right)$are comparable. Assume that one of the following holds:

(i) 

ξ is continuous.

(ii) 

For all$\vartheta ,\nu \in \mathcal{B},$the order intervals$[\vartheta ,\to )$and$(\leftarrow ,\nu ]$are closed.

Then, ξ admits a fixed point.

Proof. 

We distinguish the following two cases:

• Case 1. If $b>0$. By the definition of monotone $(b,\theta )$-enriched contraction, we have

  $$\parallel b(\vartheta -\nu )+\xi \left(\vartheta \right)-\xi \left(\nu \right)\parallel \le \theta \parallel \vartheta -\nu \parallel$$

  (6)

  for all $\vartheta ⪯\nu .$ Take $\mu =\frac{1}{b+1}\in (0,1)$ and put $b=\frac{1-\mu }{\mu }$ in (6), then the above inequality is equivalent to

  $$\parallel (1-\mu )(\vartheta -\nu )+\mu \left(\xi \right(\vartheta )-\xi (\nu \left)\right)\parallel \le \mu \theta \parallel \vartheta -\nu \parallel .$$

  (7)
  Define the mapping S as follows:

  $$S\left(\vartheta \right)=(1-\mu )\vartheta +\mu \xi \left(\vartheta \right)\mathrm{for} \mathrm{all}\vartheta \in \mathcal{B}.$$

  (8)
  Since $\xi$ is monotone, for all $\vartheta ⪯\nu$, we have

  $$\begin{array}{c}\hfill S\left(\vartheta \right)=(1-\mu )\vartheta +\mu \xi \left(\vartheta \right)⪯(1-\mu )\vartheta +\mu \xi \left(\nu \right)⪯(1-\mu )\nu +\mu \xi \left(\nu \right)=S\left(\nu \right)\end{array}$$

  so, the mapping S is also monotone. Then from (7), we get

  $$\parallel S\left(\vartheta \right)-S\left(\nu \right)\parallel \le k\parallel \vartheta -\nu \parallel$$

  (9)

  for all $\vartheta ⪯\nu$, where $k=\mu \theta .$ Since $\mu =\frac{1}{b+1}\in (0,1)$, $k\in (0,1)$. Thus from (9) S is a monotone contraction mapping. Since ${\vartheta }_1⪯\xi \left({\vartheta }_1\right)$

  $${\vartheta }_1=(1-\mu ){\vartheta }_1+\mu {\vartheta }_1⪯(1-\mu ){\vartheta }_1+\mu \xi \left({\vartheta }_1\right)=S\left({\vartheta }_1\right).$$
  Next, for given ${\vartheta }_1\in \mathcal{B}$ consider the sequence

  $${\vartheta }_{n+1}=S\left({\vartheta }_n\right)=(1-\mu ){\vartheta }_n+\mu \xi \left({\vartheta }_n\right).$$

  (10)
  Now we show that

  $${\vartheta }_n⪯{\vartheta }_{n+1} \mathrm{for} \mathrm{all} n\in \mathbb{N}.$$
  Since ${\vartheta }_1⪯S\left({\vartheta }_1\right),$ by the monotonicity of $S,$

  $${\vartheta }_2=S\left({\vartheta }_1\right)⪯S^2\left({\vartheta }_1\right)=S\left({\vartheta }_2\right)={\vartheta }_3,$$

  and successively, we can write ${\vartheta }_n⪯{\vartheta }_{n+1}=S\left({\vartheta }_n\right)$ for all $n\in \mathbb{N}.$ Take $\vartheta ={\vartheta }_n$ and $\nu ={\vartheta }_{n-1}$ in (9), we have

  $$\parallel {\vartheta }_{n+1}-{\vartheta }_n\parallel \le \parallel {\vartheta }_n-{\vartheta }_{n-1}\parallel \mathrm{for} \mathrm{all} \ge 2.$$

  (11)
  Successively from (11), we can obtain

  $$\parallel {\vartheta }_{n+m}-{\vartheta }_n\parallel \le k^{n-1}\left(\frac{1-k^m}{1-k}\right)\parallel {\vartheta }_2-{\vartheta }_1\parallel$$

  (12)

  for all $n\ge 2$ and $m\in \mathbb{N}.$ It implies that $\left\{{\vartheta }_n\right\}$ is a Cauchy sequence and must converge to a point in Banach space $\mathcal{B}$. Take

  $$u=\underset{n\to \infty }{lim}{\vartheta }_n.$$
  First, we assume that $\xi$ is continuous, then from (10)

  $$\underset{n\to \infty }{lim}{\vartheta }_{n+1}=\underset{n\to \infty }{lim}\{(1-\mu ){\vartheta }_n+\mu \xi \left({\vartheta }_n\right)\}$$

  and

  $$u=(1-\mu )u+\mu \xi \left(u\right).$$
  Therefore, $\xi \left(u\right)=u$, and $\xi$ has a fixed point in $\mathcal{B}.$ If we assume that (ii) is true, then it can be seen that

  $${\vartheta }_n⪯u \mathrm{for} \mathrm{all} n\in \mathbb{N}.$$
  Take $\vartheta ={\vartheta }_n$ and $\nu =u$ in (9), we get

  $$\parallel {\vartheta }_{n+1}-S\left(u\right)\parallel \le k\parallel {\vartheta }_n-u\parallel \to 0 \mathrm{as} n\to \infty .$$
  Thus $S\left(u\right)=u$, from Lemma 1, $F\left(S\right)=F\left(\xi \right),$ u is a fixed point of $\xi$.
• Case 2. If $b=0$, then $\xi$ is a monotone contraction mapping and following the similar steps for $\xi$ in place of S, we can complete the proof. □

In the next theorem, we prove the uniqueness of the fixed point and the global convergence of the Krasnosel’skiĭ iterative method.

Theorem 2.

If all the hypotheses of Theorem 1 hold. In addition, one of the following holds:

• (X1) Every pair of elements has an upper bound or lower bound.
• (X2) If$F\left(\xi \right)$(the set of fixed points of ξ) is totally ordered.

Then ξ has a unique fixed point. Moreover, if$\left(X1\right)$is true then the sequence$\left\{{\vartheta }_n\right\}$defined by

$${\vartheta }_{n+1}=\left(1-\frac{1}{b+1}\right){\vartheta }_n+\frac{1}{b+1}\xi \left({\vartheta }_n\right)$$

converges to a point in$F\left(\xi \right)$for any initial guess${\vartheta }_1\in \mathcal{B}.$

Proof. 

Let $\vartheta \in \mathcal{B}$ be another fixed point of $\xi$. First, we suppose that hypothesis (X1) is true. We follow the same technique as in [3]. Let

$$\nu =\underset{n\to \infty }{lim}\left\{\left(1-\frac{1}{b+1}\right){\vartheta }_n+\frac{1}{b+1}\xi \left({\vartheta }_n\right)\right\}$$

for given ${\vartheta }_1\in \mathcal{B}$ (given point as in Theorem 1). We consider the following two cases:

• Case 1. If $\vartheta$ is comparable to $\nu$ then $\vartheta =S^n\left(\vartheta \right)$ is comparable to $\nu =S^n\left(\nu \right)$ for all $n\in \mathbb{N}\cup \left\{0\right\}$, where S is a mapping defined in (8). Thus,

  $$\parallel \vartheta -\nu \parallel =\parallel S^n\left(\vartheta \right)-S^n\left(\nu \right)\parallel \le k^n\parallel \vartheta -\nu \parallel \to 0 \mathrm{as} n\to \infty$$

  which implies that $\vartheta =\nu .$
• Case 2. If $\vartheta$ is not comparable to $\nu$, from (X1) there exists either a lower or an upper bound of $\vartheta$ and $\nu$, that is, there is a $z\in \mathcal{B}$ such that z is comparable to $\vartheta$ and $\nu$. Since S is a monotone, $S^n\left(z\right)$ is comparable to $\vartheta =S^n\left(\vartheta \right)$ and $\nu =S^n\left(\nu \right)$ for all $n\in \mathbb{N}\cup \left\{0\right\}$. Now

  $$\begin{array}{ccc}\hfill \parallel \vartheta -\nu \parallel =\parallel S^n\left(\vartheta \right)-S^n\left(\nu \right)\parallel & \le & \parallel S^n\left(\vartheta \right)-S^n\left(z\right)\parallel +\parallel S^n\left(z\right)-S^n\left(\nu \right)\parallel \hfill \\ & \le & k^n\parallel \vartheta -z\parallel +k^n\parallel z-\nu \parallel \to 0 \mathrm{as} n\to \infty .\hfill \end{array}$$

Thus $\vartheta =\nu .$ Next, we show that

$$\underset{n\to \infty }{lim}{S}^n\left(p\right)=\underset{n\to \infty }{lim}{S}^n\left({\vartheta }_1\right)=\nu =\underset{n\to \infty }{lim}\left\{\left(1-\frac{1}{b+1}\right){\vartheta }_n+\frac{1}{b+1}\xi \left({\vartheta }_n\right)\right\} \mathrm{for} \mathrm{all} p\in \mathcal{B}.$$

If p is comparable to $\nu$. Since S is a monotone, $S^n\left(p\right)$ is comparable to $\nu =S^n\left(\nu \right)$ for all $n\in \mathbb{N}\cup \left\{0\right\}$. Then

$$\parallel S^n\left(p\right)-\nu \parallel \le k^n\parallel p-\nu \parallel \to 0 \mathrm{as} n\to \infty .$$

Therefore, $\underset{n\to \infty }{lim}{S}^n\left(p\right)=\nu .$ Again p is not comparable to $\nu$, then from (X1), there exists $z\in \mathcal{B}$ such that z is comparable to p and $\nu$. Since S is a monotone, $S^n\left(z\right)$ is comparable to $S^n\left(p\right)$ and $\nu =S^n\left(\nu \right)$ for all $n\in \mathbb{N}\cup \left\{0\right\}$. Thus

$$\begin{array}{ccc}\hfill \parallel S^n\left(p\right)-\nu \parallel =\parallel S^n\left(\vartheta \right)-S^n\left(\nu \right)\parallel & \le & \parallel S^n\left(p\right)-S^n\left(z\right)\parallel +\parallel S^n\left(z\right)-S^n\left(\nu \right)\parallel \hfill \\ & \le & k^n\parallel p-z\parallel +k^n\parallel z-\nu \parallel \to 0 \mathrm{as} n\to \infty .\hfill \end{array}$$

Hence $\underset{n\to \infty }{lim}{S}^n\left(p\right)=\nu$. If $F\left(\xi \right)$ is totally ordered, then following the same technique as in Case 1, we can complete the proof. □

4. Solutions to Linear Matrix Equation

In this section, we discuss the solution of the matrix Equation (1). We define a mapping G on $\mathcal{H}\left(n\right)$ (the set of all Hermitian matrices of order $n\times n$) as follows:

$$G\left(U\right)=Q+\sum _{j=1}^m{A}_m^{*}U{A}_m$$

(13)

where $A_1,\cdots ,A_m$, $A_i^{*}$ (for each i) and Q are the same as in (1). It can be seen that solutions of (1) are the fixed points of G. Let $A\in \mathcal{M}\left(n\right)$ (set of all matrices of order $n\times n$), then ${\parallel A\parallel }_1={\displaystyle \sum _{j=1}^n}{s}_j\left(A\right),$ where $s_j\left(A\right)$ are the singular values of A for $j=1,2,\cdots ,n.$ For given $Q_{+}\in \mathcal{P}\left(n\right)$ (the set of all positive definite matrices of order $n\times n$), the following norm can be defined:

$${\parallel A\parallel }_{1,Q_{+}}={\parallel Q_{+}^{\frac{1}{2}}A{Q}_{+}^{\frac{1}{2}}\parallel }_1.$$

It is can be seen that $\mathcal{H}\left(n\right)$ equipped with the norm ${\parallel .\parallel }_{1,Q_{+}}$ is a partially ordered Banach space for any $Q_{+}\in \mathcal{P}\left(n\right).$ We write $U\ge V$ (or $U>V$) if $U-V\ge 0$ (or $U-V>0$). We denote by I an identity matrix of order $n\times n,$ and $\parallel .\parallel ,$ the spectral norm, that is, $\parallel A\parallel =\sqrt{{\lambda }_{+}\left(A^{*}A\right)}$ where ${\lambda }_{+}\left(A^{*}A\right)$ is the largest eigenvalue of $A^{*}A.$

Lemma 2

([2]). Let A and B of order $n\times n$ with $A,B\ge 0$. Then

$$tr\left(AB\right)\le \parallel A\parallel tr\left(B\right).$$

Theorem 3.

Let$Q\in \mathcal{P}\left(n\right)$and for some$Q_{+}\in \mathcal{P}\left(n\right)$, we have

$$∥bI+\sum _{j=1}^m{Q}_{+}^{\frac{-1}{2}}{A}_j{Q}_{+}{A}_j^{*}{Q}_{+}^{\frac{-1}{2}}∥<\theta ,$$

where$b\in [0,\infty )$and$\theta \in [0,b+1).$Then

(1) 

Mapping G admits a unique fixed point in$\mathcal{H}\left(n\right).$

(2) 

For given$U_0\in \mathcal{H}\left(n\right)$, the sequence$\left\{U_k\right\}$defined by

$$U_{k+1}=\left(1-\frac{1}{b+1}\right)U_k+\frac{1}{b+1}G\left(U_k\right) \mathrm{for} \mathrm{all} k\in \mathbb{N}\cup \left\{0\right\},$$

(14)

converges to the unique solution of (1), which is in $\mathcal{P}\left(n\right).$

Proof. 

It can be seen that for all $U,V\in \mathcal{H}\left(n\right)$, there exist a lower bound or an upper bound. For $U_0=0,$$G\left(0\right)=Q>0,$ so $U_0\le G\left(U_0\right).$ Now we show that G satisfies condition (5). Let $U,V\in \mathcal{H}\left(n\right)$ with $U\le V,$ then $G\left(U\right)\le G\left(V\right).$ Thus,

$$\begin{array}{ccc}& & {\parallel b(U-V)+G\left(U\right)-G\left(V\right)\parallel }_{1,Q_{+}}={∥b(U-V)+\sum _{j=1}^m{A}_j(U-V)A_j^{*}∥}_{1,Q_{+}}\hfill \\ & =& tr\left\{Q_{+}^{\frac{1}{2}}(b(U-V)+\sum _{j=1}^m{A}_j^{*}(U-V)A_j{Q}_{+}^{\frac{1}{2}}\right\}\hfill \\ & =& tr\left\{Q_{+}^{\frac{1}{2}}b(U-V)Q_{+}^{\frac{1}{2}}\right\}+\sum _{j=1}^{m}tr\left\{Q_{+}^{\frac{1}{2}}{A}_j^{*}(U-V)A_j{Q}_{+}^{\frac{1}{2}}\right\}\hfill \\ & =& tr\left\{Q_{+}^{\frac{1}{2}}b(U-V)Q_{+}^{\frac{1}{2}}\right\}+\sum _{j=1}^{m}tr\left\{A_j{Q}_{+}{A}_j^{*}(U-V)\right)\}\hfill \\ & =& tr\left\{Q_{+}^{\frac{1}{2}}b(U-V)Q_{+}^{\frac{1}{2}}\right\}+\sum _{j=1}^{m}tr\left\{A_j{Q}_{+}{A}_j^{*}{Q}_{+}^{\frac{-1}{2}}{Q}_{+}^{\frac{1}{2}}(U-V)Q_{+}^{\frac{1}{2}}{Q}_{+}^{\frac{-1}{2}}\right\}\hfill \\ & =& tr\left\{Q_{+}^{\frac{1}{2}}b(U-V)Q_{+}^{\frac{1}{2}}\right\}+\sum _{j=1}^{m}tr\left\{Q_{+}^{\frac{-1}{2}}{A}_j{Q}_{+}{A}_j^{*}{Q}_{+}^{\frac{-1}{2}}{Q}_{+}^{\frac{1}{2}}(U-V)Q_{+}^{\frac{1}{2}}\right\}\hfill \\ & =& tr\left\{Q_{+}^{\frac{1}{2}}b(U-V)Q_{+}^{\frac{1}{2}}\right\}+tr\left\{\sum _{j=1}^m\left(Q_{+}^{\frac{-1}{2}}{A}_j{Q}_{+}{A}_j^{*}{Q}_{+}^{\frac{-1}{2}}\right)\left(Q_{+}^{\frac{1}{2}}(U-V)Q_{+}^{\frac{1}{2}}\right)\right\}\hfill \\ & =& tr\left\{Q_{+}^{\frac{1}{2}}b(U-V)Q_{+}^{\frac{1}{2}}+\sum _{j=1}^m\left(Q_{+}^{\frac{-1}{2}}{A}_j{Q}_{+}{A}_j^{*}{Q}_{+}^{\frac{-1}{2}}\right)\left(Q_{+}^{\frac{1}{2}}(U-V)Q_{+}^{\frac{1}{2}}\right)\right\}\hfill \\ & =& tr\left\{\left(bI+\sum _{j=1}^m(Q_{+}^{\frac{-1}{2}}{A}_j{Q}_{+}{A}_j^{*}{Q}_{+}^{\frac{-1}{2}}\right)\left(Q_{+}^{\frac{1}{2}}(U-V)Q_{+}^{\frac{1}{2}}\right)\right\}.\hfill \end{array}$$

Thus from Lemma 2, we have

$${\parallel b(U-V)+G\left(U\right)-G\left(V\right)\parallel }_{1,Q_{+}}\le ∥bI+\sum _{j=1}^m{Q}_{+}^{\frac{-1}{2}}{A}_j{Q}_{+}{A}_j^{*}{Q}_{+}^{\frac{-1}{2}}∥{\parallel U-V\parallel }_{1,Q_{+}}$$

From the assumptions on theorem

$${\parallel b(U-V)+G\left(U\right)-G\left(V\right)\parallel }_{1,Q_{+}}\le \theta {\parallel U-V\parallel }_{1,Q_{+}}$$

Therefore, from Theorems 1 and 2, mapping G has a unique fixed point and the sequence $\left\{U_k\right\}$ converges to the solution of (1). It is evident that G maps $\mathcal{P}\left(n\right)$ into the set $\{U\in \mathcal{H}(n\left)\right|Q\le U\}$; therefore, the solution lies in this set and is positive definite. □

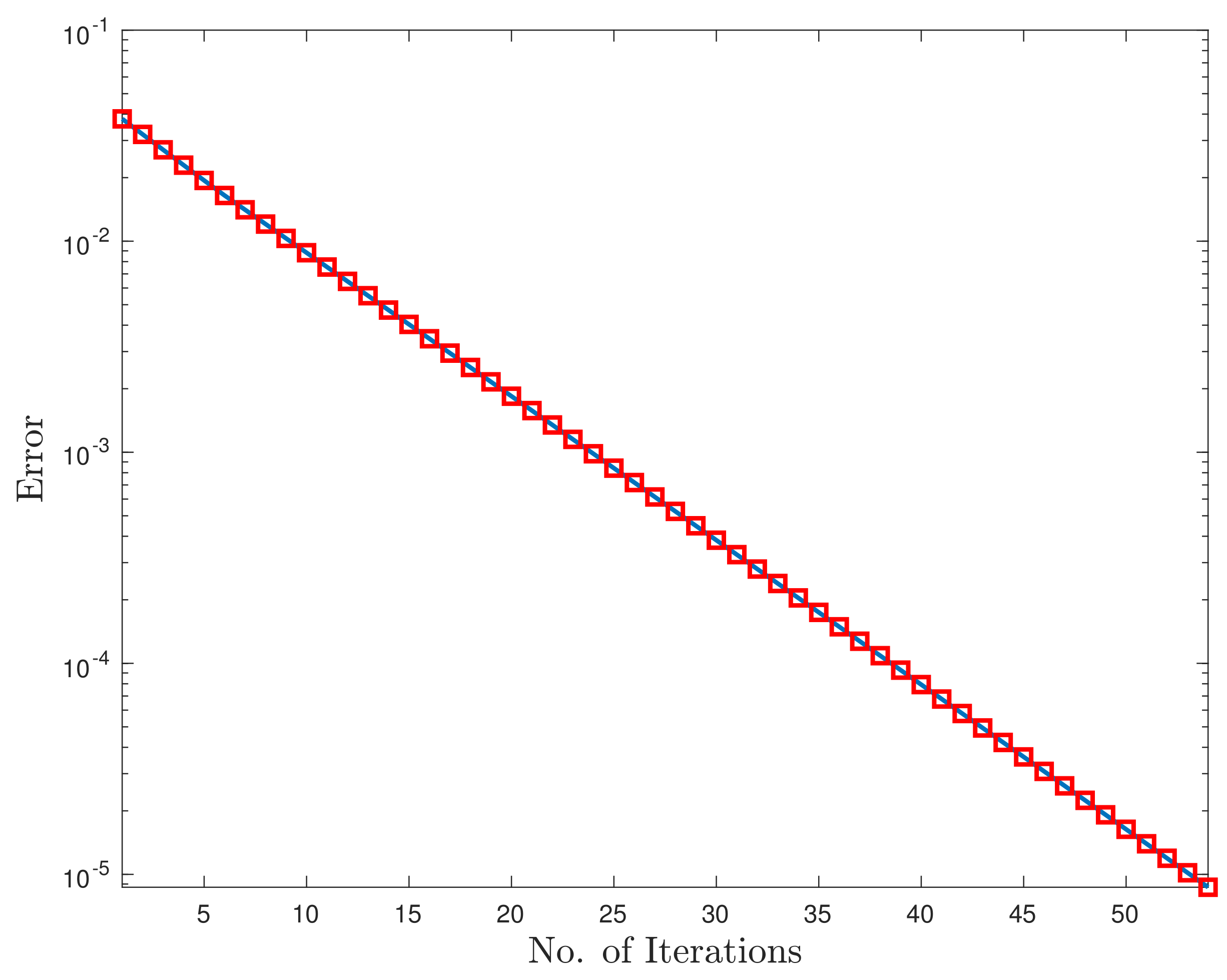
Example 5.

Consider the liner matrix Equation (13) for $m=3$, $n=4,$ i.e.,

$$U=Q+A_1^{*}U{A}_1+A_2^{*}U{A}_2+A_3^{*}U{A}_3,$$

(15)

where

$$Q=1\times {10}^{-3}\times \left[\begin{array}{cccc}0.1009& 0.0009& 0.0006& 0.0006\\ 0.0009& 0.1014& 0.0008& 0.0007\\ 0.0006& 0.0008& 0.1008& 0.0006\\ 0.0006& 0.0007& 0.0006& 0.1006\end{array}\right],$$

$$A_1=\left[\begin{array}{cccc}0.0435& 0.0153& 0.0423& 0.0735\\ 0.0779& 0.0248& 0.0671& 0.0346\\ 0.0827& 0.0702& 0.1104& 0.0991\\ 0.0871& 0.0826& 0.0099& 0.0587\end{array}\right],$$

$$A_2=\left[\begin{array}{cccc}0.1963& -0.0649& -0.0362& 0.1658\\ -0.0584& 0.0267& 0.0403& -0.0801\\ -0.0281& 0.1720& 0.1877& 0.1126\\ -0.0929& 0.0691& -0.0616& 0.1999\end{array}\right],$$

$$A_3=\left[\begin{array}{cccc}0.0223& 0.0214& 0.0174& 0.0929\\ 0.0437& 0.0473& 0.0868& 0.0728\\ 0.0303& 0.0735& 0.0168& 0.0600\\ 0.0099& 0.0544& 0.0139& 0.0655\end{array}\right].$$

The conditions of Theorem 3 can be checked numerically by considering different particular values of matrices involved. For instance, it can be tested (and verified to be true) for

$$U=\left[\begin{array}{cccc}0.0683& -0.0284& -0.0070& 0.0104\\ -0.0284& 0.0129& 0.0022& -0.0117\\ -0.0070& 0.0022& 0.0747& 0.0225\\ 0.0104& -0.0117& 0.0225& 0.0542\end{array}\right],$$

To see the behavior of convergence of the sequence$\left\{U_k\right\}$defined in (14), we take-up the initial value:

$$U_0=\left[\begin{array}{cccc}0.0809& -0.0188& 0.0118& 0.0224\\ -0.0188& 0.0246& 0.0238& 0.0003\\ 0.0118& 0.0238& 0.1121& 0.0454\\ 0.0224& 0.0003& 0.0454& 0.0751\end{array}\right].$$

If we consider$b=5$, then after 10 successive iterations, the approximations of the unique positive definite solution of the (15) is the following

$$\widehat{U}\approx U_{10}=\left[\begin{array}{cccc}0.8459& -0.0006& 0.0018& 0.006\\ -0.0006& 0.8440& 0.0069& 0.0068\\ 0.0018& 0.0069& 0.8447& 0.0038\\ 0.0060& 0.0068& 0.0038& 0.8533\end{array}\right].$$

It can also be verified that the elements of each sequence are order-preserving. The convergence behavior is shown in Figure 1.

Figure 1. Convergence behavior.

5. Solutions to Nonlinear Matrix Equations

In this section, we consider the following nonlinear matrix equations:

$$U=Q\pm \sum _{j=1}^m{A}_j^{*}F\left(U\right)A_j$$

(16)

where $F:\mathcal{P}\left(n\right)\to \mathcal{P}\left(n\right)$ is a continuous mapping. For more details of these class of equations, see [14]. In view of different conditions on mapping F, we consider the following cases:

Case 1. If F is order-preserving and considering the following equation:

$$U=Q+\sum _{j=1}^m{A}_j^{*}F\left(U\right)A_j.$$

(17)

We can define

$$G\left(U\right)=Q+\sum _{j=1}^m{A}_j^{*}F\left(U\right)A_j.$$

The mapping G is well-defined on $\mathcal{P}\left(n\right)$ and order-preserving. For all $U\in \mathcal{P}\left(n\right)$, $Q\le G\left(U\right)$. In particular, $Q\le G\left(Q\right)$. Since G is order-preserving

$$Q\le G\left(Q\right)\le G^2\left(Q\right)\le G^3\left(Q\right)\le \cdots$$

Thus, $\left\{G^j\left(Q\right)\right\}$ is an increasing sequence.

Proposition 1.

Suppose that there exists an$U_0$such that$G\left(U_0\right)\le U_0$. Then G maps the set$\{U:Q\le U\le U_0\}$into itself. The sequence$\left\{G^j\left(Q\right)\right\}$converges to a point$U_{-}$which is the smallest solution of (17). Further, the sequence $\left\{G^j\left(U_0\right)\right\}$ is a decreasing sequence, which is the largest solution in the set $[Q,U_0].$

Proof. 

Let $G\left(U_0\right)\le U_0$, then $Q\le G\left(U_0\right)\le U_0$. If $Q\le U\le U_0$, from the order-preserving property of G,

$$Q\le G\left(Q\right)\le G\left(U\right)\le G\left(U_0\right)\le U_0$$

and for all $n\in \mathbb{N}$

$$Q\le G\left(Q\right)\le G^2\left(Q\right)\le G^3\left(Q\right)\le \cdots G^j\left(Q\right)\le G^j\left(U_0\right)\cdots \le G^2\left(U_0\right)\le G\left(U_0\right)\le U_0.$$

Thus, $\left\{G^j\left(Q\right)\right\}$ is an increasing sequence and bounded above by $G^p\left(U_0\right)$ for any $p\in \mathbb{N}$. Further, the sequence $\left\{G^j\left(U_0\right)\right\}$ is bounded below the decreasing sequence. Let

$$U_{-}=\underset{j\to \infty }{lim}{G}^j\left(Q\right)$$

and

$$U_{+}=\underset{j\to \infty }{lim}{G}^j\left(U_0\right).$$

Suppose U is any solution of (17), then $Q\le U=G\left(U\right).$ For all $j\in \mathbb{N}$

$$Q\le G\left(Q\right)\le G^2\left(Q\right)\le G^3\left(Q\right)\le \cdots G^j\left(Q\right)\le U$$

Thus $U_{-}\le U.$ If $U\in [Q,U_0],$ then for all $j\in \mathbb{N}$

$$U\le G^j\left(U_0\right)\cdots \le G^2\left(U_0\right)\le G\left(U_0\right)\le U_0.$$

Hence $U\le U_{+}.$ □

The following theorem ensures the uniqueness of the solution of (17).

Theorem 4.

Assume that for all$U,V\in \mathcal{H}\left(n\right)$with$U\le V$, we have

$$\left|tr\{b(U-V)+\sum _{j=1}^m{A}_j{A}_j^{*}(F\left(U\right)-F\left(V\right))\}\right|\le \theta \left|tr(U-V)\right|$$

where$\theta \in [0,b+1)$. Then (17) has a unique solution which is positive definite. Moreover, for given $U_0\in \mathcal{H}\left(n\right)$ with $U_0\le Q+{\displaystyle \sum _{j=1}^m}{A}_j^{*}F\left(U_0\right)A_j$ the sequence $\left\{U_k\right\}$ defined as

$$U_{k+1}=\left(1-\frac{1}{b+1}\right)U_k+\frac{1}{b+1}G\left(U_k\right) \mathrm{for} \mathrm{all} k\in \mathbb{N}\cup \left\{0\right\}$$

(18)

converges (in sense of norm ${\parallel .\parallel }_1$) to the solution of (17).

Proof. 

Let $U,V\in \mathcal{H}\left(n\right)$ with $U\le V$

$$\begin{array}{ccc}\hfill {\parallel b(U-V)+G\left(U\right)-G\left(V\right)\parallel }_1& =& tr\left\{(b(U-V)+\sum _{j=1}^m{A}_j^{*}(F\left(U\right)-F\left(V\right))A_j\right\}\hfill \\ & =& tr\left(b(U-V)\right)+\sum _{j=1}^{m}tr\left(A_j^{*}(F\left(U\right)-F\left(V\right))A_j\right)\hfill \\ & =& tr(b(U-V))+\sum _{j=1}^{m}tr\left(A_j{A}_j^{*}(F\left(U\right)-F\left(V\right))\right)\hfill \\ & =& tr\{b(U-V)+\sum _{j=1}^m\left(A_j{A}_j^{*}\right)(F\left(U\right)-F\left(V\right))\}.\hfill \end{array}$$

From the assumptions in the theorem, all the hypotheses of Theorem 2 are fulfilled and we obtain the desired result. □

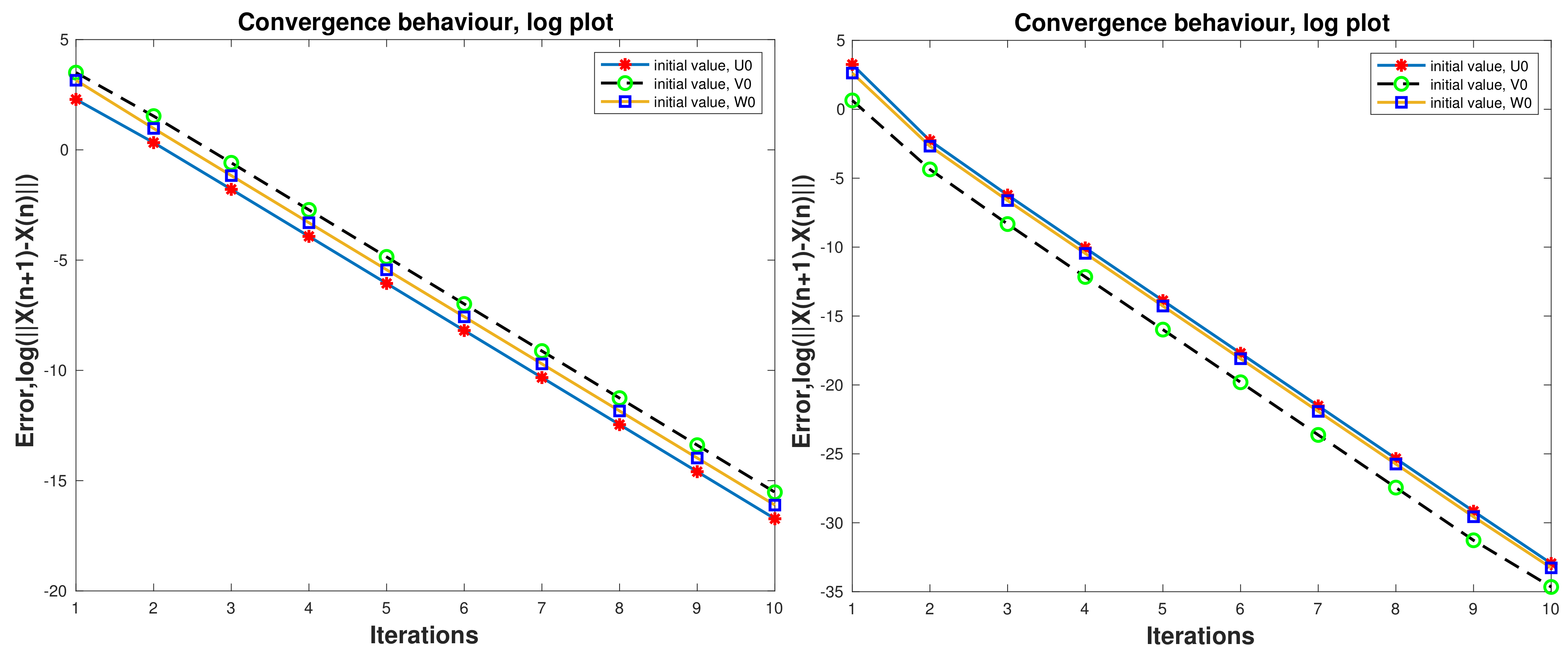
Example 6.

Consider the nonlinear matrix Equation (17) for $m=3$, $n=3$, $F\left(U\right)=U^{1/3}$, i.e.,

$$U=Q+A_1^{*}{U}^{1/3}{A}_1+A_2^{*}{U}^{1/3}{A}_2+A_3^{*}{U}^{1/3}{A}_3,$$

(19)

where

$$Q=\left[\begin{array}{ccc}11.1151& 0.6001& 0.9889\\ 0.6001& 10.5468& 0.8197\\ 0.9889& 0.8197& 11.3649\end{array}\right],A_1=\left[\begin{array}{ccc}0.0728& 0.1080& 0.1934\\ 0.0787& 0.0477& 0.1978\\ 0.2027& 0.0800& 0.0378\end{array}\right],$$

$$A_2=\left[\begin{array}{ccc}0.0224& 0.0290& 0.0330\\ 0.0470& 0.0314& 0.0368\\ 0.0490& 0.0478& 0.0318\end{array}\right],A_3=\left[\begin{array}{ccc}0.5500& 0.8600& 0.2700\\ 0.4600& 0.2400& 0.5200\\ 0.9600& 0.3600& 0.5600\end{array}\right].$$

The conditions of Theorem 4 can be checked numerically by considering different particular values of matrices involved. For instance, it can be tested (and verified to be true) for

$$U=\left[\begin{array}{ccc}1.1150& 0.5998& 0.9888\\ 0.5998& 0.5396& 0.8192\\ 0.9888& 0.8192& 1.3648\end{array}\right],V=\left[\begin{array}{ccc}10.0001& 0.0003& 0.0001\\ 0.0003& 10.0072& 0.0005\\ 0.0001& 0.0005& 10.0001\end{array}\right].$$

To see the behavior of convergence of the sequence$\left\{U_k\right\}$defined in (18), we take-up three initial values considered below:

$$U_0=\left[\begin{array}{ccc}10.0031& 0.0076& 0.00253\\ 0.00756& 10.01903& 0.0064\\ 0.00253& 0.0064& 10.0023\end{array}\right],$$

$$V_0=\left[\begin{array}{ccc}2& 0& 0\\ 0& 2& 0\\ 0& 0& 2\end{array}\right],W_0=\left[\begin{array}{ccc}6& 0& 0\\ 0& 6& 0\\ 0& 0& 6\end{array}\right].$$

For$b=0$, then after 10 successive iterations, the approximations of the unique positive definite solution of (19) is the following

$$\widehat{U}\approx U_{10}=\left[\begin{array}{ccc}15.0766& 3.2581& 3.5772\\ 3.2581& 13.0707& 2.4963\\ 3.5772& 2.4963& 13.3121\end{array}\right]$$

$$\widehat{V}\approx V_{10}=\left[\begin{array}{ccc}15.0766& 3.2581& 3.5772\\ 3.2581& 13.0707& 2.4963\\ 3.5772& 2.4963& 13.3121\end{array}\right]$$

$$\widehat{W}\approx W_{10}=\left[\begin{array}{ccc}15.0766& 3.2581& 3.5772\\ 3.2581& 13.0707& 2.4963\\ 3.5772& 2.4963& 13.3121\end{array}\right].$$

For$b=30$, then after 10 successive iterations, the approximations of the unique positive definite solution of (19) is the following

$$\widehat{U}\approx U_{10}=\left[\begin{array}{ccc}1.3809& 0.0548& 0.0673\\ 0.0548& 1.3426& 0.0484\\ 0.0673& 0.0484& 1.3613\end{array}\right]$$

$$\widehat{V}\approx V_{10}=\left[\begin{array}{ccc}15.0766& 3.2581& 3.5772\\ 3.2581& 13.0707& 2.4963\\ 3.5772& 2.4963& 13.3121\end{array}\right]$$

$$\widehat{W}\approx W_{10}=\left[\begin{array}{ccc}15.0766& 3.2581& 3.5772\\ 3.2581& 13.0707& 2.4963\\ 3.5772& 2.4963& 13.3121\end{array}\right]$$

The convergence behavior is shown in Figure 2.

Figure 2. Convergence behavior for $b=0$ (left) and $b=30$ (right).

Case 2. Consider the following equation

$$U=Q-\sum _{j=1}^m{A}_j^{*}F\left(U\right)A_j.$$

(20)

We can define

$$G\left(U\right)=Q-\sum _{j=1}^m{A}_j^{*}F\left(U\right)A_j.$$

Assume that F is order-reversing in (20), then G is order-preserving. Assume that there exists $U_0\le Q$ such that $U_0\le G\left(U_0\right)$. Then

$$U_0\le G\left(U_0\right)\le G\left(Q\right)\le G\left(Q\right).$$

One can easily see that $[U_0,Q]$ is mapped into itself.

Proposition 2.

Suppose that there exists a$U_0$such that$U_0\le G\left(U_0\right)$. Then G maps the set$\{U:U_0\le U\le Q\}$into itself. The sequence$\left\{G^j\left(Q\right)\right\}$converges to a point$U_{+}$which is the largest solution of (20). Further, the sequence $\left\{G^j\left(U_0\right)\right\}$ is an increasing sequence and converges to a point $U_{-}$, which is the smallest solution in the set $[U_0,Q].$

Theorem 5.

Let$Q\in \mathcal{P}\left(n\right)$and suppose that there exists$U_0\le Q$such that$U_0\le G\left(U_0\right)$. Further, assume that for$U_0\le U\le V\le Q,$we have

$$\left|tr\{b(U-V)+\sum _{j=1}^m{A}_j{A}_j^{*}(F\left(V\right)-F\left(U\right))\}\right|\le \theta \left|tr(U-V)\right|$$

where$\theta \in [0,b+1)$. Then (20) has a unique solution, which is positive definite. Moreover, given $U_0\in \mathcal{H}\left(n\right)$ with $U_0\le Q-{\displaystyle \sum _{j=1}^m}{A}_j^{*}F\left(U_0\right)A_j$, the sequence $\left\{U_n\right\}$ is defined as

$$U_{k+1}=\left(1-\frac{1}{b+1}\right)U_k+\frac{1}{b+1}G\left(U_k\right) \mathrm{for} \mathrm{all} k\in \mathbb{N}\cup \left\{0\right\},$$

(21)

converges (in the sense of norm ${\parallel .\parallel }_1$) to the solution of (20).

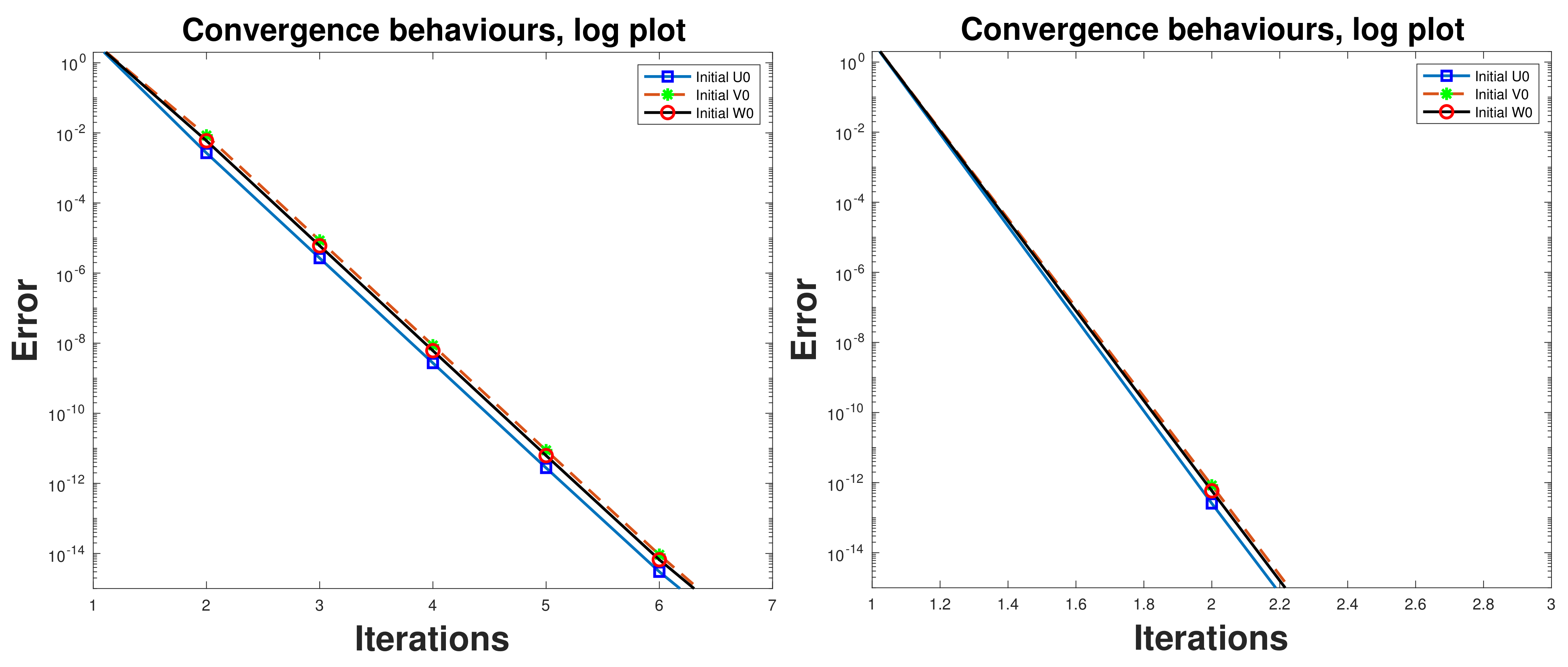
Example 7.

Consider the nonlinear matrix Equation (20) for $m=3$, $n=4$, $F\left(U\right)=U^{-1/100}$ i.e.,

$$U=Q-A_1^{*}{U}^{-1/10}{A}_1-A_2^{*}{U}^{-1/100}{A}_2-A_3^{*}{U}^{-1/100}*A_3,$$

(22)

where

$$Q=\left[\begin{array}{cccc}1.0006& 0.0008& 0.0010& 0.0012\\ 0.0008& 1.0011& 0.0014& 0.0017\\ 0.0010& 0.0014& 1.0018& 0.0021\\ 0.0012& 0.0017& 0.0021& 1.0026\end{array}\right],A_1=\left[\begin{array}{cccc}0.0061& 0.0121& 0.0182& 0.0242\\ 0.0121& 0.0182& 0.0242& 0.0303\\ 0.0181& 0.0242& 0.0303& 0.0364\\ 0.0242& 0.0303& 0.0363& 0.0423\end{array}\right],$$

$$A_2=\left[\begin{array}{cccc}0.0182& 0.0364& 0.0545& 0.0727\\ 0.0364& 0.0544& 0.0727& 0.0909\\ 0.0545& 0.0727& 0.0902& 0.1091\\ 0.0727& 0.0909& 0.1091& 0.1252\end{array}\right],A_3=\left[\begin{array}{cccc}0.0045& 0.0091& 0.0136& 0.0182\\ 0.0091& 0.0136& 0.0182& 0.0227\\ 0.0136& 0.0182& 0.0227& 0.0273\\ 0.0182& 0.0227& 0.0273& 0.0318\end{array}\right].$$

The conditions of Theorem 5 can be checked numerically by considering different particular values of matrices involved. For instance, it can be tested (and verified to be true) for

$$U=\left[\begin{array}{cccc}0.0198& 0.0264& 0.0330& 0.0394\\ 0.0264& 0.0357& 0.0448& 0.0538\\ 0.0330& 0.0448& 0.0566& 0.0681\\ 0.0394& 0.0538& 0.0681& 0.0823\end{array}\right],V=\left[\begin{array}{cccc}0.0223& 0.0297& 0.0371& 0.0443\\ 0.02974& 0.0401& 0.0504& 0.0606\\ 0.0371& 0.0504& 0.0637& 0.0767\\ 0.0443& 0.0606& 0.0767& 0.0927\end{array}\right].$$

To see the behavior of convergence of the sequence$\left\{U_k\right\}$defined in (21), we take-up three initial values:

$$U_0=\left[\begin{array}{cccc}0.0110& 0.0147& 0.0183& 0.0219\\ 0.0147& 0.01981686727& 0.0249& 0.0299\\ 0.0183& 0.0249& 0.0314& 0.0379\\ 0.0219& 0.0299& 0.0379& 0.0458\end{array}\right],$$

$$V_0=1\times {10}^{-3}\times \left[\begin{array}{cccc}0.0551& 0.0734& 0.0916& 0.1094\\ 0.0734& 0.0991& 0.1245& 0.1496\\ 0.0916& 0.1245& 0.1573& 0.1895\\ 0.1094& 0.1496& 0.1895& 0.2288\end{array}\right],$$

$$W_0=\left[\begin{array}{cccc}0.0005& 0.0007& 0.0009& 0.001\\ 0.0007& 0.001& 0.0012& 0.0014\\ 0.0009& 0.0012& 0.0016& 0.0019\\ 0.0011& 0.0015& 0.0019& 0.0023\end{array}\right].$$

For$b={10}^{10}$, then after three successive iterations, the approximations of the unique positive definite solution of the (22) are the following

$$\widehat{U}\approx U_{10}=\left[\begin{array}{cccc}1.0000& 0.0000& 0.0000& 0.0000\\ 0.0000& 1.0000& 0.0000& 0.0000\\ 0.0000& 0.0000& 1.0000& 0.0000\\ 0.0000& 0.0000& 0.0000& 1.0000\end{array}\right]$$

$$\widehat{V}\approx V_{10}=\left[\begin{array}{cccc}1.0000& 0.0000& 0.0000& 0.0000\\ 0.0000& 1.0000& 0.0000& 0.0000\\ 0.0000& 0.0000& 1.0000& 0.0000\\ 0.0000& 0.0000& 0.0000& 1.0000\end{array}\right]$$

$$\widehat{W}\approx W_{10}=\left[\begin{array}{cccc}1.0000& 0.0000& 0.0000& 0.0000\\ 0.0000& 1.0000& 0.0000& 0.0000\\ 0.0000& 0.0000& 1.0000& 0.0000\\ 0.0000& 0.0000& 0.0000& 1.0000\end{array}\right].$$

The convergence behavior and solution graph are shown in Figure 3and Figure 4.

Figure 3. Convergence behavior for $b=0$ (left) and $b={10}^{10}$ (right).

Figure 4. Surface graph of solution for $b={10}^{10}$.

6. Conclusions

In this paper, we studied new existence and convergence conditions for solutions of linear and nonlinear matrix equations.