Hybrid Inertial Accelerated Algorithms for Solving Split Equilibrium and Fixed Point Problems
Abstract
:1. Introduction
| Algorithm 1: The general alternative regularization algorithm. |
Initialization: Set and let be arbitrary. Step 1. Compute: , where is chosen to be the largest satisfying the following: If , then set and go to Step 3. Otherwise, do Step 2. Step 2. Compute: Step 3. Compute , where Set and return to Step 1. |
| Algorithm 2: The new inertial Tseng’s extragradient iterative algorithm. |
Initialization: Set , and let be arbitrary. Step 1. Given and , , compute
Step 2. Compute , where is chosen to be the largest satisfying the following: If or , then stop. Otherwise, go to Step 3. Step 3. Compute
Step 4. Compute . Set and return to Step 1. |
2. Preliminaries
- (1)
- nonexpansive, if
- (2)
- γ-contractive, if there exists such that
- (3)
- quasi-nonexpansive, if and
- (4)
- α-strongly pseudo-contractive, if there exists a constant , such that
- (5)
- pseudo-monotone, if
- (6)
- k-demicontractive, if and there exists , such that
- (7)
- k-demimetric, if and there exists , such that
- (A1)
- , ;
- (A2)
- F is monotone, i.e., , ;
- (A3)
- For all
- (A4)
- For all is convex and lower semicontinuous.
- (1)
- if
- (2)
- T is a quasi-nonexpansive mapping for ;
- (3)
- is a closed convex subset of .
- (i)
- ,
- (ii)
- ,
- (iii)
- .
- (i)
- is single-valued;
- (ii)
- is a firmly nonexpansive mapping, i.e., for all
- (iii)
- (iv)
- is closed and convex.
3. Main Results
- (C1)
- , and ;
- (C2)
- , ;
- (C3)
- and , where is generated by Algorithm 3;
- (C4)
- and .
| Algorithm 3: The hybrid inertial accelerated algorithm. |
Initialization: Set and let be arbitrary. Step 1. Given and , compute
Step 2. Compute , where is chosen to be the largest satisfying the following: If , then stop and is a solution of the SEP. Otherwise, Step 3. Compute
Step 4. Compute , where Set and return to Step 1. |
- (1)
- ;
- (2)
- .
- (1)
- If is a solution of the , then ;
- (2)
- Assume that . Then, is a solution of the .
- The proofs of our main results are simple and different from those in early and recent literature manly due to Lemma 8. More precisely, Lemma 8 together with Lemma 13 presents an interesting and simple method to prove under the conditions and .
- Theorem 2 extends, improves, and develops the corresponding results in [12,13,14,17] from finding a solution for the VIP, a solution for the the EP, or a common solution for the SEP and the fixed point problem for demicontractive mappings to finding a common solution for the SEP and the fixed point problem for demimetric mappings. Moreover, our proof is also different from the one used in those paper.
| Algorithm 4: The hybrid inertial accelerated algorithm for the SVIP and the fixed point problem. |
Initialization: Set and let be arbitrary. Step 1. Given and , compute
Step 2. Compute , where is chosen to be the largest satisfying the following: If , then stop and is a solution of the SVIP. Otherwise, Step 3. Compute
Step 4. Compute , where Set and return to Step 1. |
4. Application to Split Minimization Problems
| Algorithm 5: The general alternative regularization algorithm. |
Initialization: Set and let be arbitrary. Step 1.
Given and , compute
Step 2.
Compute , where is chosen to be the largest satisfying the following:
If , then stop and is a solution of the . Otherwise, Step 3.
Compute
Step 4.
Compute , where Set and return to
Step 1. |
5. Numerical Examples
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blum, E.; Oettli, W. From optimization and variational inequalities to equilibrium problems. Math. Stud. 1994, 63, 123–145. [Google Scholar]
- Cho, Y.J.; Petrot, N.; Suantai, S. Fixed point theorems for nonexpansive mappings with applications to generalized equilibrium and system of nonlinear variational inequalities problems. J. Nonl. Anal. Opt. 2010, 1, 45–53. [Google Scholar]
- Yao, Y.; Cho, Y.J.; Liou, Y.C. Algorithms of common solutions for variational inclusions, mixed equilibrium problems and fixed point problems. Eur. J. Oper. Res. 2011, 212, 242–250. [Google Scholar] [CrossRef]
- Tan, B.; Qin, X.; Yao, J.C. Strong convergence of self-adaptive inertial algorithms for solving split variational inclusion problems with applications. J. Sci. Comput. 2021, 87, 1–34. [Google Scholar] [CrossRef]
- Tseng, P. A modified forward-backward splitting method for maximal monotone mappings. SIAM J. Control Optim. 2000, 38, 431–446. [Google Scholar] [CrossRef]
- Alakoya, T.O.; Jolaoso, L.O.; Mewomo, O.T. A general iterative method for finding common fixed point of finite family of demicontractive mappings with accretive variational inequality problems in Banach spaces. Nonlinear Stud. 2020, 27, 1–24. [Google Scholar]
- Ogwo, G.N.; Izuchukwu, C.; Mewomo, O.T. Inertial methods for finding minimum-norm solutions of the split variational inequality problem beyond monotonicity. Numer. Algorithms 2021. [Google Scholar] [CrossRef]
- Chidume, C.E.; Maˇruşter, Şt. Iterative methods for the computation of fixed points of demicontractive mappings. J. Comput. Appl. Math. 2010, 234, 861–882. [Google Scholar] [CrossRef] [Green Version]
- Cai, G.; Dong, Q.-L.; Peng, Y. Strong convergence theorems for solving variational inequality problems with pseudo-monotone and non-Lipschitz operators. J. Opt. Theory Appl. 2021, 188, 447–472. [Google Scholar] [CrossRef]
- Censor, Y.; Bortfeld, T.; Martin, B.; Trofimov, A. A unified approach for inversion problem in intensity-modulated radiation therapy. Phys. Med. Biol. 2006, 51, 2353–2365. [Google Scholar] [CrossRef] [Green Version]
- Ansari, Q.H.; Rehan, A. Split feasibility and fixed point problems. In Nonlinear Analysis: Approximation Theory, Optimization and Application; Ansari, Q.H., Ed.; Springer: New York, NY, USA, 2014; pp. 281–322. [Google Scholar]
- Kazmi, K.R.; Rizvi, S.H. Iterative approximation of a common solution of a split equilibrium problem, a variational inequality problem and a fixed point problem. J. Egypt. Math. Soc. 2013, 21, 44–51. [Google Scholar] [CrossRef] [Green Version]
- Jolaoso, L.O.; Karahan, I. A general alternative regularization method with line search technique for solving split equilibrium and fixed point problems in Hilbert spaces. Comput. Appl. Math. 2020, 39, 1–22. [Google Scholar] [CrossRef]
- Alvarez, F.; Attouch, H. An inertial proximal method for monotone operators via discretization of a nonlinear oscillator with damping. Set-Valued Anal. 2001, 9, 3–11. [Google Scholar] [CrossRef]
- Polyak, B.T. Introduction to Optimization; Optimization Software: New York, NY, USA, 1987. [Google Scholar]
- Polyak, B.T. Some methods of speeding up the convergence of iterarive methods. Z. Vychisl. Mat. Mat. Fiz. 1964, 4, 1–17. [Google Scholar]
- Cai, G.; Shehu, Y.; Iyiola, O.S. Inertial Tseng’s extragradient method for solving variational inequality problems of pseudo-monotone and non-Lipschitz operators. J. Ind. Manag. Optim. 2021. [Google Scholar] [CrossRef]
- Takahashi, W. Introduction to Nonlinear and Convex Analysis; Yokohama Publishers: Yokohama, Japan, 2009. [Google Scholar]
- Marino, G.; Xu, H.K. Weak and strong convergence theorems for strict pseudo-contractions in Hilbert spaces. J. Math. Anal. Appl. 2007, 329, 336–349. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, W. The split common fixed point problem and the shrinking projection method in banach spaces. J. Convex Anal. 2017, 24, 1015–1028. [Google Scholar]
- Browder, F.E. Convergence of approximants to fixed points of nonexpansive nonlinear mappings in Banach spaces. Arch. Ration. Mech. Anal. 1967, 24, 82–90. [Google Scholar] [CrossRef]
- Takahashi, W.; Wen, C.F.; Yao, J.C. The shrinking projection method for a finite family of demimetric mappings with variational inequality problems in a Hilbert space. Fixed Point Theory 2018, 19, 407–420. [Google Scholar] [CrossRef]
- Song, Y. Iterative methods for fixed point problems and generalized split feasibility problems in Banach spaces. J. Nonl. Sci. Appl. 2018, 11, 198–217. [Google Scholar] [CrossRef] [Green Version]
- Maingé, P.E. The viscosity approximation process for quasi-nonexpansive mappings in Hilbert spaces. Comput. Math. Appl. 2010, 59, 74–79. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.K. Iterative algorithm for nonlinear operators. J. Lond. Math. Soc. 2002, 2, 1–17. [Google Scholar] [CrossRef]
- Combettes, P.L. Hirstoaga, S.A. Equilibrium programming in Hilbert spaces. J. Nonlinear Convex Anal. 2005, 6, 117–136. [Google Scholar]
- Su, M.; Xu, H.-K. Remarks on the gradient-projection algorithm. J. Nonlinear Anal. Optim. 2010, 1, 35–43. [Google Scholar]
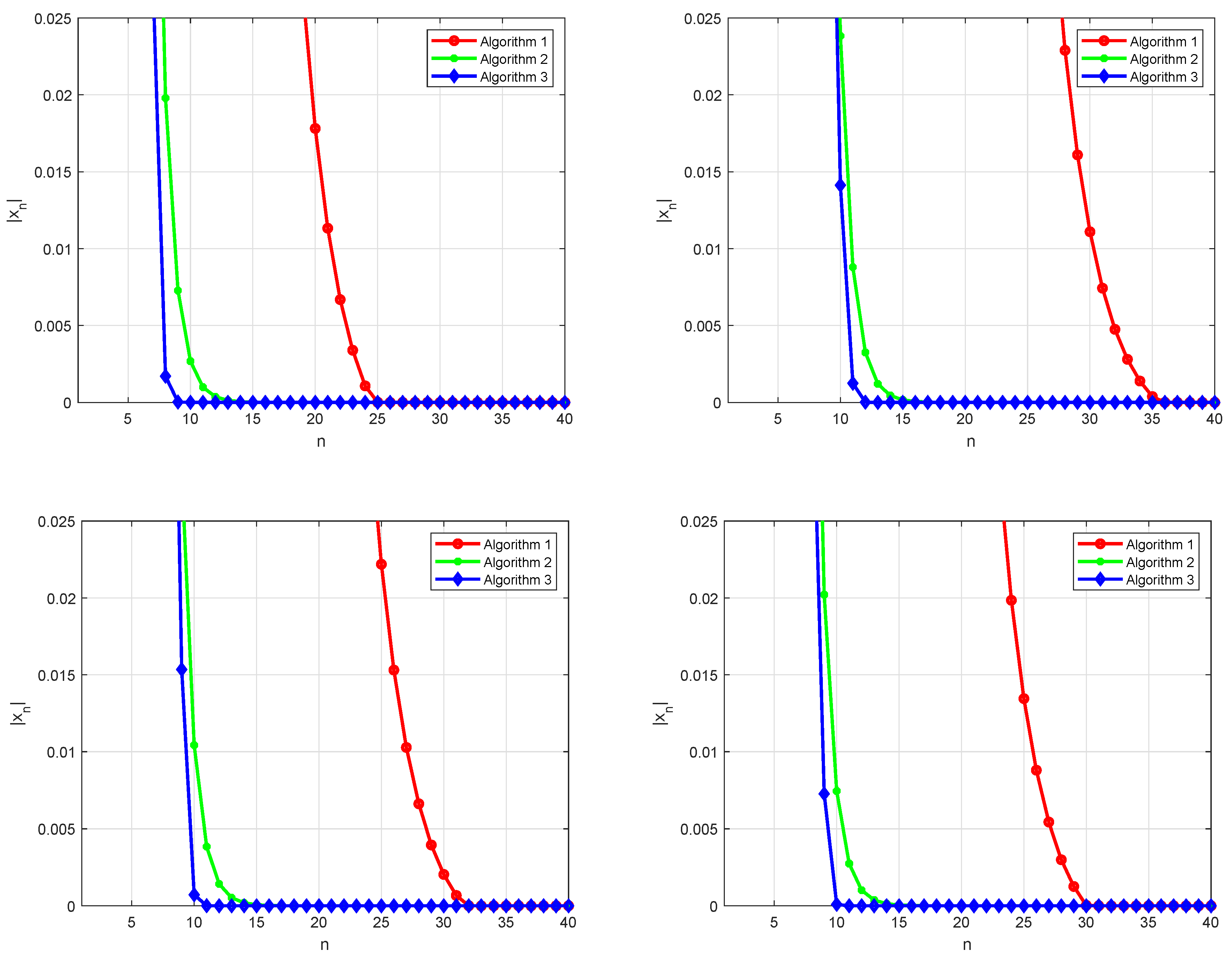
| Err | Algorithm 1 | Algorithm 2 | Algorithm 3 | |||
|---|---|---|---|---|---|---|
| 1.0947111779190 | 25 | 9.8932802287582 | 11 | 2.5084018650195 | 9 | |
| 1.0947111779190 | 25 | 5.0103649467704 | 14 | 2.5084018650195 | 9 | |
| 1.0732462528617 | 26 | 6.8899484598943 | 16 | 3.3005287697625 | 10 | |
| Err | Algorithm 1 | Algorithm 2 | Algorithm 3 | |||
|---|---|---|---|---|---|---|
| 3.8495238046047 | 36 | 5.5670721630783 | 14 | 3.8440832718020 | 12 | |
| 2.6366601401402 | 37 | 7.6554982887714 | 16 | 3.8440832718020 | 12 | |
| 2.6366601401402 | 37 | 3.9225807673322 | 19 | 3.8440832718020 | 13 | |
| Err | Algorithm 1 | Algorithm 2 | Algorithm 3 | |||
|---|---|---|---|---|---|---|
| 6.7539211424883 | 31 | 5.2608831941090 | 13 | 7.1926227474796 | 10 | |
| 5.3602548749907 | 32 | 7.2227962115800 | 15 | 8.5626461279519 | 11 | |
| 5.3602548749907 | 32 | 9.9463481554871 | 17 | 8.5626461279519 | 11 | |
| Err | Algorithm 1 | Algorithm 2 | Algorithm 3 | |||
|---|---|---|---|---|---|---|
| 3.0475500166712 | 30 | 3.7577737100778 | 13 | 9.5530385596659 | 10 | |
| 3.0475500166712 | 30 | 5.1591401511286 | 15 | 9.5530385596659 | 10 | |
| 2.4979918169436 | 31 | 7.1045343967765 | 17 | 1.1372664951983 | 11 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y. Hybrid Inertial Accelerated Algorithms for Solving Split Equilibrium and Fixed Point Problems. Mathematics 2021, 9, 2680. https://doi.org/10.3390/math9212680
Song Y. Hybrid Inertial Accelerated Algorithms for Solving Split Equilibrium and Fixed Point Problems. Mathematics. 2021; 9(21):2680. https://doi.org/10.3390/math9212680
Chicago/Turabian StyleSong, Yanlai. 2021. "Hybrid Inertial Accelerated Algorithms for Solving Split Equilibrium and Fixed Point Problems" Mathematics 9, no. 21: 2680. https://doi.org/10.3390/math9212680
APA StyleSong, Y. (2021). Hybrid Inertial Accelerated Algorithms for Solving Split Equilibrium and Fixed Point Problems. Mathematics, 9(21), 2680. https://doi.org/10.3390/math9212680





