Alikhanov Legendre—Galerkin Spectral Method for the Coupled Nonlinear Time-Space Fractional Ginzburg–Landau Complex System
Abstract
1. Introduction
2. Preliminaries
3. Numerical Scheme
3.1. Discretization
3.2. Algorithmic Implementation
| Algorithm 1: Iterative algorithm for the problem (1). |
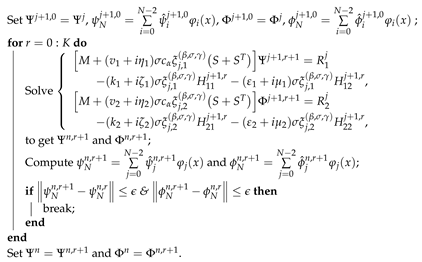 |
4. Convergence Analysis
4.1. Semi-Discrete form Convergence Analysis
4.2. Full-Discrete form Convergence Analysis
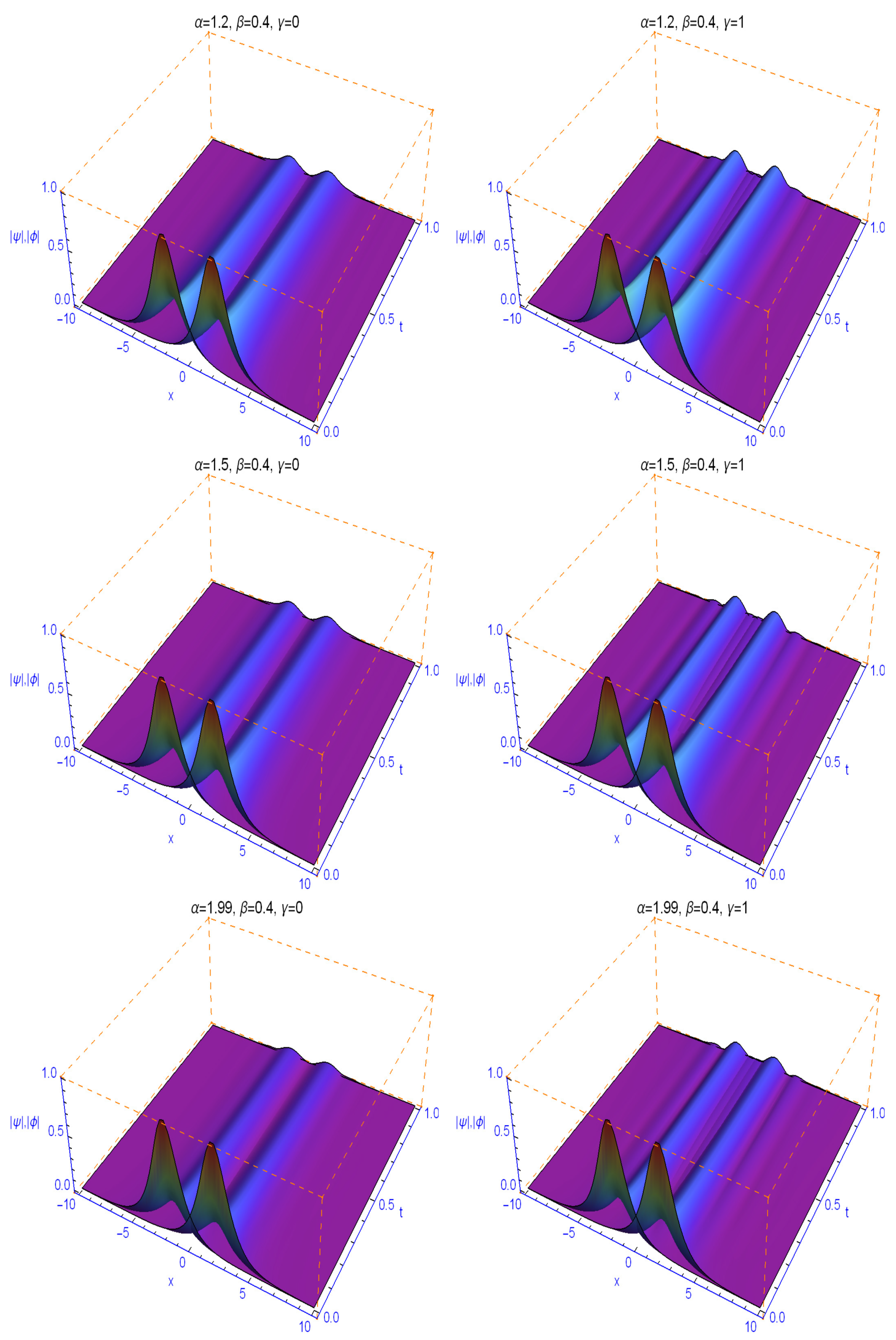
5. Numerical Experiments
6. Conclusions
- Our proposed high order hybrid numerical scheme is a linearized scheme of second order of convergence with respect to time inspite of the nonlinearity of the problem under consideration. The spectral accuracy is achieved due to the use of Galerkin Legendre approximation. Up to our knowledge, it is the first time that scheme is used to solve that kind of problems, especially noting the appearance of time and space fractional derivatives in the model under study. Unconditional convergence and stability of that scheme is secured, which means the error estimates of the numerical model has no dependence on time and spatial steps. This work reflects the possibility of that kind of schemes to be extended to deal with success with the singularity near the initial values of time fractional Caputo operators appearing in the generalized Ginzburg–Landau system. The latter can be secured by using nonuniform Alikhanov schemes combined with Legendre Galerkin spectral and it would be a near future plan for us.
- Due to the intrinsically nonlocal property and historical dependence of the fractional derivative, numerical applications of the numerical methods are always time-consuming. Therefore, fast schemes based on local approximations [41,42] can be implemented to avoid the high computational costs coming from the prehistory feature of spatial fractional order operators. Fast L1 and Fast Alikhanov formulas of the Caputo derivative which are based on the sum of exponentials can be used to to reduce the huge storage and computational cost [43,44]. Invoking these approaches to reduce the computational cost of finite difference/Galerkin spectral methods would be a target of our new works in the near future.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ginzburg, V.L.; Landau, L.D. On the theory of superconductivity. In On Superconductivity and Superfluidity; Springer: Berlin/Heidelberg, Germany, 2009; pp. 113–137. [Google Scholar]
- Aranson, I.S.; Kramer, L. The world of the complex Ginzburg–Landau equation. Rev. Mod. Phys. 2002, 74, 99. [Google Scholar] [CrossRef]
- Tarasov, V.E.; Zaslavsky, G.M. Fractional Ginzburg–Landau equation for fractal media. Phys. A Stat. Mech. Its Appl. 2005, 354, 249–261. [Google Scholar] [CrossRef]
- Yang, L.; Huang, Q.W.; Dai, Z.D. Global attractor of nonlinear optical fibre materials with two cores. J. Hunan Univ. Nat. Sci. 2009, 3, 2621–2636. [Google Scholar]
- Sakaguchi, H.; Malomed, B.A. Stable solitons in coupled Ginzburg–Landau equations describing Bose–Einstein condensates and nonlinear optical waveguides and cavities. Phys. D Nonlinear Phenom. 2003, 183, 282–292. [Google Scholar] [CrossRef][Green Version]
- Pu, X.; Guo, B. Well-posedness and dynamics for the fractional Ginzburg–Landau equation. Appl. Anal. 2013, 92, 318–334. [Google Scholar] [CrossRef]
- Shen, T.; Huang, J. Well-posedness and dynamics of stochastic fractional model for nonlinear optical fiber materials. Nonlinear Anal. Theory Methods Appl. 2014, 110, 33–46. [Google Scholar] [CrossRef]
- Shen, J.; Tang, T.; Wang, L.L. Spectral Methods: Algorithms, Analysis and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Zeng, F.; Liu, F.; Li, C.; Burrage, K.; Turner, I.; Anh, V. A Crank–Nicolson ADI spectral method for a two-dimensional Riesz space fractional nonlinear reaction-diffusion equation. SIAM J. Numer. Anal. 2014, 52, 2599–2622. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, X.; Wang, C.; Fan, W. Galerkin-Legendre spectral schemes for nonlinear space fractional Schrödinger equation. Numer. Algorithms 2018, 79, 337–356. [Google Scholar] [CrossRef]
- Guo, S.; Mei, L.; Zhang, Z.; Chen, J.; He, Y.; Li, Y. Finite difference/Hermite–Galerkin spectral method for multi-dimensional time-fractional nonlinear reaction–diffusion equation in unbounded domains. Appl. Math. Model. 2019, 70, 246–263. [Google Scholar] [CrossRef]
- Liu, H.; Lü, S. Galerkin spectral method for nonlinear time fractional Cable equation with smooth and nonsmooth solutions. Appl. Math. Comput. 2019, 350, 32–47. [Google Scholar] [CrossRef]
- Guo, S.; Mei, L.; Zhang, Z.; Jiang, Y. Finite difference/spectral-Galerkin method for a two-dimensional distributed-order time–space fractional reaction–diffusion equation. Appl. Math. Lett. 2018, 85, 157–163. [Google Scholar] [CrossRef]
- Guo, S.; Mei, L.; Zhang, Z.; Li, C.; Li, M.; Wang, Y. A linearized finite difference/spectral-Galerkin scheme for three-dimensional distributed-order time–space fractional nonlinear reaction–diffusion-wave equation: Numerical simulations of Gordon-type solitons. Comput. Phys. Commun. 2020, 252, 107144. [Google Scholar] [CrossRef]
- Zaky, M.A.; Hendy, A.S.; Macías-Díaz, J.E. Semi-implicit Galerkin–Legendre spectral schemes for nonlinear time-space fractional diffusion–reaction equations with smooth and nonsmooth solutions. J. Sci. Comput. 2020, 82, 1–27. [Google Scholar] [CrossRef]
- Zaky, M.A.; Hendy, A.S. Convergence analysis of an L1-continuous Galerkin method for nonlinear time-space fractional Schrödinger equations. Int. J. Comput. Math. 2020, 1–20. [Google Scholar] [CrossRef]
- Hendy, A.S.; Zaky, M.A. Global consistency analysis of L1-Galerkin spectral schemes for coupled nonlinear space-time fractional Schrödinger equations. Appl. Numer. Math. 2020, 156, 276–302. [Google Scholar] [CrossRef]
- Liao, H.l.; McLean, W.; Zhang, J. A discrete grönwall inequality with applications to numerical schemes for subdiffusion problems. SIAM J. Numer. Anal. 2019, 57, 218–237. [Google Scholar] [CrossRef]
- Hendy, A.S.; Macías-Díaz, J.E. A novel discrete Gronwall inequality in the analysis of difference schemes for time-fractional multi-delayed diffusion equations. Commun. Nonlinear Sci. Numer. Simul. 2019, 73, 110–119. [Google Scholar] [CrossRef]
- Hendy, A.S.; Macías-Díaz, J.E. A Discrete Grönwall Inequality and Energy Estimates in the Analysis of a Discrete Model for a Nonlinear Time-Fractional Heat Equation. Mathematics 2020, 8, 1539. [Google Scholar] [CrossRef]
- Zaky, M.A.; Hendy, A.S.; Macías-Díaz, J.E. High-order finite difference/spectral-Galerkin approximations for the nonlinear time–space fractional Ginzburg–Landau equation. Numer. Methods Partial Differ. Eq. 2020, 1–26. [Google Scholar] [CrossRef]
- Hendy, A.S.; Zaky, M.A. Graded mesh discretization for coupled system of nonlinear multi-term time-space fractional diffusion equations. Eng. Comput. 2020, 1–13. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, Some Methods of Their Solution and Some of Their Applications; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Burrage, K.; Burrage, P.; Turner, I.; Zeng, F. On the analysis of mixed-index time fractional differential equation systems. Axioms 2018, 7, 25. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M. Numerical investigation of reproducing kernel particle Galerkin method for solving fractional modified distributed-order anomalous sub-diffusion equation with error estimation. Appl. Math. Comput. 2021, 392, 125718. [Google Scholar] [CrossRef]
- Abdullah, F.; Liu, F.; Burrage, P.; Burrage, K.; Li, T. Novel analytical and numerical techniques for fractional temporal SEIR measles model. Numer. Algorithms 2018, 79, 19–40. [Google Scholar] [CrossRef]
- Loghman, E.; Kamali, A.; Bakhtiari-Nejad, F.; Abbaszadeh, M. Nonlinear free and forced Vibrations of fractional modeled viscoelastic FGM micro-beam. Appl. Math. Model. 2021, 92, 297–314. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M. A POD-based reduced-order Crank-Nicolson/fourth-order alternating direction implicit (ADI) finite difference scheme for solving the two-dimensional distributed-order Riesz space-fractional diffusion equation. Appl. Numer. Math. 2020, 158, 271–291. [Google Scholar] [CrossRef]
- Zaky, M.A.; Hendy, A.S. An efficient dissipation–preserving Legendre–Galerkin spectral method for the Higgs boson equation in the de Sitter spacetime universe. Appl. Numer. Math. 2021, 160, 281–295. [Google Scholar] [CrossRef]
- Zaky, M.A.; Hendy, A.S.; Alikhanov, A.A.; Pimenov, V. Numerical analysis of multiterm fractional nonlinear subdiffusion equations with time delay: What could possibly go wrong? Commun. Nonlinear Sci. Numer. Simul. 2021, 96, 105672. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M. Direct meshless local Petrov–Galerkin (DMLPG) method for time-fractional fourth-order reaction–diffusion problem on complex domains. Comput. Math. Appl. 2020, 79, 876–888. [Google Scholar] [CrossRef]
- Xu, Y.; Zeng, J.; Hu, S. A fourth-order linearized difference scheme for the coupled space fractional Ginzburg–Landau equation. Adv. Differ. Equ. 2019, 2019, 455. [Google Scholar] [CrossRef]
- Li, M.; Huang, C. An efficient difference scheme for the coupled nonlinear fractional Ginzburg–Landau equations with the fractional Laplacian. Numer. Methods Partial Differ. Equ. 2019, 35, 394–421. [Google Scholar] [CrossRef]
- Pan, K.; Jin, X.; He, D. Pointwise error estimates of a linearized difference scheme for strongly coupled fractional Ginzburg–Landau equations. Math. Methods Appl. Sci. 2020, 43, 512–535. [Google Scholar] [CrossRef]
- Alikhanov, A.A. A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 2015, 280, 424–438. [Google Scholar] [CrossRef]
- Ervin, V.J.; Roop, J.P. Variational solution of fractional advection dispersion equations on bounded domains in Rd. Numer. Methods Partial Differ. Equ. 2007, 23, 256–281. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, F.; Mei, L.; Anh, V.V. A novel alternating-direction implicit spectral Galerkin method for a multi-term time-space fractional diffusion equation in three dimensions. Numer. Algorithms 2020. [Google Scholar] [CrossRef]
- Shen, J. Efficient spectral-Galerkin method I. Direct solvers of second-and fourth-order equations using Legendre polynomials. SIAM J. Sci. Comput. 1994, 15, 1489–1505. [Google Scholar] [CrossRef]
- Cheng, B.; Guo, Z.; Wang, D. Dissipativity of semilinear time fractional subdiffusion equations and numerical approximations. Appl. Math. Lett. 2018, 86, 276–283. [Google Scholar] [CrossRef]
- Li, M.; Huang, C.; Wang, N. Galerkin finite element method for the nonlinear fractional Ginzburg–Landau equation. Appl. Numer. Math. 2017, 118, 131–149. [Google Scholar] [CrossRef]
- Zeng, F.; Turner, I.; Burrage, K. A stable fast time-stepping method for fractional integral and derivative operators. J. Sci. Comput. 2018, 77, 283–307. [Google Scholar] [CrossRef]
- Guo, L.; Zeng, F.; Turner, I.; Burrage, K.; Karniadakis, G.E. Efficient multistep methods for tempered fractional calculus: Algorithms and simulations. SIAM J. Sci. Comput. 2019, 41, A2510–A2535. [Google Scholar] [CrossRef]
- Liao, H.l.; Yan, Y.; Zhang, J. Unconditional convergence of a fast two-level linearized algorithm for semilinear subdiffusion equations. J. Sci. Comput. 2019, 80, 1–25. [Google Scholar] [CrossRef]
- Li, X.; Liao, H.l.; Zhang, L. A second-order fast compact scheme with unequal time-steps for subdiffusion problems. Numer. Algorithms 2020, 1–29. [Google Scholar] [CrossRef]
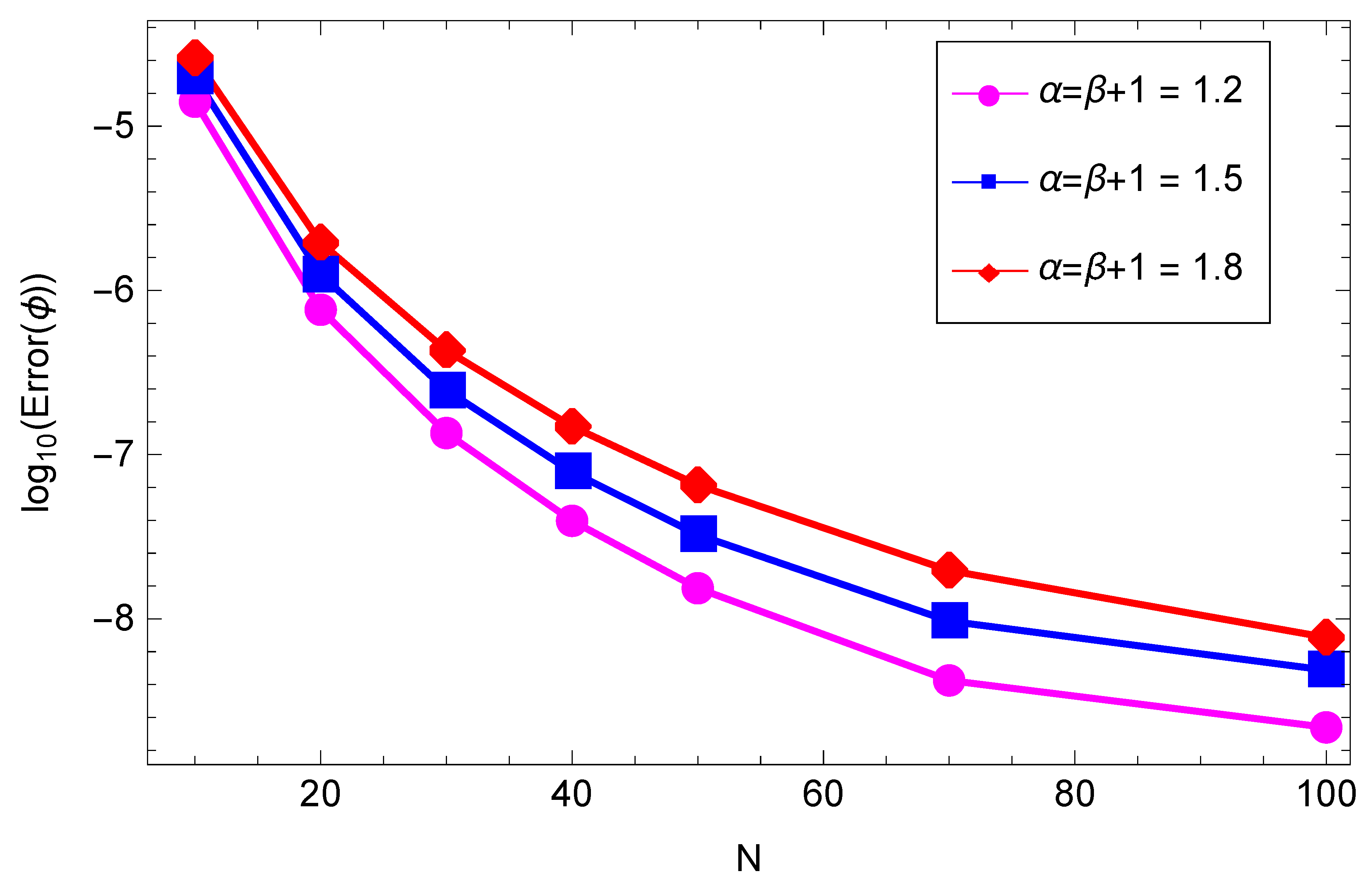
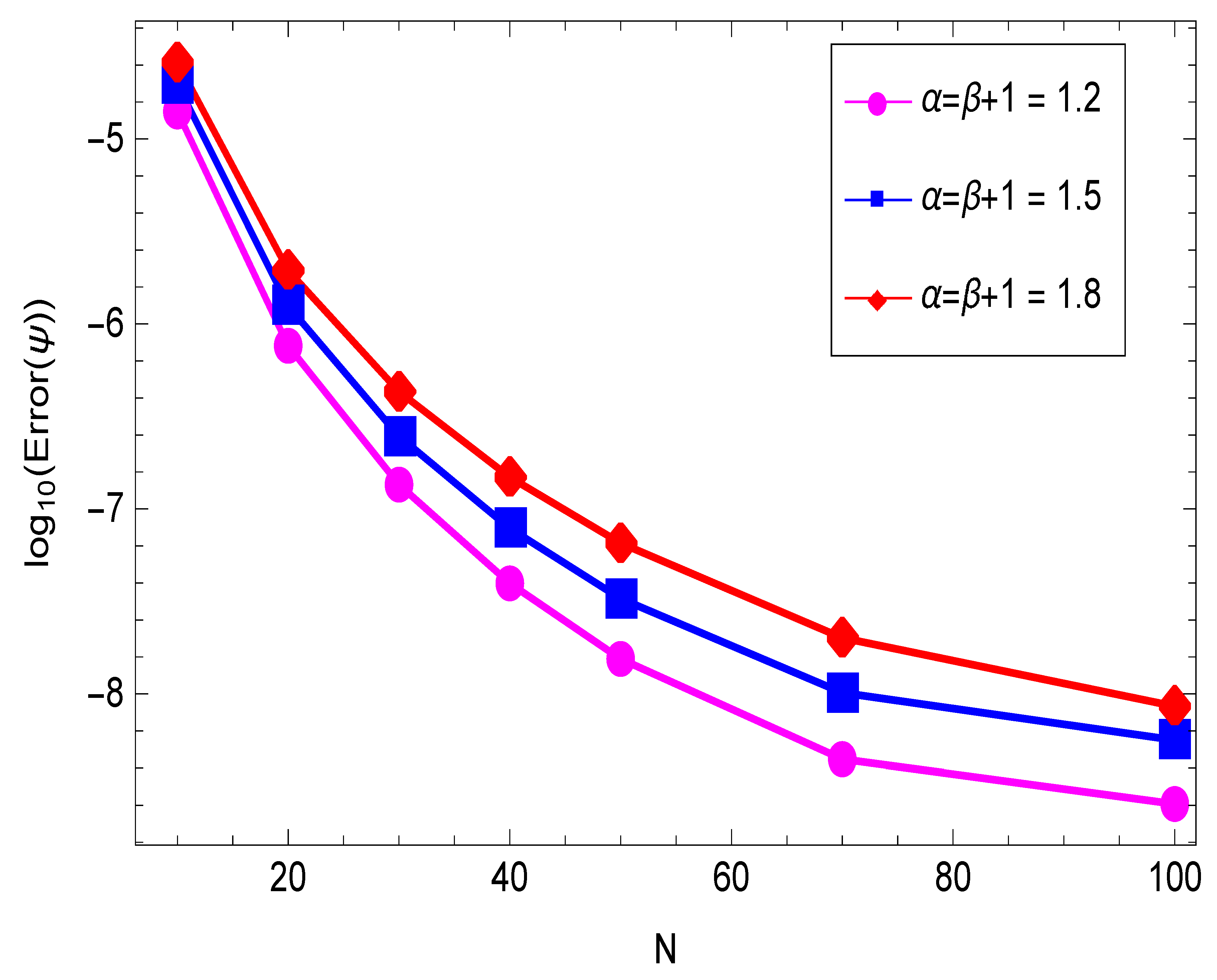
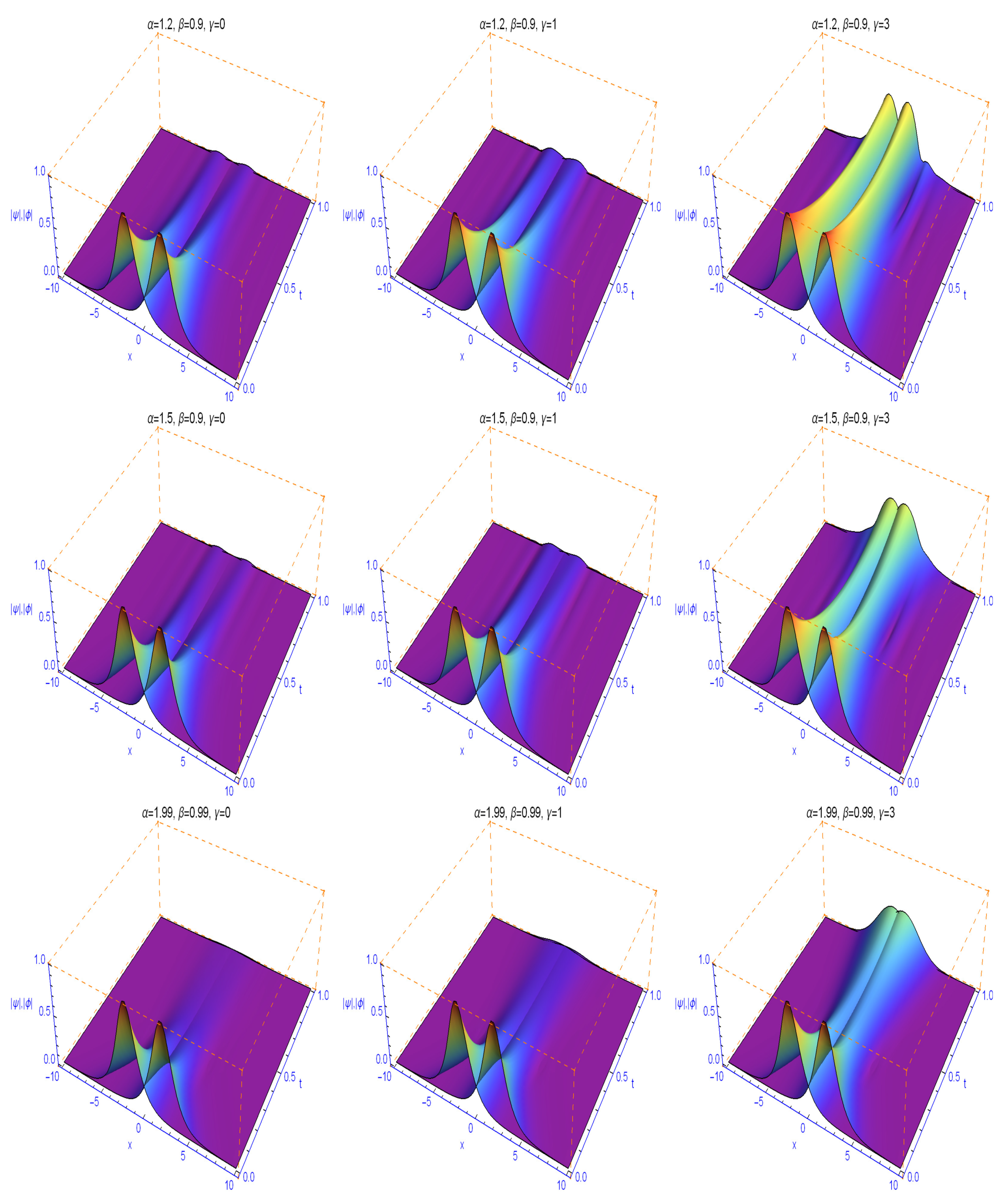
| M | ||||||
|---|---|---|---|---|---|---|
| Error | Order | Error | Order | Error | Order | |
| 100 | ||||||
| 200 | ||||||
| 400 | ||||||
| 800 | ||||||
| 1600 | ||||||
| M | ||||||
|---|---|---|---|---|---|---|
| Error | Order | Error | Order | Error | Order | |
| 100 | ||||||
| 200 | ||||||
| 400 | ||||||
| 800 | ||||||
| 1600 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaky, M.A.; Hendy, A.S.; De Staelen, R.H. Alikhanov Legendre—Galerkin Spectral Method for the Coupled Nonlinear Time-Space Fractional Ginzburg–Landau Complex System. Mathematics 2021, 9, 183. https://doi.org/10.3390/math9020183
Zaky MA, Hendy AS, De Staelen RH. Alikhanov Legendre—Galerkin Spectral Method for the Coupled Nonlinear Time-Space Fractional Ginzburg–Landau Complex System. Mathematics. 2021; 9(2):183. https://doi.org/10.3390/math9020183
Chicago/Turabian StyleZaky, Mahmoud A., Ahmed S. Hendy, and Rob H. De Staelen. 2021. "Alikhanov Legendre—Galerkin Spectral Method for the Coupled Nonlinear Time-Space Fractional Ginzburg–Landau Complex System" Mathematics 9, no. 2: 183. https://doi.org/10.3390/math9020183
APA StyleZaky, M. A., Hendy, A. S., & De Staelen, R. H. (2021). Alikhanov Legendre—Galerkin Spectral Method for the Coupled Nonlinear Time-Space Fractional Ginzburg–Landau Complex System. Mathematics, 9(2), 183. https://doi.org/10.3390/math9020183






