Coverability of Graphs by Parity Regular Subgraphs

Abstract

A graph is even (resp. odd) if all its vertex degrees are even (resp. odd). We consider edge coverings by prescribed number of even and/or odd subgraphs. In view of the 8-Flow Theorem, a graph admits a covering by three even subgraphs if and only if it is bridgeless. Coverability by three odd subgraphs has been characterized recently [Petruševski, M.; Škrekovski, R. Coverability of graph by three odd subgraphs. J. Graph Theory 2019, 92, 304–321]. It is not hard to argue that every acyclic graph can be decomposed into two odd subgraphs, which implies that every graph admits a decomposition into two odd subgraphs and one even subgraph. Here, we prove that every 3-edge-connected graph is coverable by two even subgraphs and one odd subgraph. The result is sharp in terms of edge-connectivity. We also discuss coverability by more than three parity regular subgraphs, and prove that it can be efficiently decided whether a given instance of such covering exists. Moreover, we deduce here a polynomial time algorithm which determines whether a given set of edges extends to an odd subgraph. Finally, we share some thoughts on coverability by two subgraphs and conclude with two conjectures.

1. Introduction and Preliminaries

We consider only undirected and finite graphs. Loops and/or parallel edges are allowed. Throughout, we use standard graph notation and terminology from [1]. There are only two types of graphs that are ‘parity regular’, that is, having all of their vertex degrees with the same parity. These are called ‘even graphs’ and ‘odd graphs’, where a graph is said to be even (or odd, respectively) if each of its vertex degrees is even (or odd, respectively). A covering (also called a cover) of given graph G is a family $\mathcal{F}$ of (not necessarily edge-disjoint) subgraphs of G, such that ${\bigcup }_{F\in \mathcal{F}}E\left(F\right)=E\left(G\right)$; in the more restrictive case of edge-disjointness, $\mathcal{F}$ is said to be a decomposition. A fundamental process in mathematics is that of partitioning (resp. covering) a set of objects into (resp. by) classes according to certain rules. Graph theory deals with a situation where the rules translate to ‘simpler’ subgraphs. In this article we prove several results about graph coverings comprised of parity regular subgraphs.

Let $G=(V,E)$ be a graph. For an orientation D of $E\left(G\right)$, the resulting digraph is denoted $D\left(G\right)$, and for each vertex $v\in V\left(G\right)$, $E^{+}\left(v\right)$ and $E^{-}\left(v\right)$ denote the sets of arcs in $D\left(G\right)$ having their tails and heads, respectively, at v. An integer-valued mapping f with domain $E\left(G\right)$ makes the ordered pair $(D,f)$ an integer flow of G if the equation

$$\sum _{e\in E^{+}\left(v\right)}f\left(e\right)=\sum _{e\in E^{-}\left(v\right)}f\left(e\right)$$

holds for each vertex $v\in V\left(G\right)$. The support of f is the set $\mathrm{supp}\left(f\right)=\{e\in E(G):f(e)\ne 0\}$, and if $\mathrm{supp}\left(f\right)=E\left(G\right)$ then the integer flow $(D,f)$ is said to be nowhere-zero. Given an integer k, $(D,f)$ is called a k-flow if $\left|f\right(e\left)\right|<k$ for each edge $e\in E\left(G\right)$.

The study of nowhere-zero flows was initiated by Tutte [2]. He demonstrated that nowhere-zero k-flows are dual to proper k-colorings in planar graphs. Three famous conjectures of his, known as the 5-flow, 4-flow, and 3-flow conjectures, extend various coloring theorems concerning planar graphs to arbitrary graphs. These conjectures still serve as the driving motivation for the subject of nowhere-zero flows, and, despite considerable effort, all three remain open. The reader eager to learn more about the topic should consult [3,4].

An old result of Matthews [5] states a connection between nowhere-zero flows in graphs and coverings by even subgraphs. Namely, in view of the basic result on product of flows, the obvious correspondence between the supports of 2-flows of graph and its even subgraphs, gives:

Theorem 1

(Matthews, 1978). A graph admits a covering by k even subgraphs, if and only if, it has a nowhere-zero $2^k$-flow.

Since Jaeger-Kilpatrick’s 8-Flow Theorem (c.f. [6,7,8,9]) asserts that every bridgeless graph admits a nowhere-zero 8-flow, Theorem 1 (see also [10]) implies the following:

Theorem 2.

A graph can be covered by three even subgraphs if and only if it is bridgeless.

A result which serves as a parity counterpart to Theorem 2, that is, a characterization of graphs in terms of coverability by three odd subgraphs, has been recently obtained in [11] through the following. Noting that apart from ‘isolated loops’ (vertices incident only to loops) other presence of loops has no influence on the coverability by three odd subgraphs, the proper framework for this particular coverability issue is the class of loopless graphs.

Theorem 3.

A connected loopless graph G admits a covering by three odd subgraphs if and only if it cannot be obtained from a graph depicted in Figure 1 by a (possibly void) sequence of additions of two parallel edges to a pair of adjacent vertices.

Motivated by the above two results, in this article we consider coverability by a combination of even and odd subgraphs (alternatively called ‘parts’). In Section 3, keeping three as the total number of available parity regular subgraphs, we consider coverability by one even subgraph and two odd subgraphs, and then coverability by two even subgraphs and one odd subgraph. With regard to the former covering notion, we prove that such a decomposition always exists (compare with Proposition 3). Concerning the latter covering notion, we show that every 3-edge-connected graph admits a covering by two even and one odd subgraphs. The principal method of proof is the use of T-joins, a graph theoretic concept defined below. This result is tight in terms of edge-connectivity, as we also demonstrate the existence of infinitely many 2-edge-connected graphs which are uncoverable in that sense (compare with Theorem 5). Afterwards, in Section 4, we discuss coverability by more than three (parity regular) parts, and prove that it can be efficiently decided whether any given instance of such a covering exists (compare with Theorem 6 and Corollary 2). Finally, Section 5 contains some of our thoughts on coverability by two parts.

Our work here can be seen as bridging two seemingly unrelated concepts, namely coverings by odd subgraphs and flows. Although the contribution of this paper is purely theoretical in that sense, graph theory also provides key tools for disciplines in which there is a connectedness of elements or components that seem to be related in a system-type. For example, families of graphs, and their subgraphs with suitable properties, are used to construct proof of fixed point results. An additional motivation to carry out this study comes from the emerging field of signal processing on graphs, which extends classical discrete signal processing to signals with graphs as underlying structure.

All proofs are postponed for the upcoming sections. We conclude the present section by introducing some general terminology and notation that are used throughout the paper.

The graph parameters $n\left(G\right)=\left|V\right(G\left)\right|$ and $m\left(G\right)=\left|E\right(G\left)\right|$ are called order and size of G, respectively; a graph of order 1 (resp. size 0) is said to be trivial (resp. empty). For any vertex $v\in V\left(G\right)$, the set of edges incident with v is denoted by $E_G\left(v\right)$. A vertex v having degree $d_G\left(v\right)$ (being the number of incident edges with every loop being counted twice) equal to k is a k-vertex of G; whenever k equals 0 (resp. 1), v is said to be isolated (resp. pendant). If $d_G\left(v\right)$ is even (resp. odd) we speak of an even (resp. odd) vertex of G. The collections of even vertices of G and of odd vertices of G are respectively denoted $EvenV\left(G\right)$ and $OddV\left(G\right)$. From the degree-sum formula ${\sum }_{v\in V\left(G\right)}{d}_G\left(v\right)=2m\left(G\right)$ it follows that the set $OddV\left(G\right)$ is even-sized. This well-known fact is referred to as the handshaking lemma. Given a subset T of $V\left(G\right)$, a spanning subgraph H is a T-join of G if $OddV\left(H\right)=T$. In other words, the requirement is that $d_H\left(v\right)$ is odd for all $v\in T$ and even (possibly zero) for all $v\in V\left(G\right)\backslash T$.

While considering coverings, each subgraph H is often identified with its edge set $E\left(H\right)$, and for notational simplicity we abbreviate the latter to H. Likewise, we won’t make distinction between a spanning tree F and its edge set of F. The complement $E\left(G\right)\backslash H$ of a subgraph H (seen as subset of $E\left(G\right)$) is the edge-complement of H, denoted $\overline{H}$, the role of G being implicit here. The edge-complement $\overline{F}$ of a spanning tree F of G is a cotree in G.

For a subset $X\subseteq V\left(G\right)\cup E\left(G\right)$, $G\left[X\right]$ denotes the subgraph of G induced on X. Similarly, $G-X$ is the subgraph obtained from G by removing X; $G-\left\{x\right\}$ is usually abbreviated to $G-x$. A vertex v is a cut vertex of G if the (deleted) subgraph $G-v$ has more (connected) components than G. Likewise, an edge $e\in E\left(G\right)$ is a cut edge (or bridge) of G if $G-e$ has more components than G. The connectivity (resp. edge-connectivity) of a graph G, written $\kappa \left(G\right)$ (resp. ${\kappa }^{\prime }\left(G\right)$), is the minimum size of a subset $S\subseteq V\left(G\right)$ (resp. $S\subseteq E\left(G\right)$) such that $G-S$ is disconnected or of order 1 (resp. size 0); graph G is said to be k-connected (resp. k-edge-connected) if $\kappa \left(G\right)\ge k$ (resp. ${\kappa }^{\prime }\left(G\right)\ge k$).

For $X\subseteq V\left(G\right)$, the set of edges from G with one end-vertex in X and the other in $\overline{X}$ form the edge cut associated to X, denoted ${\partial }_G\left(X\right)$. Thus, a cut edge is simply an edge cut of size 1. Depending on the parity of the size $|{\partial }_G\left(X\right)|$, we speak of an odd edge cut or an even edge cut of G.

A block graph is a connected graph having no cut vertex. For a graph G, each maximal block subgraph is called a block of G. Given a block B, any $v\in V\left(B\right)$ which is not a cut vertex of G is an internal vertex of B (and of G). The internal vertices of B comprise the interior of B in respect to G, ${\mathrm{Int}}_G\left(B\right)$. If at most one cut vertex of G is contained in $V\left(B\right)$, then B is an end-block of G. The block forest of a graph G is an acyclic bipartite graph $B\left(G\right)$ having bipartition $(\mathcal{B},\mathcal{C})$, where $\mathcal{B}$ and $\mathcal{C}$ are, respectively, the set of blocks of G and the set of cut vertices of G, such that the block B and the cut vertex v are adjacent in $B\left(G\right)$ if and only if $v\in V\left(B\right)$. If G is connected then $B\left(G\right)$ is a tree, termed the block tree of G. The end-blocks of G correspond to the leaves of $B\left(G\right)$. Tarjan [12] showed that the block tree of a connected graph can be obtained efficiently by means of depth-first search.

A partition of a set X is a collection of arbitrary nonempty subsets of X that are pairwise disjoint and contain each element of X. Given a partition $\mathcal{P}=\{V_1,V_2,\dots ,V_k\}$ of $V\left(G\right)$, $G/\mathcal{P}$ denotes the graph obtained from G by shrinking each set $V_i,1\le i\le k$, that is, by first deleting all edges whose end-vertices lie in the same partition set, and then identifying the vertices of each $V_i$.

For two vertex-disjoint graphs G and H, take their disjoint union $G⊍H$ and add edges joining every vertex of G to every vertex of H; the obtained graph $G\vee H$ is the join of G and H.

2. Mathematical Background

We shall use the following classical result about T-joins (see [13]) in order to derive two useful results regarding containment within parity regular subgraphs.

Lemma 1.

Let G be a connected graph, and let T be a subset of $V\left(G\right)$. Then a T-join of G exists, if and only if, T is even-sized. In the affirmative case, a T-join of G can be found efficiently. Moreover, if G is a tree, then the T-join is unique.

In both upcoming propositions we consider a connected spanning subgraph H of a (connected) graph G and discuss the containment of its edge-complement $\overline{H}=G-E\left(H\right)$ into an even (resp. odd) subgraph of G. The proofs are straightforward applications of Lemma 1 for a suitable choice of T.

Proposition 1.

Let G be a connected graph, and let H be a connected spanning subgraph of G. Then the edge-complement $\overline{H}$ is contained in an even subgraph K of G. Moreover, if H is a spanning tree of G, then K is unique.

Proof. 

Let us set $T=OddV\left(\overline{H}\right)$. Consider a subgraph K of G that contains $\overline{H}$. Clearly, K is even if and only if the spanning subgraph of G with edge set $K\cap H$ is a T-join of H. Now the assertion follows from Lemma 1. □

Proposition 2.

Let G be a connected graph of even order, and let H be a connected spanning subgraph of G. Then the edge-complement $\overline{H}$ is contained in an odd subgraph K of G. Moreover, if H is a spanning tree of G, then K is unique.

Proof. 

This time we set $T=EvenV\left(\overline{H}\right)$. As $n\left(G\right)$ and $\left|OddV\right(\overline{H}\left)\right|$ are even, the former by assumption and the latter by the handshaking lemma, the set T is even-sized. A subgraph K of G containing $\overline{H}$ is odd if and only if the spanning subgraph of G with edge set $K\cap H$ is a T-join of H. The assertion once again follows from Lemma 1. (Note that the obtained K is a spanning odd subgraph of G.) □

A fundamental structural theorem, found independently by Nash-Williams [14] and Tutte [15], has numerous applications.

Theorem 4

(Nash-Williams–Tutte, 1961). A graph G contains at least k edge-disjoint spanning trees, if and only if, for every partition $\mathcal{P}$ of $V\left(G\right)$ it holds that

$$m(G/\mathcal{P})\ge k\left(\right|\mathcal{P}|-1).$$

The following straightforward corollary of Theorem 4 (c.f. [16]) guaranties that sufficiently high edge-connectivity implies the existence of k edge-disjoint spanning trees. In order to make the paper self-contained we also include a brief proof.

Corollary 1.

Let G be a $2k$-edge-connected graph, and let subset $S\subset E\left(G\right)$ be of size $\left|S\right|\le k$. Then $G-S$ contains k edge-disjoint spanning trees. In particular, every $2k$-edge-connected graph contains k edge-disjoint spanning trees.

Proof. 

Consider a partition $\mathcal{P}=\{V_1,\dots ,V_t\}$ of $V\left(G\right)$, and let $v_i$ be the vertex of $G/\mathcal{P}$ corresponding to $V_i$ for each $i=1,\dots ,t$. Since G is $2k$-edge-connected, each degree $d_{G/\mathcal{P}}\left(v_i\right)\ge 2k$. Therefore,

$$2m(G/\mathcal{P})=\sum _{i=1}^t{d}_{G/\mathcal{P}}\left(v_i\right)\ge 2k·t,$$

gives

$$m(G/\mathcal{P})\ge k\left|\mathcal{P}\right|.$$

Consequently,

$$m\left(\right(G-S)/\mathcal{P})\ge m(G/\mathcal{P})-\left|S\right|\ge k\left|\mathcal{P}\right|-k=k\left(\right|\mathcal{P}|-1).$$

In view of the arbitrariness of the partition $\mathcal{P}$, $G-S$ contains k edge-disjoint spanning trees by Theorem 4. □

3. Coverability by Three Parts

This section considers coverability by three parity regular subgraphs, and it is organized as follows. We begin by considering coverability by one even and two odd subgraphs, and then discuss the existence of a covering by two even and one odd subgraphs. It turns out that the former covering always exists (even more so, it can always be made edge-disjoint, that is, a decomposition). Contrarily, the latter coverability aspect is not that trivial.

Proposition 3.

Every graph admits a decomposition into one even and at most two odd subgraphs.

Proof. 

Given a graph G, consider a maximal even subgraph H of G. The maximality of H implies that its edge-complement $\overline{H}=G-E\left(H\right)$ is acyclic. Thus, it suffices to show the following assertion: Every nontrivial tree T decomposes into at most two odd subgraphs. Proceed by induction on the number $e\left(T\right)=\left|EvenV\right(T\left)\right|$ of vertices v of even degree $d_T\left(v\right)$. The inductive base $e\left(T\right)=0$ is trivially true, since then T is an odd graph itself. For the inductive step, split a vertex $v\in EvenV\left(T\right)$ into two vertices, say $v_1$ and $v_2$, of odd degree each. The absence of cycles in T assures that the described splitting procedure furnishes two disjoint nontrivial trees, say $T_1$ and $T_2$, such that $e\left(T_i\right)<e\left(T\right),i=1,2$. Assuming $v_i\in V\left(T_i\right)$, by the inductive hypothesis there exist ‘odd decompositions’ $\{H_i^{\prime },H_i^{″}\}$ of $T_i$, with $v_i\in V\left(H_i^{\prime }\right)$ (and $v_i\notin V\left(H_i^{″}\right)$ as it is of odd degree in $T_i$). Here we allow that $H_1^{″}$ and $H_2^{″}$ are possibly void graphs. Then $\{H_1^{\prime }\cup H_2^{″},H_1^{″}\cup H_2^{\prime }\}$ is a decomposition of T into two odd subgraphs. □

An alternative argument for the assertion used in the above proof can be found in [17].

Let us turn to coverability of graphs by two even subgraphs and one odd subgraph. We prove the following result conjectured in [18].

Theorem 5.

Every 3-edge-connected graph is coverable by two even subgraphs and one odd subgraph. There exists an infinite family of 2-edge-connected graphs none of which admits such a covering.

Proof. 

Let us first prove that 3-edge-connectedness suffices for coverability by two even subgraphs and one odd subgraph. This will be achieved as follows. First, we shall reduce the problem to graphs of edge-connectivity 3. Next, we shall resolve the case when there is a vertex of degree 3, i.e., when a trivial edge 3-cut is present. Finally, we shall deal with the case of a graph G having only nontrivial edge 3-cuts: namely, we will look at an edge 3-cut $\{e_1,e_2,e_3\}$ at the ‘periphery’ of G, and consider the two smaller graphs obtained by contracting the components of $G-\{e_1,e_2,e_3\}$, one at a time. ☐

We begin the task at hand by noting a well-known fact (see Theorem 7 in Section 5): 4-edge-connectedness implies coverability by two even subgraphs. For the sake of completeness, here is a sketch of the standard textbook proof of this fact: the 4-edge-connectedness guarantees existence of two edge-disjoint spanning trees, by Corollary 1; their respective cotrees form a cover of the graph; each of these cotrees is fully contained within an even subgraph, by Proposition 1, which gives the desired covering. Therefore, we may confine to graphs G of edge-connectivity ${\kappa }^{\prime }\left(G\right)=3$.

Claim 1.

If there is a 3-vertex $v\in V\left(G\right)$, then G admits a covering $\{K^{\prime },K^{″},H\}$ consisting of two even subgraphs $K^{\prime },K^{″}$ and an odd subgraph H such that $E_G\left(v\right)⊈E\left(H\right)$.

Denote by $2G$ the graph obtained from G by duplicating each edge $e\in E\left(G\right)$. Since G is 3-edge-connected, $2G$ is 6-edge-connected. Let S be the duplicate of $E_G\left(v\right)$. Consider the graph $G^{*}=2G-S$. In other words, $G^{*}$ is obtained from G by duplicating each edge from $\overline{E_G\left(v\right)}=E\left(G\right)\backslash E_G\left(v\right)$. (Notice that S is a set of size 3 and $E\left(G\right)\subseteq E\left(G^{*}\right)$.) Then $G^{*}$ has three edge-disjoint spanning trees, by Corollary 1. These trees of $G^{*}$ correspond to three spanning trees of G, call them $T^{\prime },T^{″},$ and $T^{‴}$, such that $T^{\prime }\cap T^{″}\cap T^{‴}=\varnothing$ (seen as edge sets) and $E_{T^{\prime }}\left(v\right)⊍E_{T^{″}}\left(v\right)⊍E_{T^{‴}}\left(v\right)=E_G\left(v\right)$. Consequently, $d_{\overline{T^{\prime }}}\left(v\right)=d_{\overline{T^{″}}}\left(v\right)=d_{\overline{T^{‴}}}\left(v\right)=2$ and the collection $\{\overline{T^{\prime }},\overline{T^{″}},\overline{T^{‴}}-E_G\left(v\right)\}$ constitutes a covering of G. In view of Proposition 1, there are even subgraphs $K^{\prime },K^{″}$ of G such that $K^{\prime }\supseteq \overline{T^{\prime }}$ and $K^{″}\supseteq \overline{T^{″}}$. We show containment of $\overline{T^{‴}}-E_G\left(v\right)$ within an odd subgraph H of G such that $E_G\left(v\right)⊈E\left(H\right)$ by separately considering two cases regarding the parity of the order $n\left(G\right)$.

Case 1:

The order $n\left(G\right)$ is even. Since $\overline{T^{‴}}-E_G\left(v\right)$ is of even order, the set $EvenV(\overline{T^{‴}}-E_G\left(v\right))$ is of even size, by the handshaking lemma. Say $N_{T^{‴}}\left(v\right)=\left\{u\right\}$ and $E_{T^{‴}}\left(v\right)=\left\{e\right\}$. Then $S=EvenV(\overline{T^{‴}}-E_G\left(v\right))\oplus \{u,v\}$ is an even-sized subset of $V\left(G\right)\backslash \left\{v\right\}$. As v is a leaf of $T^{‴}$, the graph $T^{‴}-v$ is connected. In view of Lemma 1, take an S-join of $T^{‴}-v$ and form its (disjoint) union with $\overline{T^{‴}}-E_G\left(v\right)$. The only even vertices of the constructed graph are precisely u and v; moreover, v is isolated. By adding the edge e to the resulting graph, we obtain the desired H. Notice that the only edge from $E_G\left(v\right)$ included in H is e.

Case 2:

The order $n\left(G\right)$ is odd. Then $S=EvenV(\overline{T^{‴}}-v)$ is an even-sized subset of $V\left(G\right)\backslash \left\{v\right\}$. Since $T^{‴}-v$ is connected, take an S-join of $T^{‴}-v$ and combine it with $\overline{T^{‴}}-v$. We thus obtain an odd spanning subgraph of $G-v$, which serves as our H. Moreover, no edge of $E_G\left(v\right)$ is in H. This settles the claim.

Let $\{e_1,e_2,e_3\}$ be an edge 3-cut of G that induces two connected components $G\left[V_1\right]$ and $G\left[V_2\right]$ of $G-\{e_1,e_2,e_3\}$ (with $\{V_1,V_2\}$ being the corresponding partition of $V\left(G\right)$) such that $|V_2|$ is minimized (see Figure 2). For $i=1,2$, define $G_i=G/V_{3-i}$; that is, let $G_i$ be the graph obtained from G by contracting $V_{3-i}$ into an new vertex $v_{3-i}$. The graph $G_1$ is clearly 3-edge-connected, hence Claim 1 guarantees the existence of a covering $\{K_1^{\prime },K_1^{″},H\}$ of $G_1$ such that $K_1^{\prime },K_1^{″}$ are even subgraphs, whereas H is an odd subgraph for which $\{e_1,e_2,e_3\}⊈E\left(H\right)$.

If $|V_2|=1$ then $G=G_1$ and we are done. Assuming $|V_2|>1$, let $G_2^{\prime }=G\left[V_2\right]$. The minimality choice of $\{e_1,e_2,e_3\}$ enforces certain structural properties on $G_2$ and $G_2^{\prime }$. The following property regarding $G_2$ is a known fact, but for sake of completeness, we include a proof of it.

Claim 2.

The 3-set $E_{G_2}\left(v_1\right)$ is the only edge cut of size less than 4 in $G_2$.

By contradiction, as $G_2$ is surely 3-edge-connected, suppose S is an edge 3-cut of $G_2$ distinct from $\{e_1,e_2,e_3\}$. Say S disconnects $G_2$ by splitting it into two parts L and R. We may assume that $e_1\notin S$ with $e_1,v_1$ belonging in L. Consequently, S presents an edge 3-cut of G itself. Indeed, it splits it into parts $V_1\cup L\backslash \left\{v_1\right\}$ and R. However, $R⊊V_2$, contradicting the choice of $\{e_1,e_2,e_3\}$.

Claim 3.

The graph $G_2^{\prime }$ contains two edge-disjoint spanning trees.

In view of Claim 2, apart from the edge 3-cut ${\partial }_{G_2}\left(v_1\right)$, every other edge cut of $G_2$ has size at least 4. Duplicate a selected edge $e\in E_{G_2}\left(v_1\right)$. The obtained graph $G^{*}$ is 4-edge-connected. Let $S\subseteq E\left(G^{*}\right)$ be the 2-set consisting of e and its copy. Then $G^{*}-S$ has two edge-disjoint spanning trees, by Corollary 1. Seen in $G_2$, both these trees have $v_1$ as a pendant vertex. By removing $v_1$ from each, we obtain two edge-disjoint spanning trees of $G_2^{\prime }$. This establishes the claim.

Let us return to the graph $G_1$, and its covering $\{K_1^{\prime },K_1^{″},H\}$ by two even subgraphs $K_1^{\prime },K_1^{″}$ and an odd subgraph H such that $\{e_1,e_2,e_3\}⊈E\left(H\right)$. Consider the respective subgraphs of $G-E\left(G_2^{\prime }\right)$, that is, the graphs induced by the edge sets $E\left(K_1^{\prime }\right),E\left(K_1^{″}\right),E\left(H\right)$. For simplicity of notation, in what follows we denote the latter three subgraphs also by $K_1^{\prime },K_1^{″},H$. Obviously, $K_1^{\prime },K_1^{″}$ may no longer be even, but notice that the condition $\{e_1,e_2,e_3\}⊈E\left(H\right)$ guarantees that H is still odd. Let $x_1,x_2,x_3$ be the respective end-vertices of $e_1,e_2,e_3$ in $V_2$. (Here, vertices $x_1,x_2,x_3$ may not all be pairwise distinct.) We extend $K_1^{\prime }$ and $K_1^{″}$ to respective even subgraphs $K^{\prime }$ and $K^{″}$ of G as follows.

By Claim 3, there exist two edge-disjoint spanning trees $T^{\prime },T^{″}$ of $G_2^{\prime }$. Let $S^{\prime }=E\left(K_1^{\prime }\right)\cap \{e_1,e_2,e_3\}$. Notice that that $S^{\prime }$ is of size 2 or 0. In the former case, assuming $S^{\prime }=\{e_i,e_j\}$, set $V^{\prime }=\left\{x_i\right\}\oplus \left\{x_j\right\}$. In the latter case, let $V^{\prime }=\varnothing$. Take $J^{\prime }$ to be an $OddV\left(\overline{T^{\prime }}\right)\oplus V^{\prime }$-join of $T^{\prime }$, where the cotree $\overline{T^{\prime }}$ is seen in $G_2^{\prime }$. Then $K^{\prime }=K_1^{\prime }\cup J^{\prime }\cup \overline{T^{\prime }}$ is an even subgraph of G that extends $K_1^{\prime }\cup \overline{T^{\prime }}$ and has $E\left(K^{\prime }\right)\cap \{e_1,e_2,e_3\}=S^{\prime }$. Define $S^{″}$ and $V^{″}$ in a similar fashion. Namely, set $S^{″}=E\left(K_1^{″}\right)\cap \{e_1,e_2,e_3\}$. If $S^{″}=\{e_i,e_j\}$ take $V^{″}=\left\{x_i\right\}\oplus \left\{x_j\right\}$. Otherwise, $S^{″}=\varnothing$ and then set $V^{″}=\varnothing$. Let $J^{″}$ be an $OddV\left(\overline{T^{″}}\right)\oplus V^{″}$-join of $T^{″}$, again with the cotree $\overline{T^{″}}$ seen in $G_2^{\prime }$. The union $K^{″}=K_1^{″}\cup J^{″}\cup \overline{T^{″}}$ is an even subgraph of G that extends $K_1^{″}\cup \overline{T^{″}}$ and has $E\left(K^{″}\right)\cap \{e_1,e_2,e_3\}=S^{″}$.

Notice that, as $\overline{T^{\prime }},\overline{T^{″}}$ form a cover of $G_2^{\prime }$, the collection $\{K^{\prime },K^{″},H\}$ is the desired covering of G by two even subgraphs and one odd subgraph. This settles the first part of Theorem 5.

We show next that the first part of Theorem 5 is sharp in terms of edge-connectivity by exhibiting an infinite family of 2-edge-connected graphs that are uncoverable by two even subgraphs and one odd subgraph (see Figure 3 for an example). Consider a 2-edge-connected graph G that has no nowhere-zero 4-flow, that is, uncoverable by two even subgraphs, by Theorem 1. Note that the family of such graphs G is infinite, as any snark (being a cubic essentially 4-edge-connected loopless graph of chromatic index 4) is a member. Subdivide every edge of G at least once; in other words, produce a ‘complete’ subdivision $G^{\prime }$ of G. Observe that $G^{\prime }$ has edge-connectivity 2. To conclude our proof of Theorem 5 it suffices to show the following.

Claim 4.

The graph $G^{\prime }$ does not admit a covering by two even and one odd subgraphs.

Start by recognizing that every even subgraph $H^{\prime }$ of $G^{\prime }$ corresponds to an even subgraph H of G obtained by suppressing in $H^{\prime }$ each 2-vertex belonging to $V\left(H^{\prime }\right)\backslash V\left(G\right)$. Now for the claim, arguing by contradiction, suppose there exist even subgraphs $H_1^{\prime },H_2^{\prime }$ and an odd subgraph $K^{\prime }$ of $G^{\prime }$ such that $\{H_1^{\prime },H_2^{\prime },K^{\prime }\}$ constitute a covering of $G^{\prime }$. Let v be any 2-vertex of $G^{\prime }$ contained in $V\left(G^{\prime }\right)\backslash V\left(G\right)$. Clearly, $E_{G^{\prime }}\left(v\right)$ is not entirely covered by $K^{\prime }$. Thus, v belongs to at least one of the subgraphs $H_1^{\prime },H_2^{\prime }$. Consequently, v is a 2-vertex in at least one of those two even subgraphs.

Consider now an arbitrary edge $e\in E\left(G\right)$, and let $v_1,\dots ,v_k$ be the 2-vertices ‘introduced’ on e while constructing $G^{\prime }$ from G. Assuming $v_1$ belongs in $H_1^{\prime }$, we successively conclude that $v_2,v_3,\dots ,v_k$ are also in $H_1^{\prime }$. It follows that $e\in E\left(H_1\right)$, where $H_i$ denotes the even subgraph of G rendered by $H_i^{\prime },i=1,2$. The arbitrariness of e tells that $\{H_1,H_2\}$ constitutes a covering of G by two even subgraphs, a contradiction. This establishes the claim.

Note in passing that Figure 3 depicts a complete subdivision of the Petersen graph, the smallest snark. Thus, it is uncoverable by two even and one odd subgraphs. □

Remark 1.

The first part of Theorem 5 allows a succinct argument in the case of even-ordered graphs. Indeed, by duplicating the edges of G, the obtained 6-edge-connected graph surely contains three edge-disjoint spanning trees. These trees correspond to three spanning trees of G, call them $T^{\prime },T^{″},$ and $T^{‴}$, such that the collection of their edge-complements $\{\overline{T^{\prime }},\overline{T^{″}},\overline{T^{‴}}\}$ constitutes a covering of G. Applying Proposition 1 to $\overline{T^{\prime }},\overline{T^{″}}$ and Proposition 2 to $\overline{T^{‴}}$ gives a covering of G by two even and one odd subgraphs. In fact, in this case the requirement for 3-edge-connectedness can be slightly relaxed by admitting the presence of a single edge 2-cut. Namely, then the duplication of each edge would furnish a graph that is just two edges ‘short’ from being 6-edge-connected, which in view of Corollary 1, would nevertheless guarantee the existence of three edge-disjoint spanning trees in it.

Remark 2.

The examples provided in the proof of the second part of Theorem 5 point to an infinite family of 2-edge-connected graphs, uncoverable by two even and one odd subgraphs, that are pairwise topologically inequivalent.

One naturally wonders if the decision problem whether a graph admits a covering by two even and one odd subgraphs can be solved efficiently. It turns out that this answers in the negative.

Proposition 4.

The decision problem whether a graph is coverable by two even subgraphs and one odd subgraph is $\mathcal{NP}$-hard.

Proof. 

As already observed in the second part of the proof of Theorem 5 (c.f. Claim 4), given a graph G and one of its complete subdivisions $G^{\prime }$, G is coverable by two even subgraphs if and only if $G^{\prime }$ is coverable by two even subgraphs and one odd subgraph. Thus, generally speaking, the latter decision problem must be at least as hard as the former. However, the following facts are known to be true (see e.g., [19]). (1) The chromatic index of each cubic loopless graph (simple or not) equals three or four; accordingly, the graph is said to be in Class 1 or Class 2. (2) A cubic loopless graph belongs to Class 1 if and only if it can be covered by two even subgraphs. (3) The classification problem, that decides to which class a graph belongs, is $\mathcal{NP}$-hard even in the cubic case (Holyer [20] and Leven and Galil [21]).

Consequently, the decision problems regarding coverability by two even subgraphs and by two even and one odd subgraphs, respectively, are both $\mathcal{NP}$-hard. □

4. Coverability by Many Parts

In this section we discuss the coverability of graphs by more than three parity regular subgraphs. We commence by noting several conclusions in this direction that are straightforward consequences of Theorems 2, 3 and Proposition 3. Afterwards we deal with the only remaining facet of the matter.

• Coverability by four or more even subgraphs. An obvious necessary condition for coverability by (any number of) even subgraphs is the absence of bridges, and once this condition is fulfilled, three even subgraphs suffice (by Theorem 2). Thus, coverability by more than three even subgraphs brings nothing new.
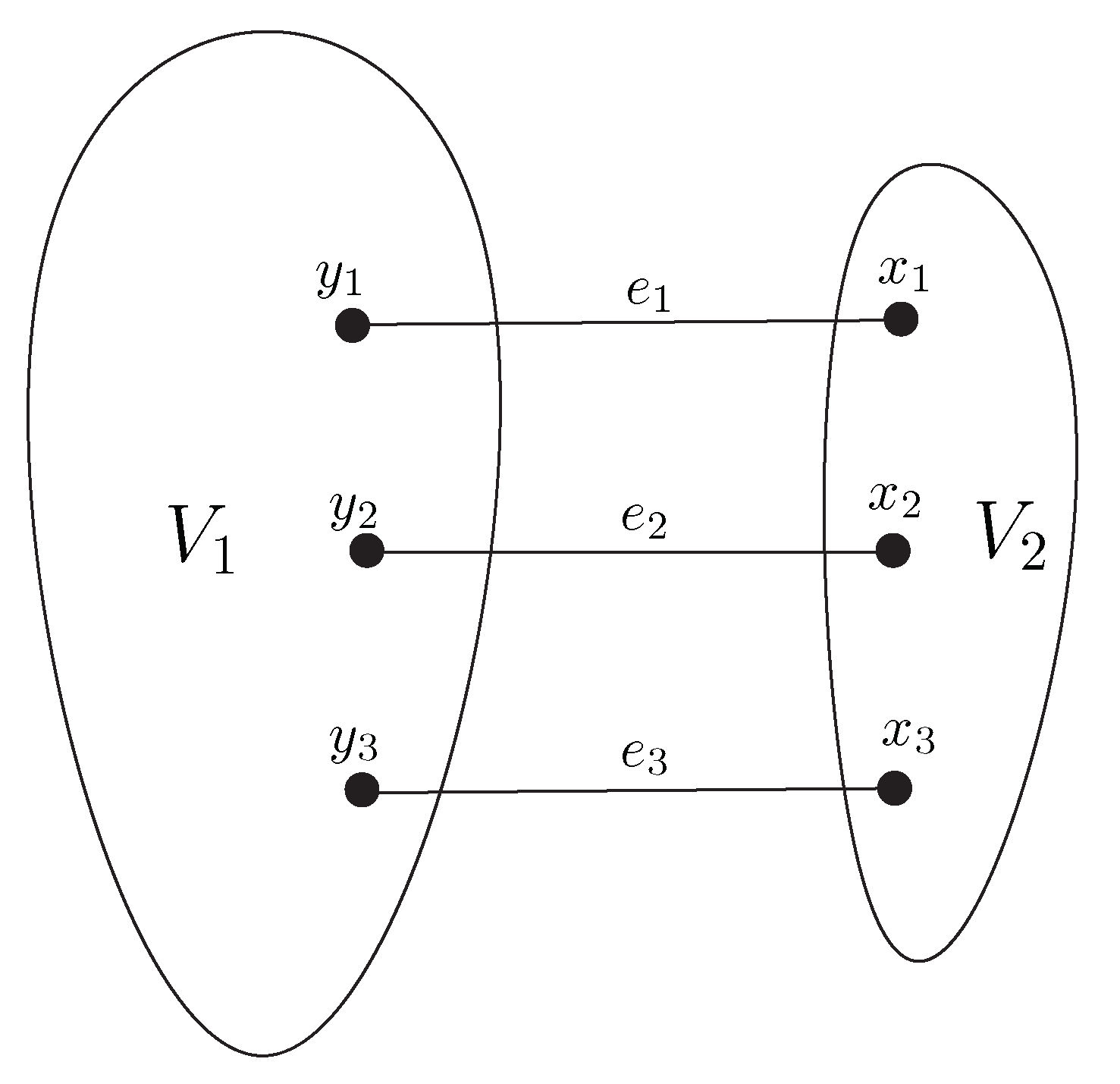
• Coverability by four or more odd subgraphs. As already mentioned in the introductory section, an obvious necessary condition for coverability by (any number of) odd subgraphs is the absence of isolated loops, and once this requirement is met, other presence of loops has no influence on the minimum size of such a covering. Thus, loopless graphs are the rightful setting for this particular coverability issue. In view of Theorem 3, apart from four types of graphs of order 3, every other connected loopless graph is coverable by three odd subgraphs. The remaining four cases (in the realm of connected loopless graphs) are captured through the following observation: If G is obtainable from a graph H depicted in Figure 1 by a (possibly void) sequence of additions of two parallel edges to a pair of adjacent vertices (such G’s form one of the mentioned four types of connected loopless graphs), then the minimum size of a covering of G by odd subgraphs equals $m\left(H\right)$. Indeed, since $n\left(G\right)=3$, every non-void odd subgraph of G must be of order 2.
• Combined coverings by even and odd subgraphs. If at least two odd subgraphs are allowed then Proposition 3 assures that such a covering always exists (it can even be made a decomposition). Thus, the only remaining aspect to be considered is the coverability by three (or more) even subgraphs and one odd subgraph. In fact, in view of Theorem 2, it makes no difference if more than three even subgraphs are allowed because no bridge can be covered by an even subgraph. In other words, the set of bridges has to be contained within the odd subgraph used in such a covering.

We shall show that the decision problem whether a graph is coverable by three even and one odd subgraphs can be solved efficiently. This will be deduced from the following result.

Theorem 6.

The existence of an odd subgraph H of G that contains a given set $S\subseteq E\left(G\right)$ can be decided in polynomial time. In the affirmative, such a subgraph can be efficiently found.

Proof. 

The proof is organized as follows. Our initial observation is that the problem is equivalent to the existence of a certain ‘compatibility’ subgraph in each component of $G-S$. We approach this alternative existence problem for an arbitrary connected graph $G_0$, by first settling particular cases (in Claims 1–3). Afterwards, we induct on the number of blocks of $G_0$. In the inductive step (realized in Claim 4) we look at an end-block $B_0$ of $G_0$, and reduce the problem to the graph $G_0-\mathrm{Int}\left(B_0\right)$. These four claims lead to an efficient algorithm since the case of a 2-connected graph $G_0$, amounting to $G_0=\mathrm{Int}\left(G_0\right)$, is already covered in Claims 1–3.

Let us consider the induced subgraph $G\left[S\right]$ and the (possibly empty) sets $EvenV\left(G\right[S\left]\right)$ and $OddV\left(G\right[S\left]\right)$ of even and odd vertices of $G\left[S\right]$, respectively. It is straightforward that the existence of H amounts to the existence of a subgraph K of $G-S$ such that $EvenV\left(G\left[S\right]\right)\subseteq OddV\left(K\right)\subseteq \overline{OddV\left(G\right[S\left]\right)}$ and $EvenV\left(K\right)\subseteq OddV\left(G\right[S\left]\right)$.

We introduce the following ad-hoc terminology. Given a connected graph $G_0$ and disjoint (possibly empty) subsets $S^{\prime },S^{″}\subseteq V\left(G_0\right)$, say that $G_0$ is $(S^{\prime },S^{″})$-compatible if there exists a subgraph $K\subseteq G_0$ with $S^{\prime }\subseteq OddV\left(K\right)\subseteq \overline{S^{″}}$ and $EvenV\left(K\right)\subseteq S^{″}$. We proceed to explain how it can be efficiently decided on the $(S^{\prime },S^{″})$-compatibility of $G_0$, since the considered existence problem reduces to such compatibility issues for the components of $G-S$.

Claim 1.

If $\overline{S^{″}}$ is even-sized, then $G_0$ is $(S^{\prime },S^{″})$-compatible.

Let K be an $\overline{S^{″}}$-join of $G_0$. Then $OddV\left(K\right)=\overline{S^{″}}\supseteq S^{\prime }$ and $EvenV\left(K\right)=S^{″}$. Hence, the subgraph K confirms that $G_0$ is $(S^{\prime },S^{″})$-compatible, which settles Claim 1.

Claim 2.

If $V\left(G_0\right)=S^{\prime }\cup S^{″}$, then $G_0$ is $(S^{\prime },S^{″})$-compatible if and only if $S^{\prime }$ is even-sized.

Under the assumptions, $\{S^{\prime },S^{″}\}$ is a partition of $V\left(G\right)$. Thus, the $(S^{\prime },S^{″})$-compatibility of $G_0$ amounts to the existence of a subgraph K with $OddV\left(K\right)=S^{\prime }$. In other words, if and only if there is a subgraph K which (seen as spanning) forms an $S^{\prime }$-join of $G_0$. Therefore, the claimed is a consequence of the handshake lemma and Claim 1.

In what follows we assume that $V\left(G_0\right)\ne S^{\prime }\cup S^{″}$.

Claim 3.

If $\mathrm{Int}\left(G_0\right)⊈S^{\prime }\cup S^{″}$, then $G_0$ is $(S^{\prime },S^{″})$-compatible.

By Claim 1, we may suppose that $\overline{S^{″}}$ is odd-sized. Select a vertex $v\in \mathrm{Int}\left(G_0\right)\backslash (S^{\prime }\cup S^{″})$. Then $\overline{S^{″}\cup \left\{v\right\}}$ is even-sized and $G_0-v$ is connected. Form an $\overline{S^{″}\cup \left\{v\right\}}$-join K of $G_0-v$. Since $OddV\left(K\right)=\overline{S^{″}}\backslash \left\{v\right\}\supseteq S^{\prime }$ and $EvenV\left(K\right)=S^{″}$, the subgraph K of $G_0$ has the desired properties, which confirms Claim 3.

Let us further assume that $\mathrm{Int}\left(G_0\right)\subseteq S^{\prime }\cup S^{″}$. In view of Claims 2 and 3, we may confine to $\kappa \left(G_0\right)=1$, and consider an end-block $B_0$ of $G_0$. Say $v_0$ is the cut vertex of $G_0$ belonging in $V\left(B_0\right)$. As $V\left(B_0\right)\backslash \left\{v_0\right\}={\mathrm{Int}}_{G_0}\left(B_0\right)\subseteq \mathrm{Int}\left(G_0\right)$, it follows that ${\mathrm{Int}}_{G_0}\left(B_0\right)\subseteq S^{\prime }\cup S^{″}$. Thus, ${\mathrm{Int}}_{G_0}\left(B_0\right)\cap S^{\prime }={\mathrm{Int}}_{G_0}\left(B_0\right)\cap \overline{S^{″}}$. Denote $G_1=G_0-{\mathrm{Int}}_{G_0}\left(B_0\right)$. Form disjoint (possibly empty) subsets $S_1^{\prime },S_1^{″}$ of $V\left(G_1\right)$ from the respective restrictions $S^{\prime }\cap V\left(G_1\right),S^{″}\cap V\left(G_1\right)$ by adjusting the membership of $v_0$ as follows:

• If ${\mathrm{Int}}_{G_0}\left(B_0\right)\cap S^{\prime }$ is even-sized, then simply take $S_1^{\prime }=S^{\prime }\cap V\left(G_1\right)$ and $S_1^{″}=S^{″}\cap V\left(G_1\right)$;
• If ${\mathrm{Int}}_{G_0}\left(B_0\right)\cap S^{\prime }$ is odd-sized, then define $S_1^{″}=(S^{″}\cap V\left(G_1\right))\oplus \left\{v_0\right\}$ and

  $$S_1^{\prime }=\left\{\begin{array}{cc}(S^{\prime }\cap V\left(G_1\right))\cup \left\{v_0\right\}\hfill & \mathrm{if}{v}_0\in S^{″},\hfill \\ (S^{\prime }\cap V\left(G_1\right))\backslash \left\{v_0\right\}\hfill & \mathrm{if}{v}_0\notin S^{″}.\hfill \end{array}\right.$$

The above cumbersome definition of the sets $S^{\prime },S^{″}$ is justified by the following.

Claim 4.

The graph $G_0$ is $(S^{\prime },S^{″})$-compatible if and only if $G_1$ is $(S_1^{\prime },S_1^{″})$-compatible.

Assuming $G_0$ is $(S^{\prime },S^{″})$-compatible, take a subgraph K with $S^{\prime }\subseteq OddV\left(K\right)\subseteq \overline{S^{″}}$ and $EvenV\left(K\right)\subseteq S^{″}$. Form the subgraph $K_1=G_1\cap K$ of $G_1$. We show that:

$S_1^{\prime }\subseteq OddV\left(K_1\right)\subseteq \overline{S_1^{″}}$ (complement taken in $V\left(G_1\right)$) and $EvenV\left(K_1\right)\subseteq S_1^{″}$. $(*)$

Indeed, putting $v_0$ aside, clearly every other vertex of $K_1$ is in order with $(*)$. Assuming $v_0\in K_1$, consider the graph $K_0=B_0\cap K$. Then $S^{\prime }\cap {\mathrm{Int}}_{G_0}\left(B_0\right)\subseteq OddV\left(K_0\right)\subseteq (\overline{S^{″}}\cap {\mathrm{Int}}_{G_0}\left(B_0\right))\cup \left\{v_0\right\}$ and $EvenV\left(K_0\right)\subseteq (S^{″}\cap {\mathrm{Int}}_{G_0}\left(B_0\right))\cup \left\{v_0\right\}$. Since $\overline{S^{″}}\cap {\mathrm{Int}}_{G_0}\left(B_0\right)=S^{\prime }\cap {\mathrm{Int}}_{G_0}\left(B_0\right)$, we have:

$$OddV\left(K_0\right)=\left\{\begin{array}{cc}{S}^{\prime }\cap {\mathrm{Int}}_{G_0}\left(B_0\right)\hfill & \mathrm{if}{S}^{\prime }\cap {\mathrm{Int}}_{G_0}\left(B_0\right)\mathrm{is}\mathrm{even}-\mathrm{sized},\hfill \\ (S^{\prime }\cap {\mathrm{Int}}_{G_0}\left(B_0\right))\cup \left\{v_0\right\}\hfill & \mathrm{if}{S}^{\prime }\cap {\mathrm{Int}}_{G_0}\left(B_0\right)\mathrm{is}\mathrm{odd}-\mathrm{sized}.\hfill \end{array}\right.$$

Hence, it holds that $d_{K_1}\left(v_0\right){\equiv }_2{d}_K\left(v_0\right)+|S^{\prime }\cap {\mathrm{Int}}_{G_0}\left(B_0\right)|$. Consequently, if $S^{\prime }\cap {\mathrm{Int}}_{G_0}\left(B_0\right)$ is even-sized then $(*)$ follows from $d_{K_1}\left(v_0\right){\equiv }_2{d}_K\left(v_0\right)$ and the choice of K. On the other hand, if $S^{\prime }\cap {\mathrm{Int}}_{G_0}\left(B_0\right)$ is odd-sized then degrees $d_{K_1}\left(v_0\right)$ and $d_K\left(v_0\right)$ are of different parities, and proceed by distinguishing between two possibilities: $\left(i\right)$ if $v_0\notin S^{″}$, by definition $v_0\in S_1^{″}$, and $(*)$ is satisfied at $v_0$ (as $d_K\left(v_0\right)$ is odd, and thus $d_{K_1}\left(v_0\right)$ is even); $\left(ii\right)$ if $v_0\in S^{″}$, by definition $v_0\in S_1^{\prime }$, yielding $(*)$ at $v_0$ (as $d_K\left(v_0\right)$ is even and $d_{K_1}\left(v_0\right)$ is odd). This completes the verification of $(*)$, and shows $(S_1^{\prime },S_1^{″})$-compatibility of $G_1$.

Proving the other direction, assume that $G_1$ is $(S_1^{\prime },S_1^{″})$-compatible. Hence, for a subgraph $K_1$ of $G_1$ condition $(*)$ holds. We construct a subgraph $K_0\subseteq B_0$ as follows. If the intersection $S^{\prime }\cap {\mathrm{Int}}_{G_0}\left(B_0\right)$ is even-sized, simply let $K_0$ be an $S^{\prime }\cap {\mathrm{Int}}_{G_0}\left(B_0\right)$-join of $B_0$. Then $OddV\left(K_0\right)=S^{\prime }\cap {\mathrm{Int}}_{G_0}\left(B_0\right)$ and $EvenV\left(K_0\right)=(S^{″}\cap {\mathrm{Int}}_{G_0}\left(B_0\right))\cup \left\{v_0\right\}$. The definition of $S_1^{\prime },S_1^{″}$ implies that the graph $K=K_0\cup K_1$ meets the requirements granting $(S^{\prime },S^{″})$-compatibility of $G_0$. On the other hand, if $S^{\prime }\cap {\mathrm{Int}}_{G_0}\left(B_0\right)$ is odd-sized, take as $K_0$ an $(S^{\prime }\cap {\mathrm{Int}}_{G_0}\left(B_0\right))\cup \left\{v_0\right\}$-join of $B_0$. Then $OddV\left(K_0\right)=(S^{\prime }\cap {\mathrm{Int}}_{G_0}\left(B_0\right))\cup \left\{v_0\right\}$ and $EvenV\left(K_0\right)=S^{″}\cap {\mathrm{Int}}_{G_0}\left(B_0\right)$. One readily checks that in each of the possibilities regarding the membership of $v_0$, the graph $K=K_0\cup K_1$ once again shows $(S^{\prime },S^{″})$-compatibility of $G_0$. This settles the claim.

As the number of blocks decreases with passing from $G_0$ to $G_1$ in Claim 4, the four claims together clearly lead to an efficient algorithm for deciding whether $G_0$ is $(S^{\prime },S^{″})$-compatible. Applied to each component C of the graph $G-S$ by taking $S^{\prime }=EvenV\left(G\left[S\right]\right)\cap V\left(C\right)$ and $S^{″}=OddV\left(G\left[S\right]\right)\cap V\left(C\right)$ this efficiently solves our initial decision problem. □

A straightforward consequence of Theorem 6 is that it can be efficiently decided whether a given graph is coverable by three even subgraphs and one odd subgraph.

Corollary 2.

Given a graph G, it can be decided in polynomial time whether it admits a covering by three even subgraphs and one odd subgraph.

Proof. 

Denote by S the (possibly empty) set of bridges of G. Since $G-S$ is bridgeless, it can be covered by three even subgraphs, by Theorem 2. Hence the considered coverability issue is equivalent to the existence of an odd subgraph H of G such that $S\subseteq E\left(H\right)$. The assertion follows from Theorem 6. □

We end this section by noting that the parity counterpart to Theorem 6 regarding the existence of an even subgraph K of G that contains a given set $S\subseteq E\left(G\right)$ can also be decided efficiently. Indeed, one readily observes that such a subgraph K exists, if and only if, every component of $G-S$ contains an even number (possibly zero) of vertices from $OddV\left(G\right[S\left]\right)$. In the affirmative, such a subgraph can be found in polynomial time.

5. Coverability by Two Parts

Jaeger [8] proved that sufficiently high edge-connectivity guarantees coverability by two even subgraphs. Obviously, no higher edge-connectivity could provide further decrease in the number of required even subgraphs.

Theorem 7

(Jaeger, 1979). Every 4-edge-connected graph is coverable by two even subgraphs.

This result is sharp in terms of edge-connectivity, as every snark presents a 3-edge-connected (cubic) graph uncoverable by two even subgraphs. Note that a ‘full’ parity counterpart to Theorem 7, that is, a positive general result on coverability of graphs having sufficiently high edge-connectivity by two odd subgraphs, is impossible because every nontrivial Eulerian graph of odd order clearly cannot be covered by two odd subgraphs. Thus, not even sufficiently high connectivity would guarantee such coverability. On the other hand, in view of Corollary 1 and Proposition 2, it is easily seen that every 4-edge-connected even-ordered graph is coverable by two odd subgraphs.

In this section we consider the possibilities for a semi parity counterpart to Theorem 7, namely, coverability by one even and one odd subgraph. The next result will provide a useful criterion.

Proposition 5.

Let G be a graph, and let H be an odd subgraph of G. The following four statements are equivalent:

$\left(i\right)$

There exists an even subgraph K of G such that $\{H,K\}$ is a covering of G.

$\left(ii\right)$

There exists an $OddV\left(\overline{H}\right)$-join of H.

$\left(iii\right)$

H meets every odd edge cut of G.

$\left(iv\right)$

$OddV\left(G\right)\subseteq V\left(H\right)$ and every component of H intersects the set $EvenV\left(G\right)$ in an even (possibly zero) number of vertices.

Proof. 

To establish equivalence between $\left(i\right)$ and $\left(ii\right)$ simply note that each of them is equivalent to the requirement that the edge set of $\overline{H}$ is fully contained within an even subgraph of G. On the other hand, this equivalent form of $\left(ii\right)$ clearly implies $\left(iii\right)$. Indeed, as every even subgraph has even-sized (possibly empty) intersection with every edge cut, no odd edge cut of G could lie entirely in $E\left(\overline{H}\right)$. Let us show that $\left(iii\right)$ implies $\left(ii\right)$. Denote $T=OddV\left(\overline{H}\right)$ and consider an arbitrary component C of H. Since ${\partial }_{\overline{H}}\left(V\left(C\right)\right)={\partial }_G\left(V\left(C\right)\right)$ must be even-sized by $\left(iii\right)$, we deduce that

$$|T\cap V\left(C\right)|{\equiv }_2\sum _{v\in V\left(C\right)}{d}_{\overline{H}}\left(v\right)=|{\partial }_{\overline{H}}\left(V\left(C\right)\right)|+\sum _{v\in V\left(C\right)}{d}_{\overline{H}\left[V\left(C\right)\right]}\left(v\right){\equiv }_2\left|{\partial }_{\overline{H}}\left(V\left(C\right)\right)\right|{\equiv }_{2}0.$$

Using that $T\cap V\left(C\right)$ is even-sized, statement $\left(iii\right)$ follows from the arbitrariness of C and Lemma 1.

Finally, we show the equivalence of $\left(ii\right)$ and $\left(iv\right)$. For this it suffices to observe that

$$OddV\left(\overline{H}\right)=(OddV\left(G\right)\backslash V\left(H\right))⊍(V\left(H\right)\cap EvenV\left(G\right)).$$

Thus, an $OddV\left(\overline{H}\right)$-join of H exists if and only if $OddV\left(G\right)\backslash V\left(H\right)=\varnothing$ and every component of H meets $EvenV\left(G\right)$ in an even number of vertices. □

The equivalence of statements $\left(i\right)$ and $\left(iv\right)$ in Proposition 5 yields the promised criterion.

Corollary 3.

A graph G is coverable by one even subgraph and one odd subgraph, if and only if, there is an odd subgraph H of G satisfying that $OddV\left(G\right)\subseteq V\left(H\right)$ and every component of H intersects the set $EvenV\left(G\right)$ in an even (possibly zero) number of vertices.

It turns out that it cannot be efficiently decided whether such an odd subgraph H of G exists.

Proposition 6.

The decision problem whether a graph is coverable by an even subgraph and an odd subgraph is $\mathcal{NP}$-hard.

Proof. 

Given a graph G, let $G^{\prime }$ be its crown, that is, the graph obtained by appending a pendant edge to each vertex $v\in V\left(G\right)$. Since every vertex of G becomes incident with a bridge of $G^{\prime }$, the graph $G^{\prime }$ is coverable by an even subgraph and an odd subgraph, if and only if, G is coverable by two even subgraphs. Consequently, the considered decision problem is at least as hard as the problem of deciding whether a graph is coverable by two even subgraphs. As already mentioned in the proof of Proposition 4, the latter problem is known to be $\mathcal{NP}$-hard. □

Interestingly, the analogous decomposition issue is quite easily solvable in polynomial time, since it amounts to finding the components of a certain induced subgraph.

Proposition 7.

A graph G decomposes into an even subgraph and an odd subgraph, if and only if, each component of $G\left[OddV\right(G\left)\right]$ has an even order.

Proof. 

Assuming such a decomposition $\{K,H\}$ exists, with H being the odd subgraph, it must be that $V\left(H\right)=OddV\left(G\right)$ and thus $E\left(H\right)\subseteq E\left(G\right[OddV\left(G\right)\left]\right)$. Consequently, for each component C of $G\left[OddV\right(G\left)\right]$, the intersection $C\cap H$ constitutes a spanning odd subgraph of C. Hence every component of $G\left[OddV\right(G\left)\right]$ is of even order.

Proving the other direction, Lemma 1 guarantees the existence of an odd spanning subgraph in each component of $G\left[OddV\right(G\left)\right]$. Denote by H the union of those odd subgraphs. Then H is an odd subgraph of G such that $\overline{H}$ is an even subgraph of G. □

We shall make use of Corollary 3 while proving the following result.

Proposition 8.

Every 4-edge-connected graph of even order admits a covering by one even subgraph and one odd subgraph. Contrarily, there exist graphs of odd order with arbitrarily high edge-connectivity none of which admits such a covering.

Proof. 

Let G be a 4-edge-connected graph of even order $n\left(G\right)$. In view of Proposition 1, the edge-connectivity alone guarantees two edge-disjoint spanning trees of G, say $T^{\prime }$ and $T^{″}$. Thus, $\{\overline{T^{\prime }},\overline{T^{″}}\}$ constitute a covering of G. By Proposition 1, there exists an even subgraph $K^{\prime }$ of G such that $K^{\prime }\supseteq \overline{T^{\prime }}$. Since $n\left(G\right)$ is even, Proposition 2 yields an odd spanning subgraph $K^{″}$ of G such that $K^{″}\supseteq \overline{T^{″}}$. Then $\{K^{\prime },K^{″}\}$ is a covering of G consisting of an even and an odd subgraph.

Let us note in passing that, due to the fact that $2k$-edge-connectedness is a slightly stronger requirement than the condition given in Theorem 4, by Corollary 1, the requirement for 4-edge-connectedness in the first part of Proposition 8 can be slightly relaxed by admitting the presence of a single edge 2-cut (and no edge 1-cuts nor 3-cuts), or the presence of at most two edge 3-cuts (and no edge 1-cuts nor 2-cuts). Indeed, in either relaxation, two edge-disjoint spanning trees of G would still exist.

Turning to the second part of the statement, consider a pair $G^{\prime },G^{″}$ of disjoint Eulerian graphs of odd order each. We assert that the graph $G=(G^{\prime }⊍G^{″})\vee K_1$ does not admit a covering by one even subgraph and one odd subgraph. Indeed, arguing by contradiction, suppose G admits such a covering. Then, according to Corollary 3, there is an odd subgraph H of G such that $OddV\left(G\right)\subseteq V\left(H\right)$ and every component of H intersects the set $EvenV\left(G\right)$ in an even (possibly zero) number of vertices. However, this is impossible, as $EvenV\left(G\right)$ is a singleton and $G\left[OddV\right(G\left)\right]$ consists of two odd components. To assure high edge-connectivity of G, simply take for $G^{\prime },G^{″}$ large enough complete graphs of odd order. □

One cannot help but notice that the examples of ‘uncoverable’ graphs provided in the proof of Proposition 8, besides being of odd order, have all but one odd vertices, and moreover, the unique even vertex constitutes a (vertex) 1-cut of the graph. Each such example can be seen as being obtained from $K_2$ by subdividing (once) the edge, thus creating a new vertex, and then ‘blowing up’ every old vertex to an Eulerian graph of odd order. Analogously, starting from $K_{1,n}$ for an odd n, subdividing each edge, and then ‘blowing up’ every old vertex to an Eulerian graph of odd order, we obtain an example of a graph that is uncoverable by an even subgraph and an odd subgraph, in view of Corollary 3. This construction clearly includes graphs of arbitrarily high edge-connectivity, that contain an arbitrary odd number of even vertices, and such that each even vertex constitutes a 1-cut.

Note in passing that, given a connected graph G, if $EvenV\left(G\right)$ is a singleton that additionally does not present a 1-cut of G, then the mere connectedness of $G-EvenV\left(G\right)$ guarantees the existence of a covering of G by an even and an odd subgraph; indeed, Proposition 7 tells that a graph G decomposes into an even and an odd subgraph, if and only if, each component of $G-EvenV\left(G\right)$ is of even order.

However, if the set $EvenV\left(G\right)$ becomes larger than a singleton than 2-connectedness alone does not suffice for the considered coverability. Namely, $K_{3,4}$ is an example of a 2-connected graph that does not admit a covering by one even subgraph and one odd subgraph, by Corollary 3. (Note that $K_{3,4}$ is a graph of edge-connectivity 3.)

We also wish to bring attention to a pair of sufficient conditions for coverability by an even and an odd subgraphs.

Proposition 9.

Let G be a graph, and consider the following three statements:

(a) 

There are two edge-disjoint spanning trees of G such that a vertex $v\in EvenV\left(G\right)$ is pendant in each of them.

(b) 

There are an Eulerian spanning subgraph $G_e$ of G and a vertex $v\in EvenV\left(G\right)$ such that $d_{G_e}\left(v\right)=d_G\left(v\right)$ and $G_e-v$ is connected.

(c) 

G admits a covering by an even subgraph and an odd subgraph.

Then $\left(a\right)\Rightarrow \left(b\right)\Rightarrow \left(c\right)$.

Proof. 

We justify the implications $\left(a\right)\Rightarrow \left(b\right)$ and $\left(b\right)\Rightarrow \left(c\right)$.

Proof of $\left(a\right)\Rightarrow \left(b\right)$: Let $T^{\prime }$ and $T^{″}$ be such a pair of spanning trees. Note that $\overline{T^{\prime }}$ is a connected spanning subgraph of G (since $T^{″}\subseteq \overline{T^{\prime }}$). Moreover, $v\in OddV\left(\overline{T^{\prime }}\right)$. Take an $OddV\left(\overline{T^{\prime }}\right)$-join H of $T^{\prime }$ and form the union $G_e=H\cup \overline{T^{\prime }}$. Then $G_e$ is an Eulerian spanning subgraph of G such that $d_{G_e}\left(v\right)=d_G\left(v\right)$. Moreover, since $T^{″}-v$ is connected and fully contained within $G_e-v$, the latter graph is connected.

Proof of $\left(b\right)\Rightarrow \left(c\right)$: Let $G_e$ be such an Eulerian spanning subgraph of G. Consider the set $S=EvenV\left(\overline{G_e}\right)$. Assume first that $n\left(G\right)$ is even. As then S is even-sized, there exists an S-join H of $G_e$. The union $G_o=H\cup \overline{G_e}$ is a spanning odd subgraph of G. Clearly, $\{G_e,G_o\}$ constitutes a cover of G by an even and an odd (spanning) subgraphs. Assume now that $n\left(G\right)$ is odd. This time S is odd-sized. Baring in mind that v is an isolated vertex of $\overline{G_e}$, take an $S\backslash \left\{v\right\}$-join $H^{\prime }$ of $G_e-v$ and form the union $G_o^{\prime }=H^{\prime }\cup (\overline{G_e}-v)$. Then $G_o^{\prime }$ is an odd subgraph of G, and $\{G_e,G_o^{\prime }\}$ is a cover of G. □

Now we promptly obtain the following.

Corollary 4.

Let G be a 4-edge-connected graph that contains an even vertex $v\in V\left(G\right)$ of degree $d_G\left(v\right)=4$. Then G admits a covering by one even subgraph and one odd subgraph.

Proof. 

Let $S\subset E_G\left(v\right)$ be an arbitrary 2-set. Take a pair of edge-disjoint spanning trees of $G-S$, guaranteed by Corollary 1, and apply the implication $\left(a\right)\Rightarrow \left(c\right)$ from Proposition 9. □

It is therefore tempting to conclude the current discussion with a pair of conjectures. Note that Corollary 4 supports the former, which in turn readily implies the latter. In view of the first part of Proposition 8, for even-ordered graphs the 4-edge-connectedness requirement alone grants both conjectures.

Conjecture 1.

G be a 4-edge-connected graph that contains an even non-cut vertex. Then G admits a covering by one even subgraph and one odd subgraph.

Conjecture 2.

Every 2-connected and 4-edge-connected graph admits a covering by one even subgraph and one odd subgraph.