Heat Transport Phenomena for the Darcy–Forchheimer Flow of Casson Fluid over Stretching Sheets with Electro-Osmosis Forces and Newtonian Heating
Abstract
:1. Introduction
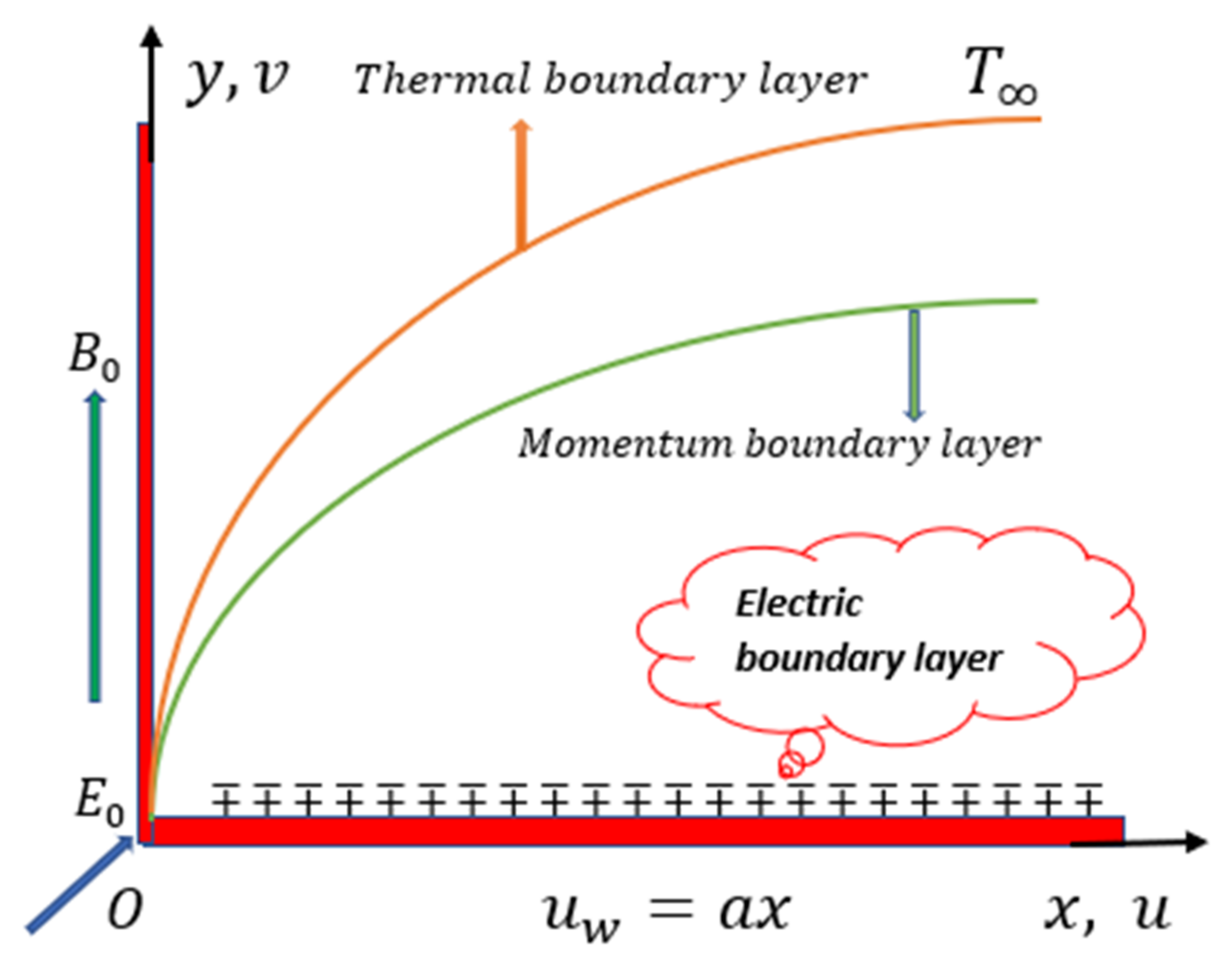
2. Mathematical Formulation
3. Solution Methodology
4. Results and Discussion
5. Numerical Outcomes
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Velocity components (m/s) | Prandtl number | ||
| Cartesian coordinates (m) | Skin friction coefficient | ||
| Eckert number | Forchheimer number | ||
| Non-Newtonian Casson fluid | Permeability of porous space | ||
| Ambient temperature (K) | Local Nusselt number | ||
| Electric parameter | Dimensionless similarity variable | ||
| Stretching velocity | Fluid density (kg/m3) | ||
| Permeability parameter | Generalized Newtonian viscosity (Pa·s) | ||
| Specific heat | Local Reynolds number | ||
| Mass flux velocity (m/s) | Thermal conductivity (W/m K) | ||
| Non-uniform inertia factor | Chemical reaction | ||
| Magnetic parameter (kg/A s2) Tesla | Kinematic viscosity (m2/s) | ||
| Fluid temperature (K) | Stream function | ||
| Dimensionless temperature | Constants (m) |
References
- Takhar, H.S.; Chamka, A.J.; Nath, G. Unsteady three-dimensional MHD-boundary-layer flow due to the impulsive motion of a stretching surface. Acta Mech. 2001, 146, 59. [Google Scholar] [CrossRef]
- Fredrickson, A.G. Principles and Applications of Rheology; Prentice-Hall: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Mukhopadhyay, S. Effects of thermal radiation on Casson fluid flow and heat transfer over an unsteady stretching surface subjected to suction/blowing. Chin. Phys. B 2013, 22, 114702. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. J. Appl. Math. Phys. 1970, 21, 645. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Akbar, N.S.; Khan, Z.H. MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet. Alex. Eng. J. Fac. Eng. Alex. Univ. 2013, 52, 577–582. [Google Scholar] [CrossRef]
- Mustafa, M.; Hayat, T.; Pop, I.; Aziz, A. Unsteady boundary layer flow of a Casson fluid due to an impulsively started moving flat plate. Heat Transfer. 2011, 40, 563–576. [Google Scholar] [CrossRef]
- Ibrahim, W.; Makinde, O.D. Magnetohydrodynamic stagnation point flow and heat transfer of Casson nanofluid past a stretching sheet with slip and convective boundary condition. J. Aerosp. Eng. 2015, 29, 04015037. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Hayat, T.; Alsaedi, A. Exact solution for boundary layer flow of Casson fluid over a permeable stretching/shrinking sheet. Z. für Angew. Math. und Mech. 2013, 94, 522–528. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Hayat, T.; Alsaedi, A. Analytic solution for magnetohydrodynamic boundary layer flow of Casson fluid over a stretching/shrinking sheet with wall mass transfer. Chin. Phys. B 2013, 22, 024702. [Google Scholar] [CrossRef]
- Oyelakin, I.S.; Mondal, S.; Sibanda, P. Unsteady Casson nanofluid flow over a stretching sheet with thermal radiation, convective and slip boundary conditions. Alex. Eng. J. Fac. Eng. Alex. Univ. 2016, 55, 1025–1035. [Google Scholar] [CrossRef] [Green Version]
- Sajid, T.; Jamshed, W.; Shahzad, F.; Eid, M.R.; Alshehri, H.M.; Goodarzi, M.; Akgül, E.K.; Nisar, K.S. Micropolar fluid past a convectively heated surface embedded with nth order chemical reaction and heat source/sink. Phys. Scr. 2021, 96, 104010. [Google Scholar] [CrossRef]
- Jamshed, W.; Devi, S.U.; Goodarzi, S.M.; Prakash, M.; Nisar, K.S.; Zakarya, M.; Abdel-Aty, A.-H. Evaluating the unsteady Casson nanofluid over a stretching sheet with solar thermal radiation: An optimal case study. Case Stud. Therm. Eng. 2021, 26, 101160. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Khan, S.A.; Alshehri, H.M.; Goodarzi, M. Numerical analysis of dual variable of conductivity in bioconvection flow of Carreau–Yasuda nanofluid containing gyrotactic motile microorganisms over a porous medium. J. Therm. Anal. Calorim. 2021, 145, 2033–2044. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Mekheimer, K.S.; Zaher, A.Z. Alterations in blood stream by electroosmotic forces of hybrid nanofluid through diseased artery: Aneurysmal/stenosed segment. Chin. J. Phys. 2020, 65, 123–138. [Google Scholar] [CrossRef]
- Akolade, M.T.; Adeosun, T.; Olabode, J. Influence of thermophysical features on MHD squeezed flow of dissipative Casson fluid with chemical and radiative effects. J. Appl. Comput. Mech. 2020, 2021, 1–11. [Google Scholar]
- Mekheimer, K.S.; Zaher, A.Z.; Hasona, W.M. Entropy of ac electro-kinetics for blood mediated gold or copper nanoparticles as a drug agent for thermotherapy of oncology. Chin. J. Phys. 2020, 65, 123–138. [Google Scholar] [CrossRef]
- Nagaraja, B.; Gireesha, B.J. Exponential space-dependent heat generation impact on MHD convective flow of Casson fluid over a curved stretching sheet with chemical reaction. J. Therm. Anal. Calorim. 2021, 143, 4071–4079. [Google Scholar] [CrossRef]
- Hussain, M.; Ali, A.; Ghaffar, A.; Inc, M. Flow and thermal study of MHD Casson fluid past a moving stretching porous wedge. J. Therm. Anal. Calorim. 2021, 102, 1–11. [Google Scholar]
- Ramudu, A.V.; Kumar, K.A.; Sugunamma, V.; Sandeep, N. Impact of Soret and Dufour on MHD Casson fluid flow past a stretching surface with convective–diffusive conditions. J. Therm. Anal. Calorim. 2021, 182, 1–11. [Google Scholar]
- Hussain, M.; Ghaffar, A.; Ali, A.; Shahzad, A.; Nisar, K.S.; Alharthi, M.R.; Jamshed, W. MHD thermal boundary layer flow of a Casson fluid over a penetrable stretching wedge in the existence of nonlinear radiation and convective boundary condition. Alex. Eng. J. 2021, 60, 5473–5483. [Google Scholar] [CrossRef]
- Takhar, H.S.; Chamkha, A.J.; Nath, G. Flow and mass transfer on a stretching sheet with a magnetic field and chemically reactive species. Int. J. Eng. Sci. 2000, 38, 1303–1314. [Google Scholar] [CrossRef]
- Pavlov, K.B. Magnetohydrodynamic flow of an incompressible viscous fluid caused by the deformation of a plane surface. Magnetohydrodynamics 1974, 10, 146–148. [Google Scholar]
- Imtiaz, M.; Hayat, T.; Alsaedi, A. Flow of magneto nanofluid by a radiative exponentially stretching surface with dissipation effect. Adv. Powder Technol. 2016, 27, 2214–2222. [Google Scholar] [CrossRef]
- Venkata Ramudu, A.C.; Anantha Kumar, K.; Sugunamma, V.; Sandeep, N. Influence of suction/injection on MHD Casson fluid flow over a vertical stretching surface. J. Therm Anal. Calorim. 2019, 113, 3675–3682. [Google Scholar] [CrossRef]
- Khan, W.A.; Makinde, O.D.; Khan, Z.H. Non-aligned MHD stagnation point flow of variable viscosity nanofluids past a stretching sheet with radiative heat. Int. J. Heat Mass Transf. 2016, 96, 525–534. [Google Scholar] [CrossRef]
- Andersson, H.I. MHD flow of a viscoelastic fluid past a stretching surface. Acta Mech. 1992, 95, 227–230. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Layek, G.C.; Samad, S.A. Study of MHD boundary layer flow over a heated stretching sheet with variable viscosity. Int. J. Heat Mass Transf. 2005, 48, 4460–4466. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Ahmed, N.; Khan, U.; Waheed, A.; Hussain, S.; Darus, M. On Combined Effects of Heat Transfer and Chemical Reaction for the Flow through an Asymmetric Channel with Orthogonally Deformable Porous Walls. Math. Probl. Eng. 2016, 2016, 2568785. [Google Scholar] [CrossRef]
- Khan, U.; Ahmed, N.; Mohyud-Din, S.T. Thermo-diffusion, diffusion-thermo and chemical reaction effects on MHD flow of viscous fluid in divergent and convergent channels. Chem. Eng. Sci. Elsevier 2016, 141, 17–27. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Layek, G.C. Chemically reactive solute distribution in MHD boundary layer flow over a permeable stretching sheet with suction or blowing. Chem. Eng. Commun. 2010, 197, 1527–1540. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, M.; Nadeem, S.; Mesloub, S. Falkner-Skan wedge flow of a power-law fluid with mixed convection and porous medium. Comput. Fluids 2011, 49, 22–28. [Google Scholar] [CrossRef]
- Gireesha, B.J.; Shankaralingappa, B.M.; Prasannakumar, B.C.; Nagaraja, B. MHD flow and melting heat transfer of dusty Casson fluid over a stretching sheet with Cattaneo–Christov heat flux model. Int. J. Ambient Energy 2020, 41, 1–9. [Google Scholar] [CrossRef]
- Hussain, A.; Sana, A.; Rizwana, R.; Malik, M.Y. MHD stagnation point flow of a Casson fluid with variable viscosity flowing past an extending/shrinking sheet with slip effects. Phys. A Stat. Mech. Its Appl. 2020, 553, 124080. [Google Scholar] [CrossRef]
- Hamid, A.; Khan, M. Multiple solutions for MHD transient flow of Williamson nanofluids with convective heat transport. J. Taiwan Inst. Chem. Eng. 2019, 103, 126–137. [Google Scholar]
- Kumar, C.P. Thermal Diffusion and Inclined Magnetic Field Effects on MHD Free Convection Flow of Casson Fluid Past an Inclined Plate in Conducting Field. Turk. J. Comput. Math. Educ. (TURCOMAT) 2021, 12, 960–977. [Google Scholar]
- Misra, J.C.; Sinha, A. Electro-osmotic flow and heat transfer of a non-Newtonian fluid in a hydrophobic microchannel with Navier slip. J. Hydrodyn. Ser. B 2015, 27, 647–657. [Google Scholar] [CrossRef]
- Nagler, J. On the electroosmotic and MHD Jeffery–Hamel flow of Nano fluid influenced by wall slip conditions. J. Polytech. 2016, 19, 555–568. [Google Scholar]
- El-Dabe, N.T.M.; Moatimid, G.M.; Hassan, M.A.; Godh, W.A. Electro-osmotic and Hall Current Effects on the Nanofluid Flow through Porous Medium with Wall Properties. Int. J. Appl. Eng. Res. 2019, 14, 3552–3565. [Google Scholar]
- Wang, X.; Xu, H.; Qi, H. Transient magnetohydrodynamic flow and heat transfer of fractional Oldroyd-B fluids in a microchannel with slip boundary condition. Phys. Fluids 2020, 32, 103104. [Google Scholar] [CrossRef]
- Yang, C.; Jian, Y.; Xie, Z.; Li, F. Electromagnetohydrodynamic Electroosmotic Flow and Entropy Generation of Third-Grade Fluids in a Parallel Microchannel. Micromachines 2020, 11, 418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Siva, T.; Jangili, S.; Kumbhakar, B. Heat transfer analysis of MHD and electroosmotic flow of non-Newtonian fluid in a rotating microfluidic channel: An exact solution. Appl. Math. Mech. 2021, 42, 1047–1062. [Google Scholar] [CrossRef]
- Zaher, A.Z.; Ali, K.K.; Mekheimer, K.S. Electroosmosis forces EOF driven boundary layer flow for a non-Newtonian fluid with planktonic microorganism: Darcy Forchheimer model, Electroosmosis forces EOF driven boundary layer flow for a non-Newtonian fluid with planktonic microorganism: Darcy Forchheimer model. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 2534–2559. [Google Scholar]
- Rajaram, V.; Varadharaj, B.; Jayavel, P. Impact of electroosmotic flow on a Casson fluid driven by chemical reaction and convective boundary conditions. Heat Transf. 2021, 50, 4993–5019. [Google Scholar] [CrossRef]
- Hamid, A.; Hashim; Khan, M. Impacts of binary chemical reaction with activation energy on unsteady flow of magneto-Williamson nanofluid. J. Mol. Liq. 2018, 262, 435–442. [Google Scholar] [CrossRef]
- Hamid, A.; Hashim; Khan, M.; Hafeez, A. Unsteady stagnation-point flow of Williamson fluid generated by stretching/shrinking sheet with Ohmic heating. Int. J. Heat Mass Transf. 2018, 126, 933–940. [Google Scholar] [CrossRef]
- Hamid, A.; Khan, M.; Alghamdi, M. Numerical simulation for transient flow of Williamson fluid with multiple slip model in the presence of chemically reacting species. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 4445–4461. [Google Scholar] [CrossRef]
- Hamid, A. Terrific effects of Ohmic-viscous dissipation on Casson nanofluid flow over a vertical thin needle: Buoyancy assisting & opposing. J. Mater. Res. Technol. 2020, 9, 11220–11230. [Google Scholar]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Tran. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Alsaedi, A.; Awais, M.; Hayat, T. Effects of heat generation/absorption on stagnation point ow of nanofluid over a surface with convective boundary conditions. Comm. Non-Linear Sci. Numer. Simul. 2012, 17, 4210–4223. [Google Scholar] [CrossRef]





| 0.1 | 0.1 | 0.1 | 2 | 6.1508 |
| 0.2 | 6.1457 | |||
| 0.3 | 6.1454 | |||
| 0.4 | 6.1453 | |||
| 0.2 | 6.2304 | |||
| 0.3 | 6.3101 | |||
| 0.4 | 6.3897 | |||
| 0.3 | 6.1107 | |||
| 0.5 | 6.0706 | |||
| 0.7 | 6.0307 | |||
| 2.1 | 5.9135 | |||
| 2.2 | 5.6978 | |||
| 2.3 | 5.5009 |
| 0.1 | 0.3 | 0.1 | 2 | 0.51881 |
| 0.2 | 0.67938 | |||
| 0.3 | 0.83994 | |||
| 0.4 | 1.0005 | |||
| 0.5 | 0.99323 | |||
| 0.7 | 1.6334 | |||
| 0.9 | 2.5444 | |||
| 0.3 | 0.51643 | |||
| 0.5 | 0.51431 | |||
| 0.7 | 0.51244 | |||
| 2.1 | 0.5156 | |||
| 2.2 | 0.51268 | |||
| 2.3 | 0.51001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Yang, D.; Israr Ur Rehman, M.; Hamid, A. Heat Transport Phenomena for the Darcy–Forchheimer Flow of Casson Fluid over Stretching Sheets with Electro-Osmosis Forces and Newtonian Heating. Mathematics 2021, 9, 2525. https://doi.org/10.3390/math9192525
Zhang X, Yang D, Israr Ur Rehman M, Hamid A. Heat Transport Phenomena for the Darcy–Forchheimer Flow of Casson Fluid over Stretching Sheets with Electro-Osmosis Forces and Newtonian Heating. Mathematics. 2021; 9(19):2525. https://doi.org/10.3390/math9192525
Chicago/Turabian StyleZhang, Xianqin, Dezhi Yang, Muhammad Israr Ur Rehman, and Aamir Hamid. 2021. "Heat Transport Phenomena for the Darcy–Forchheimer Flow of Casson Fluid over Stretching Sheets with Electro-Osmosis Forces and Newtonian Heating" Mathematics 9, no. 19: 2525. https://doi.org/10.3390/math9192525
APA StyleZhang, X., Yang, D., Israr Ur Rehman, M., & Hamid, A. (2021). Heat Transport Phenomena for the Darcy–Forchheimer Flow of Casson Fluid over Stretching Sheets with Electro-Osmosis Forces and Newtonian Heating. Mathematics, 9(19), 2525. https://doi.org/10.3390/math9192525





