Stochastic Analysis of the RT-PCR Process in Single-Cell RNA-Seq
Abstract
:1. Introduction
2. Materials and Methods
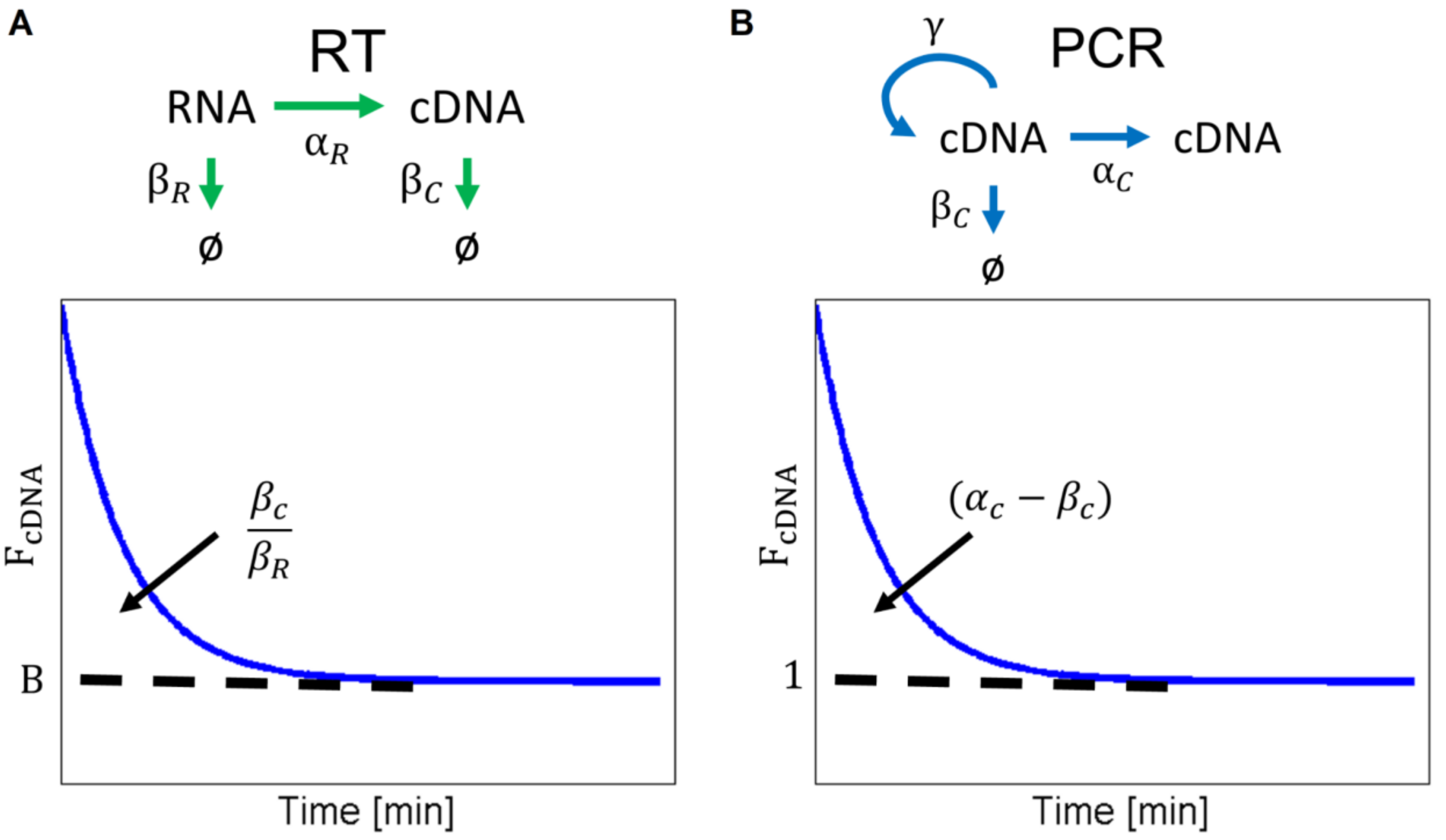
2.1. RT-PCR Model
2.2. Chemical Master Equation
2.3. Parameter Values
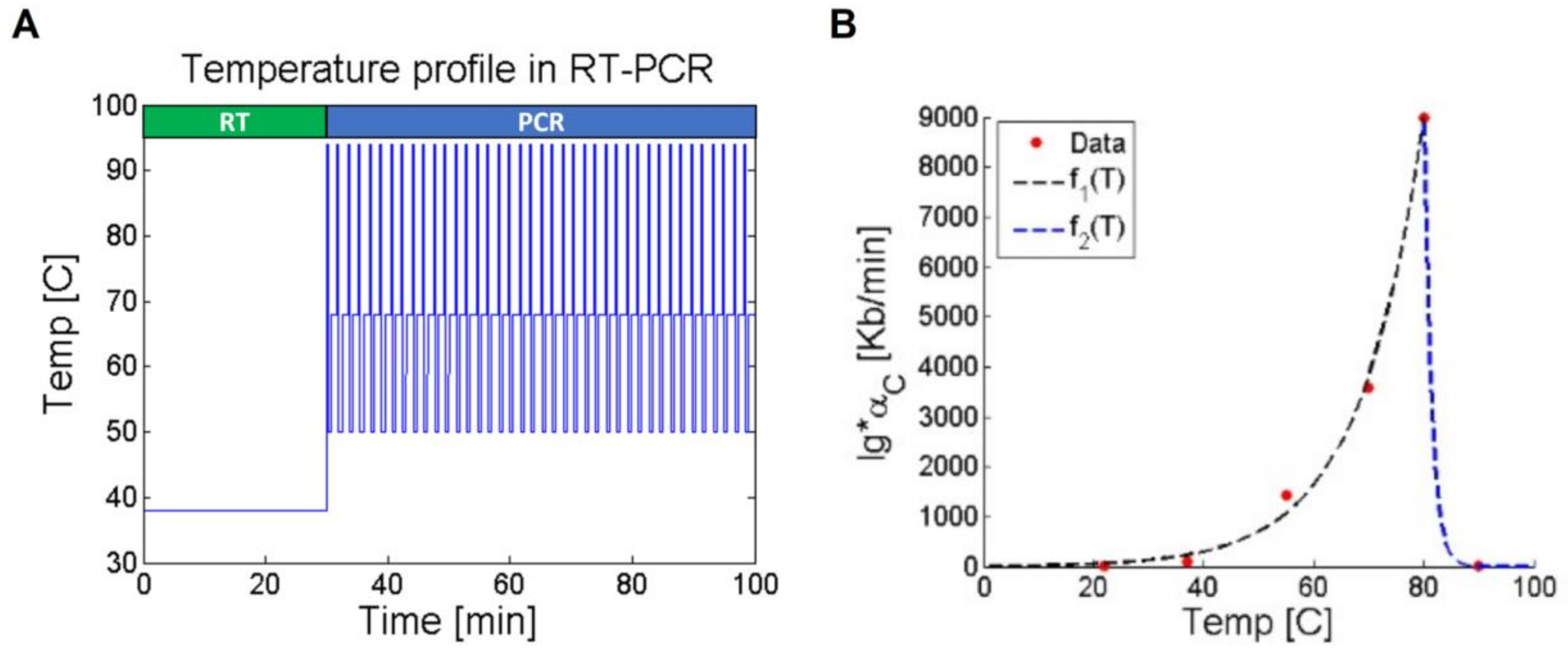
2.4. Temperature Considerations
2.5. Deterministic Solution
2.6. Simulation
3. Results
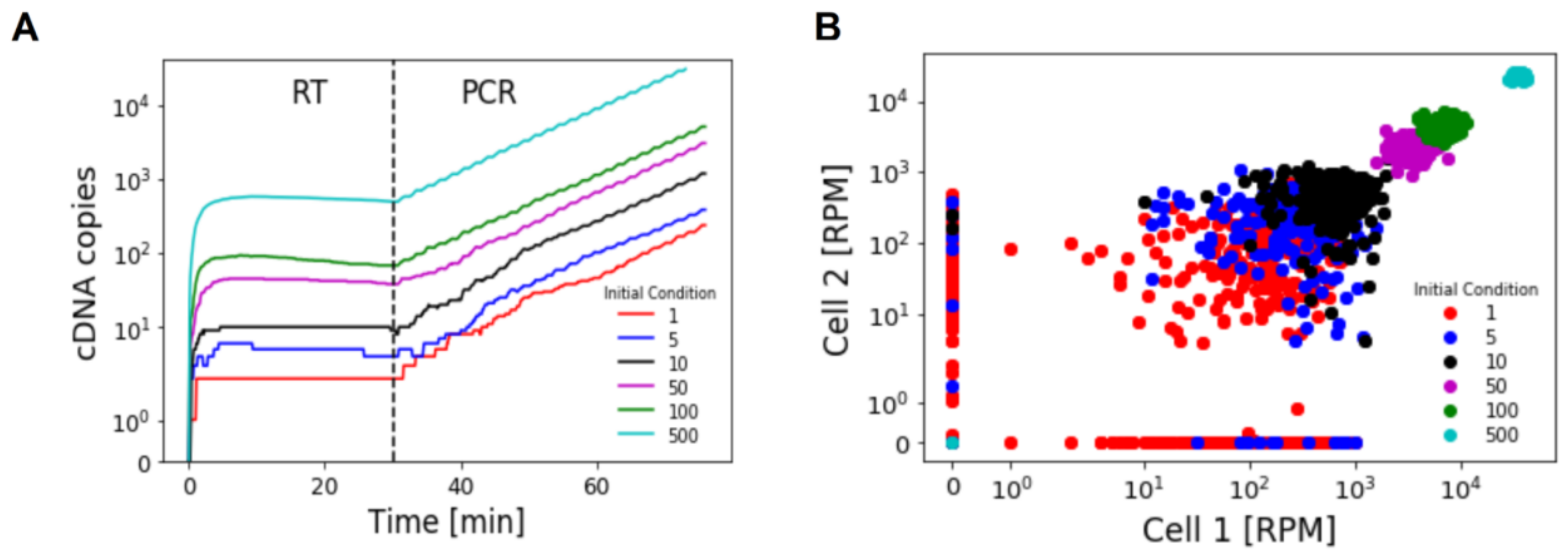
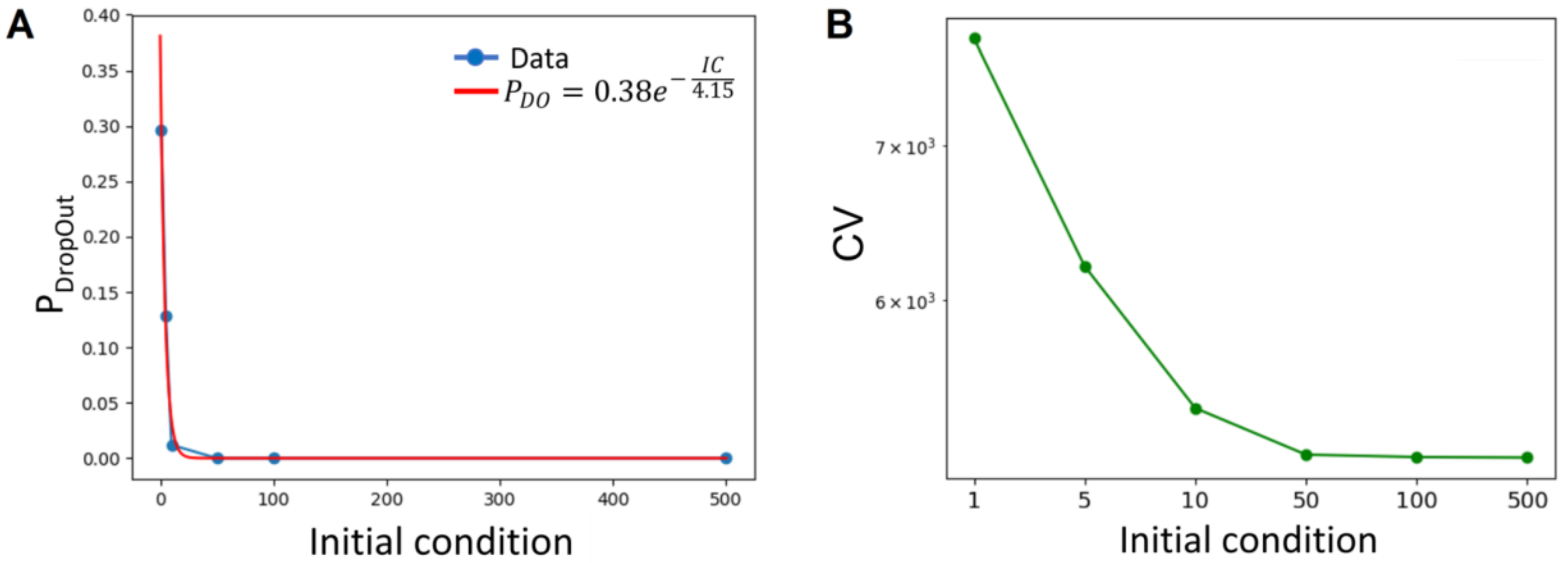
3.1. Numerical Solution of CME
3.2. Analytical Description
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Z.; Gerstein, M.; Snyder, M. RNA-Seq: A revolutionary tool for transcriptomics. Nat. Rev. Genet. 2009, 10, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Kashima, Y.; Sakamoto, Y.; Kaneko, K.; Seki, M.; Suzuki, Y.; Suzuki, A. Single-cell sequencing techniques from individual to multiomics analyses. Exp. Mol. Med. 2020, 52, 1419–1427. [Google Scholar] [CrossRef] [PubMed]
- Kharchenko, P.V.; Silberstein, L.; Scadden, D.T. Bayesian approach to single-cell differential expression analysis. Nat. Methods 2014, 11, 740–742. [Google Scholar] [CrossRef] [PubMed]
- Muciño-Olmos, E.A.; Vázquez-Jiménez, A.; De León, U.A.-P.; Matadamas-Guzman, M.; Maldonado, V.; López-Santaella, T.; Hernández-Hernández, A.; Resendis-Antonio, O. Unveiling functional heterogeneity in breast cancer multicellular tumor spheroids through single-cell RNA-seq. Sci. Rep. 2020, 10, 12728. [Google Scholar] [CrossRef] [PubMed]
- Robert, C.; Watson, M. Errors in RNA-Seq quantification affect genes of relevance to human disease. Genome Biol. 2015, 16, 177. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laehnemann, D.; Köster, J.; Szczurek, E.; McCarthy, D.; Hicks, S.; Robinson, M.D.; Vallejos, C.; Campbell, K.; Beerenwinkel, N.; Mahfouz, A.; et al. Eleven grand challenges in single-cell data science. Genome Biol. 2020, 21, 31. [Google Scholar] [CrossRef]
- Andrews, T.S.; Hemberg, M. False Signals Induced by Single-Cell Imputation. F1000Research 2018, 7, 1740. [Google Scholar] [CrossRef] [PubMed]
- Kharchenko, P.V. The triumphs and limitations of computational methods for scRNA-seq. Nat. Methods 2021, 18, 723–732. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, M.J.; Vila-Ortiz, G.J.; Salibe, M.C.; Podhajcer, O.L.; Pitossi, F.J. Model based analysis of real-time PCR data from DNA binding dye protocols. BMC Bioinform. 2007, 8, 85. [Google Scholar] [CrossRef]
- Pfaffl, M.W. A new mathematical model for relative quantification in real-time RT-PCR. Nucleic Acids Res. 2001, 29, e45. [Google Scholar] [CrossRef] [PubMed]
- Van Kampen, N.G. Stochastic processes. In Stochastic Processes in Physics and Chemistry, 3rd ed.; Elsevier: Amsterdan, The Netherlands, 2007; pp. 52–72. ISBN 9780444529657. [Google Scholar]
- Gillespie, D.T. Jump Markov processes with discrete states. In Markov Processes: An Introduction for Physical Scientists; Academic Press: San Diego, CA, USA, 1992; pp. 317–373. [Google Scholar] [CrossRef]
- Gillespie, D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Baudrimont, A.; Voegeli, S.; Viloria, E.C.; Stritt, F.; Lenon, M.; Wada, T.; Jaquet, V.; Becskei, A. Multiplexed gene control reveals rapid mRNA turnover. Sci. Adv. 2017, 3, e1700006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laguerre, S.; González, I.; Nouaille, S.; Moisan, A.; Villa-Vialaneix, N.; Gaspin, C.; Bouvier, M.; Carpousis, A.J.; Cocaign-Bousquet, M.; Girbal, L. Large-Scale Measurement of mRNA Degradation in Escherichia coli: To Delay or Not to Delay. Methods Enzymol. 2018, 612, 47–66. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.A.; Ezzeddine, N.; Shyu, A. Chapter 17 Messenger RNA Half-Life Measurements in Mammalian Cells. Methods Enzymol. 2008, 448, 335–357. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Innis, M.A.; Gelfand, D.H.; Sninsky, J.J.; White, T.J. PCR Protocols: A Guide to Methods and Applications; Academic Press: Cambridge, MA, USA, 2012; ISBN 9780080886718. [Google Scholar]
- Poulin, N.M.; Nielsen, T.O. Expression arrays: Discovery and validation. In Cell and Tissue Based Molecular Pathology; Churchill Livingstone: London, UK, 2009; pp. 70–83. ISBN 9780443069017. [Google Scholar]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Wohnhaas, C.T.; Leparc, G.G.; Fernandez-Albert, F.; Kind, D.; Gantner, F.; Viollet, C.; Hildebrandt, T.; Baum, P. DMSO cryopreservation is the method of choice to preserve cells for droplet-based single-cell RNA sequencing. Sci. Rep. 2019, 9, 10699. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vallejos, C.; Risso, D.; Scialdone, A.; Dudoit, S.; Marioni, J.C. Normalizing single-cell RNA sequencing data: Challenges and opportunities. Nat. Methods 2017, 14, 565–571. [Google Scholar] [CrossRef] [PubMed]
- Risso, D.; Ngai, J.; Speed, T.P.; Dudoit, S. Normalization of RNA-seq data using factor analysis of control genes or samples. Nat. Biotechnol. 2014, 32, 896–902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sambrook, J.; Russell, D.W. The Condensed Protocols from Molecular Cloning: A Laboratory Manual; Cold Spring Harbor Laboratory Press: New York, NY, USA, 2006; ISBN 9780879697716. [Google Scholar]
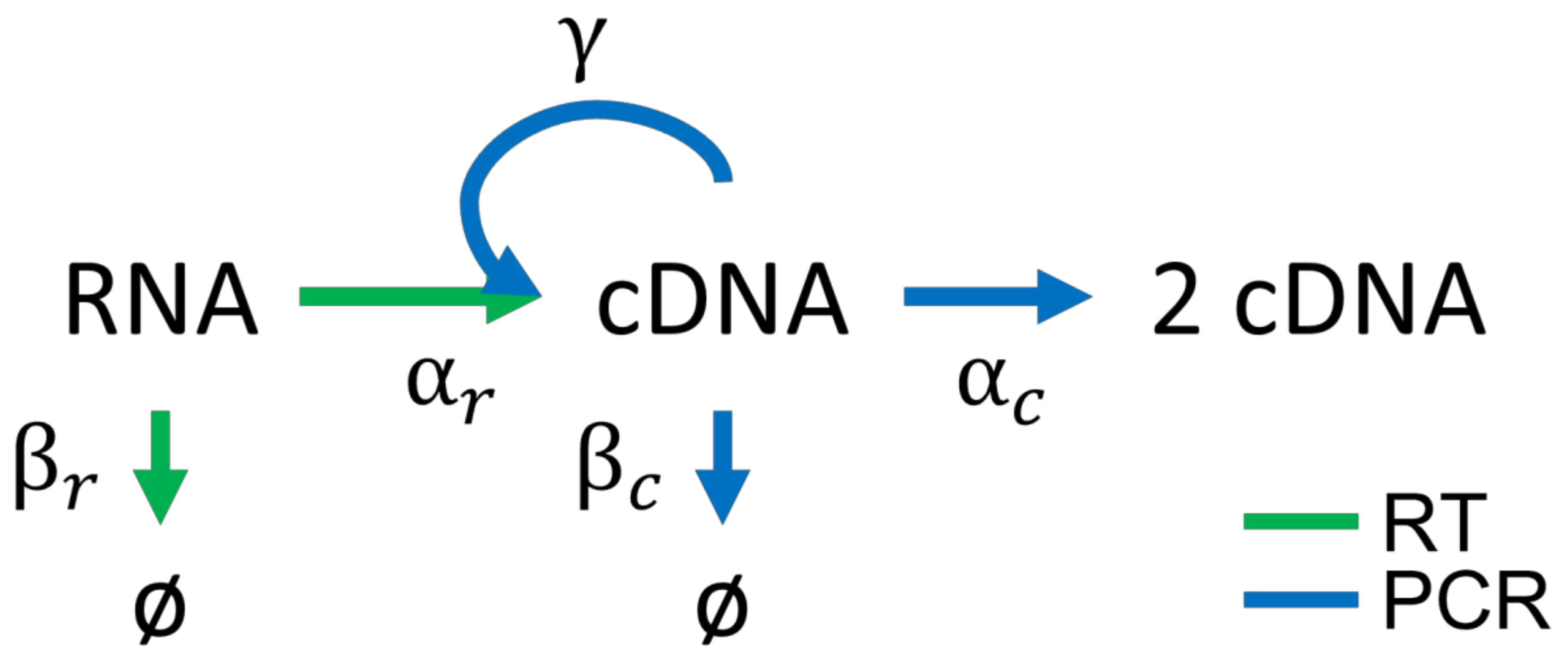

| Reaction | Propensities | Parameter Value | Description |
|---|---|---|---|
| Reverse Transcription | |||
| Reverse transcription. | |||
| Degradation of one RNA molecule. | |||
| Degradation of one cDNA molecule. | |||
| Polymerase Chain Reaction | |||
| Equation (5) | Synthesis of one cDNA molecule. | ||
| Deficient synthesis of one cDNA molecule | |||
| Degradation of the cDNA. | |||
| 1: INPUT: initial time , state and final time equal to ; |
| 2: SET: and ; |
| 3: WHILE: less than |
| 4: SET the temperature () value according to the Figure 2A profile; |
| 5: IF: less than |
| 6: SET: and equal to zero; |
| 7: ELSE |
| 8: SET equal to Equation (5); |
| 9: SET: count equal to zero; |
| 10: END IF |
| 11: DEFINE a as the sum of the propensities; |
| 12: DETERMINE the next jump τ given a; |
| 13: DETERMINE the next reaction to occur given a; |
| 14: UPDATE the system counts () and time (); |
| 15: END WHILE |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vázquez-Jiménez, A.; Resendis-Antonio, O. Stochastic Analysis of the RT-PCR Process in Single-Cell RNA-Seq. Mathematics 2021, 9, 2515. https://doi.org/10.3390/math9192515
Vázquez-Jiménez A, Resendis-Antonio O. Stochastic Analysis of the RT-PCR Process in Single-Cell RNA-Seq. Mathematics. 2021; 9(19):2515. https://doi.org/10.3390/math9192515
Chicago/Turabian StyleVázquez-Jiménez, Aarón, and Osbaldo Resendis-Antonio. 2021. "Stochastic Analysis of the RT-PCR Process in Single-Cell RNA-Seq" Mathematics 9, no. 19: 2515. https://doi.org/10.3390/math9192515
APA StyleVázquez-Jiménez, A., & Resendis-Antonio, O. (2021). Stochastic Analysis of the RT-PCR Process in Single-Cell RNA-Seq. Mathematics, 9(19), 2515. https://doi.org/10.3390/math9192515






