Investigation of Drift Phenomena at the Pore Scale during Flow and Transport in Porous Media
Abstract
:1. Introduction
Pore-Scale Radial Diffusion Models with Drift
2. Pore-Scale Fluid Flow and Transport of Tracer Model
Pore-Scale Convection–Diffusion Equation
3. Mathematical Formulation of Pore-Scale Radial Transport Equation with Linear Drifts
3.1. Formulation of Linear Drift
3.2. Pore-Scale Analytical Solution of Radial Transport Equation with Linear Drift
4. Analysis of Results
5. Conclusions
- An analytical solution to the radial transport of tracers in porous media under the influence of linear drift and radial convection at pore scale was developed. The introduction of Poiseuille velocity into the convection–dispersion equation makes it possible to investigate the drift phenomena at the pore-scale.
- The analysis we present in this work is consistent with the idea proposed by Akanji and Falade, 2019. However, this work extends it by incorporating the analytical solution to the Stokes equation. The solution to the resulting equation was used to describe the observed behaviour of the fluid over a full range of creeping flow regimes or Poiseuille velocities.
- Variation of dispersion coefficients from the solution was found to affect the concentration distribution even at low Reynolds number region.
- Linear drift effect at low creeping flow regime was found to affect tracer concentration distribution at a later time.
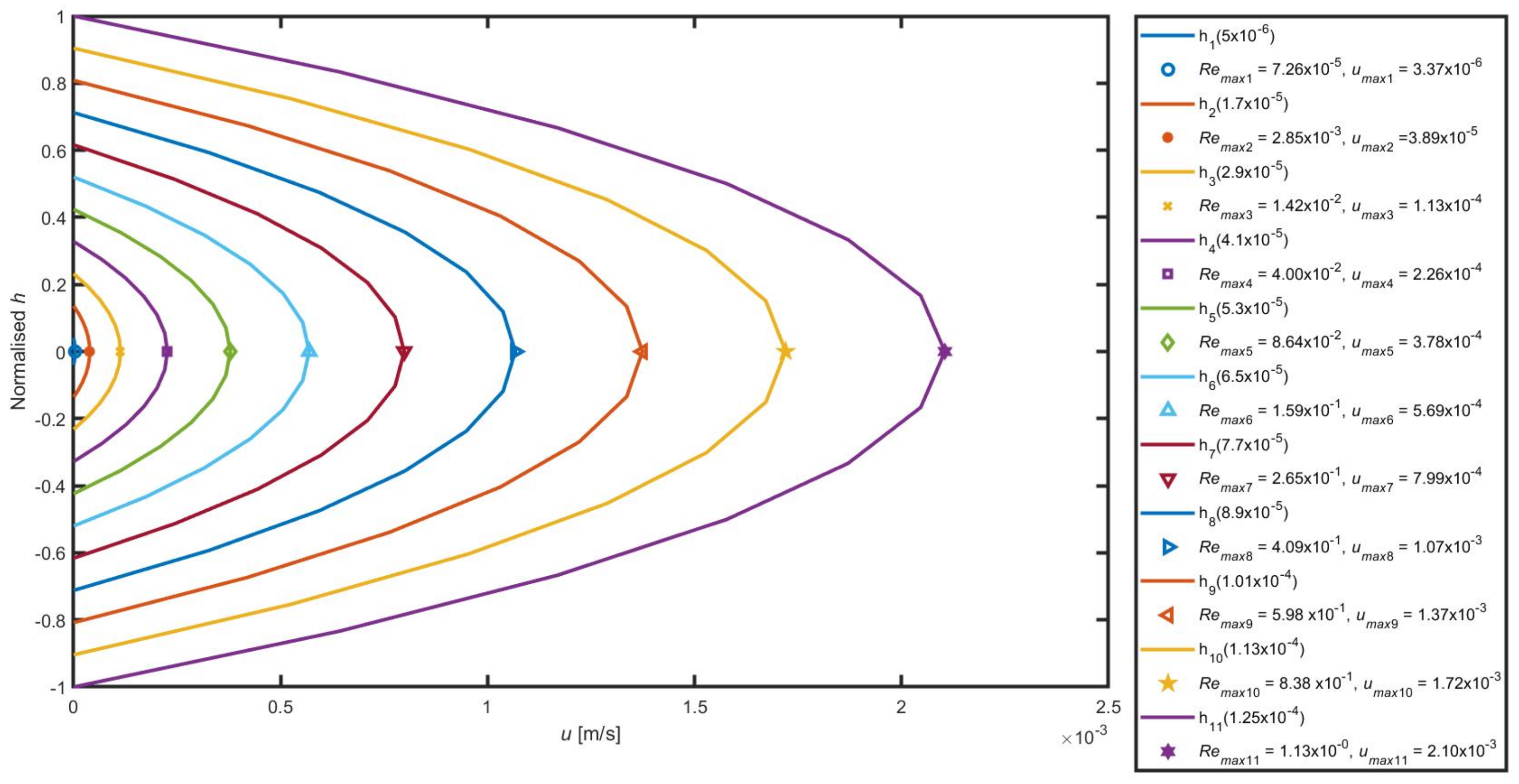
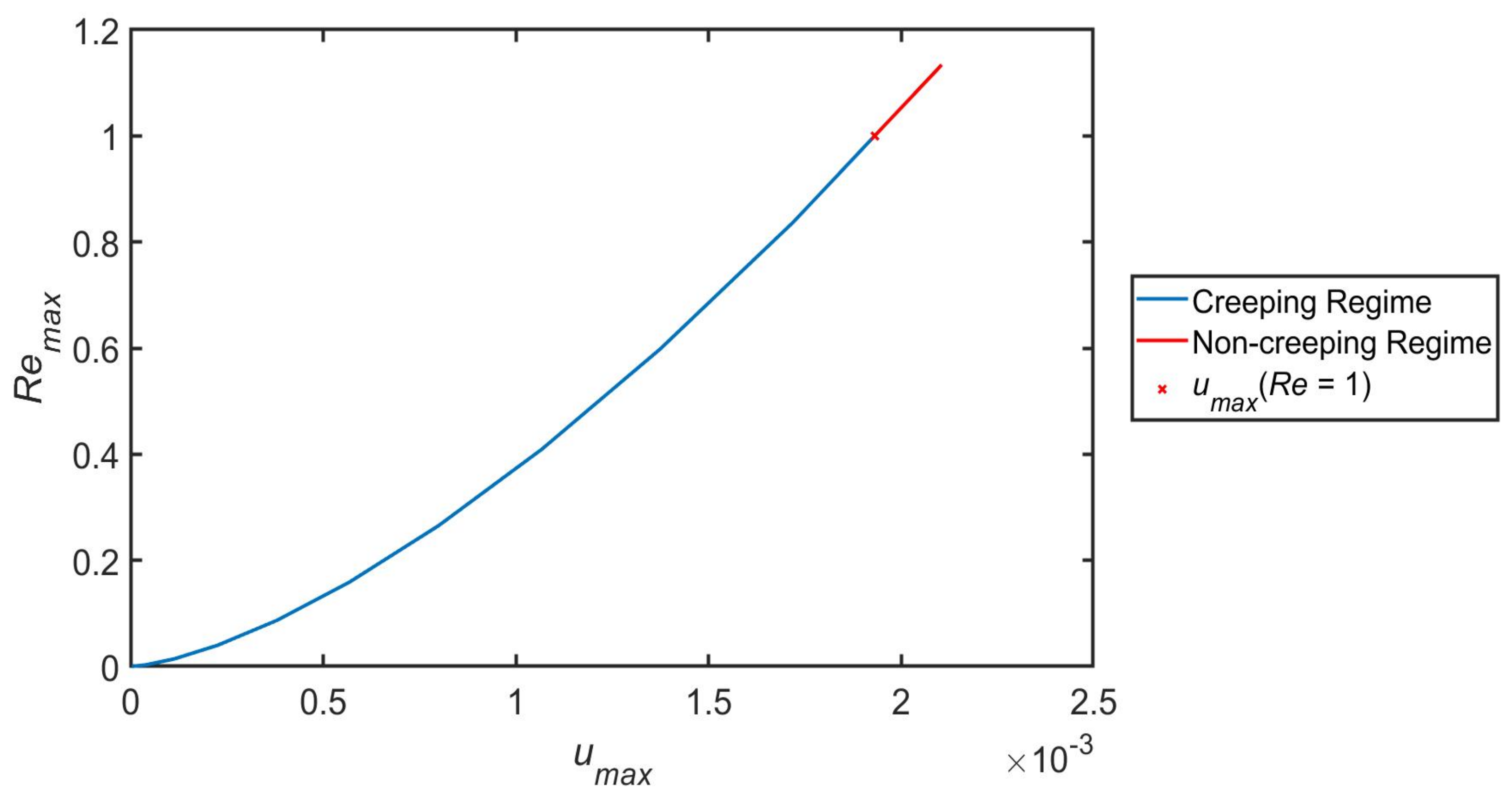
- Stokes flow approximation has been invoked and consequently the analysis of the results is valid in the limits of small Reynolds numbers of <1. However, the behaviour of the flow is likely to change for higher values of Reynolds number. The drift effect is then evaluated at a creeping flow regime. An increase in the flow velocity at the centre of the channel/porous media is noticed in all the cases from a creeping flow regime to a non-creeping flow regime.
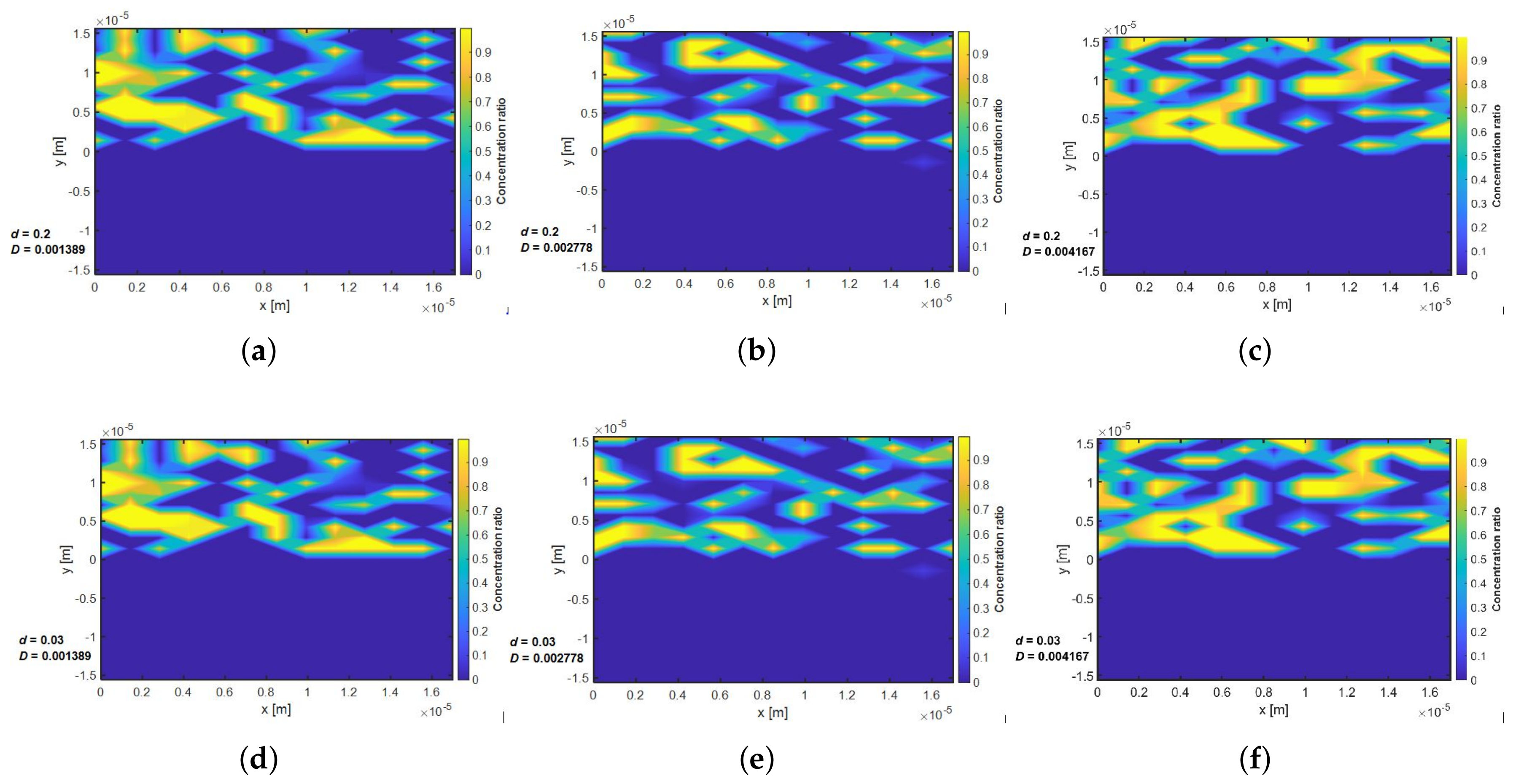
- The influence of linear drift on the concentration profile was evaluated in all the directions for a system with non-homogeneous porosity distribution and variable velocity profiles. Analysis of the results shows that the effect of linear drift on concentration profile depends on system heterogeneity and increases at later times.
- Flow velocities and concentration distribution data sets collected in this study proved to be essential and valuable for the development and testing of pore-scale numerical transport model under the influence of drift.
- This study can be used to identify the main transport path of tracers during enhanced oil recovery studies in porous media.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Chemical reaction constant, | |
| s | Laplace transform parameter |
| Gamma function | |
| Whittaker and Kummer functions parameters | |
| i | Unit vector along the x-axis |
| Concentration function | |
| j | Unit vector along the y-axis |
| k | Unit vector along the z-axis |
| L | Length of dispersion, (m) |
| Q | Injection rate, |
| Whittaker function with parameter | |
| Whittaker function with parameter | |
| Tricomi Kummer U-function with parameters (a,b,z) | |
| Absolute value of separation constant | |
| Porosity, dimensionless | |
| Angle, | |
| C | Tracer concentration |
| D | Flow hydrodynamic dispersion |
| d | Drift ratio |
| Molecular diffusion constant | |
| Shear mixing constant | |
| h | Channel thickness, in Nano-metre () |
| t | d |
| saturation of the mobile fluid phase | |
| u | Poiseuille velocity |
| r | Radial distance from the pore, (m) |
| Φ | Chromatographic response function |
| γ | Retardation constant |
Appendix A. Derivation of the Analytical Solution to the Navier–Stokes Equation
- Steady state, the transient acceleration term i.e = 0
- Unidirectional, pressure gradient is only in the X-direction and the plates are motionless.
- Velocity vector and the velocity gradient tensor are off-diagonal; therefore, the dot product is zero. Hence Equation (A1) reduces to:
Appendix B. Derivation of the Transport Flow Equation with Linear Drift
Appendix C. Transformation and Simplification of Pore-Scale Convection–Diffusion Equation to the General Whittaker Equation
Appendix D. Analytical Solution of Tracer Concentration and Its Weak-Form Solution
Appendix E. Analytical Solution—Dimensionless Representation and Inverse Laplace Transform
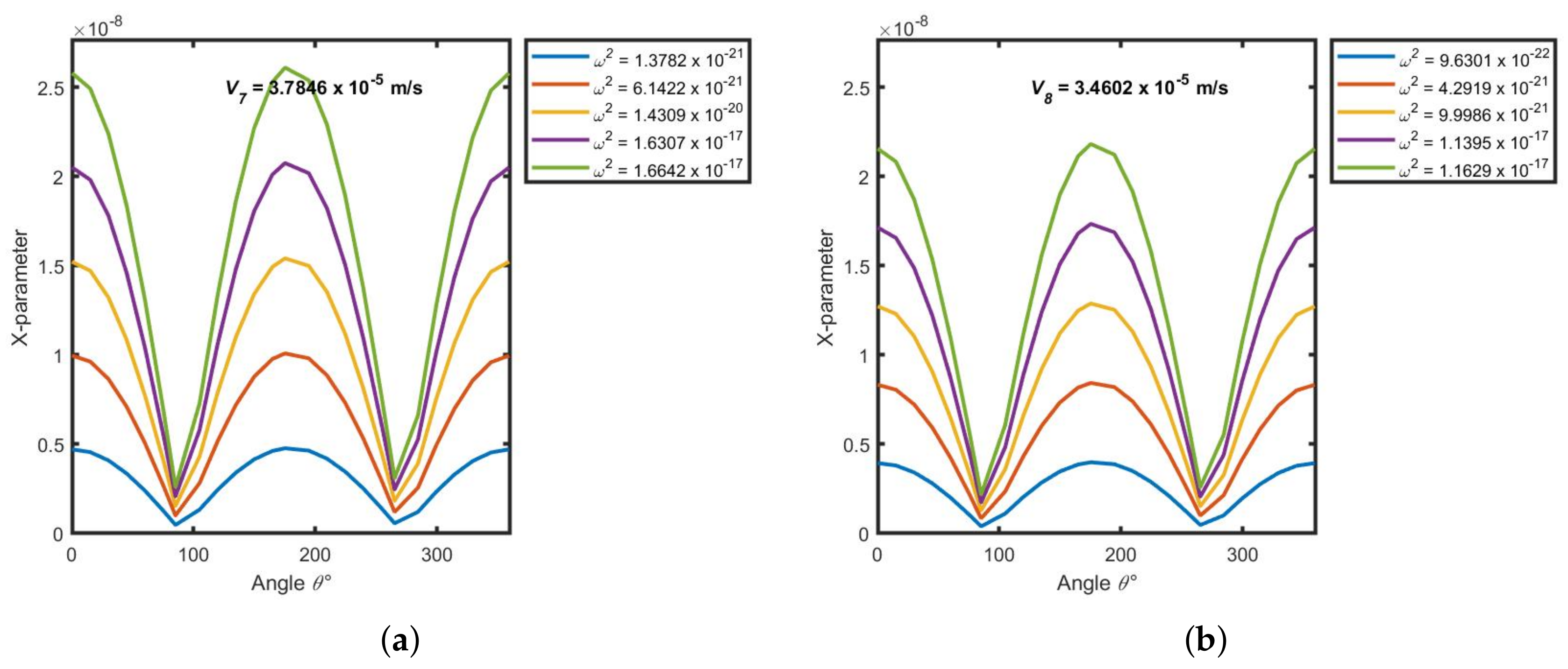
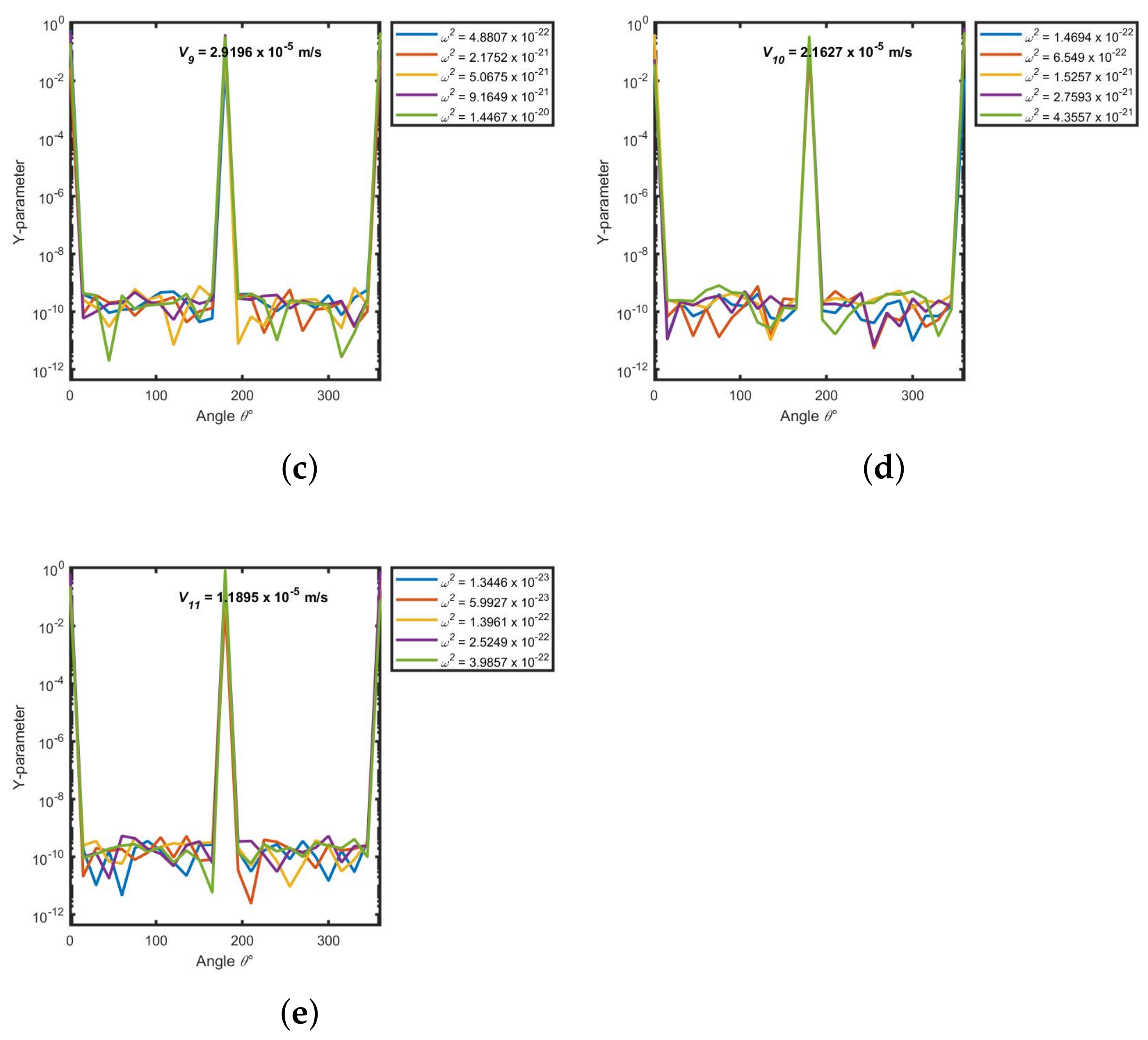
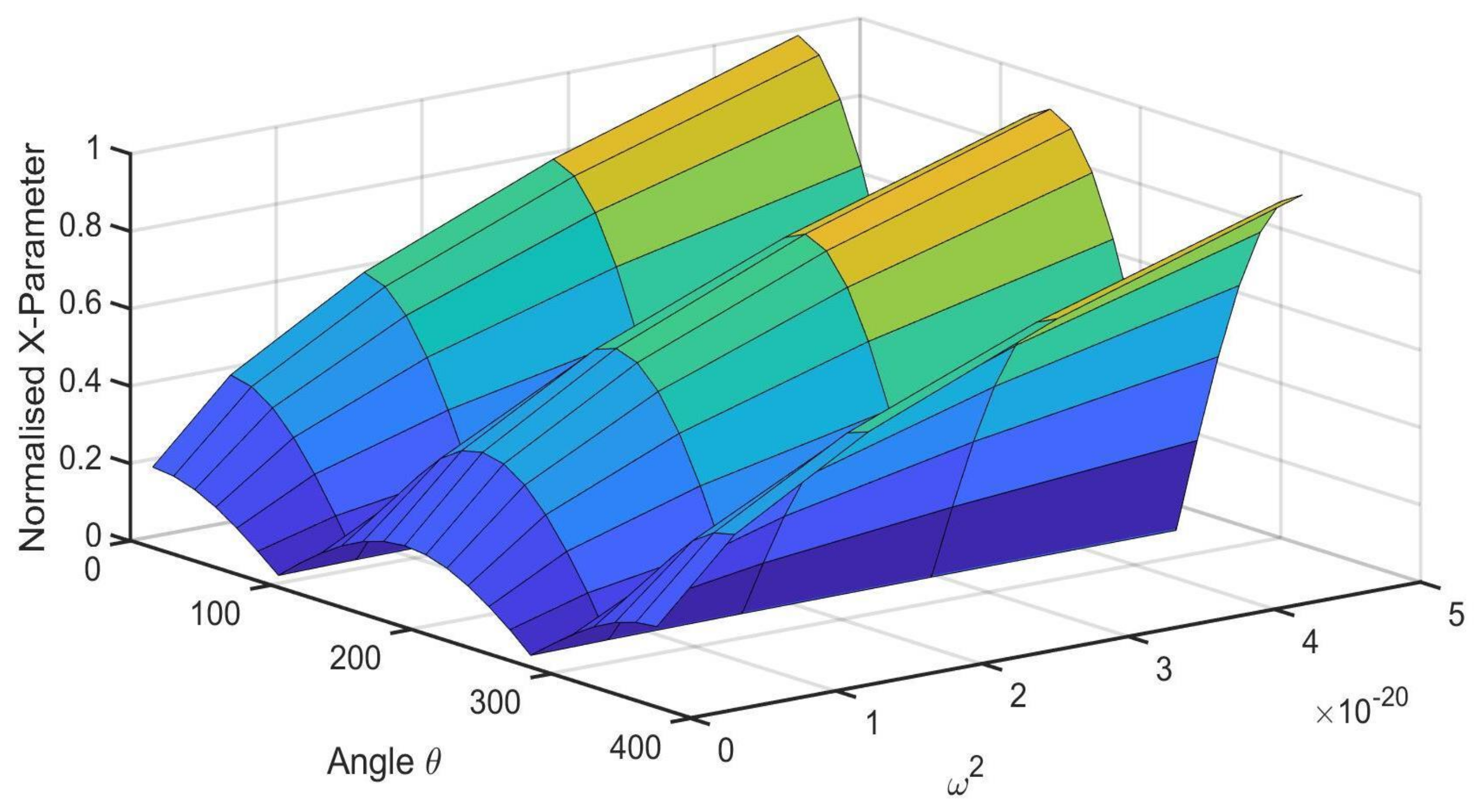
Appendix F. Symmetrical X-Parameter(Xp) and Y-Parameter (Yp) as a Function of Angle (θ) at a Thickness of h = 1.7 × 10−5 m, time t = 10 Days and Varying Separation Constant (ω2)


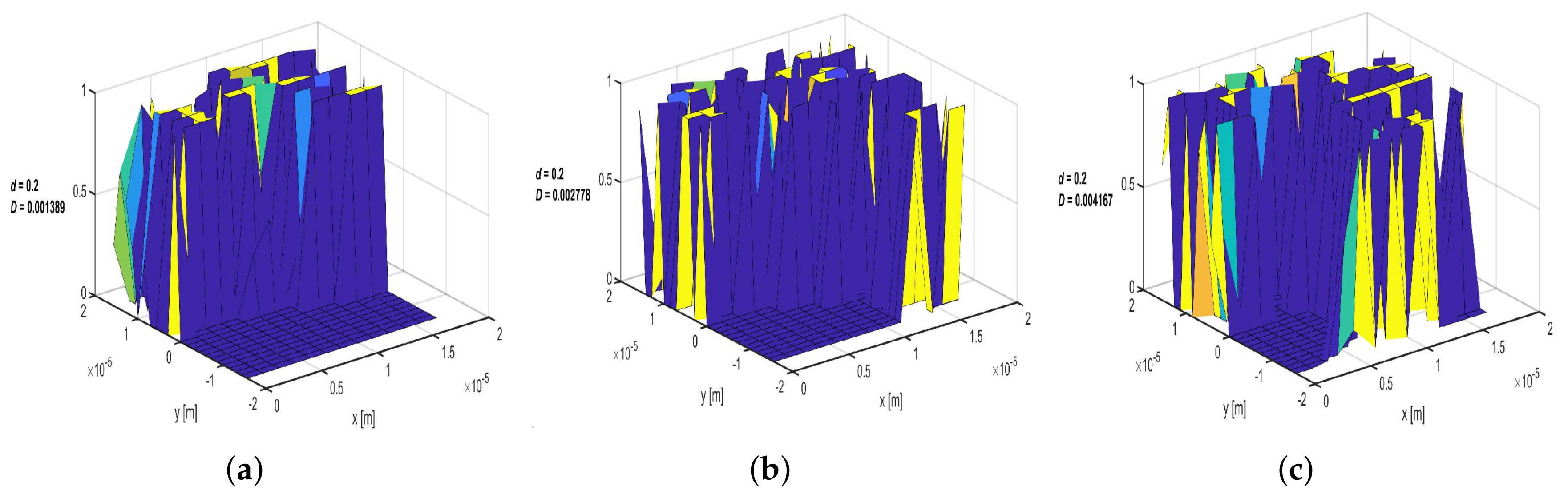
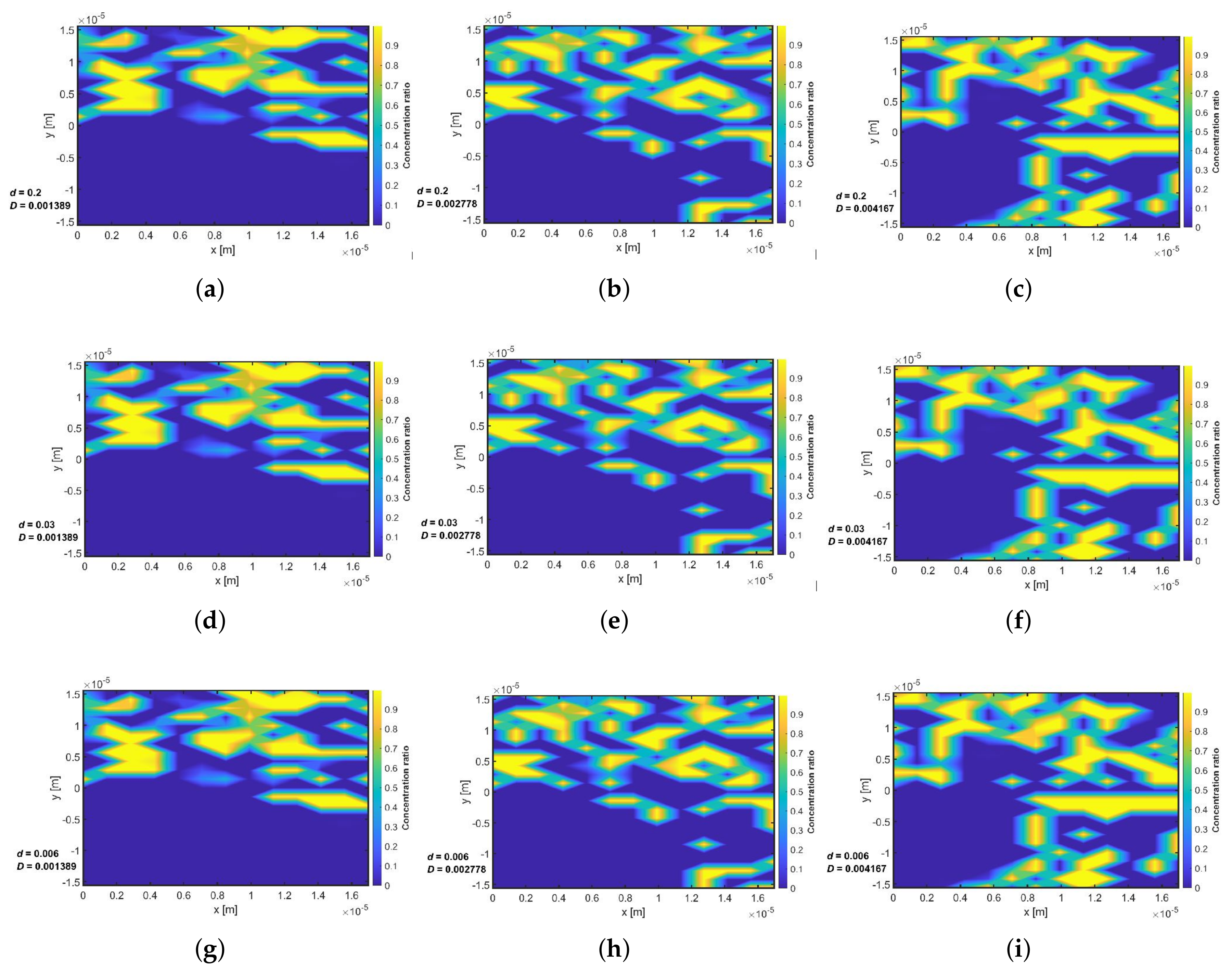
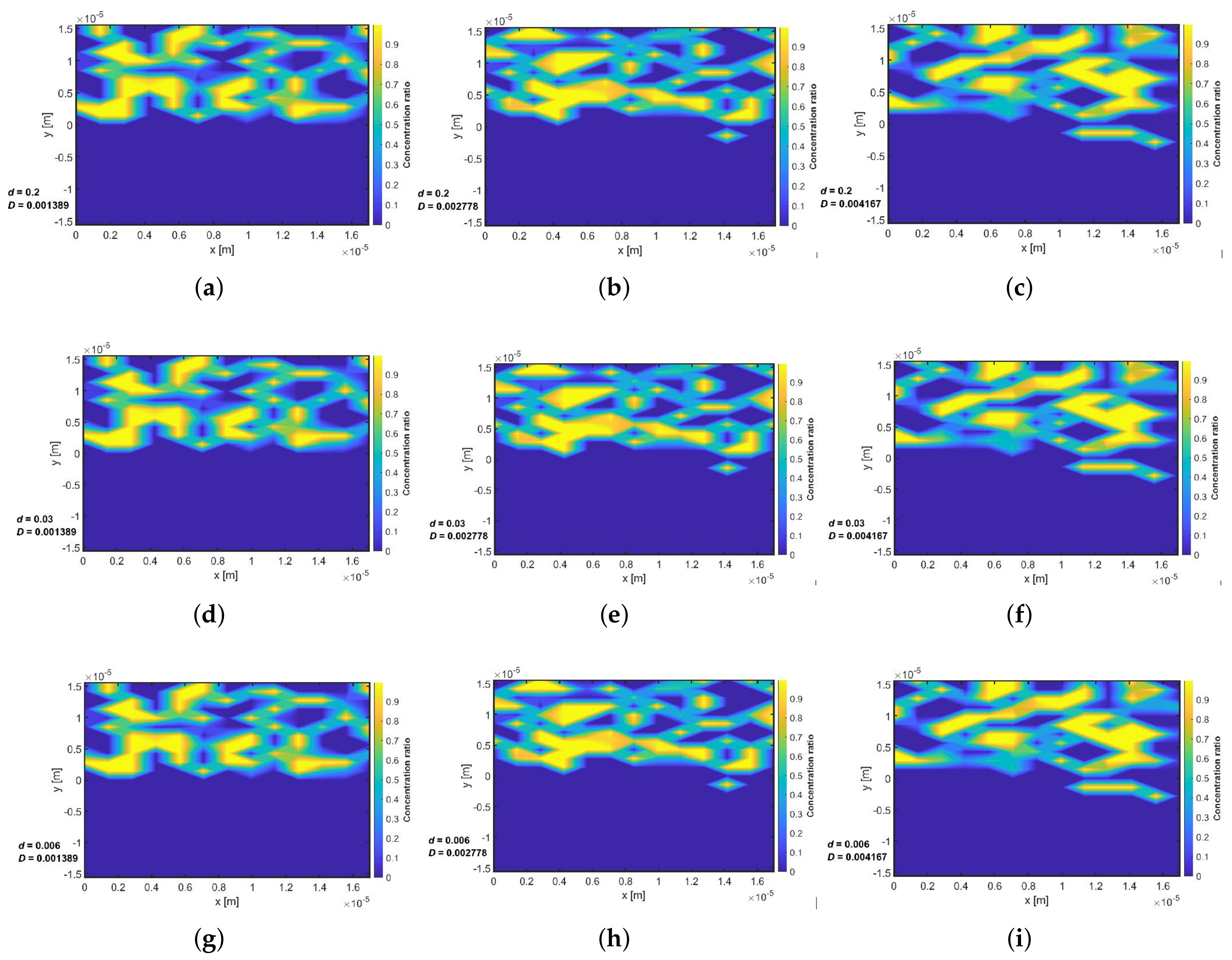
Appendix G. Concentration Distribution within the Porous Media with Linear Drift Ratio d = 0.006, 0.03 and 0.2 at Three Selected Time Intervals (t = 10, 50 and 70 Days) and a Variable Dispersion Coefficient of Do = 0.001389, 0.002778 and 0.004167 m2/s
Appendix G.1. 10 Days
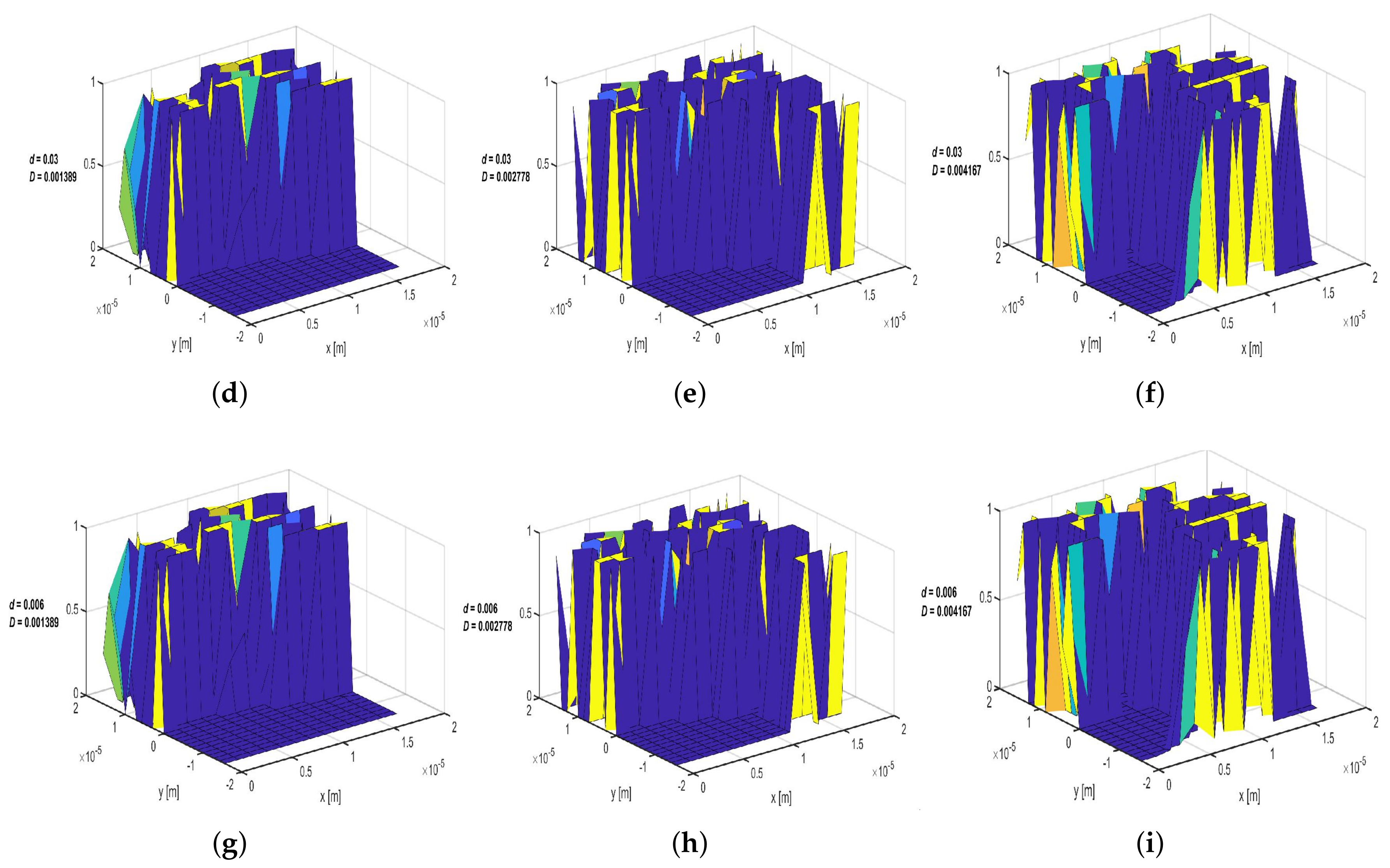
Appendix G.2. t = 50 Days
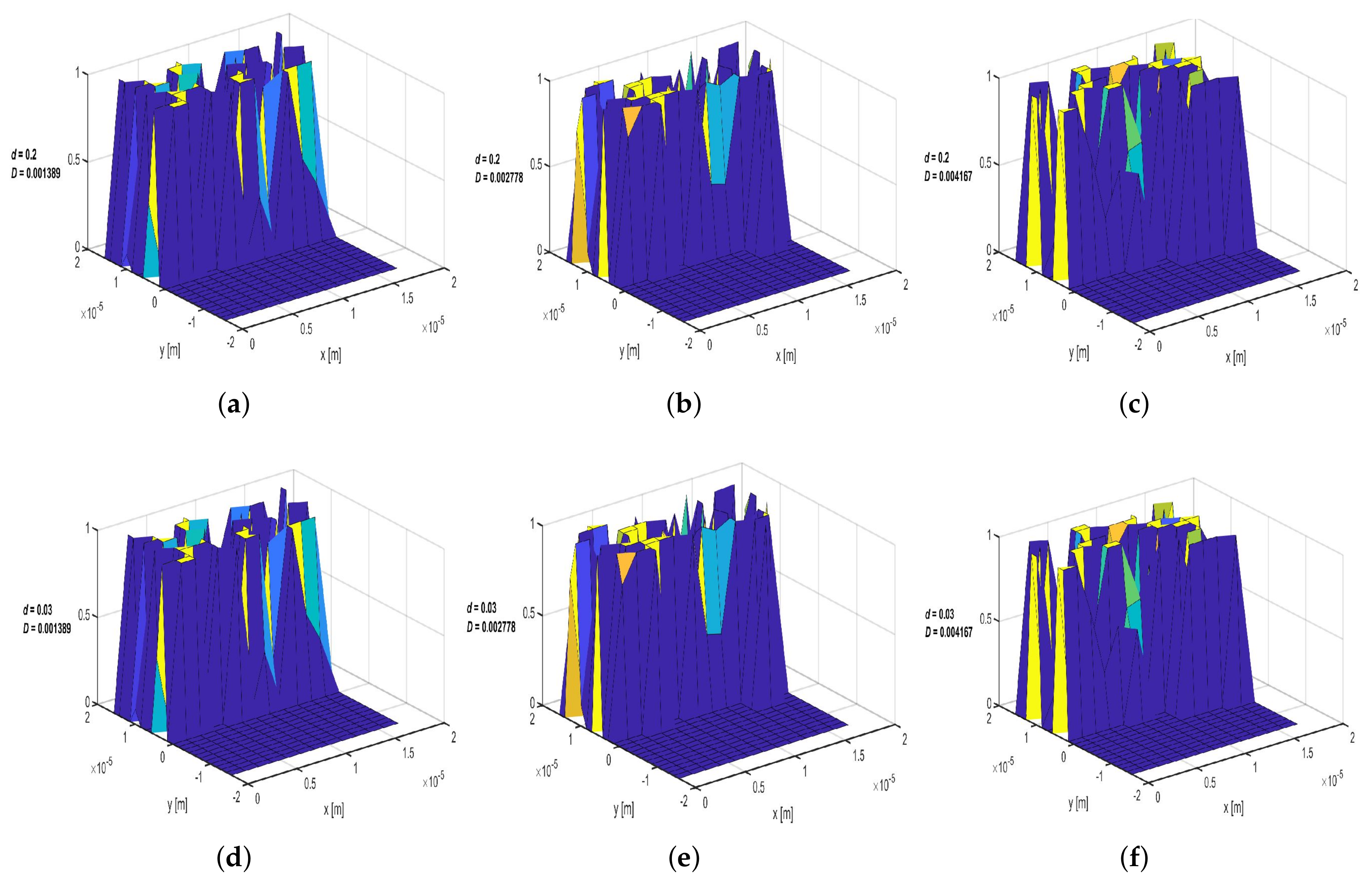
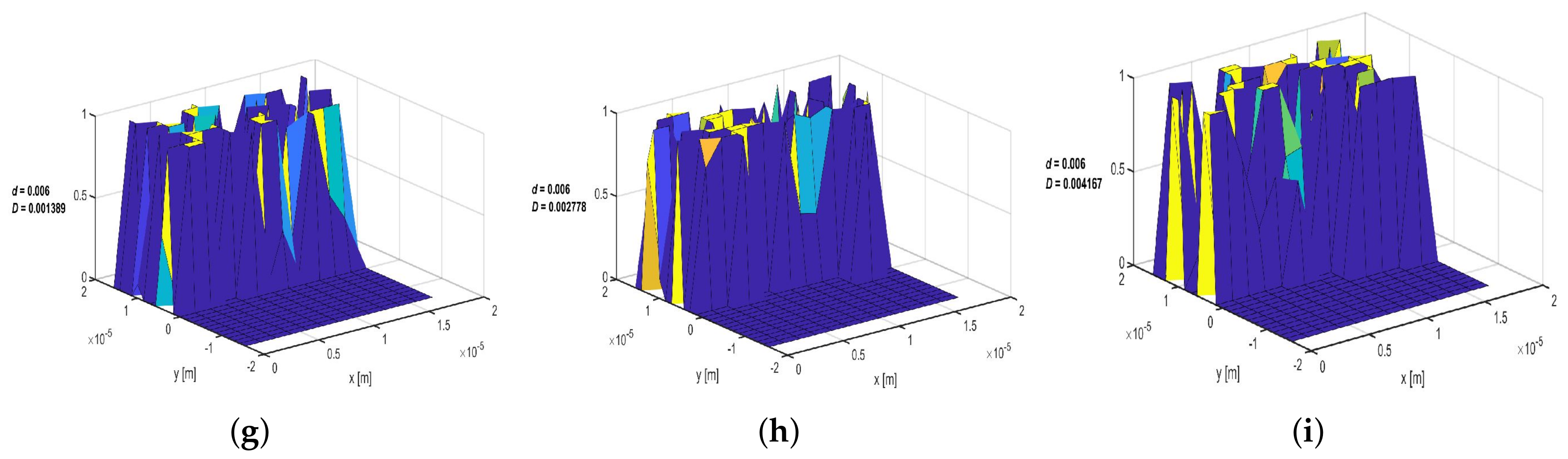
Appendix G.3. t = 70 Days

References
- Ghoraba, S.; Zyedan, B.; Rashwan, I. Solute transport modeling of the groundwater for quaternary aquifer quality management in Middle Delta, Egypt. Alex. Eng. J. 2013, 52, 197–207. [Google Scholar] [CrossRef] [Green Version]
- Bekins, B.; Rittmann, B.E.; MacDonald, J.A. Natural attenuation strategy for groundwater cleanup focuses on demonstrating cause and effect, Eos. Trans. Am. Geophys. Union 2001, 82, 53–58. [Google Scholar] [CrossRef] [Green Version]
- Offenwert, S.V.; Cnudde, V.; Bultreys, T. Pore-scale visualization and quantification of transient solute transport using fast microcomputed tomography. Water Resour. Res. 2019, 55, 9279–9291. [Google Scholar] [CrossRef] [Green Version]
- Axelsson, G. Tracer tests in geothermal resource management. In Proceedings of the EPJ Web of Conferences, Oslo, Norway, 6–8 June 2021; Volume 50 (EDP Sciences), p. 02001. [Google Scholar]
- Omofana, E. Effect of Linear Drift on Radial Transport of Tracer in Homogeneous Porous Media. Unpublished Master’s Thesis, African University of Science and Technology, Abuja, Nigeria, 2014; pp. 1–6. [Google Scholar]
- Dugstad, O. An Experimental Study of Tracers for Labelling of Injection Gas in Oil Reservoirs. Unpublished Ph.D. Thesis, University of Bergen, Bergen, Norway, 1992; pp. 1–2. [Google Scholar]
- Phirani, J.; Roy, S.; Pant, H. Predicting stagnant pore volume in porous media using temporal moments of tracer breakthrough curves. J. Petroleum Sci. Eng. 2018, 165, 640–646. [Google Scholar] [CrossRef]
- Dentz, M.; Borgne, T.L.; Englert, A.; Bijeljic, B. Mixing, spreading and reaction in heterogeneous media: A brief review. J. Contam. Hydrol. 2011, 120, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Hess, N.J.; Oostrom, M.; Celia, M.A.; Hilpert, M.; Kang, Q.; Pyrak-Nolte, L.J.; Scheibe, T.D.; Tartakovsky, A.M.; Werth, C.J.; Wildenschild, D.; et al. EMSL Pore Scale Modeling Challenge/Workshop; Tech. Rep.; (Pacific Northwest National Lab (PNNL): Richland, WA, USA, 2011. [Google Scholar]
- Milligen, B.P.V.; Bons, P.D. Analytical model for tracer dispersion in porous media. Phys. Rev. E 2012, 85, 01130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berezhkovskii, A.M.; Skvortsov, A.T. Aris-taylor dispersion with drift and diffusion of particles on the tube wall. J. Chem. Phys. 2013, 139, 084101. [Google Scholar] [CrossRef] [PubMed]
- Becker, M. Distinguishing advection, dispersion, and diffusion in fractured bedrock. In Proceedings of the U.S. EPA/NGWA Fractured Rock Conference: State of the Science and Measuring Success in Remediation, Portland, Maine, 13–15 September 2004; pp. 685–693. [Google Scholar]
- Mukahal, F.A.; Duffy, B.; Wilson, S. Advection and taylor—Aris dispersion in rivulet flow. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20170524. [Google Scholar] [CrossRef] [Green Version]
- Dorfman, K.D.; Brenner, H. Generalized taylor-aris dispersion in discrete spatially periodic networks: Microfluidic applications. Phys. Rev. E 2002, 65, 021103. [Google Scholar] [CrossRef]
- Vedel, S.; Bruus, H. Transient taylor-aris dispersion for time-dependent flows in straight channels. J. Fluid Mech. 2012, 691, 95. [Google Scholar] [CrossRef] [Green Version]
- Akanji, L.T.; Falade, G.K. Closed-form solution of radial transport of tracers in porous media influenced by linear drift. Energies 2019, 12, 29. [Google Scholar] [CrossRef] [Green Version]
- Kuttanikkad, S. Pore-Scale Direct Numerical Simulation of Flow and Transport in Porous Media. Ph.D. Thesis, Ruprecht-Karls-Universitt, Heidelberg, Germany, 2009. [Google Scholar]
- Godinez-Brizuela, O.E.; Niasar, V.J. Simultaneous pressure and electro-osmosis driven flow in charged porous media: Pore-scale effects on mixing and dispersion. J. Colloid Interface Sci. 2020, 561, 162–172. [Google Scholar] [CrossRef] [PubMed]
- Bear, J. Dynamics of Fluids in Porous Media; Courier Corporation: Washington, DC, USA, 2013. [Google Scholar]
- Scheibe, T.D.; Perkins, W.A.; Richmond, M.C.; McKinley, M.I.; Romero-Gomez, P.D.; Oostrom, M.; Wietsma, T.W.; Serkowski, J.A.; Zachara, J.M. Pore-scale and multiscale numerical simulation of flow and transport in a laboratory-scale column. Water Resour. Res. 2015, 51, 1023–1035. [Google Scholar] [CrossRef]
- Tsang, Y.; Tsang, C.; Neretnieks, I.; Moreno, L. Flow and tracer transport in fractured media: A variable aperture channel model and its properties. Water Resour. Res. 1988, 24, 2049–2060. [Google Scholar] [CrossRef]
- Attinger, S.; Abdulle, A. Effective velocity for transport in heterogeneous compressible flows with mean drift. Phys. Fluids 2008, 20, 016102. [Google Scholar] [CrossRef] [Green Version]
- Falade, G.; Brigham, W. Analysis of radial transport of reactive tracer in porous media. SPE Reserv. Eng. 1989, 4, 85–90. [Google Scholar] [CrossRef]
- Sanskrityayn, A.; Kumar, N. Analytical solution of advection–diffusion equation in heterogeneous infinite medium using green’s function method. J. Earth Syst. Sci. 2016, 125, 1713–1723. [Google Scholar] [CrossRef]
- Aichi, M.; Akitaya, K. Analytical solution for a radial advection–dispersion equation including both mechanical dispersion and molecular diffusion for a steady-state flow field in a horizontal aquifer caused by a constant rate injection from a well. Hydrol. Res. Lett. 2018, 12, 23–27. [Google Scholar] [CrossRef] [Green Version]
- Akanji, L.T.; Chidamoio, J. A finite-element algorithm for stokes flow through oil and gas production tubing of uniform diameter. Oil and Gas Science and Technology. Rev. IFP Energies Nouv. 2020, 75, 79. [Google Scholar]
- Ayuba, I.; Akanji, T.L.; Gomes, J.L. Velocity Dependence and Tracer Dispersion in Newtonian Fluids Undergoing Creeping Flow. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 2–4 August 2021. OnePetro. [Google Scholar]
- Drazin, P.G.; Riley, N. The Navier-Stokes Equations: A Classification of Flows and Exact Solutions; Cambridge University Press: Cambridge, UK, 2006; p. 334. [Google Scholar]
- Abate, J.; Whitt, W. The fourier-series method for inverting transforms of probability distributions. Queueing Syst. 1992, 10, 5–87. [Google Scholar] [CrossRef]
- Abate, J.; Whitt, W. Numerical inversion of laplace transforms of probability distributions. ORSA J. Comput. 1995, 7, 36–43. [Google Scholar] [CrossRef] [Green Version]
- Gaver, D.P., Jr. Observing stochastic processes, and approximate transform inversion. Oper. Res. 1966, 14, 444–459. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of laplace transforms [d5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Talbot, A. The accurate numerical inversion of laplace transforms. IMA J. Appl. Math. 1979, 23, 97–120. [Google Scholar] [CrossRef]
- Staben, M.E.; Zinchenko, A.Z.; Davis, R.H. Motion of a particle between two parallel plane walls in low-reynolds-number poiseuille flow. Phys. Fluids 2004, 15, 1711, Erratum in 2004, 16, 4206–4206. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayuba, I.; Akanji, L.T.; Gomes, J.L.; Falade, G.K. Investigation of Drift Phenomena at the Pore Scale during Flow and Transport in Porous Media. Mathematics 2021, 9, 2509. https://doi.org/10.3390/math9192509
Ayuba I, Akanji LT, Gomes JL, Falade GK. Investigation of Drift Phenomena at the Pore Scale during Flow and Transport in Porous Media. Mathematics. 2021; 9(19):2509. https://doi.org/10.3390/math9192509
Chicago/Turabian StyleAyuba, Ibrahim, Lateef T. Akanji, Jefferson L. Gomes, and Gabriel K. Falade. 2021. "Investigation of Drift Phenomena at the Pore Scale during Flow and Transport in Porous Media" Mathematics 9, no. 19: 2509. https://doi.org/10.3390/math9192509
APA StyleAyuba, I., Akanji, L. T., Gomes, J. L., & Falade, G. K. (2021). Investigation of Drift Phenomena at the Pore Scale during Flow and Transport in Porous Media. Mathematics, 9(19), 2509. https://doi.org/10.3390/math9192509





