Formulas, Algorithms and Examples for Binomial Distributed Data Confidence Interval Calculation: Excess Risk, Relative Risk and Odds Ratio
Abstract
1. Introduction
2. Research Aim
| Algorithm 1: Probability mass function (PMF) for binomial distribution, Equation (9). |
| Input:z, o //z←x or y, o←m or n |
| procedure PMF_B(z, o, &r) |
| If( = 0) |
| for(; ; ) ; if() else ; exit |
| EndIf |
| If() |
| for(; ; ) |
| Else |
| for(; ; ) |
| EndIf |
| for(; ; ) |
| for(; ; ) |
| end procedure |
| Output:r // or |
| Algorithm 2: Expression for ER, OR, RR (Equations (10)–(12)) as irreducible fraction. |
| Input: //x←x, m←m,y←y, n←n |
| procedure FR(a, b, &c, &d) |
| ; ; |
| If() if() ; ; exit EndIf |
| if() ; if() exit; if() |
| For(; ;) |
| ; ; //% is the modulo operator |
| EndFor //a is the greatest common divisor |
| ; // is irreducible fraction |
| end procedure |
| procedure ER(x, y, m, n, &c, &d) //excess risk, ER |
| FR(x*n - y*m, m*n, c, d) |
| end procedure // ER (Equation (10)) |
| procedure OR(x, y, m, n, &c, &d) //odds ratio, OR |
| FR(x*(n-y), y*(m-x), c, d) |
| end procedure // OR (Equation (11)) |
| procedure RR(x, y, m, n, &c, &d) //relative risk, RR |
| FR(x*n, y*m, c, d) |
| end procedure // RR (Equation (12)) |
| Output: // is a irreducible fraction |
| Algorithm 3: Bivariate binomial experiment, Equation (14). |
| Input:x, y, m, n, F //x←x, y←y, m←m, n←n, ER, OR or RR |
| procedure B2F(x, y, m, n, F, &p, &g, &h) |
| PMF_B(); PMF_B(); ; ; |
| For() For() |
| ; ; ; |
| EndFor EndFor |
| end procedure |
| Output: // probabilities; numerators; denominators |
| Algorithm 4: PMF for bivariate binomial expressions (B2E), Equation (15). |
| Input:k, p, g, h //k←k, p←p, g←g, h←h procedure PMF_B2E(&k, &p, &g, &h) procedure S0FR(l,r) ; ; For(; ;) for(; ; ); for(; ; ); If() ; ; EndIf EndFor if() ; if() end procedure ; ; ; ; For(; ;) For(; ;) if() ; if() ; EndFor ; ; ; ; EndFor ; ; ; end procedure Output: //k→k, p→p, g→g, h→h |
| Algorithm 5: CIs in increasing coverage for B2E. |
| Input:, , k, p, g, h //nu, de←de, k←mn, p←p, g←g, h←h function CC(&g, &h, k, i, j) ; If() if() ; endif; if() ; endif EndIf ; if() ; if() ; if() ; if() ; end function procedure CI_B2E(nu, de, &k, &p, &g, &h, &ci) ; for(; ; ) if(() AND ()) ; ; ; ; ; For(; ;) if() else ; ; ; ; if(() AND ()) if() ; ; ; endif if() ; ; ; endif If() ; ; ; ; EndIf if() ; ; ; endif if() ; ; ; endif EndFor end procedure Output: // array (ci_min, ci_max, coverage, 1-coverage) |
3. Background
- For an ideal gas, the value of a speed component (for instance x) takes (hypothetically) any value from , so () continuous Maxwell–Boltzmann distribution of particles by speed components is obtained, which is a Gaussian ( in Equation (7));
4. Material and Method
- Continuous asymptotic (normal) case, when CI is given by the inverse of the cumulative distribution function also called the percent-point function or quantile function: (where is the variance); for the occurrence of the proportion in a sample of size n, CI is ;
- Continuous non-asymptotic (student) case, proportion coming from a measurement through sampling of size m, when CI is given with Student t-value instead of the z-value: ; for the incidence in a sample of size n, CI is ;
- Discrete case, when a proportion comes from a sample in a (no matter how large) population, one needs to know the value of the binomial variable (x) and the sample size (m) in order to express its CI; it always becomes suitable to use the binomial distributed CI in the calculation; one of the first proposed CI is in [48] (, where ), and is its inverse—providing a CI at least as large as it is supposed to be and being most of the time too large; since the discreteness transforms the matter of integration (back) into a matter of summation and the calculation of each CI is a problem of combinatorics; there is no unique solution. One alternative is given in [9] and another one in [49], both of those alternatives have no analytical formula, only recipes (algorithms) leading to the solution.
- At least one continuous asymptotic (normal) case. When comparing two true values in a (very) large population (of an unknown size), then both proportions fall into the asymptotic continuous case; it may be suitable to use the z-value in the calculation (for studies involving z-value, z-statistics, z-test, see [50,51,52,53]);
- At least one continuous non-asymptotic (student) case. When comparing two true values obtained from a large number of repeated samplings (of known size) in a (very) large population, then both proportions fall into the continuous but not asymptotic case; it is much more suitable (than the call for the previous case) to use the Student t-value (for some typical cases, see [54,55,56,57]);
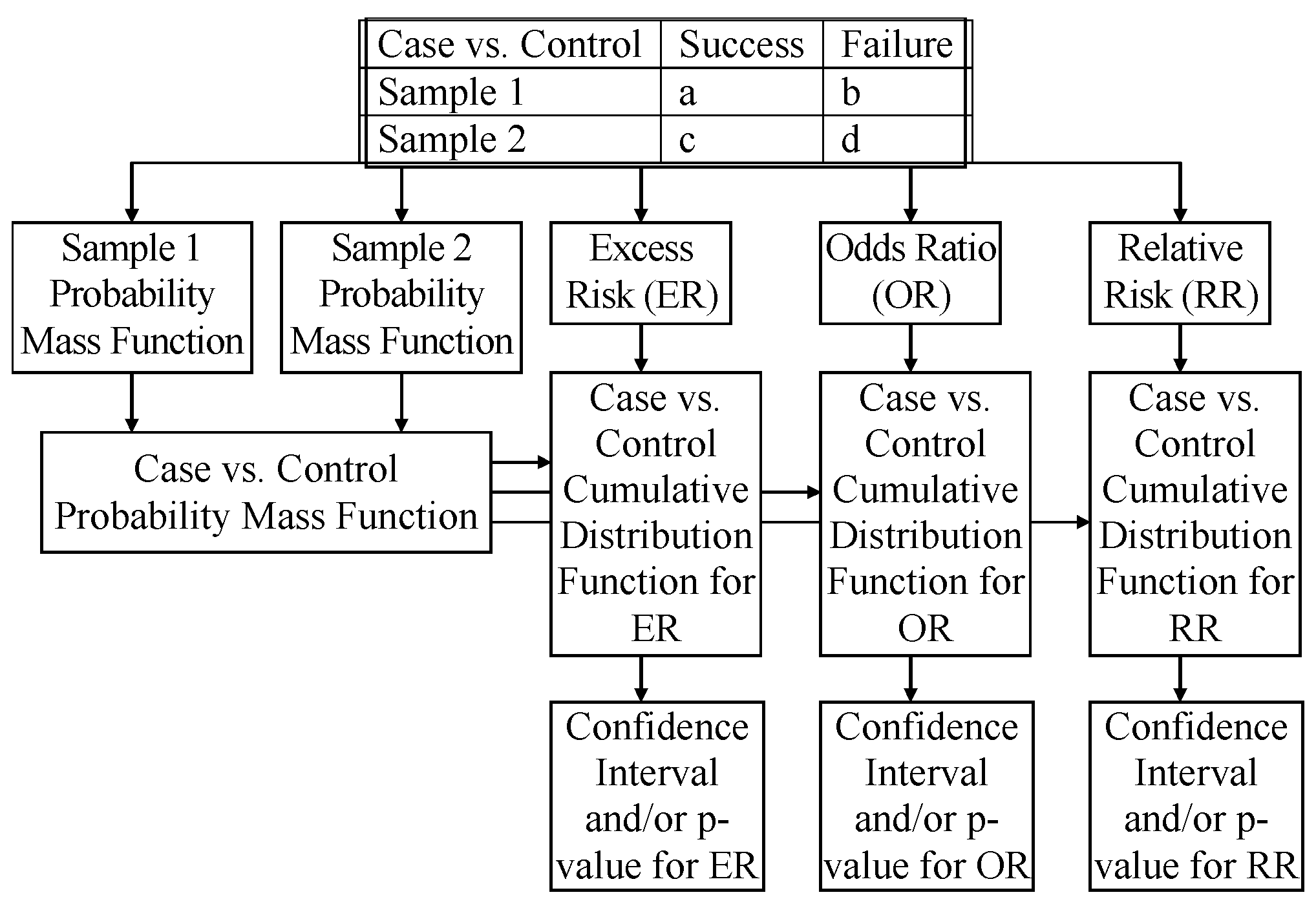
- 2 × 2 discrete case. In most of the cases, the results compared are coming from two samples (of necessary known sizes), when actually a bidimensional binomial distribution is involved and the probability for the difference is to be calculated from it [36]. This case is detailed in the next paragraph and in the remainder of the paper.
5. Results and Discussion
- It is not efficient to directly evaluate Equation (10); the complexity of the evaluation is and, for large values of the samples sizes (m and n), one will never see the result of the direct evaluation of Equation (10) (if for the evaluation takes 4 s, then for 10,000, it takes 40,000 s, which is over 11 h);
- It is not advisable to blindly use a recursion formula either (see, for example, the recursion formulas below, Equation (13)); for instance, for m = n = 300, x = 15 and y = 30, by using a recursion formula starting from and going to by using a series of recursion formulas (such as the ones in Equation (13)), one will evaluate everything to 0 in a double (8 bytes, 64 bits) floating point precision for the simple reason that is already lower () than the lowest absolute value on the scale () and is evaluated to 0 on any platform operating on IEEE 754 double-storage format;
- It is inefficient to use the general formula Equation (10) for the evaluation since for each u (or v) the same half-part (or , respectively) of it is used m (or n, respectively) times, thus inducing an inflation of the calculations by m (or n, respectively) times; it is much more convenient to evaluate (and store) the and probabilities first, and later to simply multiply them ().
5.1. The Expressions of Two Binomials and Their CIs
- If one wants a CI of (say, 5%) risk of being in error, then it may start from the pair cumulating the probability for and (it will always be a unique entry for it in , list, the one for which is the irreducible fraction of the expression subjected to analysis). Let’s label that index with (for instance = 13 in Table A4 since ER() = , = 10 in Table A5 since OR() = , and = 12 in Table A6 since RR() = ). Let us use a variable to cumulate the probability, (). The open interval (, ) contains exactly one possibility (when and ) and has the probability to appear ; thus, . By using two pointers ( and ) to move down () and up () the CI (, ) is expanded (when also , and when also ) until (and no further than) . Regarding the data given in Table A4, Table A5 and Table A6 as example, the CI is to be obtained (in each case) by summing the values for a block delimited by two boundaries; all the work is exemplified in the (next) series of three tables (Table 3 and Table A8).
- In order to gain a better understanding, another case is added here: the list of the successive expanding of the CI along with its CP. This is essentially the previous case with no stop limit and it is a more convenient arrangement of the data from Equation (15). Reviewing the described algorithm (Equation (16)):The example case listed in Table A4 (excess risk) is continued with the result of the above given recipe in Table 3. Examining entry 14 in Table 3, any interval between and will produce the closest to (and greater than) the 95% (probability) coverage (which is about 95.40%, see entry 14 in Table 3); similarly, if one wants a 2% risk of being in error (a 98% CI), one should look to the entry 16 in Table 3; if 1% is the accepted level of risk of being in error, then the answer is on line 18 in Table 3 and, finally, for 1‰the answer is in line 21 in Table 3.Moving on to the example cases listed in the appendix in Table A5 (OR) and in Table A6 (RR), the results of the above given recipe are listed in Table A7 and Table A8, respectively (in the appendix too). For both (OR and RR of (x = 2, y = 1, m = 6, n = 4) configuration), the CI at no more than 5% risk of being in error is identical with the ones at 2%, 1% and 1‱ covering all possible cases, (see entries 15 and 16 in Table A7 and 16 and 17 in Table A8).
- If someone wants to assess the probability of a no excess risk (ER, Equation (10), data arranged as in Equation (15)), that is the probability to pass through 0 trying to express the confidence; that is, in a much common language, the probability to be different from 0; then, the results given in the form of Equation (16) must be inspected. If ER () is positive, then any positive () will satisfy the requirement and the associated probability is and if ER < 0, then any < 0 will satisfy the requirement and the probability is . Inspecting Table 3, the last interval not containing 0 is at entry (iteration) 4, and its CP is 44.07%; the first interval containing 0 is at entry 5 in Table 3 and its CP is 51.47%; since the case of being 0 is the undesired, one should be excluded and, thus, the probability (for the excess risk, calculated at , to be different from 0 for (x = 2, y = 1, m = 6, n = 4) configuration) is the one given at entry 4 in Table 3, 44.07%.
- Similarly, if someone wants to assess the probability of different odds (OR, Equation (11), data arranged as in Equation (15)), then again the results given in the form of Equation (16) must be inspected. If OR > 1, then any > 1 will satisfy the requirement and the associated probability is and if OR < 1, then any < 1 will satisfy the requirement and the probability is . Inspecting Table A7, the last interval not containing 1 is at entry (iteration) 0, and its CP is 13.89%, thus giving a probability (for the OR, calculated at , to be greater than 1 for (x = 2, y = 1, m = 6, n = 4) configuration) of 13.89%.
- The same is for a non-equal risk (RR, Equation (12), data arranged as in Equation (15)), the results given in Equation (16) providing the answer. If RR > 1, then any > 1 will satisfy the requirement and the probability is and if RR < 1, then any < 1 will satisfy the requirement and the probability is . Inspecting Table A8, for the RR calculated at , the last interval not containing 1 is at entry (iteration) 1, thus giving a probability (for RR > 1 for the (x = 2, y = 1, m = 6, n = 4) configuration) of 15.98%.
5.2. The Needed Algorithms for CIs of the Expressions of Two Proportions
- Algorithm 1 calculates the binomial probability mass function; the results of and (B in Algorithm 1) are in Table 2;
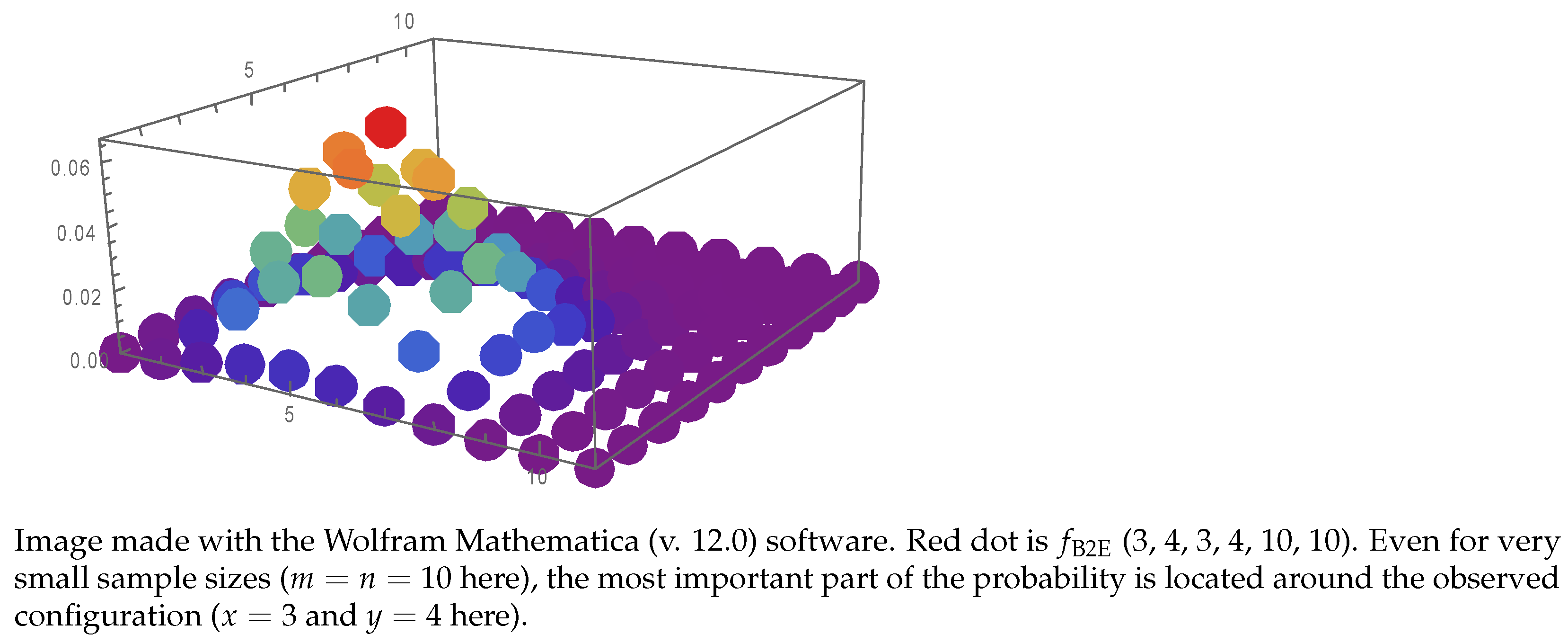
- Algorithm 3 collects all possible drawings from the bivariate binomial distribution and pairs the probabilities with one (at the time) defined function operating on binomial proportion; the output of is a entries list (Equation (14)); the output of for F ← ER is listed in Table A1, F ← OR in Table A2, and F ← RR in Table A3;
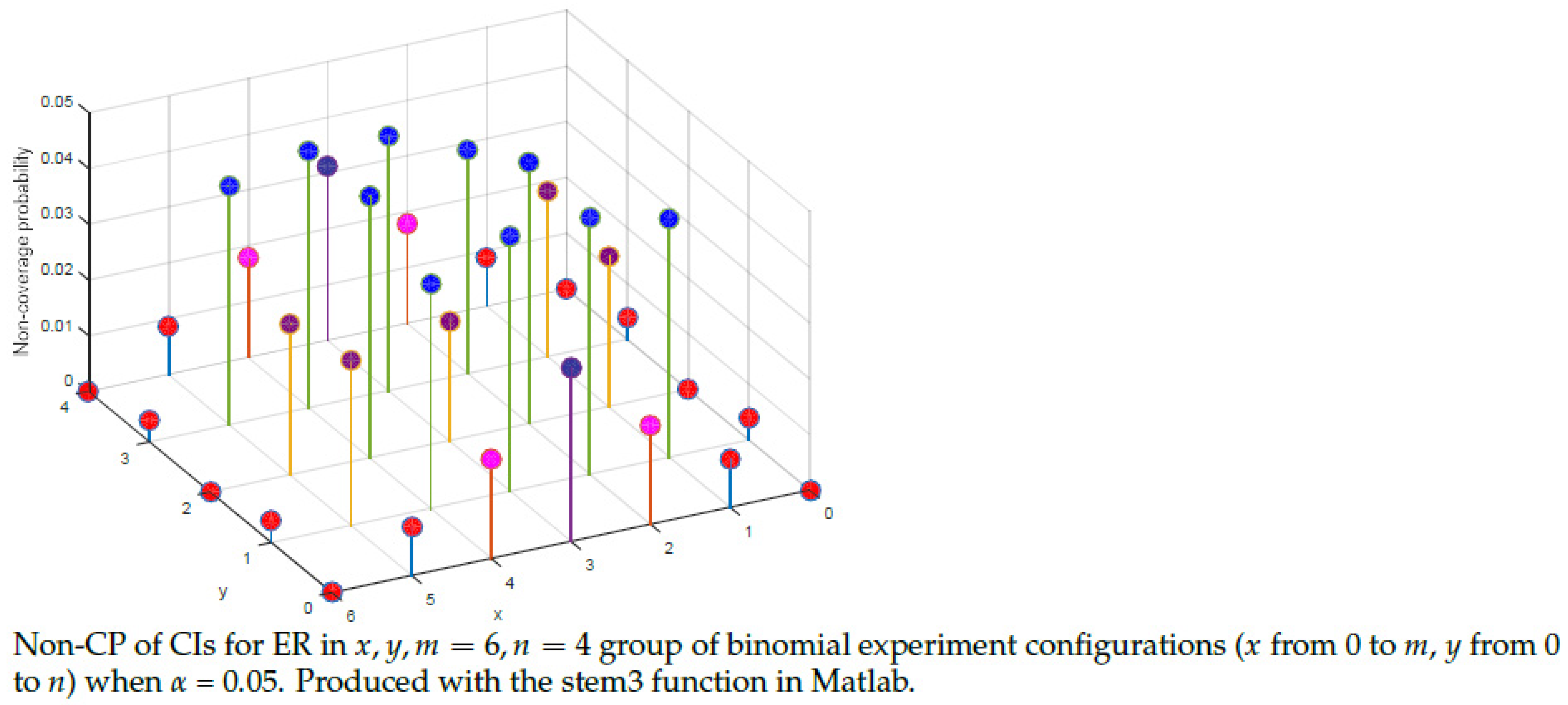
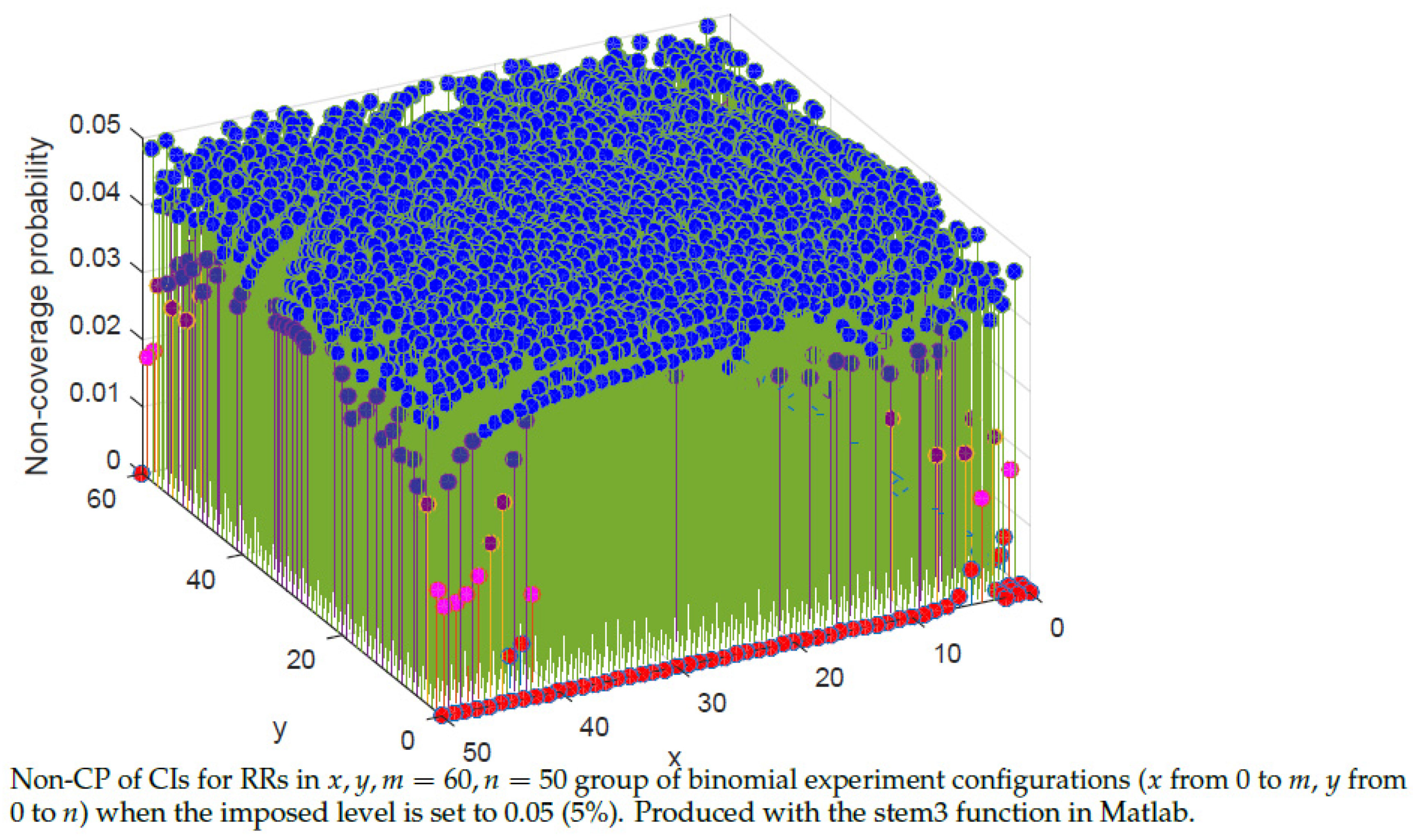
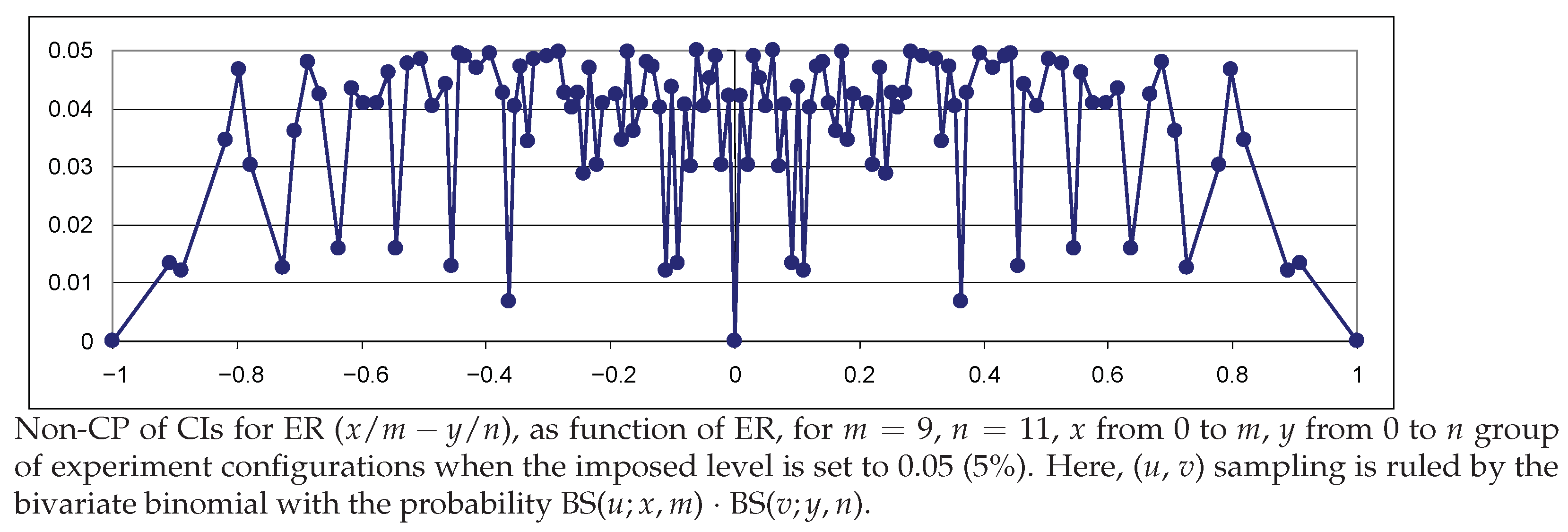
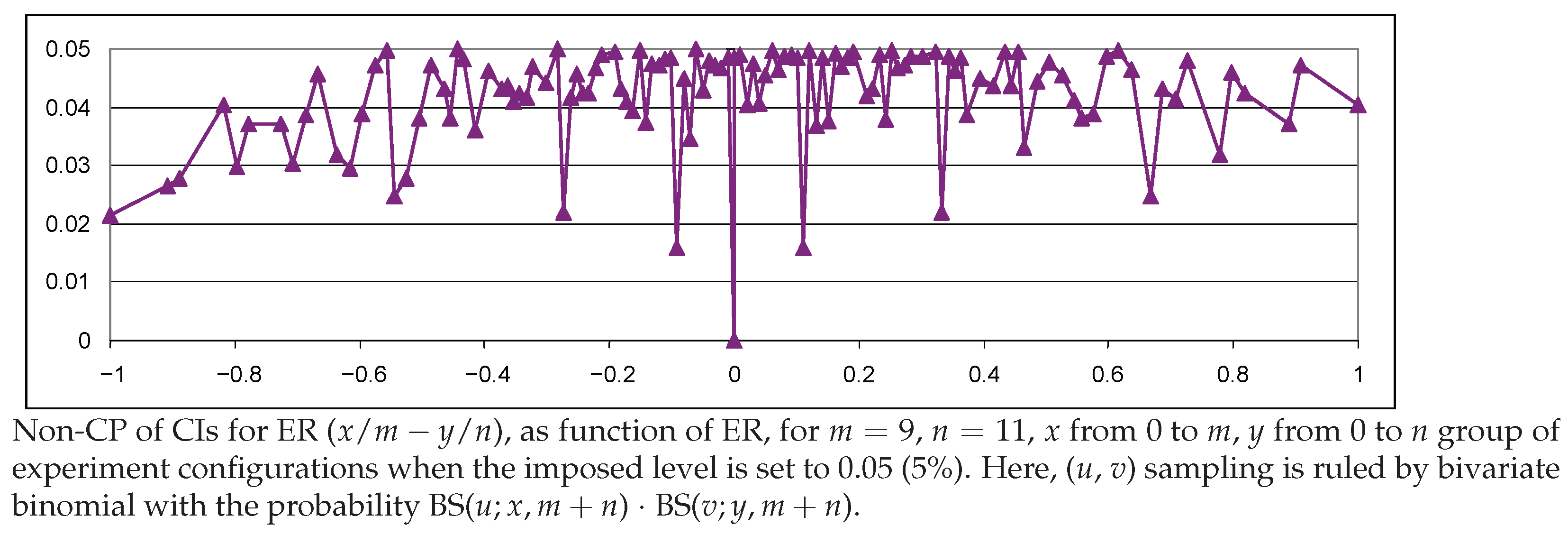
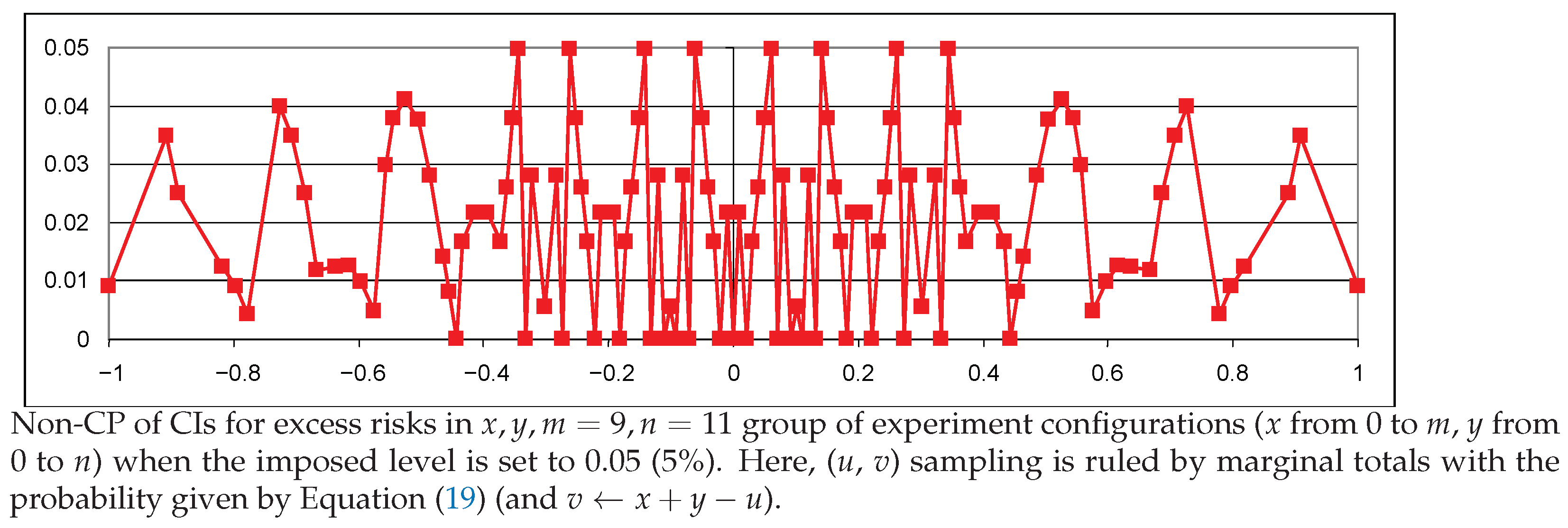
5.3. Properties of the CIs
5.4. General Discussion
- To collect all possible drawings and their associated probabilities (by using a possibly modified form of from Algorithm 3) for one (at the time) defined function F (ER, Equation (10), ; OR, Equation (11), ; RR, Equation (12), –all defined in Algorithm 2); the result is formally defined by Equation (14);
- Sort and group values and their associated probabilities (construct the probability mass function with PMF_B2E(k,p,g,h) from Algorithm 4); the result is formally defined by Equation (15);
- Construct the cumulative distribution function from which the CIs in increasing coverage (with and from the evaluation of the selected (one of ER, OR, and RR) defined function (with from Algorithm 5); the result is formally defined by Equation (16).
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Appendix A
| u vs. v | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 1 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 2 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 3 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 4 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 5 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 6 | (, ) | (, ) | (, ) | (, ) | (, ) |
| u vs. v | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 1 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 2 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 3 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 4 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 5 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 6 | (, ) | (, ) | (, ) | (, ) | (, ) |
| u vs. v | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 1 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 2 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 3 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 4 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 5 | (, ) | (, ) | (, ) | (, ) | (, ) |
| 6 | (, ) | (, ) | (, ) | (, ) | (, ) |
| j | Group j | j | Group j | j | Group j | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | {} | 9 | {, } | 17 | {} | ||||||
| 2 | {} | 10 | {, } | 18 | {, } | ||||||
| 3 | {} | 11 | {, } | 19 | {} | ||||||
| 4 | {} | 12 | {, , } | 20 | {} | ||||||
| 5 | {} | 13 | {, } | 21 | {} | ||||||
| 6 | {, } | 14 | {, } | 22 | {} | ||||||
| 7 | {} | 15 | {, } | 23 | {} | ||||||
| 8 | {, } | 16 | {, } |
| j | Group j | j | Group j | j | Group j | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Group 0 | 7 | {} | 13 | {} | ||||||
| 2 | {} | 8 | {} | 14 | {} | ||||||
| 3 | {} | 9 | {, , } | 15 | {} | ||||||
| 4 | {} | 10 | {} | 16 | {} | ||||||
| 5 | {} | 11 | {} | 17 | Group 17 | ||||||
| 6 | {} | 12 | {} |
| j | Group j | j | Group j | j | Group j | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | {, , , } | 7 | {, , , } | 13 | {} | ||||||
| 2 | {} | 8 | {} | 14 | {, } | ||||||
| 3 | {} | 9 | {} | 15 | {} | ||||||
| 4 | {, } | 10 | {, , } | 16 | {} | ||||||
| 5 | {} | 11 | {} | 17 | {} | ||||||
| 6 | {} | 12 | {, , } | 18 | {, , , , , } |
| i | MinCI | MaxCI | i | MinCI | MaxCI | i | MinCI | MaxCI | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.1389 | 0.8611 | 6 | 0.4632 | 0.5368 | 12 | 0.6653 | 0.3347 | ||||||
| 1 | 0.2130 | 0.7870 | 7 | 0.4787 | 0.5213 | 13 | 0.6688 | 0.3312 | ||||||
| 2 | 0.2168 | 0.7832 | 8 | 0.4910 | 0.5090 | 14 | 0.7035 | 0.2965 | ||||||
| 3 | 0.3279 | 0.6721 | 9 | 0.5546 | 0.4454 | 15 | 0.7104 | 0.2896 | ||||||
| 4 | 0.3974 | 0.6026 | 10 | 0.5553 | 0.4447 | 16 | 1.0000 | 0.0000 | ||||||
| 5 | 0.4077 | 0.5923 | 11 | 0.5727 | 0.4273 |
| i | MinCI | MaxCI | i | MinCI | MaxCI | i | MinCI | MaxCI | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.1563 | 0.8437 | 6 | 0.3692 | 0.6308 | 12 | 0.8543 | 0.1457 | ||||||
| 1 | 0.1598 | 0.8402 | 7 | 0.3730 | 0.6270 | 13 | 0.8698 | 0.1302 | ||||||
| 2 | 0.2527 | 0.7473 | 8 | 0.3736 | 0.6264 | 14 | 0.9266 | 0.0734 | ||||||
| 3 | 0.2874 | 0.7126 | 9 | 0.6623 | 0.3377 | 15 | 0.9390 | 0.0610 | ||||||
| 4 | 0.2943 | 0.7057 | 10 | 0.6623 | 0.3377 | 16 | 0.9400 | 0.0600 | ||||||
| 5 | 0.2951 | 0.7049 | 11 | 0.8535 | 0.1465 | 17 | 1.0000 | 0.0000 |
References
- Johnson, S.S.; Jackson, K.C.; Mietchen, M.S.; Sbai, S.; Schwartz, E.J.; Lofgren, E.T. Excess Risk of COVID-19 to University Populations Resulting from In-Person Sporting Events. Int. J. Environ. Res. Public Health 2021, 18, 8260. [Google Scholar] [CrossRef] [PubMed]
- Sovicova, M.; Zibolenova, J.; Svihrova, V.; Hudeckova, H. Odds Ratio Estimation of Medical Students’ Attitudes towards COVID-19 Vaccination. Int. J. Environ. Res. Public Health 2021, 18, 6815. [Google Scholar] [CrossRef] [PubMed]
- Montoya, F.J.; Margolis, M.L. Impact of 95% confidence intervals on pulmonary function test interpretations. Chest 1996, 110, 195S. [Google Scholar] [CrossRef]
- Monaghan, T.F.; Rahman, S.N.; Agudelo, C.W.; Wein, A.J.; Lazar, J.M.; Everaert, K.; Dmochowski, R.R. Foundational Statistical Principles in Medical Research: A Tutorial on Odds Ratios, Relative Risk, Absolute Risk, and Number Needed to Treat. Int. J. Environ. Res. Public Health 2021, 18, 5669. [Google Scholar] [CrossRef] [PubMed]
- Greenland, S.; Senn, S.J.; Rothman, K.J.; Carlin, B.J.; Poole, C.; Goodman, S.N.; Altman, D.G. Statistical tests, P values, confidence intervals, and power: A guide to misinterpretations. Eur. J. Epidemiol. 2016, 31, 337. [Google Scholar] [CrossRef] [PubMed]
- Jakobsen, J.C.; Wetterslev, J.; Winkel, P.; Lange, T.; Gluud, C. Thresholds for statistical and clinical significance in systematic reviews with meta-analytic methods. BMC Med. Res. Methodol. 2014, 14, 120. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, F.; Hunter, J.E. The impact of data-analysis methods on cumulative research knowledge: Statistical significance testing, confidence intervals, and meta-analysis. Eval. Health Prof. 1995, 18, 408. [Google Scholar] [CrossRef]
- Agresti, A.; Coull, B.-A. Approximate is Better than “Exact” for Interval Estimation of Binomial Proportions. Am. Stat. 1998, 52, 119–126. [Google Scholar] [CrossRef]
- Casella, G. Refining binomial confidence intervals. Can. J. Stat. 1986, 14, 113. [Google Scholar] [CrossRef]
- Blyth, C.R.; Still, H.A. Binomial Confidence Intervals. J. Am. Stat. Assoc. 1983, 78, 108. [Google Scholar] [CrossRef]
- Pang, G.; Alemayehu, D.; de la Peña, V.; Klass, M.J. On the bias and variance of odds ratio, relative risk and false discovery proportion. Commun. Stat.-Theory Methods 2021. Online first. [Google Scholar] [CrossRef]
- De la Peña, V.H. From decoupling and self-normalization to machine learning. Not. Am. Math. Soc. 2019, 66, 1641. [Google Scholar] [CrossRef]
- Gauss, C.F.J. Theoria combinations observationum erroribus minnimis obnoxiae. Comm. Soc. Reg. Scient. Got. Rec. Bd. V 1823, IV, 1–53. [Google Scholar]
- Newton, I. PhilosophiæNaturalis Principia Mathematica; Pepys: Londini, UK, 1687; pp. 1–411. [Google Scholar]
- Bernoulli, J. Ars Conjectandi; Thurnistorum: Basileæ, Switzerland, 1713; pp. 1–358. [Google Scholar]
- De Moivre, A. A method of approximating the sum of the terms of the binomial (a + b)n expanded to a series from whence are deduced some practical rules to estimate the degree of assent which is to be given to experiments. In The Doctrine of Chances, or, a Method of Calculating the Probability of Events in Play, 2nd ed.; Woodfall: London, UK, 1738; pp. 1–258. [Google Scholar]
- Gosset, W.S. The probable error of a mean. Biometrika 1908, 6, 1. [Google Scholar] [CrossRef]
- Maxwell, J.C. Illustrations of the dynamical theory of gases. Part I. On the motions and collisions of perfectly elastic spheres. Dublin Phil. Mag. J. Sci. Ser. 4 1860, 19, 19. [Google Scholar] [CrossRef]
- Boltzmann, L. Studien über das Gleichgewicht der lebendigen Kraft zwischen bewegten materiellen Punkten. Wien. Berichte 1868, 58, 517. [Google Scholar] [CrossRef]
- Fodor, M.-P.; Bolboacă, S.-D.; Jäntschi, L. Distribution of Molecules by Kinetic Energy Revisited. Bull. UASVM Hortic. 2013, 70, 10. [Google Scholar]
- Bose, S.N. Plancks Gesetz und Lichtquantenhypothese. Z. Phys. 1924, 26, 178. [Google Scholar] [CrossRef]
- Einstein, A. Quantentheorie des einatomigen idealen Gases. Sitzungsberichte Preuss. Akad. Wiss. 1924, XXII, 261. [Google Scholar]
- Hăşmăşanu, M.-G.; Bolboacă, S.-D.; Jäntschi, L. Bose-Einstein and Fermi-Dirac distributions and their use in biological sciences. BUASVMCN. Vet. Med. 2014, 71, 114. [Google Scholar]
- Fermi, E. Sulla quantizzazione del gas perfetto monoatomico. Rend. Lincei 1926, 3, 145. [Google Scholar]
- Dirac, P.A.M. On the Theory of Quantum Mechanics. Proc. Roy. Soc. Ser. A 1926, 112, 661. [Google Scholar] [CrossRef]
- Stirling, J. Methodus Differentialis: Sive Tractatus de Summatione et Interpolatione Serierum Infinitarum; Bowyer: Londini, UK, 1730; pp. 1–167. [Google Scholar]
- Avogadro, A. Fisica De’ Corpi Ponderabili. Trattato Della Costituzione Generale De’ Corpi. Tomo 1; Reale: Torino, Italy, 1837; pp. 1–910. [Google Scholar]
- Pearson, K. On the general theory of multiple contingency with special reference to partial contingency. Biometrika 1916, 11, 145. [Google Scholar] [CrossRef]
- Jäntschi, L.; Bolboacă, S.-D. First order derivatives of thermodynamic functions under assumption of no chemical changes revisited. J. Comput. Sci. 2014, 5, 597. [Google Scholar] [CrossRef]
- Fisher, R.A. On an Absolute Criterion for Fitting Frequency Curves. Messenger Math. 1912, 41, 155. [Google Scholar]
- Lagrange, J.L. Mécanique Analytique; Nouvele Édition. Revue et Augmentée Par L’auteur. Tome Premier; Mme Ve Courcier: Paris, France, 1811; pp. 1–428. [Google Scholar]
- Muqattash, I.; Yahdi, M. Infinite family of approximations of the Digamma function. Math. Comput. Model. 2006, 43, 1329. [Google Scholar] [CrossRef]
- Euler, L. Institutiones Calculi Differentialis Cum Eius vsu in Analysi Finitorum ac Doctrina Serierum; Academiæ Imperialis Scientiarum Petropolitanæ: St. Petersburg, Russia, 1755; pp. 1–899. [Google Scholar]
- Planck, M. Vorlesungen über die Theorie der Wärmestrahlung; Johann Ambrosius-Barth: Leipzig, Germany, 1906; pp. 1–222. [Google Scholar]
- Agresti, A. Dealing with discreteness: Making ‘exact’ confidence intervals for proportions, differences of proportions, and odds ratios more exact. Stat. Methods Med. Res. 2003, 12, 3. [Google Scholar] [CrossRef] [PubMed]
- Jäntschi, L.; Bolboacă, S.-D. Exact Probabilities and Confidence Limits for Binomial Samples: Applied to the Difference between Two Proportions. Sci. World J. 2010, 10, 865. [Google Scholar] [CrossRef]
- Hăşmăşanu, M.-G.; Bolboacă, S.-D.; Drugan, T.-C.; Matyas, M.; Zaharie, G.-C. Parental factors associated with intrauterine growth restriction. Srp. Ark. Celok. Lek. 2015, 143, 701. [Google Scholar] [CrossRef]
- Juncar, M.; Bran, S.; Juncar, R.I.; Băciuţ, M.F.; Băciuţ, G.; Onisor-Gligor, F. Odontogenic cervical necrotizing fasciitis, etiological aspects. Niger. J. Clin. Pract. 2016, 19, 391. [Google Scholar] [CrossRef]
- Cordos, A.-A.; Bolboacă, S.-D.; Drugan, C. Social Media Usage for Patients and Healthcare Consumers: A Literature Review. Publications 2017, 5, 9. [Google Scholar] [CrossRef]
- Bolboacă, S.-D.; Buhai, D.-V.; Aluaş, M.; Bulboacă, A.-E. Post retraction citations among manuscripts reporting a radiology-imaging diagnostic method. PLoS ONE 2019, 14, e0217918. [Google Scholar] [CrossRef]
- Bulboacă, A.-E.; Stănescu, I.-C.; Bolboacă, S.-D.; Bulboacă, A.-C.; Bodizs, G.-I.; Nicula, C.-A. Retinal Nerve Fiber Layer Thickness and Oxidative Stress Parameters in Migraine Patients without Aura: A Pilot Study. Antioxidants 2020, 9, 494. [Google Scholar] [CrossRef]
- Gherman, C.-D.; Mironiuc, A.-I. Evaluation of Serum Adipokines in Peripheral Arterial Occlusive Disease. Mediat. Inflamm. 2012, 2012, 257808. [Google Scholar] [CrossRef] [PubMed]
- Maniu, A.; Cosgarea, M. Mastoid Obliteration with Concha Cartilage Graft and Temporal Muscle Fascia. J. Otolaryngol-Head Neck Surg. 2012, 74, 141. [Google Scholar] [CrossRef] [PubMed]
- Micu, M.-C.; Alcalde, M.; Sáenz, J.-I.; Crespo, M.; Collado, P.; Bolboacă, S.-D.; Naredo, E. Impact of Musculoskeletal Ultrasound in an Outpatient Rheumatology Clinic. Arthritis Care Res. 2013, 65, 615. [Google Scholar] [CrossRef] [PubMed]
- Marina, M.E.; Botar Jid, C.; Bolboacă, S.-D.; Bocşa, C.; Mihu, C.-M.; Tătaru, A.-D. High-frequency sonography in the evaluation of nail psoriasis. Med. Ultrason. 2016, 18, 312. [Google Scholar] [CrossRef] [PubMed]
- Bulboacă, A.E.; Bolboacă, S.-D.; Bulboacă, A.C.; Prodan, C.I. Association between low thyroid-stimulating hormone, posterior cortical atrophy and nitro-oxidative stress in elderly patients with cognitive dysfunction. Arch. Med. Sci. 2017, 13, 1160. [Google Scholar] [CrossRef]
- Capraş, R.-D.; Bulboacă, A.-E.; Bolboacă, S.-D. Evidence-based medicine self-assessment, knowledge, and integration into daily practice: A survey among Romanian physicians and comparison between trainees and specialists. BMC Med. Educ. 2020, 20, 19. [Google Scholar] [CrossRef]
- Clopper, C.; Pearson, E.-S. The use of confidence or fiducial limits illustrated in the case of the binomial. Biometrika 1934, 26, 404. [Google Scholar] [CrossRef]
- Bolboacă, S.-D.; Jäntschi, L. Optimized confidence intervals for binomial distributed samples. Int. J. Pure App. Math. 2008, 47, 1. [Google Scholar]
- Micu, C.-M.; Micu, R.; Surd, S.; Gîrlovanu, M.; Bolboacă, S.-D.; Ostensen, M. TNF-a inhibitors do not impair sperm quality in males with ankylosing spondylitis after short-term or long-term treatment. Rheumatology 2014, 53, 1250. [Google Scholar] [CrossRef]
- Chirilă, M.; Bolboacă, S.-D. Clinical efficiency of quadrivalent HPV (types 6/11/16/18) vaccine in patients with recurrent respiratory papillomatosis. Eur. Arch. Oto-Rhino-Laryn. 2014, 271, 1135. [Google Scholar] [CrossRef]
- Mihu, D.; Ciortea, R.; Malutan, A.; Mihu, C.-M. Evaluation of maternal systemic inflammatory response in preeclampsia. Taiwan J. Obstet. Gynecol. 2015, 54, 160. [Google Scholar] [CrossRef]
- Botar-Jid, C.-M.; Cosgarea, R.; Bolboacă, S.-D.; Senilă, S.-C.; Lenghel, L.-M.; Rogojan, L.; Dudea, S.-M. Assessment of Cutaneous Melanoma by Use of Very- High-Frequency Ultrasound and Real-Time Elastography. Am. J. Roentgenol. 2016, 206, 699. [Google Scholar] [CrossRef]
- Bolboacă, S.-D.; Jäntschi, L. Predictivity Approach for Quantitative Structure–Property Models. Application for Blood–Brain Barrier Permeation of Diverse Drug–Like Compounds. Int. J. Mol. Sci. 2011, 12, 4348. [Google Scholar] [CrossRef] [PubMed]
- Pocol, C.-B.; Bolboacă, S.-D. Trends of honey consumption in North–West Romania. Int. J. Consum. Stud. 2013, 37, 642. [Google Scholar] [CrossRef]
- Juncar, M.; Popa, A.-R.; Băciuţ, M.-F.; Juncar, R.-I.; Onişor-Gligor, F.; Bran, S.; Băciuţ, G. Evolution assessment of head and neck infections in diabetic patients—A case control study. J. Cranio-MaxilloFac. Surg. 2014, 42, 498. [Google Scholar] [CrossRef] [PubMed]
- Hăşmăşanu, M.-G.; Bolboacă, S.-D.; Baizat, M.-I.; Drugan, T.-C.; Zaharie, G.-C. Neonatal short–term outcomes in infants with intrauterine growth restriction. Saudi Med. J. 2015, 36, 947. [Google Scholar] [CrossRef] [PubMed]
- Bolboacă, S.-D.; Achimaş-Cadariu, B.-A. Binomial Distribution Sample Confidence Intervals Estimation 5. Odds Ratio. Leonardo J. Sci. 2004, 4, 26. [Google Scholar]
- Bolboacă, S.-D.; Achimaş-Cadariu, B.-A. Binomial Distribution Sample Confidence Intervals Estimation 6. Excess Risk. Leonardo Electron. J. Pract. Technol. 2004, 4, 1. [Google Scholar]
- Bolboacă, S.-D.; Jäntschi, L. Binomial distribution sample confidence intervals estimation for positive and negative likelihood ratio medical key parameters. AMIA Annu. Symp. Proc. 2005, 2005, 66. [Google Scholar]
- Newcombe, R.-G. Interval estimation for the difference between independent proportions: Comparison of eleven methods. Stat. Med. 1988, 17, 873. [Google Scholar] [CrossRef]
- Pearson, K. Mathematical Contributions to the Theory of Evolution; On the Theory of Contingency and Its Relation to Association and Normal Correlation, pp. 1–34; Dulau & Co.: London, UK, 1904; pp. 1–228. [Google Scholar]
- Fisher, R.A. On the Interpretation of χ2 from Contingency Tables, and the Calculation of P. J. Roy. Stat. Soc. 1922, 85, 87. [Google Scholar] [CrossRef]
- Flanagan, J.L.; House, A.S. Development and Testing of a Formant-Coding Speech Compression System. J. Acoust. Soc. Am. 1956, 28, 1099. [Google Scholar] [CrossRef]
- Congalton, R.G.; Oderwald, R.G.; Mead, R.A. Assessing Landsat classification accuracy using discrete multivariate analysis statistical techniques. Photogrumm. Eng. Remote Sens. 1983, 49, 1671. [Google Scholar]
- Yates, F. Contingency Tables Involving Small Numbers and the χ2 Test. Supp. J. R. Stat. Soc. 1934, 1, 217. [Google Scholar] [CrossRef]
- Stegenga, J. Measuring Effectiveness. Stud. Hist. Philos. Sci. Part C-Stud. Hist. Philos. Biol. Biomed. Sci. 2015, 54, 62. [Google Scholar] [CrossRef]
- Fisher, R.A. Statistical Methods for Research Workers, 5th ed.; §21.02. The Exact Treatment of 2 × 2 tables, pp. 99–101; Oliver and Boyd: Edinburgh, UK, 1934; pp. 1–320. [Google Scholar]
- Botar-Jid, C.-M.; Bolboacă, S.-D.; Cosgarea, R.; Senilă, S.-C.; Rogojan, L.; Lenghel, L.-M.; Vasilescu, D.; Dudea, S.-M. Doppler ultrasound and strain elastography in the assessment of cutaneous melanoma: Preliminary results. Med. Ultrason. 2015, 17, 509. [Google Scholar] [CrossRef][Green Version]
- Tian, G.-L.; Zhang, C.; Jiang, X. Valid statistical inference methods for a case–control study with missing data. Stat. Methods Med. Res. 2018, 27, 1001. [Google Scholar] [CrossRef]
- Drugan, T.-C.; Bolboacă, S.-D.; Jäntschi, L.; Achimaş-Cadariu, B.-A. Binomial distribution sample confidence intervals estimation 1. Sampling and medical key parameters calculation. Leonardo Electron. J. Pract. Technol. 2003, 3, 45. [Google Scholar]
- Tharwat, A. Classification assessment methods. Appl. Comput. Inform. 2021, 17, 168. [Google Scholar] [CrossRef]
- Sui, J.; Jiao, J.; Sun, Y.; Liu, J.; Bastero, R.; Koch, G. Evaluation of alternative confidence intervals to address non-inferiority through the stratified difference between proportions. Pharmaceut. Stat. 2021, 20, 146. [Google Scholar] [CrossRef] [PubMed]




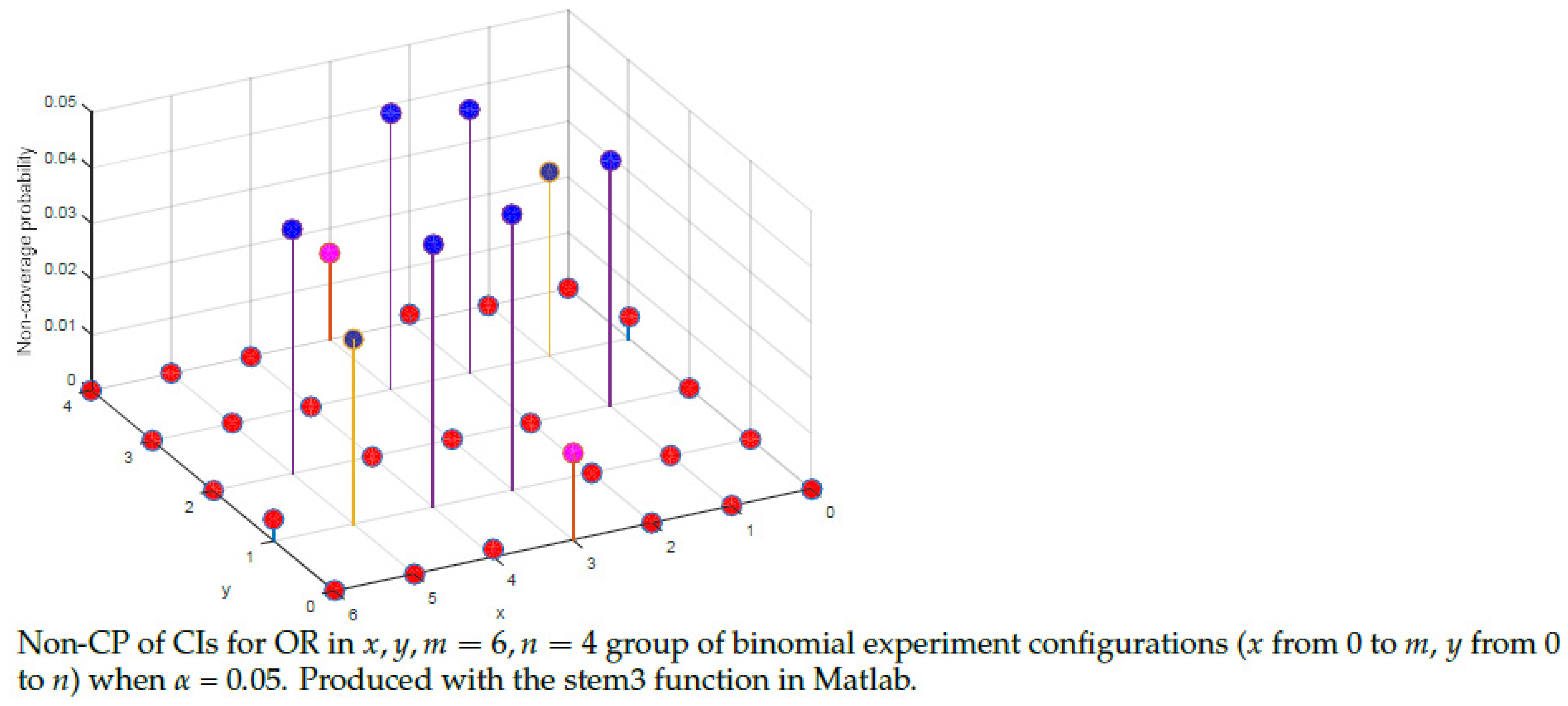
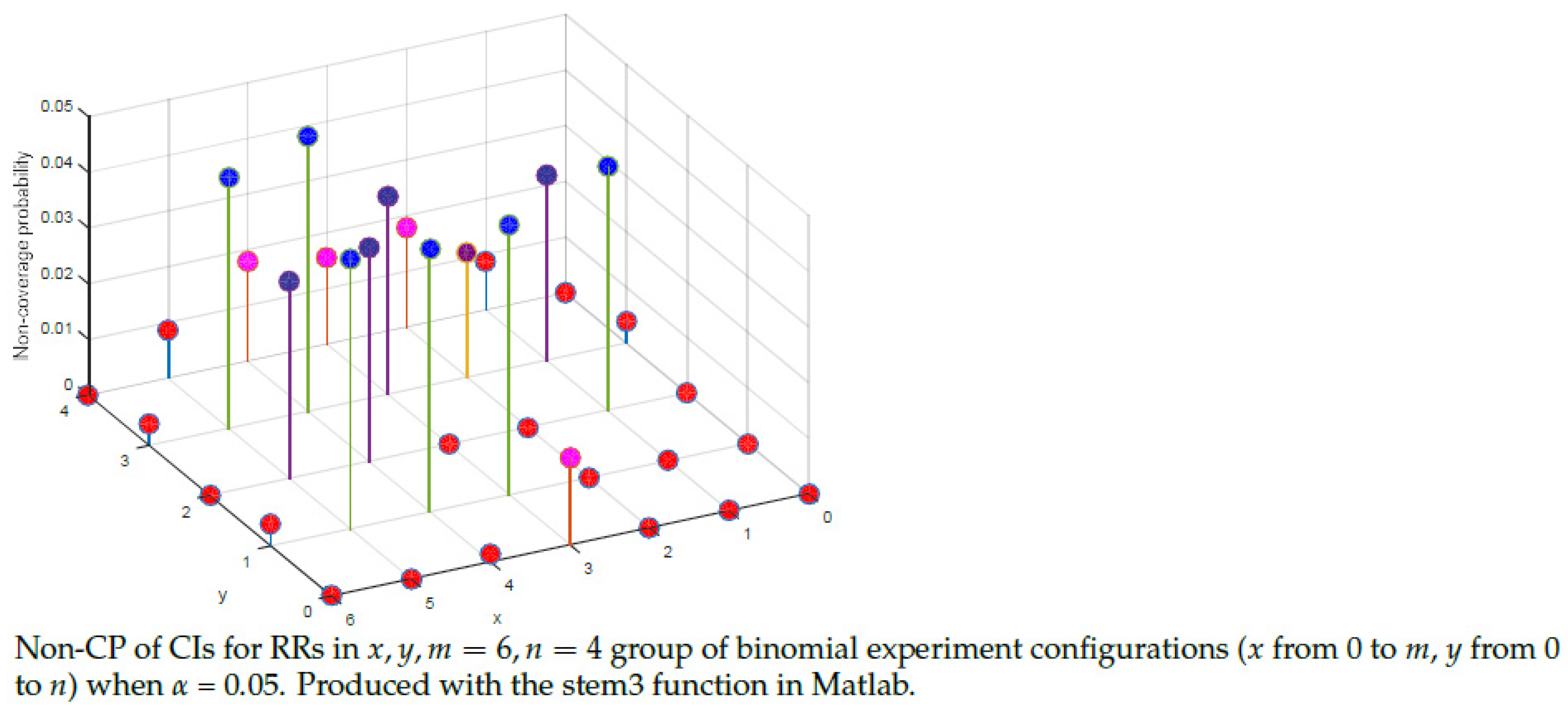
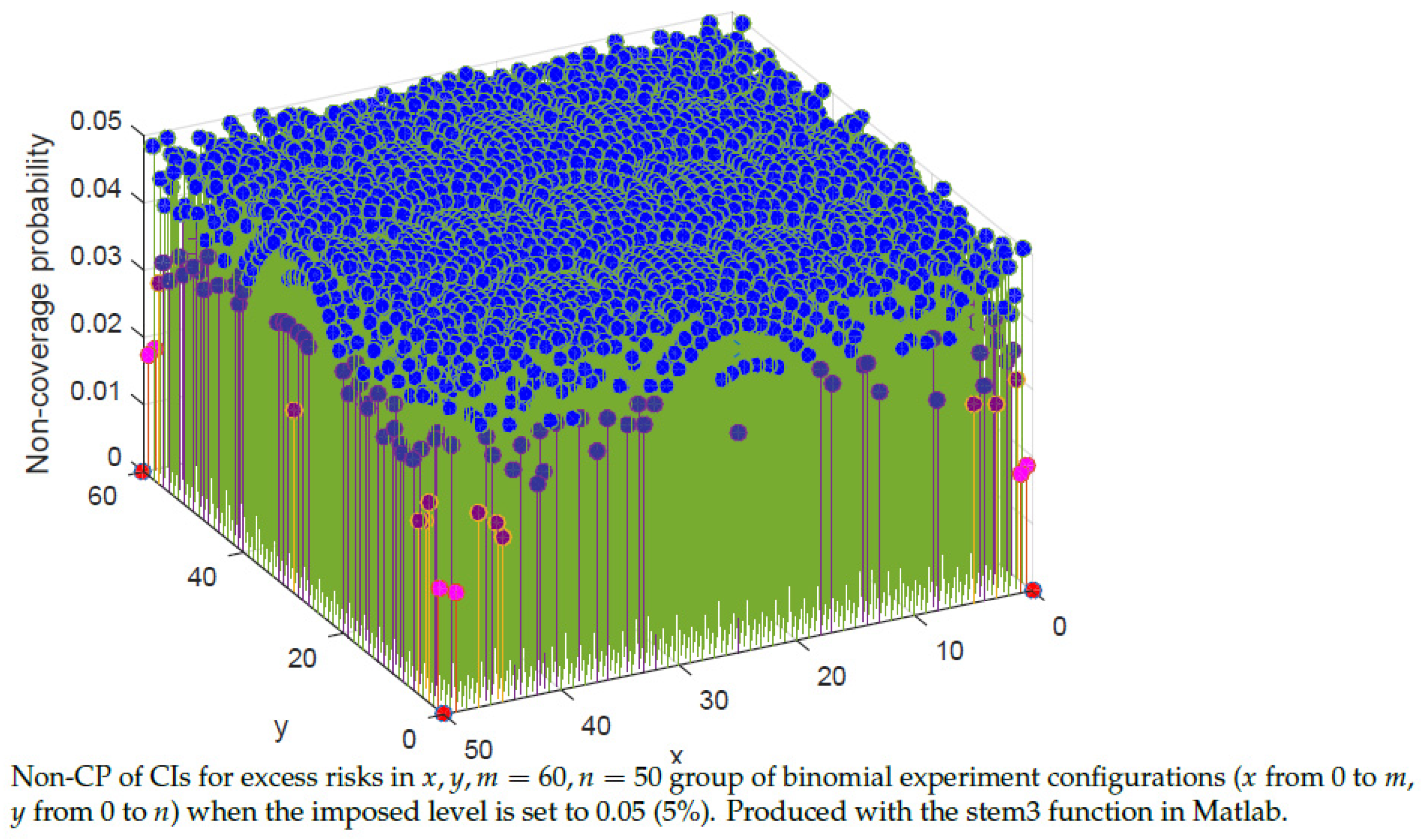
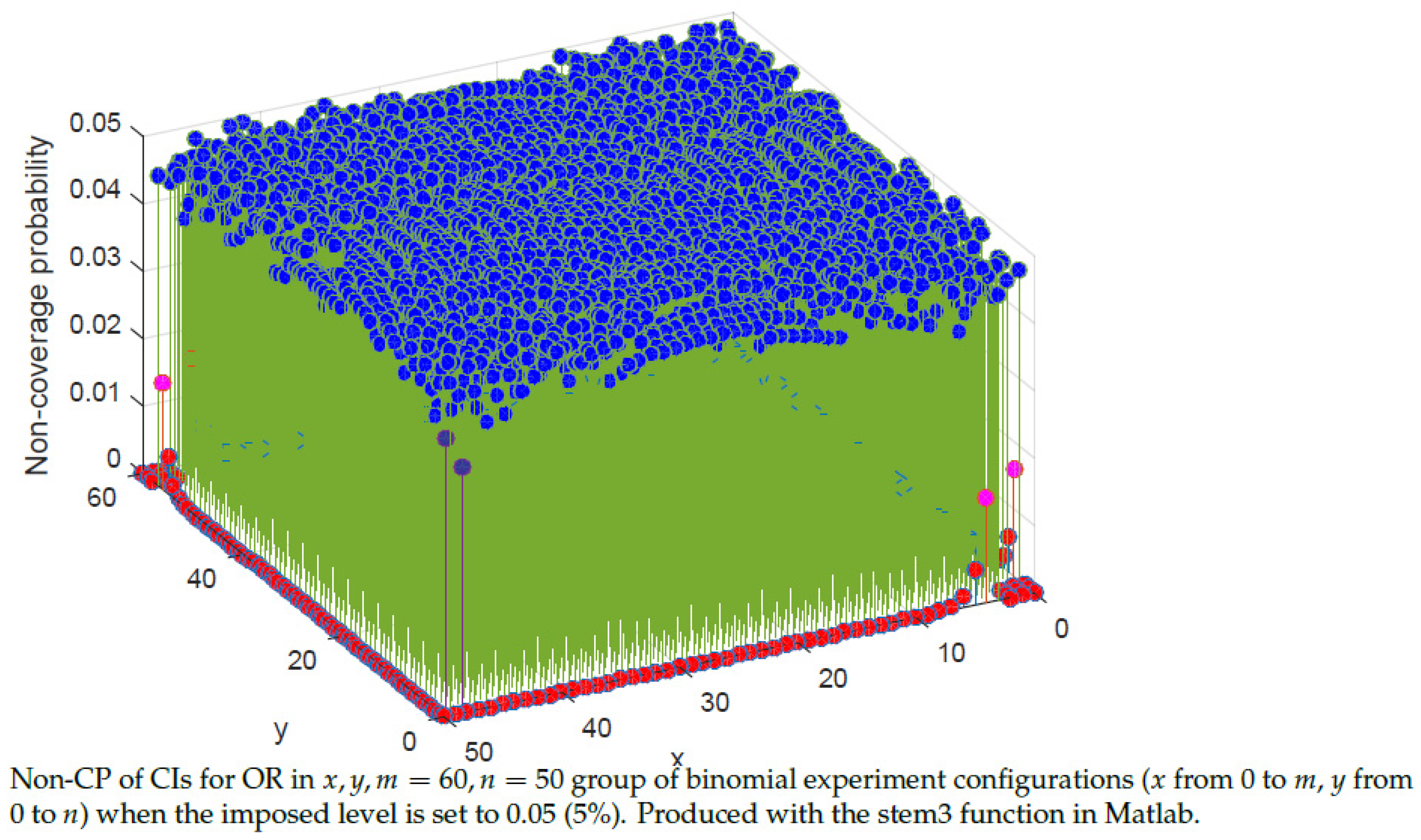
| Events | Probability Mass Function |
|---|---|
| () replica of () | , , …, , …, |
| () replica of () | , , …, , …, |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| i | MinCI | MaxCI | pCI | 1 − pCI | i | MinCI | MaxCI | pCI | 1 − pCI |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.1397 | 0.8603 | 12 | 0.9417 | 0.0583 | ||||
| 1 | 0.2404 | 0.7596 | 13 | 0.9540 | 0.0460 | ||||
| 2 | 0.3330 | 0.6670 | 14 | 0.9610 | 0.0390 | ||||
| 3 | 0.4407 | 0.5593 | 15 | 0.9870 | 0.0130 | ||||
| 4 | 0.5147 | 0.4853 | 16 | 0.9883 | 0.0117 | ||||
| 5 | 0.6297 | 0.3703 | 17 | 0.9924 | 0.0076 | ||||
| 6 | 0.6992 | 0.3008 | 18 | 0.9934 | 0.0066 | ||||
| 7 | 0.7465 | 0.2535 | 19 | 0.9940 | 0.0060 | ||||
| 8 | 0.8024 | 0.1976 | 20 | 0.9992 | 0.0008 | ||||
| 9 | 0.8371 | 0.1629 | 21 | 0.9997 | 0.0003 | ||||
| 10 | 0.9069 | 0.0931 | 22 | 1.0000 | 0.0000 | ||||
| 11 | 0.9223 | 0.0777 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jäntschi, L. Formulas, Algorithms and Examples for Binomial Distributed Data Confidence Interval Calculation: Excess Risk, Relative Risk and Odds Ratio. Mathematics 2021, 9, 2506. https://doi.org/10.3390/math9192506
Jäntschi L. Formulas, Algorithms and Examples for Binomial Distributed Data Confidence Interval Calculation: Excess Risk, Relative Risk and Odds Ratio. Mathematics. 2021; 9(19):2506. https://doi.org/10.3390/math9192506
Chicago/Turabian StyleJäntschi, Lorentz. 2021. "Formulas, Algorithms and Examples for Binomial Distributed Data Confidence Interval Calculation: Excess Risk, Relative Risk and Odds Ratio" Mathematics 9, no. 19: 2506. https://doi.org/10.3390/math9192506
APA StyleJäntschi, L. (2021). Formulas, Algorithms and Examples for Binomial Distributed Data Confidence Interval Calculation: Excess Risk, Relative Risk and Odds Ratio. Mathematics, 9(19), 2506. https://doi.org/10.3390/math9192506






