On a Bivariate Generalization of Berrut’s Barycentric Rational Interpolation to a Triangle

Abstract

We discuss a generalization of Berrut’s first and second rational interpolants to the case of equally spaced points on a triangle in ${\mathbb{R}}^2$.

1. Introduction

Berrut [1,2,3] introduced two versions of a univariate rational interpolation procedure that has proven to be efficient and effective, even for equally spaced points in an interval. Of note is that the complexity of these procedures is linear in the number of points. The derivation of these procedures is based on the classical Whittaker–Shannon sampling theorem [4,5,6]).

Theorem 1.

Suppose that $f\in C\left(\mathbb{R}\right)\cap L^1\left(\mathbb{R}\right)$ and that $\widehat{f}\left(\omega \right)=0$ for $\left|\omega \right|\ge h/2$. Then

$$f\left(x\right)=\sum _{k=-\infty }^{\infty }f\left(kh\right)\mathrm{sinc}\left(\frac{1}{h}(x-kh)\right).$$

(1)

where, as usual,

$$\mathrm{sinc}\left(x\right):=\frac{sin\left(\pi x\right)}{\pi x},$$

is the sinc function.

In the case of f with domain restricted to some compact subinterval of $\mathbb{R},$ say to $[0,1],$ considering equally spaced points with $h=1/n,$ we may consider the partial sum

$$\begin{array}{cc}\hfill f\left(x\right)\approx F_n\left(x\right)& :=\sum _{k=0}^{n}f(k/n)\mathrm{sinc}\left(n(x-k/n)\right)\hfill \\ \hfill & =\sum _{k=0}^{n}f\left(x_k\right)\mathrm{sinc}\left(n(x-x_k)\right)\hfill \end{array}$$

(2)

where we have set $x_k:=k/n,0\le k\le n$.

Figure 1 shows a plot of the approximant $F_{11}$ and $F_{41}$ of the function $f\left(x\right)=x^2$ where it is evident that when increasing n the quality of the approximation improves.

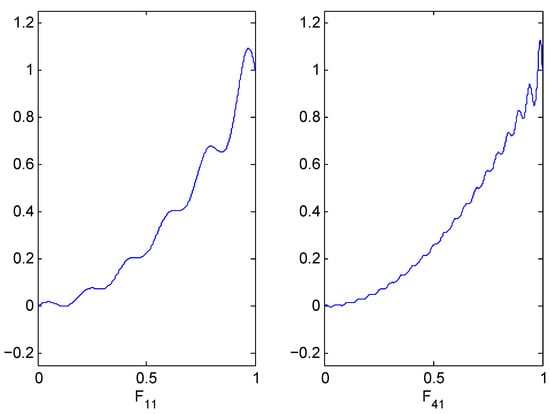
Figure 1. $F_n\left(x\right)$ for $f\left(x\right)=x^2$ and $n=11$ and $n=41$.

While (2) no longer reproduces f for all $x\in [0,1],$ it is an interpolant in that

$$F_n\left(x_j\right)=f\left(x_j\right),0\le j\le n,$$

(3)

as easily follows from the cardinality property of the translated sinc functions, i.e.,

$$\mathrm{sinc}\left(n(x_j-x_k)\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}j=k\\ \\ 0\hfill & \mathrm{if}j\ne k\end{array}\right..$$

This interpolant $F_n$ was already studied by de la Vallée Poussin (1908) who showed that under some weak regularity conditions on $f\left(x\right),$

$$\underset{n\to \infty }{lim}{F}_n\left(x\right)=f\left(x\right),x\in [0,1],$$

with error essentially of $O(1/n)$. The reader interested in further details may find them in the excellent survey by Butzer and Stens [7].

In order to alleviate the poor approximation quality of $F_n$, Berrut in [2] suggested normalizing the Formula (2) for $F_n$ to obtain what we refer to as the first Berrut rational interpolant:

$$B_n^{\left(1\right)}\left(x\right):=\frac{{\displaystyle \sum _{k=0}^{n}f\left(x_k\right)\mathrm{sinc}\left(n(x-x_k)\right)}}{{\displaystyle \sum _{k=0}^n\mathrm{sinc}\left(n(x-x_k)\right)}}.$$

(4)

$B_n^{\left(1\right)}$ remains an interpolant of f at the nodes $x_k,$$k=0,\cdots ,n$ but has the advantage of reproducing constants, that is if $f\left(x\right)=1$ then $B_n^{\left(1\right)}\left(x\right)=1$.

The Formula (4) may be simplified. Notice that

$$\mathrm{sinc}\left(n(x-x_k)\right)={(-1)}^k\frac{sin\left(n\pi x\right)}{n\pi (x-x_k)}.$$

hence,

$$\begin{array}{cc}\hfill B_n^{\left(1\right)}\left(x\right)& =\frac{{\sum }_{k=0}^{n}f\left(x_k\right)\mathrm{sinc}\left(n(x-x_k)\right)}{{\sum }_{k=0}^n\mathrm{sinc}\left(n(x-x_k)\right)}\hfill \\ \hfill & =\frac{sin\left(n\pi x\right){\sum }_{k=0}^n{(-1)}^k\frac{f\left(x_k\right)}{x-x_k}}{sin\left(n\pi x\right){\sum }_{k=0}^n{(-1)}^k\frac{1}{x-x_k}}\hfill \\ \hfill & =\frac{{\sum }_{k=0}^n{(-1)}^{k}f\left(x_k\right)/(x-x_k)}{{\sum }_{k=0}^n{(-1)}^k/(x-x_k)}.\hfill \end{array}$$

(5)

An example of this first interpolant is shown in Figure 2 again for $f=x^2$ and $n=11,41$.

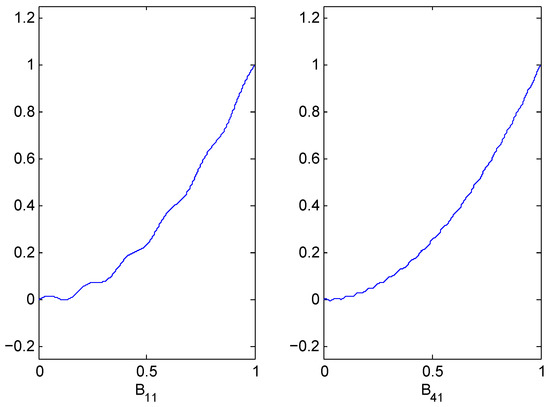
Figure 2. Berrut $B_n^{\left(1\right)}$ for $f\left(x\right)=x^2$ and $n=11$ and $n=41$.

Remark 1.

Besides being an improved approximant, $B_n^{\left(1\right)}$ is also numerically stable as its associated Lebesgue constant has $O(log(n\left)\right)$ growth, as was shown in [8].

Berrut also proposed a second improvement by making a simple boundary adjustment in the definition of $B_n^{\left(1\right)}$ to obtain an interpolant that also reproduced polynomials of degree one. Specifically, let

$$B_n^{\left(2\right)}\left(x\right):=\frac{{\displaystyle \sum _{k=0}^n{(-1)}^k{\beta }_{k}f\left(x_k\right)/(x-x_k)}}{{\displaystyle \sum _{k=0}^n{(-1)}^k{\beta }_k/(x-x_k)}}$$

(6)

where

$${\beta }_k=\left\{\begin{array}{cc}1\hfill & 1\le k\le (n-1),\hfill \\ 1/2\hfill & k=0,n\hfill \end{array}\right..$$

Remark 2.

Floater and Hormann ([9]) subsequently introduced the more general formula

$$F{H}_n\left(x\right):=\frac{{\displaystyle \sum _{k=0}^n{(-1)}^k{\beta }_k^{\left(d\right)}f\left(x_k\right)/(x-x_k)}}{{\displaystyle \sum _{k=0}^n{(-1)}^k{\beta }_k^{\left(d\right)}/(x-x_k)}}.$$

(7)

where the weights ${\beta }_k^{\left(d\right)}$ are chosen so that $F{H}_n$ reproduces polynomials of degree at most d

In the specific case of equally spaced nodes their formula for the ${\beta }_k^{\left(d\right)}$ reduces to

$${\beta }_k^{\left(d\right)}:=\left\{\begin{array}{cc}{\sum }_{j=0}^k\left(\genfrac{}{}{0pt}{}{d}{k}\right)& 0\le k\le d\hfill \\ \\ 2^d& d\le k\le n-d\hfill \\ \\ {\beta }_{n-k}& n-d\le k\le n\hfill \end{array}\right.$$

(8)

where $n\ge 2d$, by assumption.

The cases of $d=0,1$ correspond to Berrut’s first and second interpolants, respectively.

In this work we will consider bivariate extensions of Berrut’s first and second interpolants. The more general Floater-Hormann case will be the topic of a subsequent paper.

In Figure 3 we show a comparison between the Berrut interpolants for $f\left(x\right)=x^4$ and $n=12$.

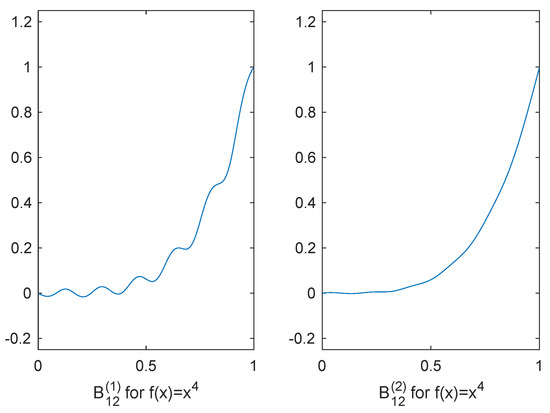
Figure 3. $B_n^{\left(1\right)}$ and $B_n^{\left(2\right)}$ for $f\left(x\right)=x^4$ and $n=12$.

2. The Extension of Berrut’s First Interpolant to Equally Spaced Points on a Triangle

The bivariate Whittaker–Shannon sampling operator is defined as follows. Set $x_i:=i/n$ and $y_j:=j/n$ then

$$f(x,y)=\sum _{i=-\infty }^{\infty }\sum _{j=-\infty }^{\infty }f(x_i,y_j)\mathrm{sinc}\left(n(x-x_i)\right)\mathrm{sinc}\left(n(y-y_j)\right)$$

(9)

We can now truncate triangularly (this is equivalent to consider equally spaced points on the triangle, as illustrated in Figure 4). Let

$$T:=\{(x,y)\in {\mathbb{R}}^2:0\le x,y,x+y\le 1\}$$

be the standard triangle in ${\mathbb{R}}^2$ and set

$$\begin{array}{cc}\hfill F_n(x,y)& :=\sum _{(i,j)/n\in T}f(x_i,y_j)\mathrm{sinc}\left(n(x-x_i)\right)\mathrm{sinc}\left(n(y-y_j)\right)\hfill \\ \hfill & =\sum _{0\le i+j\le n}f(x_i,y_j)\mathrm{sinc}\left(n(x-x_i)\right)\mathrm{sinc}\left(n(y-y_j)\right).\hfill \end{array}$$

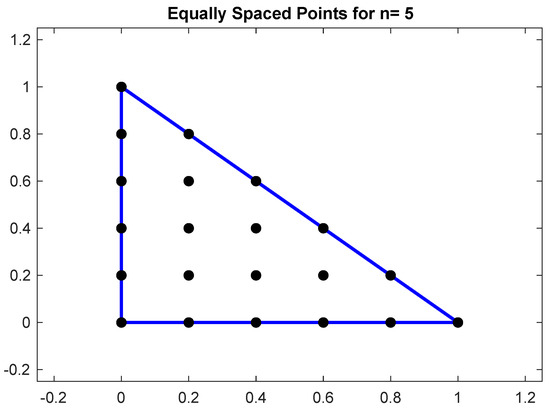
Figure 4. Equally Spaced Points in a Triangle.

Furthermore, by normalizing as in the one-dimensional Berrut case, we get

$$B_n^{\left(1\right)}(x,y):=\frac{{\displaystyle \sum _{0\le i+j\le n}f(x_i,y_j)\mathrm{sinc}\left(n(x-x_i)\right)\mathrm{sinc}\left(n(y-y_j)\right)}}{{\displaystyle \sum _{0\le i+j\le n}\mathrm{sinc}\left(n(x-x_i)\right)\mathrm{sinc}\left(n(y-y_j)\right)}}$$

(10)

Finally we simplify, just as in the univariate case, to get

$$B_n^{\left(1\right)}(x,y):=\frac{{\displaystyle \sum _{0\le i+j\le n}{(-1)}^{i+j}\frac{f(x_i,y_j)}{(x-x_i)(y-y_j)}}}{{\displaystyle \sum _{0\le i+j\le n}{(-1)}^{i+j}\frac{1}{(x-x_i)(y-y_j)}}},$$

(11)

Remark 3.

Of course the summation can be truncated to regions P other than just the triangle to obtain multivariate versions of the Berrut rational interpolation at integer lattice points contained in P. However, we consider in this first work only the case of $P=T$ a triangle.

Proposition 1.

We have that $B_n^{\left(1\right)}(x,y)$ is an interpolant, i.e.,

$$B_n^{\left(1\right)}(x_{\alpha },y_{\beta })=f(x_{\alpha },y_{\beta }),0\le \alpha +\beta \le n,$$

and that $B_n^{\left(1\right)}$ reproduces constants. Moreover, restricted to the vertical grid lines $x=x_s$ and horizontal grid lines $y=y_t,$$B_n^{\left(1\right)}$ agrees with the univariate Berrut interpolant for the interpolation points along those lines.

Proof. 

It is easy to verify these properties. Interpolation is guaranteed by the singularities at the interpolation points while the reproduction of constants is self evident.

To see the grid line first rationalize by multiplying the numerator and denominator by ${\omega }_n\left(x\right){\omega }_n\left(y\right)$ where

$${\omega }_n\left(z\right):=\prod _{i=0}^n(z-x_i)$$

to obtain

$$B_n^{\left(1\right)}(x,y)=\frac{{\displaystyle \sum _{0\le i+j\le n}{(-1)}^{i+j}f(x_i,y_j)\prod _{k=0,k\ne i}^n(x-x_k)\prod _{k=0,k\ne j}^n(y-y_j)}}{{\displaystyle \sum _{0\le i+j\le n}{(-1)}^{i+j}\prod _{k=0,k\ne i}^n(x-x_k)\prod _{k=0,k\ne j}^n(y-y_j)}}.$$

Restricting, for example to the vertical grid line $x=x_s$ we obtain

$$B_n^{\left(1\right)}(x_s,y)=\frac{{\displaystyle \sum _{0\le i+j\le n}{(-1)}^{i+j}f(x_i,y_j)\prod _{k=0,k\ne i}^n(x_s-x_k)\prod _{k=0,k\ne j}^n(y-y_j)}}{{\displaystyle \sum _{0\le i+j\le n}{(-1)}^{i+j}\prod _{k=0,k\ne i}^n(x_s-x_k)\prod _{k=0,k\ne j}^n(y-y_j)}}.$$

However the product

$$\prod _{k=0,k\ne i}(x_s-x_k)=0$$

unless $i=s$. Hence

$$\begin{array}{cc}\hfill B_n^{\left(1\right)}(x_s,y)& =\frac{{\displaystyle \sum _{j=0}^{n-s}{(-1)}^{s+j}f(x_s,y_j)\prod _{k=0,k\ne s}^n(x_s-x_k)\prod _{k=0,k\ne j}^n(y-y_j)}}{{\displaystyle \sum _{j=0}^{n-s}{(-1)}^{s+j}\prod _{k=0,k\ne s}^n(x_s-x_k)\prod _{k=0,k\ne j}^n(y-y_j)}}\hfill \\ \hfill & =\frac{{\displaystyle \sum _{j=0}^{n-s}{(-1)}^{s+j}f(x_s,y_j)\prod _{k=0,k\ne j}^n(y-y_j)}}{{\displaystyle \sum _{j=0}^{n-s}{(-1)}^j\prod _{k=0,k\ne j}^n(y-y_j)}}\hfill \end{array}$$

which is exactly the univariate Berrut interpolant for the function $f(x_s,y)$ along that the line $x=x_s$. □

Remark 4.

The restriction of $B_n^{\left(1\right)}(x,y)$ to the upper edge $x+y=1$ is not a univariate Berrut interpolant, as is easy to confirm. It follows that $B_n^{\left(1\right)}$ is not symmetric with respect to the barycentric coordinates of the triangle.

As we have seen, the formula (11) can be rationalized by multiplying the numerator and denominator by ${\omega }_n\left(x\right){\omega }_n\left(y\right),$ where

$${\omega }_n\left(z\right):=\prod _{i=0}^n(z-x_i).$$

Indeed, writing $B_n^{\left(1\right)}(x,y)=N_n(x,y)/D_n(x,y),$ let

$$\begin{array}{cc}\hfill d_n(x,y):& ={\omega }_n\left(x\right){\omega }_n\left(y\right)D_n(x,y)\hfill \\ \hfill & ={\omega }_n\left(x\right){\omega }_n\left(y\right)\sum _{i=0}^n\sum _{j=0}^{n-i}\frac{{(-1)}^{i+j}}{(x-x_i)(y-y_j)}\hfill \end{array}$$

be the resulting polynomial for the denominator in (11). The zeros of $d_n(x,y)$ correspond to poles in the expression for $B_n^{\left(1\right)}$ and are obviously problematic. We conjecture however that there are no poles inside the triangle, but have been able to prove this only for $n\le 20,$ to date. We remark that although the univariate arguments used by Berrut (and more generally by Floater and Hormann) do extend easily to the tensor product case, they do not, to the best of our knowledge, extend easily to the triangular case which we are considering.

Our method to do this is elementary, but computationally expensive. Consider first the $n=1$ case. Then

$$\begin{array}{cc}\hfill d_1(x,y)& ={\omega }_1\left(x\right){\omega }_1\left(y\right)\sum _{i=0}^1\sum _{j=0}^{1-i}\frac{{(-1)}^{i+j}}{(x-i/1)(y-j/1)}\hfill \\ \hfill & =x(x-1)y(y-1)\left\{\frac{1}{xy}-\frac{1}{(x-1)y}-\frac{1}{x(y-1)}\right\}\hfill \\ \hfill & =(x-1)(y-1)-x(y-1)-(x-1)y\hfill \\ \hfill & =1-xy.\hfill \end{array}$$

Clearly $d_1(x,y)>0$ for $(x,y)\in T,$ but this can also be confirmed by the use of barycentric coordinates. Indeed, let $z:=(1-x-y)$ so that $x+y+z=1$. In particular, the triangle T is given by

$$T=\{(x,y)\in {\mathbb{R}}^2:0\le x,y,z\}.$$

Then, homogenizing and simplifying we have

$$\begin{array}{cc}\hfill d_1(x,y)& ={(x+y+z)}^2-xy\hfill \\ \hfill & =x^2+y^2+z^2+xy+2xz+2yz.\hfill \end{array}$$

As all the coefficients of $d_1$ are non-negative, it follows that $d_1>0$ on the interior of the triangle T. By, the previous proposition, we know that there are also no boundary poles on the edges $x=0$ and $y=0$. The upper edge ($z=0$) needs to be checked separately, which is easily done.

For higher degrees n it is convenient to change variables letting $x^{\prime }:=nx,$$y^{\prime }:=ny,$$z^{\prime }=n-x^{\prime }-y^{\prime }$ so that

$$d_n(x,y)=n^{-2n}{\omega }_n^{\prime }\left(x^{\prime }\right){\omega }_n^{\prime }\left(y^{\prime }\right)\sum _{i=0}^n\sum _{j=0}^{n-i}\frac{{(-1)}^{i+j}}{(x^{\prime }-i)(y^{\prime }-j)}$$

where

$${\omega }_n^{\prime }\left(t\right)=\prod _{i=0}^n(t-i).$$

Then, ignoring the $n^{-2n}$ factor and, by an abuse of notation, suppressing the primes,

$$\begin{array}{cc}\hfill d_2(x,y)& ={\omega }_2\left(x\right){\omega }_2\left(y\right)\sum _{i=0}^2\sum _{j=0}^{2-i}\frac{{(-1)}^{i+j}}{(x-i)(y-j)}\hfill \\ \hfill & =x(x-1)(x-2)y(y-1)(y-2)\times \hfill \\ \hfill & \left\{\frac{1}{xy}-\frac{1}{(x-1)y}-\frac{1}{x(y-1)}+\frac{1}{x(y-2)}+\frac{1}{(x-1)(y-1)}+\frac{1}{x(y-2)}\right\}\hfill \\ \hfill & =2x^2{y}^2-4x^{2}y+2x^2-4x{y}^2+7xy-4x+2y^2-4y+4,\hfill \end{array}$$

a polynomial of degree 4. It can be homogenized to

$$2x^2{y}^2-4x^{2}yt+2x^2{t}^2-4x{y}^{2}t+7xy{t}^2-4x{t}^3+2y^2{t}^2-4y{t}^3+4t^4$$

which becomes, upon setting $t=(x+y+z)/2$ ($=1$ in barycentric coordinates),

$$\begin{array}{cc}\hfill 4d_2(x,y)& =x^4-x^{3}y+2x^{3}z+4x^2{y}^2+4x^{2}yz+2x^2{z}^2-x{y}^3\hfill \\ \hfill & +4x{y}^{2}z+7xy{z}^2+2x{z}^3+y^4+2y^{3}z+2y^2{z}^2+2y{z}^3+z^4.\hfill \end{array}$$

Not all the coefficients are non-negative and hence we cannot immediately conclude that $d_2>0$ on T. However, we may degree elevate this expression, i.e., multiply by a factor ${(x+y+z)}^r$ (cf. e.g., [10]). If it is the case that all the coefficients of the product

$${(x+y+z)}^r{d}_2(x,y)$$

are non-negative, it follows that $d_2>0$ on T. (The lowest power r with this property is related to the so-called Bernstein degree of $d_2(x,y)$.) In this case, consider what occurs if $r=1$. Then

$$\begin{array}{cc}\hfill 4{(x+y+z)}^1{d}_2(x,y)& =x^5+3x^{4}z+3x^3{y}^2+5x^{3}yz+4x^3{z}^2+3x^2{y}^3\hfill \\ \hfill & +12x^2{y}^{2}z+13x^{2}y{z}^2+4x^2{z}^3+5x{y}^{3}z+13x{y}^2{z}^2\hfill \\ \hfill & +11xy{z}^3+3x{z}^4+y^5+3y^{4}z+4y^3{z}^2+4y^2{z}^3+3y{z}^4+z^5.\hfill \end{array}$$

The minimum non-zero coefficient, 1 in this case, provides a certificate of positivity for $d_2(x,y)$ on the interior of T (where $x,y,z>0$). Separate certificates for the boundary can be obtained by setting $x=0,$$y=0$ and $z=0,$ respectively. However, as already noted, the restrictions of the bivariate interpolant to the edges $x=x_0=0$ and $y=y_0=0$ are the univariate Berrut interpolants and hence have no poles there. The upper edge $z=0$ needs to be done separately.

By these means we may, with the assistance of a computer algebra system, prove the following positivity result.

Proposition 2.

For at least $n=1,2,\cdots ,20,$

$$d_n(x,y)>0,(x,y)\in T.$$

Proof. 

We produced a positivity certificate for the stated values of n using the Matlab Symbolic Toolbox and the following code.

The minimal values of degree elevation are shown in Table 1.

Table 1. Degree Elevation r for Degree n.

n	r	||	n	r
1	0	||	11	89
2	1	||	12	103
3	5	||	13	123
4	8	||	14	143
5	14	||	15	169
6	22	||	16	188
7	33	||	17	215
8	44	||	18	238
9	56	||	19	271
10	70	||	20	296

Notice that the minimal elevation degree r grows quite quickly with n. In principle one can continue with this procedure proving positivity for one degree n at a time. A general proof evades us for the time being. □

In the univariate case it is known that in fact there are no real poles whatsoever. In contrast, in the bivariate case there are real poles, however, due to Proposition 2 they are necessarily outside the triangle.

Proposition 3.

For any set of weights $w_{ij},$ the denominator

$$d_n(x,y):={\omega }_n\left(x\right){\omega }_n\left(y\right)\sum _{0\le i+j\le n}{w}_{ij}\frac{1}{(x-i/n)(y-j/n)}$$

has real zeros at $\left(\frac{\alpha }{n},\frac{\beta }{n}\right)$ for $0\le \alpha ,\beta \le n$ and $\alpha +\beta >n$.

Proof. 

Notice that

$$d_n(x,y)=\sum _{0\le i+j\le n}{w}_{ij}\left(\prod _{k=0,k\ne i}^n(x-k/n)\right)\left(\prod _{m=0,m\ne j}^n(y-m/n)\right).$$

However, for $\alpha +\beta >n$ we must have $(\alpha ,\beta )\ne (i,j),$ for all $(i,j)$ with $i+j\le n,$ i.e., either $\alpha \ne i$ or $\beta \ne j$ (or both). Hence at least one of the products

$$\prod _{k=0,k\ne i}^n(\alpha /n-k/n),\prod _{m=0,m\ne j}^n(\beta /n-m/n)$$

must be zero, and thus $d_n(\alpha /n,\beta /n)=0$. □

Remark 5.

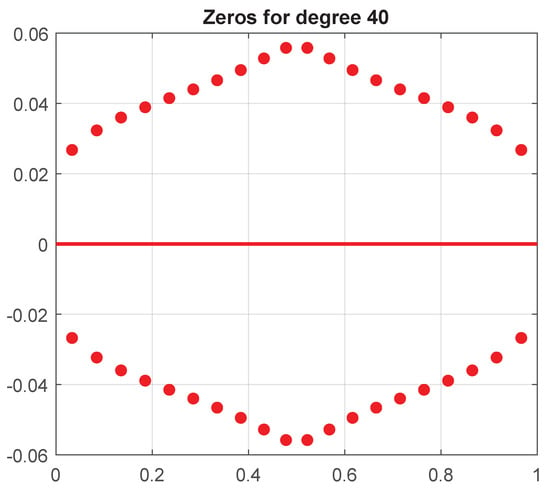
While there are no real poles in the univariate case, there are complex poles. Figure 5 shows these poles for degree $n=40$. In fact it is possible to analyze the asymptotics of these poles. Indeed, it was shown in [4] that

$$D_n\left(x\right):=\sum _{j=0}^n\frac{{(-1)}^j}{x-j/n}=\frac{n}{2}\left\{2\pi csc\left(n\pi x\right)+G(nx+1)+{(-1)}^{n+1}G(n(1-x)+1)\right\}$$

where $G\left(x\right)$ is the so-called Bateman G-function

$$G\left(x\right)=2{\int }_0^{\infty }\frac{e^{-xt}}{1+e^{-t}}dt,\Re \left(x\right)>0.$$

Letting $z:=nx,$ we obtain

$$D_n(z/n)=\frac{n}{2}\left\{2\pi csc\left(\pi z\right)+G(z+1)+{(-1)}^{n+1}G(n+1-z)\right\}.$$

However, notice, from the defining formula, that

$$\underset{n\to \infty }{lim}G(n+1-z)=0$$

so that the zeros of $D_n\left(x\right)$ are aysmptotically the zeros of $2\pi csc\left(\pi z\right)+G(z+1),$ divided by n. In particular, one may find numerically that

$$z_0:\approx 1.346516491475860+1.055160064278170i$$

is a zero of $2\pi csc\left(\pi z\right)+G(z+1)$ and hence $z_0/n$ is approximately a zero of $D_n\left(x\right)$. Consequently, in the univariate case, there are complex poles of distance order $1/n$ to the interval $[0,1],$ whereas in the bivariate case there are real poles of this same order of distance to the triangle T.

Figure 5. Univariate Poles for Degree $n=40$.

Finally, we show some examples of this bivariate interpolant. Figure 6 shows the bivariate extension of Berrut’s first interpolant for the function $f(x,y)=x^2+y^2$ and $n=13,27$.

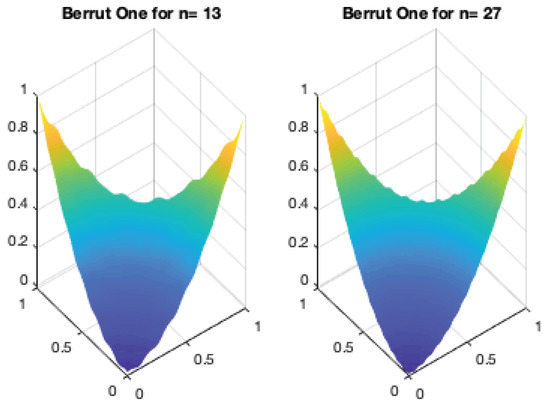
Figure 6. Bivariate Berrut One for $f(x,y)=x^2+y^2,$$n=13,27$.

Figure 7 shows the interpolant of $f(x,y)=sin\left(2\pi ({(x-1/3)}^2+{(y-1/3)}^2)\right)$ for the same degrees.

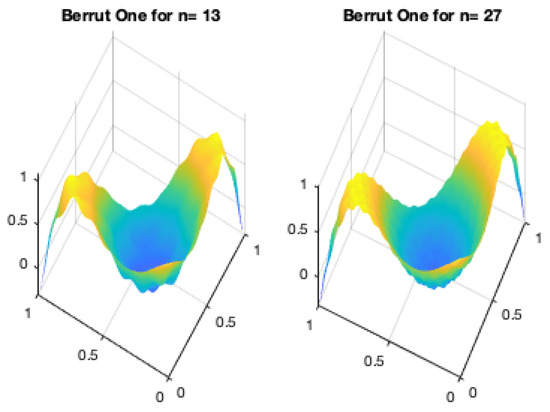
Figure 7. Bivariate Berrut One for $f(x,y)=sin\left(2\pi ({(x-1/3)}^2+{(y-1/3)}^2)\right),$$n=13,27$.

One may notice that the interpolant is reasonable for higher values of n but leaves room for improvement.

A Hybrid Interpolant

For any linear interpolant it is possible, by means of a so-called Boolean sum, to create a hybrid version that reproduces any specifed finite dimensional subspace of functions, the most common example of such being the space of polynomials of degree one. Indeed, for example, if $L\left(f\right)$ denotes the linear interpolant of f at the three vertices of $T,$ i.e.,

$$Lf(x,y)=f(0,0)(1-x-y)+f(1,0)x+f(0,1)y$$

then for $\widehat{f}(x,y):=f(x,y)-Lf((x,y),$ we may defined

$$B{h}_n^{\left(1\right)}(x,y):=B_n^{\left(1\right)}(x,y)+Lf(x,y)$$

where $B_n^{\left(1\right)}$ is the interpolant of $\widehat{f}$.

Figure 8 give a comparison between the original $B_n^{\left(1\right)}$ and its hybrid version, for $f(x,y)=1+2x+3y$ and $n=7$.

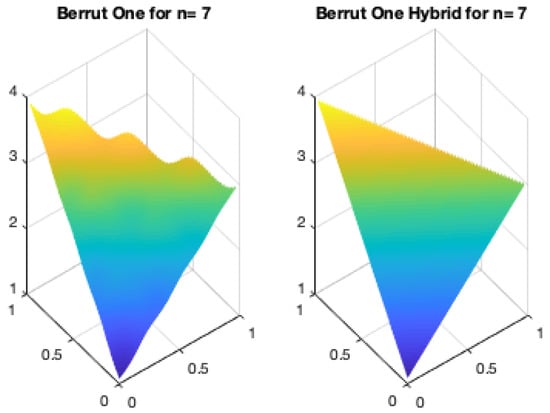
Figure 8. Berrut One and its Hybrid for $n=7$ and $f(x,y)=1+2x+3y$.

3. The Extension of Berrut’s Second Interpolant to Equally Spaced Points on a Triangle

Berrut’s second interpolant (for when the boundary points are included) involves the introduction of weights, adjusted at the boundary, to ensure the reproduction of linears. In general, for weights ${\beta }_{ij},$$0\le i+j\le n,$ we define

$$B_n^{\left(2\right)}(x,y)=\frac{{\sum }_{i+j\le n}{\beta }_{ij}f(i/n,j/n)\frac{{(-1)}^{i+j}}{(x-i/n)(y-j/n)}}{{\sum }_{i+j\le n}{\beta }_{ij}\frac{{(-1)}^{i+j}}{(x-i/n)(y-j/n)}}.$$

(12)

In the bivariate case the reproduction of linears splits into n odd and n even cases. We consider first the n odd case for which we define the weights

$${\beta }_{ij}:=\left\{\begin{array}{cc}0& (i,j)=(0,0),(n,0),(0,n)\hfill \\ 1/2& 1\le i\le n-1,j=0\hfill \\ 1/2& 1\le j\le n-1,i=0\hfill \\ 1/2& 1\le i\le n-1,j=i\hfill \\ 1& \mathrm{otherwise}\hfill \end{array}\right.$$

(13)

(i.e., 0 at the three vertices, $1/2$ at the interior edge points and 1 at the triangle interior points). The $n=5$ case is shown in Figure 9.

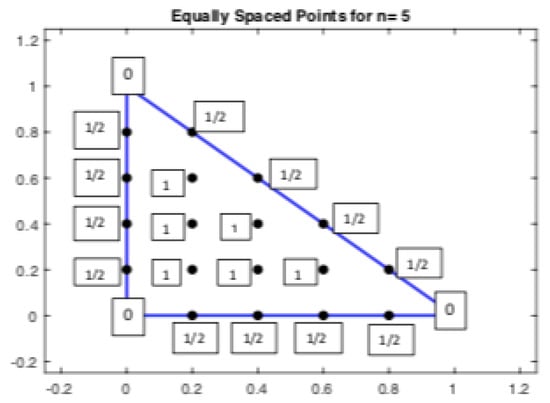
Figure 9. Weights on the triangle.

Proposition 4.

For $n>1$ odd and weights given by (13), $B_n^{\left(2\right)}(x,y)$ reproduces polynomials of degree one.

Proof. 

We remark that the $n=1$ case has all weights zero, and hence is not relevant. □

We will make use of univariate reproduction formulas for Berrut’s second interpolant.

Lemma 1.

For any points $x_0<x_1<\cdots <x_m$ and weights $w_i\in \mathbb{R},$

$$\sum _{i=0}^m{w}_i\frac{{(-1)}^i}{x-x_i}{x}_i=x\left\{\sum _{i=0}^m{w}_i\frac{{(-1)}^i}{x-x_i}\right\}$$

if and only if

$$\sum _{i=0}^m{w}_i{(-1)}^{i+1}=0.$$

Proof. 

We calculate

$$\begin{array}{cc}\hfill \sum _{i=0}^m{w}_i\frac{{(-1)}^i}{x-x_i}{x}_i& =\sum _{i=0}^m{w}_i\frac{{(-1)}^i}{x-x_i}((x_i-x)+x)\hfill \\ \hfill & =\sum _{i=0}^m{w}_i{(-1)}^{i+1}+x\left\{\sum _{i=0}^m{w}_i\frac{{(-1)}^i}{x-x_i}\right\}\hfill \\ \hfill & =x\left\{\sum _{i=0}^m{w}_i\frac{{(-1)}^i}{x-x_i}\right\}\hfill \\ \hfill & \iff \sum _{i=0}^m{w}_i{(-1)}^{i+1}=0.\hfill \end{array}$$

□

Lemma 2.

Consider the weights

$$w_i:=\left\{\begin{array}{cc}a& i=0,m\hfill \\ 1& 1\le i\le m-1\hfill \end{array}\right.$$

with $a\in \mathbb{R}$ a parameter. Then for $a=1/2$ and any $m\ge 1,$ or $a=0$ and m odd

$$\sum _{i=0}^m{w}_i\frac{{(-1)}^i}{x-x_i}{x}_i=x\left\{\sum _{i=0}^m{w}_i\frac{{(-1)}^i}{x-x_i}\right\}.$$

Proof. 

By Lemma 1 we need only show that ${\sum }_{i=0}^m{w}_i{(-1)}^{i+1}=0$.

The $a=1/2$ case is the result first proved by Berrut and hence we leave out the details. In case $a=0$ and m is odd then we calculate

$$\sum _{i=0}^m{w}_i{(-1)}^{i+1}=\sum _{i=1}^{m-1}{(-1)}^{i+1}=0$$

as this is an alternating sum of $\pm 1$ with an even ($m-1$) number of terms. □

Now to prove Proposition 4. We wish to show that

$$\sum _{i+j\le n}{\beta }_{ij}f(i/n,j/n)\frac{{(-1)}^{i+j}}{(x-i/n)(y-j/n)}=f(x,y)\sum _{i+j\le n}{\beta }_{ij}\frac{{(-1)}^{i+j}}{(x-i/n)(y-j/n)}$$

for any $f(x,y)=ax+by+c$. Clearly it suffices to show this for $f(x,y)=x,$ which we now proceed to do. First note that, by scaling by a factor of n this is equivalnet to showing that

$$\sum _{i+j\le n}{\beta }_{ij}i\frac{{(-1)}^{i+j}}{(x-i)(y-j)}=x\sum _{i+j\le n}{\beta }_{ij}\frac{{(-1)}^{i+j}}{(x-i)(y-j)}.$$

Now write the summation by rows as

$$\sum _{j=0}^n{(-1)}^j\left\{\sum _{i=0}^{n-j}{\beta }_{ij}i\frac{{(-1)}^i}{(x-i)(y-j)}\right\}.$$

For the first row, $j=0,$ the weights correspond to the lower edge and are

$$0,1,1,\cdots ,1,0$$

and we apply the univariate Lemma with $a=0$ and $m=n$ to obtain

$$\sum _{i=0}^{n-0}{\beta }_{i0}i\frac{{(-1)}^{i+j}}{(x-i)(y-j)}=x\sum _{i=0}^{n-0}{\beta }_{i0}\frac{{(-1)}^{i+j}}{(x-i)(y-j)}.$$

For the other rows, $j=1,\cdots ,(n-1)$ the weights are

$$\frac{1}{2},1,\cdots ,1,\frac{1}{2}$$

and we may apply the univariate Lemma with $a=1/2$ and $m=n-j$ to obtain

$$\sum _{i=0}^{n-j}{\beta }_{ij}i\frac{{(-1)}^{i+j}}{(x-i)(y-j)}=x\sum _{i=0}^{n-j}{\beta }_{ij}\frac{{(-1)}^{i+j}}{(x-i)(y-j)}.$$

For the top row (actually a singleton), ${\beta }_{0,n}=0$ and so there is nothing to do. □

Remark 6.

The zero weights at the vertices means that $B_n^{\left(2\right)}(x,y)$ will not interpolate at those points. It will however provide an order $1/n$ approximation to the corresponding value of f, provided it is minimally smooth. The approximation properties of these interpolants will be discussed in a forthcoming work.

Just as in the first interpolant case, by Lemma 3, there are poles at $(\alpha ,\beta ),$$0\le \alpha ,\beta \le n,$$\alpha +\beta >n$. However, just as in the first case, there are no poles in the triangle T.

Proposition 5.

For at least $n=1,3,\cdots ,21,$

$$d_n(x,y)>0,(x,y)\in T.$$

Proof. 

We do this in exactly the same manner as in the first case, by using degree elevation to produce a positivity certificate, one degree at a time. The minimal values of degree elevation are displayed in Table 2. □

Table 2. Degree Elevation r for Degree n.

n	r	||	n	r
3	0	||	13	75
5	7	||	15	101
7	17	||	17	131
9	33	||	19	165
11	51	||	21	203

The n even case splits into two subcases.

n, A Multiple of Four

In case n is a multiple of four we introduce the weights of 1 at interior points and along each edge

$$0,\frac{1}{2},\cdots ,\frac{1}{2},\frac{1}{4},\frac{1}{2},\frac{1}{4},\frac{1}{2}.\cdots ,\frac{1}{2},0$$

(14)

where the $1/2$ bracketed by $1/4$ to the left and right is the middle entry, $i=n/2$ (Figure 10).

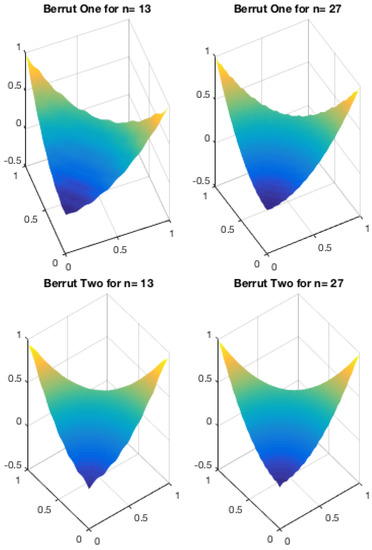
Figure 10. Above: Berrut’s one. Below: Berrut’s two.

We first remark that in the univariate case the rational interpolant with these weights, for n a multiple of four, reproduces linears.

Lemma 3.

For n a multiple of four and the weights given by (14),

$$\sum _{i=0}^n{w}_i\frac{{(-1)}^i}{x-x_i}{x}_i=x\left\{\sum _{i=0}^n{w}_i\frac{{(-1)}^i}{x-x_i}\right\}.$$

Proof. 

Applying Lemma 1 we calculate

$$\begin{array}{cc}\hfill \sum _{i=0}^n{w}_i{(-1)}^{i+1}& =\sum _{i=1}^{n-1}{w}_i{(-1)}^{i+1}(\mathrm{as}{w}_0=w_n=0)\hfill \\ \hfill & =\frac{1}{2}\sum _{i=1}^{n-1}{(-1)}^{i+1}-\frac{1}{4}\left\{{(-1)}^{(n/2-1)+1}+{(-1)}^{(n/2+1)+1}\right\}\hfill \\ \hfill & =\frac{1}{2}\sum _{i=1}^{n-1}{(-1)}^{i+1}-\frac{1}{4}\left\{(+1)+(+1)\right\}(\mathrm{as}n/2\mathrm{is}\mathrm{even})\hfill \\ \hfill & =\frac{1}{2}(+1)-\frac{1}{2}\hfill \\ \hfill & =0\hfill \end{array}$$

and the result follows. □

Proposition 6.

For the weights $q_{ij}$ given by (14) and n a multiple of four, the Berrut two extension reproduces linears.

Proof. 

We will show that

$$\sum _{i+j\le n}{\beta }_{ij}f(x_i,y_j)\frac{{(-1)}^{i+j}}{(x-x_i)(y-y_j)}=\sum _{i+j\le n}{\beta }_{ij}\frac{{(-1)}^{i+j}}{(x-x_i)(y-y_j)}$$

for any $f(x,y)=ax+by+c$. Again, it suffices to show this for $f(x,y)=x,$ i.e., that

$$\sum _{i+j\le n}{\beta }_{ij}{x}_i\frac{{(-1)}^{i+j}}{(x-x_i)(y-y_j)}=x\left\{\sum _{i+j\le n}{\beta }_{ij}\frac{{(-1)}^{i+j}}{(x-x_i)(y-y_j)}\right\}.$$

We again proceed row by row. The bottom row $j=0$ is the case discussed in Lemma 3. The other rows, other than for $j=n/2\pm 1,$ follow from the $a=1/2$ case of Lemma 2. For $j=n/2-1$ we have

$$\begin{array}{cc}\hfill \sum _{i=0}^{n-j}{q}_{ij}\frac{{(-1)}^{i+j}}{(x-x_i)(y-y_j)}{x}_i& =\frac{{(-1)}^j}{y-y_j}\sum _{i=0}^{n-(n/2-1)}{q}_{ij}\frac{{(-1)}^i}{x-x_i}{x}_i\hfill \\ \hfill & =\frac{{(-1)}^j}{y-y_j}\sum _{i=0}^{n/2+1}{q}_{ij}\frac{{(-1)}^i}{x-x_i}((x_i-x)+x)\hfill \\ \hfill & =\frac{{(-1)}^j}{y-y_j}\left\{\sum _{i=0}^{n/2+1}{q}_{ij}{(-1)}^{i+1}+x\left[\sum _{i=0}^{n/2+1)}{q}_{ij}\frac{{(-1)}^i}{x-x_i}\right]\right\}.\hfill \end{array}$$

Now we claim that

$$\sum _{i=0}^{n/2+1}{q}_{ij}{(-1)}^{i+1}=0$$

from which the result for the $j=(n/2-1)$th row follows. To see this just note that for row $j=n/2-1,$

$$\begin{array}{cc}\hfill \sum _{i=0}^{n/2+1}{q}_{ij}{(-1)}^{i+1}& =\sum _{i=1}^{n/2}{(-1)}^{i+1}+\frac{1}{4}\left\{{(-1)}^{0+1}+{(-1)}^{(n/2+1)+1}\right\}\hfill \\ \hfill & =0+\frac{1}{4}\left\{(-1)+(+1)\right\}(\mathrm{as}n/2\mathrm{even})\hfill \\ \hfill & =0.\hfill \end{array}$$

The row $j=n/2+1$ is completely analogous. □

Just as in the previous cases, by Lemma 3, there are poles at $(\alpha ,\beta ),$$0\le \alpha ,\beta \le n,$$\alpha +\beta >n$. However, we conjeture that there are no poles in the triangle T.

Proposition 7.

For at least $n=4,8,\cdots ,20,$

$$d_n(x,y)>0,(x,y)\in T.$$

Proof. 

We do this in exactly the same manner as before, by using degree elevation to produce a positivity certificate, one degree at a time. The minimal values of degree elevation are displayed in Table 3.

Table 3. Degree Elevation r for Degree n.

n	r
4	0
8	59
12	175
16	341
20	550

This concludes the proof. □

Figure 11 shows the result of interpolating $f(x,y)=x^2+y^2$ for $n=8$ and $n=12$.

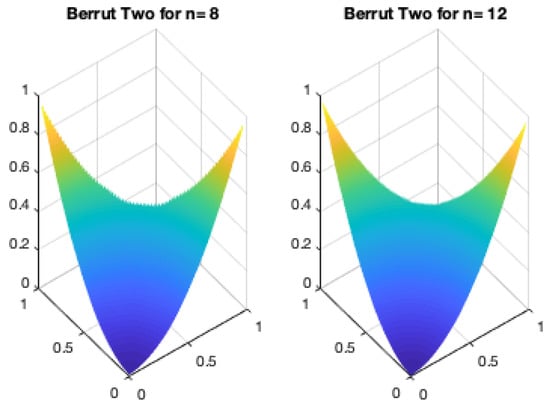
Figure 11. Berrut Two for n a multiple of four.

4. n Even, But n/2 Odd

In case n is even but not a multiple of four, i.e., $n/2$ is odd, we introduce the weights of 1 at interior points and along each edge

$$0,\frac{1}{2},\cdots ,\frac{1}{2},0,\frac{1}{2},\frac{1}{2}.\cdots ,\frac{1}{2},0$$

(15)

where the 0 in the middle is the entry, $i=n/2$.

We first remark that in the univariate case the rational interpolant with these weights, for n even but $n/2$ odd, reproduces linears.

Lemma 4.

For n even but $n/2$ odd, and the weights given by (15),

$$\sum _{i=0}^n{w}_i\frac{{(-1)}^i}{x-x_i}{x}_i=x\left\{\sum _{i=0}^n{w}_i\frac{{(-1)}^i}{x-x_i}\right\}.$$

Proof. 

By Lemma 1, we need only show that

$$\sum _{i=0}^n{w}_i{(-1)}^{i+1}=0.$$

However, in this case

$$\begin{array}{c}\hfill \sum _{i=0}^n{w}_i{(-1)}^{i+1}=\frac{1}{2}\left\{\sum _{i=1}^{n/2-1}{(-1)}^{i+1}+\sum _{i=n/2-1}^{n-1}{(-1)}^{i+1}\right\}=\frac{1}{2}\{0+0\}\end{array}$$

as both are alternating sums of $\pm 1$ with an even number of terms, $n/2-1$ for the first sum and $(n-1)-(n/2+1)+1=n/2-1$ for the second. □

Proposition 8.

For n even but $n/2$ odd and the edge weights given by (15), the generalized Berrut interpolant reproduces linears.

Proof. 

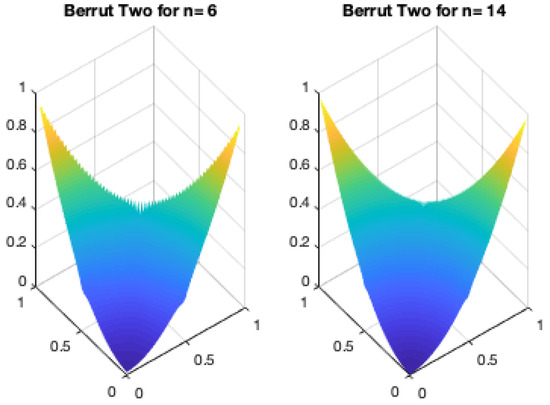
We again go row by row. The bottom row is the case of Lemma 4. The rows with $1/2$ at the beginning and end are the classical Berrut case, whereas the middle row $j=n/2$ with weights

$$0,1,1,\cdots ,1,1,0$$

is handled by Lemma 2 as, by assumption, $n/2$ is odd (Figure 12). □

Figure 12. Berrut Two for n even but $n/2$ odd and $f(x,y)=x^2+y^2$.

Remark 7.

There are, as always, poles oustide of the triangle T and we conjecture that there are again no poles inside T.