1. Introduction
The stability analysis and control design of a nonlinear system is a difficult task. In fact, the controlled object of the control system is always nonlinear. Sometimes it is difficult to use linearization or recognition techniques to describe complex nonlinear systems. Recently, the so-called fuzzy model [
1,
2], which uses fuzzy implication to express the local linear input/output relationship of nonlinear systems, is used to approximate nonlinear objects. The study conducted by [
1] used fuzzy logic to model two effective factors that affect melatonin regarding Major Depressive Disorder (MDD). The Fuzzy Logic Direct Model Reference Adaptive Control (DMRAC) is the choice of insulin infusion control for Type I diabetes, as shown in [
2]. Takagi-Sugeno (TS)-type fuzzy is a special case of fuzzy systems, where Takagi-Sugeno (TS)-type fuzzy controllers have been fully applied to stabilize controller design. In addition, based on the parallel distributed compensation (PDC) technology, the control design of this type of fuzzy control system is derived according to [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13]. A new, observer-based fuzzy controller design method with a time-delay adaptability is proposed in the study conducted by [
3]. The designed controller contains both current and past state information of the system and can be derived by solving a set of linear matrix inequalities (LMI). In the study put forth by [
4], the so-called fuzzy Lyapunov function (i.e., multiple Lyapunov function) is used to solve the stability analysis and stability problems of the Takagi-Sugeno fuzzy system. In order to make full use of the fuzzy Lyapunov function, we propose a new parallel distributed compensation (PDC) scheme, which feeds back the time derivative of the premise membership function. The study conducted by [
5] considers the observer design for a class of nonlinear systems with unknown inputs. The Parallel Distributed Observer (PDO), composed of a local linear observer and an appropriate level of membership function, is a conventional observer of the Takagi-Sugeno fuzzy bilinear system. The study conducted by [
6] used the Takagi-Sugeno (TS) fuzzy model to design a controller and assuming that uncertainty affects system behavior through state and control input, an observer that can capture part of the uncertainty trajectory related to control input is proposed. The nonlinear system and the system demonstrate the proposed fault-tolerant control scheme. The proposed fault-tolerant controller is implemented and verified on three interconnected cones. The tank system has two constraints in terms of failure, one is the construction of the actuator, the other is the system composition (leakage). The MATLAB Simulink platform with linear fuzzy model and The LMI toolbox is used to solve the LMI and determine the recommended controller gain design method [
7]. Based on Mayer’s convergence theorem, [
8] studied the stability analysis of the linear Takagi-Sugeno (T-S) free fuzzy systems with corresponding parameter uncertainties. Three numerical iterative schemes are proposed, namely: Jacobi, Gauss-Seidel, and continuous over-relaxation (SOR) to solve the fuzzy system of linear equations (FSLE). The convergence characteristics of these iterative schemes have been discussed [
9]. The study conducted by [
10] proposed to use the approximation of the CKM algorithm in the original harmony search algorithm (HS) to adjust the pitch adjustment rate (PArate) parameter in the Type 2 fuzzy system. The study conducted by [
11] applied construct to the control system in the multivariable nonlinear system stability theory, applied the Lyapunov theory, performed input-output stability analysis, and verified the stability domain. The proposed considerations can be applied to various structures to adjust the speed of electric drives using various PI fuzzy controllers. The study conducted by [
12] proposed a fuzzy controller design method based on the interval type 2 (IT2) T-S fuzzy model for stochastic nonlinear systems affected by actuator saturation. Using Lyapunov’s theory, the stability analysis of the IT2 T-S fuzzy model and some corresponding sufficient conditions are established [
13]. The idea is to design a compensator for each rule of the fuzzy system. The final overall fuzzy controller is usually non-linear; it is a fuzzy blend of each individual linear controller.
Over the years, the stability problem and control design of time-delay systems have also been explored, because delays are common in engineering systems [
14,
15,
16,
17]. The work of [
14] studies the stability of discrete time-delay systems. The type of system considered is represented by a delay difference equation, and a nonlinear discrete-time system with time-varying delay is modeled. It converts from a matrix representation to an arrow, allowing the use of aggregation techniques and M matrix properties to determine new sufficient stability conditions. The robust stability of a class of linearly switched time-varying delay systems with all unstable subsystems and interval uncertainties are studied [
15]. By establishing a suitable time scheduling multiple co-positive Lyapunov-Krasovskii functional (MCLKF) and adopting a mode-dependent dwell time (MDDT) switching strategy, a new delay-related sufficient condition is formulated to ensure the global uniform asymptotic stability of the system under consideration. The study conducted by [
16] aimed at a class of high-order, nonlinear systems with a time delay, where a design method of an output feedback tracking controller is proposed. In order to deal with the time lag, a suitable Lyapunov-Krasovskii tracking analysis is cleverly constructed, and the output feedback tracking controller is designed using the homogeneous dominance method. In the works of [
17], the delay-related stability of the haptic system is studied by developing a new stability criterion. First, the haptic system inevitably introduces time delays by using a communication network to transmit information between the controller and the haptic device. When discussing the stability of the haptic system near its operating point, the original nonlinear system is modeled as a linear system with the above-mentioned time delay. In summary, the stability problem and control design of the T-S fuzzy time-delay system have aroused people’s great interest, and it is naturally worth studying ([
18,
19,
20,
21]). In the study conducted by [
18], the event-triggered communication (ETC) scheme is used to study the design of fuzzy
filters for nonlinear network control systems. First, a new adaptive ETC scheme is given to determine whether the sampled measurement output should be released to the communication network. In addition, the augmented fuzzy line integral Lyapunov function is introduced into the
performance analysis of the filter error system, and the time derivative information of the membership function is fully considered to reduce the conservativeness of the network fuzzy filter design. The author of [
19] proposes an adaptive fuzzy hierarchical sliding mode control method for a class of multi-input, multi-output unknown nonlinear time-delay systems with input saturation. Based on the Takagi-Sugeno fuzzy model method, an output feedback control strategy is developed for a class of continuous-time nonlinear time-delay systems through an improved repetitive control scheme [
20]. The author of [
21] studies the sampling data stabilization problem of Takagi-Sugeno (T-S) fuzzy system with time delay. By considering the state information in the interval from
to t and t to
, a new two-sided delay-related cyclic functional is introduced, which can not only relax the monotonic constraint (LKF) of the Lyapunov-Krasovskii functional, but also make better use of the actual sampling mode.
In this paper, based on the properties of matrix and norm measurements, we first give sufficient conditions for the robust stability test of uncertain fuzzy time-delay systems, the conditions of test results include delay-independent and delay-dependent. It needs only to solve r (the number of rules of the fuzzy model) inequality, not to find a common positive definite matrix P. It is a difficult task to find such a P, especially when the number of rules of the fuzzy model is large. Three numerical examples and one particular example are provided to illustrate the effectiveness of the proposed method. The following notations will be used throughout the paper: the identity matrix with dimension n is denoted by , λ(A) stands for the eigenvalues of matrix , ‖A‖ denotes the norm of matrix A, i.e., means the matrix measure of matrix A, i.e.,
2. System Description and Problem Statement
Consider a time-delay system described by the following T-S fuzzy model. This T-S fuzzy time-delay system is composed of
r rules that can be represented as follows:
: If
is
and
is
Then
And
is a bounded nonlinear perturbation vector satisfying
where
.
By using a center-average defuzzifer, product inference and singleton fuzzifier, the fuzzy time-delay system (1) can be inferred as
where
and
.
is the grade of membership of
in the fuzzy set
. It is seen that
and
.
For simplicity, we use the symbol to denote First we will derive the delay-independent stability condition of an unforced system (1). For this objective, some helpful lemmas are given below.
Consider the time-delay system
where
,
A and
are matrices in proper dimensions,
is the delay duration.
Lemma 1 [22]. The stability of system (4) implies the stability for the following systems and vice versa.
where z = exp(jw),
,
and
C.
In light of Lemma 1, it is obvious that the stability of the fuzzy time-delay system (3) is equivalent to that of the system
Lemma 2 [23]. For matrix
,
, the following relation holds:
Furthermore, we assume , and , the following relation holds:
Lemma 3. It is true that .
Proof 1. = 0
This completes the proof. □
3. Main Results
3.1. A. Delay-Independent Robust Stability
Now, we present a delay-independent condition of robust stability for the fuzzy time-delay system (1).
Theorem 1. The fuzzy time-delay system (1) will have robust stability with a delay-independence if
holds. Furthermore, the max perturbation bound b satisfies
Proof 2. The trajectory response of system (6) can be written as follows:
Applying the norm on both sides of Equation (9) and in view of Lemma 1, we can obtain the following equation.
Then, Equation (10) is a solution of the following system (11):
Since (from the comparison theorem), the exponential stability of implies that of . Hence, the system (6) is globally exponentially stable, if is negative. Furthermore, the system (1) is also stable due to the system (6) and (1) having the same stability properties. This completes the proof. □
Corollary 1. Consider the fuzzy system (1) without delay and perturbation is asymptotically stable, if the following condition is satisfied
Remark 1. In view of Theorem 1, the stability criterion of fuzzy system (1)doesn not need to find a common positive definite matrix to satisfy any inequality.
3.2. B. Delay-Dependent Robust Stability
Next, we will derive a sufficient stability condition for fuzzy time-delay system (1) with delay-dependence. One can obtain the following equation:
Hence, the system (3) can be written as
Furthermore, assume , , and .
Prior to the examination of robust stability problem for system (1), one useful concept is given below.
Lemma 4. Let for and if . Then there exist a and a such that for .
In the following, a sufficient condition for ensuring the asymptotic stability of a fuzzy time-delay system is proposed.
Theorem 2. Suppose
, then the fuzzy time-delay system (1) will have robust stability with delay-dependence, if
is satisfied.
Proof 3. The trajectory response of system (14) can be written as follows
Applying the norm on both sides of Equation (16), we obtain
Then, the Equation (18) is a solution of the following system (19).
Since
(from the comparison theorem), the exponentially stable of
implies that of
. From Lemma 4, system (1) is asymptotically stable, if the following equation is satisfied:
This completes the proof. □
3.3. C. Controller Design
In the subsection, this paper investigates the problem of designing a fuzzy state feedback controller to stabilize the system (1). Based on the concept of PDC, we consider the following fuzzy control rules:
Hence, the overall output of this fuzzy controller is
By substituting (21) into (3), the global closed-loop fuzzy system becomes
In light of Lemma 1, it is obvious that the stability of the fuzzy time-delay system (22) is equivalent to that of the system
Furthermore, we assume and . Next, we shall discuss the robust stabilization problem of the system (1).
Theorem 3. Suppose the state feedback gains
satisfy the following conditions:
For
i,
j = 1, 2,…,
r, then the perturbed fuzzy time-delay system (1) can be stabilized asymptotically by the fuzzy controller (21). Furthermore, the tolerable perturbation bound
b satisfies
Proof 4. The trajectory response of system (22) can be written as follows:
Applying the norm on both sides of Equation (26) and in view of lemma 1, we can obtain the following equation.
Then, Equation (28) is a solution of the following system (29).
Since (from the comparison theorem), the exponential stability of implies that of . Hence, the system (26) is globally exponential stability, if is negative, Furthermore, the system (1) is also stable due to the system (26) and (1) having the same as stability properties. This completes the proof. □
Remark 2. In fact, we can simplify state feedback gains
to
, for i = 1, 2,…,r, from the condition (24). Hence, we only need to consider the r fuzzy rules for the system (1) then we can find the controller gain F, (i.e., the controller (20) and condition (24) can be turned into the following controller and condition, respectively).
Corollary 2. In view of Remark 2, the condition (31) can be easily transformed into the following problem of LMIs:
Corollary 3. If the tolerable perturbation bound b can be known, and the state feedback gains
, satisfy the following problem of LMIs.
For i = 1,2,…,r, then the perturbed fuzzy time-delay system (1) can be stabilized asymptotically by the fuzzy controller (30).
Corollary 4. The system (1) without time-delay and perturbation is asymptotically stable, if there exists state feedback gains
such that
4. Example
Example 1. Consider the following simple T-S fuzzy time-delay model with Perturbation where the fuzzy rules are given by
where
,
,
,
and
.
The membership function for
are the Gaussian function forms
and
Now we want to analyze the system’s stability. Using Theorem 1, we obtain and . Hence, , the uncertain fuzzy time-delay System (35) is robust stable with delay-independence under the tolerable perturbation bound .
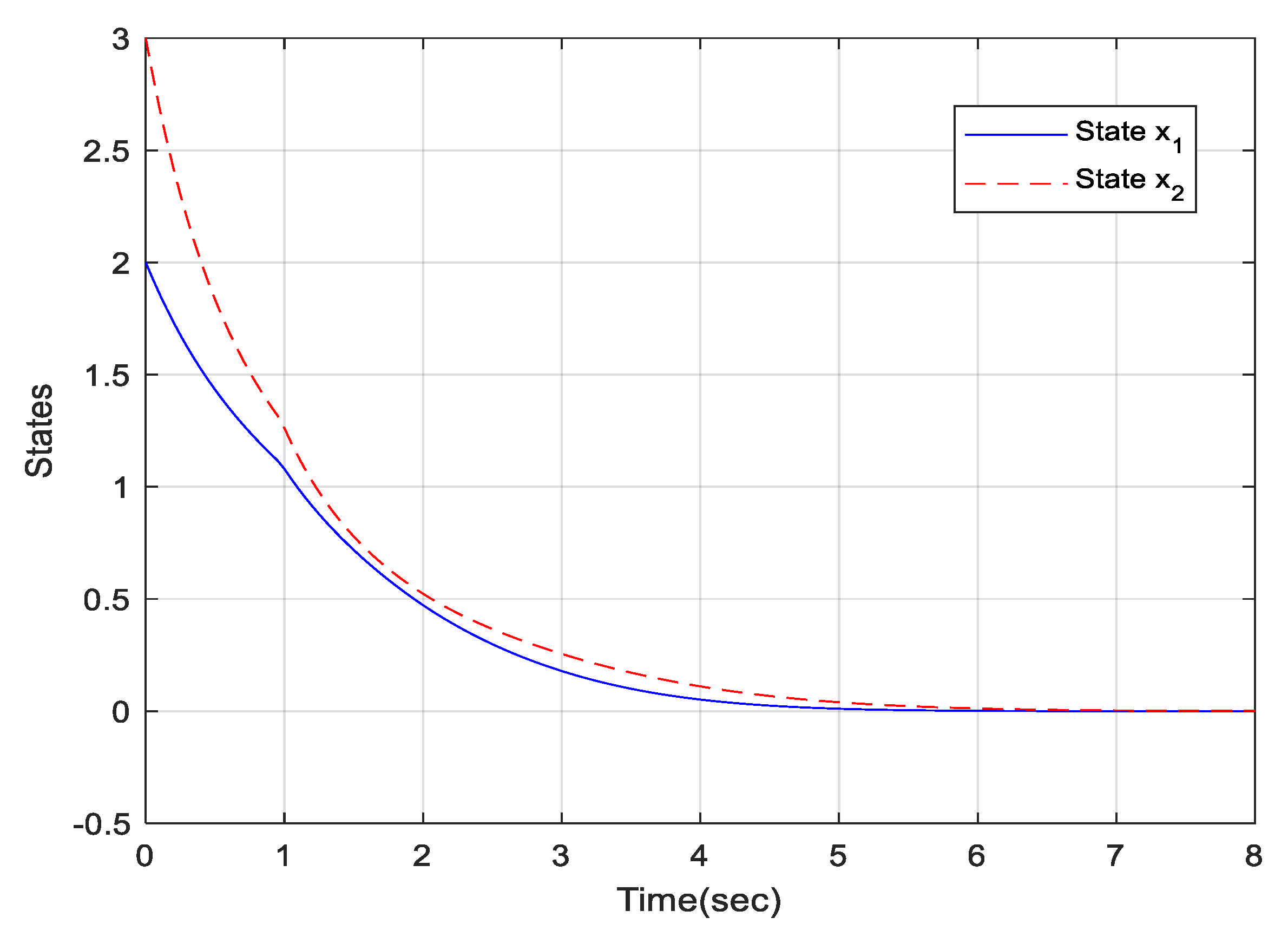
The trajectories for states of the T-S fuzzy time-delay System (35) is shown in
Figure 1 with initial value
and
. The solid line is the state of
and the dotted line is the state of
.
Example 2. Consider the following simple T-S fuzzy time-delay model with Perturbation where the fuzzy rules are given by
where
,
,
,
and
.
The membership function for
is as the same as for Example 1. Firstly, we can easily calculate
,
,
,
and
. In view of Theorem 2, the System (36) is robust stable, if the relationship between the delay and the tolerable perturbation bound b satisfy the following inequality
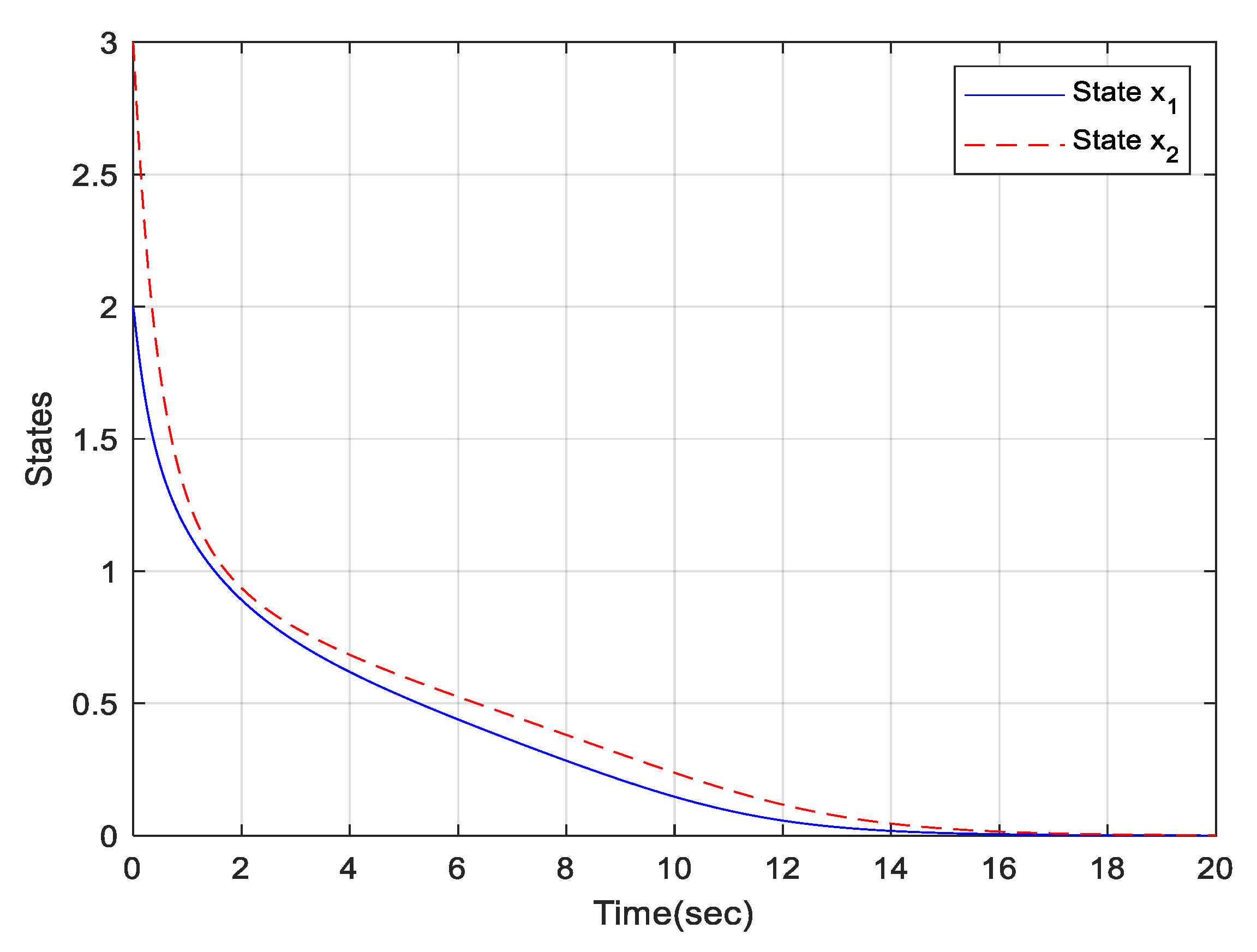
The trajectories for states of the T-S fuzzy time-delay System (36) is shown in
Figure 2 with initial value
and
. The solid line is the state of
and the dotted line is the state of
.
Example 3. Consider the following simple T-S fuzzy time-delay model with Perturbation where the fuzzy rules are given by
where
and
,
and
.
The membership function for is as the same for Example 1. We get controller gain matrices satisfying (32) by using the LMI technique as follows:
, then , , and . Hemce, and check the inequality (25), the tolerable bound is .
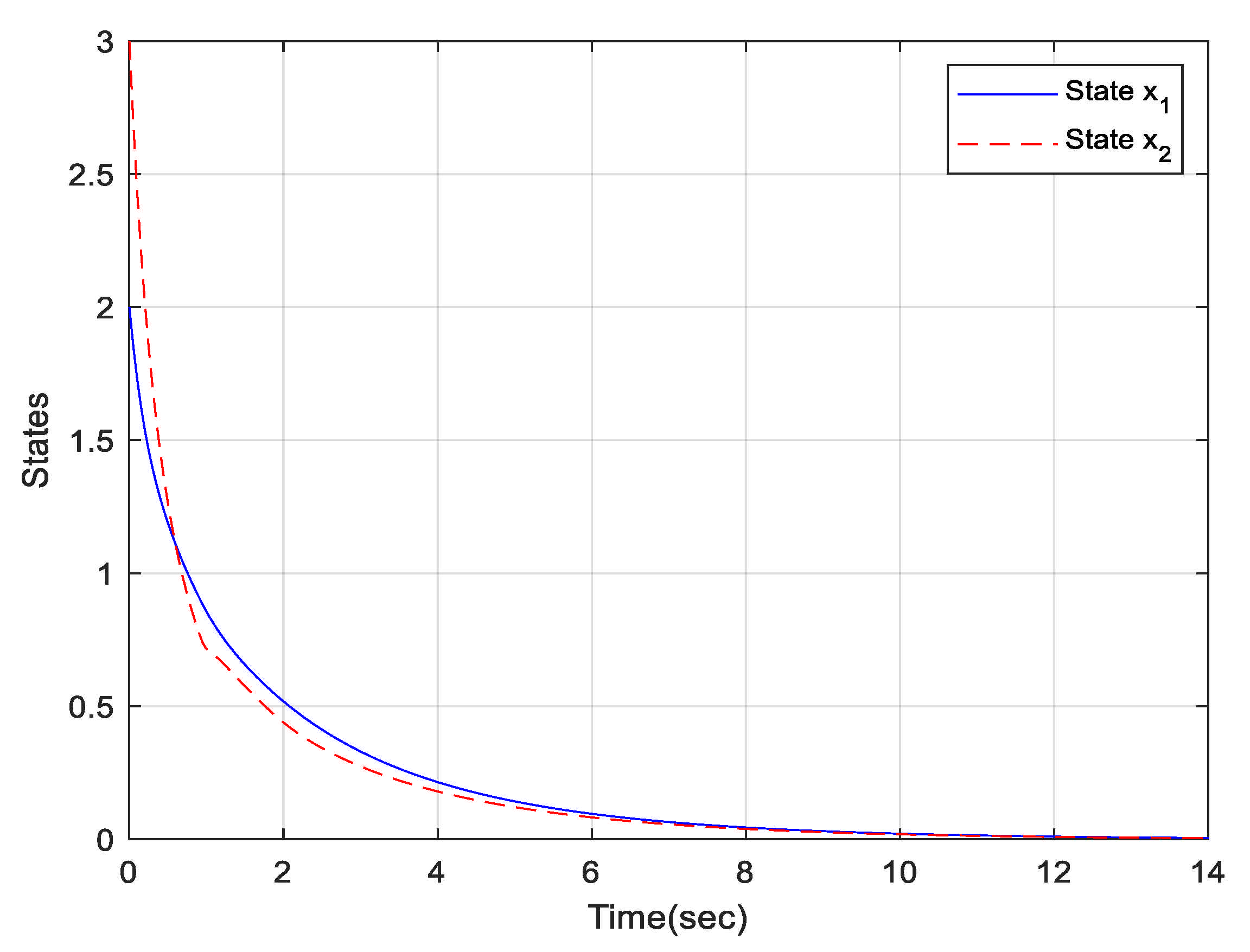
The trajectories for states of the T-S fuzzy time-delay System (37) is shown in
Figure 3 with initial value
and
. The solid line is the state of
and the dotted line is the state of
.
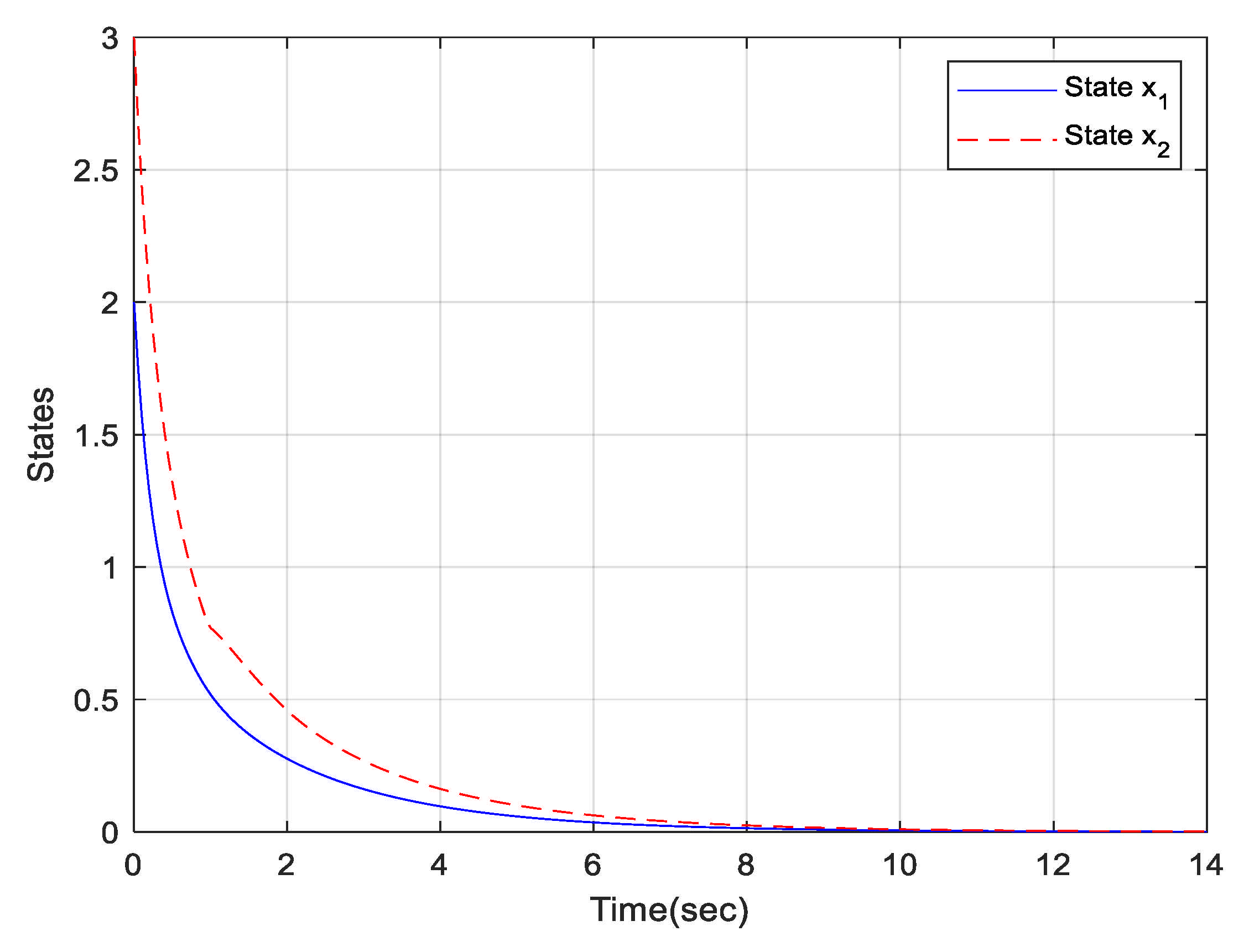
Furthermore, if we choose the gain matrices , then , , and Hence, and the perturbation bound can be obtained via Corollary 2.
The trajectories for states of the T-S fuzzy time-delay system (37) is shown in
Figure 4 with initial value
and
. The solid line is the state of
and the dotted line is the state of
.
Example 4. Consider the first order, irreversible, exothermic reaction
carried out in a well-mixed continuously stirred tank reactor (CSTR) [
21].
The membership function for
are
By using corollary 3 under the perturbation bound
b < 0.5, we get controller gain matrices (33) as follows:
The trajectories for states of the T-S fuzzy time-delay system (38) is shown in
Figure 5 with initial value
and
. The solid line is the state of
and the dotted line is the state of
.