Inferential Reasoning of Secondary School Mathematics Teachers on the Chi-Square Statistic
Abstract
:1. Introduction
2. Theoretical Framework
3. Methodology
3.1. Teachers Participating in the Study
3.2. Instrument of Inquiry
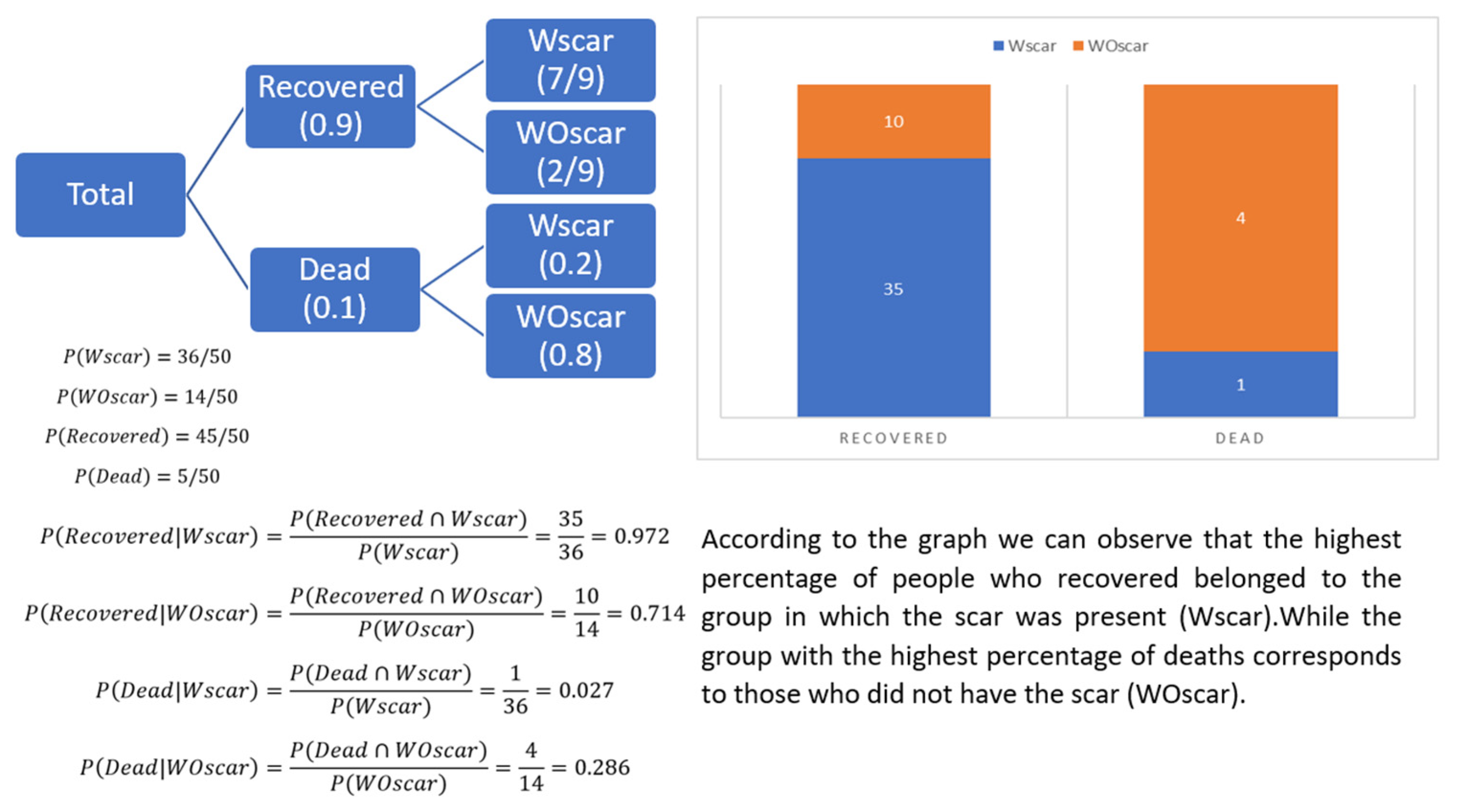
4. Analysis of Teachers’ Practices
4.1. Practices Associated with Activity 1
4.2. Practices Associated with Activity 2
5. Final Reflections
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
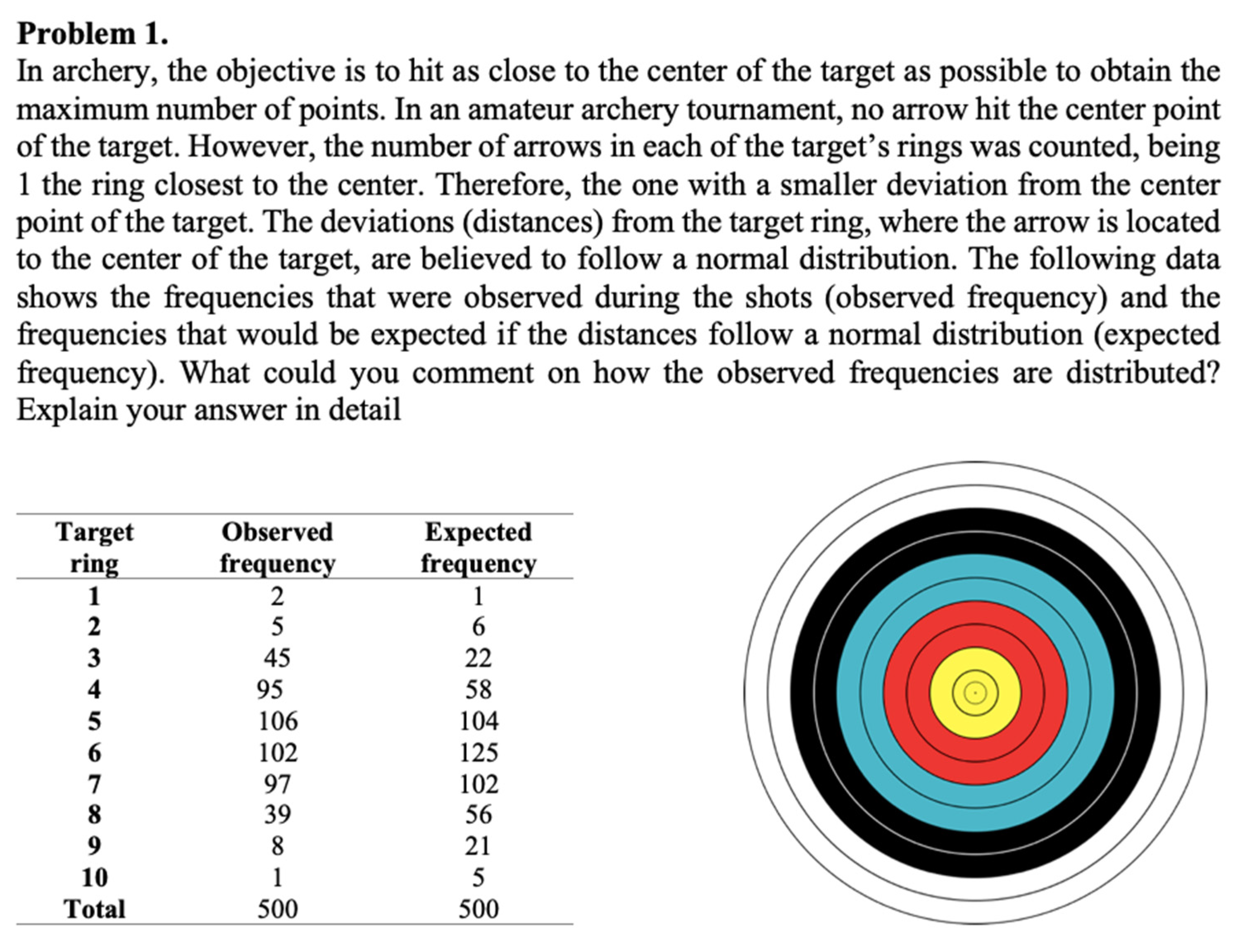
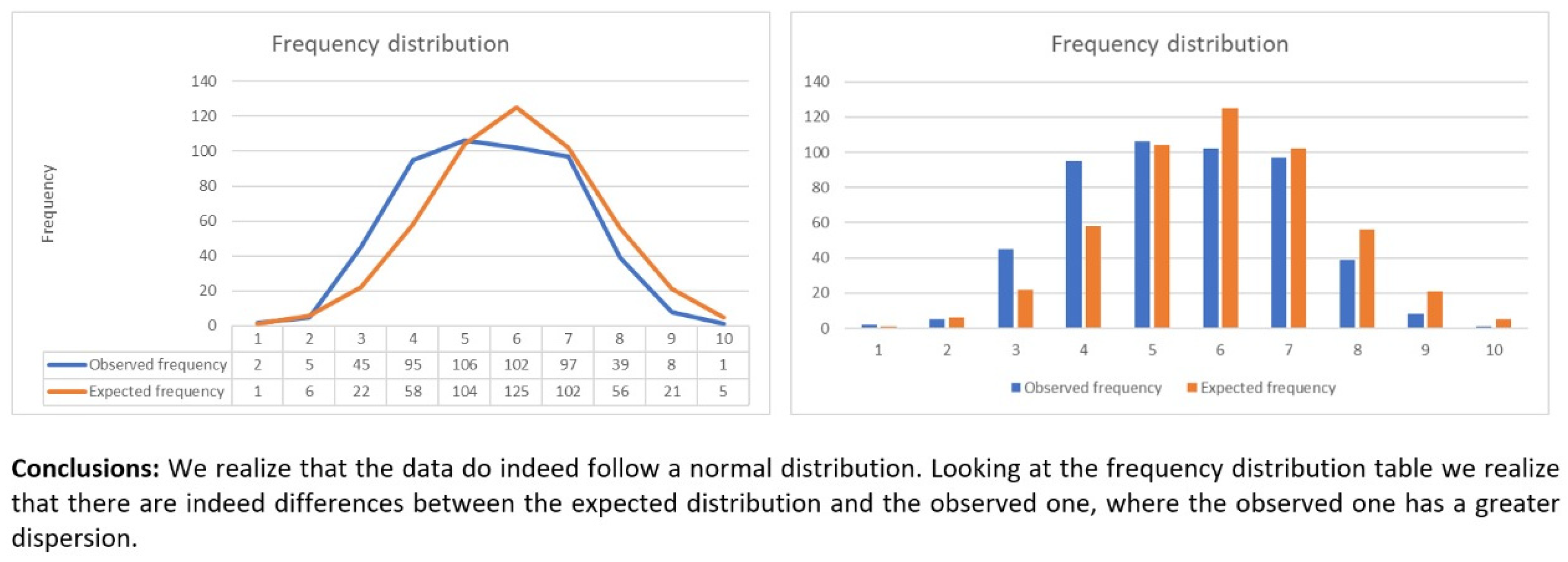
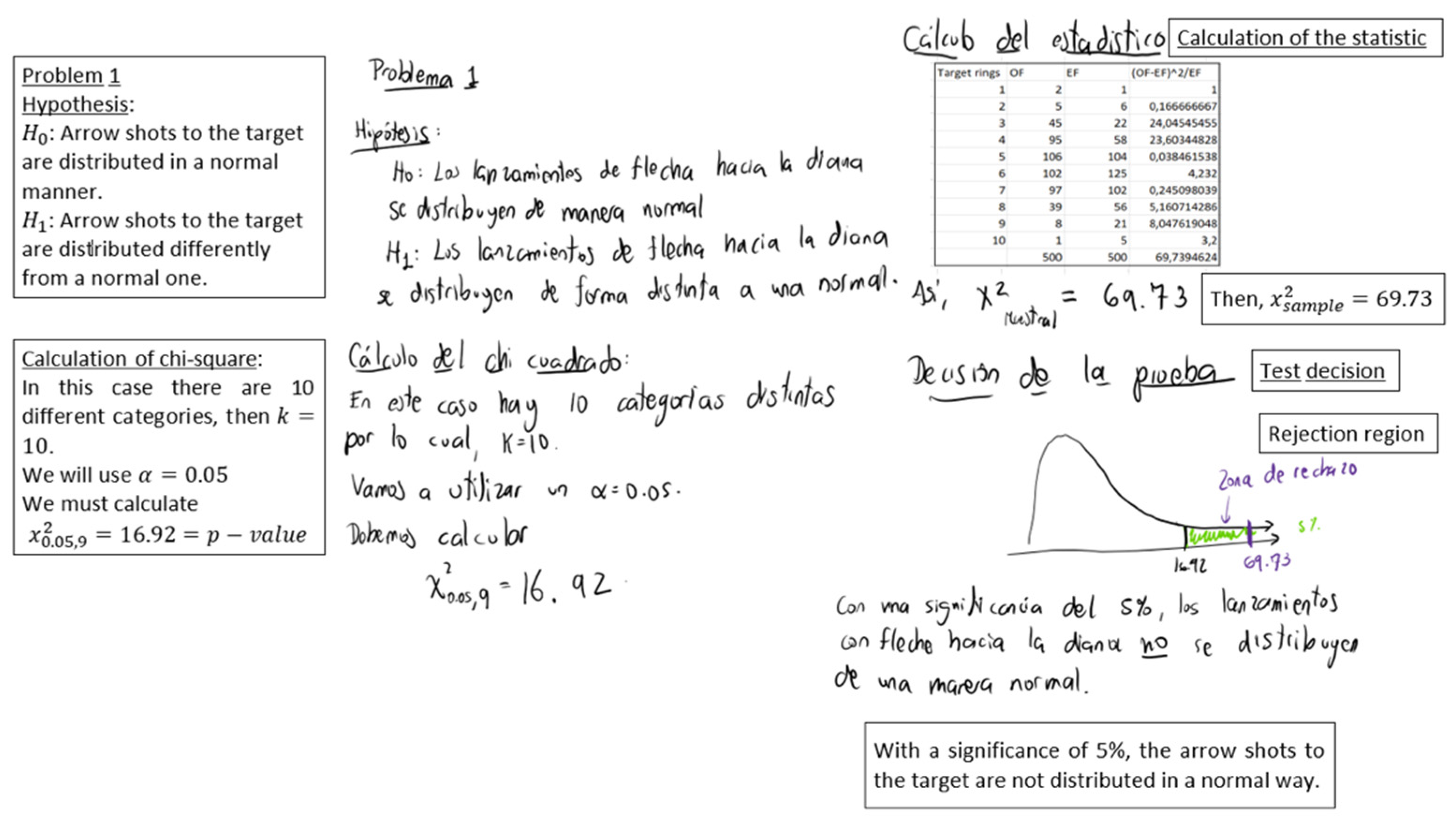
Appendix A


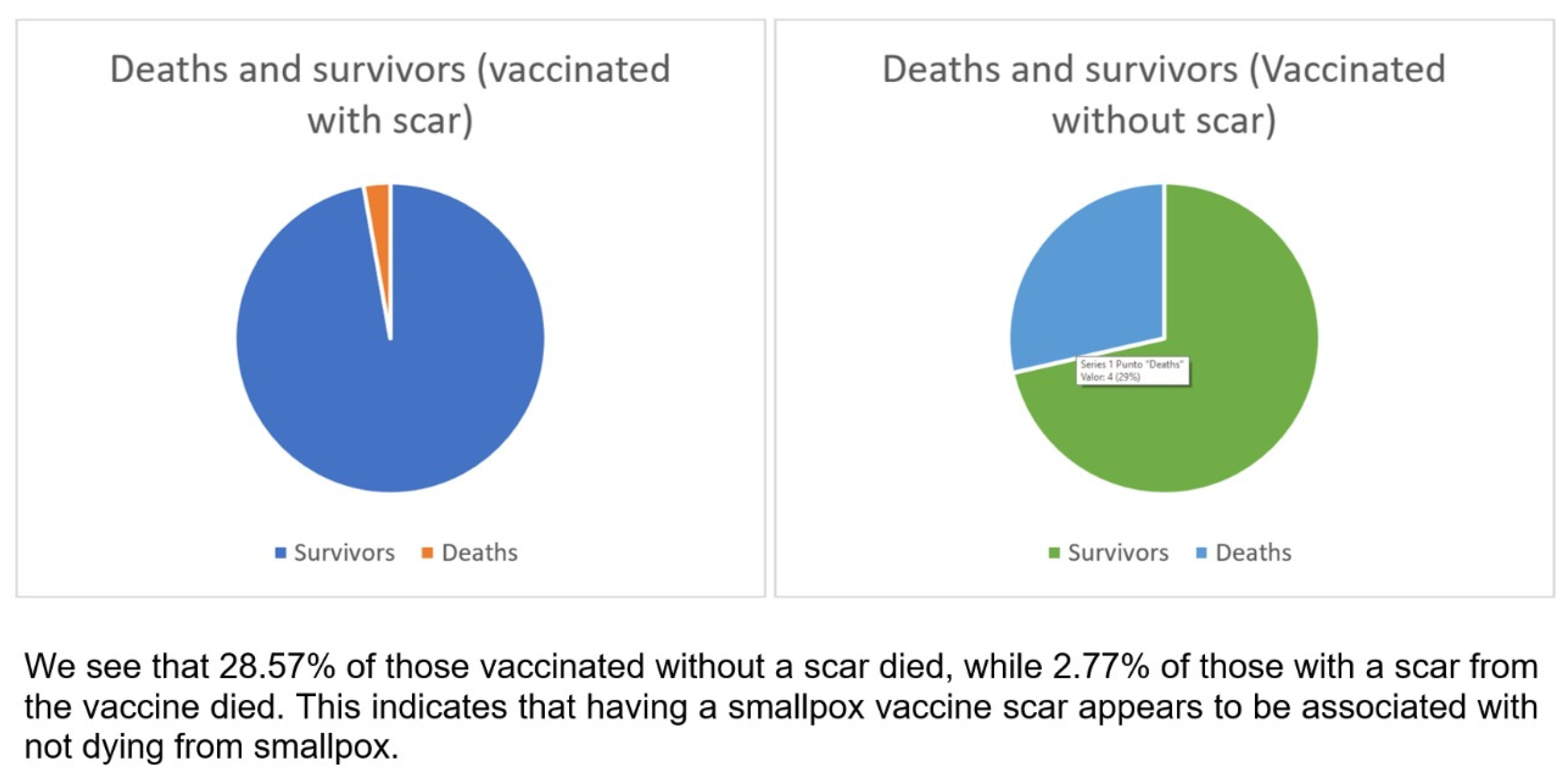
Appendix B


References
- Ministerio de Educación de Chile [Mineduc]. Bases Curriculares 3° y 4° Medio [Curricular Bases 3rd and 4th of Secondary Education]; Unidad de Currículum y Evaluación: Santiago, Chile, 2019.
- Callingham, R.; Watson, J.M. The development of statistical literacy at school. Stat. Educ. Res. J. 2017, 16, 181–201. [Google Scholar] [CrossRef]
- Pfannkuch, M. Reimagining curriculum approaches. In International Handbook of Research in Statistics Education, 1st ed.; Ben-Zvi, D., Makar, K., Garfield, J., Eds.; Springer International: Cham, Switzerland, 2018; pp. 387–413. [Google Scholar] [CrossRef]
- Sotos, A.E.C.; Vanhoof, S.; Van den Noortgate, W.; Onghena, P. Students’ misconceptions of statistical inference: A review of the empirical evidence from research on statistics education. Educ. Res. Rev. 2007, 2, 98–113. [Google Scholar] [CrossRef]
- Garfield, J.; Ben-Zvi, D. Developing Students’ Statistical Reasoning: Connecting Research and Teaching Practice, 1st ed.; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar] [CrossRef]
- Harradine, A.; Batanero, C.; Rossman, A. Students and teachers’ knowledge of sampling and inference. In Teaching Statistics in School Mathematics-Challenges for Teaching and Teacher Education, 1st ed.; Batanero, C., Burril, G., Reading, C., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 235–246. [Google Scholar] [CrossRef]
- Batanero, C.; Vera, O.D.; Díaz, C. Dificultades de estudiantes de psicología en la comprensión del contraste de hipótesis [Psychology students’ difficulties on understanding the contrast of hypotheses]. Números. Rev. Didáctica Matemáticas 2012, 80, 91–101. [Google Scholar]
- López-Martín, M.M.; Batanero, C.; Gea, M.M.; Arteaga, P. Assessing prospective high school teachers’ understanding of statistical hypotheses. In INTED 2018, Proceedings of the 12th International Technology, Education and Development Conference, Valencia, Spain, 5–7 March 2018; Gómez, L., López, A., Candel, I., Eds.; IATED: Valencia, Spain, 2018; pp. 2808–2813. [Google Scholar] [CrossRef]
- Batanero, C. Del análisis de datos a la inferencia: Reflexiones sobre la formación del razonamiento estadístico [Reflections on the formation of statistical reasoning]. Cuad. Investig. Form. Educ. Matemática 2013, 11, 277–291. [Google Scholar]
- Zieffler, A.; Garfield, J.; delMas, R.; Reading, C. A framework to support research on informal inferential reasoning. Stat. Educ. Res. J. 2008, 7, 40–58. [Google Scholar]
- Makar, K.; Rubin, A. A framework for thinking about informal statistical inference. Stat. Educ. Res. J. 2009, 8, 82–105. [Google Scholar]
- Doerr, H.M.; delMas, R.; Makar, K. A modeling approach to the development of students’ informal inferential reasoning. Stat. Educ. Res. J. 2017, 16, 86–115. [Google Scholar] [CrossRef]
- Jacob, B.L.; Doerr, H.M. Statistical reasoning with the sampling distribution. Quadrante 2014, 23, 123–146. [Google Scholar] [CrossRef]
- Pfannkuch, M.; Arnold, P.; Wild, C.J. What I see is not quite the way it really is: Students’ emergent reasoning about sampling variability. Educ. Stud. Math. 2015, 88, 343–360. [Google Scholar] [CrossRef]
- Makar, K.; Rubin, A. Learning about statistical inference. In International Handbook of Research in Statistics Education, 1st ed.; Ben-Zvi, D., Makar, K., Garfield, J., Eds.; Springer International: Cham, Switzerland, 2018; pp. 261–294. [Google Scholar] [CrossRef]
- Nilsson, P.; Schindler, M.; Bakker, A. The Nature and Use of Theories in Statistics Education. In International Handbook of Research in Statistics Education, 1st ed.; Ben-Zvi, D., Makar, K., Garfield, J., Eds.; Springer International: Cham, Switzerland, 2018; pp. 359–386. [Google Scholar] [CrossRef]
- Bakker, A.; Ben-Zvi, D.; Makar, K. An inferentialist perspective on the coordination of actions and reasons involved in making a statistical inference. Math. Educ. Res. J. 2017, 29, 455–470. [Google Scholar] [CrossRef] [Green Version]
- Cañadas, G.R.; Díaz, C.; Batanero, C.; Estepa, A. Precisión de los Estudiantes de Psicología en la Estimación de la Asociación [Psychology student’s estimation of association]. Bolema Bol. Educ. Matemática 2013, 27, 759–778. [Google Scholar] [CrossRef] [Green Version]
- Cañadas, G.R.; Batanero, C.; Arteaga, P.; Gea, M.M. Medidas de asociación en tablas 2 × 2: Evaluación de una experiencia de enseñanza con estudiantes universitarios [Association coefficients in 2 × 2 tables: Assessing a teaching experience with university students]. In Investigación en Educación Matemática XVIII; González, M.T., Codes, M., Arnau, D., Ortega, T., Eds.; SEIEM: Salamanca, Spain, 2014; pp. 207–216. [Google Scholar]
- Cañadas, G.; Arteaga, P.; Contreras, J.M.; Gea, M.M. Comprensión de medidas de asociación en tablas RxC por estudiantes de psicología [Measures of association in tables RxC for student’s in Psychology]. In Investigación en Educación Matemática XX; Berciano, A., Fernández, C., Fernández, T., González, J.L., Hernández, P., Jiménez, A., Macías, J.A., Ruiz, F.J., Sánchez, M.T., Eds.; SEIEM: Malaga, Spain, 2016; pp. 187–196. [Google Scholar]
- Estrada, A.; Díaz, C. Computing probabilities from two way tables. In An exploratory study with future teachers. In Proceedings of Seventh International Conference on Teaching of Statistics, Bahia, Salvador; Rossman, A., Chance, B., Eds.; International Association for Statistical Education: Bahia, Salvador, 2006; pp. 1–4. [Google Scholar]
- Batanero, C.; Estepa, A.; Godino, J.D.; Green, D.R. Intuitive strategies and preconceptions about association in contingency tables. J. Res. Math. Educ. 1996, 27, 151–169. [Google Scholar] [CrossRef]
- Cañadas, G.R.; Batanero, C.; Díaz, C.; Roa, R. Psychology students’ understanding of the Chi-squared test. Stat. Enseign. 2012, 3, 3–18. [Google Scholar]
- Cañadas, G.; Batanero, C.; Díaz, C.; Gea, M.M. Comprensión del test chi-cuadrado por estudiantes de Psicología [undertanding of chi-squared test by psychology students]. In Investigación en Educación Matemática XVI; Estepa, A., Contreras, A., Deulofeu, J., Penalva, M.C., García, F.J., Ordóñez, L., Eds.; Universidad de Granada: Granada, Spain, 2012; pp. 153–163. [Google Scholar]
- Contreras, J.M.; Estrada, A.; Díaz, C.; Batanero Bernabeu, M.D.C. Dificultades de futuros profesores en la lectura y cálculo de probabilidades de doble entrada [Difficulties of future teachers in reading and calculating double-entry probabilities]. In Investigación en Educación Matemática XIV; Moreno, M.M., Estrada, A., Carrillo, J., Sierra, T.A., Eds.; SEIEM: Lleida, Spain, 2010; pp. 271–280. [Google Scholar]
- Lugo-Armenta, J.G.; Pino-Fan, L.R. An approach to inferential reasoning levels. Educ. Stud. Math. 2021. submitted. [Google Scholar]
- Ben-Zvi, D.; Garfield, J.B. Statistical Literacy, Reasoning, and Thinking: Goals, Definitions, and Challenges. In The Challenge of Developing Statistical Literacy, Reasoning and Thinking, 1st ed.; Ben-Zvi, D., Garfield, J., Eds.; Springer: Dordrecht, The Netherlands, 2004; pp. 3–16. [Google Scholar] [CrossRef]
- Lugo-Armenta, J.G.; Pino-Fan, L.R. Niveles de razonamiento inferencial para el estadístico t-Student [Inferential reasoning Levels about the t-Student statistic]. Bolema Bol. Educ. Matemática 2021, 71, in press. [Google Scholar]
- Godino, J.D.; Batanero, C.; Font, V. The onto-semiotic approach to research in mathematics education. ZDM Int. J. Math. Educ. 2007, 39, 127–135. [Google Scholar] [CrossRef] [Green Version]
- Godino, J.D.; Batanero, C.; Font, V. The onto-semiotic approach: Implications for the prescriptive character of didactics. Learn. Math. 2019, 39, 37–42. [Google Scholar]
- Godino, J.D.; Batanero, C. Significado institucional y personal de los objetos matemáticos [Institutional and personal meaning of mathematical objects]. Rech. Didact. Mathématiques 1994, 14, 325–355. [Google Scholar]
- Godino, J.D.; Font, V.; Wilhelmi, M.R.; Lurduy, O. Why is the learning of elementary arithmetic concepts difficult? Semiotic tools for understanding the nature of mathematical objects. Educ. Stud. Math. 2011, 77, 247–265. [Google Scholar] [CrossRef]
- Pino-Fan, L.R.; Godino, J.D.; Font, V. Assessing key epistemic features of didactic-mathematical knowledge of prospective teachers: The case of the derivative. J. Math. Teach. Educ. 2018, 21, 63–94. [Google Scholar] [CrossRef]
- Font, V.; Rubio, N.V. Procesos matemáticos en el enfoque ontosemiótico [Mathematical processes in the onto-semiotic approach]. In Actas del Segundo Congreso Internacional Virtual de Educación Estadística; Contreras, J.M., Arteaga, P., Cañadas, G.R., Gea, M.M., Giacomone, B., López-Martín, M.M., Eds.; Departamento de Didáctica de la Matemática, Universidad de Granada: Granda, Spain, 2017. [Google Scholar]
- Lugo-Armenta, J.G.; Pino-Fan, L.R.; Ruiz, B.R. Chi-square reference meanings: A historical-epistemological overview. Revemop 2021, 3, 1–33. [Google Scholar] [CrossRef]
- Cohen, L.; Manion, L.; Morrison, K. Research Methods in Education, 6th ed.; Routledge: New York, NY, USA, 2011. [Google Scholar]
- Lugo-Armenta, J.G.; Pino-Fan, L.R. Inferential statistical reasoning of math teachers: Experiences in virtual contexts generated by the COVID-19 pandemic. Educ. Sci. 2021, 11, 363. [Google Scholar] [CrossRef]
- Galton, F., IV. Statistics by intercomparison, with remarks on the law of frequency of error. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1875, 49, 33–46. [Google Scholar] [CrossRef]
- Pfannkuch, M.; Wild, C. Towards an understanding of statistical thinking. In The Challenge of Developing Statistical Literacy, Reasoning and Thinking, 1st ed.; Ben-Zvi, D., Garfield, J., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004; pp. 17–46. [Google Scholar] [CrossRef]
- Pfannkuch, M.; Budgett, S.; Fewster, R.; Fitch, M.; Pattenwise, S.; Wild, C.; Ziedins, I. Probability modeling and thinking: What can we learn from practice? Stat. Educ. Res. J. 2016, 15, 11–37. [Google Scholar] [CrossRef]
- Stohl Lee, H.; Angotti, R.L.; Tarr, J.E. Making comparisons between observed data and expected outcomes: Students’ informal hypothesis testing with probability simulation tools. Stat. Educ. Res. J. 2010, 9, 68–96. [Google Scholar]
- Chance, B.; Rossman, A. Using simulation to teach and learn statistics. In Proceedings of the Seventh International Conference on Teaching Statistics, Voorburg, The Netherlands, 2–7 July 2006; International Statistical Institute: Voorburg, The Netherlands; pp. 1–6. [Google Scholar]
- Tintle, N.L.; Topliff, K.; Van der Stoep, J.; Holmes, V.L.; Swanson, T. Retention of statistical concepts in a preliminary randomization-based introductory statistics curriculum. Stat. Educ. Res. J. 2012, 11, 21–40. [Google Scholar] [CrossRef]
- Rossman, A.J.; Chance, B.L. Using simulation-based inference for learning introductory statistics. Wiley Interdiscip. Rev. Comput. Stat. 2014, 6, 211–221. [Google Scholar] [CrossRef]
- Fisher, R.A. Statistical Methods for Research Workers, 1st ed.; Oliver and Boyd: Edinburgh, Scotland, 1925. [Google Scholar]
- Rossman, A.J. Reasoning about Informal Statistical Inference: One Statistician’s View. Stat. Educ. Res. J. 2008, 7, 5–19. [Google Scholar]
- Yule, G.U. On the association of attributes in statistics: With illustrations from the material of the childhood society. Philos. Trans. R. Soc. Lond. 1900, 194, 257–319. [Google Scholar] [CrossRef] [Green Version]
- Batanero, C.; Borovcnik, M. Statistics and Probability in High School; Sense Publishers: Rotterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Batanero, C.; Gea, M.M.; Álvarez-Arroyo, R. Comprendiendo la independencia y el condicionamiento [Understanding independence and conditioning]. UNO Rev. Didáctica Mat. 2020, 89, 7–13. [Google Scholar]
- Wild, C.; Pfannkuch, M. Statistical thinking in empirical enquiry. Int. Stat. Rev. 1999, 67, 223–248. [Google Scholar] [CrossRef]
- Bakker, A.; Gravemeijer, K. Learning to reason about distribution. In The Challenge of Developing Statistical Literacy, Reasoning, and Thinking; Ben-Zvi, D., Garfield, J., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004; pp. 147–168. [Google Scholar] [CrossRef]
- Reading, C.; Reid, J. An emerging hierarchy of reasoning about distribution: From a variation perspective. Stat. Educ. Res. J. 2006, 5, 46–68. [Google Scholar]
- Dinov, I.D.; Palanimalai, S.; Khare, A.; Christou, N. Randomization-based statistical inference: A resampling and simulation infrastructure. Teach. Stat. 2018, 40, 64–73. [Google Scholar] [CrossRef] [PubMed]
- Bakker, A.; Derry, J. Lessons from inferentialism for statistics education. Math. Think. Learn. 2011, 13, 5–26. [Google Scholar] [CrossRef]
- Makar, K.; Ben-Zvi, D. The Role of Context in Developing Reasoning about Informal Statistical Inference. Math. Think. Learn. 2011, 13, 1–4. [Google Scholar] [CrossRef]
- Vallecillos, A. El papel de las hipótesis estadísticas en los contrastes: Concepciones y dificultades de aprendizaje [The role of statistical hypotheses on contrasts: Conceptions and learning difficulties]. Educ. Matemática 1997, 9, 5–20. [Google Scholar]
- López-Martín, M.M.; Batanero, C.; Gea, M.M. ¿Conocen los futuros profesores los errores de sus estudiantes en la inferencia estadística? [Do prospective teachers know their students’ errors in statistical inference?]. Bolema Bol. Educ. Matemática 2019, 33, 672–693. [Google Scholar] [CrossRef] [Green Version]
- Inzunza, S.; Jiménez, J.V. Caracterización del razonamiento estadístico de estudiantes universitarios acerca de las pruebas de hipótesis [The characteristics of college students’ statistical reasoning on hypothesis testing]. Rev. Latinoam. Investig. Matemática Educ. 2013, 16, 179–211. [Google Scholar] [CrossRef]
- Cohen, J. Cosas que he aprendido (hasta ahora) [Things I have learned (up to now)]. An. Psicol. Ann. Psychol. 1992, 8, 3–18. [Google Scholar]
- Batanero, C. Treinta años de investigación didáctica sobre el análisis inferencial de datos [Thirty years of educational research on inferential data analysis]. In Rutas de la Educación Matemática; Avila, A., Ed.; Sociedad Mexicana de Investigación y divulgación de la Educación Matemática: Mexico City, Mexico, 2018; pp. 186–199. [Google Scholar]
- DePaolo, C.A.; Robinson, D.F.; Jacobs, A. Café Data 2.0: New Data from a New and Improved Café. J. Stat. Educ. 2016, 24, 85–103. [Google Scholar] [CrossRef] [Green Version]
- Fellers, P.S.; Kuiper, S. Introducing Undergraduates to Concepts of Survey Data Analysis. J. Stat. Educ. 2020, 28, 18–24. [Google Scholar] [CrossRef]
- Woodard, V.; Lee, H.; Woodard, R. Writing Assignments to Assess Statistical Thinking. J. Stat. Educ. 2020, 28, 32–44. [Google Scholar] [CrossRef]
- Gibbs, A.L.; Goossens, E.T. The Evidence for Efficacy of HPV Vaccines: Investigations in Categorical Data Analysis. J. Stat. Educ. 2013, 21. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lugo-Armenta, J.G.; Pino-Fan, L.R. Inferential Reasoning of Secondary School Mathematics Teachers on the Chi-Square Statistic. Mathematics 2021, 9, 2416. https://doi.org/10.3390/math9192416
Lugo-Armenta JG, Pino-Fan LR. Inferential Reasoning of Secondary School Mathematics Teachers on the Chi-Square Statistic. Mathematics. 2021; 9(19):2416. https://doi.org/10.3390/math9192416
Chicago/Turabian StyleLugo-Armenta, Jesús Guadalupe, and Luis Roberto Pino-Fan. 2021. "Inferential Reasoning of Secondary School Mathematics Teachers on the Chi-Square Statistic" Mathematics 9, no. 19: 2416. https://doi.org/10.3390/math9192416
APA StyleLugo-Armenta, J. G., & Pino-Fan, L. R. (2021). Inferential Reasoning of Secondary School Mathematics Teachers on the Chi-Square Statistic. Mathematics, 9(19), 2416. https://doi.org/10.3390/math9192416





