A Coupling between Integral Equations and On-Surface Radiation Conditions for Diffraction Problems by Non Convex Scatterers
Abstract
1. Introduction
2. Two-Dimensional Scattering-Integral Equation Formulations
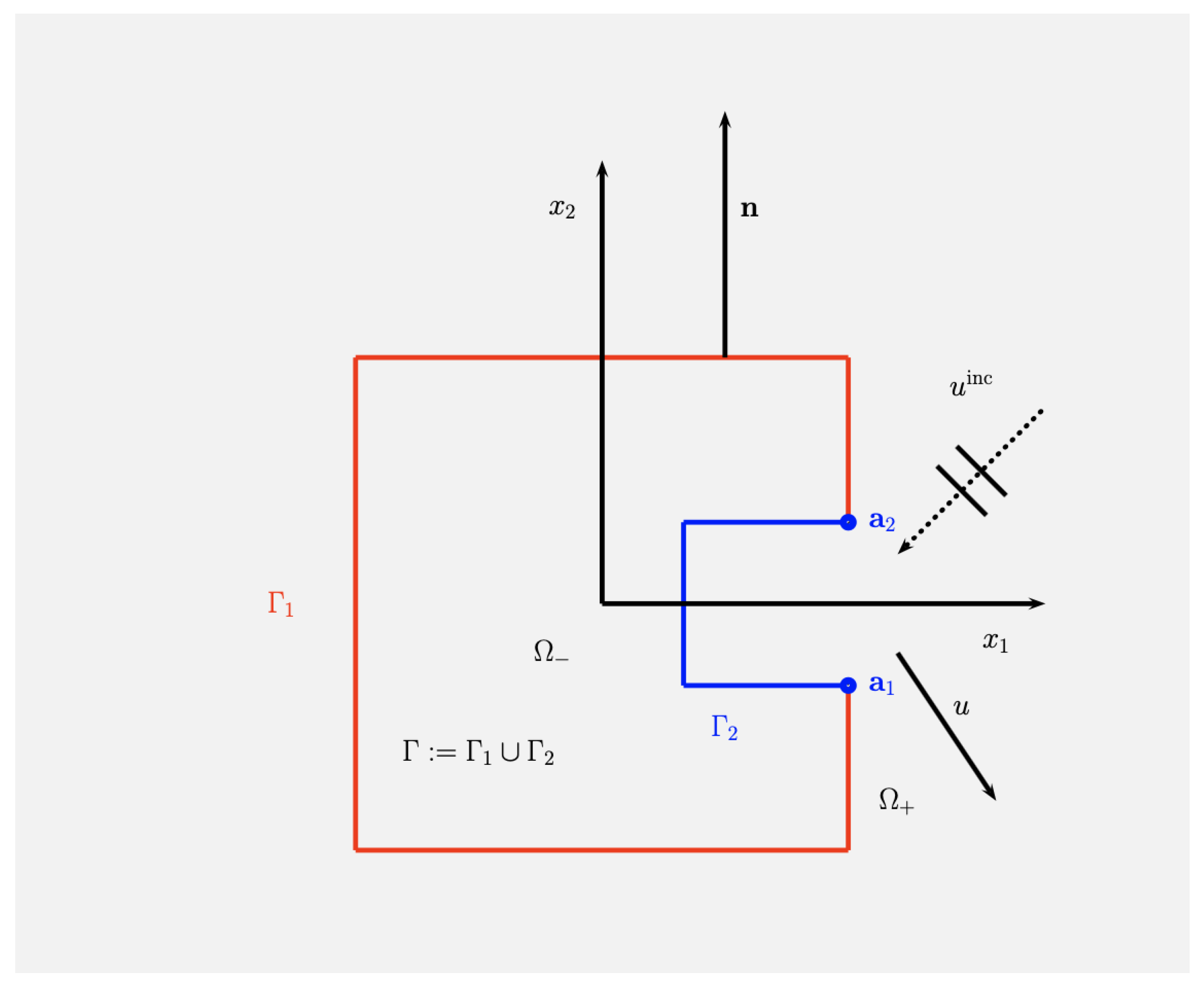
2.1. The Two-Dimensional Scattering Problem
2.2. Integral Operators for Scattering
2.3. Direct Boundary Integral Equations for the Dirichlet Problem
2.4. Numerical Approximation
3. Loss of Accuracy of the OSRC Method for Non Convex Scatterers
3.1. First and Second-Order OSRCs
3.2. Numerical Approximation
4. The Coupling Procedure for Non Convex Scatterers
4.1. Weak Coupling Procedure and Boundary Element Approximation
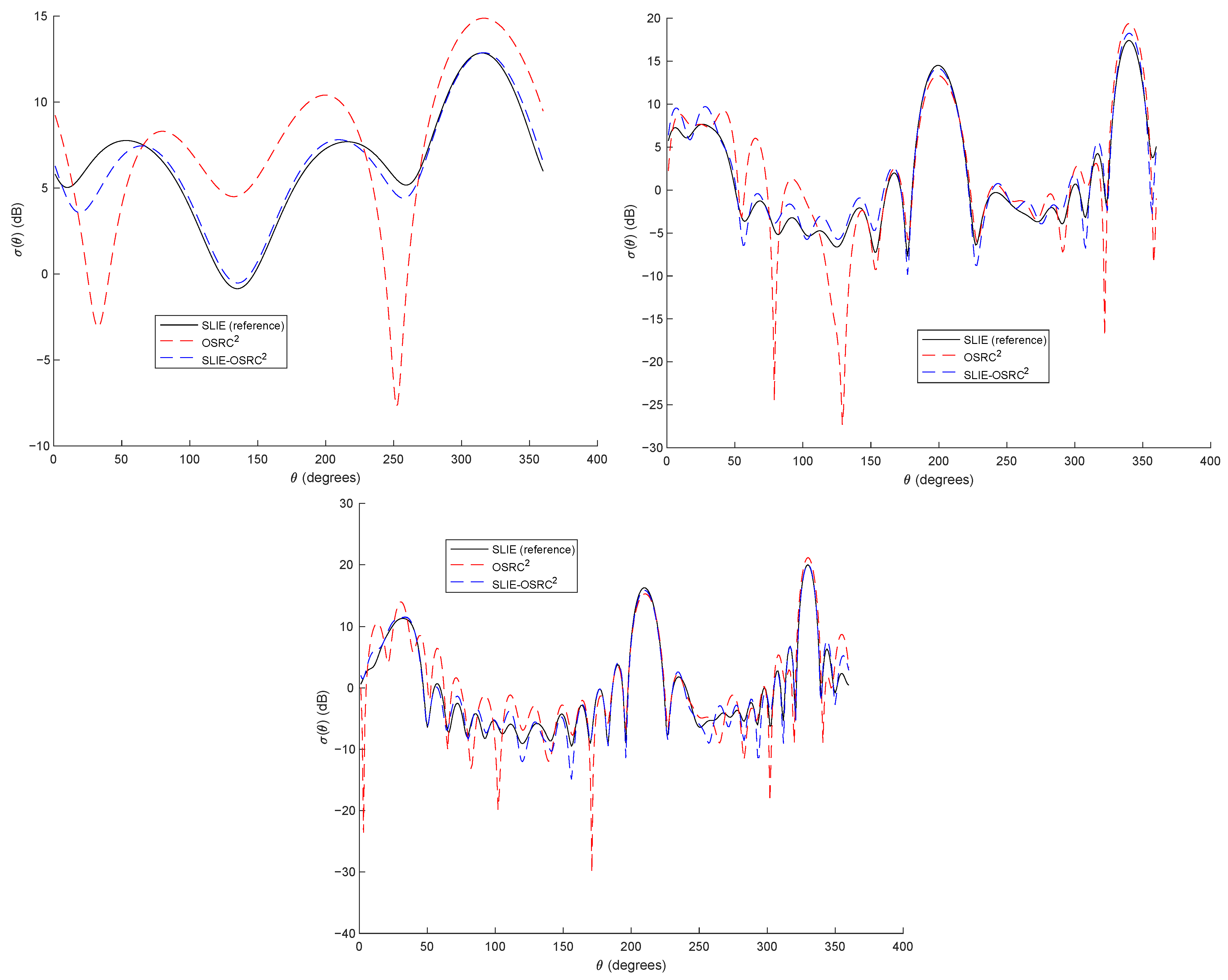
4.2. A Numerical Example-Validation of the Procedure
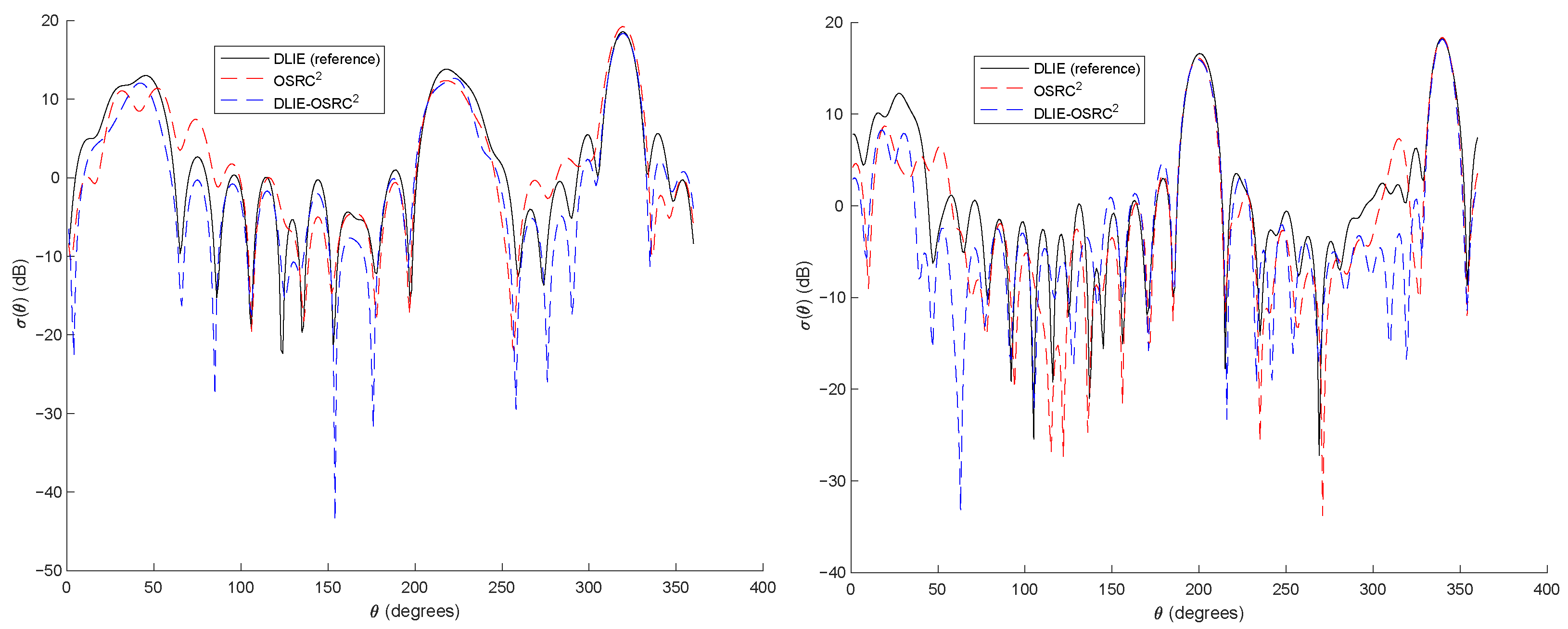
5. The Neumann Scattering Problem
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
Abbreviations
| OSRC | On-Surface Radiation Condition |
| EFIE | Electric Field Integral Equation |
| SLIE | Single-Layer Integral Equation |
| MFIE | Magnetic Field Integral Equation |
| CFIE | Combined Field Integral Equation |
| BWIE | Burton-Miller Integral Equation |
| SCS | Sonar Cross Section |
| BEM | Boundary Element Method |
| DtN | Dirichlet-to-Neumann |
| DLIE | Double-Layer Integral Equation |
References
- Antoine, X.; Barucq, H.; Bendali, A. Bayliss-Turkel-like Radiation Condition on Surfaces of Arbitrary Shape. J. Math. Anal. Appl. 1999, 229, 184–211. [Google Scholar] [CrossRef]
- Antoine, X.; Darbas, M.; Lu, Y. An Improved Surface Radiation Condition for High-Frequency Acoustic Scattering Problems. Comput. Methods Appl. Mech. Eng. 2006, 195, 4060–4074. [Google Scholar] [CrossRef]
- Givoli, D. High-order local non-reflecting boundary conditions: A review. Wave Motion 2004, 39, 319–326. [Google Scholar] [CrossRef]
- Hagstrom, T. Radiation boundary conditions for the numerical simulation of waves. Acta Numer. 1999, 8, 47–106. [Google Scholar] [CrossRef]
- Hagstrom, T.; Warburton, T. A new auxiliary variable formulation of high-order local radiation boundary conditions: Corner compatibility conditions and extensions to first-order systems. Wave Motion 2004, 39, 327–338. [Google Scholar] [CrossRef]
- Modave, A.; Geuzaine, C.; Antoine, X. Corner treatments for high-order local absorbing boundary conditions in high-frequency acoustic scattering. J. Comput. Phys. 2020, 401, 109029. [Google Scholar] [CrossRef]
- Tsynkov, S. Numerical solution of problems on unbounded domains. A review. Appl. Numer. Math. 1998, 27, 465–532. [Google Scholar] [CrossRef]
- Bérenger, J.P. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Bérenger, J.P. Perfectly matched layer (PML) for computational electromagnetics. Synth. Lect. Comput. Electromagn. 2007, 2, 1–117. [Google Scholar] [CrossRef]
- Bermúdez, A.; Hervella-Nieto, L.; Prieto, A.; Rodríguez, R. Perfectly matched layers. In Computational Acoustics of Noise Propagation in Fluids-Finite and Boundary Element Methods; Springer: Berlin/Heidelberg, Germany, 2008; pp. 167–196. [Google Scholar]
- Bermúdez, A.; Hervella-Nieto, L.; Prieto, A.; Rodríguez, R. Perfectly matched layers for time-harmonic second order elliptic problems. Arch. Comput. Methods Eng. 2010, 17, 77–107. [Google Scholar] [CrossRef]
- Druskin, V.; Güttel, S.; Knizhnerman, L. Near-optimal perfectly matched layers for indefinite Helmholtz problems. SIAM Rev. 2016, 58, 90–116. [Google Scholar] [CrossRef]
- Turkel, E.; Yefet, A. Absorbing PML boundary layers for wave-like equations. Appl. Numer. Math. 1998, 27, 533. [Google Scholar] [CrossRef]
- Bériot, H.; Prinn, A.; Gabard, G. Efficient implementation of high-order finite elements for Helmholtz problems. Int. J. Numer. Methods Eng. 2016, 106, 213–240. [Google Scholar] [CrossRef]
- Ihlenburg, F. Finite Element Analysis of Acoustic Scattering; Number 132 in Applied Mathematical Sciences; Springer: New York, NY, USA, 1998. [Google Scholar]
- Solin, P.; Segeth, K.; Dolezel, I. Higher-Order Finite Element Methods; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Antoine, X.; Darbas, M. An Introduction to Operator Preconditioning for the Fast Iterative Integral Equation Solution of Time-Harmonic Scattering Problems. Multiscale Sci. Eng. 2021, 1, 1–35. [Google Scholar] [CrossRef]
- Antoine, X.; Geuzaine, C.; Ramdani, K. Wave Propagation in Periodic Media-Analysis, Numerical Techniques and Practical Applications; Progress in Computational Physics; Chapter Computational Methods for Multiple Scattering at High Frequency with Applications to Periodic Structures Calculations; Bentham Books: Sharjah, United Arab Emirates, 2010; Volume 1, pp. 73–107. [Google Scholar]
- Burton, A.J.; Miller, G.F. The application of integral equation methods to the numerical solution of some exterior boundary-value problems. Proc. R. Soc. Lond. A Math. Phys. Sci. 1971, 323, 201–210. [Google Scholar]
- Chandler-Wilde, S.; Graham, I.; Langdon, S.; Spece, E. Numerical-asymptotic boundary integral methods in high-frequency acoustic scattering. Acta Numer. 2012, 21, 89–305. [Google Scholar] [CrossRef]
- Colton, D.; Kress, R. Inverse Acoustic and Electromagnetic Scattering Theory, 2nd ed.; Applied Mathematical Sciences; Springer: Berlin, Germany, 1998; Volume 93. [Google Scholar]
- Colton, D.L.; Kress, R. Integral Equation Methods in Scattering Theory; Pure and Applied Mathematics (New York); John Wiley & Sons Inc.: New York, NY, USA, 1983. [Google Scholar]
- Harrington, R.; Mautz, J. H-field, E-field and combined field solution for conducting bodies of revolution. Arch. Elektron. Uebertragungstechnik 1978, 4, 157–164. [Google Scholar]
- Liu, Y. Fast Multipole Boundary Element Method: Theory and Applications in Engineering; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Martin, P.A. Multiple Scattering. Interaction of Time-Harmonic Waves with N Obstacles; Encyclopedia of Mathematics and its Applications; Cambridge University Press: Cambridge, UK, 2006; Volume 107, p. xii+437. [Google Scholar]
- McLean, W. Strongly Elliptic Systems and Boundary Integral Equations; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Nédélec, J.C. Acoustic and Electromagnetic Equations. Integral Representations for Harmonic Problems; Applied Mathematical Sciences; Springer: New York, NY, USA, 2001; Volume 144. [Google Scholar]
- Thierry, B. Analyse et Simulations Numériques du Retournement Temporel et de la Diffraction Multiple. Ph.D. Thesis, Nancy University, Nancy, France, 2011. [Google Scholar]
- Hackbusch, W. Hierarchical Matrices: Algorithms and Analysis; Springer: Berlin/Heidelberg, Germany, 2015; Volume 49. [Google Scholar]
- Kriegsmann, G.; Taflove, A.; Umashankar, K. A new formulation of electromagnetic wave scattering using an on-surface radiation boundary condition approach. IEEE Trans. Antennas Propag. 1987, 35, 153–161. [Google Scholar] [CrossRef]
- Antoine, X. Computational Methods for Acoustics Problems; Chapter Advances in the On-Surface Radiation Condition Method: Theory, Numerics and Applications; Saxe-Coburg Publications: Stirling, UK, 2008; pp. 169–194. [Google Scholar]
- Antoine, X. An algorithm coupling the OSRC and FEM for the computation of an approximate scattered acoustic field by a non-convex body. Int. J. Numer. Methods Eng. 2002, 54, 1021–1041. [Google Scholar] [CrossRef]
- Alzubaidi, H.; Antoine, X.; Chniti, C. Formulation and accuracy of On-Surface Radiation Conditions for acoustic multiple scattering problems. Appl. Math. Comput. 2016, 277, 82–100. [Google Scholar] [CrossRef]
- Acosta, S. On-surface radiation condition for multiple scattering of waves. Comput. Methods Appl. Mech. Eng. 2015, 283, 1296–1309. [Google Scholar] [CrossRef][Green Version]
- Sauter, S.; Schwab, C. Boundary Element Methods; Springer Series in Computational Mathematics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Antoine, X. Fast Approximate Computation of a Time-Harmonic Scattered Field using the On-Surface Radiation Condition Method. IMA J. Appl. Math. 2001, 66, 83–110. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems; PWS Publishing Company: Boston, MA, USA, 1996. [Google Scholar]
- Saad, Y.; Schultz, M. GMRES: A Generalized Minimal Residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 1986, 7, 856–869. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzahrani, S.M.; Antoine, X.; Chniti, C. A Coupling between Integral Equations and On-Surface Radiation Conditions for Diffraction Problems by Non Convex Scatterers. Mathematics 2021, 9, 2299. https://doi.org/10.3390/math9182299
Alzahrani SM, Antoine X, Chniti C. A Coupling between Integral Equations and On-Surface Radiation Conditions for Diffraction Problems by Non Convex Scatterers. Mathematics. 2021; 9(18):2299. https://doi.org/10.3390/math9182299
Chicago/Turabian StyleAlzahrani, Saleh Mousa, Xavier Antoine, and Chokri Chniti. 2021. "A Coupling between Integral Equations and On-Surface Radiation Conditions for Diffraction Problems by Non Convex Scatterers" Mathematics 9, no. 18: 2299. https://doi.org/10.3390/math9182299
APA StyleAlzahrani, S. M., Antoine, X., & Chniti, C. (2021). A Coupling between Integral Equations and On-Surface Radiation Conditions for Diffraction Problems by Non Convex Scatterers. Mathematics, 9(18), 2299. https://doi.org/10.3390/math9182299





