Two Different Views for Generalized Rough Sets with Applications
Abstract
:1. Introduction
- (1)
- To initiate a novel neighborhood (so-called basic-neighborhood) construct from any general binary relation and study its properties;
- (2)
- To propose new generalized rough approximations and investigate their properties based on this neighborhood;
- (3)
- To solve some problems in set-valued ordered information systems concerning finding the key foods suitable in order to be healthy.
2. Pawlak Rough Sets and Some of Its Generalizations
2.1. Pawlak Rough Set Theory
2.2. Yao’s Rough Sets
2.3. Allam et al.’s Rough Sets
2.4. Dai et al.’s Rough Sets
2.5. Marei’s Rough Sets
- (i)
- The first kind of-lower (resp.-upper) approximation of is given by:
- (ii)
- The first kind of-lower (resp.-upper) approximation of is given by:whereand.
- whereand.
3. New Types of Generalized Neighborhoods
| . |
- (a)
- For each,;
- (b)
- For each,if and only if;
- (a)
- By using Definition 10, the proof is obvious;
- (b)
- By using Definition 10, if . Then … (1)
- (a)
- The inclusion sign in (a) of Lemma 1 need not be equal, in general;
- (b)
- The “basic-neighborhood” and “initial-neighborhood” are independent (non-comparable);
- (c)
- The neighborhoods,,, and, for each, are independent (i.e., non-comparable) in general.
- (a)
- .
- (b)
- and.
- (a)
- ;
- (b)
- .
- (a)
- The opposite of Lemma 3 is not true in general;
- (b)
- The neighborhoodsandare independent in the case of a reflexive relation.
- (a)
- ;
- (b)
- .
- (a)
- The converse of Lemma 4 is not true in general;
- (b)
- The neighborhoodsandare independent in the case of a transitive relation;
- (c)
- The neighborhoodsandare independent in the case of a transitive relation.
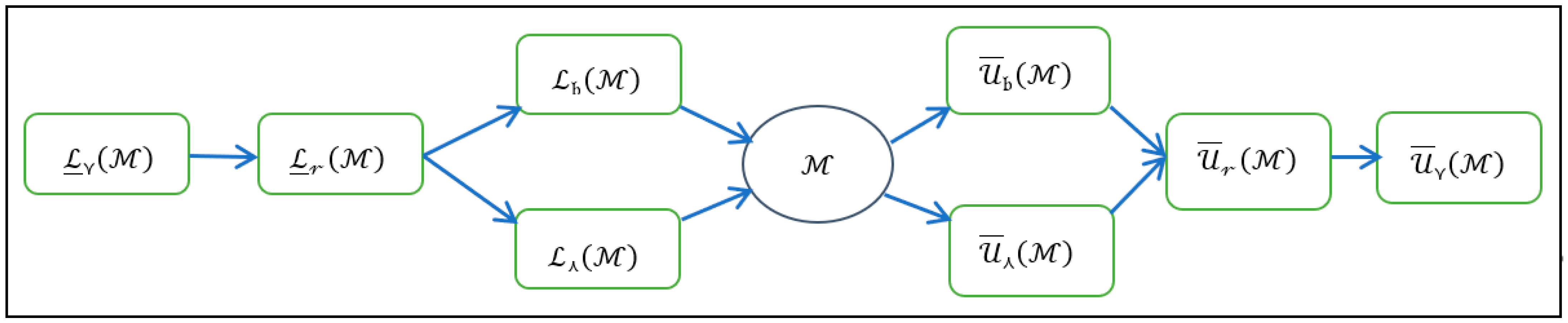
4. Two Different Views for Generalized Rough Sets via Basic Neighborhoods
4.1. The First Method to Generalization Based on a One Binary Relation
4.2. The Second Method to Generalization Based on a Finite Number of Binary Relations
- (i)
- The first kind of-basic lower (resp.-basic upper) approximation of is given by:
- (ii)
- The second kind of-basic lower (resp.-basic upper) approximation of is given by:whereand.
- (i)
- and;
- (ii)
- and;
- (iii)
- Ifis of second kind-basic exact, then it is of first kind-basic exact.
4.3. Comparisons between the Suggested Approaches and the Other Methods
- (i)
- The Yao, Allam, and Dai methods are not suitable to approximate the rough sets in the general case, since they could not be applied for any relation (since the main properties of the approximations did not hold), and thus these methods restrict the applications of rough set theory, for instance:
- a.
- ,,.
- b.
- and.
- (ii)
- On the other hand, our methods in the present paper were the best methods for approximating the sets in the general case, since these approximations satisfied all properties of Pawlak’s rough sets without any conditions or restrictions. Therefore, the suggested method can help in discovering the vagueness in the data.
- (a)
- ;
- (b)
- .
- (a)
- ;
- (b)
- ;
- (c)
- ;
- (d)
- ;
- (e)
- Ifis-exactis-exactis-exact.Ifis-exactis-exactis-exact.
- (a)
- and;
- (b)
- and.
- (i)
- , for each;
- (ii)
- and, for each;
- (iii)
- Ifis-exact, then it is-basic exact.
5. Applications
5.1. Set-Valued Information Systems
5.2. Decision-Making of Multi-Information System of Nutrition Modeling via B-Rough Approximations
- (1)
- We could not use Pawlak’s rough set model in the previous application because of its transitivity as we applied Pawlak’s rough set model only in the case of equivalence relation. Moreover, these methods were applied easily without restrictions, so this may expand the field of the application of Pawlak’s rough sets;
- (2)
- Using Marei’s methods was not suitable for obtaining an accurate decision, since they produced some contradictions and vagueness. Consequently, we were unable to decide the suitable healthy food;
- (3)
- On the other hand, by using the suggested approximations, we confirmed between the experimental data and its mathematical analysis. The mathematical study depends on the classification of data by using the -neighborhoods. Hence, we minimized the vagueness in the data and also obtained a higher accuracy measure. Accordingly, we can say that the suggested approximations were more accurate than the previous methods for extracting the information and helping to eliminate the ambiguity of the data in the real-life problems, especially in the medical diagnosis which needed accurate decisions.
5.3. A Medical Application in Decision-Making of the Heart Attacks Problem
- , , , , , and .
- , and .
- , , , , , and .
- (1)
- Pawlak’s rough set model cannot be used in the above application because the used relation was transitive. Pawlak’s rough set model was applied only when the relation was an equivalence relation. On the other hand, the suggested 664 methods were applied and hence, this extended the application fields of Pawlak’s rough sets;
- (2)
- Using Dai et al.’s methods was not suitable for obtaining an accurate decision, since the boundary region was , and the accuracy measure was , which meant that all patients in may have been infected, although the infected patients were surely specified with the set . Consequently, we were unable to decide whether the patient was infected with heart attacks, and this produced vagueness in decision making regarding the medical diagnosis;
- (3)
- On the other hand, using the suggested approximations, we attained the boundary , and the accuracy measure was . Hence, we minimized the vagueness in the data and also obtained a higher accuracy measure. Accordingly, we can say that the suggested approximations were more accurate than the previous methods for extracting the information and helping to eliminate the ambiguity of the data in real-life problems, especially in the medical diagnosis which needed accurate decisions.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pawlak, Z. Rough sets. Int. J. Inf. Comput. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough Sets, Theoretical Aspects of Reasoning about Data; Springer: Dordrecht, Netherlands, 1991. [Google Scholar] [CrossRef]
- Amer, W.S.; Abbas, M.I.; El-Bably, M.K. On j-near concepts in rough sets with some applications. J. Intell. Fuzzy Syst. 2017, 32, 1089–1099. [Google Scholar] [CrossRef]
- Lashin, E.F.; Kozae, A.M.; Abo Khadra, A.A.; Medhat, T. Rough set theory for topological spaces. Int. J. Approx. Reason. 2005, 40, 35–43. [Google Scholar] [CrossRef] [Green Version]
- Abd El-Monsef, M.E.; EL-Gayar, M.A.; Aqeel, R.M. On relationships between revised rough fuzzy approximation operators and fuzzy topological spaces. Int. J. Granul. Comput. Rough Sets Intell. Syst. 2014, 3, 257–271. [Google Scholar]
- El-Bably, M.K.; Abo-Tabl, E.A. A topological reduction for predicting of a lung cancer disease based on generalized rough sets. J. Intell. Fuzzy Syst. 2021, 1–16. [Google Scholar] [CrossRef]
- Skowron, A.; Dutta, S. Rough Sets, Past, Present, and Future. Nat. Comput. 2018, 17, 855–876. [Google Scholar] [CrossRef] [Green Version]
- El Sayed, M.; El Safty, M.A.; El-Bably, M.K. Topological approach for decision-making of COVID-19 infection via a nano-topology model. AIMS Math. 2021, 6, 7872–7894. [Google Scholar] [CrossRef]
- Lu, H.; Khalil, A.M.; Alharbi, W.; El-Gayar, M.A. A new type of generalized picture fuzzy soft set and its application in decision making. J. Intell. Fuzzy Syst. 2021, 40, 1–17. [Google Scholar] [CrossRef]
- Guan, Y.; Wang, H. Set-valued information systems. Inf. Sci. 2006, 176, 2507–2525. [Google Scholar] [CrossRef]
- Qian, Y.; Dang, C.; Liang, J.; Tang, D. Set-valued ordered information systems. Inf. Sci. 2009, 179, 2809–2832. [Google Scholar] [CrossRef]
- Slowinski, R.; Vanderpooten, D. A generalized definition of rough approximations based on similarity. IEEE Trans. Knowl. Data Eng. 2000, 12, 331–336. [Google Scholar] [CrossRef]
- Abo-Tabl, E.A. A comparison of two kinds of definitions of rough approximations based on a similarity relation. Inf. Sci. 2011, 181, 2587–2596. [Google Scholar] [CrossRef]
- Abo Khadra, A.A.; El-Bably, M.K. Topological approach to tolerance space. Alex. Eng. J. 2008, 47, 575–580. [Google Scholar]
- Dai, J.H.; Gao, S.C.; Zheng, G.J. Generalized rough set models determined by multiple neighborhoods generated from a similarity relation. Soft Comput. 2018, 22, 2081–2094. [Google Scholar] [CrossRef]
- Kin, K.; Yang, J.; Pei, Z. Generalized rough sets based on reflexive and transitive relations. Inf. Sci. 2008, 178, 4138–4141. [Google Scholar]
- Kondo, M. On the structure of generalized rough sets. Inf. Sci. 2006, 176, 589–600. [Google Scholar] [CrossRef]
- Yao, Y.Y. Two views of the theory of rough sets in finite universes. Int. J. Approx. Reason. 1996, 15, 291–317. [Google Scholar] [CrossRef] [Green Version]
- Allam, A.A.; Bakeir, M.Y.; Abo-Tabl, E.A. New approach for basic rough set concepts. In International Workshop on Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing; Lecture Notes in Artificial Intelligence; Springer: Regina, SK, Canada, 2005; Volume 3641, pp. 64–73. [Google Scholar]
- Yao, J.; Ciucci, D.; Zhang, Y. Generalized Rough Sets. In Springer Handbook of Computational Intelligence. Springer Handbooks; Kacprzyk, J., Pedrycz, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Ali, M.I.; Davvaz, B.; Shabir, M. Some properties of generalized rough sets. Inf. Sci. 2013, 224, 170–179. [Google Scholar] [CrossRef]
- Abd El-Monsef, M.E.; Embaby, O.A.; El-Bably, M.K. Comparison between rough set approximations based on different topologies. Int. J. Granul. Comput. Rough Sets Intell. Syst. 2014, 3, 292–305. [Google Scholar]
- El-Bably, M.K.; Fleifel, K.K.; Embaby, O.A. Topological approaches to rough approximations based on closure operators. Granul. Comput. 2021, 1–14. [Google Scholar] [CrossRef]
- Nawar, A.S. Approximations of some near open sets in ideal topological spaces. J. Egypt. Math. Soc. 2020, 28, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Abd El-Monsef, M.E.; EL-Gayar, M.A.; Aqeel, R. A comparison of three types of rough fuzzy sets based on two universal sets. Int. J. Mach. Learn. Cyber. 2017, 1, 343–353. [Google Scholar] [CrossRef]
- Hosny, M. On generalization of rough sets by using two different methods. J. Intell. Fuzzy Syst. 2018, 35, 979–993. [Google Scholar] [CrossRef]
- Tripathy, B.K.; Mitra, A. Some topological properties of rough sets and their applications. Int. J. Granul. Comput. Rough Sets Intell. Syst. 2010, 1, 355–375. [Google Scholar] [CrossRef]
- Xu, W.H.; Zhang, W.X. Measuring roughness of generalized rough sets induced by a covering. Inf. Sci. 2007, 158, 2443–2455. [Google Scholar] [CrossRef]
- Abd El-Monsef, M.E.; Kozae, A.M.; El-Bably, M.K. On generalizing covering approximation space. J. Egypt. Math. Soc. 2015, 23, 535–545. [Google Scholar] [CrossRef] [Green Version]
- Nawar, A.S.; El-Bably, M.K.; El-Atik, A.A. Certain types of coverings based rough sets with application. J. Intell. Fuzzy Syst. 2020, 39, 3085–3098. [Google Scholar] [CrossRef]
- Marei, E.A. Neighborhood System and Decision Making. Master’s Thesis, Zagazig University, Zagazig, Egypt, 2007. [Google Scholar]
- Al-shami, T.M.; Fu, W.Q.; Abo-Tabl, E.A. New rough approximations based on E-neighborhoods. Complexity 2021, 2021, 6. [Google Scholar] [CrossRef]
- Abo-Tabl, E.A. Rough sets and topological spaces based on similarity. Int. J. Mach. Learn. Cybern. 2013, 4, 451–458. [Google Scholar] [CrossRef]
- Ma, L. On some types of neighborhood-related covering rough sets. Int. J. Approx. Reason. 2012, 53, 901–911. [Google Scholar] [CrossRef] [Green Version]
- El-Bably, M.K.; El Atik, A. Soft β-rough sets and their application to determine COVID-19. Turk. J. Math. 2021, 45, 1133–1148. [Google Scholar] [CrossRef]
- Yu, Z.; Bai, X.; Yun, Z. A study of rough sets based on 1-neighborhood systems. Inf. Sci. 2013, 248, 103–113. [Google Scholar] [CrossRef]
- De Baets, B.; Kerre, E. A revision of Bandler-Kohout compositions of relations. Math. Pannonica 1993, 4, 59–78. [Google Scholar]
- Azzam, A.A.; Khalil, A.M.; Li, S.-G. Medical applications via minimal topological structure. J. Intell. Fuzzy Syst. 2020, 39, 4723–4730. [Google Scholar] [CrossRef]
| Yao’s Method | Allam’s Method | Dai’s Method | Current Method | |||||
|---|---|---|---|---|---|---|---|---|
| Students | Group II (A2) | Group III (A3) | Group IV (A4) | Group V (A5) | Decision (D) | |
|---|---|---|---|---|---|---|
| Unhealthy | ||||||
| Healthy | ||||||
| Healthy | ||||||
| Unhealthy | ||||||
| Healthy | ||||||
| Healthy | ||||||
| Unhealthy | ||||||
| Healthy |
| Students | |||||
|---|---|---|---|---|---|
| Students | |||||
|---|---|---|---|---|---|
| yes | yes | yes | yes | no | yes | |
| no | no | no | yes | yes | no | |
| yes | yes | yes | yes | yes | yes | |
| no | no | no | yes | no | no | |
| yes | no | no | yes | yes | no | |
| no | no | no | yes | no | no | |
| yes | yes | yes | yes | yes | yes | |
| yes | yes | no | yes | yes | yes | |
| yes | no | yes | yes | no | yes | |
| no | no | no | yes | yes | no | |
| yes | no | yes | yes | no | yes | |
| yes | no | no | yes | yes | no |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abu-Gdairi, R.; El-Gayar, M.A.; El-Bably, M.K.; Fleifel, K.K. Two Different Views for Generalized Rough Sets with Applications. Mathematics 2021, 9, 2275. https://doi.org/10.3390/math9182275
Abu-Gdairi R, El-Gayar MA, El-Bably MK, Fleifel KK. Two Different Views for Generalized Rough Sets with Applications. Mathematics. 2021; 9(18):2275. https://doi.org/10.3390/math9182275
Chicago/Turabian StyleAbu-Gdairi, Radwan, Mostafa A. El-Gayar, Mostafa K. El-Bably, and Kamel K. Fleifel. 2021. "Two Different Views for Generalized Rough Sets with Applications" Mathematics 9, no. 18: 2275. https://doi.org/10.3390/math9182275
APA StyleAbu-Gdairi, R., El-Gayar, M. A., El-Bably, M. K., & Fleifel, K. K. (2021). Two Different Views for Generalized Rough Sets with Applications. Mathematics, 9(18), 2275. https://doi.org/10.3390/math9182275







