Taxonomy of Polar Subspaces of Multi-Qubit Symplectic Polar Spaces of Small Rank ^†

Abstract

We study certain physically-relevant subgeometries of binary symplectic polar spaces $W(2N-1,2)$ of small rank N, when the points of these spaces canonically encode N-qubit observables. Key characteristics of a subspace of such a space $W(2N-1,2)$ are: the number of its negative lines, the distribution of types of observables, the character of the geometric hyperplane the subspace shares with the distinguished (non-singular) quadric of $W(2N-1,2)$ and the structure of its Veldkamp space. In particular, we classify and count polar subspaces of $W(2N-1,2)$ whose rank is $N-1$. $W(3,2)$ features three negative lines of the same type and its $W(1,2)$’s are of five different types. $W(5,2)$ is endowed with 90 negative lines of two types and its $W(3,2)$’s split into 13 types. A total of 279 out of 480 $W(3,2)$’s with three negative lines are composite, i.e., they all originate from the two-qubit $W(3,2)$. Given a three-qubit $W(3,2)$ and any of its geometric hyperplanes, there are three other $W(3,2)$’s possessing the same hyperplane. The same holds if a geometric hyperplane is replaced by a ‘planar’ tricentric triad. A hyperbolic quadric of $W(5,2)$ is found to host particular sets of seven $W(3,2)$’s, each of them being uniquely tied to a Conwell heptad with respect to the quadric. There is also a particular type of $W(3,2)$’s, a representative of which features a point each line through which is negative. Finally, $W(7,2)$ is found to possess 1908 negative lines of five types and its $W(5,2)$’s fall into as many as 29 types. A total of 1524 out of 1560 $W(5,2)$’s with 90 negative lines originate from the three-qubit $W(5,2)$. Remarkably, the difference in the number of negative lines for any two distinct types of four-qubit $W(5,2)$’s is a multiple of four.

1. Introduction

Some fifteen years ago, it was discovered (see, e.g., [1,2,3,4]) that there exists a deep connection between the structure of the N-qubit Pauli group and that of the binary symplectic polar space of rank N, $W(2N-1,2)$, where commutation relations between elements of the group are encoded in collinearity relations between points of $W(2N-1,2)$. This connection has subsequently been used to obtain a deeper insight into, for example, finite geometric nature of observable-based proofs of quantum contextuality (for a recent review, see [5]), properties of certain black-hole entropy formulas [6] and the so-called black-hole/qubit correspondence [7], leading to a finite-geometric underpinning of four distinct Hitchin’s invariants and the Cartan invariant of form theories of gravity [8] and even to an intriguing finite-geometric toy model of space-time [9]. This group-geometric connection was further strengthened by making use of the concept of geometric hyperplane and that of the Veldkamp space of $W(2N-1,2)$[10]. As per quantum contextuality, famous two-qubit Mermin–Peres magic squares were found to be isomorphic to a special class of geometric hyperplanes of $W(3,2)$ called grids [11], whereas three-qubit Mermin pentagrams were found to have their natural settings in the magic Veldkamp line of $W(5,2)$[12], being also isomorphic—under the Grassmannian correspondence of type Gr$(2,4)$—to ovoids of $W(3,2)$[13]. Concerning the black-hole/qubit correspondence, here a key role is played by the geometric hyperplane isomorphic to an elliptic quadric of $W(5,2)$. Interestingly, form theories of gravity seem to indicate that a certain part of the magic Veldkamp line in the four-qubit symplectic polar space, $W(7,2)$, and the associated extended geometric hyperplanes are of physical relevance as well.

From the preceding paragraph it is obvious that revealing finer traits of the structure of binary symplectic polar spaces of small rank can be vital for further physical applications of these spaces. Having this in view, we will focus on sets of $W(2N-3,2)$’s located in $W(2N-1,2)$, for $N=2,3,4$, providing their comprehensive observable-based taxonomy. Key parameters of our classification of such subspaces of $W(2N-1,2)$ will be: the number of negative lines they contain (which is also an important parameter when it comes to quantum contextuality), the distribution of different types of observables they feature, the character of the geometric hyperplane a subspace of a given type shares with the distinguished (non-singular) quadric of $W(2N-1,2)$ and, in the case of refined ‘decomposition’ of three-qubit $W(3,2)$’s, also the very structure of their Veldkamp lines.

The paper is organized as follows. Section 2 provides the reader with the necessary finite-geometric background and notation. Section 3 deals with $W(3,2)$ and the hierarchy of its triads. Section 4 addresses the three-qubit $W(5,2)$ and its $W(3,2)$’s; here we classify $W(3,2)$’s in two distinct ways and illustrate the fact that there are four $W(3,2)$’s sharing a geometric hyperplane, or a specific tricentric triad. Section 5 focuses on prominent septuplets of $W(3,2)$’s that are closely related to Conwell heptads with respect to a hyperbolic quadric of $W(5,2)$. Section 6 classifies $W(5,2)$’s living in the four-qubit $W(7,2)$ and furnishes a couple of examples of their composite types. Finally, Section 7 is devoted to concluding remarks.

2. Finite Geometry Background

Given a d-dimensional projective space PG$(d,2)$ over GF$\left(2\right)$, a polar space $\mathcal{P}$ in this projective space consists of the projective subspaces that are totally isotropic/singular with respect to a given non-singular bilinear form; PG$(d,2)$ is called the ambient projective space of $\mathcal{P}$. A projective subspace of maximal dimension in $\mathcal{P}$ is called a generator; all generators have the same (projective) dimension $r-1$. One calls r the rank of the polar space.

Polar spaces of relevance for us are of three types (see, for example, [14,15]): symplectic, hyperbolic and elliptic. The symplectic polar space $W(2N-1,2)$, $N\ge 1$, consists of all the points of PG$(2N-1,2)$, $\{(x_1,x_2,\dots ,x_{2N}):x_j\in \{0,1\},j\in \{1,2,\dots ,2N\}\}\setminus$$\left\{\right(0,0,\dots ,0\left)\right\}$, together with the totally isotropic subspaces with respect to the standard symplectic form

$$\sigma (x,y)=x_1{y}_{N+1}-x_{N+1}{y}_1+x_2{y}_{N+2}-x_{N+2}{y}_2+\cdots +x_N{y}_{2N}-x_{2N}{y}_N.$$

(1)

This space features

$${\left|W\right|}_p=4^N-1$$

(2)

points and

$${\left|W\right|}_g=(2+1)(2^2+1)\cdots (2^N+1)$$

(3)

generators. The hyperbolic orthogonal polar space ${\mathcal{Q}}^{+}(2N-1,2)$, $N\ge 1$, is formed by all the subspaces of PG$(2N-1,2)$ that lie on a given non-singular hyperbolic quadric, with the standard equation

$$x_1{x}_{N+1}+x_2{x}_{N+2}\dots +x_N{x}_{2N}=0.$$

(4)

Each ${\mathcal{Q}}^{+}(2N-1,2)$ contains

$$|Q^{+}{|}_p=(2^{N-1}+1)(2^N-1)$$

(5)

points and there are

$${\left|W\right|}_{Q^{+}}={\left|Q^{+}\right|}_p+1=(2^{N-1}+1)(2^N-1)+1$$

(6)

copies of them in $W(2N-1,2)$. Finally, the elliptic orthogonal polar space ${\mathcal{Q}}^{-}(2N-1,2)$, $N\ge 2$, comprises all points and subspaces of PG$(2N-1,2)$ satisfying the standard equation

$$f(x_1,x_{N+1})+x_2{x}_{N+2}+\cdots +x_N{x}_{2N}=0,$$

(7)

where f is an irreducible quadratic polynomial over GF$\left(2\right)$. Each ${\mathcal{Q}}^{-}(2N-1,2)$ contains

$$|Q^{-}{|}_p=(2^{N-1}-1)(2^N+1)$$

(8)

points and there are

$${\left|W\right|}_{Q^{-}}={\left|Q^{-}\right|}_p+1=(2^{N-1}-1)(2^N+1)+1$$

(9)

copies of them in $W(2N-1,2)$. For both symplectic and hyperbolic polar spaces $r=N$, whereas for the elliptic one $r=N-1$. The smallest non-trivial symplectic polar space is the $N=2$ one, $W(3,2)$, often referred to as the doily. It features 15 points (see Equation (2)) and the same number of lines (that are also its generators, see Equation (3)), with three points per line and three lines through a point; it is a self-dual ${15}_3$-configuration and the only one out of 245,342 such configurations that is triangle-free, being, in fact, isomorphic to the generalized quadrangle of order two (GQ$(2,2)$). This symplectic polar space features ten ${\mathcal{Q}}^{+}(3,2)$’s (by Equation (6)) and six ${\mathcal{Q}}^{-}(3,2)$’s (by Equation (9)). A ${\mathcal{Q}}^{+}(3,2)$ contains nine points and six lines forming a $3\times 3$ grid, so it is also called a grid. A ${\mathcal{Q}}^{-}(3,2)$ features five pairwise non-collinear points, hence it is an ovoid. A triple of mutually non-collinear points of $W(3,2)$ is called a triad and a point collinear with all the three points of a triad is called a center of the triad; $W(3,2)$ contains 60 unicentric and 20 tricentric triads.

The N-qubit observables we will be dealing with belong to the set

$${\mathcal{S}}_N=\{G_1\otimes G_2\otimes \cdots \otimes G_N:G_j\in \{I,X,Y,Z\},j\in \{1,2,\dots ,N\}\}\setminus \left\{{\mathcal{I}}_N\right\}$$

(10)

where ${\mathcal{I}}_N\equiv I_{\left(1\right)}\otimes I_{\left(2\right)}\otimes \dots \otimes I_{\left(N\right)}$,

$$X=\left(\begin{array}{cc}\hfill 0& \hfill 1\\ \hfill 1& \hfill 0\end{array}\right),Y=\left(\begin{array}{cc}\hfill 0& \hfill -i\\ \hfill i& \hfill 0\end{array}\right),\mathrm{and}Z=\left(\begin{array}{cc}\hfill 1& \hfill 0\\ \hfill 0& \hfill -1\end{array}\right)$$

(11)

are the Pauli matrices, I is the identity matrix and ‘⊗’ stands for the tensor product of matrices. ${\mathcal{S}}_N$, whose elements are simply those of the N-qubit Pauli group if the global phase is disregarded, features two kinds of observables, namely symmetric (i.e., observables featuring an even number of Y’s) and skew-symmetric; the number of symmetric observables is $(2^{N-1}+1)(2^N-1)$. We shall further employ a finer classification where an observable having $N-1$, $N-2$, $N-3$, …I’s will be, respectively, of type A, B, C, …; also, whenever it is clear from the context, $G_1\otimes G_2\otimes \cdots \otimes G_N$ will be short-handed to $G_1{G}_2\cdots G_N$.

For a particular value of N, the $4^N-1$ elements of ${\mathcal{S}}_N$ can be bijectively identified with the same number of points of $W(2N-1,2)$ in such a way that the images of two commuting elements lie on the same line of this polar space, and generators of $W(2N-1,2)$ correspond to maximal sets of mutually commuting elements. If we take the symplectic form defined by Equation (1), then this bijection acquires the form

$$G_j\leftrightarrow (x_j,x_{j+N}),j\in \{1,2,\cdots ,N\},$$

(12)

assuming that

$$I\leftrightarrow (0,0),X\leftrightarrow (0,1),Y\leftrightarrow (1,1),\mathrm{and}Z\leftrightarrow (1,0).$$

(13)

Employing the above-introduced bijection (for more details see, e.g., [12]), it can be shown that given an observable O, the set of symmetric observables commuting with O together with the set of skew-symmetric observables not commuting with O will lie on a certain non-degenerate quadric of $W(2N-1,2)$, this quadric being hyperbolic (resp. elliptic) if O is symmetric (resp. skew-symmetric). We can express this important property by making, whenever appropriate, this associated observable explicit in a subscript, ${\mathcal{Q}}_{\left(O\right)}^{\pm }(2N-1,2)$, noting that there exists a particular hyperbolic quadric associated with $\mathcal{I}$:

$$\begin{array}{c}\hfill {\mathcal{Q}}_{\left(\mathcal{I}\right)}^{+}(2N-1,2):=\{(x_1,x_2,\cdots ,x_{2N})\in W(2N-1,2)|x_1{x}_{N+1}+x_2{x}_{N+2}+\\ \hfill \dots +x_N{x}_{2N}=0\}.\end{array}$$

(14)

Given a point-line incidence geometry $\Gamma (P,L)$, a geometric hyperplane of $\Gamma (P,L)$ is a subset of its point set such that a line of the geometry is either fully contained in the subset or has with it just a single point in common. The Veldkamp space $\mathcal{V}\left(\Gamma \right)$ of $\Gamma (P,L)$ is the space in which [16]: (i) a point is a geometric hyperplane of $\Gamma$ and (ii) a line is the collection, denoted $H^{\prime }{H}^{\prime \prime }$, of all geometric hyperplanes H of $\Gamma$ such that $H^{\prime }\cap H^{\prime \prime }=H^{\prime }\cap H=H^{\prime \prime }\cap H$ or $H=H^{\prime },H^{\prime \prime }$, where $H^{\prime }$ and $H^{\prime \prime }$ are distinct points of $\mathcal{V}\left(\Gamma \right)$. For a $\Gamma (P,L)$ with three points on a line, all Veldkamp lines are of the form $\{H^{\prime },H^{\prime \prime },\overline{H^{\prime }\Delta H^{\prime \prime }}\}$ where $\overline{H^{\prime }\Delta H^{\prime \prime }}$ is the complement of symmetric difference of $H^{\prime }$ and $H^{\prime \prime }$, i.e., they form a vector space over GF$\left(2\right)$. As demonstrated in [10], $\mathcal{V}\left(W\right(2N-1,2\left)\right)\cong$ PG$(2N,2)$. Its points are both hyperbolic and elliptic quadrics of $W(2N-1,2)$, as well as its perp-sets. Given a point x of $W(2N-1,2)$, the perp-set ${\widehat{\mathcal{Q}}}_{\left(x\right)}(2N-1,2)$ of x consists of all the points collinear with it,

$${\widehat{\mathcal{Q}}}_{\left(x\right)}(2N-1,2):=\{y\in W(2N-1,2)|\sigma (x,y)=0\};$$

(15)

the point x being referred to as the nucleus of ${\widehat{\mathcal{Q}}}_{\left(x\right)}(2N-1,2)$.

We shall briefly recall basic properties of the Veldkamp space of the doily, $\mathcal{V}\left(W\right(3,2\left)\right)\simeq$ PG(4, 2), whose in-depth description can be found in [11]. The 31 points of $\mathcal{V}\left(W\right(3,2\left)\right)$ comprise fifteen perp-sets, ten grids and six ovoids—as also illustrated in Figure 1. The 155 lines of $\mathcal{V}\left(W\right(3,2\left)\right)$ split into five distinct types as summarized in

Table 1. An overview of the properties of the five different types of lines of $\mathcal{V}\left(W\right(3,2\left)\right)$ in terms of the core (i.e., the set of points common to all the three hyperplanes forming the line) and the types of geometric hyperplanes featured by a generic line of a given type. The last column gives the total number of lines per each type.

Type	Core	Perps	Ovoids	Grids	#
I	Two Secant Lines	1	0	2	45
II	Single Line	3	0	0	15
III	Tricentric Triad	3	0	0	20
IV	Unicentric Triad	1	1	1	60
V	Single Point	1	2	0	15

and depicted in Figure 2. (Table 1, as well as Figure 1 and Figure 2, were taken from [17].)

In what follows, we will mainly be focused on $W(2N-3,2)$’s that are located in $W(2N-1,2)$. These are, in general, of two different kinds [10]. A $W(2N-3,2)$ of the first kind, to be called linear, is isomorphic to the intersection of two perp-sets with non-collinear nuclei and their number in $W(2N-1,2)$ is

$${\left|W\right|}_{W_l}=\frac{1}{3}{4}^{N-1}(4^N-1).$$

(16)

A $W(2N-3,2)$ of the second kind, to be called quadratic, is isomorphic to the intersection of a hyperbolic quadric and an elliptic quadric and $W(2N-1,2)$ features

$${\left|W\right|}_{W_q}=4^{N-1}(4^N-1)$$

(17)

of them. By way of example, in $W(3,2)$ a linear (resp. quadratic) $W(1,2)$ corresponds to a tricentric (resp. unicentric) triad.

In the sequel, when referring to $W(2N-1,2)$ and its subspaces, we will always have in mind the $W(2N-1,2)$ and its subspaces whose points are labelled by N-qubit observables from the set ${\mathcal{S}}_N$ as expressed by Equations (12) and (13). Moreover, a linear subspace of such $W(2N-1,2)$ will be called positive or negative according as the (ordinary) product of the observables located in it is $+{\mathcal{I}}_N$ or $-{\mathcal{I}}_N$, respectively. Let us illustrate this point, taking again the $N=2$ case. Up to isomorphism, there is just one type of the two-qubit doily. Its six observables of type A are $IX$, $XI$, $IY$, $YI$, $IZ$ and $ZI$ and its nine ones of type B are $XX$, $XY$, $XZ$, $YX$, $YY$, $YZ$, $ZX$, $ZY$ and $ZZ$, the latter lying on a particular hyperbolic quadric, ${\mathcal{Q}}_{\left(YY\right)}^{+}(3,2)$. Among the fifteen lines only the three lines $\{XX,YY,ZZ\}$, $\{XY,YZ,ZX\}$ and $\{XZ,YX,ZY\}$ are negative, forming also one system of generators of ${\mathcal{Q}}_{\left(YY\right)}^{+}(3,2)$.

3. W(3,2) and Its Two-Qubit W(1,2)’s

This is a rather trivial case. As already mentioned in Section 2, the doily contains three negative lines, which are all of the same ($B-B-B$) type. Among its $W(1,2)$’s, we find two types of linear ones and three types of quadratic ones whose properties are summarized in

Table 2. Classification of $W(1,2)$’s living in $W(3,2)$. Column one (T) shows the type, columns two and three ($O_A$ and $O_B$) indicate the number of observables of corresponding types and columns four ($W_l$) and five ($W_q$) yield, respectively, the number of ‘linear’ and ‘quadratic’ $W(1,2)$’s of a given type.

T	${\mathit{O}}_{\mathit{A}}$	${\mathit{O}}_{\mathit{B}}$	${\mathit{W}}_{\mathit{l}}$	${\mathit{W}}_{\mathit{q}}$
1	0	3	−	6
2	1	2	−	36
3	1	2	18	−
4	2	1	−	18
5	3	0	2	−

.

It is worth noticing that the six quadratic $W(1,2)$’s (i.e., unicentric triads) of Type 1 lie on the distinguished quadric ${\mathcal{Q}}_{\left(YY\right)}^{+}(3,2)$, being in fact its six ovoids.

4. W(5,2) and Its Three-Qubit Doilies

The space $W(5,2)$ contains 63 points, 315 lines and 135 generators, the latter being all Fano planes. Among the 63 canonical three-qubit observables associated to the points, nine are of type A, twenty-seven are type B and twenty-seven are of type C. Through an observable of type C, there pass six negative lines, all being of type $C-C-B$; thus the total number of negative lines of this type is $\frac{27\times 6}{2}=81.$ Through an observable of type B, there pass four negative lines. Of them, three are of the above-mentioned type and the fourth one is of type $B-B-B$; the total number of negative lines of the latter type is $\frac{27\times 1}{3}=9.$ As no negative line features an observable of type A, one finds that the $W(5,2)$ accommodates as many as $(81+9=)90$ negative lines.

When we pass to $W(3,2)$’s, we find a (much) richer structure, because alongside the types of observables we can employ one more parameter, namely the number of negative lines a given $W(3,2)$ contains. In fact, we find that the 336 linear doilies (see Equation (16)) fall into six different types and the 1008 quadratic ones (see Equation (17)) into seven types; we note in passing that Type 9 splits further into two subtypes depending on whether the two observables of type A do (Type $9A$, 162 members) or do not (Type $9B$, 54 members) commute. This classification is summarized in

Table 3. Classification of doilies living in $W(5,2)$. Column one (T) shows the type, column two ($C^{-}$) the number of negative lines in a doily of the given type, columns three to five ($O_A$ to $O_C$) indicate the number of observables of corresponding types and columns six ($D_l$) and seven ($D_q$) yield, respectively, the number of ‘linear’ and ‘quadratic’ doilies of a given type.

T	${\mathit{C}}^{-}$	${\mathit{O}}_{\mathit{A}}$	${\mathit{O}}_{\mathit{B}}$	${\mathit{O}}_{\mathit{C}}$	${\mathit{D}}_{\mathit{l}}$	${\mathit{D}}_{\mathit{q}}$
1	7	0	7	8	−	81
2	7	0	9	6	27	−
3	6	1	5	9	−	108
4	5	2	5	8	162	−
5	5	2	7	6	−	162
6	4	3	5	7	−	324
7	3	0	9	6	9	−
8	3	0	15	0	−	36
9	3	2	7	6	−	216
10	3	2	9	4	81	−
11	3	4	5	6	54	−
12	3	4	7	4	−	81
13	3	6	9	0	3	−

and is also pictorially illustrated in Figure 3. It is worth noticing here that there are two different types of doilies (Type 3 and Type 6) exhibiting an even number of negative lines.

The 27 observables of type B lie on an elliptic quadric of $W(5,2)$, which can be defined as follows:

$${\mathcal{Q}}_{\left(YYY\right)}^{-}(5,2):=x_1^2+x_1{x}_4+x_4^2+x_2^2+x_2{x}_5+x_5^2+x_3^2+x_3{x}_6+x_6^2=0.$$

(18)

Here, we took a coordinate basis of $W(5,2)$ in which the symplectic form $\sigma (x,y)$ is given by Equation (1),

$$\begin{array}{c}\hfill \sigma (x,y)=(x_1{y}_4-x_4{y}_1)+(x_2{y}_5-x_5{y}_2)+(x_3{y}_6-x_6{y}_3),\end{array}$$

so that the correspondence between the 63 three-qubit observables (see Equation (10))

$$\begin{array}{c}\hfill {\mathcal{S}}_3=\{G_1\otimes G_2\otimes G_3:G_j\in \{I,X,Y,Z\},j\in \{1,2,3\}\}\setminus {\mathcal{I}}_3\end{array}$$

and the 63 points of $W(5,2)$ is of the form (see Equation (12))

$$\begin{array}{c}\hfill G_j\leftrightarrow (x_j,x_{j+3}),j\in \{1,2,3\},\end{array}$$

taking also into account Equation (13).

This special quadric ${\mathcal{Q}}_{\left(YYY\right)}^{-}(5,2)$, as any non-degenerate quadric, is a geometric hyperplane of $W(5,2)$. As a doily is also a subgeometry of $W(5,2)$, it either lies fully in ${\mathcal{Q}}_{\left(YYY\right)}^{-}(5,2)$ (Type 8), or shares with ${\mathcal{Q}}_{\left(YYY\right)}^{-}(5,2)$ a set of points that form a geometric hyperplane; an ovoid (Types 3, 4, 6 and 11), a perp-set (Types 1, 5, 9 and 12) and a grid (Types 2, 7, 10 and 13). One also observes that no quadratic doily shares a grid with ${\mathcal{Q}}_{\left(YYY\right)}^{-}(5,2)$.

In addition to the distinguished elliptic quadric, there are also three distinguished hyperbolic quadrics in $W(5,2)$, namely: the quadric whose 35 observables feature either two $X^{\prime }$s or no X,

$${\mathcal{Q}}_{\left(ZZZ\right)}^{+}(5,2):=x_4^2+x_5^2+x_6^2+x_1{x}_4+x_2{x}_5+x_3{x}_6=0,$$

(19)

the one whose 35 observables feature either two $Y^{\prime }$s or no Y (see Equation (14)),

$${\mathcal{Q}}_{\left(III\right)}^{+}(5,2):=x_1{x}_4+x_2{x}_5+x_3{x}_6=0,$$

(20)

and the one whose 35 observables feature either two $Z^{\prime }$s or no Z,

$${\mathcal{Q}}_{\left(XXX\right)}^{+}(5,2):=x_1^2+x_2^2+x_3^2+x_1{x}_4+x_2{x}_5+x_3{x}_6=0.$$

(21)

Accordingly, there are three distinguished doilies of Type 8, namely the ones the quadric ${\mathcal{Q}}_{\left(YYY\right)}^{-}(5,2)$ shares with these three hyperbolic quadrics.

Take the two-qubit doily. Add formally to each observable, at the same position, the same mark from the set $\{X,Y,Z\}$. Pick up a geometric hyperplane in this three-qubit labeled doily and replace by I the added mark in each observable that belongs to this geometric hyperplane. One obviously gets a three-qubit doily. Now, there are 31 geometric hyperplanes in the doily, three possibilities $(X,Y,Z)$ to pick up a mark and three possibilities (left, middle, right) where to insert the mark; so there will be $31\times 3\times 3=279$ doilies created this way. In particular, out of the $15\times 9=135$ doilies ‘induced’ by perp-sets, 81 are of Type 10 and 54 of Type 11; out of the $10\times 9=90$ doilies ‘generated’ by grids, eighty-one are of Type 12 and nine of Type 8; finally, the $6\times 9=54$ doilies stemming from ovoids are all of the same type $9B$. So, if we look at Table 3, all doilies of Types 1 to 7, 27 doilies of Type 8 and all doilies of Type $9A$ can be regarded as ‘genuine’ three-qubit guys, nine doilies of Type 8 that originate from grids (henceforth referred to as Type $8^{\prime }$) and all doilies of Types $9B$ to 13 can be viewed as ‘built from the two-qubit guy’; with Type 13 doilies being even more two-qubit-like.

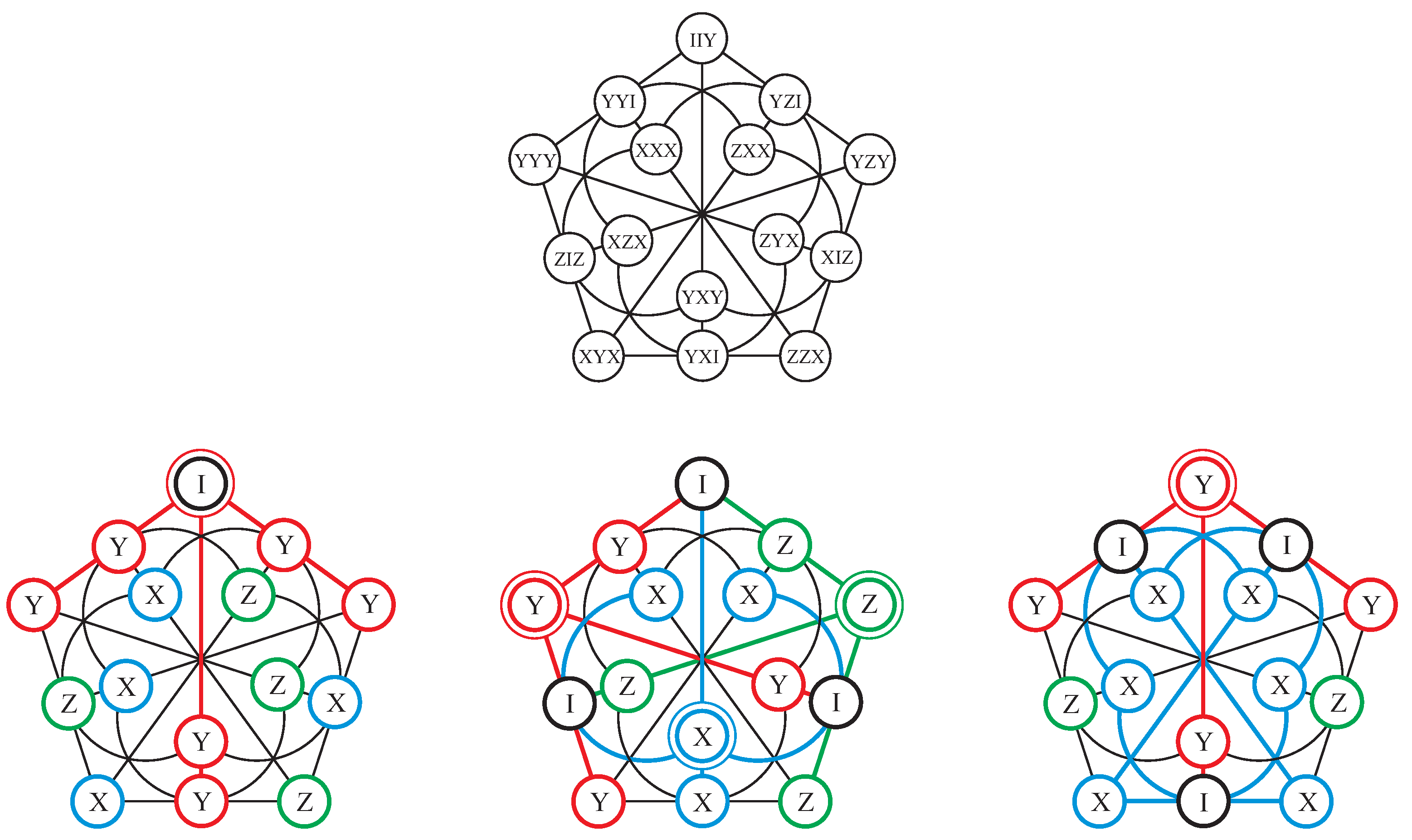
This stratification of three-qubit doilies can also be spotted in a different way. Take a representative doily of a particular type, for example, that of Type 3 depicted in Figure 4, top. From its three-qubit labels, keep first only the left mark (bottom left figure), then the middle mark (bottom middle figure) and, finally, the right mark (bottom right figure). In each of these three ‘residual’ doilies it is easy to see that if you take the points featuring a given non-trivial mark (i.e., X, Y or Z) together with the points featuring I, these always form a geometric hyperplane and the whole set form a Veldkamp line of the doily where the points featuring I represent its core. Employing Table 1 we readily see that this Veldkamp line is of type V (the core is a single point) for the left residual doily, type III (the core is a tricentric triad) for the middle doily and of type IV (the core is a unicentric triad) for the right one. To account this way for the 13 types of three-qubit doilies, we also need the concept of a trivial Veldkamp line of the doily, i.e., a line consisting of a geometric hyperplane counted twice and the full doily, which exactly accounts for those doilies ‘generated’ by the two-qubit doily. This classification is summarized in

Table 4. A refined classification of doilies living in $W(5,2)$. We use the following abbreviations for the cores of Veldkamp lines: 2cl—two concurrent lines, le—line, ttr—tricentric triad, utr—unicentric triad, pt—point, ov—ovoid, ps—perp-set, gr—grid and fl stands for the full doily.

T	2cl	le	ttr	utr	pt	ov	ps	gr	fl
1	1	−	−	−	2	−	−	−	−
2	−	3	−	−	−	−	−	−	−
3	−	−	1	1	1	−	−	−	−
4	−	1	2	−	−	−	−	−	−
5	1	−	−	2	−	−	−	−	−
6	1	−	1	1	−	−	−	−	−
7	−	3	−	−	−	−	−	−	−
8	3	−	−	−	−	−	−	−	−
$9A$	1	−	−	2	−	−	−	−	−
$8^{\prime }$	−	−	2	−	−	−	−	1	−
$9B$	−	−	2	−	−	1	−	−	−
10	−	−	2	−	−	−	1	−	−
11	−	−	2	−	−	−	1	−	−
12	−	−	2	−	−	−	−	1	−
13	−	−	2	−	−	−	−	−	1

. Here, columns two to six give the number of ordinary Veldkamp lines of a given type, columns seven to nine show the same for trivial Veldkamp lines and the last column corresponds to the degenerate case when all the points of a residual doily bear the label I. Note that all doilies stemming from the two-qubit doily (i. e., Types $8^{\prime }$ to 13) feature ordinary Veldkamp lines of the same type.

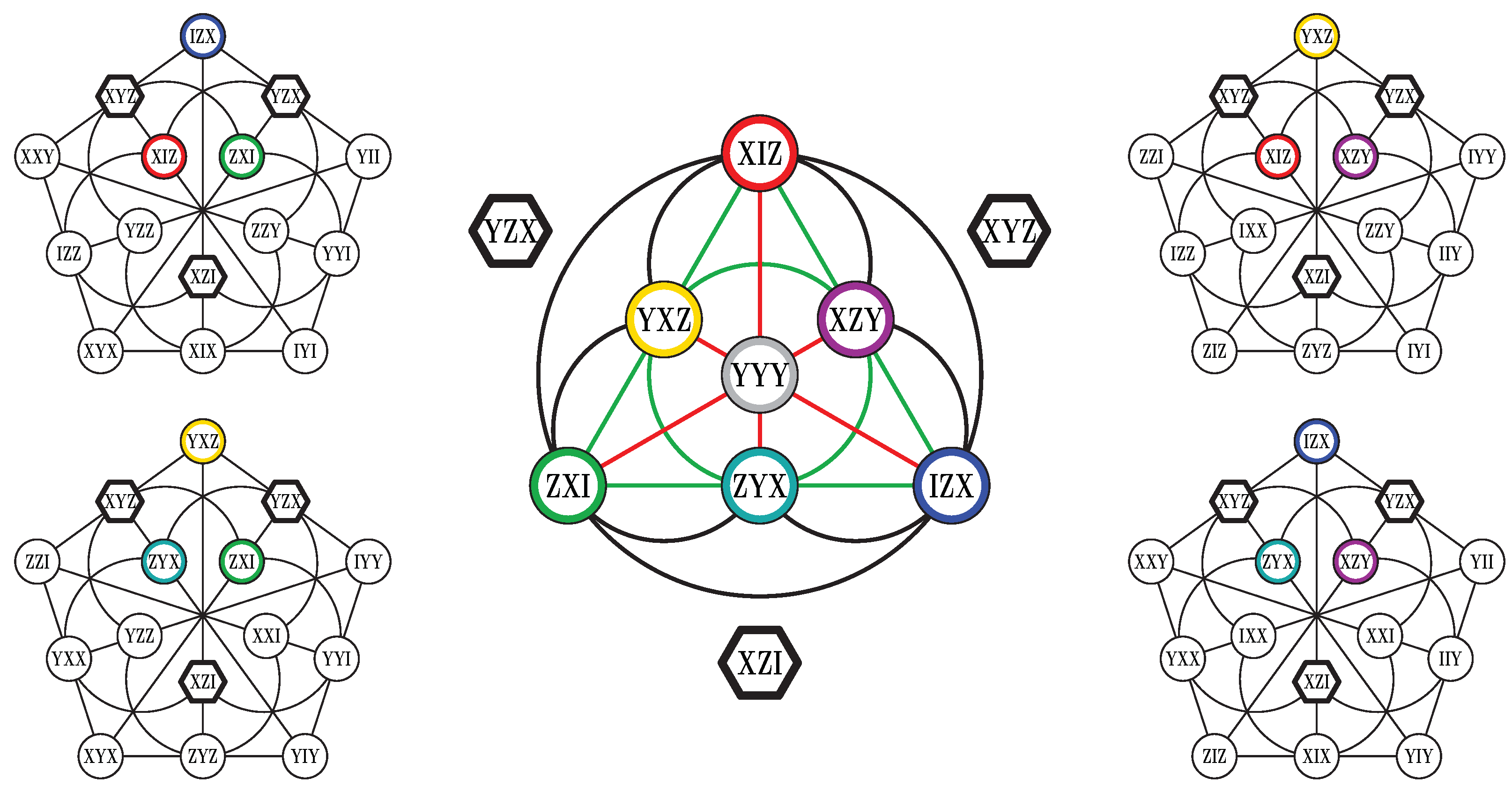
Using a computer, we have also found out a very interesting property that given a doily and any geometric hyperplane in it, there are three other doilies having the same geometric hyperplane. Figure 5 serves as a visualisation of this fact when the common geometric hyperplane is an ovoid. The four doilies sharing a geometric hyperplane, however, do not stand on the same footing. This is quite easy to spot from our example depicted in Figure 5. A point of the doily is collinear with three distinct points of an ovoid, the three points forming a unicentric triad. Let us pick up such a triad, say $\{ZYI,XYI,YYI\}$ and look for its centers in each of the four doilies. These are $IYI$ (top doily), $IIX$ (left doily), $IIY$ (right doily) and $IYZ$ (bottom doily). We see that the last three observables are mutually anticommuting, whereas the first observable commutes with each of them. This property is found to hold for each of $\left(\genfrac{}{}{0pt}{}{5}{3}\right)=10$ triads contained in an ovoid. Hence, the top doily of Figure 5 has indeed a different footing than the remaining three. A similar $3+1$ split up is also observed in any quadruple of doilies having a grid in common because a point of the doily is also collinear with three points of a grid that form a unicentric triad. However, when the shared hyperplane is a perp-set, one gets a different, namely a $2+2$ split, because in this case the corresponding triple of points forms a tricentric triad.

A tricentric triad of a linear resp. quadratic doily of $W(5,2)$ defines a line resp. plane in the ambient PG$(5,2)$. The latter type of a triad is found to be shared by four quadratic doilies. Given the three observables of such a triad, there are seven observables commuting with each of them, the corresponding seven points lying in a Fano plane (namely in the polar plane to the plane defined by the triad) in the ambient PG$(5,2)$. One of the seven observables has a distinguished footing as it commutes with each of the remaining six ones, with these six observables forming three commuting pairs. Out of the six observables, one can form just four tricentric triads of which each is complementary to the triad we started with and thus defines with the latter a unique quadratic doily. These properties are also illustrated in Figure 6.

Among the 13 different types of three-qubit doilies, there is one type, namely Type 3, which has two remarkable properties. The first property is that there is one point (to be called a deep point) such that all three lines passing through it are negative. Let us take a representative doily of such a type shown in Figure 3, 1st row right. The deep point is $ZIZ$. Then one sees that there are just two points (to be called zero-points) such that neither of them lies on a negative line; one is $IIY$ and the other is $XIZ$. These two points and the deep point form in the doily a tricentric triad, hence a copy of ‘linear’ $W(1,2)$. The second property is related to the fact that through each observable of type B there pass four negative lines. Three of them are such that each features one observable of type B and two observables of type C, whereas the remaining one consists of all observables of type B. Written vertically, the four negative lines passing through our deep point $ZIZ$ are:

$ZIZ$	$ZIZ$	$ZIZ$	$ZIZ$
$XXX$	$XYX$	$XZX$	$XIX$
$YXY$	$YYY$	$YZY$	$YIY$

We see that the three lines that are located in the doily are of the same type, viz. $B-C-C$. If we also include the fourth negative line, viz. the $B-B-B$ one, we obtain what we can call a ‘doily with a tail.’ Taking into account the above-mentioned four-doilies-per-hyperplane property, we see that there are altogether 12 doilies, four per each observable, having the same tail and all being of Type 3.

5. ‘Conwell’ Heptads of Doilies in W(5,2)

Recall Sylvester’s famous construction of $W(3,2)$, see [18]. Given a six-element set $M_6\equiv \{1,2,3,4,5,6\}$, a duad is an unordered pair $\left(ij\right)\in M_6$, $i\ne j$ and a syntheme is a set of three pairwise disjoint duads, i.e., a set $\left\{\right(ij),(kl),(mn\left)\right\}$ where $i,j,k,l,m,n\in M_6$ are all distinct. The point-line incidence structure whose points are duads and whose lines are synthemes, with incidence being inclusion, is isomorphic to $W(3,2)$, as also illustrated in Figure 7.

Next, take a seven-element set, $M_7\equiv \{1,2,3,4,5,6,7\}$. One can form from it $\left(\genfrac{}{}{0pt}{}{7}{3}\right)=35$ unordered triples $\left(ijk\right)$, $i\ne j\ne k\ne i$. From each set of fifteen triples having the same element in common, we can create a doily using the duad-syntheme construction on that six-element subset of $M_7$ where the common element is omitted. So, we achieve seven different doilies, one per each element, as depicted in Figure 8. Any two of them have an ovoid in common; because each ovoid is characterized by two elements, say a and b, and it is of the form $\left\{\right(abc),(abd),(abe),(abf),(abg\left)\right\}$, where $a,b,c,d,e,f,g\in M_7$ are all different, hence it belongs to both the a-doily and the b-doily. Also, any triple is shared by three doilies.

A remarkable fact is that this abstract heptad of doilies has a neat realization in our three-qubit $W(5,2)$. To see this, we have to introduce the notion of a Conwell heptad of PG$(5,2)$. Given a ${\mathcal{Q}}^{+}(5,2)$ of PG$(5,2)$, a Conwell heptad [19] (in the modern language [20] also known as a maximal exterior set) with respect to ${\mathcal{Q}}^{+}(5,2)$ is a set of seven off-quadric points such that each line joining two distinct points of the heptad is skew to the ${\mathcal{Q}}^{+}(5,2)$. There are exactly 8 heptads with respect to ${\mathcal{Q}}^{+}(5,2)$. Any two of them have exactly one point in common and any point off ${\mathcal{Q}}^{+}(5,2)$ is exactly in two heptads; also any six points of a heptad are linearly independent in PG$(5,2)$. Next [21], let P be a point on ${\mathcal{Q}}^{+}(5,2)$. The tangent hyperplane of ${\mathcal{Q}}^{+}(5,2)$ at P intersects a heptad C in exactly three points $P_1,P_2$ and $P_3$ such that the points $P,P_1,P_2$ and $P_3$ are coplanar and $P_1,P_2$ and $P_3$ are not collinear; that is, the points $P_1,P_2$ and $P_3$ represent a conic in the plane and the point P is its knot (the common intersection of its tangents). Hence, there exists a bijection from the set of the 35 points of ${\mathcal{Q}}^{+}(5,2)$ onto the set of the 35 triples of points of C.

Now, let us take a ${\mathcal{Q}}^{+}(5,2)$ that belongs to $W(5,2)$, for example, ${\mathcal{Q}}_{\left(III\right)}^{+}(5,2)$ (see Equation (20)) that accommodates all symmetric observables from ${\mathcal{S}}_3$. The eight Conwell heptads with respect to this distinguished hyperbolic quadric, expressed in terms of three-qubit observables, are:

1	2	3	4	5	6	7	8
$ZYX$	$YZI$	$YIZ$	$YZI$	$YIZ$	$YXI$	$XYI$	$YII$
$YIX$	$YXZ$	$YZX$	$YXI$	$YIX$	$YZZ$	$ZYZ$	$ZYI$
$YZZ$	$YXX$	$YXX$	$IYZ$	$XYI$	$YZX$	$ZYX$	$XYZ$
$XYX$	$IYI$	$IYX$	$IYX$	$IZY$	$IYI$	$ZIY$	$XYX$
$IYZ$	$IXY$	$ZYZ$	$ZIY$	$IXY$	$IZY$	$XZY$	$XIY$
$YXZ$	$XZY$	$IIY$	$YYY$	$YYY$	$XXY$	$XXY$	$ZZY$
$IIY$	$ZZY$	$XYZ$	$XIY$	$$ZYI$$	$ZXY$	$YII$	$ZXY$

We see that each Conwell heptad entails seven pairwise anticommuting observables and so, in fact, corresponds to a set of generators of a seven-dimensional Clifford algebra [22]. Let us pick up one of them, say the heptad number 1, and associate its observables with the elements of $M_7$ as follows:

$$1\leftrightarrow ZYX,2\leftrightarrow YIX,3\leftrightarrow YZZ,4\leftrightarrow XYX,5\leftrightarrow IYZ,6\leftrightarrow YXZ,7\leftrightarrow IIY.$$

From the above-described relation between tangent hyperplanes to a hyperbolic quadric and a Conwell heptad it follows that any unordered triple $\left(ijk\right)$, $i,j,k\in M_7$, will be associated with a particular point on ${\mathcal{Q}}_{\left(III\right)}^{+}(5,2)$ and its associated observable is the (ordinary) product of the observables associated with elements/points i, j and k; for example, $146\leftrightarrow ZYX.XYX.YXZ=IXZ$. Hence, all seven doilies of the heptad lie fully in ${\mathcal{Q}}_{\left(III\right)}^{+}(5,2)$ and, since no two of them share a line, they partition the set of 105 lines of ${\mathcal{Q}}_{\left(III\right)}^{+}(5,2)$. Figure 9 serves as a visualization of this particular ‘Conwell’ heptad of doilies. As $W(5,2)$ contains 36 hyperbolic quadrics (see Equation (6)), it features altogether $36\times 8=288$ such heptads of doilies. It is also worth mentioning that employing the well-known Klein correspondence between the points of ${\mathcal{Q}}^{+}(5,2)$ and the lines of PG$(3,2)$ (see, e.g., Table 15.10 of [23] for more details) and taking into account that the doily is a self-dual object, any Conwell heptad of doilies corresponds to a heptad of mutually azygetic doilies in PG(3,2) (see, e.g., [24]).

6. W(7,2) and Its Four-Qubit W(5,2)’s

The space $W(7,2)$ possesses 255 points, 5355 lines, 11,475 planes and 2295 generators, the latter being all PG(3,2)’s. Among the 255 canonical four-qubit observables associated to the points, 12 are of type A, 54 of type B, 108 of type C and 81 of type D. Through an observable of type D there pass: four negative lines of type $D-D-D$, totaling to $\frac{81\times 4}{3}=108$; twelve negative lines of type $D-D-B$, totaling to $\frac{81\times 12}{2}=486$; and twelve negative lines of type $D-C-C$, totaling to $81\times 12=972$. Through an observable of type C there pass, apart from the above-mentioned lines of type $D-C-C$, six negative lines of type $C-C-B$, totaling to $\frac{108\times 6}{2}=324$. Through an observable of type B there passes, apart from the already discussed two types of lines, a single negative line of type $B-B-B$, the total number of such lines being $\frac{54\times 1}{3}=18$. Since no negative line can contain an observable of type A, the four-qubit $W(7,2)$ thus exhibits five distinct types of negative lines whose total number is $(108+486+972+324+18=)1908$.

When it comes to $W(5,2)$’s, we find 11 types among their 5440 linear members and as many as 18 types among their 16,320 quadratic cousins, as summarized in

Table 5. Classification of $W(5,2)$’s living in $W(7,2)$. Column one (T) shows the type, column two ($C^{-}$) the number of negative lines in a $W(5,2)$ of the given type, columns three to six ($O_A$ to $O_D$) indicate the number of observables featuring three I’s, two I’s, one I or no I, respectively, columns seven ($W_l$) and eight ($W_q$) yield, respectively, the number of ‘linear’ and ‘quadratic’ $W(5,2)$’s of a given type, the last but one column depicts the type of intersection of a representative $W(5,2)$ with the distinguished hyperbolic quadric and the last column indicates the type of geometric hyperplane featuring the trivial mark (I) for composite $W(5,2)$’s.

T	${\mathit{C}}^{-}$	${\mathit{O}}_{\mathit{A}}$	${\mathit{O}}_{\mathit{B}}$	${\mathit{O}}_{\mathit{C}}$	${\mathit{O}}_{\mathit{D}}$	${\mathit{W}}_{\mathit{l}}$	${\mathit{W}}_{\mathit{q}}$	Int	GH
1	130	3	9	33	18	108	−	ell	$---$
2	126	0	24	0	39	−	108	full	$---$
3	126	1	13	27	22	−	1944	hyp	$---$
4	126	2	10	30	21	−	1620	perp	$---$
5	122	1	15	27	20	972	−	hyp	$---$
6	122	2	10	30	21	−	648	perp	$---$
7	118	0	16	32	15	−	324	perp	$---$
8	118	3	9	33	18	648	−	ell	$---$
9	118	3	11	25	24	−	1296	hyp	$---$
10	114	1	15	27	20	324	−	hyp	$---$
11	114	1	17	27	18	−	216	hyp	$---$
12	114	3	13	25	22	1944	−	hyp	$---$
13	114	4	12	28	19	−	1944	perp	$---$
14	110	3	15	25	20	−	1944	hyp	$---$
15	110	5	11	23	24	648	−	hyp	$---$
16	106	5	13	23	22	−	1944	hyp	$---$
17	102	1	21	27	14	−	648	hyp	$---$
18	102	2	18	30	13	−	324	perp	$---$
19	102	3	15	25	20	−	648	hyp	$---$
20	102	4	12	28	19	−	1944	perp	$---$
21	90	0	36	0	27	−	12	full	ell: $O=YYY$
22	90	2	22	30	9	−	108	perp	hyp: all 9 O’s featuring two Y’s
23	90	3	9	33	18	36	−	ell	$---$
24	90	3	21	25	14	324	−	hyp	perp: all 27 O’s of type C
25	90	4	16	28	15	−	324	perp	ell: all 27 O’s featuring one Y
26	90	5	15	31	12	324	−	ell	perp: all 27 O’s of type B
27	90	6	18	26	13	−	324	perp	hyp: 26 O’s having no Y + $III$
28	90	7	17	21	18	108	−	hyp	perp: all 9 O’s of type A
29	90	9	27	27	0	4	−	ell	full $W(5,2)$

. It represents no difficulty to check that 54 observables of type B and 81 of type D lie on a particular hyperbolic quadric in $W(7,2)$, to be referred to as the distinguished hyperbolic quadric ${\mathcal{Q}}_{\left(YYYY\right)}^{+}(7,2)$, which is also a geometric hyperplane in the latter space. A $W(5,2)$ either lies fully in this quadric (Types 2 and 21) or shares with it a set of points that forms a geometric hyperplane. Hence, the sum of $O_B$ and $O_D$ in each row of Table 5 must be one of the following numbers: 27 (when the hyperplane of $W(5,2)$ is an elliptic quadric), 31 (a perp-set) and/or 35 (a hyperbolic quadric); for the reader’s convenience, the type of such geometric hyperplane is explicitly listed in column 9 of Table 5. One sees that no linear $W(5,2)$ shares with ${\mathcal{Q}}_{\left(YYYY\right)}^{+}(7,2)$ a perp-set and no quadratic $W(5,2)$ cuts this distinguished quadric in an elliptic quadric. Comparing Table 5 with Table 3, one readily discerns that whereas $W(3,2)$’s in $W(5,2)$ are endowed with both an even and odd number of negative lines, for $W(5,2)$’s in $W(7,2)$ this number is always even; in addition, the difference in $C^{-}$ for any two distinct types of four-qubit $W(5,2)$’s is a multiple of four.

Let us have a closer look at $W(5,2)$’s featuring 90 (i.e., the smallest possible number of) negative lines. We can easily show that almost all of them originate from the three-qubit $W(5,2)$. First, by adding I to each three-qubit observable at the same position we achieve the four trivial four-qubit $W(5,2)$’s of Type 29. Next, adding to each observable at the same position a mark from the set $\{X,Y,Z\}$, picking up a geometric hyperplane in this four-qubit labeled $W(5,2)$ and replacing by I the added mark of each observable in the geometric hyperplane one gets a four-qubit $W(5,2)$ with 90 negative lines. Now, there are 28 (# of elliptic quadrics) + 36 (# of hyperbolic quadrics) + 63 (# of perp-sets) = 127 geometric hyperplanes in the $W(5,2)$, three possibilities $(X,Y,Z)$ to pick up a mark and four possibilities (left, middle-left, middle-right, right) where to insert the mark. So, there will be $127\times 3\times 4=1524$ four-qubit $W(5,2)$’s created this way, which only falls short by 36 the total number of $W(5,2)$’s endowed with 90 negative lines (the four guys of Type 29 being, of course, disregarded). A concise summary is given in the last column of Table 5, where the type of geometric hyperplane is further specified by the character/type of the associated (three-qubit) observable. One observes that Type 23 is the only irreducible type of $W(5,2)$’s having 90 negative lines.

We shall illustrate this process by a couple of examples. Let us start with the perp-set of the three-qubit $W(5,2)$ whose nucleus is an observable of type A, say $XII$. Out of 31 observables commuting with this observable there are seven of type A ($XII$, $IXI$, $IIX$, $IYI$, $IIY$, $IZI$ and $IIZ$), fifteen of type B ($IXX$, $IXY$, $IXZ$, $XXI$, $XIX$, $IYX$, $IYY$, $IYZ$, $XYI$, $XIY$, $IZX$, $IZY$, $IZZ$, $XZI$, and $XIZ$) and nine of type C ($XXX$, $XXY$, $XXZ$, $XYX$, $XYY$, $XYZ$, $XZX$, $XZY$, and $XZZ$). Hence, out of 32 observables off the perp, there will be $9-7=2$ of type A, $27-15=12$ of type B and $27-9=18$ of type C:

${\widehat{\mathcal{Q}}}_{\left(XII\right)}$	$O_A$	$O_B$	$O_C$
on	7	15	9
off	2	12	18

Next, each observable of the perp-set acquires a trivial mark I and hence goes into the four-qubit observable of the same type. However, an observable lying off the perp-set gets a non-trivial label X, Y or Z and so yields the four-qubit observable of the subsequent type; that is, $O_A^{\left(3\right)}\to O_B^{\left(4\right)}$, $O_B^{\left(3\right)}\to O_C^{\left(4\right)}$ and $O_C^{\left(3\right)}\to O_D^{\left(4\right)}$. Hence, in our case, we get:

(${\widehat{\mathcal{Q}}}_{\left(XII\right)}$)	$O_A$	$O_B$	$O_C$	$O_D$
(on – type intact)	7	15	9	0
(off – type shifted)	0	2	12	18
Total	7	17	21	18

Comparing with Table 5 we see that this is a four-qubit $W(5,2)$ of Type 28.

As the second example we shall take the case when the geometric hyperplane of $W(5,2)$ is an elliptic quadric generated by an antisymmetric observable of type B, say $YXI$. This quadric, ${\mathcal{Q}}_{\left(YXI\right)}^{-}(5,2)$, consists of all symmetric observables that commute with $YXI$ and all antisymmetric observables that anticommute with $YXI$. In particular, it contains 4 observables of type A ($IXI$, $IIX$, $IIZ$ and $IYI$), 11 observables of type B ($XZI$, $ZZI$, $YIY$, $IXX$, $IXZ$, $YZI$, $IYX$, $IYZ$, $XIY$, $ZIY$ and $IZY$) and 12 observables of type C ($XZX$, $ZZX$, $XZZ$, $ZZZ$, $YXY$, $XYY$, $ZYY$, $YZX$, $YZZ$, $XXY$, $ZXY$ and $YYY$). So, out of 36 observables off the quadric, there will be 5, 16 and 15 of type A, B and C, respectively. In a succinct form,

${\mathcal{Q}}_{\left(YXI\right)}^{-}(5,2)$	$O_A$	$O_B$	$O_C$
on	4	11	12
off	5	16	15

From this it follows that the corresponding four-qubit $W(5,2)$ is of Type 25:

(${\mathcal{Q}}_{\left(YXI\right)}^{-}(5,2)$)	$O_A$	$O_B$	$O_C$	$O_D$
(on – type intact)	4	11	12	0
(off – type shifted)	0	5	16	15
Total	4	16	28	15

7. Conclusions

We have introduced a remarkable observable-based taxonomy of subspaces of $W(2N-1,2)$, $2\le N\le 4$, whose rank is just one less than that of the ambient space. Alongside the distribution of various types of observables, an important parameter of the classification was the number of negative lines contained in a subspace. As already mentioned in the introduction, this latter parameter is essential in checking whether a given finite geometric configuration is contextual or not. For example, our preliminary analysis shows that all three-qubit and four-qubit doilies are, as their two-qubit sibling, contextual. In a separate paper we plan to address this question in more detail, also employing the degree of contextuality for a variety of other symplectic subspaces. However, when approaching subspaces of higher rank this way, it would be natural to include as parameters the number of negative linear subspaces of every viable dimension from 1 to $N-2$, i.e., consider negative lines, negative planes, …, negative generators; so, already in the case of $N=4$ we can add one more parameter, the number of negative planes a four-qubit $W(5,2)$ is endowed with, to achieve an interesting refinement of our Table 5. As the three-qubit $W(5,2)$ features 54 negative planes [25], each composite four-qubit $W(5,2)$ must have the same number of negative planes; in connection with this fact, it would be interesting to check whether each irreducible four-qubit $W(5,2)$ having 90 lines (Type 23) also enjoys this property.

Another interesting extension/variation of our taxonomy would be to take into account the number of negative lines passing through a point of the subspace. Let us call this number the order of a point and for each subspace $W(2s-1,2)$ define the following string of parameters $[p_0,p_1,p_2,\dots ,p_{4^{s-1}-1}]$, where $p_k$, $0\le k\le 4^{s-1}-1$ stands for the number of points of order k the subspace contains. Applying this to three-qubit doilies ($s=2$), we find the following five patterns (as readily discerned from Figure 3): $[0,9,6,0]$ (Types 1 and 2), $[2,9,3,1]$ (Type 3), $[5,5,5,0]$ (Types 4 and 5), $[6,6,3,0]$ (Type 6) and $[6,9,0,0]$ (Types 7 to 13).

A slightly different possibility of employing our strategy is to analyse other distinguished subgeometries of $W(2N-1,2)$ such as, for example, the split Cayley hexagon of order two [26]. This generalized polygon can be embedded into $W(5,2)$, and in two different ways [27], classical and skew. We have already discerned two distinct kinds of the former and as many as thirteen different types of the latter. Yet a full understanding of the case requires a more rigorous computer-assisted approach and will, therefore, be treated in a separate paper.