Abstract
A novel multi-server vacation queuing model is considered. The distinguishing feature of the model, compared to the standard queues, is the self-sufficiency of servers. A server can terminate service and go on vacation independently of the system manager and the overall situation in the system. The system manager can make decisions whether to allow the server to start work after vacation completion and when to try returning some server from a vacation to process customers. The arrival flow is defined by a general batch Markov arrival process. The problem of optimal choice of the total number of servers and the thresholds defining decisions of the manager arises. To solve this problem, the behavior of the system is described by the three-dimensional Markov chain with the special block structure of the generator. Conditions for the ergodicity of this chain are derived, the problem of computation of the steady-state distribution of the chain is discussed. Expressions for the key performance indicators of the system in terms of the distribution of the chain states are derived. An illustrative numerical result is presented.
1. Introduction
Queuing theory is one of the most quickly developing branches of applied probability due to the intensive appearance of new queuing models of real-world systems, telecommunication networks, in particular. As a consequence of the creation of various new schemes of resource sharing and multiplexing, the role of multi-server systems grows. The most common assumption made in the literature about multi-server queues is that there exists a finite or infinite pool of servers that provide service to arriving customers under the control of the system manager. The simplest, traditional, case assumes the existence of the fixed finite number of servers. The arriving customer occupies one of the idle servers to receive service. If all servers are occupied, the arrived customer is lost or stored into the buffer of a finite or infinite capacity or temporarily leaves the system and makes retrials to find a free server.
The process of servers’ occupation is usually completely defined by the arrival of customers. The arrival of a new customer implies the occupation of one more server if some server is free. The traditional service disciplines for the systems with a buffer are so-called conservative. This means that the situation when the input buffer is not empty while some servers are idle is not possible. The extreme diversity of real-world systems and processes that can be modeled by multi-server queuing systems gave raise to consideration of other scenarios of involvement of the servers into the processing of customers. Some of them are briefly listed below.
- Systems with unreliable servers in which any server (or all servers together) can be broken after a random period of time and require recovering. During the server recovering, it is not able to provide service. After the end of the recovering, the server resumes service if the input buffer is not empty. The literature about unreliable queuing systems (or queues with service interruption) is huge. We can mention, e.g., [1,2,3,4,5,6,7,8,9,10].
- Systems with server vacation in which in some situations the server can temporally stop operation and go to so-called vacation. Usually, the decision of whether or not to go on vacation does not depend on the wish of the server. Vacation is automatically taken if the buffer is empty or restriction on the continuous time of operation of the server or the number of sequentially provided services is violated. The existing literature about queuing systems with server vacation is also huge. We can mention, e.g., [11,12,13,14,15,16]; however, it is worth noting that the research of queuing systems with vacations mainly focuses on the analysis of single-server queues, e.g., [17].
- Systems with randomly varying number of available servers as the partial case of queues operating in the random environment, see, e.g., [18,19] and references therein. Note that in the majority of the papers devoted to the queues operating in the random environment the number of the servers does not change. Only the arrival, service and other rates are changed at the epochs of the change of the state of the random environment. These systems can be regarded as the generalization of unreliable queues to the cases of more flexible mechanisms of server activation and deactivation as well as partial reliability of the servers. The study of systems operating in a random environment was apparently initiated in [20] under the name of systems with partial failure of the device. Links to numerous more recent publications can be found, e.g., in [10,21,22,23].
- Systems with a controllable number of active servers in which a certain part of existing servers is switched-off and is activated (one-by-one or in blocks) only when the number of customers in the system grows above some fixed threshold values, see, e.g., [24,25,26,27].
- Systems in which arriving customers require occupation of a random number of servers, see, e.g., [28], or when all servers not engaged currently into service have to start service of an arriving customer, see, e.g., [29,30].
- Systems with additional resource required for service, see, e.g., [31,32,33,34,35,36]. Such systems are called in the literature as queuing-inventory systems, assembly-like systems, double-sided or queues with paired customers. These systems are non-conservative because the servers can stay idle in the presence of a non-empty buffer if some additional resource required for service is currently unavailable.
The model considered in this paper combines certain features of systems with vacations and systems with a controllable number of active servers. The common features are an opportunity of taking a vacation by a server and the possibility of influence, to some extent, on these vacations. The distinguishing feature of the considered model is the self-sufficiency of the servers. This self-sufficiency manifests itself as follows.
(i) Any server that just finished service of a customer may decide to take a vacation or start a new service, independently of the situation in the system and desire of the system manager;
(ii) The server being on vacation (we refer to such a server as the vacated server) that obtains an invitation (offer) of the system manager to terminate a vacation, due to accumulation of a long queue, can accept this offer and start service or decline this offer and continue its vacation.
Note that the leverage of influence of the system manager on the servers is the option not to allow to finish a vacation and start service if the queue length in the system is small.
The goal of this paper is to apply the matrix-analytical methods of queuing theory for analysis of the queuing system with self-sustained servers, which have many important applications. Analysis is far from being easy due to the space-inhomogeneous behavior of the multi-dimensional Markov chain describing the dynamics of the system. Nevertheless, the stability condition of the system is obtained in a nice analytically tractable form, algorithms for computation of the main performance measures of the system are elaborated and numerically verified.
The novelty of this paper is defined by the fact that, to the best of our knowledge, the systems with the self-sufficiency of servers defined in this paper are not considered in the existing literature.
One of the numerous possible practical applications of the considered queuing model is as follows. Let us consider a manufacturing company that produces some product. Products arrive at the warehouse from where they need to be delivered to consumers by trucks. The business model of the company does not assume the purchase, storage and maintenance of trucks. Instead, the company hires some pool of independent individual cargo carriers (freelancers, individual entrepreneurs) having their own truck for delivering the products. The contract between the company and the truck driver (server) assumes the obligation of the driver to finish any started service and its right not to provide further services for a while. The obligation of the company may be providing an opportunity to each server to implement a certain minimum average number of services during a fixed period of time. The company has the right to ignore the wish of the server to provide a service (if the queue is empty or short) and to invite the vacated server for resuming the service (if the queue becomes long).
A similar system arises in modeling Internet-based taxi companies in which the majority of engaged taxi drivers work only part-time in comfortable periods of time for them.
The proposed model can be used by the company owner for managerial goals. Namely, he/she can decide the optimal number of contracts with servers to be signed, conditions of proposing to the server to interrupt vacation and declining the attempt of the server to start working after vacation completion. Various costs can be taken into account, e.g., average waiting time in the queue, queue length, probability of a customer loss due to impatience, and charge for not providing the chances to implement the negotiated number of services. The problem of optimization of the number of required servers is far from trivial. If this number is too small, a queue may be pretty high. Customers may leave the queue without service (if the products are perishable or must be delivered to the consumer by a certain time), which may provoke substantial losses for the company. If this number is too large, problems with providing enough work to the servers can arise. The solution of the optimization problem requires the computation of the values of the various performance indicators of the system under the fixed values of the system parameters and the thresholds of defining decisions about sending invitations to the vacated servers and declining their offers to start working. As the mandatory step to make this computation, it is necessary to describe the behavior of the system by the multi-dimensional Markov chain and analyze its stationary distribution. Taking into account the nice properties of the Kronecker product of matrices, it is possible to write down the generator of the Markov chain describing the operation of the transportation company in a transparent form. Then, it is necessary to analyze the stationary behavior of the chain, compute performance measures of the system and implement numerical analysis of these indicators.
Correspondingly, the outline of the content of the sections of the paper is as follows. Section 2 contains a precise description of the queuing system under study. The process describing the behavior of the system is defined in Section 3 as the three-dimensional Markov chain. The infinitesimal generator of this Markov chain is written down. Section 4 is devoted to the derivation of the ergodicity condition of this Markov chain. Section 5 concerns the problem of computation of the stationary distribution of this Markov chain. Formulas for computing the values of several performance indicators of the system based on the known stationary distribution of the Markov chain are presented in Section 6. Section 7 contains numerical illustrations and Section 8 concludes the paper.
2. Mathematical Model
We consider a queuing system having the structure presented in Figure 1.
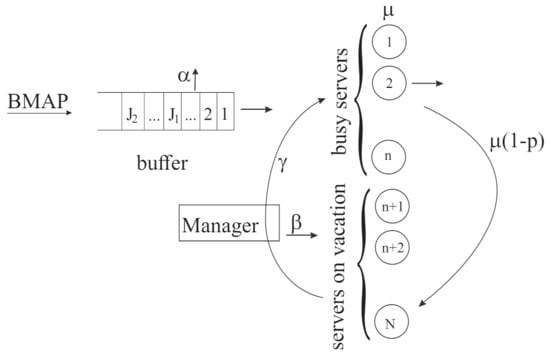
Figure 1.
Structure of queuing system under study.
The system has N identical and independent of each other servers. All arriving customers are temporarily placed into the buffer of an infinite capacity. The service discipline is First-In-First-Out. The arrival of customers is described by the batch Markov arrival process (). The is a rich class of point processes that allows to adequately model the majority of real-world processes, including those having correlated inter-arrival times and (or) large variance of these times. This makes them valuable for modeling real-world arrival flows. A detailed description of the can be found, e.g., in [37,38,39]; therefore, we present only very dense information about the that is necessary for the goals of this paper.
Arrivals of customers in the occur under control of an irreducible Markov chain with a finite state space were W is the fixed integer number. Intensities of transitions of the process which are accompanied by the arrival of a batch of k customers, are given by the entries of the matrix Here we assume that for where K is the maximum batch size. This assumption is just a technical one. It is non-necessary and made just for receiving a possibility to use for further analysis the numerically more efficient algorithms from [40] along with the algorithms from [41].
The diagonal entries of the matrix are negative and define, up to the sign, the intensity of departing of process from the corresponding states. The matrix is the generator of Markov chain The stationary distribution of Markov chain is defined by the row vector that is the unique solution to the system
Here and in the sequel, is a column vector of appropriate size consisting of 1 s, is a row vector of appropriate size consisting of 0 s.
The average rate of customers arrival is defined by
The average rate of batches arrival is defined by
We assume that the service time of a customer is exponentially distributed with the parameter If during the service completion epoch at some server the buffer is idle, the server takes a vacation. If the buffer is not idle, the server starts a new service with probability and with the complementary probability takes a vacation independently on the number of customers in the buffer. We assume that the vacation times of different servers are independent and have an exponential distribution with the parameter When the vacation time of a server expires, the server tries to start work. If during the vacation completion moment the number of customers in the buffer is greater than or equal to the predefined threshold the server picks up the customer from the head of the queue and starts its service. In the opposite case, i.e., the queue length is less than the server has to repeat vacations until it will obtain permission to resume service.
We assume that when the number of customers in the buffer becomes greater or equal to another predefined threshold such that the system starts searching a server being on vacation and offers to the server to terminate a vacation ahead of the schedule and start service. The search time has the exponential distribution with the parameter During each search, the system offers to start working to vacated servers sequentially. If any server agrees to start work, the search is stopped. If a server declines the offer, the system makes an offer to another vacated server. We assume that each vacated server declines the offer with probability and accepts the offer with the complementary probability. Thus, with the probability where n is the number of servers on the vacation, no one vacated server wants to interrupt the vacation and start working. With the complementary probability, the search results function by finding the server who accepts the offer. This server starts to work immediately. After the end of any search, the system starts the new search if the number of customers in the buffer is still greater or equal to the threshold Otherwise, new searches are not implemented until the queue length increases again to the level
Customers can be impatient and leave the buffer without service, independently of other customers. A customer leaves the system without service after an exponentially distributed patience time with the parameter
Our goal is to analyze the described queuing model.
3. Process of the System States
The behavior of the system under study can be described by the regular irreducible continuous-time Markov chain
where, during the epoch
- •
- is the number of customers in the buffer,
- •
- is the number of busy servers,
- •
- is the state of the underlying process of the ,
Here and further, the notation such as means that the parameter n admits values from the set
To formally define the continuous-time Markov it is necessary to write down, for any pair of the states and the intensities of transition between these states.
To avoid bulky denotations, following the standard methodology of investigation of multi-dimensional Markov chains having one denumerable component, we enumerate the states of the Markov chain in the direct lexicographic order of the components and combine the set of states into the level i,
Let be the matrix constituted by the transition intensities from level i to level j and let Q be the block matrix constituted by the blocks It is clear that the matrix Q is the infinitesimal generator of the Markov chain
Theorem 1.
The generator Q of the Markov chain has the following block upper-Hessenbergian structure
The non-zero blocks are defined as follows:
where
⊗ indicates the symbol of the Kronecker product matrices, see [42];
denotes the diagonal matrix with the diagonal entries listed in the brackets;
is the identity matrix having size indicated in the suffix (if the size of the matrix is clear from the context, it can be omitted);
Proof.
The proof of Theorem 1 is implemented via careful analysis of all possible transitions of the Markov chain and further combining the intensities of these transitions into the blocks of the generator.
The diagonal entries of the matrix Q are negative. The modulus of each diagonal entry defines the intensity of leaving the corresponding state of the Markov chain If the number of customers in the buffer is equal to zero, the Markov chain can leave its state only if the underlying process of the makes a transition without generation of a customer (the intensities of such transitions are given by the diagonal entries of the matrix ) or the service of a customer is finished (the intensities of such events are given as the diagonal entries of the matrix ). When the number of customers in the buffer is more than zero, additionally the Markov chain can leave its state due to the departure of a customer from the buffer due to impatience (the intensities of such events are given as the diagonal entries of the matrix ). If the number of customers in the buffer is greater than or equal to the Markov chain can also change its state when a vacant server decides to start work (the intensities of such events are given as the diagonal entries of the matrix ). If the number of customers in the buffer is greater than or equal to , the system can find a vacant server who agrees to start working, which also leads to the change of the state of the chain (the intensities of such events are given as the diagonal entries of the matrix ).
The non-diagonal entries of the matrix define the intensities of the transition of the chain that do not lead to the change of the number of customers in the buffer. In the case such intensities are the intensity of service completion in one busy server (such intensities are the entries of the matrix ). In the case such intensities are the intensity of service completion and unwillingness to continue the work in one busy server (such intensities are the entries of the matrix ). Note, that in these cases the number of busy servers decreases by one. This explains the appearance of the matrix in the corresponding formulas. Further, the transitions of the underlying process without generation of batches of customers (the intensities of such transitions are given as the non-diagonal entries of the matrix ) does not imply the change of the number of customers in the buffer.
Taking into account all the above reasonings, we obtain the form of the non-diagonal blocks
The entries of the matrix define the intensities of the Markov chain transitions that lead to the decrease in the number of customers in the buffer by one. In the case the events that lead to the decreasing the number of customers in the buffer by one are the following:
- 1.
- The server finishes service and wants to continue the work (the corresponding intensities are given as the entries of the matrix );
- 2.
- One of the customers staying in the buffer abandons it due to impatience (the corresponding intensities are given as the entries of the matrix );
- 3.
- One of the vacant servers decides to start working (the corresponding intensities are given as the entries of the matrix );
- 4.
- The system finds a vacant server who agrees to work (the corresponding intensities are given as the entries of the matrix );
Note that the occurrence of events 3 and 4 leads to an increase in the number of working servers by one, which is indicated by the matrix in the corresponding formulas. In the case only events 1 and 2 are possible. In the case possible events are 1, 2 and 3.
Taking these reasons into account we obtain the presented above form of the blocks
The entries of the matrix define the intensities of the Markov chain transitions that lead to the increase in the number of customers in the buffer by . This can happen only in the case of the arrival of a batch of customers of size The corresponding intensities are given as the entries of the matrices , which explains the form of the blocks □
4. Ergodicity Condition
Before computing the stationary distribution of the Markov chain it is necessary to find the conditions that have to be imposed on the parameters of the system to guarantee the existence of this distribution (ergodicity conditions).
Theorem 2.
If the customers in the buffer are impatient, i.e., then the stationary distribution of the considered Markov chain exists for any set of the system parameters.
If the customers in the buffer are patient, i.e., then the necessary and sufficient condition of the existence of the stationary distribution of the considered Markov chain is defined by the inequality
where is the probability that at an arbitrary moment when the system is overloaded, i.e., the number of customers in the buffer is huge, the number of busy servers is equal to
The probabilities are defined by formulas:
where
Proof.
Let us firstly consider the case . In this case, the Markov chain belongs to the class of asymptotically quasi-Toeplitz Markov chains, see [41]. This follows from the fact that the following limits exist:
where is the diagonal matrix with the diagonal entries equal to the corresponding diagonal entries of the matrix taken with the opposite sign, and is the Kronecker delta.
Let the matrix Y be defined as The matrix Y can be reducible. We denote as the irreducible blocks of the canonical normal form of the matrix and let be the corresponding blocks of the matrices
For the ergodicity of an asymptotically quasi-Toeplitz Markov chain, it is required that for each irreducible block the following inequality
holds true.
Here, the vectors are the unique solutions to the equations
One can verify that in the considered case the matrix and the matrices Thus, ergodicity conditions (7) is transformed to the inequalities which are true for all possible system parameters.
Now, let us consider the case In this case, the matrices and do not depend on the value i and are defined as
Thus, the Markov chain belongs to the class of quasi-Toeplitz (or type) Markov chains. The sufficient and necessary condition for the ergodicity condition of a quasi-Toeplitz Markov chain, see, e.g., [39], is the fulfillment of the following inequality:
or
Here, the vector is the unique solution of the system
where
It is easy to verify that the matrix has the form
Using the so-called mixed product rule for the Kronecker product of matrices, see [42], it is not difficult to verify by the direct substitution that the vector that is the solution of the system (10) can be computed in the form
where is the invariant probability vector of the stationary distribution of the underlying process of the
The vector is the unique solution to the system
The vector is the vector of the stationary distribution of the number of busy servers when the system is overloaded and defines the stationary distribution of the birth-and-death process with the state space The intensities of the birth and the death in the state n are defined, correspondingly, by Formulas (4) and (5). From the theory of the birth-and-death processes, it is well known that the vector in the partitioned form is defined by its components given by Formulas (2) and (3). By substituting the vector in form (11) into inequality (9), after some algebraic transformations, including the use of mixed product rule, we obtain inequality (1). □
Remark 1.
Ergodicity condition (1) is intuitively clear. The left-hand side of (1) is the rate of customers’ arrival to the system. The right-hand side of (1) is the rate of customers’ departure from the buffer when the system is overloaded. Indeed, as it was stated above, is the probability that n servers are busy at an arbitrary moment when the system is overloaded (correspondingly, servers are on vacation). Under the condition that n servers are busy, the rate of customers departure from the queue is the sum of:
(i) The rate of service completion without taking a vacation by the server that finished the service;
(ii) The rate of vacation completion (and starting service) by one of the vacated servers;
(iii) The rate of finishing a search of a server having a vacation that is accompanied by an agreement of one of vacated servers to interrupt vacation and start service.
Then (1) reflects the evident condition of stability of the system: when the system is overloaded, customers’ arrival rate must be less than the average customers’ departure rate from the buffer.
Remark 2.
Ergodicity condition (1) can be used for the preliminary, rough, choice of the system parameters, in particular, the number N of servers. If for the given (or evaluated by some experts) intensity λ of arrival, rates of service μ, vacations γ and successful invitations to interrupt vacation, and the fixed value N inequality (1) is not fulfilled, then the number of servers must be increased.
Remark 3.
It is easy to see that the statement of Theorem 2 is valid under assumptions that the following inequalities are fulfilled: and In the case of violation of these inequalities, the birth-and-death process with the generator A becomes the death process and (all servers are permanently vacated) or the birth process and (in the overloaded system all servers are permanently busy). Note that the imposed assumption (from the beginning) that and can be weakened. One of the rates γ and β can be equal to 0 if another one is positive. If (the server cannot take a vacation before the queue is exhausted), the servers are no longer self-sustained and the considered queuing system is the usual multi-server queue with vacations. The ergodicity condition is trivial
5. Computation of the Stationary Distribution of the Markov Chain
Let us assume that the ergodicity condition of the Markov chain is fulfilled. Then, the stationary probabilities
exists.
Enumerating the states of the Markov chain in the direct lexicographic order of the components and combining the stationary probabilities of the states included into the level we obtain the row vectors
It is well-known that the vectors can be found as the solution to so-called Chapman–Kolmogorov equations:
In the case as it was mentioned above, the generator Q of this Markov chain has an upper-Hessenbergian quasi-Toeplitz structure. The methods for computation of the stationary distribution of such Markov chains are well-known, see, e.g., [39,43]. To make computations for the queuing system under study, we propose the algorithm presented in Section 2.4.4 in [39].
In the case the solution of (12) encounters tremendous difficulties and we cannot cite any reference in the existing literature where system (12) is solved. Because the generator Q has the upper-Hessenbergian structure, it is possible to write down the recursion by which all the vectors can be calculated via the vectors and, eventually, via the vector ; however: (i) this recursion is not numerically stable due to multiple sequential implementations of subtraction of sub-stochastic vectors and (ii) what is more important, the impossibility to compute the vector Even in the case of type Markov chains, the problem of computation of the vector is solved based on some additional considerations, e.g., it was offered to use the interpretation of the stationary probability of a state of a discrete-time Markov chain in terms of the average time between the successive visits of the chain to this state. Alternatively, the reasonings of the analyticity of the generating function of the vectors in the unit disc of the complex plane are exploited. In the case of the chain with the non-quasi-Toeplitz structure of the generator, both these approaches do not work and no other approach is offered in the literature.
In such a situation, a very popular approach among the researchers in the matrix methods in queuing theory is to make some kind of truncation (rough or soft) of the state space of the chain, for more details see, e.g., [44]. The evident disadvantages of this approach consist of the difficulty of choosing the proper level of truncation and, as a rule, the high dimension of the finite system of equations for the stationary probabilities, which has to be solved numerically.
The analysis of Markov chains having the generator of a structure similar to the generator defined by Theorem 1, which are called in [41] as asymptotically quasi-Toeplitz Markov chains, is very important from the perspective of modeling various systems with customer retrials, see, e.g., [44], systems with impatient customers, systems and tandems of queues with an infinite number of servers; therefore, in [41], a new approach for the computation of the vectors is offered. This approach suggests that the vectors are computed not via solving the system (12) but by means of a solution of another, specially constructed, system of equations for the vectors The procedure of constructing this another system is described in detail in [41]. In two words, this procedure assumes the construction of series of so-called censored Markov chains with respect to the original Markov chain with different censoring levels. By means of varying the censoring levels, a new, alternative, system of equations for the vectors is obtained.
To solve this system, again, as it was described above with respect to the initial system (12), all vectors are recursively expressed via the vector This recursion is numerically stable; however, more important is the fact that using the censoring level 0, it is possible to derive the system of equations for the components of the vector Under fulfillment of the ergodicity condition, this system supplemented by one more equation derived via the use of normalization condition has a unique solution. The problem of computation of the vectors is completely solved.
In [41], more or less comprehensive analysis is implemented for continuous and discrete-time Markov chains, including the account of the possibility of irreducibility and reducibility of certain matrices arising during analysis. Ergodicity conditions and stable numerical algorithms for computation of the stationary distribution of Markov chains are presented.
It is worth mentioning that recently several papers by Japanese authors appeared in which the Markov chains having the upper-Hessenbergian non-quasi-Toeplitz structure of the generator appeared, see, e.g., [45,46]. They also use the idea of derivation of the system of equations for the stationary probabilities or conditional probabilities via the construction of the family of the censored Markov chains; however, in contrast to [41] where the states with large values of a denumerable component are censored, they censor other groups of states. The advantage of [45] over [41] is that no assumption about the form of heterogeneity in the generator is made while in [41] suggestion about the existence of the limiting behavior of the blocks of the generator when i tends to infinity is imposed; however, this advantage turns into a disadvantage because the problem of the derivation of the ergodicity condition is completely solved in [41] and is not touched in [45]. Further, the results from [45] are applicable only if the sub-diagonal blocks of the generator are non-singular matrices while in [41] they are allowed to be singular. This is very important for the application of the results to the analysis of multi-server queues where these blocks are usually singular.
For the implementation of the numerical experiments described below, we used the algorithms from the recent paper [40] in which the Markov chains having the upper-Hessenbergian non-quasi-Toeplitz structure of the generator are considered. In [40], no assumptions about the form of heterogeneity are made and the presented algorithm for computation of the stationary distribution is much faster than the algorithm based on the results of [41].
6. Performance Indicators
Having computed the row vectors and sub-vectors defined by we can compute various performance measures of the system. Expressions for some of them are presented below.
The average number of customers in the buffer can be found as
The average number of busy servers is computed as
The average number of servers on vacation is computed as
The average intensity of the output flow of successfully serviced customers can be found as
The loss probability of an arbitrary customer due to impatience is computed as
The probability that the system’s search for a vacant server who agrees to interrupt the vacation will be successful is computed as
The intensity of forced vacation of a working server due to empty buffer during service completion epoch can be found as
The probability that after the service completion moment the server would like to start a new service but is forced to take a vacation because the buffer is empty can be found as
The intensity of the refuses to the servers who would like to start work after vacation completion due to the presence of less than customers in the buffer can be found as
The probability that the server would like to start work after vacation completion but the system does not give permission to start due to the presence of less than customers in the buffer can be found as
7. Numerical Examples
We assume that the arrival flow at the system is the , which is defined by the following matrices
and has the following characteristics:
The average arrival rate of customers
The average arrival rate of batches
The coefficient of correlation of successive inter-arrival times
The squared coefficient of variation of inter-arrival times
The service intensity is assumed to be equal to The intensity of each customer’s impatience is
The parameter of the exponential distribution of the vacation time is equal to The intensity of each customer’s impatience is The probability p that the server starts a new service after the service completion, if the buffer is not idle, is equal to The parameter of the exponential distribution of the search time is The probability that each vacated server declines the offer to interrupt the vacation and start to work is
The aim of the numerical example is to define the control parameters and , which maximize the following economical criterion:
Here, a is a profit gained by the system from the service of one customer, b is a charge for the loss of one customer, c is a charge paid by the system when the server wants to start a new service after the service completion, but the buffer is empty and d is a charge paid by the system when the vacant server wants to start work, but the number of customers in the buffer is less than
In the numerical example, we fix the following values of costs coefficients:
Let us assume that the number of servers N can take the value from the range [5, 200], the parameter can vary from 1 to 20, and the parameter can vary from to 25.
Computations implemented under the fixed above values of parameters of the system and values show that the maximal value of the economical criterion is Thus, to maximize the profit of the system it is required to have servers, allow for the vacant server to start work when at least customers stay in the buffer and start the search of a server who wants to work among vacant servers when the number of customers in the buffer is more or equal to
Note, that if the manager of the system does not perform any control, i.e., the parameter (each vacant server can start work if the buffer is not empty) and the intensity (the system never searches servers who wants to start work), the optimal value of the cost criterion is and achieved for
Because it is not possible to present 4D figures, let us fix the value of the parameter and vary the number of servers N over the interval [5, 200] and the parameter over the interval .
Figure 2 illustrates the dependence of the average number of customers in the buffer on the number of servers N and the parameter .
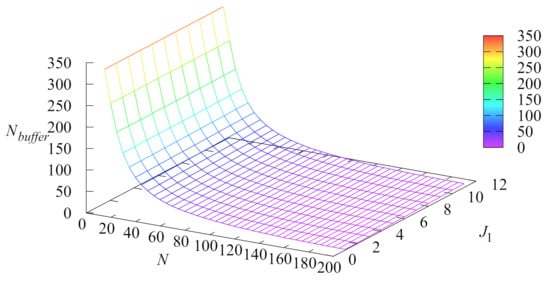
Figure 2.
Dependence of the average number of customers in the buffer on N and .
As it is seen from Figure 2, the average number of customers in the buffer decreases with the increase in the number of servers N and increases with the increase in the parameter
Figure 3 illustrates the dependence of the average number of busy servers on the number of servers N and the parameter .
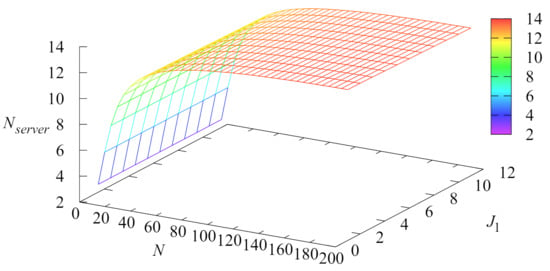
Figure 3.
Dependence of the average number of busy servers on N and .
As it is seen from Figure 3, the average number of busy servers decreases with the increase in the parameter and increases with the increase in the number of servers
Figure 4 illustrates the dependence of the loss probability on the number of servers N and the parameter .
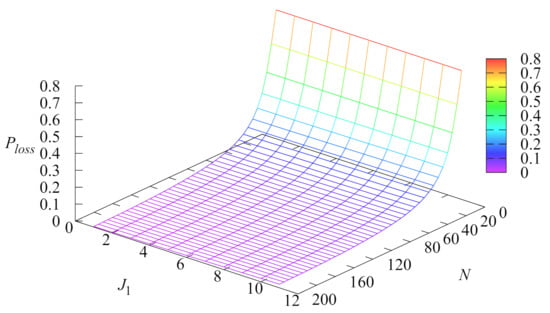
Figure 4.
Dependence of the loss probability on N and .
As it is seen from Figure 4, the loss probability increases with the increase in the parameter and decreases with the increase in the number of servers
The dependence of the probability that after the service completion moment the server would like to start a new service but is forced to take a vacation because the buffer is empty on the number of servers N and the parameter is illustrated in Figure 5.
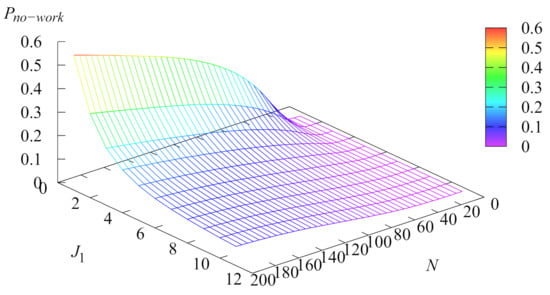
Figure 5.
Dependence of the probability on N and .
One can see from Figure 5 that the probability grows with the increase in the number of customers and decreases when the parameter increases.
Figure 6 illustrates the dependence of the probability that the server would like to start work after vacation completion but the system does not give permission to start due to the presence of less than customers in the buffer on the number of servers N and the parameter .
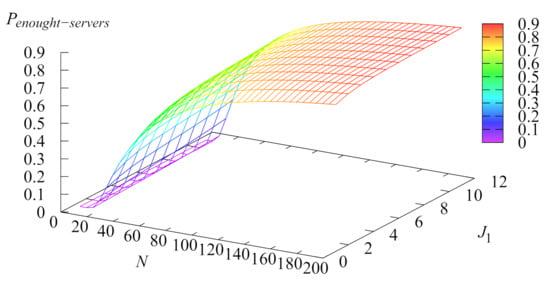
Figure 6.
Dependence of the probability on N and .
As it is seen from Figure 6, the probability increases with the increase in the parameter and the number of servers
The dependence of the values of the cost criterion E on the number of servers N and the parameter is illustrated in Figure 7.
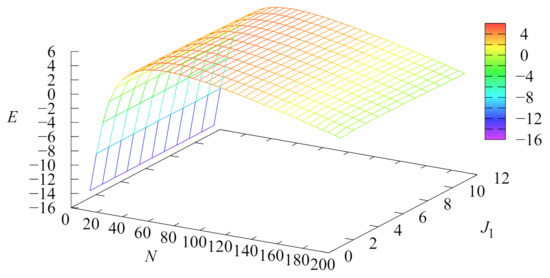
Figure 7.
Dependence of the probability on N and .
Some of the dependencies presented in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 are quite qualitatively clear. The values of Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 characterize these dependencies quantitatively, which allows to solve various optimization problems.
8. Conclusions
In this paper, we introduce into consideration a new kind of multi-server queuing systems with servers vacation. A novel feature of the model is a high degree of independence of servers of the decision-maker of the system. Any server from the finite pool of servers can stop operation after service completion of another customer and go for vacation. The manager of the system can implicitly influence performance of the system via the proper choice of the thresholds defining the providing to a server an opportunity to start work after vacation completion. Further, the manager can use the right to try to interrupt the ongoing vacation of a server if congestion occurs. The arrival flow is assumed to be defined by the that allows fitting modern flows. Such a type of model can have potential applications for the investigation of real systems with low centralization of operation of the system and the possibility of flexible choice of a working schedule by the servers, e.g., some modern systems with workers that are the freelancers that work at their free time when they wish, e.g., transportation systems, in particular, taxi drivers.
The model deserves to be generalized in many directions including consideration of the phase-type distribution of service or search times (which allows to more exactly fit the statistics about the values of these times, comparing the exponential distribution suggested in this paper), more involved strategies of control by beginning/finishing vacations, presence of a certain pool of permanent servers that completely obey the manager, account of retrial phenomenon (see [44,47,48]), random fluctuation of the system parameters, etc.
Author Contributions
Conceptualization, S.D., K.S. and A.D.; methodology, S.D., O.D. and K.S.; software, S.D. and O.D.; validation, S.D. and O.D.; formal analysis, S.D., K.S. and A.D.; investigation, A.D.; writing, original draft preparation, K.S. and A.D.; writing, review and editing A.D. and S.D.; supervision A.D. and K.S.; project administration O.D. and A.D. All authors read and agreed to the published version of the manuscript.
Funding
The publication was prepared with the support of the RUDN University Strategic Academic Leadership Program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mitrani, I.L.; Avi-Itzhak, B. A many-server queue with server interruptions. Oper. Res. 1968, 163, 628–638. [Google Scholar] [CrossRef]
- Neuts, M.F.; Lucantoni, D.M. A Markovian queue with N servers subject to breakdowns and repairs. Manag. Sci. 1979, 25, 849–861. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Pramod, P.K.; Chakravarthy, S.R. Queues with interruptions: A survey. Top 2014, 22, 290–320. [Google Scholar] [CrossRef]
- Chakravarthy, S.R.; Kulshrestha, R. A queueing model with server breakdowns, repairs, vacations, and backup server. Oper. Res. Perspect. 2020, 7, 100131. [Google Scholar] [CrossRef]
- Kim, C.S.; Klimenok, V.I.; Dudin, A.N. Analysis of unreliable BMAP/PH/N type queue with Markovian flow of breakdowns. Appl. Math. Comput. 2017, 314, 154–172. [Google Scholar] [CrossRef]
- Chakravarthy, S.R.; Ozkar, S.; Shruti, S. Analysis of M/M/c Retrial Queue with Thresholds, PH Distribution of Retrial Times and Unreliable Servers. J. Appl. Math. Inform. 2021, 39, 173–196. [Google Scholar]
- Yang, X.; Alfa, A.F. A class of multi-server queueing systems with server failures. Comput. Ind. Eng. 2009, 56, 33–43. [Google Scholar] [CrossRef]
- Klimenok, V.I.; Orlovsky, D.S.; Kim, C.S. The BMAP/PH/N retrial queue with Markovian flow of breakdowns. Eur. J. Oper. Res. 2008, 189, 1057–1072. [Google Scholar]
- Dudin, A.; Dudin, S. Analysis of a priority queue with phase-type service and failures. Int. J. Stoch. Anal. 2016, 2016, 9152701. [Google Scholar] [CrossRef] [Green Version]
- Kim, C.; Dudin, A.; Dudin, S.; Dudina, O. Analysis of an MMAP/PH1,PH2/N/∞ queueing system operating in a random environment. Int. J. Appl. Math. Comput. Sci. 2014, 24, 485–501. [Google Scholar] [CrossRef] [Green Version]
- Doshi, B.T. Queueing systems with vacations—A survey. Queueing Syst. 1986, 1, 29–66. [Google Scholar] [CrossRef]
- Tian, N.Z.; Zhang, G. Vacation Queueing Models-Theory and Applications; Springer: Heidelberg, Germany, 2006. [Google Scholar]
- Chao, X.; Zhao, Y.Q. Analysis of multi-server queues with station and server vacations. Eur. J. Oper. Res. 1998, 110, 392–406. [Google Scholar] [CrossRef]
- Kim, B.; Kim, J.; Bueker, O. Non-preemptive priority M/M/m queue with servers’ vacations. Comput. Ind. Eng. 2021, 160, 107390. [Google Scholar] [CrossRef]
- Chakravarthy, S.R. A Comparative Study of Vacation Models Under Various Vacation Policies: A Simulation Approach. In Mathematical Modeling and Computation of Real-Time Problems; CRC Press: Boca Raton, FL, USA, 2021; pp. 3–20. [Google Scholar]
- Kim, C.S.; Dudin, A.; Dudina, O.; Klimenok, V. Analysis of queueing system with non-preemptive time limited service and impatient customers. Methodol. Comput. Appl. Probab. 2020, 22, 401–432. [Google Scholar] [CrossRef]
- Takagi, H. Queueing Analysis: A Foundation of Performance Evaluation; North-Holland: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Dudin, A.; Kim, C.S.; Dudin, S.; Dudina, O. Priority Retrial Queueing Model Operating in Random Environment with Varying Number and Reservation of Servers. Appl. Math. Comput. 2015, 269, 674–690. [Google Scholar] [CrossRef]
- Kim, C.S.; Dudin, S. Analysis of Type Queueing System Operating in Random Environment. J. Korean Inst. Ind. Eng. 2016, 42, 30–37. [Google Scholar]
- Gnedenko, B.V.; Kovalenko, I.N. Introduction in Queueing Theory; KVIRTU: Kiev, Ukraine, 1963. (In Russian) [Google Scholar]
- Bin, S.; Dudin, S.A.; Dudina, O.S.; Dudin, A.N. A Customer Service Model in an Adaptive-Modulation Mobile Communication Cell with Allowance for Random Environment. Autom. Remote Control 2021, 82, 812–826. [Google Scholar] [CrossRef]
- Kim, C.S.; Klimenok, V.; Mushko, V.; Dudin, A. The BMAP/PH/N retrial queueing system operating in Markovian random environment. Comput. Oper. Res. 2010, 37, 1228–1237. [Google Scholar] [CrossRef]
- Yang, G.; Yao, L.G.; Ouyang, Z.S. The MAP/PH/N retrial queue in a random environment. Acta Math. Appl. Sin. Engl. Ser. 2013, 29, 725–738. [Google Scholar] [CrossRef]
- Lui, J.C.S.; Golubchik, L. Stochastic complement analysis of multi-server threshold queues with hysteresis. Perform. Eval. 1999, 35, 19–48. [Google Scholar] [CrossRef]
- Li, H.; Yang, T. Queues with a variable number of servers. Eur. J. Oper. Res. 2000, 124, 615–628. [Google Scholar] [CrossRef]
- Kim, C.S.; Dudin, A.; Dudin, S.; Dudina, O. Hysteresis Control by the Number of Active Servers in Queueing System with Priority Service. Perform. Eval. 2016, 101, 20–33. [Google Scholar] [CrossRef]
- Mitrani, I. Trading power consumption against performance by reserving blocks of servers. In Computer Performance Engineering; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–15. [Google Scholar]
- Green, L. A queueing system in which customers require a random number of servers. Oper. Res. 1980, 28, 1335–1346. [Google Scholar] [CrossRef] [Green Version]
- Kim, C.S.; Lee, M.H.; Dudin, A.; Klimenok, V. Multi-server queueing systems with cooperation of the servers. Ann. Oper. Res. 2008, 162, 57–68. [Google Scholar] [CrossRef]
- Dudin, A.N.; Sun, B. Unreliable Multi-server System with Controllable Broadcasting Service. Autom. Remote Control 2009, 70, 2073–2084. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Manikandan, R.; Shajin, D. Analysis of a multiserver queueing-inventory system. Adv. Oper. Res. 2015, 2015, 747328. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Shajin, D.; Lakshmy, B. On a queueing-inventory with reservation, cancellation, common life time and retrial. Ann. Oper. Res. 2016, 247, 365–389. [Google Scholar] [CrossRef]
- Gelenbe, E. Synchronising energy harvesting and data packets in a wireless sensor. Energies 2015, 8, 356–369. [Google Scholar] [CrossRef] [Green Version]
- Dudin, A.N.; Lee, M.H.; Dudin, S.A. Optimization of Service Strategy in Queueing System with Energy Harvesting and Customers Impatience. Int. J. Appl. Math. Comput. Sci. 2016, 26, 367–378. [Google Scholar] [CrossRef] [Green Version]
- Baek, J.H.; Dudina, O.; Kim, C.S. Queueing System with Heterogeneous Impatient Customers and Consumable Additional Items. Int. J. Appl. Math. Comput. Sci. 2017, 27, 367–384. [Google Scholar] [CrossRef] [Green Version]
- Sun, B.; Dudin, A.; Dudin, S. Queueing system with impatient customers, visible queue and replenishable inventory. Appl. Comput. Math. 2018, 17, 161–174. [Google Scholar]
- Chakravarthy, S.R. The batch Markovian arrival process: A review and future work. In Advances in Probability Theory and Stochastic Processes; Krishnamoorthy, A., Raju, N., Ramaswami, V., Eds.; Notable Publications Inc.: Princeton, NJ, USA, 2001; pp. 21–29. [Google Scholar]
- Lucantoni, D. New results on the single server queue with a batch Markovian arrival process. Commun. Statist.-Stoch. Model. 1991, 7, 1–46. [Google Scholar] [CrossRef]
- Dudin, A.N.; Klimenok, V.I.; Vishnevsky, V.M. The Theory of Queuing Systems with Correlated Flows; Springer Nature: Heidelberg, Germany, 2019. [Google Scholar]
- Dudin, S.; Dudin, A.; Kostyukova, O.; Dudina, O. Analysis of single-server retrial queueing model with a finite buffer, batch arrivals, and unreliable service. J. Comput. Appl. Math. 2020, 366. [Google Scholar]
- Klimenok, V.I.; Dudin, A.N. Multi-dimensional asymptotically quasi-Toeplitz Markov chains and their application in queueing theory. Queueing Syst. 2006, 54, 245–259. [Google Scholar] [CrossRef]
- Graham, A. Kronecker Products and Matrix Calculus with Applications; Horwood, E., Ed.; Courier Dover Publications: Cichester, UK, 1981. [Google Scholar]
- Neuts, M.F. Structured Stochastic Matrices of M/G/1 Type and Their Applications; Marcel Dekker: New York, NY, USA, 1989. [Google Scholar]
- Falin, G.; Templeton, J.G.C. Retrial Queues; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Takine, T. Analysis and computation of the stationary distribution in a special class of Markov chains of level-dependent M/G/1-type and its application to BMAP/M/∞ and BMAP/M/c + M queues. Queueing Syst. 2016, 84, 49–77. [Google Scholar] [CrossRef]
- Masuyama, H. A sequential update algorithm for computing the stationary distribution vector in upper block-Hessenberg Markov chains. Queueing Syst. 2019, 92, 173–200. [Google Scholar] [CrossRef] [Green Version]
- Breuer, L.; Dudin, A.N.; Klimenok, V.I. A retrial BMAP/PN/Nsystem. Queueing Syst. 2002, 40, 433–457. [Google Scholar] [CrossRef]
- Breuer, L.; Klimenok, V.; Birukov, A.; Dudin, A.; Krieger, U.R. Modeling the access to a wireless network at hot spots. Eur. Trans. Telecommun. 2005, 16, 309–316. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).