A New Algorithm for Computing Disjoint Orthogonal Components in the Parallel Factor Analysis Model with Simulations and Applications to Real-World Data
Abstract
1. Introduction, Notations, and Objectives
1.1. Introduction and Bibliographical Review
1.2. Acronyms, Notations, and Symbols
1.3. Objectives and Description of Sections
2. The Parafac Model and the Disjoint Approach
2.1. The Parafac Model
2.2. The ParafacALS Algorithm
| Algorithm 1: ParafacALS approach |
 |
2.3. A Disjoint Approach for the Parafac Model
| Definition of disjoint orthogonal matrix. |
| Let be an matrix, where . Then, is disjoint if and only if, for any i, there exists a unique j such that , and for any j, there exists i such that . If also satisfies , where is the identity matrix, then is a disjoint orthogonal matrix. |
3. The DisjointParafacALS Algorithm
3.1. Definitions
- : Three-way table of data;
- R: Number of components in modes A, B, and C;
- ALSMaxIter: Maximum number of iterations of the ALS algorithm; and
- Tol: Maximum distance allowed in the fit of the model for two consecutive iterations.
3.2. Stages of the Algorithm
- [Stage 1] Computation of a disjoint orthogonal loading matrix with the DisjointPCA algorithm: The first stage is computing the disjoint loading matrix. In order to obtain R disjoint orthogonal components in the loading matrices , , or , the DisjointPCA algorithm is applied to the matrices , , or , respectively. If , , and are required to be disjoint orthogonal, then we have that: Tol; Tol; and , respectively.
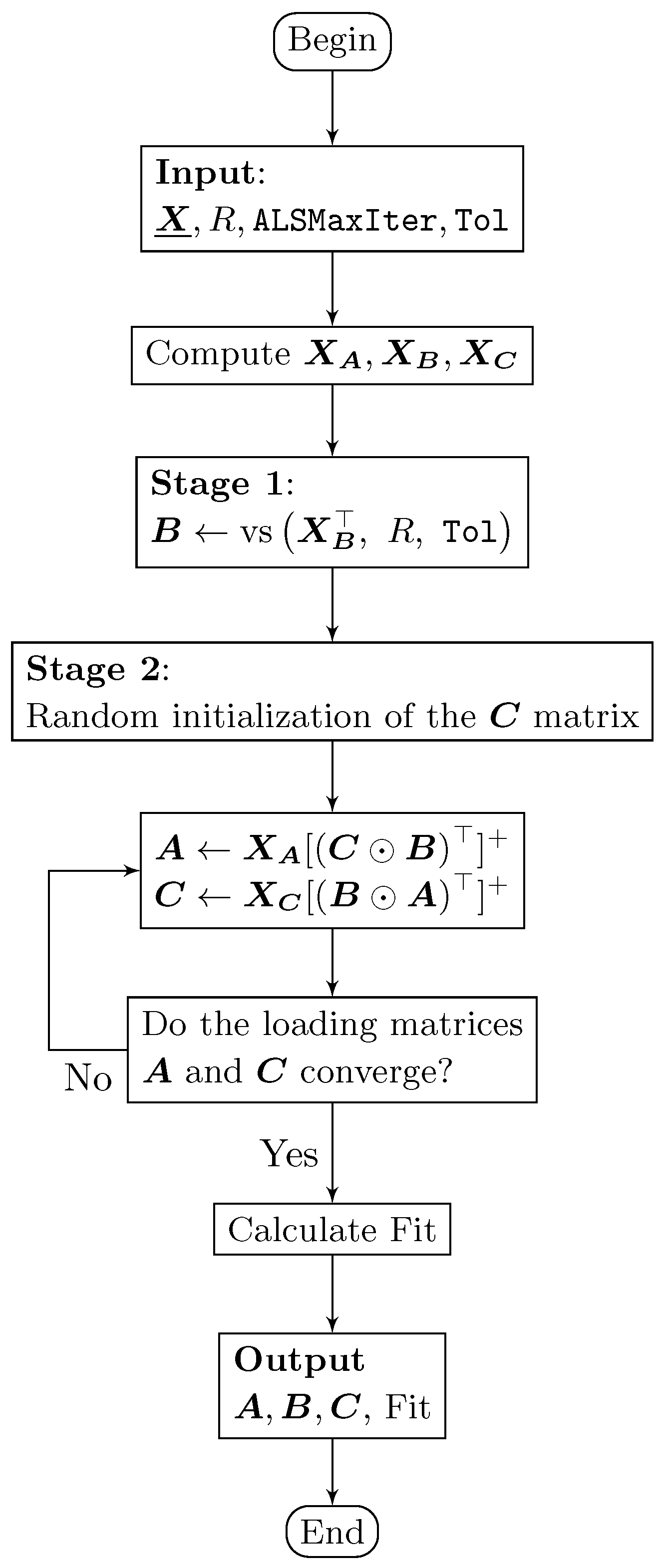
- [Stage 2] Computation of non-disjoint orthogonal loading matrices: The second stage is computing the non-disjoint loading matrices. For instance, if it is required that the matrix has disjoint orthogonal components, the ALS algorithm must be applied to compute loading matrices and ( matrix is fixed) as happens in the ParafacALS algorithm, initializing or ; see Figure 1. The other two cases can be developed from the illustration based on in this figure. The DisjointParafacALS algorithm finishes by outputing the matrices , , and , and the fit of the model.
3.3. Algorithm and Flowchart
| Algorithm 2: Procedure for using the DisjointParafacALS algorithm |
|
4. Computational Aspects
4.1. Characteristics of Hardware and Software
4.2. Experimental Settings for Simulated Data
4.3. Experimental Application with Simulated Data
5. Applications with Real-World Data
5.1. Applying the DisjointParafacALS Algorithm to TV Data
5.2. Applying the DisjointParafacALS Algorithm to Kojima Data
5.3. Applying the DisjointParafacALS Algorithm to Tongue Data
6. Conclusions, Other Potential Applications, and Future Work
- (i)
- (ii)
- (iii)
- There are also applications in environmental sciences related to water [36].
- (iv)
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hached, M.; Jbilou, K.; Koukouvinos, C.; Mitrouli, M. A multidimensional principal component analysis via the C-product Golub–Kahan–SVD for classification and face recognition. Mathematics 2021, 9, 1249. [Google Scholar] [CrossRef]
- Martin-Barreiro, C.; Ramirez-Figueroa, J.A.; Cabezas, X.; Leiva, V.; Galindo-Villardón, M.P. Disjoint and functional principal component analysis for infected cases and deaths due to COVID-19 in South American countries with sensor-related data. Sensors 2021, 21, 4094. [Google Scholar] [CrossRef]
- Hitchcock, F.L. The expression of a tensor or a polyadic as a sum of products. J. Math. Phys. 1927, 6, 164–189. [Google Scholar] [CrossRef]
- Hitchcock, F.L. Multiple invariants and generalized rank of a p-way matrix or tensor. J. Math. Phys. 1927, 7, 39–79. [Google Scholar] [CrossRef]
- Harshman, R.A. Foundations of the Parafac procedure: Models and conditions for an explanatory multimodal factor analysis. UCLA Work. Pap. Phon. 1970, 16, 1–84. [Google Scholar]
- Carroll, J.D.; Chang, J.J. Analysis of individual differences in multidimensional scaling via an N-way generalization of “Eckart-Young” decomposition. Psychometrika 1970, 35, 283–319. [Google Scholar] [CrossRef]
- Bro, R.; Kiers, H.A.L. A new efficient method for determining the number of components in Parafac models. J. Chemom. 2003, 17, 274–286. [Google Scholar] [CrossRef]
- Harshman, R.A.; Desarbo, W.S. An Application of Parafac to a Small Sample Problem, Demonstrating Preprocessing, Orthogonality Constraints, and Split-Half Diagnostic Techniques. In Research Methods for Multimode Data Analysis; Law, H.G., Snyder, C.W., Jr., Hattie, J.A., McDonald, R.P., Eds.; Praeger: New York, NY, USA, 1984; pp. 602–642. [Google Scholar]
- Leardi, R. Multi-Way Analysis with Applications in the Chemical Sciences, Age Smilde; Bro, R., Geladi, P., Eds.; Wiley: Chichester, UK, 2004. [Google Scholar]
- Harshman, R.; Lundy, M.E. Data preprocessing and the extended Parafac model. In Research Methods for Multimode Data Analysis; Law, H.G., Snyder, C.W., Jr., Hattie, J.A., McDonald, R.P., Eds.; Praeger: New York, NY, USA, 1984; pp. 216–284. [Google Scholar]
- Kroonenberg, P. Applied Multiway Data Analysis; Wiley: New York, NY, USA, 2008. [Google Scholar]
- Smilde, A.; Geladi, P.; Bro, R. Multi-Way Analysis: Applications in the Chemical Sciences; Wiley: New York, NY, USA, 2005. [Google Scholar]
- Amigo, J.M.; Marini, F. Multiway methods. In Data Handling in Science and Technology; Elsevier: Amsterdam, The Netherlands, 2011; Volume 28, pp. 265–313. [Google Scholar]
- Favier, G.; de Almeida, A.L. Overview of constrained Parafac models. EURASIP J. Adv. Signal Process. 2014, 2014, 142. [Google Scholar] [CrossRef]
- Giordani, P.; Kiers, H.; Ferraro, M.D. Three-way component analysis using the R package threeWay. J. Stat. Softw. Artic. 2014, 57, 1–23. [Google Scholar]
- Papalexakis, E.; Faloutsos, C.; Sidiropoulos, N.D. ParCube: Sparse parallelizable tensor decompositions. In Machine Learning and Knowledge Discovery in Databases; Springer: Berlin, Germany, 2012; pp. 521–536. [Google Scholar]
- Kaya, O.; Ucar, B. Scalable sparse tensor decompositions in distributed memory systems. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Austin, TX, USA, 15–20 November 2015; pp. 1–11. [Google Scholar]
- Li, J.; Ma, Y.; Wu, X.; Li, A.; Barker, K. PASTA: A parallel sparse tensor algorithm benchmark suite. CCF Trans. High Perform. Comput. 2019, 1, 111–130. [Google Scholar] [CrossRef]
- Kiers, H.A.; Giordani, P. Candecomp/Parafac with zero constraints at arbitrary positions in a loading matrix. Chemom. Intell. Lab. Syst. 2020, 207, 104145. [Google Scholar] [CrossRef]
- Wilderjans, T.F.; Ceulemans, E. Clusterwise Parafac to identify heterogeneity in three-way data. Chemom. Intell. Lab. Syst. 2013, 129, 87–97. [Google Scholar] [CrossRef]
- Cariou, V.; Wilderjans, T.F. Consumer segmentation in multi-attribute product evaluation by means of non-negatively constrained CLV3W. Food Qual. Prefer. 2018, 67, 18–26. [Google Scholar] [CrossRef]
- Vichi, M.; Saporta, G. Clustering and disjoint principal component analysis. Comput. Stat. Data Anal. 2009, 53, 3194–3208. [Google Scholar] [CrossRef]
- Macedo, E.; Freitas, A. The alternating least-squares algorithm for CDPCA. In EURO Mini-Conference on Optimization in the Natural Sciences; Plakhov, A., Tchemisova, T., Freitas, A., Eds.; Springer: Cham, Switzerland, 2015; pp. 173–191. [Google Scholar]
- Ferrara, C.; Martella, F.; Vichi, M. Dimensions of well-being and their statistical measurements. In Topics in Theoretical and Applied Statistics; Springer: Cham, Switzerland, 2016; pp. 85–99. [Google Scholar]
- Ramirez-Figueroa, J.A.; Martin-Barreiro, C.; Nieto-Librero, A.B.; Leiva, V.; Galindo-Villardón, M.P. A new principal component analysis by particle swarm optimization with an environmental application for data science. Stoch. Environ. Res. Risk Assess. 2021. [Google Scholar] [CrossRef]
- Martin-Barreiro, C.; Ramirez-Figueroa, J.A.; Nieto-Librero, A.B.; Leiva, V.; Martin-Casado, A.; Galindo-Villardón, M.P. A new algorithm for computing disjoint orthogonal components in the three-Way Tucker model. Mathematics 2021, 9, 203. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Tomasi, G.; Bro, R. A comparison of algorithms for fitting the Parafac model. Comput. Stat. Data Anal. 2006, 50, 1700–1734. [Google Scholar] [CrossRef]
- Caro-Lopera, F.J.; Leiva, V.; Balakrishnan, N. Connection between the Hadamard and matrix products with an application to matrix-variate Birnbaum–Saunders distributions. J. Multivar. Anal. 2012, 104, 126–139. [Google Scholar] [CrossRef]
- Lundy, M.E.; Harshman, R.; Kruskal, J. A two stage procedure incorporating good features of both trilinear and quadrilinear models. In Multiway Data Analysis; Elsevier: Amsterdam, The Netherlands, 1989; pp. 123–130. [Google Scholar]
- Kroonenberg, P.M.; Harshman, R.A.; Murakami, T. Analysing three-way profile data using the Parafac and Tucker3 models illustrated with views on parenting. Appl. Multivar. Res. 2009, 13, 5–41. [Google Scholar] [CrossRef][Green Version]
- Harshman, R.; Ladefoged, P.; Goldstein, L. Factor analysis of tongue shapes. J. Acoust. Soc. Am. 1977, 62, 693–707. [Google Scholar] [CrossRef] [PubMed]
- Andersen, C.M.; Bro, R. Practical aspects of Parafac modeling of fluorescence excitation-emission data. J. Chemom. 2003, 17, 200–215. [Google Scholar] [CrossRef]
- Bro, R.; Heimdal, H. Enzymatic browning of vegetables. Calibration and analysis of variance by multiway methods. Chemom. Intell. Lab. Syst. 1996, 34, 85–102. [Google Scholar] [CrossRef]
- Bro, R. Exploratory study of sugar production using fluorescence spectroscopy and multi-way analysis. Chemom. Intell. Lab. Syst. 1999, 46, 133–147. [Google Scholar] [CrossRef]
- Leardi, R.; Armanino, C.; Lanteri, S.; Alberotanza, L. Three-mode principal component analysis of monitoring data from Venice lagoon. J. Chemom. 2000, 14, 187–195. [Google Scholar] [CrossRef]
| Acronym / Notation / Symbol | Definition |
|---|---|
| PCA | Principal component analysis. |
| Parafac | Parallel factor analysis. |
| Tensor or three-way table (three dimensional). | |
| Data matrix (two dimensional). | |
| Number of entities in the first, second and third mode of the tensor, respectively. | |
| R | Number of components in the Parafac model. |
| Indices. | |
| Tensor element at position , with . | |
| Approximation of the element . | |
| Error when approximating the element . | |
| , , | Loading matrices of the first, second and third mode of the Parafac model, respectively. |
| Element of loading matrix at position , with . | |
| Element of loading matrix at position , with . | |
| Element of loading matrix at position , with . | |
| , , | Frontal, horizontal and vertical slices matrices from , respectively. |
| , , | Error matrices when approximating matrices , and , respectively. |
| Component correlation matrix. | |
| The identity matrix. | |
| ∘ | Hadamard product. |
| ⊙ | Khatri–Rao product. |
| The transpose of matrix . | |
| The Moore–Penrose generalized inverse of matrix . | |
| The Frobenius norm of matrix . | |
| Tol | The DisjointPCA algorithm with tolerance Tol is applied to the data matrix , and the |
| disjoint orthogonal loading matrix with R components is obtained as a result using | |
| the Vichi-Saporta (vc) algorithm [22]. |
| Course | COMP1 | COMP2 | COMP3 |
|---|---|---|---|
| Grammar | 0 | 0.42683051 | 0 |
| Math | 0.58009486 | 0 | 0 |
| Physics | 0.56675657 | 0 | 0 |
| Psychology | 0 | 0.52692660 | 0 |
| Literature | 0 | 0.51315878 | 0 |
| History | 0 | 0.52614840 | 0 |
| Chemistry | 0.58504440 | 0 | 0 |
| Sports | 0 | 0 | 1 |
| Element | Characterist |
|---|---|
| Operating System | Windows 10 for 64 bits |
| RAM | 8 Gigabytes |
| Processor | Intel Core i7-4510U 2-2.60 GHZ |
| Development tool—IDE— | Microsoft Visual Studio Express |
| Programming language | C#.NET |
| Statistical software | R |
| Data entry and presentation of results | Microsoft Excel |
| Communication between C#.NET and Excel | COM+ |
| Communication between C#.NET and R | R.NET |
| Random number generation | runif function of the stats package |
| Singular value decomposition (SVD) | irlba function of the irlba package |
| Moore–Penrose generalized inverse of a matrix | ginv function of the MASS package |
| COMP1 | COMP2 | COMP3 | |
|---|---|---|---|
| COMP1 | 1 | 0.019363 | 0.024297 |
| COMP2 | 0.019363 | 1 | 0.010313 |
| COMP2 | 0.024297 | 0.010313 | 1 |
| Disjoint Orthogonal Components | Fit (in %) | Runtime (in Minutes) |
|---|---|---|
| None (ParafacALS) | 99.31 | 0.0007 |
| (DisjointParafacALS) | 95.70 | 0.1736 |
| (DisjointParafacALS) | 93.71 | 0.1862 |
| (DisjointParafacALS) | 95.76 | 0.1325 |
| Subject (individual) | COMP1 | COMP2 | COMP3 |
|---|---|---|---|
| −0.39987415 | 0 | 0 | |
| −0.38886439 | 0 | 0 | |
| −0.46369775 | 0 | 0 | |
| −0.47750129 | 0 | 0 | |
| −0.49584480 | 0 | 0 | |
| 0 | 0.45327357 | 0 | |
| 0 | 0.40688744 | 0 | |
| 0 | 0.37939130 | 0 | |
| 0 | 0.34345457 | 0 | |
| 0 | 0.41482141 | 0 | |
| 0 | 0.44159947 | 0 | |
| 0 | 0 | −0.54088342 | |
| 0 | 0 | −0.41894439 | |
| 0 | 0 | −0.53459196 | |
| 0 | 0 | −0.49612716 |
| Variable | COMP1 | COMP2 | COMP3 |
|---|---|---|---|
| −0.40287714 | 0 | 0 | |
| −0.38117182 | 0 | 0 | |
| −0.38769074 | 0 | 0 | |
| −0.34328899 | 0 | 0 | |
| −0.31499905 | 0 | 0 | |
| −0.34929550 | 0 | 0 | |
| −0.45057171 | 0 | 0 | |
| 0 | −0.39457824 | 0 | |
| 0 | −0.33906833 | 0 | |
| 0 | −0.37809945 | 0 | |
| 0 | −0.30556330 | 0 | |
| 0 | −0.32902385 | 0 | |
| 0 | −0.32439850 | 0 | |
| 0 | −0.33306471 | 0 | |
| 0 | −0.41059636 | 0 | |
| 0 | 0 | −0.46109260 | |
| 0 | 0 | −0.43821079 | |
| 0 | 0 | −0.41637465 | |
| 0 | 0 | −0.38723790 | |
| 0 | 0 | −0.52157826 |
| Time | COMP1 | COMP2 | COMP3 |
|---|---|---|---|
| −0.72171067 | 0 | 0 | |
| −0.69219484 | 0 | 0 | |
| 0 | −0.43505908 | 0 | |
| 0 | −0.39485340 | 0 | |
| 0 | −0.49233526 | 0 | |
| 0 | −0.42701150 | 0 | |
| 0 | −0.47966818 | 0 | |
| 0 | 0 | −0.59150295 | |
| 0 | 0 | −0.53266172 | |
| 0 | 0 | −0.60530633 |
| COMP1 | COMP2 | COMP3 | |
|---|---|---|---|
| COMP1 | 1 | 0.05652381 | −0.97495543 |
| COMP2 | 0.05652381 | 1 | −0.11506567 |
| COMP3 | −0.97495543 | −0.11506567 | 1 |
| COMP1 | COMP2 | COMP3 | |
|---|---|---|---|
| COMP1 | 1 | 0 | 0 |
| COMP2 | 0 | 1 | 0 |
| COMP3 | 0 | 0 | 1 |
| Scenario | Fit (in %) | Runtime (in Minutes) |
|---|---|---|
| ParafacALS - Degeneracy | 47.93 | 0.4258 |
| ParafacALS with Orthogonal | 47.27 | 0.0182 |
| DisjointParafacALS with Disjoint Orthogonal | 41.12 | 0.5664 |
| DisjointParafacLAS with Disjoint Orthogonal | 41.21 | 0.5456 |
| Bipolar Scale | Humor | Sensitivity | Violence |
|---|---|---|---|
| (1) Thrilling-Boring | −0.09 | 0.29 | −0.12 |
| (2) Intelligent-Idiotic | 0.30 | 0.17 | 0.12 |
| (3) Erotic-Not Erotic | −0.25 | −0.06 | −0.27 |
| (4) Sensitive-Insensitive | 0.03 | −0.43 | 0.12 |
| (5) Interesting-Uninteresting | 0.00 | 0.37 | 0.26 |
| (6) Fast-Slow | −0.08 | 0.19 | −0.29 |
| (7) Intell. Stimulating-Intell. Dull | 0.27 | 0.20 | 0.25 |
| (8) Violent-Peaceful | 0.08 | 0.04 | −0.68 |
| (9) Caring-Callous | 0.04 | −0.47 | 0.02 |
| (10) Satirical-Not Satirical | −0.46 | 0.09 | 0.18 |
| (11) Informative-Uninformative | 0.31 | 0.20 | 0.19 |
| (12) Touching-Leave Me Cold | −0.07 | −0.31 | 0.15 |
| (13) Deep-Shallow | 0.21 | −0.14 | 0.16 |
| (14) Tasteful-Crude | 0.19 | −0.31 | 0.02 |
| (15) Real-Fantasy | 0.38 | 0.06 | −0.06 |
| (16) Funny-Not Funny | −0.46 | 0.06 | 0.30 |
| Bipolar Scale | Humor | Sensitivity | Violence |
|---|---|---|---|
| (1) Thrilling-Boring | 0 | 0.40 | 0 |
| (2) Intelligent-Idiotic | 0.39 | 0 | 0 |
| (3) Erotic-Not Erotic | −0.35 | 0 | 0 |
| (4) Sensitive-Insensitive | 0 | −0.50 | 0 |
| (5) Interesting-Uninteresting | 0 | 0.37 | 0 |
| (6) Fast-Slow | 0 | 0 | −0.52 |
| (7) Intell. Stimulating-Intell. Dull | 0.39 | 0 | 0 |
| (8) Violent-Peaceful | 0 | 0 | −0.47 |
| (9) Caring-Callous | 0 | −0.52 | 0 |
| (10) Satirical-Not Satirical | −0.39 | 0 | 0 |
| (11) Informative-Uninformative | 0.40 | 0 | 0 |
| (12) Touching-Leave Me Cold | 0 | −0.41 | 0 |
| (13) Deep-Shallow | 0 | 0 | 0.51 |
| (14) Tasteful-Crude | 0 | 0 | 0.50 |
| (15) Real-Fantasy | 0.36 | 0 | 0 |
| (16) Funny-Not Funny | −0.38 | 0 | 0 |
| TV Program | Humor | Sensitivity | Violence |
|---|---|---|---|
| (1) Mash | 0.14 | 0.03 | −0.11 |
| (2) Charlie’s angels | 0.21 | 0.13 | 0.54 |
| (3) All in the family | 0.20 | 0.04 | −0.18 |
| (4) 60 min | −0.35 | −0.19 | −0.18 |
| (5) The tonight show | 0.16 | −0.23 | −0.19 |
| (6) Let’s make a deal | 0.19 | 0.00 | 0.25 |
| (7) The Waltons | −0.13 | 0.55 | −0.23 |
| (8) Saturday night live | 0.35 | −0.31 | 0.11 |
| (9) News | −0.39 | −0.27 | 0.00 |
| (10) Kojak | 0.09 | −0.04 | 0.37 |
| (11) Mork and Mindy | 0.38 | 0.12 | −0.10 |
| (12) Jacques Cousteau | −0.40 | −0.10 | −0.29 |
| (13) Football | −0.07 | −0.32 | 0.39 |
| (14) Little house on the prairie | −0.06 | 0.54 | −0.18 |
| (15) Wild kingdom | −0.31 | 0.04 | −0.21 |
| TV Program | Humor | Sensitivity | Violence |
|---|---|---|---|
| (1) Mash | 0.17 | 0 | 0 |
| (2) Charlie’s angels | 0 | 0 | 0.53 |
| (3) All in the family | 0.28 | 0 | 0 |
| (4) 60 min | −0.51 | 0 | 0 |
| (5) The tonight show | 0 | −0.24 | 0 |
| (6) Let’s make a deal | 0 | 0 | 0.36 |
| (7) The Waltons | 0 | 0.60 | 0 |
| (8) Saturday night live | 0 | −0.44 | 0 |
| (9) News | −0.63 | 0 | 0 |
| (10) Kojak | 0 | 0 | 0.25 |
| (11) Mork and Mindy | 0.49 | 0 | 0 |
| (12) Jacques Cousteau | 0 | 0 | −0.58 |
| (13) Football | 0 | −0.31 | 0 |
| (14) Little house on the prairie | 0 | 0.55 | 0 |
| (15) Wild kingdom | 0 | 0 | −0.44 |
| COMP1 | COMP2 | COMP3 | |
|---|---|---|---|
| COMP1 | 1 | −0.20159703 | −0.93725207 |
| COMP2 | −0.20159703 | 1 | 0.06099119 |
| COMP3 | −0.93725207 | 0.06099119 | 1 |
| COMP1 | COMP2 | COMP3 | COMP4 | |
|---|---|---|---|---|
| COMP1 | 1 | 0.09060317 | −0.17620287 | 0.02597586 |
| COMP2 | 0.09060317 | 1 | −0.93490587 | 0.06082605 |
| COMP3 | −0.17620287 | −0.93490587 | 1 | −0.14096143 |
| COMP4 | 0.02597586 | 0.06082605 | −0.14096143 | 1 |
| Scenario | Fit (in %) | Runtime (in Min) |
|---|---|---|
| ParafacALS () - Degeneracy | 38.82 | 0.0753 |
| ParafacALS () with orthogonal | 38.01 | 0.0084 |
| DisjointParafacALS () with disjoint orthogonal | 32.28 | 0.2396 |
| ParafacALS () - Degeneracy | 45.95 | 0.0492 |
| DisjointParafacALS () with disjoint orthogonal | 36.69 | 0.4473 |
| Scale | Scale Type | COMP1 | COMP2 | COMP3 |
|---|---|---|---|---|
| (1) Acceptance | PSA | 0.64 | 0.27 | 0.24 |
| (2) Child centredness | PSA | 0.54 | 0.32 | 0.27 |
| (3) Possessiveness | BPC | 0.06 | 0.47 | 0.38 |
| (4) Rejection | R | −0.53 | 0.36 | 0.24 |
| (5) Control | BPC | 0.02 | 0.32 | 0.56 |
| (6) Enforcement | BPC | −0.18 | 0.34 | 0.49 |
| (7) Positive involvement | PSA | 0.54 | 0.4 | 0.3 |
| (8) Intrusiveness | BPC | 0.16 | 0.37 | 0.49 |
| (9) Control through guilt | R | −0.34 | 0.36 | 0.35 |
| (10) Hostile control | BPC | −0.17 | 0.34 | 0.61 |
| (11) Inconsistent discipline | LD | −0.3 | 0.43 | 0.14 |
| (12) Nonenforcement | LD | 0.28 | −0.22 | 0.01 |
| (13) Acceptance individuation | PSA | 0.64 | 0.29 | 0.17 |
| (14) Lax discipline | LD | 0.37 | 0 | 0.04 |
| (15) Instilling persistent anxiety | BPC | −0.11 | 0.41 | 0.49 |
| (16) Hostile detachment | R | −0.58 | 0.24 | 0.16 |
| (17) Withdrawal of relations | R | −0.45 | 0.35 | 0.23 |
| (18) Extreme autonomy | LD | 0.32 | −0.2 | 0.02 |
| Scale | Scale Type | COMP1 | COMP2 | COMP3 |
|---|---|---|---|---|
| (1) Acceptance | PSA | 0.49 | 0 | 0 |
| (2) Child centredness | PSA | 0.46 | 0 | 0 |
| (3) Possessiveness | BPC | 0 | 0.26 | 0 |
| (4) Rejection | R | 0 | 0.35 | 0 |
| (5) Control | BPC | 0 | 0.29 | 0 |
| (6) Enforcement | BPC | 0 | 0.33 | 0 |
| (7) Positive involvement | PSA | 0.47 | 0 | 0 |
| (8) Intrusiveness | BPC | 0.33 | 0 | 0 |
| (9) Control through guilt | R | 0 | 0.34 | 0 |
| (10) Hostile control | BPC | 0 | 0.36 | 0 |
| (11) Inconsistent discipline | LD | 0 | 0.26 | 0 |
| (12) Nonenforcement | LD | 0 | 0 | 0.57 |
| (13) Acceptance individuation | PSA | 0.46 | 0 | 0 |
| (14) Lax discipline | LD | 0 | 0 | 0.59 |
| (15) Instilling persistent anxiety | BPC | 0 | 0.34 | 0 |
| (16) Hostile detachment | R | 0 | 0.28 | 0 |
| (17) Withdrawal of relations | R | 0 | 0.33 | 0 |
| (18) Extreme autonomy | LD | 0 | 0 | 0.57 |
| Scale | Scale Type | COMP1 | COMP2 | COMP3 | COMP4 |
|---|---|---|---|---|---|
| (1) Acceptance | PSA | 0.52 | 0 | 0 | 0 |
| (2) Child centredness | PSA | 0.49 | 0 | 0 | 0 |
| (3) Possessiveness | BPC | 0 | 0.34 | 0 | 0 |
| (4) Rejection | R | 0 | 0 | 0.55 | 0 |
| (5) Control | BPC | 0 | 0.39 | 0 | 0 |
| (6) Enforcement | BPC | 0 | 0.37 | 0 | 0 |
| (7) Positive involvement | PSA | 0.50 | 0 | 0 | 0 |
| (8) Intrusiveness | BPC | 0 | 0.35 | 0 | 0 |
| (9) Control through guilt | R | 0 | 0.35 | 0 | 0 |
| (10) Hostile control | BPC | 0 | 0.43 | 0 | 0 |
| (11) Inconsistent discipline | LD | 0 | 0 | 0.45 | 0 |
| (12) Nonenforcement | LD | 0 | 0 | 0 | 0.57 |
| (13) Acceptance individuation | PSA | 0.50 | 0 | 0 | 0 |
| (14) Lax discipline | LD | 0 | 0 | 0 | 0.59 |
| (15) Instilling persistent anxiety | BPC | 0 | 0.41 | 0 | 0 |
| (16) Hostile detachment | R | 0 | 0 | 0.50 | 0 |
| (17) Withdrawal of relations | R | 0 | 0 | 0.49 | 0 |
| (18) Extreme autonomy | LD | 0 | 0 | 0 | 0.57 |
| Disjoint Orthogonal Components | Fit (in %) | Runtime (in Min) |
|---|---|---|
| None (ParafacALS) | 92.62 | 0.0016 |
| (DisjointParafacALS) | 86.62 | 0.0913 |
| (DisjointParafacALS) | 85.23 | 0.1432 |
| (DisjointParafacALS) | 85.31 | 0.0765 |
| COMP1 | COMP2 | |
|---|---|---|
| COMP1 | 1 | 0.06890887 |
| COMP2 | 0.06890887 | 1 |
| Vowel | COMP1 | COMP2 |
|---|---|---|
| 1 | 1.52 | 0.69 |
| 2 | 0.97 | 0.33 |
| 3 | 1.04 | 0.42 |
| 4 | 0.77 | −0.17 |
| 5 | 0.33 | −0.53 |
| 6 | −0.31 | −2.04 |
| 7 | −1.07 | −1.24 |
| 8 | −1.38 | 0.26 |
| 9 | −1.05 | 0.58 |
| 10 | −0.83 | 1.69 |
| Vowel | COMP1 | COMP2 |
|---|---|---|
| 1 | 0.55 | 0 |
| 2 | 0.33 | 0 |
| 3 | 0.37 | 0 |
| 4 | 0.19 | 0 |
| 5 | 0 | −0.12 |
| 6 | 0 | −0.91 |
| 7 | −0.51 | 0 |
| 8 | −0.35 | 0 |
| 9 | −0.20 | 0 |
| 10 | 0 | 0.40 |
| Tongue Point | COMP1 | COMP2 |
|---|---|---|
| 4 | −0.60 | −1.19 |
| 5 | −0.88 | −1.09 |
| 6 | −1.05 | −0.95 |
| 7 | −1.16 | −0.59 |
| 8 | −1.14 | −0.01 |
| 9 | −0.95 | 0.46 |
| 10 | −0.55 | 0.93 |
| 11 | 0.14 | 1.24 |
| 12 | 0.87 | 1.42 |
| 13 | 1.26 | 1.37 |
| 14 | 1.41 | 1.22 |
| 15 | 1.32 | 0.93 |
| 16 | 0.91 | 0.49 |
| Tongue Point | COMP1 | COMP2 |
|---|---|---|
| 4 | −0.25 | 0 |
| 5 | −0.30 | 0 |
| 6 | −0.31 | 0 |
| 7 | −0.29 | 0 |
| 8 | 0 | −0.66 |
| 9 | 0 | −0.61 |
| 10 | 0 | −0.43 |
| 11 | 0.18 | 0 |
| 12 | 0.34 | 0 |
| 13 | 0.40 | 0 |
| 14 | 0.41 | 0 |
| 15 | 0.36 | 0 |
| 16 | 0.23 | 0 |
| Speaker | COMP1 | COMP2 |
|---|---|---|
| 1 | −0.43 | −0.27 |
| 2 | −0.70 | −0.36 |
| 3 | −0.37 | −0.37 |
| 4 | −0.34 | −0.49 |
| 5 | −0.47 | −0.31 |
| Speaker | COMP1 | COMP2 |
|---|---|---|
| 1 | −0.46 | 0 |
| 2 | −0.72 | 0 |
| 3 | 0 | −0.66 |
| 4 | 0 | −0.75 |
| 5 | −0.52 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martin-Barreiro, C.; Ramirez-Figueroa, J.A.; Cabezas, X.; Leiva, V.; Martin-Casado, A.; Galindo-Villardón, M.P. A New Algorithm for Computing Disjoint Orthogonal Components in the Parallel Factor Analysis Model with Simulations and Applications to Real-World Data. Mathematics 2021, 9, 2058. https://doi.org/10.3390/math9172058
Martin-Barreiro C, Ramirez-Figueroa JA, Cabezas X, Leiva V, Martin-Casado A, Galindo-Villardón MP. A New Algorithm for Computing Disjoint Orthogonal Components in the Parallel Factor Analysis Model with Simulations and Applications to Real-World Data. Mathematics. 2021; 9(17):2058. https://doi.org/10.3390/math9172058
Chicago/Turabian StyleMartin-Barreiro, Carlos, John A. Ramirez-Figueroa, Xavier Cabezas, Victor Leiva, Ana Martin-Casado, and M. Purificación Galindo-Villardón. 2021. "A New Algorithm for Computing Disjoint Orthogonal Components in the Parallel Factor Analysis Model with Simulations and Applications to Real-World Data" Mathematics 9, no. 17: 2058. https://doi.org/10.3390/math9172058
APA StyleMartin-Barreiro, C., Ramirez-Figueroa, J. A., Cabezas, X., Leiva, V., Martin-Casado, A., & Galindo-Villardón, M. P. (2021). A New Algorithm for Computing Disjoint Orthogonal Components in the Parallel Factor Analysis Model with Simulations and Applications to Real-World Data. Mathematics, 9(17), 2058. https://doi.org/10.3390/math9172058










