Business Cycles in a Two-Sided Altruism Model

Abstract

This study demonstrates that business cycles with complex periodic fluctuations may arise in an overlapping generations model with two-sided altruism. The structure of an equilibrium dynamical system strongly depends on the degree of altruism in the model. If either altruism of a generation to the parent or the child disappears, the study also demonstrates that complex periodic fluctuations never occur. In this sense, two-sided altruism is essential for a complex business cycle.

1. Introduction

In an infinite time horizon model in which each generation has an identical time-inconsistent preference, existing studies considered a sub-game perfect Nash equilibrium as an equilibrium concept and characterized it as a sequence consisting of each generation’s policy function. In an overlapping generations model with intergenerational altruism, in which time inconsistency arises, recent studies revealed a condition under which each generation’s policy function is linear, and found that its sequence is determined by a simple dynamical system (see the research of Fujiu and Yano [1,2]). This finding implies that generations may have different policy functions from each other. In the study on intergenerational altruism and transfers, revealing how the policy functions may vary from generation to generation is significant. Thus, examining the dynamical system which determines a sequence of them is also significant. However, little has been done in this regard.

The study analyzes a dynamical system which determines a sequence of each generation’s policy function. Based on this analysis, it demonstrates that the dynamical system may produce a cyclical sequence of period-3 in an overlapping generations model with two-sided altruism. By the theorem of Li and Yorke [3], period-3 implies chaos. Thus, complex business cycles may occur in the model.

This study examines time-inconsistent preferences, which have been studied by Strotz [4]; Phelps and Pollak [5]; Laibson [6]. Recent studies conduct research on the relationship between intergenerational altruism and time inconsistency (see Galperti and Strulovici [7]; Gonzalez, Lazkano and Smulders [8]; Aoki, Yano, and Nishimura [9]). To examine the rational behavior of an agent with time-inconsistent preferences, many studies have mainly considered a stationary equilibrium in which all generations have an identical policy function, e.g., [10,11,12,13]. Hori and Kanaya studied an overlapping generations model with two-sided altruism, under which each generation is altruistic to its parent and child generations (see [14,15,16]). Fujiu and Yano [2] found a dynamic equation determining a sequence of policy functions in equilibrium of a similar model. The present paper is fundamentally based on the model and extends the result in [2].

This study also examines endogenous business cycles, e.g., [17,18,19,20], and chaos in economic dynamics, e.g., [21,22,23,24,25,26]. Recent studies examine conditions under which equilibrium dynamical systems generate paths with periodic fluctuations, as well as paths that converge to a steady state (see [27,28,29]). Several studies consider endogenous growth models with innovation and investigate the range of parameters in which complex periodic fluctuations can occur (see [30,31,32,33,34,35]). In these studies, endogenous cycles can occur by characteristics and constraints in the production sector. The present paper, however, asserts that rational behavior by a generation with two-sided altruism may cause business cycles with complex structures. It demonstrates that chaotic fluctuations in the sense of Li and Yorke [3] may occur when the degree of altruism to the parents is sufficiently high, while the degree of altruism to the children is low but not zero. In other words, this paper reveals that two-sided altruism is a new explanatory factor of an endogenous fluctuation with a complex periodic structure. This has not been indicated in the existing literature.

In this study, each generation’s policy function represents the function of human capital investment. The findings on the relationship between the degree of altruism and a sequence of the policy functions provide an important aspect for the study of economic growth through the accumulation of human capital. The growth rate may go up and down repeatedly in an economy with the high degree of altruism to the parents, while it may remain low when altruism to the parents generation disappears.

This paper sets up an overlapping generations model with two-sided altruism in Section 2, and then presents the fundamental and main results in Section 3 and Section 4, respectively. Section 5 contains the discussion and conclusion.

2. A Two-Sided Altruism Model

In this section, this paper introduces an overlapping generations model in which intergenerational altruism exists from children to parents and from parents to children (two-sided altruism). To define an equilibrium, which is expressed as a sequence consisting of each generation’s policy function, the paper adopts the model studied by Hori [16].

Assume that in each period, a generation of parents and a generation of adult children exist. Each generation lives for two periods. Denote by $U_t$ the total utility of generation t. Generation t gains utility from its own consumption in the first and the second periods, $c_t^1$ and $c_{t+1}^2$, respectively. In addition, assume that each generation is altruistic to its parents and children generations; that is, generation t also gains utility from the parent’s utility $U_{t-1}$ and the child’s utility $U_{t+1}$. Then, generation t’s utility is represented as follows:

$$U_t=a{U}_{t-1}+u\left(c_t^1\right)+\rho u\left(c_{t+1}^2\right)+b{U}_{t+1},$$

(1)

where

$$a>0,b>0\mathrm{and}a+b<1.$$

(2)

Note that parameters a and b capture the degree of altruism of generation t to its parent and child, respectively, and that $\rho >0$ is a discount factor and constant over generations.

Let $g_t$ and $x_t$ be the transfers that generation t makes for its parent and child, respectively. The transfer to the child, generation $t+1$, takes the form of human capital investment, which determines the child’s income. Let $y_{t+1}$ be the income of generation $t+1$. Denote a relationship between the human capital investment and the income by the function,

$$y_{t+1}=f\left(x_t\right).$$

(3)

Generation t’s transfer to the parent, generation $t-1$, takes the form of a gift, which determines generation $t-1$’s consumption in the second period, $c_t^2$. That is,

$$c_t^2=g_t.$$

(4)

Each generation, say t, divides its income, $y_t=f\left(x_{t-1}\right)$, into own consumption in the first period of life $c_t^1$, gifts to its parents $g_t$, and human capital investment in its children $x_t$. Given (4), the budget constraint of generation t may be expressed as

$$c_t^1+g_t+x_t\le y_t.$$

(5)

Assume that each generation does not consider dead ancestors. Then, from (1), generation t’s utility is rewritten as follows.

$$\begin{array}{ccc}\hfill {\widehat{U}}_t& =& u\left(c_t^1\right)+{\alpha }^{-1}\rho u\left(g_t\right)+\beta [u\left(c_{t+1}^1\right)+{\beta }^{-1}\rho u\left(g_{t+1}\right)]\hfill \\ & & +{\beta }^2[u\left(c_{t+2}^1\right)+{\beta }^{-1}\rho u\left(g_{t+2}\right)]+{\beta }^3[u\left(c_{t+3}^1\right)+{\beta }^{-1}\rho u\left(g_{t+3}\right)]+\dots ,\hfill \end{array}$$

where

$$\alpha =\frac{1+\sqrt{1-4ab}}{2a},\beta =\frac{1-\sqrt{1-4ab}}{2a}.$$

(6)

Note that we show the derivation of ${\widehat{U}}_t$ in Appendix A.

As indicated by Hori [16], an optimal choice by each generation leads to time-inconsistent results over generations under preferences such as ${\widehat{U}}_t$. If each generation is rational, it should make choices based on the descendant generation’s policy functions, which are time-consistent choices. To formalize a sub-game perfect Nash equilibrium in the model, let a generation t’s choices be denoted by

$$c_t^1=c^1(y_t-x_t)\mathrm{and}{g}_t=g(y_t-x_t).$$

If for every $t\ge 1$, $x_t={\xi }_t\left(y_t\right)$ maximizes ${\widehat{U}}_t$ subject to

$$0\le x_t\le y_t,$$

$$c_t^1=c^1(y_t-x_t),g_t=g(y_t-x_t),$$

$$y_{t+s}=f\left(x_{t+s-1}\right),s\ge 1,$$

$$x_{t+s}={\xi }_{t+s}\left(y_{t+s}\right),s\ge 1,$$

$$c_{t+s}^1=c^1(y_{t+s}-x_{t+s}),g_{t+s}=g(y_{t+s}-x_{t+s}),s\ge 1,$$

$$\mathrm{given}{y}_t\ge 0\mathrm{and}{\left\{{\xi }_{t+s}\right\}}_{s=1}^{\infty },$$

then call ${\left\{{\xi }_t\right\}}_{t=1}^{\infty }$ a sub-game perfect Nash equilibrium or an equilibrium. Furthermore, if it satisfies ${\xi }_t=\xi$ for every $t\ge 1$, then call $\xi$ a stationary equilibrium.

We define a periodic cycle equilibrium as follows. If ${\left\{{\xi }_t\right\}}_{t=1}^{\infty }$ is an equilibrium, and if for some integer $k>1$, it satisfies

$$\begin{array}{ccc}\hfill {\xi }_t& =& {\xi }_{t+k};\hfill \\ \hfill {\xi }_t& \ne & {\xi }_{t+\tau },\tau =1,..,k-1,\hfill \end{array}$$

for every $t\ge 1$, then say that ${\left\{{\xi }_t\right\}}_{t=1}^{\infty }$ has a period-k cycle or call it an equilibrium with period-k cycle. Note that in this equilibrium, it follows from the definition that ${\xi }_t={\xi }_{t+nk}$ for $n=1,2,\dots$

To characterize an equilibrium in the model, by (3) and (5), let the utility function ${\widehat{U}}_t$ be rewritten as follows:

$${\widehat{U}}_t=\underset{x_t\in [0,y_t]}{max}\{w(y_t-x_t)+\beta V_{t+1}\left(x_t\right)\},$$

where

$$w(y_t-x_t)=u\left(c^1(y_t-x_t)\right)+{\alpha }^{-1}\rho u\left(g(y_t-x_t)\right),$$

(7)

$$\left(c^1\left(m\right),g\left(m\right)\right)=arg\underset{(c^1,g)}{max}\{u\left(c^1\right)+{\alpha }^{-1}\rho u\left(g\right)\},\mathrm{subject}\mathrm{to}{c}^1+g\le m,$$

(8)

$$\begin{array}{ccc}\hfill V_{t+1}\left(x_t\right)& =& u\left(c^1(f\left(x_t\right)-{\xi }_{t+1}\left(f\left(x_t\right)\right))\right)+{\beta }^{-1}\rho u\left(g(f\left(x_t\right)-{\xi }_{t+1}\left(f\left(x_t\right)\right))\right)\hfill \\ & & +\beta V_{t+2}\left({\xi }_{t+1}\left(f\left(x_t\right)\right)\right).\hfill \end{array}$$

A value function associated with generation t’s optimization problem for $t\ge 1$ is described as

$$\begin{array}{ccc}\hfill V_t\left(x_{t-1}\right)& =& ({\beta }^{-1}-{\alpha }^{-1})\rho u(g(f\left(x_{t-1}\right)-{\xi }_t\left(f\left(x_{t-1}\right)\right))\hfill \\ & & +\underset{x_t}{max}\left\{w(f\left(x_{t-1}\right)-x_t)\right)+\beta V_{t+1}\left(x_t\right)\},\hfill \end{array}$$

(9)

where $x_t={\xi }_t\left(f\left(x_{t-1}\right)\right)$, by letting $y_1=f\left(x_0\right)$ be given. As for (9), the first-order conditions are denoted as follows:

$$-w^{\prime }(y_t-x_t)+\beta V_{t+1}^{\prime }\left(x_t\right)=0,$$

(10)

and

$$\begin{array}{ccc}\hfill V_t^{\prime }\left(x_{t-1}\right)& =& ({\beta }^{-1}-{\alpha }^{-1})\rho u^{\prime }{g}^{\prime }[f^{\prime }\left(x_{t-1}\right)-{\xi }_t^{\prime }{f}^{\prime }\left(x_{t-1}\right)]\hfill \\ & & +w^{\prime }(f\left(x_{t-1}\right)-x_t)f^{\prime }\left(x_{t-1}\right),\hfill \end{array}$$

which imply that

$$\begin{array}{ccc}\hfill V_{t+1}^{\prime }\left(x_t\right)& =& ({\beta }^{-1}-{\alpha }^{-1})\rho u^{\prime }{g}^{\prime }[f^{\prime }\left(x_t\right)-{\xi }_{t+1}^{\prime }{f}^{\prime }\left(x_t\right)]\hfill \\ & & +w^{\prime }(f\left(x_t\right)-x_{t+1})f^{\prime }\left(x_t\right).\hfill \end{array}$$

(11)

Thus, from (10) and (11), it follows that

$$\begin{array}{ccc}\hfill w^{\prime }(y_t-x_t)& =& (1-{\alpha }^{-1}\beta )\rho u^{\prime }{g}^{\prime }[f^{\prime }\left(x_t\right)-{\xi }_{t+1}^{\prime }{f}^{\prime }\left(x_t\right)]\hfill \\ & & +\beta w^{\prime }(f\left(x_t\right)-{\xi }_{t+1}\left(f\left(x_t\right)\right))f^{\prime }\left(x_t\right).\hfill \end{array}$$

(12)

This equation leads to the following functionals:

$${\xi }_t\left(y_t\right)\in H(y_t,{\xi }_{t+1}),$$

and

$${\xi }_{t+\tau }\left(y\right)\in H(y,{\xi }_{t+\tau +1}),\tau \ge 1.$$

3. Fundamental Results

In this section, the fundamental results are demonstrated by specifying functional forms of the utility and production functions and characterizing the equilibrium dynamics in the model. As discussed by Fujiu and Yano [2], if the utility and production functions are characterized by the constant elasticity of substitution, an equilibrium is expressed as a sequence of linear policy functions; that is, in equilibrium, for every $t\ge 1$, ${\xi }_t$ satisfies

$${\xi }_t\left(y\right)={\gamma }_{t}y,{\gamma }_t\in (0,1),\forall y\ge 0.$$

To confirm this, let the utility and production functions be assumed as follows:

$$u\left(c\right)=\frac{c^{1-\sigma }}{1-\sigma },0<\sigma <1,$$

(13)

$$f\left(x\right)=\mu x,\mu >0.$$

(14)

Then, the following theorem is obtained.

Theorem 1.

Assume (13) and (14). Then, there is a continuous function $h:[0,1]\to [0,1]$ such that ${\left\{{\xi }_t\right\}}_{t=1}^{\infty }$ satisfying that for every $t\ge 1$,

$${\xi }_t\left(y\right)={\gamma }_{t}y,{\gamma }_t\in (0,1),\forall y\ge 0,$$

where

$${\gamma }_t=h\left({\gamma }_{t+1}\right),$$

is an equilibrium.

Proof. 

See Appendix B. □

In Theorem 1, a continuous function h plays the role of a dynamic equation, which determines an equilibrium ${\left\{{\xi }_t\right\}}_{t=1}^{\infty }$; that is, the equilibrium dynamics is represented by the linear policy function ${\xi }_t$ and the dynamic equation h. By investigating the dynamic equation h, this paper shows two types of equilibrium: one is a stationary equilibrium; the other is an equilibrium with periodic cycle.

From Appendix B, the dynamic equation in equilibrium, ${\gamma }_t=h\left({\gamma }_{t+1}\right)$, satisfies

$$h\left({\gamma }_{t+1}\right)=\frac{1}{1+{[\frac{(\alpha -\beta )\rho }{{\alpha }^{2-\frac{1}{\sigma }}+1}(1-{\gamma }_{t+1})+\beta ]}^{-\frac{1}{\sigma }}(1-{\gamma }_{t+1}){\mu }^{1-\frac{1}{\sigma }}}.$$

(15)

If there exists a $\gamma \in (0,1)$ such that $\gamma =h\left(\gamma \right)$, ${\left\{{\xi }_t\right\}}_{t=1}^{\infty }$ satisfying ${\xi }_t\left(y_t\right)=\gamma y_t$ is a stationary equilibrium. To guarantee that there exists a $\gamma$ satisfying $0<\gamma <1$ and $\gamma =h\left(\gamma \right)$, it is sufficient that

$$\beta {\mu }^{1-\sigma }<1.$$

(16)

Theorem 2.

Assume (16). Then, there exists a $\gamma \in (0,1)$ such that for every $t\ge 1$,

$${\xi }_t\left(y\right)=\gamma y,\forall y\ge 0,$$

is a stationary equilibrium.

Proof. 

See Appendix C. □

Based on the results obtained in this section, the main results are presented in the next section.

4. Main Results

In this section, the main results are obtained by specifying the parameters and numerically analyzing a dynamic path from the dynamic equation h.

This study shows that the dynamic equation may generate a chaotic dynamic path. However, it is difficult to analytically specify the parameter space under which a chaos occurs. So the study specified parameters as follows. In the first step, it fixed parameters to plausible values, except for those that represent the degree of altruism. It is a significant assumption that the utility function is close to linear, but not linear. In the second step, the study changed the parameters of altruism so that the dynamic equation had a structure of chaotic dynamics; the case occurred when a was sufficiently high and b was low but not zero. In the final step, it fixed the parameters of altruism. In this case, we found that each generation is strongly altruistic to its parent generation, while it is weakly altruistic to its children generation.

Let a, b, $\mu$, $\rho$, and $\sigma$ satisfy

$$a=0.799,b=0.2,\mu =3,\rho =1,\mathrm{and}\sigma =0.04.$$

(17)

Note that (17) satisfies the condition (16) and the parameter assumptions (1), $\mu >0$, $\rho >0$, and $0<\sigma <1$.

Suppose

$$\gamma =0.7533528777732662,$$

which approximates a solution of the equation $\gamma =h\left(\gamma \right)$. Then, for every $t\ge 1$,

$${\xi }_t\left(y\right)=\gamma y,\forall y\ge 0,$$

is a stationary equilibrium. Figure 1 shows ${\gamma }_t=h\left({\gamma }_{t+1}\right)$, which satisfies $\gamma ={\gamma }_t={\gamma }_{t+1}$ at the point S.

Figure 1 shows that the dynamic equation ${\gamma }_t=h\left({\gamma }_{t+1}\right)$ has a periodic solution with period-3. When $\gamma \in (0,1)$ satisfies $\gamma \ne h\left(\gamma \right),\gamma \ne h\left(h\right(\gamma \left)\right)$ and $\gamma =h\left(h\right(h\left(\gamma \right)\left)\right)$, we call $\gamma$ a periodic point of period-3. Note that $\gamma =0.999949$ approximates a periodic point of period-3 because

$$\begin{array}{ccc}\hfill h\left(\gamma \right)& =& 0.830017;\hfill \\ \hfill h\left(h\right(\gamma \left)\right)& =& 0.323087;\hfill \\ \hfill h\left(h\right(h\left(\gamma \right)\left)\right)& =& 0.999949.\hfill \end{array}$$

By referring to the theorem by Li and Yorke [3], we find that the dynamic equation ${\gamma }_t=h\left({\gamma }_{t+1}\right)$ has more complex periodic solutions.

Theorem 3.

(Li and Yorke, 1975). Let I be an interval and let $h:I\to I$ be continuous. Assume that $e\in I$ satisfies $h\left(h\right(h\left(e\right)\left)\right)\ge e>h\left(e\right)>h\left(h\right(e\left)\right)$. Then, for every positive integer k, there is a periodic point in I with period- k.

Let $I=[0,1]$. The dynamic equation h, denoted by (15), maps I into itself. Let $e=0.9999494$, which satisfies $e\in I$. Then, it holds that

$$\begin{array}{ccc}\hfill h\left(e\right)& =& 0.830957057822524;\hfill \\ \hfill h\left(h\right(e\left)\right)& =& 0.31806661602253666;\hfill \\ \hfill h\left(h\right(h\left(e\right)\left)\right)& =& 0.9999532981467422.\hfill \end{array}$$

From the theorem by Li and Yorke, this implies that h has a periodic point with period-k for every positive integer k. Therefore, we obtain the following result.

Proposition 1.

In the model, an equilibrium ${\left\{{\xi }_t\right\}}_{t=1}^{\infty }$ may have a period-k cycle for every integer $k>1$.

This proposition states that various periodic fluctuations can arise in the equilibrium of an overlapping generations model with two-sided altruism.

Generation $t+1$’s income is denoted by

$$y_{t+1}=\mu x_t,$$

and generation t’s choice of $x_t$ is denoted as a function of generation t’s income, $y_t$; that is,

$$x_t={\gamma }_t{y}_t.$$

Denote a growth rate of income over time by $R_t$, which is expressed as follows:

$$R_t=\frac{y_{t+1}}{y_t}-1=\mu {\gamma }_t-1.$$

If ${\left\{{\gamma }_t\right\}}_{t=1}^{\infty }$ has a period-k cycle for an integer $k>1$ in equilibrium, ${\left\{R_t\right\}}_{t=1}^{\infty }$ also has a period-k cycle. Thus, for every integer $k>1$, a business cycle with a period-k cycle can occur in an overlapping generations economy with two-sided altruism.

Proposition 2.

Business cycles with various periods can occur in an overlapping generations economy with two-sided altruism.

This proposition asserts that it is essential for the presence of various periodic fluctuations that all generations have two-sided altruism. In the next section, we consider this assertion.

5. Discussion and Conclusions

The main results are obtained from the finding that the dynamic equation ${\gamma }_t=h\left({\gamma }_{t+1}\right)$ has a periodic point with period-3, as drawn in Figure 1. In the model, the degree of altruism plays an essential role in determining such a structure of the dynamic equation. The degrees of altruism from each generation to its parental generation and to its descendant one are denoted by discount factors a and b, respectively. In this section, we examine each effect of a and b on the dynamic equation using the method by Fujiu and Yano [2] (they conducted a similar analysis in a two-sided altruism model with different conditions from this model).

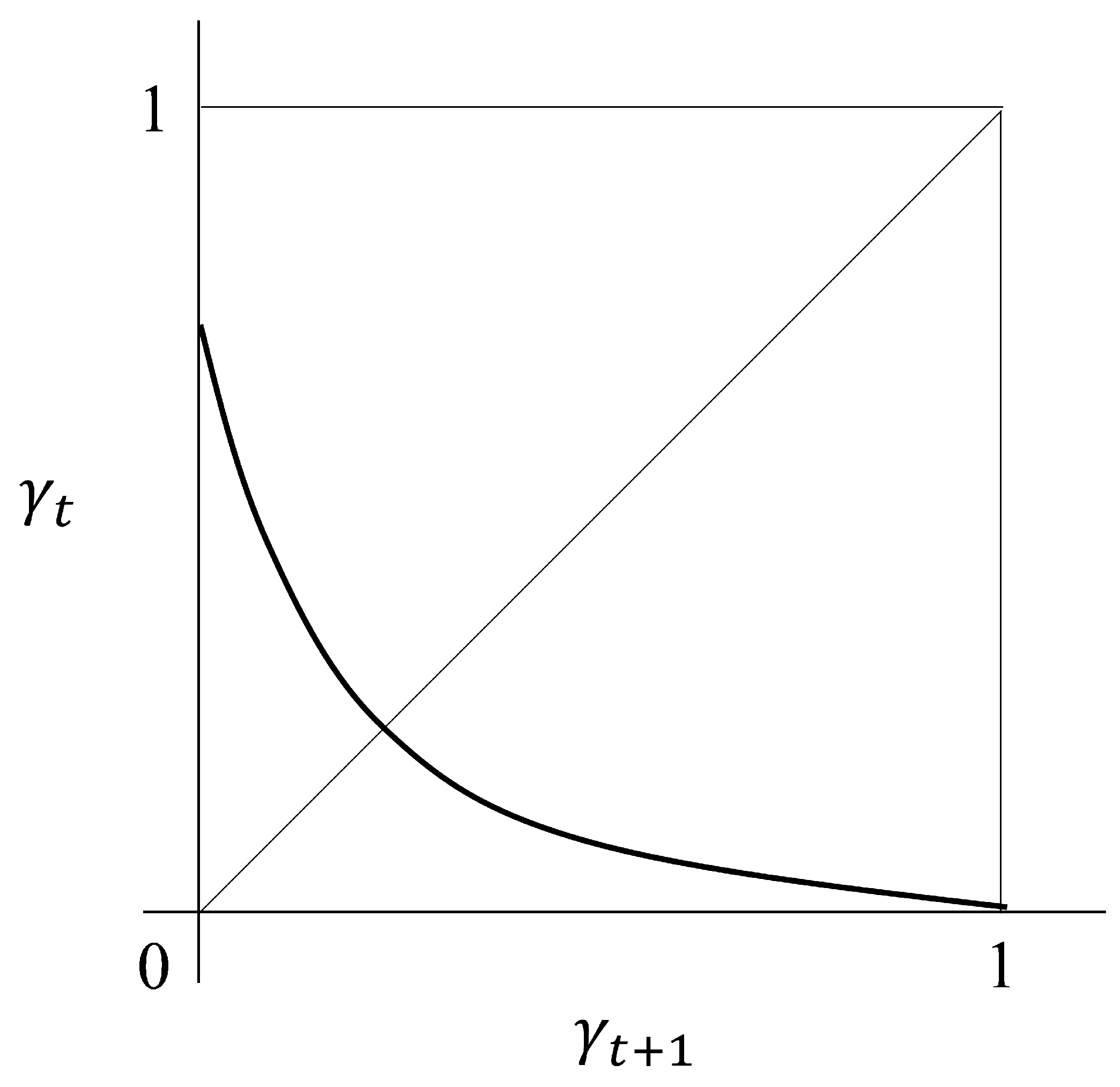
Consider the case where $a>0$ and $b=0$, which implies that each generation is altruistic only to its parental one. Note that Fujiu and Yano [1] derived a stationary policy function by finding a fixed point of the dynamic equation in this case. In our model, if b goes to zero, then the dynamic equation ${\gamma }_t=h\left({\gamma }_{t+1}\right)$ is denoted as follows:

$${\gamma }_t=\frac{1}{1+{(\frac{a^{\frac{1}{\sigma }-1}+a}{\rho })}^{\frac{1}{\sigma }}{(\frac{1}{\mu })}^{\frac{1}{\sigma }-1}{(\frac{1}{1-{\gamma }_{t+1}})}^{\frac{1}{\sigma }-1}},$$

which monotonically decreases with respect to ${\gamma }_{t+1}\in [0,1]$ and ensures that ${\gamma }_t$ is asymptotically close to zero when ${\gamma }_{t+1}$ is approaching 1, as shown in Figure 2. This implies that a period-3 cycle never arises from the dynamic equation.

In contrast, consider the case where $a=0$ and $b>0$. If $a=0$, we find that ${\alpha }^{-1}=0$ by (6) and there are no transfer flows from each generation to its parental one by (8). Then, it is natural to build a model in which such a transfer does not arise and the associated discount factor is zero, $\rho =0$. By assuming $\rho =0$, the model is reduced to an optimal growth model, in which an optimal choice of human capital investment by generation t, $x_t^{*}$, coincides with a time-consistent choice, $x_t$, shown by a stationary policy function $x_t=\gamma y_t$, where $\gamma =h\left(\gamma \right)$. Existing studies examined an equilibrium dynamics in which such optimal choices may be chaotic in an optimal growth model, although the policy function is stationary (see Nishimura and Yano [21]; Fujio [36]). 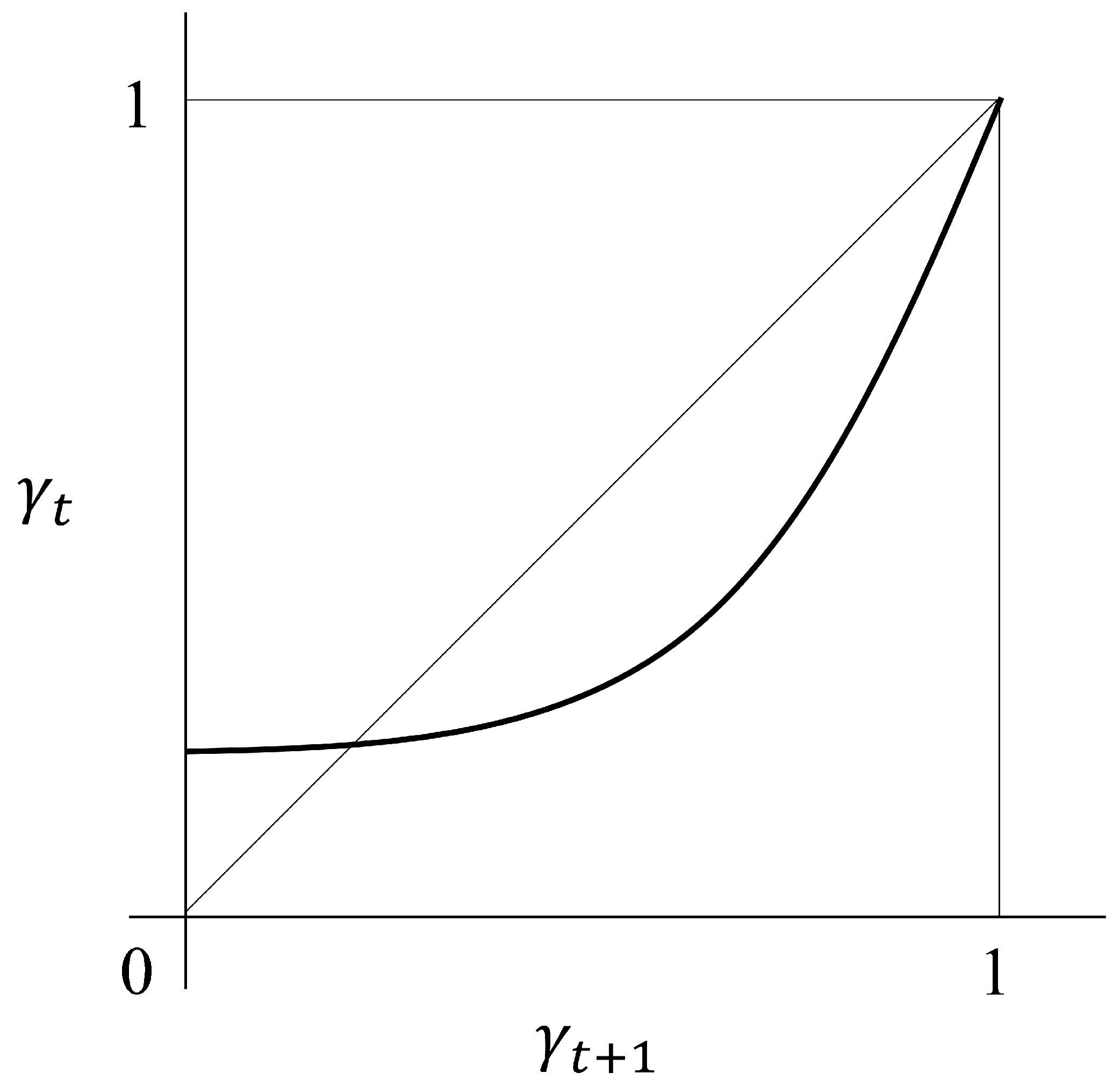If $a=0$ and $\rho =0$ in our model, the dynamic equation ${\gamma }_t=h\left({\gamma }_{t+1}\right)$ is denoted as follows:

$${\gamma }_t=\frac{1}{1+{\left(\frac{1}{b{\mu }^{1-\sigma }}\right)}^{\frac{1}{\sigma }}(1-{\gamma }_{t+1})},$$

which monotonically increases with respect to ${\gamma }_{t+1}\in [0,1]$ and satisfies that only a $\gamma \in (0,1)$ exists, such that ${\gamma }_t={\gamma }_{t+1}=\gamma$ under the condition (16), which is reduced to $b{\mu }^{1-\sigma }<1$ if a goes to zero. As shown in Figure 3, the dynamic equation only has one stable fixed point, which implies that no business cycles arise.

In this study, each generation’s policy function represents the function of human capital investment. Human capital may be rapidly accumulated when ${\gamma }_t$ is high, while it may be slowly accumulated when ${\gamma }_t$ is low. Whether the growth rate goes up or down depends on a sequence of ${\gamma }_t$. A structure of the sequence is determined by the degree of altruism. In this discussion, we find that the growth rate may go up and down repeatedly when the degree of altruism to the parents is high, while it may remain low when altruism to the parents generation disappears.

The findings in this study are as follows. The degree of altruism determines a structure of the equilibrium dynamics in the model. In particular, the presence of both altruism from a generation to its parent and child generations is essential for economic fluctuations with complex periodic structures. This is because such economic fluctuations never arise if each generation has neither altruism toward its parent or toward its child, as discussed above. In other words, two-sided altruism is a new explanatory factor of an endogenous business cycle with a complex periodic structure. This has not been identified in the existing literature.