Using an Improved Differential Evolution for Scheduling Optimization of Dual-Gantry Multi-Head Surface-Mount Placement Machine
Abstract
1. Introduction
- ♦
- The component height restriction is considered in SMP processing.
- ♦
- The proposed modified differential evolution (MDE) algorithm with two similarity measurement mechanisms using a random-key encoding mapping method is designed for minimizing the number of picks in feeder arrangement.
- ♦
- A combination of nearest-neighbor search (NNS) and 2-opt method is applied to shorten the path in component placing operations.
- ♦
- The experimental results indicate that while using the MDE algorithm for feeder arrangement, at most 30% of the number of picks can be reduced; moreover, when adding a combination of NNS and 2-opt method for component placing sequence, the whole assembly time is decreased at most by 13% using the proposed method.
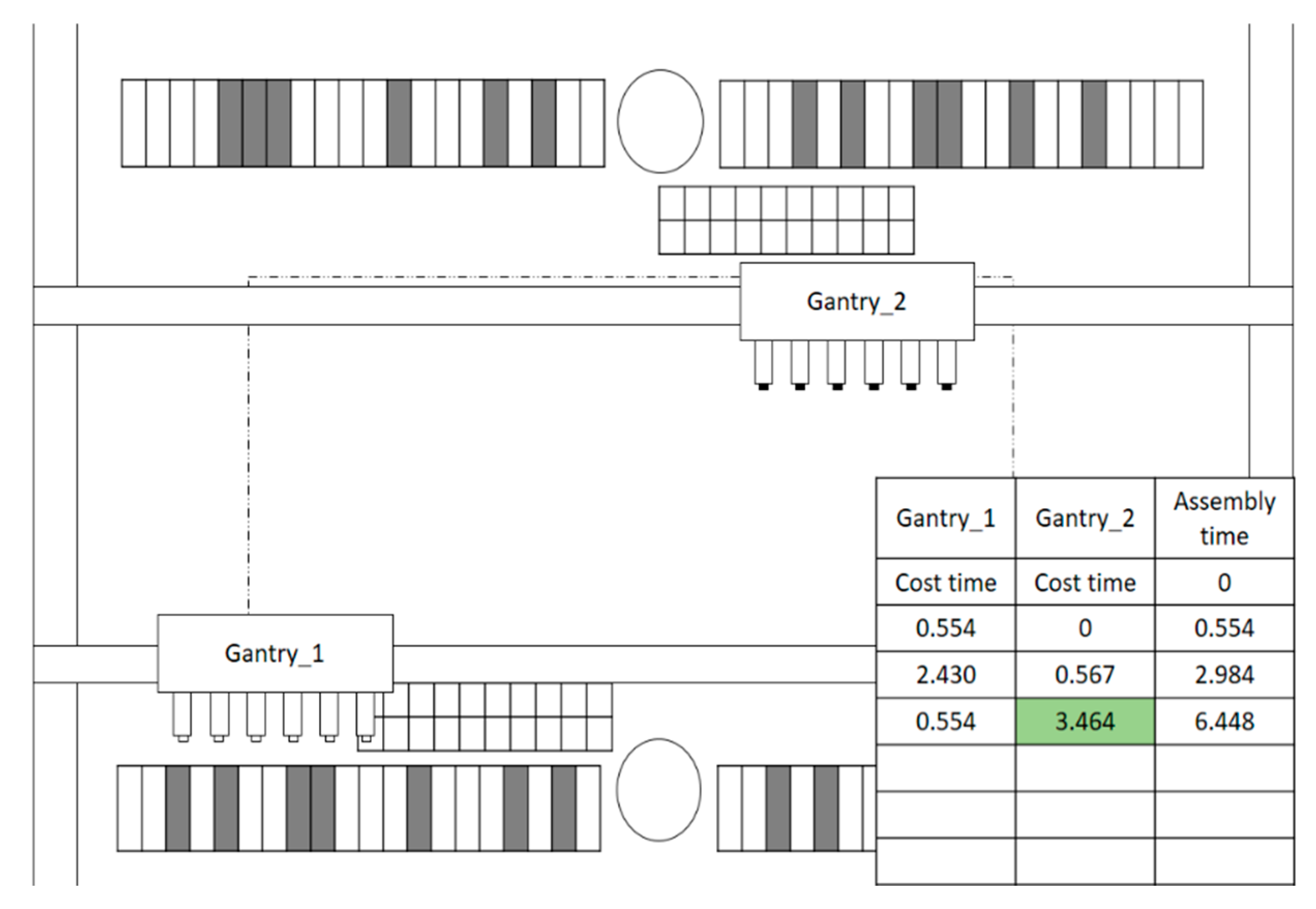
2. Description of the SMP Machine
- (a)
- Gantry: This moves above the surface-mount machine, allowing the pick-and-place heads to pick components from the correct feeder and then to place the components on the correct position of the PCB.
- (b)
- Pick-and-place head: Every pick-and-place head is equipped with a single nozzle, which is used to pick and place components.
- (c)
- ANC: This is where nozzles are placed and changed.
- (d)
- Nozzle: These are installed on pick-and-place heads for component picking and placing. Different nozzle types are required for different components. Accordingly, the pick-and-place heads move to the ANC for nozzle changes when required.
- (e)
- Feeder: The feeder is used to store and provide components. Every feeder stores only one component.
- (f)
- Feeder station: Feeders for placement operation here.
- (g)
- PCB table: PCBs are fixed and placed here.
- (h)
- Fly vision system: This is used to determine whether a component is damaged or faulty and confirm a component’s loading position by recalibrating the X–Y coordinate.
3. Problem Definition
3.1. Problem Description
- (i)
- Component allocation problem:
- (ii)
- ANC assignment problem:
- (iii)
- Feeder arrangement problem:
- (iv)
- Component height restrictions:
- (v)
- Component pick-and-place sequence:
3.2. Establishment of a Mathematical Model
4. Method
4.1. Component Allocation
4.2. ANC Assignment Using a Quantity Ratio Method
- Step 1:
- Step 2:
- Step 3:
4.3. Feeder Arrangement Using the MDE Algorithm
- (a)
- Initialization
- (b)
- Mutation
- (c)
- Selection
MDE Algorithm
- (a)
- Initialization
- (b)
- Selection
- (c)
- Similarity
- Similarity 1: This method measured the Euclidean distance between an individual and to determine their level of similarity. The mean level of similarity () is the threshold value; individuals with levels of similarity lower than this value are defined as being similar to the position. The equation is presented as follows:where variable NP is the total number of individuals, D represents dimensions, is the position, and represents individual j.
- Similarity 2: Based on the Dice coefficient [23], feeder slots loaded with components are presented in sets to obtain a set-similarity metric function. The equation is presented as follows:where {X} represents set X, {Y} represents set Y, and is the intersection of sets X and Y.
4.4. Determining Placing Sequence Using the Nearest-Neighbor Search and 2-Opt Method
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, D.S.; Lee, T.E.; Kim, K.H. Component allocation and feeder arrangement for a dual-gantry multi-head surface mount placement tool. Int. J. Prod. Econ. 2005, 95, 245–264. [Google Scholar] [CrossRef]
- Du, X.; Li, Z. Placement process optimization of dual-gantry turret placement machine. In Proceedings of the 2008 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Xi’an, China, 2–5 July 2008; pp. 1266–1271. [Google Scholar]
- Ashayeri, J.; Ma, N.; Sotirov, R. An aggregated optimization model for multi-head SMD placements. Comput. Ind. Eng. 2011, 60, 99–105. [Google Scholar] [CrossRef][Green Version]
- Torabi, S.A.; Hamedi, M.; Ashayeri, J. A new optimization approach for nozzle selection and component allocation in multi-head beam-type SMD placement machines. J. Manuf. Syst. 2013, 32, 700–714. [Google Scholar] [CrossRef]
- Zhu, G.-Y.; Zhang, W.-B. An improved Shuffled Frog-leaping Algorithm to optimize component pick-and-place sequencing optimization problem. Expert Syst. Appl. 2014, 41, 6818–6829. [Google Scholar] [CrossRef]
- He, T.; Li, D.; Yoon, S.W. A Hierarchical Restricted Balance Approach for Workload Balance of a Dual-Delivery SMT Placement Machine. In Proceedings of the IIE Annual Conference, Nashville, TN, USA, 30 May–2 June 2015; pp. 808–817. [Google Scholar]
- Li, D.; Yoon, S.W. PCB assembly optimization in a single gantry high-speed rotary-head collect-and-place machine. Int. J. Adv. Manuf. Technol. 2017, 88, 2819–2834. [Google Scholar] [CrossRef]
- He, T.; Li, D.; Yoon, S.W. A multi-phase planning heuristic for a dual-delivery SMT placement machine optimization. Robot. Comput.-Integr. Manuf. 2017, 47, 85–94. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L.; Liu, P. Applied Research of Hierarchical Multi-objective Optimization Method in High Speed and High Precision Placement Machine. J. Phys. Conf. Ser. 2020, 1605, 012029. [Google Scholar] [CrossRef]
- Lin, H.Y.; Lin, C.J.; Huang, M.L. Optimization of printed circuit board component placement using an efficient hybrid genetic Algorithm. Appl. Intell. 2016, 45, 622–637. [Google Scholar] [CrossRef]
- He, T.; Li, D.; Yoon, S.W. An adaptive clustering-based genetic algorithm for the dual-gantry pick-and place machine optimization. Adv. Eng. Inform. 2018, 37, 66–78. [Google Scholar] [CrossRef]
- Li, Z.; Yu, X.; Qiu, J.; Gao, H. Cell Division Genetic Algorithm for Component Allocation Optimization in Multi-Functional Placers. IEEE Trans. Ind. Inform. (Early Access) 2021. [Google Scholar] [CrossRef]
- Huang, X.; Li, C.; Chen, H.; An, D. Task scheduling in cloud computing using particle swarm optimization with time varying inertia weight strategies. Clust. Comput. 2019, 23, 1137–1147. [Google Scholar] [CrossRef]
- Hsu, H.P. Solving feeder assignment and component sequencing problems for printed circuit board assembly using particle swarm optimization. IEEE Trans. Autom. Sci. Eng. 2017, 14, 881–893. [Google Scholar] [CrossRef]
- Zhao, H.; Gao, W.; Deng, W.; Sun, M. Study on an Adaptive Co-Evolutionary ACO Algorithm for Complex Optimization Problems. Symmetry 2018, 10, 104. [Google Scholar] [CrossRef]
- Storn, R. On the usage of differential evolution for function optimization. In Proceedings of the Biennial Conference of the North American Fuzzy Information Processing Society (NAFIPS), Berkeley, CA, USA, 19–22 June 1996; pp. 519–523. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient adaptive scheme for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Choi, T.J.; Ahn, C.W. An Improved Differential Evolution Algorithm and Its Application to Large-Scale Artificial Neural Networks. J. Phys. Conf. Ser. 2017, 806, 012010. [Google Scholar] [CrossRef]
- Choi, T.J.; Lee, Y. Asynchronous differential evolution with self- adaptive parameter control for global numerical optimization. Matec Web Conf. 2018, 189, 03020. [Google Scholar] [CrossRef]
- Choi, T.J.; Togelius, J.; Cheong, Y.-G. Advanced Cauchy Mutation for Differential Evolution in Numerical Optimization. IEEE Access 2020, 8, 8720–8734. [Google Scholar] [CrossRef]
- Bean, J.C. Genetic Algorithms and Random Keys for Sequencing and Optimization. INFORMS J. Comput. 1994, 6, 154–160. [Google Scholar] [CrossRef]
- Faria, H.; Resende, M.G.; Ernst, D. A biased random key genetic algorithm applied to the electric distribution network reconfiguration problem. J. Heuristics 2017, 23, 533–550. [Google Scholar] [CrossRef]
- Dice, L.R. Measures of the Amount of Ecologic Association Between Species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Hsu, H.-P. Printed Circuit Board Assembly Planning for Multi-Head Gantry SMT Machine Using Multi-Swarm and Discrete Firefly Algorithm. IEEE Access 2020, 9, 1642–1654. [Google Scholar] [CrossRef]
- Kachitvichyanukul, V. Comparison of Three Evolutionary Algorithms: GA, PSO, and DE. Ind. Eng. Manag. Syst. 2012, 11, 215–223. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]






















| Component Allocation | ANC Assignment | Feeder Arrangement | Component Height | Pick-and-Place Sequence | Method | |
|---|---|---|---|---|---|---|
| Sun et al. [1] | ✓ | ✓ | ✓ | GA | ||
| Du and Li [2] | ✓ | ✓ | ✓ | Hybrid GA | ||
| Ashayeri et al. [3] | ✓ | ✓ | ✓ | MIP | ||
| Torabi et al. [4] | ✓ | ✓ | ✓ | MOPSO | ||
| Zhu and Zhang [5] | ✓ | ISFLA | ||||
| He et al. [6] | ✓ | ✓ | ✓ | ✓ | HRB | |
| Li and Yoon [7] | ✓ | ✓ | ✓ | ANNTS | ||
| He et al. [8] | ✓ | ✓ | ✓ | HS | ||
| Huang et al. [9] | ✓ | ✓ | ✓ | HMO | ||
| This study | ✓ | ✓ | ✓ | ✓ | ✓ | MDE |
| Component | Nozzle | Total Number of Components for the Nozzle | Quantity Ratio | ||
|---|---|---|---|---|---|
| Type | Quantity | Type | Size | ||
| D | 15 | AN2 | Small | 50 | 20% |
| B | 35 | ||||
| A | 20 | AN3 | Small | 20 | 8% |
| E | 80 | AN4 | Small | 80 | 32% |
| C | 100 | AN5 | Small | 100 | 40% |
| F | 10 | ANV1 | Large | 10 | 100% |
| PCB | Number of Components | Component Types | Nozzle Types |
|---|---|---|---|
| PCB-1 | 322 | 17 | 5 |
| PCB-2 | 396 | 14 | 4 |
| PCB-3 | 532 | 14 | 4 |
| PCB-4 | 586 | 16 | 3 |
| PCB-5 | 614 | 17 | 2 |
| PCB-6 | 638 | 18 | 4 |
| PCB-7 | 682 | 19 | 5 |
| PCB-8 | 696 | 17 | 5 |
| PCB-9 | 720 | 15 | 3 |
| PCB-10 | 796 | 17 | 2 |
| Methods | MDE | DE | PSO | GA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Similarity1 | Similarity2 | |||||||||
| Gantry | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 |
| PCB-1 | 44 | 61 | 51 | 68 | 62 | 70 | 67 | 75 | 64 | 77 |
| PCB-2 | 47 | 70 | 52 | 64 | 67 | 89 | 89 | 96 | 82 | 87 |
| PCB-3 | 93 | 91 | 92 | 92 | 98 | 94 | 100 | 108 | 96 | 119 |
| PCB-4 | 85 | 73 | 83 | 74 | 103 | 96 | 113 | 90 | 116 | 117 |
| PCB-5 | 106 | 100 | 99 | 100 | 118 | 114 | 119 | 116 | 128 | 124 |
| PCB-6 | 92 | 93 | 95 | 93 | 100 | 107 | 128 | 113 | 127 | 129 |
| PCB-7 | 121 | 128 | 132 | 129 | 142 | 154 | 126 | 159 | 172 | 157 |
| PCB-8 | 108 | 112 | 109 | 117 | 134 | 120 | 130 | 151 | 142 | 151 |
| PCB-9 | 93 | 109 | 94 | 107 | 127 | 117 | 134 | 122 | 129 | 132 |
| PCB-10 | 119 | 124 | 119 | 122 | 141 | 151 | 154 | 137 | 155 | 155 |
| Average | 90.8 | 96.1 | 92.6 | 96.6 | 109.2 | 111.2 | 116 | 116.7 | 121.1 | 124.8 |
| DE | PSO | GA | ||||
|---|---|---|---|---|---|---|
| Gantry | 1 | 2 | 1 | 2 | 1 | 2 |
| MDE Similarity1 | −20.3% | −15.7% | −27.7% | −21.4% | −33.4% | −30.0% |
| MDE Similarity2 | −18.0% | −15.1% | −25.2% | −20.8% | −25.3% | −29.2% |
| PCB Methods | PCB-1 | PCB-2 | PCB-3 | PCB-4 | PCB-5 | PCB-6 | PCB-7 | PCB-8 | PCB-9 | PCB-10 | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MDE Similarity 1 | Gantry_1 | 5535.9 | 6386.0 | 14,393.6 | 13,189.3 | 7890.4 | 5687.5 | 14,087.7 | 5921.0 | 14,087.7 | 8882.6 | 9606.2 |
| Gantry_2 | 22,098.5 | 24,283.0 | 35,681.5 | 38,810.7 | 45,165.2 | 53,235.6 | 52,695.1 | 49,152.5 | 52,695.1 | 51,267.8 | 42,508.5 | |
| MDE Similarity 2 | Gantry_1 | 8996.7 | 6243.4 | 8045.6 | 4909.0 | 27,345.5 | 14,804.7 | 14,339.6 | 15,061.7 | 14,339.6 | 12,437.5 | 12,652.3 |
| Gantry_2 | 28,887.4 | 24,629.2 | 36,614.3 | 38,195.4 | 45,436.8 | 43,432.9 | 52,207.5 | 58,298.6 | 52,207.5 | 52,018.6 | 43,192.8 | |
| DE | Gantry_1 | 17,300.6 | 8164.9 | 17,093.5 | 18,870.2 | 16,074.5 | 20,976.4 | 29,878.2 | 16,623.0 | 29,878.2 | 22,145.1 | 19,700.5 |
| Gantry_2 | 30,402.3 | 29,038.3 | 47,589.3 | 49,700.0 | 73,724.1 | 61,888.1 | 48,086.1 | 60,670.6 | 48,086.1 | 65,426.5 | 51,461.1 | |
| PSO | Gantry_1 | 20,085.0 | 46,903.4 | 14,901.8 | 19,732.4 | 50,936.9 | 56,762.9 | 30,744.5 | 76,028.7 | 30,744.5 | 62,205.5 | 40,904.6 |
| Gantry_2 | 26,791.4 | 65,493.1 | 68,364.6 | 44,386.8 | 56,528.2 | 51,164.0 | 52,767.6 | 75,556.7 | 52,767.6 | 61,737.6 | 55,555.8 | |
| GA | Gantry_1 | 15,732.5 | 31,684.0 | 21,321.1 | 55,354.4 | 55,776.3 | 76,430.6 | 25,093.5 | 26,523.6 | 25,093.5 | 26,929.9 | 35,993.9 |
| Gantry_2 | 34,702.8 | 27,899.8 | 66,586.1 | 22,457.9 | 52,666.3 | 37,960.3 | 48,536.2 | 72,913.3 | 48,536.2 | 63,998.6 | 47,625.8 | |
| Methods PCB | MDE | DE | PSO | GA | |
|---|---|---|---|---|---|
| Similarity1 | Similarity2 | ||||
| PCB-1 | 194.1 | 193.5 | 211.4 | 197.5 | 212.8 |
| PCB-2 | 277.3 | 282.8 | 301.9 | 324.8 | 297.2 |
| PCB-3 | 184.6 | 179.3 | 194.7 | 227.9 | 233.2 |
| PCB-4 | 233.8 | 222.3 | 242.0 | 245.7 | 250.0 |
| PCB-5 | 287.8 | 294.3 | 312.1 | 321.4 | 313.6 |
| PCB-6 | 274.0 | 284.0 | 288.3 | 314.4 | 313.7 |
| PCB-7 | 318.5 | 304.2 | 373.2 | 343.3 | 352.6 |
| PCB-8 | 245.5 | 267.4 | 284.6 | 284.0 | 282.1 |
| PCB-9 | 350.5 | 349.4 | 387.1 | 409.6 | 361.8 |
| PCB-10 | 296.5 | 305.0 | 329.0 | 340.6 | 308.6 |
| Average | 266.26 | 268.22 | 292.43 | 300.92 | 292.56 |
| DE | PSO | GA | |
|---|---|---|---|
| MDE Similarity1 | −9.8% | −13.0% | −9.8% |
| MDE Similarity2 | −9.0% | −12.2% | −9.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-J.; Lin, C.-H. Using an Improved Differential Evolution for Scheduling Optimization of Dual-Gantry Multi-Head Surface-Mount Placement Machine. Mathematics 2021, 9, 2016. https://doi.org/10.3390/math9162016
Lin C-J, Lin C-H. Using an Improved Differential Evolution for Scheduling Optimization of Dual-Gantry Multi-Head Surface-Mount Placement Machine. Mathematics. 2021; 9(16):2016. https://doi.org/10.3390/math9162016
Chicago/Turabian StyleLin, Cheng-Jian, and Chun-Hui Lin. 2021. "Using an Improved Differential Evolution for Scheduling Optimization of Dual-Gantry Multi-Head Surface-Mount Placement Machine" Mathematics 9, no. 16: 2016. https://doi.org/10.3390/math9162016
APA StyleLin, C.-J., & Lin, C.-H. (2021). Using an Improved Differential Evolution for Scheduling Optimization of Dual-Gantry Multi-Head Surface-Mount Placement Machine. Mathematics, 9(16), 2016. https://doi.org/10.3390/math9162016






