Abstract
Starting from a contact Hamiltonian description of Liénard systems, we introduce a new family of explicit geometric integrators for these nonlinear dynamical systems. Focusing on the paradigmatic example of the van der Pol oscillator, we demonstrate that these integrators are particularly stable and preserve the qualitative features of the dynamics, even for relatively large values of the time step and in the stiff regime.
MSC:
65D30; 34K28; 34A26; 34C15
1. Introduction
Liénard systems are a class of two-dimensional nonlinear dynamical systems that exhibit a stable limit cycle. Among them the most famous is the van der Pol oscillator [1,2]. Due to the existence of a stable limit cycle, such systems are of the utmost importance in modelling natural phenomena such as, e.g., electrical circuits and neuronal dynamics, and therefore an accurate investigation of their dynamics is required. However, because of the nonlinear nature of such systems, analytical results are scarce and one has to recur to perturbative techniques and numerical integration.
An immediate and paramount problem for both the development of perturbative techniques and of stable numerical schemes is the lack of a geometric structure. Indeed, apart from very specific cases in which some integrability conditions are satisfied, and where one can use the Jacobi Last Multiplier to find a Lagrangian or Hamiltonian structure [3,4], in the general case such a pursuit is hopeless. For instance, many Liénard systems present an attractor, a stable limit cycle, and thus they cannot be Hamiltonian in the symplectic sense. There have been several attempts in the literature to circumvent this problem. In [5] the authors suggested enlarging the phase–space to a four-dimensional manifold and define a particularly simple Hamiltonian system in this enlarged space so that the two-dimensional projection onto the original space recovers the original dynamics, and then they showed that this approach allows for the use of perturbative methods. In [6], the classical Bateman trick for the harmonic oscillator was extended to the van der Pol oscillator and then further generalised to all Liénard systems with a quadratic potential. Both these approaches involve a four-dimensional phase–space, and in both the authors have focused on the perturbation theory and have not explored the consequences of the Hamiltonisation for the numerical integration. From yet another perspective, in [7] the authors have presented various splitting schemes for “conditionally linear systems” (these include Liénard systems) which, although not geometric, are based on the standard splitting schemes for symplectic Hamiltonian systems, and showed good qualitative and quantitative results.
In this work, we contribute to the advancement of geometric integration for Liénard systems by using Hamiltonian flows on contact manifolds. Contact geometry was introduced in Sophus Lie’s study of differential equations, and has been the subject of intense research, especially related to low-dimensional topology [8]. In recent years, contact Hamiltonian systems have found many applications, first in the context of thermodynamics [9,10,11] and, more recently, in the context of the Hamiltonisation of several dissipative dynamical systems [12,13,14,15,16,17,18,19]. The large number of applications of contact systems that have appeared recently motivated research on geometric numerical integration [15,16,20,21]. Fortunately, contact flows possess geometric integrators (both variational and Hamiltonian) that precisely parallel their symplectic counterparts, and therefore they show remarkable numerical and analytical properties such as, e.g., increased stability, near-preservation of invariant quantities, and modified Hamiltonians.
In this work, leveraging some ideas in [5], we start a treatment of Liénard systems from the point of view of contact Hamiltonian systems: we show that they can be given a particularly simple Hamiltonian formulation on a three-dimensional contact manifold, and then we use this Hamiltonisation to construct splitting integrators for such systems and analyse their properties from an analytical point of view, exploiting the modified equations. Along the work, we use the van der Pol oscillator as a paradigmatic example.
Our results show that the resulting geometric integrators are very stable, even when the system is stiff, and they preserve the qualitative features of the limit cycle even for large values of the time step, which permits sparing computational resources and is of primal importance in applications to, e.g., neuronal dynamics [7]. Moreover, from the use of the modified equations, we can prove analytical results on the preservation and the period of the limit cycle that show a very good agreement with the numerical simulations.
The paper is organised as follows: in Section 2 we provide a Hamiltonian formulation of Liénard systems based on contact Hamiltonian dynamics, and then in Section 3 we introduce a new class of explicit geometric integrators for these systems that are naturally derived by splitting the Hamiltonian. Then in Section 4 and Section 5 we thoroughly analyse the properties of these integrators both analytically and numerically by investigating the benchmark example of the van der Pol oscillator. We conclude in Section 6 with a discussion and a perspective on future work.
All the simulations are reproducible with the code provided in [22].
2. A Contact Hamiltonian Formulation of Liénard Systems
2.1. A Brief Review of Liénard Systems
Liénard systems are a family of planar coupled differential equations of the form [1]
where for an even function and is an odd function. Alternatively, (1) is equivalent to the second order scalar equation
A third equivalent version of (1) is given by
Example 1
(The van der Pol oscillator). Perhaps the most famous example of the family of Liénard systems is the van der Pol oscillator, which can be written using dimensionless variables as follows
and can be equivalently rewritten in the form (3) as
from which we recognise that in this case and .
A crucial property of Liénard systems is encoded in the following theorem, guaranteeing the existence and uniqueness of a stable limit cycle for a large class of systems [23].
Theorem 1
(Liénard’s Theorem). Under the conditions
- ,
- if,
- and,
- has exactly one positive zero at, is monotone increasing forand;
The dynamical system (1) presents a unique, stable limit cycle.
In particular, the theorem above implies that the van der Pol Equation (4) with has a unique, stable limit cycle.
For additional information on the classical approach to the analysis of Liénard systems we refer to [23].
2.2. A Brief Review of Contact Hamiltonian Systems
Similarly to the fact that a symplectic manifold is a -dimensional differentiable manifold endowed with a 2-form that is closed () and non-degenerate (), an exact contact manifold M is a -dimensional manifold endowed with a 1-form , called the contact form, that is non-degenerate, which means
A contact version of Darboux’s theorem [24] guarantees the local existence of coordinates —called Darboux coordinates—which permit to express the contact form as , where Einstein’s summation convention over repeated indices is being used here and in the following.
The contact form allows us to define in a natural way the concept of a Hamiltonian vector field on M. Let be a real function on M, then the contact Hamiltonian vector field associated with is defined by
where is the interior product and is the Reeb vector field corresponding to [8].
In Darboux coordinates takes the form
Finally, contact manifolds carry a natural bracket structure, called the Jacobi bracket, which yields a Lie algebra on smooth functions on M and is defined as
Again, in Darboux coordinates the Jacobi bracket reads
We refer the reader to [11,13,17,24,25] for further details. For our scope, it will be important in the following to have an explicit expression for the Jacobi bracket of monomial functions, that is,
where and
2.3. A Contact Hamiltonian Formulation of Liénard Systems
It is well known that any dynamical system on a n-dimensional manifold Q of the form can be extended to a Hamiltonian system defined on the -dimensional phase–space . This can be achieved with the introduction of the conjugate momenta in order to define the Hamiltonian
A direct computation shows that when we consider only the dynamics on the original x-variables, then we recover the original n-dimensional system. For instance, in the case of Liénard systems (3), the Hamiltonian reads
In [5], such an approach was used to derive a Hamiltonisation of Liénard systems in such an extended phase–space that was then shown to be useful to perform perturbation theory. Moreover, in [26] a similar extension, but with a suitably defined new Hamiltonian that non-trivially couples the variables, was used in order to develop geometric integrators in the extended phase–space and then used, e.g., in the case of the van der Pol oscillator.
In principle one could use the Hamiltonian (13) and perform a splitting in order to obtain new geometric integrators that are symplectic in the extended phase–space. However, we see from the form of (13) that it is linear in the momenta, meaning that it is naturally associated with a contact Hamiltonian on the -dimensional projectivised cotangent bundle , endowed with the contact structure inherited from the canonical symplectic structure of [24,27]. The procedure to perform such reduction is quite simple in this case and it is reviewed, e.g., in the recent work [10]. In order to avoid clutter of notation, from now on we focus on the case , which is the relevant case for our study: We start with (13) and consider a connected component of the open set in which . On such set, we can define the coordinates , which serve as Darboux coordinates on . Finally, we define the contact Hamiltonian
A direct calculation then shows that the restriction of the resulting contact Hamiltonian system to the plane recovers the original system.
By means of the above prescription, we arrive at the following result for Liénard systems.
Theorem 2
(Hamiltonisation of Liénard systems). Liénard systems are contact Hamiltonian systems, with a Hamiltonian of the form
The associated contact Hamiltonian system is
From the first two equations we recover the original Liénard system in the-space, while the third equation is decoupled.
Example 2
(The van der Pol oscillator revisited). As we have already seen in Section 2.1 the van der Pol equation is a particular case of a Liénard system, which is obtained by choosing and as
Consequently the contact Hamiltonian in this case reads
and the corresponding contact Hamiltonian systems is
As expected, from the first two equations we recover the original van der Pol Equation (4).
Remark 1.
Forand setting the appropriate initial condition, derived from (18) turns out to be the slope of the tangentto the orbit of the system at each pointof its evolution. This stems from the fact that (16)–(18) are the characteristic equations of the Hamilton-Jacobi equation for (15). Details of this derivation are in preparation by [28].
Remark 2.
The reduction procedure that led us to (14) is not unique. Indeed, we could have selected the connected component in whichand set. The corresponding contact Hamiltonian for Liénard systems is:
Beware that in this caseand, that is, the roles of q and s are switched, and the resulting system is
which is equivalent to (16)–(18) for thepart, but not so much for p.
The choice of reduction, in the case at hand, was dictated by numerical convenience: The Hamiltonianfrom (14) resulted in a simpler form of the algorithm, providing better results overall.
3. Geometric Numerical Integration of Liénard Systems
3.1. Contact Splitting Integrators
Contact splitting integrators are a class of geometric integrators recently introduced in the context of celestial mechanics [15]. They are the contact analogues of the well-known symplectic splitting integrators.
Let be a contact Hamiltonian which is separable into a sum of functions
Then, the Hamiltonian vector field associated with is separable as well
If moreover, each of the is exactly integrable, meaning that there exists a closed-form solution for its flow, then we can approximate the dynamics of to second order in with contact maps according to the following proposition.
Proposition 1
(Contact splitting integrators). In the hypotheses above, let denote the map given by the time-t exact flow of each vector field , for . Then
is a second order contact numerical integrator, meaning that each map is a contactomorphism.
From knowledge of the second order contact integrator (27) and using Yoshida’s standard formulation for the composition [29], we can construct two types of contact integrators of any even order; the difference between the two methods is that one involves exact coefficients for the calculation of the new time step, while the other uses approximated coefficients and involves a smaller number of map computations per iteration. The two methods are summarised in the following propositions.
Proposition 2
(Integrator with exact coefficients). If is an integrator of order , then the map
with and given by
is an integrator of order .
Proposition 3
(Integrator with approximated coefficients). There exist and a set of real coefficients such that the map
is an integrator of order .
In Table 1 we list the values of the approximated coefficients for three different sixth order integrators, labelled as A, B and C. Note that .

Table 1.
The coefficients for three different 6th order integrators.
Remark 3.
The splitting integrator with approximate coefficients labelled as A is the better performer among the approximate splitting integrators of sixth order presented here. This can be related to the fact that its largest coefficient is the smallest among the approximate integrators.
3.2. Modified Hamiltonian and Error Analysis
One of the main advantages of using contact splitting integrators is the possibility to have a direct error control by using the modified equations obtained from the modified Hamiltonian that results from the Baker–Campbell–Hausdorff (BCH) formula (see [15] for further details on the derivation of the modified Hamiltonian in the contact case). Indeed, for an integrator of order multiple applications of the BCH formula give [15]
where all the corrections are Hamiltonian vector fields. Therefore, is the time- flow of a Hamiltonian vector field, and its associated Hamiltonian, called the modified Hamiltonian, can be written formally as the power series
where the subscript in denotes the fact that it is associated with an integrator of order , and are the Hamiltonian functions associated with the Hamiltonian vector fields , that is,
Plugging (32) into the contact Hamiltonian equations that stem from (8), we obtain the modified equations, which are the equations whose time- flow gives exactly the integrator . Therefore, studying the modified equations and their relation with the original equations gives us important information on the modifications introduced by the integrator on the original system.
3.3. Geometric Numerical Integration of Liénard Systems
The application of the contact splitting integrators introduced in Section 3.1 to Liénard systems starts with the splitting of the contact Hamiltonian (15) as
and the consequent identification of the corresponding vector fields
The structure of this splitting ensures the exact integrability condition for any choice of the functions and . Indeed, the time- flow maps are explicitly given by
Example 3
(The van der Pol oscillator yet again). Applying the above splitting to the Hamiltonian (20) we obtain
and the corresponding time-τ flow maps are
In the next section we present the numerical and analytical results of the application of various splitting integrators based on the maps (40) to the van der Pol oscillator. To fix the notation, when referring to a particular splitting, we will write, e.g., to indicate that we are using the second order integrator obtained using the splitting (27) of the maps (40) composed in the order indicated in parentheses.
Remark 4.
As we show in Proposition 4, the equations of motion of q and s are necessarily independent of p. In fact one could have just considered the first two rows of (21) and used the corresponding splitting integrator. The integrator itself would be identical to the restriction of (40) to theplane.
By going through the route of the contact Hamiltonian, however, we show that there is more to this scheme in certain cases: It produces geometric integrators, guaranteed to preserve an underlying contact structure. Our belief is that this hidden structure is the reason the integrator is so performant in terms of the preservation of the limit cycle, even in the stiff regime.
3.4. A Remark on Variational Integrators
We can also think of Liénard systems as forced Lagrangian systems. The discrete version of the Lagrange–D’Alembert principle can then be used to construct geometric integrators for the systems without the need to introduce an ancillary variable. The theory of variational integration for forced systems is developed in detail in [30] (Part 3), we present here only the bare minimum and the integrator that results. We will use this integrator in the following sections as an extra element of comparison for our splitting integrators.
If we denote the Lagrangian by and the external force by , the Lagrange–D’Alembert principle tells us that the trajectories of the system are the solutions of
In the case of the van der Pol oscillator, and .
For the discrete Lagrange–D’Alembert principle, we seek a discrete curve satisfying
where and are the discretisations of the Lagrangian and the force, respectively. For instance, when considering the midpoint rule,
Applying a discrete Legendre transform with forces, one ends up with the implicit integrator
where denotes the derivative with respect to the ith variable.
In all cases, however, the explicit nature of the contact integrator makes it orders of magnitude faster than the variational one, as shown in Table 2.

Table 2.
Execution time statistics for the integration of a van der Pol oscillator with initial conditions , for .
4. Geometric Numerical Integration of the van der Pol Oscillator: Numerical vs. Analytical Results
4.1. Numerical Results
We split the analysis into three different cases, labelled by the value of the nonlinear coupling parameter : For we recover the harmonic oscillator on the plane ; for and we are in the non-stiff regime; for we are in the stiff regime.
It is well-known that to approximate the limit cycle with Euler-type methods, one cannot choose the time step independently of , even in the non-stiff case [7]: For example, the Euler method requires and the exponential midpoint method requires .
In the rest of this section, we will focus on the performance of our algorithm in the preservation of the limit cycle. As we will see, our methods accurately preserve the limit cycle of the van der Pol oscillator when : This allows for much larger step sizes than Euler-type methods when integrating Liénard systems.
4.1.1. (Harmonic Oscillator)
Figure 1 shows the solutions in the -plane for different time steps and with the same initial condition .
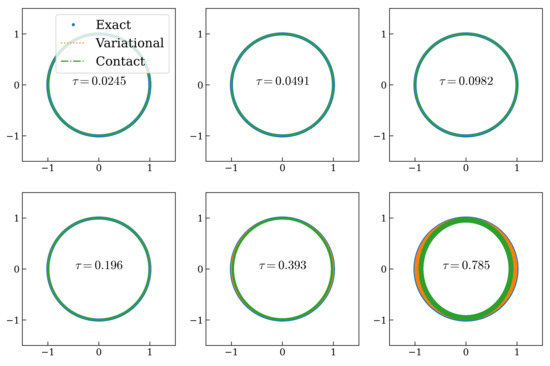
Figure 1.
Orbit of the van der Pol oscillator with (harmonic oscillator) with initial condition integrated for different values of the time step . The dashed blue line shows the exact solution.
We can observe that the integrator is stable at least until the surprisingly large value . By increasing the time step, the typical circular orbit of the harmonic oscillator becomes more elliptic, and the period changes. In this regime, in which we are effectively integrating a Hamiltonian system, we can see the extra stability of the variational integrator compared to a splitting integrator.
Let us focus for a moment only on the contact integrator. In Figure 2 we plot the relation between the time step and the period of the orbits obtained from numerical simulations. Even though the frequency changes, we can see that the variation remains well under control for all values of .
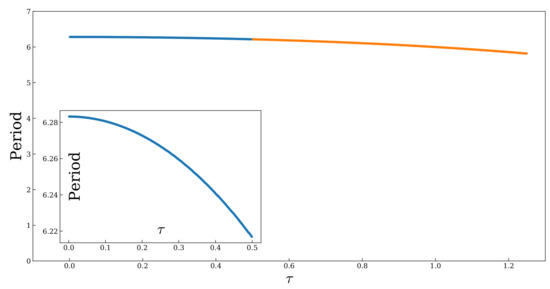
Figure 2.
van der Pol oscillator with (harmonic oscillator). Dependence of the period of the numerical solution with respect to the time step. The inset plot is a close-up of the periods for .
4.1.2. and (Non-Stiff Regime)
In Figure 3 we show the persistence of the limit cycle for different values of and increasing values of .
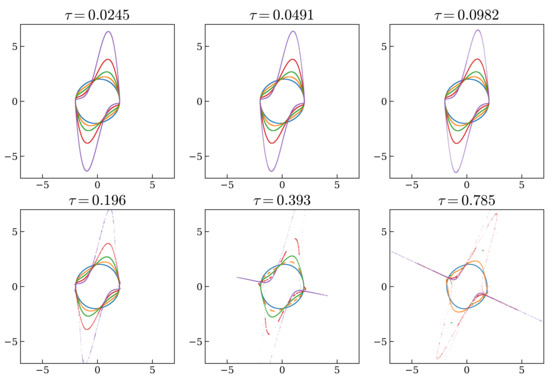
Figure 3.
Limit cycle of the van der Pol oscillator computed with the second-order contact integrator for values of 0.1 (blue), 0.5 (orange), 1 (green), 2 (red), 4 (purple) and with different time steps.
Clearly, the limit cycle is preserved also for very large values of and in this range. Moreover, the very long integration time, with , is an evidence of the stability of the integrator.
Moreover, in this case, the dependence of the period and the frequency of the limit cycle with respect to the time step shown in Figure 4 is very similar to that of the harmonic oscillator.
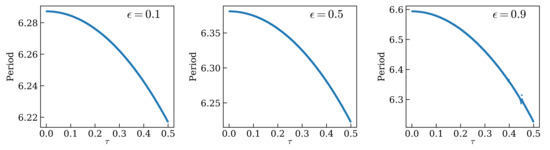
Figure 4.
Dependence of the period of the numerical solution of the van der Pol limit cycle with respect to the time step for increasing from left to right.
According to adiabatic perturbation theory [31] (Chapter XII), we can expect the variational integrator obtained in Section 3.4 to perform relatively well in the integration of Liénard systems with small coupling. However, already in this regime, we start observing a difference in stability with respect to the variational integrator. In Figure 5, where we replicate the simulation of Figure 3 with the variational integrator of Section 3.4, we can clearly see that the increase of the time step corresponds to a progressive disappearance of the limit cycle, also for small values of .
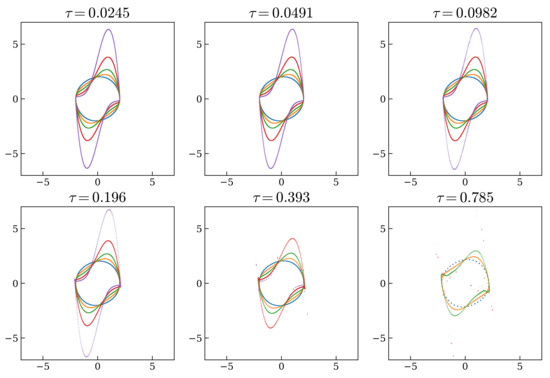
Figure 5.
Limit cycle of the van der Pol oscillator computed using the variational approach of Section 3.4 for values of 0.1 (blue), 0.5 (orange), 1 (green), 2 (red), 4 (purple) and with different time steps.
4.1.3. (Stiff Regime)
To better understand what happens in the stiff case , it is convenient to perform, after the integration, the so-called Liénard transformation [1,7]
This change of variables transforms the dynamics into
and enables a nice geometric description of the limit cycle. Indeed, the nullcline, which is the locus of points such that , is given by the cubic . Since evolves much faster than , the solutions are quickly attracted by the cubic nullcline. Once there, they move slowly along the curve until they reach an extremum, at which point they quickly jump horizontally to the other branch of the nullcline. This periodic motion that jumps back and forth on the nullcline is the attractive limit cycle of the stiff van der Pol oscillator.
Figure 6 shows the cubic nullcline and the numerically simulated attractor for and for different values of the time step. As one can observe, the limit cycle is preserved also for large values of the nonlinear coupling, although it suffers from a distortion for larger values of : This is especially clear in the first picture of the last row of plots of Figure 6, corresponding to and .
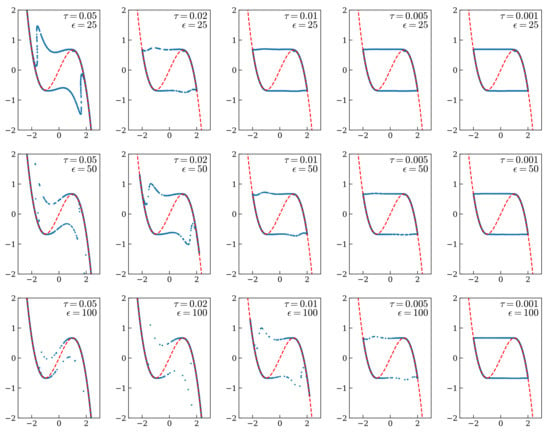
Figure 6.
Orbits for the stiff van der Pol oscillator obtained with the second-order contact integrator for different values of the coupling and of the time step after the Liénard transformation: With increasing from top to bottom and decreasing from left to right.
When we replicate the previous figure also for the variational integrator, see Figure 7, we see again that there is a sudden disappearance of the limit cycle also for values of which are relatively small compared to . This gets more and more pronounced by increasing the coupling constant and seems to indicate a complex dependence of the error on the product . In contrast, we prove in Proposition 7 that the contact integrator of order has an error of order . Thus we can expect, provided , to preserve the qualitative features of the dynamics, in agreement with the results of Figure 6.
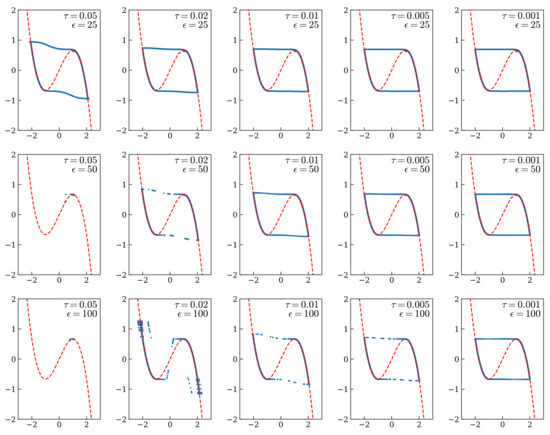
Figure 7.
Orbits for the stiff van der Pol oscillator obtained with the variational approach of Section 3.4 for different values of the coupling and of the time step after the Liénard transformation: With increasing from top to bottom and decreasing from left to right.
4.2. Analytical Results
In this section, we provide an analytical study of the contact splitting integrators for the van der Pol oscillator based on the modified equations. We start by providing two general properties of the modified equations that are of special importance.
As we have seen in Example 2, in the contact formulation of the van der Pol oscillator the equations for q and s are independent of p, as it should be. Clearly, given that the maps for q and s in (40) are all independent of p, any splitting integrator will satisfy this property too. However, it is instructive to recover this result by using the modified Hamiltonian, since in the proof we will find out an important property of , i.e., that it is linear in p, as it is the original Hamiltonian (20). This is the content of the next result.
Proposition 4.
For any contact splitting integrator, the corresponding modified Hamiltonianis linear in p. It follows that the modified equations for q and s are independent of p.
Proof.
We prove first the second part: The claim is that if is linear in p, then the corresponding modified equations for q and s do not depend on p. By a direct look at the general contact Hamiltonian Equations (8), this is clearly true. Now let us prove that is indeed linear in p: Considering the splitting in (39), we have that , , and , are all polynomials in and that only C depends (linearly) on p. Therefore, we see from (11) that by commuting A, B and C we can only obtain terms that are at most linear p. Then again, by commuting two terms that are at most linear in p, we see from (11) that we always obtain terms that are at most linear in p. We conclude that the modified Hamiltonian is at most linear in p. Indeed, is linear in p, because otherwise in the modified equations we would have , which is clearly not the case. □
Furthermore, we observe that when the time step , any truncation of the modified equations is likely to possess new spurious equilibria. This is so since at any order the corresponding vector fields are polynomials in of increasing order. Therefore, it is important to actually prove that is the only fixed point (considering only the dynamics projected to the plane) for the integrator and that it is unstable, as we show in the next result.
Proposition 5.
Restricted to the plane, the integratorhas a unique fixed point atwhich is unstable. Furthermore, both eigenvaluesof the Jacobian of the mappingsatisfyfor all and .
Proof.
The proof is based on writing explicitly the action of the integrator on an initial condition, that is, we apply to , to obtain
Now when we impose the condition for a fixed point
Using the second equation in (45) into the first equation in (44) we obtain
which is true if and only if .
Next, we substitute into the second equation in (44) and we obtain
which is true if and only if .
To prove that is unstable, we compute the Jacobian of the map (44) at , and in particular we obtain that its determinant is , indicating that at least one eigenvalue has absolute value , which proves the instability.
To conclude the proof, let and . A direct computation shows that the eigenvalues of the Jacobian of the map (44) at are
Depending on the sign of we have two cases: The eigenvalues are both real or they are complex conjugates.
- Case (I)
- : The eigenvalues are complex conjugates, therefore . Since , we have .
- Case (II)
- : This happens when , that is
The fact that follows from .
Let us now focus on . Notice that since and , we necessarily have that . Therefore, it suffices to prove that
By repeatedly rearranging (48) and observing that (47) implies , we obtain that (48) is equivalent to the following inequalities
□
In what follows we split the analysis into three different cases depending on the value of , as we did in the Section 4.1.
4.2.1. (Harmonic Oscillator)
In this case, we have a harmonic oscillator, for which each non-trivial trajectory has period . Moreover, the maps (40) in this particular case are simplified (for instance, the map becomes the identity) and the modified Hamiltonian takes the remarkably simple expression
where
The corresponding modified system is thus
which is again exactly solvable (recall that is fixed), and the solution in q and s is a harmonic oscillator with frequency
In Figure 8 we compare (57) with the numerical results for the period and the frequency obtained in Section 4.1.1. We observe that there is a very good agreement between the analytical expression up to the eighth order in and the numerical results.
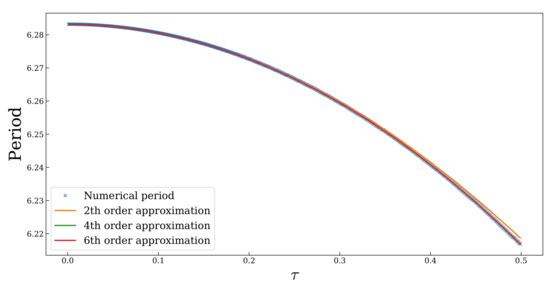
Figure 8.
Dependence of the period of the numerical solution for the harmonic oscillator () with respect to the time step. The numerically estimated period is compared with the period computed from the modified equations.
4.2.2. (Non-Stiff Regime)
This regime can be studied using perturbation theory and therefore there are many results (see, e.g., [32,33]). We study the persistence of the limit cycle for the contact splitting integrators in a way similar to [7], that means, we use the modified equations in order to provide some estimations on the amplitude and period of the limit cycle.
Proposition 6.
Proof.
Let us consider a contact splitting integrator of order ; using the BCH formula (see Section 3.2) we can argue that the modified Hamiltonian whose time- flow is given by is of the form
Thus the modified equations read
We know from Proposition 4 that the equations for and are independent of p, and from Proposition 5 that the point in the -plane is an unstable equilibrium of the system.
If we rewrite the system in polar coordinates on the plane with the change of variables and , then the equation for reads
Since the modified Hamiltonian is by construction a polynomial in the variables q and s, the dependence on of is only through sums and products of trigonometric functions. In particular, this implies that the averaged dynamics of obtained by the integration along a period has the form
One now observes that, modulo high order terms in , the stationary points of the averaged dynamics are and , which implies that the latter is the radius of the limit cycle, proving the first part of the proposition.
For any fixed order, it is possible to give a more refined estimate of the limit cycle radius by looking at the exact correction from the modified Hamiltonian.
To prove the second part of the statement, we concentrate on the integrator (since this is the integrator that has been used throughout the simulations in the paper). The corresponding modified Hamiltonian, in this case, is
leading to the following modified equations for and
and to the radial equation
An explicit computation then gives
leading to the claimed radius . □
In the non-stiff regime, we can also perform a perturbative analysis by applying the Poincaré–Lindstedt method to study the frequency (and hence the period) of the system (see, e.g., [33]). The first step consists in the time reparametrisation , which leads to the differential equation
where the derivatives are now expressed in terms of , instead of t, and, as usual, we omit the decoupled equation for . Noticing that the modified Hamiltonian vector field depends on the two parameters and , we suppose, in analogy to the traditional approach [33], that all the terms appearing in the equations can be expanded in Taylor series with respect to such parameters as follows
In particular, notice that we assume all the expressions to be of even order in , given that all the terms appearing in the modified equations are of even order.
For convenience, and without loss of generality, we follow [33] and assume that
This is equivalent to a convenient time shift that simplifies the initial conditions.
The differential equation corresponding to the order , then reads
whose solution is
Since we want and to have period , this fixes , while condition (70) implies and .
To fix A, we need to consider the order , , which gives the differential equations
Inserting the solution of the previous step we can solve (73). We find that in order to avoid secular behaviours, we need to fix and .
By repeating this procedure for higher orders of and , we can compute the matrix and the corresponding solutions. For instance, up to order and , we get
The first important remark here is that the coefficients of the first row (corresponding to fixing and taking in Equation (67)) are exactly the same as for the approximation of the frequency obtained by using the modified Hamiltonian (cf. Equation (57)), which shows a remarkable consistency between the two methods. Moreover, Equation (67), with the coefficients given in (74), allows us to extend the analytical analysis for the frequency and period of the limit cycle to the case . In Figure 9 we compare the analytical results thus obtained with the numerical results from Section 4.1.2. Clearly the match is very accurate, as the curves are almost indistinguishable, even for very large values of the nonlinear coupling and of the time step .
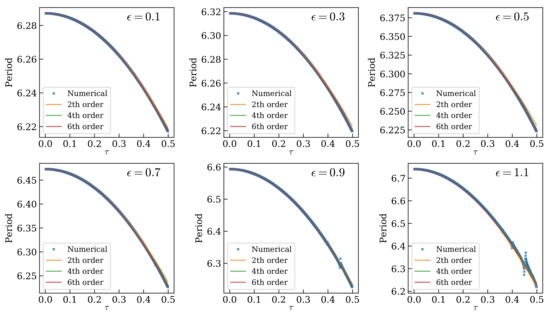
Figure 9.
Comparison between the numerical and analytical results (using perturbation theory) for the period of the limit cycle. Each figure is an analogue of Figure 8 for the value of indicated in the top right corner.
4.2.3. (Stiff Regime)
This is allegedly the most difficult regime to study, because is large, and therefore the nonlinear terms are important. Typically, we must rely on the numerical results. However, we can give an argument for a reasonable measure of the distance between the simulated numerical dynamics and the original one: An analysis of the modified Hamiltonian (see, e.g., (59)) allows now to control the error of the contact integrator of order asymptotically with . Provided that , this leads to the preservation of the qualitative features of the dynamics, in agreement with what is shown in Figure 6.
The result follows from the structure of the modified Hamiltonian itself and its explicit construction via the Jacobi brackets. It is important here to stress that this analysis holds also for large values of and not just for the adiabatic case .
Proposition 7.
For any contact splitting integrator of orderbased on the maps (40), the truncation at order(in τ),, of the modified Hamiltonian differs from the original Hamiltonian by a polynomial in ϵ of order at most. Moreover, any term of orderis of the form, and.
Proof.
Let , it can be proven that (see [15]), each correction in (32) is the result of taking nested Jacobi brackets. Since the Jacobi bracket is anti-symmetric, we may have at most equal terms inside the nested brackets. Considering that in the splitting (34) only the A term depends (linearly) on , and given the linearity of the Jacobi bracket, the greatest power in is given by the term , with P being either B or C. We conclude that the maximum degree in of is at most and the result follows from the structure of (32). □
From Proposition 7 it follows that the each correction in the modified Hamiltonian contributes a term of order . Recalling that in this case, one can expect that to keep the sum (32) under control, special attention should be given to the size of the product . This agrees with the results in Section 4.1.3, where we observed that the limit cycle presents a noticeable deformation for values of and , or and , that is, when .
5. Geometric Numerical Integration of Forced Liénard Systems
To emphasise the applicability of contact integrators to general Liénard systems, we will now present a brief numerical application of contact integrators to Liénard systems with time-dependent forcing. As usual, we take the van der Pol oscillator as our benchmark example, and study this system under the influence of a forcing term that is known to give rise to chaotic behaviour [26,34].
We stress that this section is meant as an example of possible further applications, and the results presented here are by no means meant to be exhaustive analyses or comparisons with the previous literature. Moreover, we will focus on the numerical aspects and omit the analytical treatment of the modified Hamiltonians: Since the computations are analogue to what we have already presented for the unforced van der Pol oscillator, we believe that adding them here would unnecessarily complicate the paper.
In the simulations that follow, we proceed in analogy to [26]. We test the second order contact integrator and two different sixth order integrators: , with exact coefficients, and , with approximate coefficients taken from family A in Table 1 (these are the integrators that have showed the best performance, cf. Remark 3). All the comparisons are made with respect to the LSODA solver [35] provided by SciPy [36], a robust adaptive solver with automatic and dynamic selection of the applied stiff or nonstiff methods, with a relative accuracy parameter of and an absolute accuracy parameter of .
Remark 5.
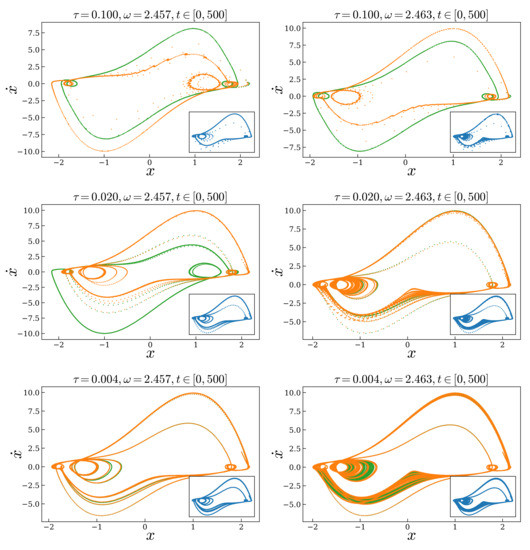
At this point, one may wonder why we are not also making a comparison with a variational integrator of the type described in Section 3.4. As a matter of fact, variational integrators with time-dependent forcing can be developed using [30] (Parts 3 and 4). However, the introduction of time into the equation comes with the introduction of an extra pair of equations involving time’s dual variable, the energy. As a direct consequence, one ends up with an implicit integrator in position, momentum, time and energy. In general, a fixed time step will not satisfy the extra equations involving the energy and the corresponding integrator is not going to be geometric [30] (Section 4.3.3). A naïve simulation using a fixed–step variational integrator with time-dependent forcing will immediately show this fact: Unless the time step is minuscule, the integrated trajectory will miss some evident qualitative features of the dynamics, see Figure 11. An additional simulation, reproducing the equivalent of Figure 10, can be found in the accessory simulation code [22].

Figure 10.
Orbit of the forced van der Pol oscillator with . The green dots correspond to the second order integrator and the orange dots to a sixth order approximate integrator (CBABC) with the coefficients taken from family A in Table 1. Left: Regular attractor. Right: Strange attractor. From top to bottom the time step is decreasing. The inset plots contain the corresponding trajectory computed with LSODA. It is plotted separately because, besides the first row, it is virtually indistinguishable from the one obtained with the sixth order integrator.
The contact splitting integrator benefits from being an explicit fixed–time integrator even in presence of time-dependent terms. This results in a simpler implementation and much faster computation times, even when the number of evaluations of the vector fields is virtually the same as the variational one.
The Forced van der Pol Oscillator
Following [26,34], we consider a forced van der Pol oscillator of the following form,
where A is the amplitude of the forcing and its frequency.
Extending (20) to a time-dependent contact Hamiltonian, we observe that the equation above can be recovered from
Indeed, on the plane, the corresponding contact Hamiltonian system reduces to
The nontrivial behaviour of this example is well known [34], e.g., for the couplings one can show that the system undergoes a bifurcation cascade from a regular attractor () to a chaotic one (for ).
In the numerical experiments, we propagate the system until and, unless differently specified, the time step is .
As one can see in Figure 10, even though we are dealing with a stiff problem, the method is capable of capturing the attractor even for large value of the time step and long integration intervals, rapidly converging to the correct solution as the time step decreases.
This system in the chaotic regime, , was also the example used to analyse the performances of the modified leapfrog methods introduced in [26]. While the numerical test in [26] uses a sixth order integrator, we will still include a test for our second order integrator.
While both integrators are geometric in nature, explicit and with fixed time step, the ones introduced in this paper present two main differences from those in [26]: They are based on contact geometry instead of symplectic one and they require the integration of only three variables (one of which is the time) instead of six.
In Figure 11 we show the trajectories computed by the aforementioned integrators. As one can see by comparing Figure 12 and Figure 4 in [26], despite the simplicity of the contact methods, their performance is comparable to the ones presented in [26], with the approximate integrator performing better than the exact one: They give results comparable to an established differential equation solver, LSODA, with less computational work: For these simulations the amounts of vector field evaluations of LSODA is , while our second order integrator requires evaluations and the sixth order one . These results can also be contrasted with the amount of evaluations for the corresponding algorithms in [26], which are (Method 1) and (Method 2). By avoiding the phase space extension, we obtained two concrete advantages: We have reduced both the computational cost of the integrator and the number of possible combinations of the splitting maps.
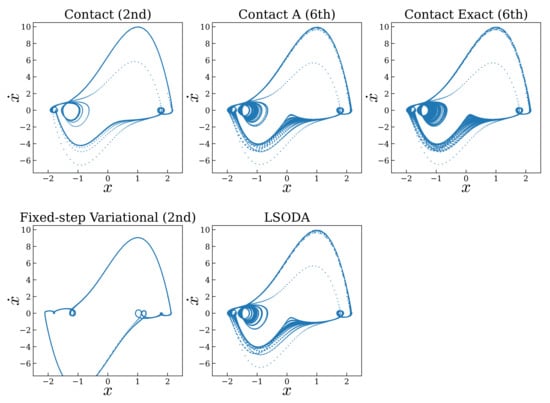
Figure 11.
Numerical orbits of the forced van der Pol oscillator (75) with , and , with the reference contact integrators and LSODA.
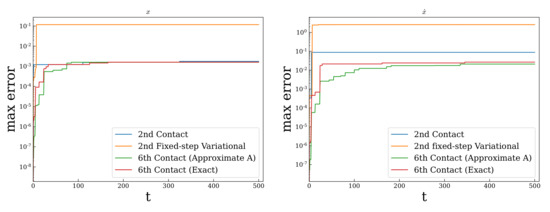
Figure 12.
Maximum absolute errors in x and up to a given time for the reference contact integrators compared to the LSODA method along the orbit in Figure 11.
As we already discussed in Remark 5, a time-dependent variational integrator requires an additional implicit equation in time and energy. As one can observe in Figure 11, the variational integrator obtained by imposing a fixed time step is unable to reproduce fine details of the system unless the time step is extremely small. In addition to this, the implicit nature of the integrator renders it extremely slower than the contact integrator, see also Table 2.
6. Conclusions
In this work we have proposed a novel approach to the geometric numerical integration of an important class of nonlinear dynamical systems, that is, Liénard systems. Such systems are planar systems having a limit cycle, and therefore they cannot be Hamiltonian in the symplectic sense in their original variables. As a minimal extension, we have considered Liénard systems as two-dimensional projections of contact Hamiltonian systems in three dimensions. This Hamiltonisation enables us to use the contact splitting integrators recently introduced in [15] and therefore to derive a new class of geometric numerical integrators for Liénard systems. We have used the paradigmatic example of the van der Pol oscillator to show that such formulation can be beneficial both for obtaining accurate numerical integrations of the dynamics at relatively small computational cost, and for deriving complementary analytical results, based on the use of the modified Hamiltonian and modified equations.
While we have shown here some interesting results, several questions still remain to be addressed. For instance, we have not fully exploited the modified Hamiltonian and modified equations in the stiff case; we have not considered further theoretical properties related to the existence of a Hamiltonian structure, such as, e.g., the preservation of volumes in the three-dimensional manifold, or the associated Lagrangian structure. In this context, we remark that the approach investigated here is based on the simplest possible Hamiltonisation of Liénard systems by means of contact Hamiltonian systems, which is obtained by a Hamiltonian that is linear (hence singular) in the momenta. Therefore, to derive an associated Lagrangian structure one would have to use the algorithm for singular contact Hamiltonian systems developed in [37]. From the numerical perspective, this could open the door to the use of contact variational integrators [16,20]. Moreover, other (contact) Hamiltonisations of Liénard and spiking systems might be possible, perhaps using non-standard contact structures, and therefore future work should also focus on alternative constructions.
Author Contributions
Software, F.Z. and M.S.; Supervision, A.B. and M.S.; Writing-original draft, F.Z., A.B. and M.S.; Writing-review and editing, F.Z., A.B. and M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the second author’s starter grant and by NWO Visitor Travel Grant 040.11.698 that sponsored the visit of AB to the Bernoulli Institute. M. Seri research is partially supported by the NWO co-fund grant 613.009.10.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors would like to thank Qihuai Liu, Arjan Van der Schaft and Mats Vermeeren for multiple interesting discussions and useful comments, and Edoardo Zadra for providing emergency computational facilities during the pandemic.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Liénard, A. Etude des oscillations entretenues. Revue Générale L’électricité 1996, 23, 901–912. [Google Scholar]
- Van der Pol, B. A theory of the amplitude of free and forced triode vibrations. Radio Rev. 1 1920, 701–710, 754–762. [Google Scholar]
- Nucci, M.C.; Tamizhmani, K.M. Lagrangians for Dissipative Nonlinear Oscillators: The Method of Jacobi Last Multiplier. J. Nonlinear Math. Phys. 2021, 17, 167. [Google Scholar] [CrossRef] [Green Version]
- Cariñena, J.F.; Guha, P. Nonstandard Hamiltonian structures of the Liénard equation and contact geometry. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1940001. [Google Scholar] [CrossRef]
- Choi, J.S.; Tapley, B.D. An extended canonical perturbation method. Celest. Mech. 1973, 7, 77–90. [Google Scholar] [CrossRef]
- Shah, T.; Chattopadhyay, R.; Vaidya, K.; Chakraborty, S. Conservative perturbation theory for nonconservative systems. Phys. Rev. E 2015, 92. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Raman, B.; Stern, A. Structure-Preserving Numerical Integrators for Hodgkin–Huxley-Type Systems. SIAM J. Sci. Comput. 2020, 42, B273–B298. [Google Scholar] [CrossRef] [Green Version]
- Geiges, H. An Introduction to Contact Topology; Cambridge University Press: Cambridge, UK, 2008; Volume 109. [Google Scholar]
- Mrugala, R.; Nulton, J.D.; Schön, J.C.; Salamon, P. Statistical approach to the geometric structure of thermodynamics. Phys. Rev. A 1990, 41, 3156–3160. [Google Scholar] [CrossRef]
- Van der Schaft, A.; Maschke, B. Geometry of Thermodynamic Processes. Entropy 2018, 20, 925. [Google Scholar] [CrossRef] [Green Version]
- Bravetti, A. Contact geometry and thermodynamics. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1940003. [Google Scholar] [CrossRef]
- Bravetti, A.; Tapias, D. Thermostat algorithm for generating target ensembles. Phys. Rev. E 2016, 93. [Google Scholar] [CrossRef] [Green Version]
- Bravetti, A.; Cruz, H.; Tapias, D. Contact Hamiltonian mechanics. Ann. Phys. 2017, 376, 17–39. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Torres, P.J.; Wang, C. Contact Hamiltonian dynamics: Variational principles, invariants, completeness and periodic behavior. Ann. Phys. 2018, 395, 26–44. [Google Scholar] [CrossRef]
- Bravetti, A.; Seri, M.; Vermeeren, M.; Zadra, F. Numerical integration in Celestial Mechanics: A case for contact geometry. Celest. Mech. Dyn. Astron. 2020, 132. [Google Scholar] [CrossRef] [Green Version]
- Vermeeren, M.; Bravetti, A.; Seri, M. Contact variational integrators. J. Phys. A Math. Theor. 2019, 52, 445206. [Google Scholar] [CrossRef] [Green Version]
- Gaset, J.; Gràcia, X.; Muñoz-Lecanda, M.C.; Rivas, X.; Román-Roy, N. New contributions to the Hamiltonian and Lagrangian contact formalisms for dissipative mechanical systems and their symmetries. Int. J. Geom. Methods Mod. Phys. 2020, 17, 2050090. [Google Scholar] [CrossRef]
- Gaset, J.; Gràcia, X.; Muñoz-Lecanda, M.C.; Rivas, X.; Román-Roy, N. A contact geometry framework for field theories with dissipation. Ann. Phys. 2020, 414, 168092. [Google Scholar] [CrossRef] [Green Version]
- Ciaglia, F.; Cruz, H.; Marmo, G. Contact manifolds and dissipation, classical and quantum. Ann. Phys. 2018, 398, 159–179. [Google Scholar] [CrossRef] [Green Version]
- Simoes, A.A.; Martín de Diego, D.; Lainz Valcázar, M.; de León, M. On the Geometry of Discrete Contact Mechanics. J. Nonlinear Sci. 2021, 31. [Google Scholar] [CrossRef]
- Goto, S.i.; Hino, H. Fast symplectic integrator for Nesterov-type acceleration method. arXiv 2021, arXiv:2106.07620. [Google Scholar]
- Zadra, F.; Seri, M.; Bravetti, A. Support Code for Geometric Numerical Integration of Liénard Systems via a Contact Hamiltonian Approach (v2.0). Zenodo. Available online: https://research.rug.nl/en/publications/support-code-for-geometric-numerical-integration-of-l%C3%ACenard-syste (accessed on 10 August 2021). [CrossRef]
- Perko, L. Differential Equations and Dynamical Systems; Springer: New York, NY, USA, 1991. [Google Scholar] [CrossRef]
- Arnol’d, V.I. Mathematical Methods of Classical Mechanics; Springer: New York, NY, USA, 2010. [Google Scholar]
- De León, M.; Lainz Valcázar, M. Contact Hamiltonian systems. J. Math. Phys. 2019, 60, 102902. [Google Scholar] [CrossRef]
- Pihajoki, P. Explicit methods in extended phase space for inseparable Hamiltonian problems. Celest. Mech. Dyn. Astron. 2014, 121, 211–231. [Google Scholar] [CrossRef] [Green Version]
- Blair, D.E. Riemannian Geometry of Contact and Symplectic Manifolds; Birkhäuser: Boston, MA, USA, 2010. [Google Scholar] [CrossRef]
- Liu, Q.; (Guilin University of Electronic Technology, Guilin, China). Personal communication, 2020.
- Yoshida, H. Construction of higher order symplectic integrators. Phys. Lett. A 1990, 150, 262–268. [Google Scholar] [CrossRef]
- Marsden, J.E.; West, M. Discrete mechanics and variational integrators. Acta Numer. 2001, 10, 357–514. [Google Scholar] [CrossRef] [Green Version]
- Hairer, E.; Wanner, G.; Lubich, C. Geometric Numerical Integration. Springer Ser. Comput. Math. 2002. [Google Scholar] [CrossRef]
- Amore, P.; Boyd, J.P.; Fernández, F.M. High order analysis of the limit cycle of the van der Pol oscillator. J. Math. Phys. 2018, 59, 012702. [Google Scholar] [CrossRef] [Green Version]
- Andersen, C.M.; Geer, J.F. Power Series Expansions for the Frequency and Period of the Limit Cycle of the Van Der Pol Equation. SIAM J. Appl. Math. 1982, 42, 678–693. [Google Scholar] [CrossRef]
- Parlitz, U.; Lauterborn, W. Period-doubling cascades and devil’s staircases of the driven van der Pol oscillator. Phys. Rev. A 1987, 36, 1428–1434. [Google Scholar] [CrossRef]
- Hindmarsh, A. ODEPACK. A Collection of ODE System Solvers. In Scientific Computing; Stepleman, R.S., Ed.; North-Holland: Amsterdam, The Netherlands, 1983; pp. 55–64. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De León, M.; Lainz Valcázar, M. Singular Lagrangians and precontact Hamiltonian systems. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950158. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).