Abstract
The Collatz dynamic is known to generate a complex quiver of sequences over natural numbers for which the inflation propensity remains so unpredictable it could be used to generate reliable proof-of-work algorithms for the cryptocurrency industry; it has so far resisted every attempt at linearizing its behavior. Here, we establish an ad hoc equivalent of modular arithmetics for Collatz sequences based on five arithmetic rules that we prove apply to the entire Collatz dynamical system and for which the iterations exactly define the full basin of attractions leading to any odd number. We further simulate these rules to gain insight into their quiver geometry and computational properties and observe that they linearize the proof of convergence of the full rows of the binary tree over odd numbers in their natural order, a result which, along with the full description of the basin of any odd number, has never been achieved before. We then provide two theoretical programs to explain why the five rules linearize Collatz convergence, one specifically dependent upon the Axiom of Choice and one on Peano arithmetic.
1. Introduction
In 1937, Lothar Collatz established a conjecture known as the problem, also known as Kakutani’s problem, the Syracuse algorithm, Hasse’s algorithm, Thwaites conjecture, and Ulam’s problem. The Collatz problem involves the iterative sequence defined as follows (see OEIS [1] for the definition of the Collatz map):
Among others, Erdős and Conway [2] conjectured that, given any initial term , the sequence always terminates at 1. Conway proved that there is no nontrivial cycle with a length less than 400, with Lagarias [3] later increasing this lower bound to 275,000. Conway [2], and Kurtz and Simon [4] also proved that the generalization of the Collatz problem is undecidable. The conjecture was first verified up to by Leavens et al. [5] and then to by Vardi [6]; then, Oliveira [7] further extended the results to , and as of 2020, it had been verified beyond . The Collatz problem is often stated differently, for example by Terras [8,9], to essentially compress the division by 2 [10,11]:
Researchers have tried to model the problem in various ways. Wolfram [12] represented it as an eight-register machine. Cloney et al. [10] and Bruschi [13] modeled it as a quasi-cellular automaton, with Zeleny [14] specifically modeling it as a six-color one-dimensional quasi-cellular automaton. Among some notable recent developments, Machado [15] provided an interesting clustering perspective on the Collatz conjecture and Tao [16] demonstrated that almost all Collatz orbits attain almost bounded values.
The dynamical system generated by the problem is known to create complex quivers (a quiver is simply a collection of arrows between points forming a set [17], where the Collatz quiver used here is simply defined as the set of all arrows connecting any natural number to the next one under the Collatz map) over , with one of the most picturesque being the so-called “Collatz Feather” or “Collatz Seaweed”, a name popularized by Clojure programmer Oliver Caldwell in 2017 [18]. The inflation propensity of Collatz orbits remains so unpredictable that Bocart showed that it can form the core of a reliable proof-of-work algorithm for Blockchain solutions [19], with groundbreaking applications to the field of number-theoretical cryptography as such algorithms are unrelated to primes yet, being based on the class of congruential graphs and still allowing for a wide diversity of practical variants. If Bocart thus demonstrated that graph-theoretical approaches to the problem can be very fertile to applied mathematics, the authors have also endeavored to demonstrate its pure number-theoretical interest prior to this work [20,21,22,23,24]. In this article, we refer to the Bocart proof-of-work in that expanding it and more precisely endowing it with a scannable certificate is an important side-result of our approach.
Our methodology consists of using the complete binary tree and the complete ternary tree (the complete binary tree over odd numbers is defined as endowed with the following two linear applications and all their possible combinations, with the complete ternary tree over the same set in turn defined as endowed with operations and all their possible combinations) over as a general coordinate system for each node of the feather. We owe this strategy to earlier discussions with Feferman [25] on his investigations on the continuum hypothesis, as it is known that the complete binary tree over natural numbers is one way of generating real numbers. The last author’s discussion with Feferman argued that morphisms, sections, and origamis of n-ary trees over could be a promising strategy to define objects of intermediate cardinalities between and , in a manner inspired from Conway’s construction of surreal numbers [26], which itself began by investigating the branching factor of the game of Go. Central to our contribution to the Collatz conjecture in this paper is also the analysis of the branching factor of a zero-player cellular game developing in the complete binary tree over odd numbers.
2. Related Research
2.1. Goodstein Sequences and Hydra Games
The idea of attacking the Collatz conjecture from the angle of logic and set theory is not new. Hydra games were first introduced by Kirby and Paris [27], and Arzarello [28] provided a rather wide outline of how their consideration could, in fact, lead to a set theoretical solution of the Collatz conjecture. The convergence of Goodstein sequences indeed, which form the core of Kirby and Paris’ demonstration that no Hydra game can be lost, cannot be proven in Peano arithmetics alone. Their founding element, however, which is the base-k hereditary representation of a number n, can be defined without the axiom of choice.
Definition 1.
Let us write any given number n as a sum of powers of a base k. Let us further write the exponents themselves as sums of powers of a base k; this process continues until we reach 1 in the exponent. This representation is denoted as the base-k hereditary representation of n.
The Goodstein sequence is generated by repeatedly increasing or “bumping” base k to and then by subtracting 1. Mathematically, it can be defined by the recursive sequence and . Here, the operator takes the base-k hereditary representation of n and then substitutes the base with . An example, as given by Klein [28], starts with 266:
Goodstein [29] proved that any such sequence always terminates at 0, but Kirby and Paris [27] also demonstrated that his theorem cannot be proven in Peano arithmetics alone. The idea of a Hydra game is similar to the Goodstein sequences, with the name “Hydra” coming from Greek mythology and describing Hercules’ battle with the Hydra of Lerna, with any of its multiple heads growing two more each time it is cut. In this game, a tree represents the Hydra and the game consists of cutting a branch of it (or one of the multiple “heads”) turn by turn. The Hydra then grows according to a set of rules, by growing a finite number of new heads in response to the cutting. Kirby and Paris [27] proved that the Hydra is killed by Hercules regardless of the strategy used to cut its heads. They also proved that, similar to Goodstein sequences, this property cannot be proven by Peano arithmetics alone, as they more precisely demonstrated that, if the well-ordering hypothesis for integers (i.e., within Peano arithmetics) could be used to demonstrate the convergence, then the theorem regarding Goodstein sequences could be reduced to the famous result of Gentzen [30] named “Gentzen’s consistency proof”, meaning that, from solving the Hydra game, one may prove the consistency of Peano arithmetics, which cannot be achieved within Peano arithmetics, as known from Gödel’s incompleteness theorem [31]. Cichon [32] and Hodgson [33] discussed a similar sequence to that of Goodstein, now called a “weak Goodstein sequence” and also used in Arzarello [28]. The weak sequence of 266 becomes
Cichon [32] proved the convergence of all weak Goodstein sequences by showing that one can assign the m-tuplet of the coefficients of the decomposition in base to each term of any such sequence and then demonstrated that the m-tuplets are well-ordered in a purely decreasing lexicographic way. In contrast with the Goodstein sequences, the convergence of the weak sequence can be proven in Peano arithmetics. The abovementioned results of Cichon [32], and Kirby and Paris [27] were alternatively proven by Caicedo [34] using proof from the theoretic results of Lob–Wainer’s fast growing hierarchy of functions. Another excellent work discussing the independence of Goodstein sequences and the axioms of Peano arithmetics has been produced in Kaplan [35] and Miller [36]’s respective theses. Kaplan further demonstrated a method for finding non-standard models of Peano arithmetics (introduced by Thoralf Skolem in 1934, non-standard models of arithmetic not only behave isomorphically to Peano arithmetic for a well-ordered initial segment of their set but also contain elements that do not belong to this segment) that satisfy Goodstein’s theorem using indicator theory, but a more significant contribution is that of Stępień and Stępień 2017 [37] with their groundbreaking approach to the demonstration of the consistency of arithmetics.
Recently, Barina [38] introduced a new algorithmic approach for computational convergence verification of the Collatz problem; his parallel OpenCL implementation reached a speed of 128-bit numbers per second on an NVIDIA GeForce RTX 2080 GPU. In conformity with the approach of Koch et al. [23], he exploited the particular optimization advantage of operating on integers represented in base 2, which we use as well in this article because the base 2 representation of whole numbers is the most natural when representing them in a complete binary tree.
It is also worth mentioning that, in an interesting preprint that has not yet been peer-reviewed as of the writing of this article, Kleinnijenhuis et al. [39] attempted to apply Hilbert’s paradox of the Grand Hotel to the Collatz problem and used Wolfram Mathematica for their computations on very large numbers, which has also been simulated by Christian Koch. (See the Collatz Python Library hosted by his GitHub repository [40]).
2.2. L-Systems and Analogies with Statistical Physics
The founding concept of our approach is to identify inevitable collisions within the phase space of the Collatz dynamical system between numbers proven to converge and numbers supposedly not converging to 1. To that end, we first defined an ad hoc coordinate system of the Collatz phase space, starting from the complete binary tree over . Then, to describe the non-ergodicity of Collatz orbits, we specifically studied the distribution of the intersections of the binary and ternary trees, as shown in Section 10. The most important contribution of this paper to solving the Collatz conjecture is the identification and demonstration of the five fundamental laws that characterize the basin of attraction of any odd number, which we can recursively apply to define an infinite L-system (initially developed by biologist Aristid Lidenmayer in 1968, L-systems are alphabets endowed with recursive production rules that allow, among others, for the easy representation of biological growth, in particular in botanics, where they show extensive industrial applications in generating vegetable shapes in the video game industry) developing within the complete binary tree and the characterization of some of their most essential emerging properties, in particular their comparative branching factor. Thus, the objective is to demonstrate that the L-system starting from number 1 cannot fail to finitely collide with the L-system starting from any other number, a methodology that may rightly evoke ergodic theory and statistical physics. Indeed, demonstrating on the one side that the Collatz dynamical system tends to compress trajectories to certain bottlenecks of its phase space and using this element of proof to further demonstrate that finite collisions between any two pairs of trajectories is therefore inevitable is a proof program we borrowed from statistical physics. However, if the already existing representations of the “Collatz feather” do already exhibit obvious bottlenecks and phase space confinements, the most essential contribution to their further understanding lies in establishing an ad hoc coordinate system, endowed with a practical metric to characterize and demonstrate the nature of these confinements precisely.
3. Contributions to the State-of-the-Art
In acknowledgement of the intellectual influence of the study of quantum non-ergodicity to the study of discrete dynamical systems (for a more precise example, see [41]) we meant to not reduce this article to its mathematical proofs but rather to accompany them with novel 3D visualizations of the Collatz phase space, along with specific empirical measurements of its behavior. As explained in the previous section, both the mathematical proofs and 3D visualizations are based on the ad hoc algebraic foundations, in particular, the coordinate system consisting of studying the intersections of both the binary and ternary trees over odd numbers that we established to gain further insight into the chaoticity of the Collatz feather. In Figure 1, we outline the fundamental contributions we intend to make here. Green charts indicate the results obtained from a two-dimensional coordinate system; purple charts indicate those obtained from a 3D analysis of the feather; and the blue chart indicates a result obtained from both.
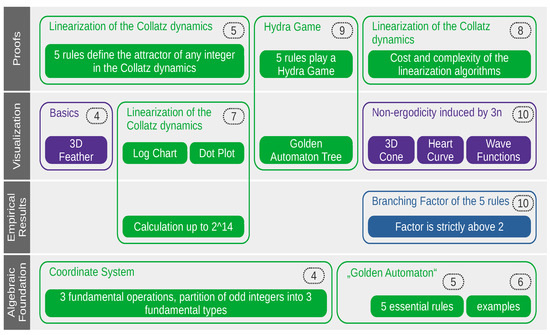
Figure 1.
Structure of the original contributions of this paper.
Fundamentally, our most essential theorems consist of the five rules that exactly define the basin of attraction of any odd number in the Collatz dynamical system. However, the emerging properties of those five rules are hard to predict and can be counterintuitive. They require equally novel developments in mathematical visualization and beyond a few novel concepts as well. This interplay between conceptual and visual progress is the reason we endeavored to develop many figures and frameworks, both in 2D and in 3D, and from graph theory to cellular automata, transfinite set theory, space-filling L-systems, and caustics. Though not intended ab initio, these many approaches practically complement each other in achieving what we believe to be one of the finest understandings of the fundamental chaoticity of Collatz orbits ever achieved.
4. Binary and Ternary Trees as a Novel Coordinate System for the Collatz Basins of Attraction
Note 1.
For all intents and purposes, we define Syr(x) or the “Syracuse action” as “the next odd number in the forward Collatz orbit of x”. Whenever two numbers a and b have a common number in their orbit, we also note a≡b, a relation that is self-evidently transitive:
The choice of symbol “≡” is a deliberate one to acknowledge a kinship between our method and modular arithmetic.
Definition 2.
Actions G, V and S: For any natural number a,
- 1.
- 2.
- .
- 3.
Definition 3. Rank:
The rank of any odd natural number a is its number of consecutive end digits 1 in base 2. For computer scientists, the rank is thus strictly equivalent to the “number of trailing ones” or “number of trailing 1 bits” of its binary representation (the number of trailing zeros in any binary string is also known as count trailing zeros (ctz), and the number of trailing ones are known as count trailing ones (cto)).
Definition 4. Types
A, B, andC:
- 1.
- A number a is of type A if its base 3 representation ends with the digit 2.
- 2.
- A number b is of type B if its base 3 representation ends with the digit 0.
- 3.
- A number c is of type C if its base 3 representation ends with the digit 1.
In other words, a number of type A belongs to the residue class , a number of type B belongs to the residue class , and a number of type C belongs to the residue class in the ring . In modular arithmetic, using the standard definition of “≡”, we simply have , b , and c . However, we adopted this ABC nomenclature as a simpler way to assign types to numbers when coding our linearizing algorithms, especially when combining different properties (e.g., Bup or A in Section 2.1, which would have been too cumbersome in the current notations of modular arithmetic. To remember which is which, one need only remember the order of ABC: if a, b, and c are respectively of types A, B, and C, then a+1 is dividable by 3, as is c-1; thus, a is on the left of b and c is on the right of b.
We intend to use the quiver of Figure 2 as a general coordinate system for each node of the Collatz feather. Paramount to our investigation is the comparative analysis of the branching factor of the feather compared with that of the binary tree.
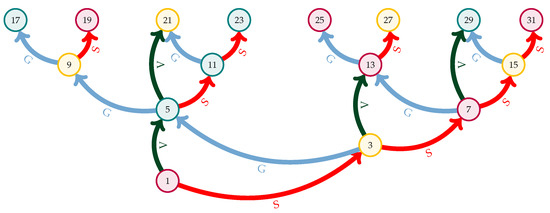
Figure 2.
Quiver connecting all odd numbers from 1 to 31 with the arrows of actions S, V, and G. The set is thus endowed with three unary operations without a general inverse that are noncommutative with . Whenever we mention the inverse of these operations, we assume that they exist on . Type A numbers are circled in teal, type B is in gold, and type C is in purple.
Figure 3 visualizes the orbits of all numbers from 1 to 15,000 in 3D, with the colors set by the types of Definition 3: the type A numbers are in teal, the type B ones are in gold, and the type C ones are in purple. Each branch is generated from the complete sequence of each number: for an even number, the current branch is rotated in one direction and rotated in the opposite one for an odd number. Two points, and containing the previous and current points of the orbit in the form , are handed over to the rotation function, which executes the rotation of the current point around a predefined axis. Rotating in opposite directions for even and odd numbers creates the feather-like construct shown in the figure.

Figure 3.
Collatz feather rendered in Blender, this time with the same ternary typology as defined in Definition 4 [42].
Listing 1.
Although the Collatz feather has often been represented in the literature and in popular mathematics circles, its fundamental geometry remains very poorly understood. In the next section, however, we identify the five fundamental rules that define the complete basin of attraction of any point of the feather.
5. The Five Fundamental Rules of the Collatz Dynamical System
Theorem 1.
The following arithmetic rules apply anywhere over the system endowed with the Collatz dynamic. Their iteration ad infinitum from any odd number precisely defines the entirety of the basin of attraction leading to it. (The reader should note that, although we call them “rules” in anticipation of their use in programming our linearizing algorithm, they are in fact theorems, which we prove in the next subsections, where operator ⋀ is defined as , with ∧ representing the “AND” boolean operator).
- Rule One: odd,
- Rule Two: if x is odd, then, with k odd. If x is even with k even.
- Rule Three:, odd non B,
- Rule Four:, odd non B,
- Rule Five:, , odd non B where is of rank 1, ,
Let us now demonstrate that each of these rules is in fact a theorem.
Definition 5.
In reference to Figure 2, we call "vertical odd" a number that can be written , where o is odd, and "vertical even" if it can be written , where e is even. For example, 5 is the first vertical odd in because and 9 is the first vertical even number in because .
5.1. Proving Rule One
If a is written , then ; therefore, .
5.2. Proving Rule Two
Lemma 2.
Let a be a number of rank 1; thus, with an odd number p such that a = G(p), Syr(S(a)) = G(3· p). Let a be a number of rank n so that S(a) = G(p); then, Syr(a) = G(3 p)
Proof.
If , p is odd; then, it follows that
Let us now generalize to the n. If can be written , it is also of rank 1, whereas is of rank 2; therefore, the Syracuse action (defined in Note 1) made it lose one rank. All we have to prove now is that = under those conditions:
If a is of rank , is of rank and . □
Note 2.
Since the action over an odd number n always yields an even result, for any odd number, the Collatz map is equivalent to computing or, in plain English, adding one to the odd number, then halving the result, and then subtracting one. How many recursive times one can add a half of itself to an even number or, equivalently, what is the largest k such that is a natural number for any even n directly depends on the base 2 representation of n, in particular, the number of n of trailing zeroes in this base. If we consider the Collatz map of Mersenne numbers m for example, which are defined as with , for any of them, one can consecutively multiply by and still yield a natural number for a number of times equal their rank − 1. Indeed, 31, which is written as in base 2 is of rank 5 because ; therefore, if one repeats the action “add to the number+1 half itself”, this yields an even result exactly four consecutive times. Thus, any strictly ascending Collatz orbit concerns only numbers a of rank and is defined by
While this may seem partly recreational, this property of Collatz orbits is in fact extremely useful to compress and characterize their non-decreasing segments, as the previous expression describes the one and only way an orbit can increase under the Syracuse action.
Lemma 4.
Let a be an odd number of rank 1 that is vertical even; then, is of rank 2 or more, and is vertical even. Let a be an odd number of rank 1 that is vertical odd; then, is of rank 2 or more, and is vertical odd.
Proof.
If a is vertical even, it can be written as and this number admits an that is , which is an odd number; therefore, is at least of rank 2.
Moreover, and this number admits a that is , an even number. Now, if a is vertical odd, it can be written as , and and . It follows that admits an and admits a of, respectively, and and that they are both odd. □
Theorem 5.
(Rule Two) Let a be a number that is vertical even; then, and for any even k. Let a be a number that is vertical odd; then, and for any odd k.
Proof.
If a is vertical even, then it can be written as , where p is necessarily vertical (odd or even). We proved that is then of rank 2 or more and that we have so it is necessarily vertical odd (since is of rank 2 or more) so and, therefore, . This behavior we can now generalize to n because, if a is vertical even with , then the lemmas we used also provide that and therefore is vertical even for any even n because is vertical (even or odd, depending on p only) for any even n.
Now, if a is vertical odd, it can be written as and p is necessarily of rank 2 or more because . Thus, is vertical (even or odd), and therefore, is vertical even. □
Note 3.
Observe that, in the process of proving Rule Two, we also demonstrated that any number of rank 2 or more is finitely turned into a rank 1 number of type A by the Collatz dynamic and that any number x of rank 2 or more so that under Rule Two is finitely mapped to a type A number that is vertical even; therefore, proving the convergence of such numbers is enough to prove the Collatz Conjecture. In the upcoming sections, they are called the “” numbers (which one may admit is more practical than calling them “the intersection of residue classes , , and ”), and identified with set .
5.3. Proving Rules Three and Four
Theorem 7.
(Rules Three and Four) Let a be a vertical even number with , where n and b are odd; then, . Let a be a vertical even number with , where m is even (zero included) and b is odd; then,
Proof.
If , by definition, . Then, As this expression can be divided by 2 no more than twice, we have .
Note that, if , then , which is of course an odd number. Therefore, is vertical odd and ; thus, we proved that .
If , then , so ; therefore, and thus . From this, we can generalize the progression of numbers that can be written , where x is of rank 2 or more. □
Definition 6.
Let x be any odd number:
- All “Variety S” numbers above x are written and
- all“Variety V” numbers above x are written or equivalently .
Any number g that can be written with x odd and may thus be finitely reduced under the Collatz dynamic to a number that can be written either or by the repeated following transformation:
Therefore, we indeed have that,
- for variety S numbers, , which proves Rule Four and
- for variety V numbers, which proves Rule Three because Rule One already provides that .
Just as in the process of proving Rule 2 we previously characterized and compressed the only way in which an orbit can ascend under the Syracuse action, proving Rules 3 and 4 incidentally allows one to compress and characterize the only way in which an orbit can descend under the Syracuse action as well, when is still understood as “the next odd number in the forward Collatz orbit”. If in plain English the ascending part could be described as “add one to a number and then half of the result, and then remove one”, the descending part may be equally described as “remove one from a number and then one quarter of the result, and then add one”. The monotonicity of this iterated transformation only depends on the base 2 representation of the initial number, hence the interest in using as a coordinate system for the Collatz orbits.
5.4. Proving Rule Five
Any type A number of rank 1 can be written , where b is of type B. In proving Rule Two, we showed that any number of rank is finitely mapped by the Collatz dynamics to , which combined with Rule Two itself gives Rule Five.
Figure 4 shows a few applications of Rules Three, Four, and Five plotted in gold. Rules One and Two are plotted in black. Whenever a number is connected to 1 by a finite path of black and/or gold edges, it is proven to converge to 1.
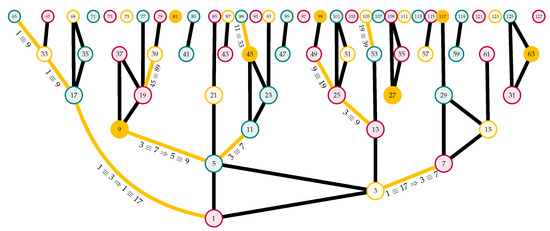
Figure 4.
Just a few applications of the five rules starting from .
6. The Golden Automaton
Definition 7.
On {; G, S}, the Turing machine recursively calculating the output of Rules One, Two, Three, Four, and Five from number 1 onward, in the natural order on is called the “Golden Automaton”.
6.1. “Golden Arithmetic”
Our purpose is to develop an ad hoc multi-unary algebra that could found a congruence arithmetic specifically made to prove the Collatz conjecture and which we intend as an epistemological extension of modular arithmetic, hence our use of the symbol ≡ in this article rather than the ∼ which is sometimes seen in Collatz-related literature. This “Golden arithmetic” involves words taken in the alphabet , which we call in their order of application, such as in turtle graphics. For example, VGS3 means
Rules 3, 4, and 5 may now be reformulated as such, without loss of generality as long as Rules One and Two are still assumed:
- Rule Three: Let b be of type B; then, from b. We will all this action and it is defined in .
- Rule Four: Let c be of type C; then, from c. We call this action and it is defined in .
- Rule Five: Let a be of type A; then, from a. We call this action and it is defined on .
As Rules One and Two ensure that the quiver generated by the Golden Automaton branches, with each type B number that is vertical even providing both a new A type and a new B type number to keep applying, respectively, Rules 5 and 3, we may follow only the pathway of type A numbers to define a single non-branching series of arrows, forming a single infinite branch of the quiver. The latter, if computed from number 15, leads straight to 31 and 27, solving a great deal of other numbers on the way:
Again, it is in no way a problem but rather a powerful property of the Golden Automaton that this particular quiver branch already covers 19 steps because each of them branches into other solutions.
We may follow another interesting sequence to show that, in the same way that Mersenne number 15 finitely solves Mersenne number 31, Mersenne number 7 solves Mersenne number 127. This time, we follow a different branch of the Golden Automaton up to , which we proved is written because 127 is the Mersenne of rank 7.
By Rule 4, we have the first equivalence and .
Therefore, by Rule 2, we also have .
Rule 3 gives and again .
The cases of 15 proving the convergence of 31 and 27 and of 7 proving the one of 127 naturally leads us to the following conjecture:
Conjecture 1.
Suppose that all odd numbers up to are proven to converge to 1 under the Collatz dynamic; then, the Golden Automaton finitely proves the convergence of those up to in Peano Arithmetic.
Indeed, we already have that the Golden Automaton starting with 1 proves 3 by Rule One; then, 3 proves all numbers from 5 to 15, which in turn prove all numbers from 33 to 127. In the next subsection, we render larger quivers generated by the Golden Automaton to provide a better understanding of their geometry and fundamental properties and to demonstrate why it is so and, more generally, how, granted Goodstein sequences converge (meaning this requires the axiom of choice), it can be proven that they can reach any number in .
7. The Golden Automaton Well-Behaves as a Collatz Convergence on the Binary Tree
Let us now represent each odd number in the binary tree over with a cell having only three possible states:
- Black, meaning the odd number is not (yet) proven to converge under the iterated Collatz transformation or, equivalently, that it is only equivalent to another black number;
- Gold, meaning the odd number is proven to converge and the consequences of its convergence have not yet been computed, i.e., it can have an offspring; and
- Blue, meaning the number is proven to converge and the consequences of its convergence have been computed i.e., its offspring has already been turned gold.
In this ad hoc yet simpler “Game of Life”-like zero-player game, each gold cell yields an offspring and then turns blue, and whenever a cell is blue or gold, the odd number it represents is proven to converge. Starting with one cell colored in gold at the positions 1, the game applies the following algorithm to each gold cell in the natural order of odd numbers:
- Rule 1: if a cell on x is gold, color the cell on in gold;
- Rule 2: if a cell on x is gold, color the cell on in gold depending on the precise conditions of rule 2;
- If a cell on x of type A is gold, then color the cell on in gold;
- If a cell on x of type C is gold, then color the cell on in gold; and
- After applying the previous rules for a gold cell, turn it blue.
Note that, when applying on a type B number equivalent to Rule 1, then for , the algorithm needs not implement a defined and we can in fact compress it to only four rules.
Whenever a complete series of odd numbers between and is colored in gold, the game takes it and returns what we call its "computational bonus" namely all numbers that are higher than are colored blue and gold, thus giving a clear measurement of the algorithmic time it takes the Golden Automaton to prove the convergence of each complete level of the binary tree over . From there, we later plot the evolution of this bonus on linear and logarithmic scales.
Figure 5 illustrates the game we defined for the case n = 6. On the middle image, row {5;7} was solved with a computational bonus of eight numbers also solved above it. On the right image, row {9; 11; 13; 15} has a computational bonus of 6. As number 1 is the neutral element of operation , we leave it in gold during the simulations.
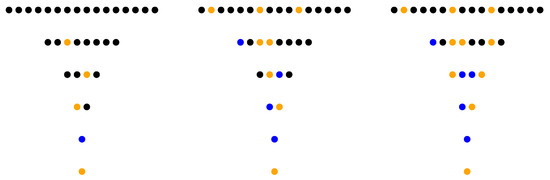
Figure 5.
The five rules completing the binary tree row by row in our first Python implementation of the Golden Automaton (“GAI”) [42].
Note that this first implementation of the Golden Automaton was made in Python to streamline its graphical output but that a later barebone version for maximal scalability has also been implemented in C++, this time with no graphical output. The Python version is called “GAI” and the C++ one is called “GAII” (see Section 8).
Now that the functioning of the Golden Automaton appears in a clearer way, in spite of the seeming complexity of its rules, we can scale it up to n = 12, which is detailed in the next six figures (Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11) (produced by GAI):

Figure 6.
Case 12, instant state of the tree when the seventh row has just been completed.

Figure 7.
Case 12, instant state of the tree when the eighth row has just been completed.

Figure 8.
State of row 8 (129 to 255) when it has just been finished.

Figure 9.
State of row 9 (257 to 511) when row 8 has just been finished.

Figure 10.
At the same instant, state of row 10 (513 to 1023).

Figure 11.
At the same instant, state of row 11 (going from 1025 to 2047: each line has about 100 dots).
To facilitate the observation of each row of the binary tree being covered by the Golden Automaton, we now zoom into each of them individually(Figure 8, Figure 9, Figure 10 and Figure 11):
The charts shown in Figure 12 (created out of the results obtained by GAI) now plot the bonus above any row n of the binary tree when the Golden Automaton just finished proving its entire convergence. The chart on the right plots the result against a logarithmic scale, with progressions (orange line), (green), and (red) in comparison, giving an early indication of the linear behavior of the Golden Automaton at the logarithmic scale, solving the rows of the binary tree in their natural order and having also solved about additional odd numbers above any full row that it just solved.
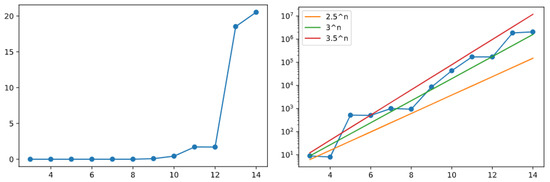
Figure 12.
Amount of extra numbers proven to converge above row n when it has just been finished by the Golden Automaton in either linear or log scales [42].
We also investigated the behavior of the Golden Automaton when mapped on the ternary tree over odd numbers, that is, the set of odd numbers endowed with operations . The automaton still demonstrated the entire rows one after another, this time with about extra numbers solved above each row. These graphs are shown in Figure 13 (created out of results obtained by GAI).
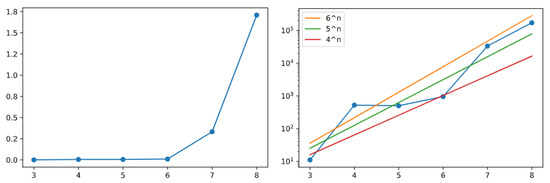
Figure 13.
Amount of extra numbers proven to converge above row n, this time in a ternary tree, when it has just been finished by the Golden Automaton, in either linear or log scales [42].
From there, we can thus provide two strategies to finalize a proof of the Collatz conjecture. The first would be to demonstrate that the Golden Automaton defines a game that is strictly simpler than a Hydra game over the graph of all unsolved numbers up to any arbitrary odd integer. The second would be to demonstrate that the comparative branching factor of the Golden Automaton, as it is diagonal to the binary tree, is strictly above 2 and that, thus, the population of solved dots can only finitely take over the population of unsolved ones, or put in another way, that the basin of attraction of any supposedly diverging odd number grows too fast not to collide with the basin of number 1.
8. Cost and Complexity of the Algorithms for Linearizing the Collatz Convergence
Following insightful comments from the reviewers, a second, leaner version of the Golden Automaton was written in C++ by Baptiste Rostalski, an intern at Strasbourg University’s department of computer science, which made it possible to push the results to line 23 (that is, in the binary tree) to further study its algorithmic complexity, in particular, to which extent the proportion of unproven nodes above any proven line n decreases in time. Here, we thus further describe the first version of our algorithm (“Golden Automaton One” or “GAI”, implemented in Python) and the second, “lean” one (“Golden Automaton Two or “GAII”, implemented in C++) for maximal scalability and the reproducible metrics it outputs.
8.1. Golden Automaton I (Implemented in Python)
The purpose of this first implementation, although it was conceived with scalability in mind, remained modularity and the ability to easily output representations within the binary tree (in 2D and 3D with Blender for the 3D outputs). To minimize complexity, all numbers that have just been proven are stored in an array and sorted by size. To make sure no new number is included in this array, it is compared with a second array storing all previously used numbers, the relevant rule introduced in Section 6.1. (The previously used numbers are now in blue in the 2D representation of Section 7. A binary search function then executes all searches, and a binary insert function executes all inserts. When a number is not included in the second array storing the already used numbers, it is inserted at the correct position of the first array of the proven numbers. After applying all five rules to all numbers in their normal ascending order, GAI deletes it from the first array (proven numbers) and inserts it into the second one (used proven numbers). Thus, the algorithm always takes the first of the proven number and applies it, depending on its type—see Definition 4). In this way, the algorithm ensures that the rows is completed as soon as possible. The algorithm counts the proven numbers per row to output the bonus as soon as it is completed. Remember that the bonus is the amount of proven numbers in all rows above the completed row. This procedure allows us to follow the exact sequence of the proven numbers as well as the exact time of completion of the individual rows.
8.2. Golden Automaton II (Implemented in C++) and Its Output
While the initial Python versions of the Golden Automaton were very modular and flexible enough to produce various graphical outputs on the fly, during the review process of this article, we also developed a barebone version to be executed in C++, which reached line 23. The exact algorithm of this version is described in the Appendix A. The first confirmation it provided was that the Golden Automaton solved every row while never proving more than extra numbers above any of them which is shown in Figure 14.
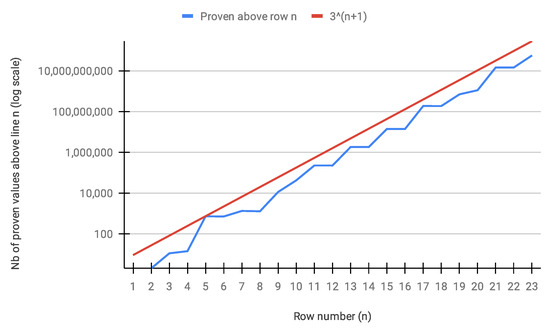
Figure 14.
Amount of extra numbers proven by Golden Automaton II (log scale) after finishing any row n of the binary tree (x-axis), fit to the function (red).
An even more interesting figure was the evolution of the relative difference between any row n and its successor , meaning, when row n is finished, how many numbers still remain to be solved in row , in which we confirmed an exponentially decreasing trend (see Figure 15). This result somehow improved in [16] in that it evidences a trend of the frequency of presumed unsolved numbers decreasing exponentially with n, yet while Tao obtained that the complement of its set of presumed unproven numbers attained only almost bounded values, here, the complementary set is that of proven numbers, of which the orbit is therefore not almost bounded but bounded.
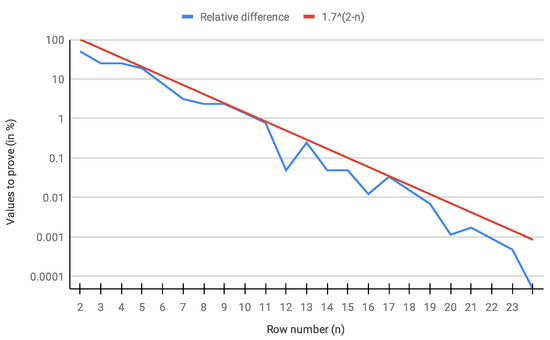
Figure 15.
Log scale of the proportion (in %) of presumed unproven numbers in each row when row n is finished by Golden Automaton II. The line of is shown in red for comparison.
Averaged across pairs of successive rows, the amount of presumed unproven numbers in every row when row n had been proven to exhibit a linear tendency (see Figure 16).
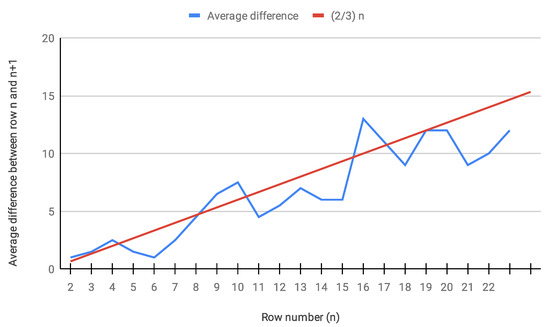
Figure 16.
Average difference between row n and in absolute values (not proportion) and not logarithmic ones.
Although the Golden Automaton II is RAM-intensive (needing a little less than 1.5 TByte of Random Access Memory to go all the way to row 23), we confirmed experimentally that its computing time, which is shown in Figure 17, in n never exceeded , which, given its barebone structure, is in accordance with the observation that the Golden Automaton proved less than extra numbers above each row n when it finished.
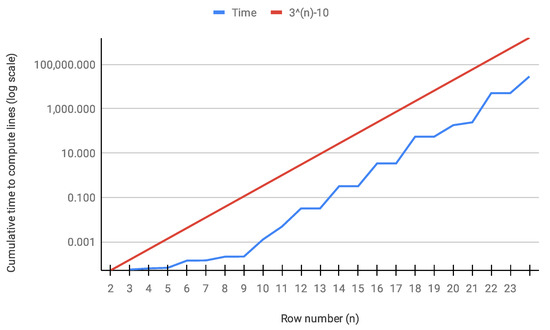
Figure 17.
Cumulative time to compute any row n, with in red for comparison (log scale).
As Golden Automaton II is based on the same, unchanging five rules we demonstrated at the beginning of this article, we can now posit that its time complexity is below , although we only intend to demonstrate that it is finite with n in the next sections.
9. The Golden Automaton as a Hydra Game
As we mentioned in Section 2.1 the idea of attacking the Collatz conjecture from the angle of transfinite arithmetic, in particular, the model of the Hydra game is not new, as Arzarello and others considered it in 2015 [28]. Both Goodstein sequences and Collatz sequences iterate base changes, but the Collatz sequences do so in a much less divergent manner, involving only bases 2, 3, and 4, with each critical step of their trajectory obeying the following rules:
- If a number is written in base 2, then it is finitely mapped to the result of operation G on the number written in base 3 with . Note that this is the one and only way an orbit can grow in the Collatz dynamics.
- If a number is written in base 4, then it is immediately mapped to a number written in base 2.
- If a number is written in base 2, then it is equivalent to the result of operation S on in base 3 with r as the base 3 representation of s.
- If a number is written in base 2, then it is equivalent to in base 3 with w as the base 3 representation of v.
The purpose of this subsection is to identify provable fundamental properties of the Golden Automaton by computationally scaling it up on the full binary tree over , but this time studying not the vertices but the edges of the graph. To streamline its algorithmic scaling, we use the simplified rules we defined in the previous subsection, again, without loss of generality. Our precise purpose is to pave the way for a formal demonstration that proving the convergence of odd numbers up to n is always isomorphic to a Hydra game, which justifies that we now study edges and not vertices. In Figure 18, Figure 19, Figure 20 and Figure 21, we color all of the elements of , for example , in red; as we demonstrate in the next section, they are precisely from the “heads” of the Hydra Game.
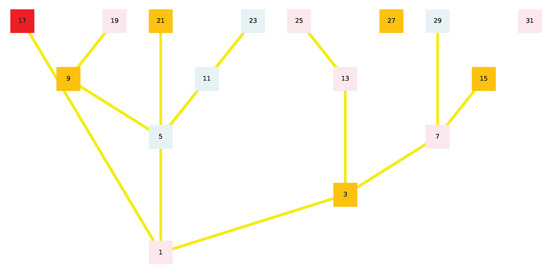
Figure 18.
Golden Automaton confined to numbers smaller than 32 [42].
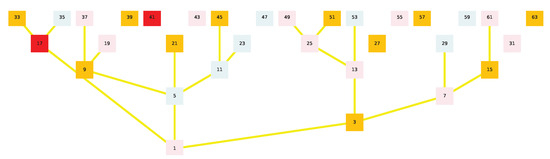
Figure 19.
Golden Automaton confined to numbers smaller than 64 [42].
Figure 20.
Golden Automaton confined to numbers smaller than 128 [42].

Figure 21.
Golden Automaton confined to numbers smaller than 256 [42].
Theorem 9.
If Goodstein sequences converge, the Collatz conjecture is true.
Definition 8.
A
Hydra
is a rooted tree with arbitrarily many and arbitrarily long finite branches. Leaf nodes are called
heads. A head is
short
if the immediate parent of the head is the root and
long
if it is neither short nor the root. The object of the
Hydra game
is to cut down the Hydra to its root. At each step, one can cut off one of the heads, after which the Hydra grows new heads according to the following rules:
- If the head was long, grow n copies of the subtree of its parent node minus the cut head, rooted in the grandparent node.
- If the head was short, grow nothing.
Lemma 10.
The Golden Automaton reaching any natural number is
at worst
a Hydra game over a finite subtree of the complete binary tree over .
Proof.
The essential questions to answer in demonstrating either a homomorphism between a Hydra game and the Golden Automaton reaching any odd number, or that the Golden Automaton is playing at worst a Hydra game are as follows:
- What are the Hydra’s heads?
- How do they grow?
- Does the Golden Automaton cut them according to the rules (at worst)?
These questions are answered in detail below. □
Definition 9.
A type A number that is
vertical even
is called an . The set of numbers is . Type B numbers that verify and type C numbers that verify under
Rule Two
are called
Bups
and
Cups, respectively.
9.1. What Are the Hydra’s Heads?
numbers are the heads of the Hydra. They are 12 points apart on (24 in nominal value, e.g., 17 to 41), and any Bup or Cup of they represent under Rule Five is smaller than them since action strictly decreases. Thus, up to the nth , there are (Bups + Cups) of rank 2 or more and half of them are equivalent to those (e.g., between 17 and 41, Bup 27 is equivalent to 41, which is equivalent to Cup 31 by Rule Four).
9.2. How Do They Grow?
Between any two consecutive in , there are
- Eight non-A numbers;
- One at most mapped to the second ;
- Three at most “ups” (Bup or Cup) of rank 2 or more.
Moreover, we always have the following:
- Let b be of type B; there are numbers of type that are smaller than ;
- Let c be of type C; there are numbers of type that are smaller than ;
- Let 3c be of type B, where c is of type C; there are numbers of type up to included; and
- Let 3a be of type B, where a is of type A; there are numbers of type smaller than ,
which define the growth of the heads. Any supposedly diverging forms a Hydra, as contains an image of all undecided Collatz numbers and any non-decreasing trajectory identifies a subtree within this set.
9.3. Does the Golden Automaton Play a Hydra Game?
It could be demonstrated that the Golden Automaton plays an even simpler game as it branches and thus cuts heads several at a time—unlike Hercules in the regular Hydra game—in particular cutting some long heads without them doubling. (The reason the Golden Automaton dominates so fast is that it plays a significantly simpler game one could call “Hecatonchire vs. Hydra”, namely a Hydra game where Hercules’ number of arms also multiplies at each step.) However, as this is needless for the final proof, we can now simply demonstrate that, even under the worst possible assumptions, it follows at least the rules of a regular Hydra game.
The computation of that we detailed in Subsection 3.1 is one case of playing the Hydra game by the Golden Automaton; we underlined each use of Rule 5 specifically so that the reader can now report it more easily because, each time this rule is used, a head (that is, an ) has just been cut.
The demonstration that 27 and 31 converge corresponds to the cutting of heads 41 and 161, respectively. This single branch of the automaton having first cut head 17 reaches head 1025 via B-typed numbers 15 and 81. It therefore plays a Hydra game with heads, of which one (17) is already cut at this point and of which at least 8 are rooted (so cutting them does not multiply any number of heads). This process being independent of the targeted number, we now have that the reach of any number by the Golden Automaton is at least equivalent to playing a Hydra game with n heads of which are rooted. Even without demonstrating more precise limit theorems for factors n and m (which could still be a fascinating endeavor), the road is now open for a final resolution of the Collatz conjecture.
From there, indeed, we know from Goodstein [29] and from Kirby and Paris [27] that assuming is well-ordered (that is, assuming the axiom of choice), no Hydra game can be lost. Since we have that reaching any number n is a Hydra game for the Golden Automaton, we have that the Golden Automaton cannot fail to finitely reach any natural number.
10. The Golden Automaton as a Winning Cellular Game Represented as a 3D L-System, with Some Important Applications in Industrial Cryptography
Beyond graph theory, we want to outline here a different strategy towards a resolution of the Collatz conjecture (this time in Peano arithmetics and thus independently of the axiom of choice) by studying the Golden Automaton as a cellular game invading the phase space defined by the complete binary tree over odd numbers. For this section, we need a 3D representation of the dynamic we studied in Section 7, designed to specifically display potential collisions between the basins of attraction of number 1 and any supposedly diverging other number. We employ the same game, that is, a zero-player game that is significantly simpler than John Conway’s Game of Life and played on the complete binary tree , except that we now allow it to start from any point rather than 1 and study its development within the basin of 1. The purpose of this approach is both to identify possibly provable patterns in the way any subbasin would be embedded in the 1-basin and to simply observe whether the five rules, for any point, finitely spawn a population of points between any starting number x and that is bigger than , which would imply that finite collisions between any two basins are inevitable. Moreover, in terms of industrial cryptographic applications, this approach provides the first 3D visualization of the Bocart [19] proof-of-work using the pseudorandomness of the inflation propensity of Collatz orbits as the asymmetric number-theoretical problem to be used to authenticate blockchain transactions yet that is independent of prime numbers. This 3D visualization, although it does provide novel theoretical insight on the Collatz conjecture, is practically important because it now makes the Bocart proof-of-work scannable, similar to a QR code.
Figure 22, Figure 23, Figure 24 and Figure 25 provide a 3D-Visualisation of the Golden Automaton. Figure 22 shows an orthogonal view of the Golden Automaton starting from 1 (in blue) merged with another starting from 1457 (in green), which is the first in the trajectory of 127. We input the rather than 127 itself to specifically study the impact of divergence on the form of the basin.
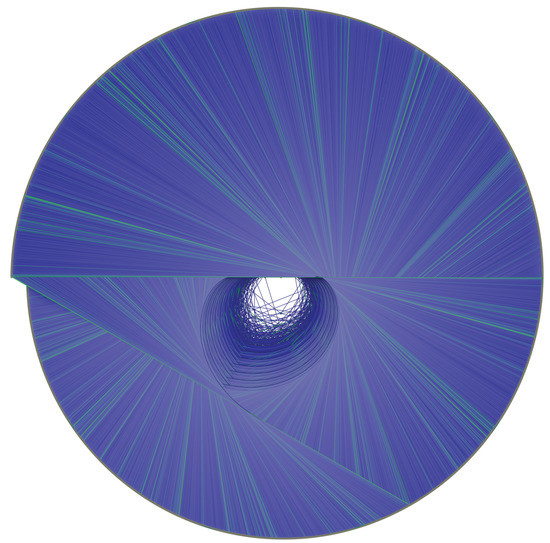
Figure 22.
Orthogonal view of the Golden Automaton starting from 1 (in blue) obtained from the code in [42]. All its intersections with the automaton starting independently from 1457 (the first in the forward Collatz trajectory of 127) are shown in green. As expected from our 2D works in Section 7, the Golden automaton starting from 1 covers all numbers. This figure also provides the first trigonometric representation of the inflation propensity of Collatz orbits, which Bocart [19] has proven constitutes a reliable proof-of-work for blockchain applications: the number of green lines (overlapping the inverse orbit of 1457 and that of 1) is directly tied to the inflation propensity of a given orbit; simply put, the more an orbit inflates, the more green lines are shown on this disc, but their distribution cannot be faked and thus forms a functional authentication fingerprint. As green lines also represent particular trajectories, this figure also suggests that other promising proofs-of-work, comparable with that of Bocart, could be obtained from the study of non-ergodic billiards.
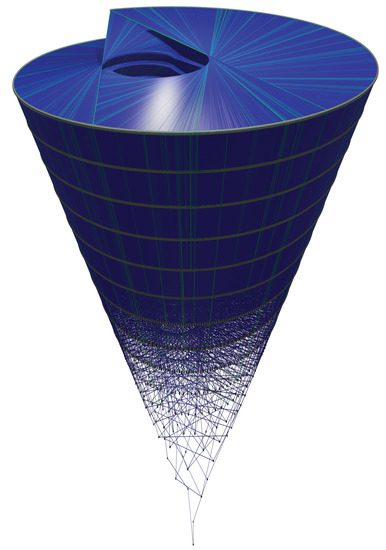
Figure 23.
Isometric projection of Figure 22 (code available at [42]). The green lines visible on the sides represent a binary transformation (e.g., operations S, V, or G) and those visible on the top of the cone represent ternary operations (e.g., ), thus decomposing the correlates (one in base 2 and one in base 3) of the inflation propensity of the number’s orbit in two dimensions. From this figure, it could be possible to implement faster proof-of-work verification of the Bocart protocol by just scanning the side lines, though this would admit a certain margin of error.
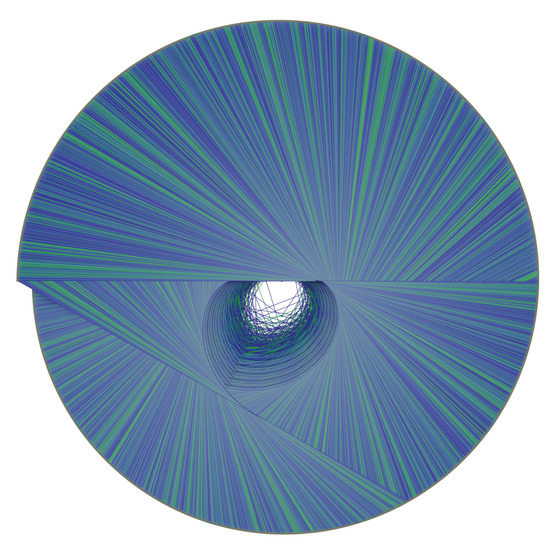
Figure 24.
Orthogonal view of the Golden Automaton starting from 1 (blue), which overlaps the one starting from 161 (green). We first observe that the basin of 161 (the first of 31) now occupies a much larger proportion of the basin of 1 than did the basin of 1457 (the first of 127). Simply put, the more a number diverges, the longer the trail of type A numbers it leaves and the more its basin of attraction inflates, ultimately making a collision with the basin starting from 1 inevitable. (Another important property of Mersenne 31 is that, as defined by OEIS [43], it is “self-contained”, meaning its orbits contains multiples of itself (i.e., the number 155).) This representation of base 3 correlates with the inflation propensity of Collatz orbits is in fact directly scannable, similar to a QR code, with the central truncated caustic forming the standard reference point of the scan and the pseudorandom distribution of the green lines using a direct verification protocol of the Bocart proof-of-work.
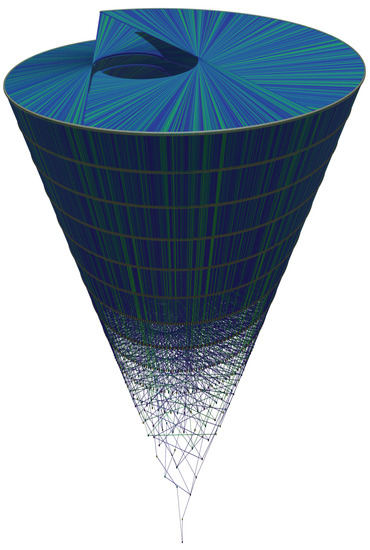
Figure 25.
The Golden Automaton starting from 161 with all its collision edges, with the one starting from 1 shown in green. Although they are related, both the side and top distributions of the green edges can be used for cryptographic applications. The angle of the display remains important for scannable applications, as only the central convexoid of the figure may be used as a standard reference for the scan and must therefore be visible or otherwise indicated even if only the side lines are scanned.
Let us now compare the inflation propensity of 31, for which Collatz orbit is much more complex than 127, and observe that, as predicted by the five rules, the figure it outputs now shows a much more voluminous basin of attraction. The reason this result was expected is that, under the five rles, the assumed divergence of a number implies that it leaves a trail of type A numbers (on each of which Rule 5 can be applied) that is strictly proportional to the inflation propensity of its orbit since for any number x of rank 2 or more, action outputs a type A number. The following Figure 24 provides an orthogonal view of the Golden Automaton starting from 1 (blue) merged with one starting from 161 (green), which is the first of number 31. As 31 is both lower than 127 in the binary tree and displays a higher orbit inflation propensity, its overlap ends up much larger than that of 127, as its basin of attraction inflates along with its orbit.
The convexoid that is the structure of the center of the basin of attraction of any number appears to be the truncated caustic generated by multiplication by 3 on the binary tree projected on the unit circle. In Figure 26, we thus implement the fundamental operations of the ternary tree, , thus visualizing the way it develops itself on top of the binary tree. Operation is shown in yellow, is in purple, and is in teal. Number 1 is at exactly , number 3 is at , number 7 is at , and number 5 is at .

Figure 26.
The ternary tree over the binary tree embedded on the unit circle. The shape of this figure is essential in generating the pseudorandomness of the inflation propensity of Collatz orbits and, thus, of the Bocart proof-of-work. More generally, it forms the base of the pseudorandomness of conversions between bases 2 and 3, which led Furstenberg to later state his eponymous conjecture.
Moreover a truncated caustic generated by the map on the binary tree is visualized in Figure 27.

Figure 27.
The truncated caustic generated by the map on the binary tree, this time with gradient-colored lines from the domain (red) to codomain (yellow), underlining the non-ergodicity of the map on the binary tree and why other number-theoretical proof-of-work comparable with that of Bocart, in particular, independent of large prime numbers, may be obtained from the study of non-ergodic number billiards. The code repository for this figure is also available at [42].
The shape of the truncated caustic that is the envelope of the family of curves generated by the map over the binary tree embedded on the unit circle gives particular insight into how the chaoticity of conversions between bases 2 and 3 and the chaoticity of the Collatz map are tightly interrelated. Although it was not our initial objective, we may comment that a further understanding of the non-ergodicity generated by the action on the binary tree, in particular its concentrating Collatz orbits to certain subtrees, may threaten the long-term solidity of the first Bocart proof-of-work, although all the while opening the way to other protocols inspired from it. The following graphs provide some measurements of the non-ergodicity generated by the truncated caustic (Figure 28).
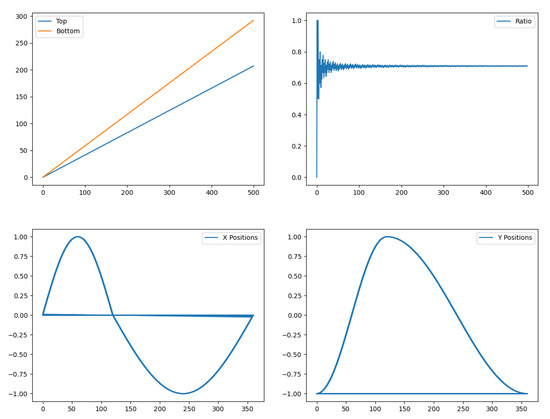
Figure 28.
Clockwise, from the upper left: number of points on each side of the unit circle (side 7 is “top”, and side 5 is “bottom") after iterations of the multiplication by 3 on number 1. The top/bottom ratio, on the next figure, converges to approximately 0.7. The next two figures display the cosine and sine of the multiplication by 3 of each point of the unit circle: on one third of the domain, this operation multiplies the angle of the starting point by 1.5, and on the other two thirds, the operation multiplies the angle by 0.75, thus explaining the asymmetry of the truncated caustic, in turn explaining the non-ergodicity of the map on the binary tree embedded in the unit circle.
To provide more information about how many numbers the five rules solve, Figure 29 finally analyzes the offspring they generate from any number, which we believe is the most promising strategy to finalize a Peano-arithmetical proof of the Collatz conjecture. Plotted are the number of points in the basin of attraction of two Mersenne numbers (31 and 511) with or without counting the points generated by their divergence to their first against how high the basin is calculated. Function is always plotted as a reference. The purpose is to show that the more the Five Rules are iterated, the more the amount of dots within the basin of attraction increases above . The top-left figure indicates the number of dots in the basin of 31, and the top-right one indicates those in 161, that is, taking into account the divergence from 31 to 161. The bottom plots represent the basins of attraction of 511 and 13,121, which is the first in the trajectory of 511, again, to take its divergence into account. The basin of 13,121 does not depart from as fast as that of 511 but starts from a larger number of dots, generated by the 511–13,121 divergence.
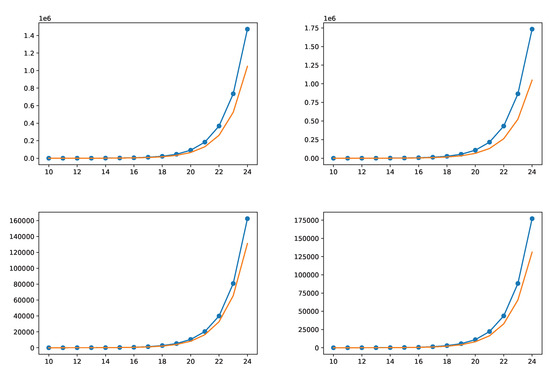
Figure 29.
The amount N of numbers proven by applying the five rules from points x to is plotted here against n. Function is shown in orange as a reference. Clockwise from the upper left, the starting points are 31, 161, 13121, and 511. [42].
The apparent growth rate of all of the Mersenne numbers from 31 to 8191 is calculated as the solution for x to , where N is the number of dots in the basin of the number that is found between itself and its first (for example, 161 is the first of 31) and n is the number of multiplications by 2 from the initial number that are needed to reach the row of this first in the binary tree (for example, n = 3 to go from 31 to 161). All of the growth rates are larger than 2 (orange line) (Figure 30), explaining why the basins of attraction of each of these numbers cannot fail to collide with that of 1.
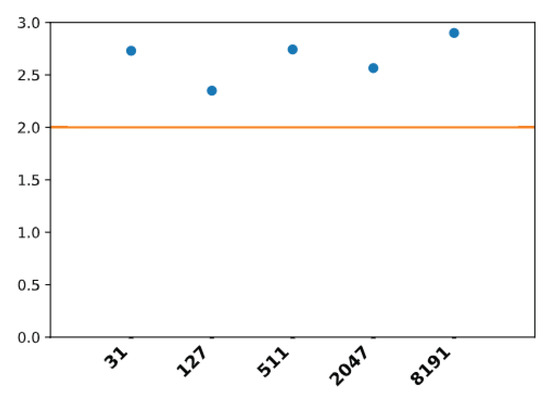
Figure 30.
The observed growth rates of the basin of attraction of different Mersenne numbers, with 2 in orange for reference.
We already demonstrated in Section 4 that any can be written , and it is precisely the catching of numbers with a large factor n by the Golden Automaton that increases the quantity of dots in its offspring per given finite series of rows of the binary tree. Specifically, those numbers, which are by definition as the ones that can be iterated upon the most by the Golden Automaton are not evenly distributed on the unit circle, and we postulate that this is the most fundamental reason behind the apparent branching factor of the Golden Automaton being strictly greater than 2 in any point we calculated. In turn, if the branching factor of the Golden automaton tends to always be greater than two, it is impossible for two separate basins of attraction to cohabitate on the binary tree.
11. Conclusions
Whenever the Collatz conjecture is studied, one cannot fail to quote Paul Erdős’ famous claim that “mathematics may not be ready for such problems"; depending on one’s epistemological attitude, the quote may either seem discouraging or an incentive to achieve a novel theoretical breakthrough. This is what we attempted in this article, primarily by establishing an ad hoc equivalent of modular arithmetic for Collatz sequences to automatically demonstrate the convergence of infinite quivers of numbers based on five arithmetic rules we proved by application in the entire dynamical system and which we further simulated to gain insight into their graph geometry and computational properties. This endeavor has led us to focus on the origins of the non-ergodicity of the Collatz dynamical system, which we found in the geometric properties of multiplication by 3 on the complete binary tree over odd numbers. These symmetry-breaking properties, indeed, could be further studied in other contexts such as cryptography, harmonic analysis, or the study of L-functions. In particular, following Bocart, 2018 [19], one can now gain a better insight into the geometric properties of the pseudorandomness generated by Collatz series and, even more, by the Collatz basins.
Furthermore, as Bocart had understood well, studying the Collatz map can lead to promising industrial applications in applied computer sciences, in particular cryptography and financial technologies (fintech). It is possible that the Golden Automaton we described in this article is used to successfully weaken the Bocart proof-of-work developed from the study of the inflation propensity of Collatz orbits; however, the endeavor of developing number theoretical Bocart proof-of-work independent of prime numbers must retain all its industrial interest. As Bocart also understood, it could be possible to extend his work to the 5x+1 map, but following this work, we believe that a stronger Bocart proof-of-work that could not be weakened by the Golden Automaton would be the one based on the inflation propensity of the Juggler sequence, which is well-known for its Collatz-like chaoticity and defined as follows:
For any
As the inflation propensity of the Collatz orbits ultimately depends on the nature of conversions between base 2 and base 3, which Shmerkin [44] has described as being the fundamental enquiry behind the Furstenberg conjecture, we predict that advances in this matter would be the likeliest to weaken the Bocart proof-of-work in the future. (Would it be so, though we already mentioned the Juggler sequence as a promising second version of the Bocart proof-of-work, we believe that the study of non-ergodic number billiards could also be most fertile in novel cryptographic protocols) To this end, we believe that the truncated caustic we describe in Figure 26 would be most relevant. In the larger field of using Physical Uncloneable Functions (or “PUF”) to ensure anonymity in electronic cash transactions, as was studied for example by Fragkos et al. [45] with their promising paradigm of an “artificially intelligent money”, we believe not only our Golden Automaton but other Number Theoretic models such as primon gas [46] could provide a useful direction to develop practical encryption protocols beyond the ubiquitous RSA.
Author Contributions
I.J.A. created the framework of studying the Collatz dynamical system in the coordinates defined by the intersection of the binary and ternary trees over , identified and demonstrated the five rules, and predicted that they would at worst be isomorphic to a Hydra game over the set of undecided Collatz numbers, which he defined as well. He directed the 3D visualization of the Golden Automaton and its 2D projection on the unit circle, and the search for its comparative growth rate. Contributing equally, A.R. and E.S. designed and coded an optimized, highly scalable 2D graphical implementation of the five rules and ran all of the simulations, confirming the Hydra game isomorphism and computing the first ever dot plot of the Golden Automaton over odd numbers, which they optimized as well. They were also the first team to ever simulate the five rules to the level achieved in this article and to confirm their emerging geometric properties on such a scale, including the linearity of their logarithmic scaling and the limit reproductive rates of single dots of the golden automaton. A.R. also designed, coded, and optimized the 3D generated feather (Figure 3). M.H. was in charge of generating the other 3D figures, and related simulations and under I.J.A.’s direction, he was the first to outline the truncated caustic at the center of the Golden Automaton’s basin of attraction. This research being interdisciplinary in nature, S.G. was tasked with giving an overview of all topics described and provided editorial guidance for the organization of the Results section. In the later stages of this article’s research, B. Rosalski provided a lightweight, optimized version of the Golden Automaton coded in the C++ language which, along with a critical estimate of its complexity, allowed us to better reproduce, scale, and confirm our results. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a personal grant to I. Aberkane from Mohammed VI University, Morocco, and by a collaboration between Capgemini, Potsdam University, The Nuremberg Institute of Technology, and Strasbourg University. Even though the last author began the initial works leading to this article at Stanford University, 42 School of Code Fremont, and the Complex Systems Digital Campus Unesco-Unitwin, the funding that financed the discovery of his most important theorems is fully attributable to Mohammed VI University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
I.J.A. thanks the late Solomon Feferman and Alan T. Waterman, Jr., along with Paul Bourgine, Yves Burnod, Pierre Collet, Françoise Cerquetti, and Oleksandra Desiateryk. Special thanks go to Baptiste Rostalski, whose excellent work allowed us to publish Figure 14, one of the most important if not the most important graphical confirmation of our work. We dedicate this work to the memories of John Horton Conway (1937–2020), Solomon Feferman (1928–2016), and Alan T. Waterman, Jr. (1918–2008).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Algorithm of the Golden Automaton II (Implemented in C++ by Baptiste Rostalski)

References
- Sloane, N.J.A. A006370: The Collatz or 3x+1 Map: a(n) = n/2 if n is even, 3n + 1 if n is Odd. Available online: https://oeis.org/A006370 (accessed on 6 April 2021).
- Conway, J. Unpredictable Iterations. In The Ultimate Challenge: The 3x+1 Problem; AMS: Providence, RI, USA, 1972; pp. 49–52. [Google Scholar]
- Lagarias, J. The 3x + 1 Problem and Its Generalizations. Amer. Math. Monthly 1985, 92, 3–23. [Google Scholar] [CrossRef]
- Kurtz, S.A.; Simon, J. The Undecidability of the Generalized Collatz Problem. In Theory and Applications of Models of Computation: Proceedings of the 4th International Conference (TAMC 2007), Shanghai, China, 22–25 May 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 542–553. [Google Scholar]
- Leavens, G.T.; Vermeulen, M. 3x + 1 Search Programs. Comput. Math. Appl. 1992, 24, 79–99. [Google Scholar] [CrossRef]
- Vardi, I. The 3x + 1 Problem. In Computational Recreations in Mathematica; Addison-Wesley: Redwood City, CA, USA, 1991; pp. 129–137. [Google Scholar]
- Oliveira e Silva, T. Computational Verification of the 3x + 1 Conjecture. 2008. Available online: https://www.ieeta.pt/~tos/3x+1.html (accessed on 6 April 2021).
- Terras, R. A Stopping Time Problem on the Positive Integers. Acta Arith. 1976, 30, 241–252. [Google Scholar] [CrossRef]
- Terras, R. On the Existence of a Density. Acta Arith. 1979, 35, 101–102. [Google Scholar] [CrossRef][Green Version]
- Cloney, T.; Goles, E.; Vichniac, G.Y. The 3x + 1 Problem: A Quasi Cellular Automaton. Complex Sys. 1987, 1, 349–360. [Google Scholar]
- Weisstein, E.W. Collatz Problem. In From MathWorld—A Wolfram Web Resource; Available online: https://mathworld.wolfram.com/CollatzProblem.html (accessed on 6 April 2021).
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002; pp. 100, 122, 904. [Google Scholar]
- Bruschi, M. Two Cellular Automata for the 3x + 1 Map. arXiv 2005, arXiv:0502061. [Google Scholar]
- Zeleny, E. Collatz Problem as a Cellular Automaton. Available online: https://demonstrations.wolfram.com/CollatzProblemAsACellularAutomaton/ (accessed on 6 April 2021).
- Machado, J.A.T.; Galhano, A.; Cao Labora, D. A Clustering Perspective of the Collatz Conjecture. Mathematics 2021, 9, 314. [Google Scholar] [CrossRef]
- Tao, T. Almost all orbits of the Collatz map attain almost bounded values. arXiv 2019, arXiv:1909.03562. [Google Scholar]
- Derksen, H.; Weyman, J. Quiver representations. Not. AMS 2005, 52, 200–206. [Google Scholar]
- Caldwell, O. The Collatz conjecture, visualised in Clojure. arXiv 2017, arXiv:1711.09197. [Google Scholar]
- Bocart, F. Inflation propensity of Collatz orbits: A new proof-of-work for blockchain applications. J. Risk Financ. Manag. 2018, 11, 83. [Google Scholar] [CrossRef]
- Aberkane, I. On the Syracuse Conjecture over the Binary Tree. Available online: https://hal.archives-ouvertes.fr/hal-01574521 (accessed on 6 April 2021).
- Aberkane, I. Endomorphisms of the Collatz Quiver. Available online: https://hal.archives-ouvertes.fr/hal-03026742 (accessed on 6 April 2021).
- Aberkane, I. Syracuse Is Solved. Available online: https://hal.archives-ouvertes.fr/hal-03001845 (accessed on 6 April 2021).
- Koch, C.; Sultanow, E.; Cox, S. Divisions by Two in Collatz Sequences: A Data Science Approach. Int. J. Pure Math. Sci. 2020, 21. [Google Scholar] [CrossRef]
- Sultanow, E.; Koch, C.; Cox, S. Collatz Sequences in the Light of Graph Theory. Tech. Rep. Potsdam. Univ. 2020. [Google Scholar] [CrossRef]
- Feferman, S. Is the continuum hypothesis a definite mathematical problem. In Draft of Paper for the Lecture to the Philosophy Deptment; Harvard University: Cambridge, MA, USA, 2012. [Google Scholar]
- Knuth, D.E. Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness, 12nd ed.; Addison-Wesley: Boston, MA, USA, 1974. [Google Scholar]
- Kirby, L.; Paris, J. Accessible independence results for Peano arithmetic. Bull. Lond. Math. Soc. 1982, 14, 285–293. [Google Scholar] [CrossRef]
- Artigue, M.; Arzarello, F.; Epp, S. Goodstein Sequences: The Power of a Detour via Infinity. Available online: http://blog.kleinproject.org/?p=674 (accessed on 6 April 2021).
- Goodstein, R. On the restricted ordinal theorem. J. Symb. Log. 1944, 9, 33–41. [Google Scholar] [CrossRef]
- Gentzen, G. Die Widerspruchsfreiheit der reinen Zahlentheorie. Math. Ann. 1936, 112, 493–565. [Google Scholar] [CrossRef]
- Godel, K. Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, I. Monatshefte Math. Phys. 1931, 38, 173–198. [Google Scholar] [CrossRef]
- Cichon, E.A. A Short Proof of Two Recently Discovered Independence Results Using Recursion Theoretic Methods. Proc. Amer. Math. Soc. 1983, 87, 704–706. [Google Scholar] [CrossRef]
- Hodgson, B. Herculean or Sisyphean tasks. EMS Newsl. 2004, 51, 11–16. [Google Scholar]
- Caicedo, A. Goodstein’s function. Rev. Colomb. MatemáTicas 2007, 41, 381–391. [Google Scholar]
- Kaplan, D. A Classification of Non-Standard Models Of Peano Arithmetic by Goodstein’s Theorem. Ph.D. Thesis, Franklin and Marshall College, Lancaster, PA, USA, 2012. [Google Scholar]
- Miller, J. On the Independence of Goodstein’s Theorem; University of Arizona: Tucson, AZ, USA, 2001. [Google Scholar]
- Stępień, T.J.; Stępień, L. On the Consistency of the Arithmetic System. J. Math. Syst. Sci. 2017, 7. [Google Scholar] [CrossRef]
- Barina, D. Convergence verification of the Collatz problem. J. Supercomput. 2021, 77, 2681–2688. [Google Scholar] [CrossRef]
- Kleinnijenhuis, J.; Kleinnijenhuis, A.M.; Aydogan, M.G. The Collatz tree as a Hilbert hotel: A proof of the 3x + 1 conjecture. arXiv 2020, arXiv:2008.13643v3. [Google Scholar]
- Koch, C. Collatz Python Library. 2021. Available online: https://github.com/c4ristian/collatz (accessed on 6 April 2021).
- Clark, L.; Torzewska, F.; Maybee, B.; Beige, A. Non-Ergodicity in open quantum systems through quantum feedback. Europhys. Lett. 2020, 130, 54002. [Google Scholar] [CrossRef]
- Sultanow, E. Sources for the exploration of Collatz Sequences: TeX, Mathematica and Python. 2020. Available online: https://github.com/Sultanow/collatz (accessed on 6 April 2021).
- Sloane, N.J.A. A005184: Self-Contained Numbers: Odd Numbers n Whose Collatz Sequence Contains a Higher Multiple of n. Available online: https://oeis.org/A005184 (accessed on 6 April 2021).
- Hochman, M.; Shmerkin, P. Local entropy averages and projections of fractal measures. Ann. Math. 2012, 175, 1001–1059. [Google Scholar] [CrossRef]
- Fragkos, G.; Minwalla, C.P.J.; Tsiropoulou, E.E. Artificially Intelligent Electronic Money. IEEE Consum. Electron. Mag. 2021, 10, 81–89. [Google Scholar] [CrossRef]
- Marcolli, M. Geometry and Physics of Numbers. Available online: http://www.its.caltech.edu/~matilde/GeomPhysPrimes.pdf (accessed on 6 April 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
