Abstract
Research on mathematics teachers’ knowledge has generally focused more on mathematics concepts than mathematical processes. This paper addresses the latter with a focus on mathematical problem solving (PS). It reports on a study that investigated the pedagogical knowledge for PS of prospective elementary school teachers of mathematics (PTs). Participants were 149 PTs at a university in Spain. They were at the end of their teacher education program. Data sources consisted of a questionnaire on knowledge of learning PS and a questionnaire on knowledge of teaching PS. Findings indicated that the PTs held combination of different levels of knowledge of PS learning and teaching. Many of them demonstrated appropriate knowledge of many characteristics for (1) PS learning consisting of student as a problem-solver, PS as a worthwhile task, non-cognitive factor related to PS, and (2) PS teaching consisting of PS teaching approaches, discourse in PS, intervention during stuck state in PS, PS assessment, and PS resources. However, there were also contradictions and limitations to their knowledge with implications for teacher education. These combination of appropriate and inappropriate knowledge resulted in some conflicts that are related to teaching actions and would limit student’ learning of PS.
1. Introduction
While research on mathematics teacher knowledge has received significant attention in the last two decades, the focus has been more on mathematics concepts than mathematical processes. In particular, when considering mathematics knowledge for teaching, e.g., [1], content knowledge and pedagogical content knowledge tends to be interpreted as knowledge of mathematics concepts and pedagogical knowledge of mathematics concepts, respectively. As Lin and Rowland [2] pointed out regarding studies on mathematics teacher knowledge reported in the Psychology of Mathematics Education conference proceedings,
[...] some draw attention to gaps or conflicts in the mainstream teacher knowledge discourse. Both Chapman (2012) and Foster, Wake and Swan (2014) take up a critique that Shulman’s [1986] framework and its derivatives focus on knowledge of mathematical concepts at the expense of problem solving proficiency.(p. 489) [2]
Chapman [3] suggested that mathematical problem solving (PS), which is central to learning and doing mathematics, should be treated as an integral part of mathematics knowledge for teaching. However, it should also be considered in its own right given that mathematical processes have a different conceptualization to mathematics concepts [4,5]. Thus, the knowledge specifically related to PS continues to be highlighted as an area in need of attention in research [6]. Chapman [3] suggested a framework of PS knowledge for teaching that can serve as a basis to further research this knowledge from the perspective of teachers. This paper reports on a study that was influenced by this framework and the importance to attend to prospective teachers’ knowledge of PS to further understand how to support its development. Specifically, the study investigated the following research question: what pedagogical PS knowledge do prospective elementary school teachers’ have at the end of their education program? The focus was on their knowledge of: (1) PS learning, consisting of characteristics of student as a problem-solver, PS as a worthwhile task, non-cognitive factor related to PS, and (2) PS teaching, consisting of characteristics of PS teaching approaches, discourse in PS, intervention during stuck state in PS, PS assessment, and PS resources.
2. Theoretical Framework of Pedagogical PS Knowledge
PS can mean different things from different perspectives. For example, some teachers may consider solving traditional, algorithmic word problems as PS. In this study, we considered PS to be an action taken by an individual or a group, who identifies a task with no direct procedure to solve it, proceeds to solve it by deploying a strategy involving a series of not necessarily linear steps and confronts the challenge with a favorable disposition [7,8]. These ideas would take the form of tasks such as: If the perimeter of a rectangle is 24 cm, what might be the area? However, it is the problem solver who finally labels problems as such [9]. Pedagogical PS knowledge was interpreted in a theoretical framework consistent with this view of PS. This framework is an adapted version of the framework proposed in Chapman [3] for mathematics PS knowledge for teaching. Chapman’s framework includes: teacher PS proficiency; knowledge of problem content, solving and posing; pedagogical knowledge of students as problem solvers and of teaching practice; and affective factors and beliefs that impact teaching and learning PS. These categories of knowledge are related to both content knowledge (i.e., PS as the content) and pedagogical content knowledge (i.e., pedagogical PS knowledge). Chapman argued that teaching for PS proficiency draws on a complex network of interdependent knowledge and teachers’ proficiency to teach PS involves these categories of knowledge and knowing what to do with them. However, in this paper, we focus only on the adapted categories for pedagogical PS knowledge, which consists of: (a) non-cognitive factors; (b) students as problem solvers; (c) school PS in terms of worthwhile tasks; and (d) PS teaching. We adopted a structure based on Schoenfeld’s [10] teaching triangle to represent the relationships among these categories of knowledge. This resulted in our theoretical framework for pedagogical PS knowledge being a pedagogical PS triangle depicted in Figure 1.
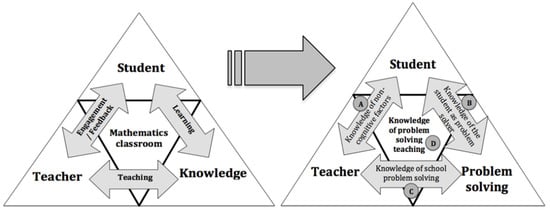
Figure 1.
Pedagogical triangle and pedagogical PS knowledge triangle.
The pedagogical PS triangle illustrates the three categories of knowledge (A, B, and C, Figure 1) teachers should hold to support the two-direction relationships between student and PS, teacher and PS, and teacher and student, respectively. The relationship between student as problem solver and teacher as facilitator involves, for example, discourse between teacher and student to support students as they engage in PS. The relationship between student as problem solver and PS as process involves, for example, students determining the PS process and the PS process offering opportunities for students as an open process or way of thinking. The relationship between teacher as facilitator and PS as process involves, for example, teacher specifying the PS process based on task selected/designed and PS process offering opportunities to teacher as an open-ended process or way of thinking. These relationships determine the category of knowledge for teaching PS (fourth category, D in Figure 1), which forms the core of the pedagogical PS knowledge. The teacher needs to hold appropriate knowledge of these four categories of knowledge for these relationships to be effectively implemented in their teaching. We next elaborate on how we consider each of these four categories of knowledge in Figure 1.
2.1. Knowledge of Student as Problem Solver
Teachers should hold knowledge of students as problem solvers to be able to effectively facilitate the relationship between the students and PS. This should include knowledge of students’ PS difficulties, characteristics for successful problem solvers, and PS thinking related to possible PS phases and strategies that students are expected to develop [3,11,12,13,14]. From a pedagogical perspective, teachers should also hold knowledge to help students (1) “build new mathematical knowledge through PS, (2) solve problems that arise in mathematics and in other contexts, (3) apply and adapt a variety of appropriate strategies to solve problems, and (4) monitor and reflect on the process of mathematical problem solving” [5] (p. 116). They should have knowledge of strategic intervention during students’ PS which includes knowledge to support “productive struggle” [15]. For example, according to NCTM [15], they must decide how to engage students in reasoning about the problem without reducing the productive struggle, recognizing that students are inclined to bypass the reasoning process to avoid the struggle. They should know strategies to support student exploration of a problem without depriving them of engaging in the PS process. These strategies should enable and support students to not only engage in reasoning about the problem but, over time, but also develop as problem solvers. They should design classroom instruction to engage all students in PS through scaffolding so that students can engage in mathematical reasoning. However, while these are all important aspects of a teacher’s knowledge associated with the student as problem solver, in this study, since the participants, as PTs, have limited classroom teaching experience with PS, the focus is only on their knowledge of characteristics of successful and novice problem solvers.
2.2. Knowledge of PS as Worthwhile Task
Engaging in PS is a worthwhile task and engaging in a worthwhile task is PS [3]. We consider it important for teachers to hold knowledge of both ways of engaging students in PS. This knowledge includes teachers knowing what are worthwhile tasks to enable them to select appropriate tasks for PS and knowing PS strategies, PS models, and problem posing to enable them to engage students in genuine PS. NCTM [14] highlighted the importance for teachers to implement problems that promote reasoning and PS. Lester and Cai [16] pointed out that the selection of a good problem is critical, as, among other issues, it has been shown that teachers tend to avoid the use of really problematic tasks that challenge students. Teachers should also hold knowledge of PS models such as those proposed by Pólya [17], Schoenfeld [14], Posamentier and Krulik [13], or Mason et al. [12] and knowledge of problem posing [18,19]. These components of pedagogical PS knowledge would also allow teachers to rethink tasks when students get stuck or provide extensions or new situations to the most advantaged students. In this study, we focused on investigating PTs’ knowledge of these components consisting of problem selection, PS strategies, PS models, and problem posing.
2.3. Knowledge of Non-Cognitive Factors Affecting PS
Past and recent studies have indicated that factors such as attitude, motivation, and beliefs are important to PS performance [3,8,20,21]. For example, Rott’s [22] comparisons of the teachers’ behavior and their beliefs revealed the importance of beliefs in the context of teaching for PS. This suggests that teachers should hold knowledge of non-cognitive factors affecting PS. Although the scope of the non-cognitive factors is broad, in this study, we focused on a meta-knowledge about the conceptions and beliefs and the mutual implications that these have in PS learning and teaching. Specifically, we considered PTs’ expectations related to non-cognitive factors involving dispositions or beliefs, e.g., [8] that are associated with successful PS performance. This includes knowledge to encourage situations that favor beliefs related to the time necessary to solve a problem and the multiple resolution options or the possibility of several responses and knowledge to make present the emotions of anxiety and frustration as natural elements of the process of solving a problem.
2.4. Knowledge of PS Instructional Practice
It is obvious that teachers should hold knowledge of instructional practice. In this study we focused on teachers’ knowledge of instructional practice in terms of: teaching approaches, discourse, stuck state, assessment and resources. Teaching approaches involves the teacher’s actions related to teaching for, about, or through PS [23]. For example, Chapman [24] has identified four approaches used by teachers to teach PS: translation-based, strategy-based, heuristic-based, and inquiry-based. Discourse, according to Lester [7], is the most successful classroom approaches for developing good problem solvers. It involves the teacher’s actions that encourage students to participate, cooperate and genuinely engage in PS. Lester and Cai [16] described it as the manner in which “teachers orchestrate pedagogically sound, active PS in the classroom” (p. 124). It includes actions such as furthering the use of multiple representations or promoting multiple solutions to a problem. Stuck state involves a situation in which the problem solver encounters an obstacle that needs to be overcome to arrive at a solution of the problem. The teacher needs to hold knowledge of specific instructional strategies of how to intervene to help students to overcome or deal with being stuck [3]. Such strategies could consist of, for example, the task and their sequence, the enabling prompts, the extending prompts, the explicit pedagogies, and how to build a learning community [25]. Assessment involves tools or methods to determine students’ progress in PS and the quality of their solution. The teacher needs knowledge of such methods to assess students’ PS performance and set goals for further learning. These methods include, for example, analytic scoring scales (Charles et al. [26]) and performance rubrics [27]. Finally, resources relates to the manipulative and intangible resources used in PS with elementary school students. The teacher needs knowledge of how to use both manipulatives in PS [28] and pictorial and abstract representations in PS [29]. Pictorial representation merits particular attention, for all students need to master a variety of notations in the various stages of PS.
To summarize, the four components of our theoretical framework (Figure 1), that is, knowledge of students as problem solvers, PS as worthwhile tasks, non-cognitive factors affecting PS, and PS instruction provided the basis for data collection and analysis, which is described later in the research methods section. The focus is to gain insights of the extent to which the PTs held appropriate knowledge for each of these four components of pedagogical PS knowledge at the end of their education program.
3. Related Literature
While studies on PTs have not investigated their knowledge of PS pedagogy with the depth undertaken in this study, they do offer insights about specific aspects of this knowledge and challenges PTs could experience in teaching PS. This is highlighted in the following summaries of studies that collectively address a variety of aspects of PTs’ knowledge of PS pedagogy.
Son and Lee’s [30] study included an investigation of how PTs conceptualized mathematical PS. Participants were 96 PTs taking a required elementary mathematics methods course. Findings indicated five conceptions of PS among the PTs: PS as (i) a means to achieve other ends (e.g., a way to exercise the brain) for 6% of PTs, (ii) a means to finding an answer or solution (i.e., a non-complex, goal-driven activity) for 45%, (iii) a skill requiring properly following steps for 25%, (iv) employing multiple approaches/strategies (similar to focus on steps but with consideration of alternatives) for 17%, and (v) art, which acknowledged not only the complexity of problems and use of multiple strategies but also the importance of metacognition for 7%. The authors concluded that a large portion of the PTs defined PS as a skill-based or means-to-an end/solution view by focusing on solutions or procedural steps and they were likely to focus on required steps toward reaching right answers.
One study that addressed PTs’ knowledge of PS strategies and its relationship to their future teaching is by Capraro, An, Ma, Rangel-Chavez, and Harbaugh [31]. They investigated the types of strategies PTs valued most in solving an open-ended puzzle problem and how they would explain their solution to students. Participants were eight PTs in a required PS course in their education program. Findings indicated that their primary strategy in solving the problem was guess and check but there were misapplications of it as a systematic PS strategy, that is, they treated it as a random process. None of them could give an explanation of the problem at the level of thinking necessary to find all four solutions. They explained that they stopped or gave up after only one solution because of frustration, time limitation, satisfaction with one solution and belief that there was only one solution. The authors concluded that many of them did not demonstrate sufficient ability in solving the problem directly to be able to explain it most effectively to their students.
Other studies have raised other issues about PTs’ knowledge or ability to engage students in PS. For example, Karp [32] suggested that PTs often lack the skill of using mathematical problems for pedagogical purposes. She examined the experiences of 25 PTs during a pre-practicum teaching methods course to identify common features in the difficulties they experienced. She found that the PTs were often unable to provide examples of problems which could be solved in different ways and could demonstrate this ‘openness’ to the students. They often lacked the ability to carry out a didactic-psychological analysis of a problem by studying both its formulation and its solution from the point of view of the student. They were challenged to help students think during PS and lacked the specific skill to guide and scaffold students in their cognitive activities. Lee’s [33] study suggested similar findings regarding PTs’ supporting students’ PS. Lee investigated how three PTs interpreted and developed in their role of facilitating students’ mathematical PS with a technology tool. Findings indicated that the PTs’ PS strategies had a direct impact on their pedagogical decisions while they were facilitating students’ PS. They recognized the need to ask non-leading questions that would guide students in their solution strategies but had difficulties posing such questions and struggled in facilitating students’ PS. In explaining a solution to students, they were influenced by their struggle to make sense of how to facilitate students’ PS.
Another study that addressed PTs’ issues regarding the use of problems in teaching PS is by González and Eli [34]. They investigated teachers’ perspectives about launching a problem. Findings indicated that the 10 PTs in the study supported the assumption that the launch is a crucial moment for motivating students to solve the problem, which provides a basis to promote student engagement, thus specifically addressing the avowed difficulty of students’ limited attention spans. This assumption refers to not only the content of the launch but also the duration of it. A majority of PTs agreed that teachers should preview the work necessary to solve the problem during the launch, for example, present a problem that is analogous to the given one, identify a fundamental idea in the problem and highlight that idea. The PTs also stated that the launch is an opportunity for teachers to clarify the key concepts of the problem and supported the assumption that teachers should not disclose procedures for solving the problem in the launch.
Finally, one study that focused on teachers’ metacognitive knowledge is by Metallidou [35]. He considered metacognitive knowledge in terms of the frequency, efficacy, and facility of applying different PS strategies in different kind of problems, which included how aware the participants were of the existence of five general PS strategies (i.e., free production (brainstorming), analogy, step-by-step analysis, visualization, and combining) and strategy-selection process for three different kinds of problems (i.e., interpersonal, practical, and study problems). Findings indicated that the 166 PTs in the study gave significantly differentiated frequency, efficacy, and facility ratings for the application of each strategy to each kind of problems, which suggested that they were metacognitively aware that different kinds of problems require the application of different strategies. The author concluded that PTs seemed to have well-developed conditional metacognitive knowledge regarding the strategy selection process in interpersonal problems but they need to be familiarized with more ‘technical’ strategies, such as combining, and with different kinds of PS situations.
These studies suggest that, for the most part, PTs hold limited or inappropriate pedagogical knowledge of PS, which include their conceptualization of PS, their understanding and use of PS strategies in their learning and teaching, and their understanding and use of discourse or appropriate intervention to support students’ PS. This study provides a more in depth and focused approach to exploring PTs’ knowledge of these and other important aspects of the pedagogical knowledge of PS that teachers should hold.
4. Research Methods
This study employed a quantitative research methodology involving the use of questionnaires to determine the participants’ pedagogical PS knowledge.
4.1. Participants
The participants of the study were 149 PTs at the end of their elementary education degree program at a university in Spain. As a requirement of their program, they completed three mathematics education courses: (1) the study of school mathematics as a discipline, (2) teaching and learning the different topics of school mathematics, concretized in cognitive and pedagogical aspects, and (3) the study of the mathematics elementary curriculum and the design and implementation of plan teaching. In these courses, PS was a transversal goal, weaved across topics, specifically, when discussing meanings and modes of use of mathematical concepts. For example, the PTs had opportunity to solve mathematical tasks that could exemplify or introduce the content of a lesson and develop skills such as semantic analysis of problems but did not study PS explicitly in these courses. However, 93 of them completed the optional course: Mathematical Competences in Elementary Education, which included an explicit focus on PS, with activities such as: (a) characterization and exemplification of the role of PS in the learning of mathematics and its link with mathematical competence, (b) development and application of strategies and heuristics for PS, (c) application of criteria for inventing problems of mathematics, and (d) analysis of appropriate teaching strategies for teaching PS in the mathematics classroom. Thus, the participants were considered as two different groups in the data analysis, with one group consisting of 56 PTs without the optional PS-oriented course (represented as GWo, i.e., group without the optional course) and the other group consisting of 93 PTs with this course (represented as GW, i.e., group with the optional course).
4.2. Data Sources
The main data sources were questionnaires, which provide a basis to collect information to describe the knowledge of a sample of people [36]. A closed questionnaire format was used since the goal was not to identify the meaning teachers held of problems, PS, and their teaching of it, in which Likert scales are usually used. Instead, the goal was to characterize their knowledge based on obtaining specific responses. This led to the use of dichotomous responses that indicate the presence or absence of certain knowledge [36].
The questionnaires were developed based on the four categories of the pedagogical PS knowledge framework (Figure 1) and included: (a) theoretical analysis of the notion of competence to solve problems; (b) study of mathematics curricular requirements of elementary education related to PS; and (c) review of research literature on PS with elementary school teachers. In order to obtain information to increase reliability, validity, and feasibility of the questionnaires, the initial versions were reviewed by experts in mathematics education and tested in a pilot study with 19 fourth-year primary school PTs enrolled in the same university program as participants of this study but in a different year. Five experts in mathematics education provided a qualitative evaluation of the degree of adequacy of the items to determine the PTs’ knowledge. For the pilot study, in addition to completing the questionnaires, the PTs indicated in writing any difficulties they encountered or perceived regarding the comprehension and wording of the items of the questionnaires. Feedback from the experts and results of the pilot study were adopted to construct the final version of the two questionnaires. Piñeiro, Chapman, Castro-Rodríguez, and Castro [37] provide further details regarding the development of and ways of validating the questionnaires.
The two questionnaires are organized in terms of the four components of the pedagogical PS knowledge framework (Figure 1). One questionnaire focuses on the three components associated with PS learning (hereafter, the PS learning questionnaire) and the other focuses on the component associated with PS teaching (hereafter, the PS teaching questionnaire). Following is a summary of what was required of participants for each category of knowledge for each questionnaire.
4.2.1. PS Learning Questionnaire
This questionnaire addressed the PTs’ knowledge of three categories of characteristics about problem solver, worthwhile tasks, and non-cognitive factors related to PS.
Student as a Problem Solver. For this category, the questionnaire consists of 15 statements (see Table 1) about characteristics the literature indicated for successful or good problem solvers and unsuccessful or novice solvers. For eight statements (1–8), participants were asked to indicate which ones correspond to a good problem solver and for the other seven statements (9–15), which correspond to a beginner or novice problem solver.
PS as Worthwhile Task. For this category, the questionnaire consists of 54 items (see Table 2) dealing with problem selection (i.e., good problem features reported in the literature) and PS strategies and possible use of strategies in teaching PS, representation of PS process (i.e., cyclic or linear model), and the benefits and characteristics of problem posing. For the seven items (16–22) dealing with problem selection, participants were asked to identify: What criteria would you use to select problems for a class as a future teacher? For the 34 items (23A–23Q2) dealing with 17 strategies and 17 corresponding uses of strategies, they responded to: What PS strategies do you know and which one would you use in a class where you teach your future students to solve problems? For the four items (24–27) dealing with PS models (include two diagrams, one of a cyclic and one of a linear PS model), they were required to indicate which items they agreed or disagreed with based on the two diagrams that represented the PS process. For example: Diagram 1 represents PS process in a real way because it shows that you can go back over what has been done or skip phases (Item 24, Table 2). For the last nine items (28–36) dealing with problem posing, participants were asked to indicate which statements are true.
Non-Cognitive Factors that Affect PS. For this category, the questionnaire consists of 11 items (see Table 3) of noncognitive factors involving some of the most common beliefs about PS and how they mutually affect teacher and student when teaching PS. Participants were required to indicate which statements could benefit the student’s ability to solve problems.
4.2.2. PS Teaching Questionnaire
This questionnaire addressed the PTs’ knowledge of five categories of characteristics about teaching approaches, discourse, stuck state, assessment, and resources related to PS.
Teaching Approaches to PS. For this category, the questionnaire consists of 12 items (see Table 4) about the goals of each of the three teaching approaches to PS (i.e., for, about, through) and some of their characteristics. For nine of the items (1–9) dealing with statements of appropriate classroom teaching strategies, participants were asked to indicate which statements reflect a class in which PS is taught. For the other three items (10–12) dealing with examples of classroom situations that are related to the teaching approaches, participants were asked: The statements below highlight ways to organize a class in which PS are taught. Do you think they are appropriate?
Discourse in PS Teaching. For this category, the questionnaire consists of 10 items (see Table 5) regarding a teacher’s possible actions to support students’ PS proficiency, that is, actions related to discussion management and ways to conduct the PS process. Participants were required to indicate: Which teacher actions are helping to develop a suitable environment for PS instruction?
Stuck State in PS. For this category, the questionnaire consists of eight items (see Table 6) about a teacher’s possible actions when students have difficulties in solving a problem with a focus on difficulties with understanding and carry out the plan. For five items (23–27), participants were required to indicate what actions should a teacher take if a student gets stuck when solving a problem. For the other three items (28–30), they were to respond to: A student who has understood an arithmetic problem, has made a good selection of the strategy, but has made a mistake in a calculation and is stuck... what action should a teacher do to help him?
Assessment of PS. For this category, the questionnaire consisted of 23 items (see Table 7) regarding criteria and instruments. The items included a list of possible criteria to assess the PS process and a list of assessment instruments for PS proficiency. For 16 of the items (31–46), participants were required to indicate what should be assessed in/about PS and for the other seven items (47A–47G), what kind of assessment tools should be used for PS proficiency.
Resources for PS teaching. For this category, the questionnaire consisted of 13 items (see Table 8 in Results section) regarding representations (concrete, pictorial, and symbolic) and their role in solving problems with special attention to concrete manipulative materials when teaching PS. For three items (48a–48c), participants were to indicate: Why is it good for students’ PS development to use resources (manipulatives and/or tools) when solving problems? For the other 10 items (49–58), participants were to indicate which of the statements are recommended teacher’s actions related to the use of representations to solve problems.
The two questionnaires were administered at the end of the 2017–2018 academic year to the two groups of PTs, i.e., to 93 participants GW and 56 participants GWo. Participants worked individually to respond to the questionnaires during two different times for 20 min each. One of the researchers was present throughout the process. Finally, the validity regarding the internal structure and reliability of the questionnaires was determined through the Kuder and Richardson’s coefficient KR-20, recommended for dichotomous items, which was 0.70 and considered to be acceptable.
4.3. Data Analysis
We carried out the analysis in order to describe the adequacy of the PT’s responses to those reported in the literature, comparing the responses between the two groups that participated in the study. This analysis included a contrast between the responses given by the participants and the recommendations reported by the literature as adequate PS teaching, e.g., [15]. This perspective allows obtaining information regarding which aspects of explicit training have had effects on PTs’ knowledge.
5. Results: PTs’ Knowledge of Teaching and Learning PS
We organized the findings in two sections that correspond to the two questionnaires: PTs’ knowledge of PS learning and PTs’ knowledge of PS teaching. Each section consists of categories and sub-categories of the PTs’ responses based on the items of the questionnaires. The findings are also presented to highlight the levels of knowledge of each of the two groups of PTs separately and in comparison to each other. The two groups are GW (i.e., PTs with the optional PS-oriented course) and GWo (i.e., PTs without the optional PS-oriented course) at the end of their education program.
5.1. PTs’ Knowledge of PS Learning
The PTs’ pedagogical PS knowledge related to PS learning refers to their knowledge of factors that can affect students’ learning of PS. We considered these factors in terms of three categories of knowledge that PTs should hold to support students’ learning of PS: student as a problem-solver, PS as worthwhile task, and non-cognitive factors that affect PS.
5.1.1. PTs’ Knowledge of Problem-Solver
Table 1 provides the questionnaire results of PTs’ knowledge of successful and novice problem solvers’ characteristics. Yes indicates agreement and no disagreement with the statement. We considered their responses to be appropriate when they corresponded to expectations of theory discussed in our theoretical framework.

Table 1.
Percentages of responses for knowledge of student as problem-solver.
Table 1.
Percentages of responses for knowledge of student as problem-solver.
| Item | GWo (N = 56) | GW (N = 93) | |||
|---|---|---|---|---|---|
| YES | NO | YES | NO | ||
| Successful-problem-solvers’ characteristics | |||||
| 1 | His mathematical knowledge is connected and well organized. | 95.6 * | 5.4 | 97.8 * | 2.2 |
| 2 | He is persistent in maintaining the selected strategy already planned | 71.4 | 28.6 * | 60.2 | 39.8 * |
| 3 | He tends to focus on the problem’s structural characteristics and not on the superficial or obvious ones | 75.0 * | 25.0 | 62.4 * | 37.6 |
| 4 | He gets frustrated more easily by not getting the results quickly | 21.4 | 78.6 * | 22.6 | 77.4 * |
| 5 | He is aware of their strengths and weaknesses | 85.7 * | 14.3 | 93.5 * | 6.5 |
| 6 | He is able to control and monitor their own work | 96.4 * | 3.6 | 92.5 * | 7.5 |
| 7 | He has a concern about his resolution process is well done, using sophisticated strategies, being clear and reasonable in their process | 96.4 * | 3.6 | 92.5 * | 7.5 |
| 8 | He is less concerned about the details and more about finishing quickly | 8.9 | 91.1 * | 10.8 | 89.2 * |
| Novice-problem-solvers’ characteristics | |||||
| 9 | He can distinguish relevant information from irrelevant | 30.4 | 69.6 * | 36.6 | 63.4 * |
| 10 | He keeps with his strategy even though it is not well-suited for the specific problem | 69.6 * | 30.4 | 64.5 * | 35.5 |
| 11 | He is impulsive in the choice of a solution strategy | 89.3 * | 10.7 | 82.8 * | 17.2 |
| 12 | He maintains his solution strategy even if he does not find partial results | 75.0 * | 25.0 | 72.0 * | 28.0 |
| 13 | He has poor clarity of the way forward to get the solution | 76.8 * | 23.2 | 80.6 * | 19.4 |
| 14 | He uses strategies not appropriate to the type of problem proposed | 66.1 * | 33.9 | 73.1 * | 26.9 |
| 15 | He finds a result without checking its accuracy or suitable | 76.8 * | 23.2 | 78.5 * | 21.5 |
* Intended response.
Most of the PTs in both groups demonstrated appropriate knowledge of almost all of the eight characteristics of successful problem solvers. More than 90% of the GWo and GW correctly identified five of the characteristics such as having connected and organized knowledge, metacognitive abilities, and concern about form and content. About 63 to 79% of both groups identified two other characteristics involving focusing on structural instead of superficial or obvious problem factors and easily frustrated by not getting solution quickly. However, only few PTs of both groups (29% of GWo and 40% of GW) were able to identify whether good problem solvers would persist in maintaining the strategy they initially selected.
Fewer PTs of both groups were able to identify appropriate characteristics of novice problem solvers compared to those of successful problem solvers. A majority of both groups (89% of GWo and 83% of GW) identified the characteristic of being impulsive in choice of a solution strategy while about 66–76% of GWo and 63–80% of GW identified the other six characteristics including stick with a strategy despite not seeing partial results, not check the coherence of the result, impulsive in the choice of a solution strategy, and has poor clarity of the way forward to get the solution.
Overall:
- While both groups demonstrated more knowledge of successful than novice problem solvers, more GWo than GW demonstrated knowledge of more characteristics of both.
- More GWo than GW appropriately agreed with five of the eight characteristics of successful problem solvers and four of the seven characteristics of novice problem solvers.
- Thus, the findings suggested that with or without engaging the PTs in a course focused on PS, most of them held or developed appropriate knowledge of several characteristics of successful problem solvers during their teacher education program and many were also able to identify most characteristics for novice problem solvers.
- The main challenge for most of them in both groups was determining whether successful problem solvers would persist in maintaining the strategy they initially selected.
- Many of them thought that both successful and novice problem solvers will persist with their initial strategy. In general, most were better at identifying characteristics of successful than novice problem solvers.
5.1.2. PTs’ Knowledge of PS as Worthwhile task
Table 2 provides the questionnaire results of the participants’ knowledge of PS as worthwhile task in terms of four themes: problem selection, strategies, PS models, and problem posing.

Table 2.
Percentages of responses regarding knowledge of PS as worthwhile task.
Table 2.
Percentages of responses regarding knowledge of PS as worthwhile task.
| Item | GWo (N = 56) | GW (N = 93) | |||
|---|---|---|---|---|---|
| YES | NO | YES | NO | ||
| Problem selection | |||||
| 16 | The task allows for exploring and developing mathematical ideas | 96.4 * | 3.6 | 97.8 * | 2.2 |
| 17 | The task is contextualized in situations close to the student’s world | 98.2 * | 1.8 | 98.9 * | 1.1 |
| 18 | The task prompt the interest to seek for the solution and motivate the students to its resolution | 98.2 * | 1.8 | 98.9 * | 1.1 |
| 19 | The task offers different levels of solution and difficulty in solving the problem | 92.9 * | 7.1 | 91.4 * | 8.6 |
| 20 | The task answer is not direct or short | 53.6 * | 46.4 | 49.5 * | 50.5 |
| 21 | The task’s mathematical structure can be used in different situations so that students can make generalizations about problem families | 91.1 * | 8.9 | 92.5 * | 7.5 |
| 22 | The task is understandable and available to students, so students believe they could solve them and know by themselves when they have reached a solution | 100 * | 0 | 94.6 * | 5.4 |
| Strategies | |||||
| 23A | Know “act it out” | 60.7 * | 39.3 | 57.0 * | 43.0 |
| 23A2 | Would use “act it out” | 78.6 * | 21.4 | 80.6 * | 19.4 |
| 23B | Know “check reasonableness of answer” | 92.9 * | 7.1 | 97.8 * | 2.2 |
| 23B2 | Would use “check reasonableness of answer” | 92.9 * | 7.1 | 98.9 * | 1.1 |
| 23C | Know “choose an operation” | 85.7 * | 14.3 | 91.4 * | 8.6 |
| 23C2 | Would use “choose an operation” | 62.5 * | 37.5 | 76.3 * | 23.7 |
| 23D | Know “draw a diagram” | 64.3 * | 35.7 | 80.6 * | 19.4 |
| 23D2 | Would use “draw a diagram” | 69.6 * | 30.4 | 83.9 * | 16.1 |
| 23E | Know “draw a picture” | 98.2 * | 1.8 | 100 * | 0 |
| 23E2 | Would use “draw a picture” | 94.6 * | 5.4 | 98.9 * | 1.1 |
| 23F | Know “estimate” | 91.1 * | 8.9 | 97.8 * | 2.2 |
| 23F2 | Would use “estimate” | 64.3 * | 35.7 | 82.8 * | 17.2 |
| 23G | Know “look for a pattern” | 76.8 * | 23.2 | 92.5 * | 7.5 |
| 23G2 | Would use “look for a pattern” | 62.5 * | 37.5 | 82.8 * | 17.2 |
| 23H | Know “make a graph” | 96.4 * | 3.6 | 98.9 * | 1.1 |
| 23H2 | Would use “make a graph” | 87.5 * | 12.5 | 93.5 * | 6.5 |
| 23I | Know “use manipulative” | 98.2 * | 1.8 | 100 * | 0 |
| 23I2 | Would use “use manipulative” | 100 * | 0 | 100 * | 0 |
| 23J | Know “building a table” | 98.2 * | 1.8 | 98.9 * | 1.1 |
| 23J2 | Would use “building a table” | 96.4 * | 3.6 | 98.9 * | 1.1 |
| 23K | Know “solve a simpler problem” | 87.5 * | 12.5 | 92.5 * | 7.5 |
| 23K2 | Would use “solve a simpler problem” | 66.1 * | 33.9 | 84.9 * | 15.1 |
| 23L | Know “solve an equivalent problem” | 91.1 * | 8.9 | 97.8 * | 2.2 |
| 23L2 | Would use “solve an equivalent problem” | 89.3 * | 10.7 | 87.1 * | 12.9 |
| 23M | Know “guess and check” | 85.7 * | 14.3 | 92.5 * | 7.5 |
| 23M2 | Would use “guess and check” | 66.1 * | 33.9 | 83.9 * | 16.1 |
| 23N | Know “sort and classify “ | 89.3 * | 10.7 | 96.8 * | 3.2 |
| 23N2 | Would use “sort and classify” | 82.1 * | 17.9 | 87.1 * | 12.9 |
| 23O | Know “use a model” | 75.0 * | 25.0 | 88.2 * | 11.8 |
| 23O2 | Would use “use a model” | 58.9 * | 41.1 | 83.9 * | 16.1 |
| 23P | Know “split the problem” | 94.6 * | 5.4 | 100 * | 0 |
| 23P2 | Would use “split the problem” | 91.1 * | 8.9 | 96.8 * | 3.2 |
| 23Q | Know “work backwards” | 26.8 * | 73.2 | 58.1 * | 41.9 |
| 23Q2 | Would use “work backwards” | 30.4 * | 69.6 | 44.1 * | 55.9 |
| PS models | |||||
| 24 | Diagram 1 represents PS process in a real way because it shows that you can go back over what has been done or skip phases | 78.6 * | 21.4 | 63.4 * | 36.6 |
| 25 | Diagram 2 represents PS process in a genuine way because it shows the beginning and the end of the process, with the steps a student must follow | 78.6 | 21.4 * | 88.2 | 11.8 * |
| 26 | Diagram 1 is incorrect because its pointers indicate that you can go back on the work done | 14.3 | 85.7 * | 19.4 | 80.6 * |
| 27 | Diagram 2 is the best way to represent PS process because it shows as moves toward the solution | 51.8 | 48.2 * | 48.4 | 51.6 * |
| Problem Posing | |||||
| 28 | Students must solve problems posed by themselves | 80.4 * | 19.6 | 84.9 * | 15.1 |
| 29 | Only the teacher should pose problems for the students | 5.4 | 94.6 * | 6.5 | 93.5 * |
| 30 | Posing problems can hamper the development of students’ mathematical knowledge | 10.7 | 89.3 * | 4.3 | 95.7 * |
| 31 | Problem posing can help students develop mathematical knowledge | 98.2 * | 1.8 | 100 * | 0 |
| 32 | Problem posing fosters mathematical creativity | 100 * | 0 | 98.9 * | 1.1 |
| 33 | Problem posing can be made before, during or after solving a problem | 82.1 * | 17.9 | 80.6 * | 19.4 |
| 34 | Problem posing can encourage the use of wrong strategies | 33.9 | 66.1 * | 24.7 | 75.3 * |
| 35 | Problem posing is reformulating a given problem | 32.1 * | 67.9 | 35.5 * | 64.5 |
| 36 | Problem posing is posing a new problem without a precondition | 39.3 * | 60.7 | 57.0 * | 43.0 |
* Intended response.
Problem Selection. More than 91% of both the GWo and GW demonstrated appropriate knowledge of six of the seven characteristics associated with problem selection for PS. These characteristics included that such problems should enable the exploration and development of mathematical ideas, offer different levels of solutions, be contextual, provoke interest, and be accessible to students. However, only about half of both groups indicated that a problem should not have a short and direct response.
PS Strategies. A majority of the PTs demonstrated appropriate knowledge of many of the 17 PS strategies with over 92% of GW and over 86% GWo indicating knowledge of the same 13 of 17 strategies. These 13 included: draw a picture, use manipulatives, check reasonableness of answer, split the problem, know estimate, make a graph, and building a table, which over 91% of both groups identified. Fewer PTs in both groups indicated knowing the strategies: act it out (61% GWo and 57% GW), draw a diagram (64% GWo and 80% GW), and work backwards (27% GWo and 58% GW). In addition to demonstrating their knowledge of the PS strategies, the PTs also indicated whether they would use each. For GW, over 82% would use 15 of the 17 strategies, while for GWo over 82% would use eight of the seventeen and about one-third will use seven of the seventeen. For both groups, all of the PTs will use manipulatives but few (30% GWo and 44% GW) will use work backwards. There was not a one-to-one match between knowing a strategy and using it. For example, 24% more of GW and 18% more of GWo would use ‘act it out’ compared to the percentage that indicated knowledge of it as a strategy. In general, both groups demonstrated appropriate knowledge and indicated use of a wide range of strategies, but not to the same extent for knowing and using the strategies. However, for most of the strategies the two groups differed in knowledge and/or use of them with more of the GW demonstration appropriate knowledge and use of them.
PS Models. More GWo than GW demonstrated appropriate knowledge of genuine PS, that is, 79% of GWo and 63% of GW considered the process as cyclical and unstructured and 86% of GWo and 81% of GW indicated that you can go back on work done. However, more than half of both groups also indicated that genuine PS is a linear process, with 79% of GWo and 88% of GW considering it to be a sequence of specific steps to the solution and 52% of GWo and 48% of GW considering it to be one-directional, that is, it goes forward to a solution. Thus, both groups demonstrated contradictions in their knowledge of PS models regarding whether the process is cyclical or linear.
Problem Posing. A majority of PTs in both groups demonstrated appropriate knowledge of most of the characteristics of problem posing. More than 80% of GWo and GW identified characteristics such as both teacher and students should do problem posing, problem posing helps to foster creativity, problem posing can occur in different class moments, and problem posing does not make learning difficult. Fewer PTs in both groups demonstrated knowledge of problem posing as reformulation of a given problem (i.e., 32% of GWo and 36% of GW) and as posing a new problem without a precondition (i.e., 39% of GWo and 57% of GW).
Summary:
- Overall, regarding the PTs’ knowledge of PS as worthwhile task, the two groups demonstrated similar level of knowledge for problem selection and different levels for strategies, PS models, and problem posing.
- About the same number of PTs for both groups correctly identified almost all of the characteristics for problem selection.
- More of the GW than the GWo appropriately identified almost all of the strategies and indicated they would use them.
- More GWo than GW identified three of the four factors for PS model. More of the GW than GWo correctly identified six of the nine characteristics of problem posing.
- Thus, while the additional focused work on problem solving seemed to give the GW an advantage over the GWo for strategies and problem posing, it did not for problem selection and PS model.
- However, there were some key issues for both. For example, while a majority of them identified knowledge of many of the PS strategies, some of them did not know act it out, draw a diagram, and work backwards.
- There was also not a one-to-one match between knowing a strategy and using it, for example, some GW knew of but will not use choose an operation, estimate, work backwards and some GWo knew but will not use look for a pattern, solve a simpler problem, and guess and check. For both groups, more of them will use act it out although they did not know it.
- Both groups also demonstrated contradictions in their knowledge of PS models regarding whether the process is cyclical or linear.
- Only about half of both groups indicated that a problem should not have a short and direct response and less than half demonstrated knowledge of problem posing as reformulation of a given problem and as posing a new problem without a precondition.
5.1.3. PTs’ Knowledge of Non-Cognitive Factors That Influence PS
Table 3 provides the questionnaire results of the PTs’ knowledge of Non-Cognitive factors that influence PS.

Table 3.
Percentages of responses of knowledge of non-cognitive factors.
Table 3.
Percentages of responses of knowledge of non-cognitive factors.
| Item | GWo (N = 56) | GW (N = 93) | |||
|---|---|---|---|---|---|
| YES | NO | YES | NO | ||
| 37 | Students should discover how to solve a problem by themselves without the teacher’s explanations | 60.7 * | 39.3 | 66.7 * | 33.3 |
| 38 | Students should know that the most important thing is to get the correct answer to a problem | 5.4 | 94.6 * | 4.3 | 95.7 * |
| 39 | Students have to assume that problems have only one correct answer | 10.7 | 89.3 * | 10.8 | 89.2 * |
| 40 | Once the students have solved the problem, they should know all the correct answers to the problems | 89.3 * | 10.7 | 90.3 * | 9.7 |
| 41 | Students who solve problems in different ways, end up getting confused | 14.3 | 85.7 * | 96.8 | 3.2 * |
| 42 | Students should use keywords (add, give, etc.) to solve word problems | 66.1 | 33.9 * | 73.1 | 26.9 * |
| 43 | It is better for the students to practice arithmetic calculations without context than use arithmetic calculations to solve word problems | 8.9 | 91.1 * | 14.0 | 86.0 * |
| 44 | Students should only solve problems once the mathematical concept has been taught | 33.9 | 66.1 * | 14.0 | 86.0 * |
| 45 | Students must solve problems as quickly as possible | 3.6 | 96.4 * | 1.1 | 98.9 * |
| 46 | It is better for the students that the teacher only teach PS after teaching mathematical concepts | 35.7 | 64.3 * | 11.8 | 88.2 * |
| 47 | To learn how to solve problems you must practice on an everyday basis | 58.9 * | 41.1 | 67.7 * | 32.3 |
* Intended response.
A majority of both groups demonstrated appropriate knowledge of at least six of the 11 factors, with over 86% of GWo correctly identifying six and 86% of GW identifying seven. The five that were common to both groups included that the PTs believed getting a right answer to a problem is not the most important aspect of PS, students do not have to solve problems quickly, students should not think there is only one correct answer or that they should know all possible answers to a problem, and students do not have to practice algorithms before solving word problems. Fewer for both groups (about two-thirds) indicated that students should be able to solve problems on their own without teacher’s help and must practice every day to develop their PS proficiency, while only 34% of GWo and 27% of GW thought that teaching keywords in the context of word problems could be counterproductive. For three factors, there were significant differences between the two groups. While 86% of GWo indicated solving a problem in different ways (with different strategies) will not confuse students, only 3% of GW agreed with this, but while about 87% of GW indicated that students do not have to learn mathematics concept first then solve problems and teachers do not have to teach PS after students know concepts and procedures, only about 65% of GWo agreed.
Overall:
- For eight of the eleven factors, about the same or fairly close amounts of both the GW and GWo indicted the appropriate factors, suggesting not a significant difference in the knowledge between them.
- However, while both groups held many beliefs that were appropriate to support students’ learning of PS, there were also many of the PTs who held some beliefs (five for GWo and four for GW) that were inconsistent with what were appropriate.
- Thus, there were mixed knowledge and contradictions demonstrated in their thinking about the beliefs that promoted an adequate development of PS in students.
5.2. PTs Pedagogical Knowledge of PS Teaching
The participants’ knowledge related to PS teaching refers to their knowledge of factors that can affect instruction in supporting students’ learning of PS. We consider these factors in terms of five categories of knowledge that PTs should hold: PS teaching approaches, discourse in PS, stuck state in PS, PS assessment, and PS resources.
5.2.1. PTs’ Knowledge of PS Teaching Approaches
Table 4 provides the questionnaire results of the participants’ knowledge of PS teaching approaches.

Table 4.
Percentages of responses of knowledge of PS teaching approaches.
Table 4.
Percentages of responses of knowledge of PS teaching approaches.
| Item | GWo (N = 56) | GW (N = 93) | |||
|---|---|---|---|---|---|
| YES | NO | YES | NO | ||
| 1 | Class discussions should focus only on the answer to the problem instead of the process to get the answer | 3.6 | 96.4 * | 0 | 100 * |
| 2 | In the class there must be an environment where it is possible to explore problems both individually and in groups, communicating all the multiple ways of solving them | 100 * | 0 | 100 * | 0 |
| 3 | You must first learn a mathematical concept and then apply it to solve problems | 48.2 | 51.8 * | 40.9 | 59.1 * |
| 4 | The focus of discussion and attention should be on the process | 87.5 * | 12.5 | 92.5 * | 7.5 |
| 5 | The teacher must show and exemplify, step by step, how problems are solved | 82.1 | 17.9 * | 77.4 | 22.6 * |
| 6 | Phase and strategies should be taught directly and explicitly | 50.0 * | 50.0 | 38.7 * | 61.3 |
| 7 | Class discussions should focus on unpacking mathematical concepts involved in PS | 58.9 * | 41.1 | 64.5 * | 35.5 |
| 8 | The class should start with a problem, then let the students explore it and discover the mathematics involve in it; while the teacher guides the process | 85.7 * | 14.3 | 97.8 * | 2.2 |
| 9 | The teacher should explain in detail how to solve the problems and the students should listen and then apply | 32.1 | 67.9 * | 30.1 | 69.9 * |
| 10 | The teacher should teach mathematical concepts first, and then apply them to solve problems | 62.5 * | 37.5 | 50.5 * | 49.5 |
| 11 | The teacher should teach general aspects of PS (i.e., PS strategies or PS phases), which enhance students’ PS proficiency | 92.9 * | 7.1 | 100 * | 0 |
| 12 | The teacher should teach a mathematical concept from solving problems | 82.1 * | 17.9 | 89.2 * | 10.8 |
* Intended response.
A majority of both groups demonstrated appropriate knowledge of about half of the twelve factors, with over 82% of GWo correctly identifying six and over 90% of GW identifying also six. The six, common to both groups, included: class discussions should focus only on the answer to the problem instead of the process to get the answer; having an environment in the classroom for students to explore problems individually and in groups; conducting class discussion focused on the process to the solution; starting the class with a problem that students explore to discover underlying mathematics on their own; teaching through PS is the most appropriate approach; and teaching about PS is the most suitable. Many of both groups (50 to 70%) demonstrated appropriate knowledge for another five of the twelve items with more GW agreeing with four, including that a mathematical concept should not be taught and then applied to PS; that the class discussion should focus on unpacking the mathematical knowledge in the problems; and the teacher should not explain how a problem is solved step by step and the student listen and repeat. More GWo (50%) agreed that PS phases and strategies should be taught directly and explicitly than GW (39%). A majority (82% of GWo and 77% of GW) inappropriately agreed that teacher must show and exemplify, step by step, how problems are solved.
Overall:
- More GW than GWo correctly agreed with 10 of the 12 factors, suggesting further exposure to formal knowledge on PS made a difference to their learning.
- One factor was particularly challenging for both groups regarding whether the teachers should demonstrate steps to a solution.
- Both groups did best on the set of items dealing with teaching through PS with a majority agreeing with three of the four items, followed by teaching about PS with a majority agreeing with two of the four items, and then teaching for PS with a range of responses for three of the four items.
5.2.2. PTs’ Knowledge of Discourse in PS Teaching
Table 5 provides the questionnaire results of the participants’ knowledge of discourse in PS teaching.

Table 5.
Percentages of responses of knowledge of discourse in PS teaching.
Table 5.
Percentages of responses of knowledge of discourse in PS teaching.
| Item | GWo (N = 56) | GW (N = 93) | |||
|---|---|---|---|---|---|
| YES | NO | YES | NO | ||
| 13 | Fostering the use of different solution strategies | 100 * | 0 | 100 * | 0 |
| 14 | To make available to the students a solution-book with all the right answers | 30.4 | 69.6 * | 22.6 | 77.4 * |
| 15 | Discussing PS strategies used by the students | 100 * | 0 | 98.9 * | 1.1 |
| 16 | Asking for argumentation and reflection on answers and the mathematics concepts involved in the problem | 100 * | 0 | 100 * | 0 |
| 17 | Finishing the PS process once the answer is found | 5.4 | 94.6 * | 10.8 | 89.3 * |
| 18 | Guiding the discussion on how the problem was solved or what procedure was used | 98.2 * | 1.8 | 100 * | 0 |
| 19 | Asking for problems to be solved quickly | 0 | 100 * | 1.1 | 98.9 * |
| 20 | Propose problems of easy resolution | 21.4 | 78.6 * | 28.0 | 72.0 * |
| 21 | Explaining explicitly to students the ways each problem is solved | 80.4 | 19.6 * | 75.3 | 24.7 * |
| 22 | Encourage indicating agreement or disagreement with classmates’ solutions, giving justified reasons | 98.2 * | 1.8 | 98.9 * | 1.1 |
* Intended response.
A majority in both groups (over 90%) demonstrated appropriate knowledge of discourse in teaching PS for seven of the 10 factors. These seven, common to both groups, included encouraging the use of different solution strategies, discussing the strategies used by the students, asking for reflections and arguing about the mathematics involved in the problems, not ending the activity once the solution has been found, guiding the discussion to how problem was solved and asking students to justify their solution process. Many (70 to 79%) in both groups also agreed with two other factors regarding not providing a solution for the proposed tasks and not proposing problems that are solved quickly. However, 80% of GWo and 75% of GW inappropriately agreed with the factor that the ways in which problems are solved must be explicitly explained to students.
Overall:
- The PTs of both groups demonstrated similar level of knowledge of discourse, about the same agreeing with six factors, GWo agreeing with two more than GW and GW agreeing with two others than GWo, suggesting little difference in the knowledge between them despite differences in exposure to formal knowledge in PS.
- However a key issue for both groups was most PTs indicating that the teacher should explain explicitly to students the ways to solve each problem and a few indicating posing problems of easy solution.
5.2.3. PTs’ Knowledge of Stuck State in PS
Table 6 provides the questionnaire results of the participants’ knowledge of stuck state in PS.

Table 6.
Percentages of responses of knowledge of stuck state in PS.
Table 6.
Percentages of responses of knowledge of stuck state in PS.
| Item | GWo (N = 56) | GW (N = 93) | |||
|---|---|---|---|---|---|
| YES | NO | YES | NO | ||
| 23 | If the student made a mistake in an arithmetic calculation, the teacher should ask to read the problem again until he understands it. | 75.0 | 25.0 * | 72.0 | 28.0 * |
| 24 | The teacher should identify if the error is related to understanding the problem or strategy’s execution | 98.2 * | 1.8 | 100 * | 0 |
| 25 | For struggles with problem’ understanding, the teacher should suggest alternative representations. | 96.4 * | 3.6 | 96.8 * | 3.2 |
| 26 | For struggles with plan’ execution, the teacher should suggest alternative strategies. | 92.9 * | 7.1 | 94.6 * | 5.4 |
| 27 | If the student struggle with PS, the teacher should give the answer so that the student does not get frustrated. | 14.3 | 85.7 * | 16.1 | 83.9 * |
| 28 | The teacher should ask the student to represent the problem’s data in a different way + | 78.6 | 21.4 * | 66.7 | 33.3 * |
| 29 | The teacher should suggest to the student to change his strategy + | 53.6 | 46.4 * | 38.7 | 61.3 * |
| 30 | The teacher should ask the student questions about how he carries out the arithmetic calculations + | 91.1 * | 8.9 | 97.8 * | 2.2 |
+ Participants were asked to respond to a specific stuck situation of a student who understands an arithmetic problem but makes a mistake in one of the calculations. * Intended response.
Most of the participants in both groups (over 91%) demonstrated appropriate knowledge for four of the eight factors related to when students are stuck. These factors included that the teacher should identify if the stuck state relates to an error in understanding problem conditions or in the execution of the strategy, and if the former, alternative representations should be suggested and if the latter, alternative strategies should be suggested. In addition, 86% of GWo and 84% of GW demonstrated knowledge that the teacher should not give the answer to the problem when students are stuck. However, only 61% of GW and 46% of GWo indicated that the teacher should not suggest to the student to change strategy. In addition, 21% of GWo and 33% of GW agreed that the teacher should not ask the student to represent the problem’s data in a different way and 25% of GWo and 28% of GW agreed that if the student made an error in an arithmetic calculation, the teacher should not ask them to reread the problem until they understands it.
Overall:
- The PTs of both groups demonstrated similar level of knowledge of teaching intervention when a student is stuck, suggesting little difference in the knowledge between them despite differences in exposure to formal knowledge on PS.
- They had difficulty identifying the same items including treating an error in arithmetic calculation as a lack of understanding of a problem.
5.2.4. PTs’ Knowledge of Assessment in PS Teaching
Table 7 provides the questionnaire results of the participants’ knowledge of assessment in PS teaching.

Table 7.
Percentages of responses of knowledge of assessment in PS teaching.
Table 7.
Percentages of responses of knowledge of assessment in PS teaching.
| Item | GWo (N = 56) | GW (N = 93) | |||
|---|---|---|---|---|---|
| YES | NO | YES | NO | ||
| 31 | The student’s understanding of the problem, for example, asking them to explain it with their own words | 94.6 * | 5.4 | 95.7 * | 4.3 |
| 32 | The organization and representation of problem data by the student | 92.9 * | 7.1 | 95.7 * | 4.3 |
| 33 | The student’s planning to get the solution | 91.1 * | 8.9 | 93.5 * | 6.5 |
| 34 | The student’s control of his own PS process, that is, if he is able to notice that if the plan does not allow to find the answer, it must be back and look for a new one | 94.6 * | 5.4 | 93.5 * | 6.5 |
| 35 | The student’s ability to select and use strategies | 100 * | 0 | 97.8 * | 2.2 |
| 36 | The existence of appropriate attitudes and beliefs in the student to solve problems | 89.3 * | 10.7 | 86 * | 14.0 |
| 37 | The student communication, his response and his justifications about what has been done | 94.6 * | 5.4 | 96.8 * | 3.2 |
| 38 | The student’s ability to use related mathematical knowledge into his PS process | 98.2 * | 1.8 | 92.5 * | 7.5 |
| 39 | The student’s ability to find the correct answer | 80.4 * | 19.6 | 78.5 * | 21.5 |
| 40 | The student’s ability to find the answer quickly | 14.3 | 85.7 * | 14 | 86.0 * |
| 41 | The student’s ability to give tidy and cleanliness work | 82.1 | 17.9 * | 81.7 | 18.3 * |
| 42 | The student’s ability to identify keywords (give away, lost, etc.) | 87.5 | 12.5 * | 79.6 | 20.4 * |
| 43 | The student’s ability to make sense of the answer according to the conditions of the problem | 94.6 * | 5.4 | 95.7 * | 4.3 |
| 44 | The student’s ability to represent ideas and answers only with symbols and numbers | 25.0 | 75.0 * | 17.2 | 82.8 * |
| 45 | The student’s perseverance to continue working despite not finding the right answer | 98.2 * | 1.8 | 95.7 * | 4.3 |
| 46 | The student’s confidence and security when facing PS | 78.6 * | 21.4 | 94.6 * | 5.4 |
| 47A | Observe students | 98.2 * | 1.8 | 82.8 * | 17.2 |
| 47B | Personal interviews | 75.0 * | 25.0 | 63.4 * | 36.6 |
| 47C | Self-reports | 83.9 * | 16.1 | 79.6 * | 20.4 |
| 47D | Problem posing | 82.1 * | 17.9 | 91.4 * | 8.6 |
| 47E | Written PS responses | 92.9 * | 7.1 | 75.3 * | 24.7 |
| 47F | Multiple-choice tests | 51.8 | 48.2 * | 52.7 | 47.3 * |
| 47G | Fill-in-the-blank tests | 30.4 | 69.6 * | 37.6 | 62.4 * |
* Intended response.
Most of both groups (over 75%) demonstrated appropriate knowledge in at least 14 of the first 16 factors regarding what to assess for students’ PS. In particular, over 91% of GWo identified nine and over 92% GW identified 10. These included that the PTs would evaluate understanding, data organization, planning, self-control of the process, the use and selection of strategies, argumentation and communication, the ability to use mathematical knowledge, the ability to make sense of the answer, perseverance in finding the answer, and the confidence and security shown. About the same number of each group (in the 80s) identified three others related to assessing the existence of appropriate attitudes and beliefs, not finding an answer quickly and ability to find the correct answer. In addition, 75% of GWo and 83% of GW will not assess ability to represent ideas and answers only with symbols and numbers. Only about 18% of both groups will not assess ability to give tidy and clean work and 13% of GWo and 20% of GW would not evaluate ability to identify keywords in word problems.
There was mixed results regarding the instruments that PTs would use to evaluate PS ability with more of the GWo than the GW agreeing with most of the seven ways. Over 80% of both groups agreed with observing students, self-reports and problem posing. However, while 93% of GWo would use written PS responses only 75% of GW would use them, and 75% of GWo would use personal interviews, while only 64% of GW would use them. Finally, approximately 50% in both groups would use fill-in-the-blank tests and less than 40% of both groups would use multiple-choice tests.
Overall:
- There was little difference between the percentage of WGo and WG with appropriate knowledge of assessing PS but more WGo than WG agreed with six of the seven ways of assessing PS with a majority of WG agreeing with problem posing, suggesting little difference or improvement in the knowledge between them despite differences in further exposure to formal knowledge on PS.
- For both groups, there was inconsistency in their knowledge by indicating they would evaluate students’ ability to identify keywords in word problems.
5.2.5. PTs’ Knowledge of Resources in PS Teaching
Table 8 provides the questionnaire results of the participants’ knowledge of resources in PS teaching.

Table 8.
Percentages of responses of knowledge of resources PS teaching.
Table 8.
Percentages of responses of knowledge of resources PS teaching.
| Item | GWo (N = 56) | GW (N = 93) | |||
|---|---|---|---|---|---|
| YES | NO | YES | NO | ||
| 48A | It will help students to systematically write their calculations while solving the problem and respond in a tidy manner | 69.6 | 30.4 * | 73.1 | 26.9 * |
| 48B | It will allow students to visualize and manipulate relationships and ideas and then generalize some aspects related to the structure of the problem | 98.2 * | 1.8 | 98.9 * | 1.1 |
| 48C | It is not necessary for students to use resources; it would be better to teach them the mathematical symbols | 10.7 | 89.3 * | 1.1 | 98.9 * |
| 49 | Promote on the student the use of a single type of representation to avoid confusion | 10.7 | 89.3 * | 4.3 | 95.7 * |
| 50 | The teacher should use only formal or symbolic representations | 10.7 | 89.3 * | 16.1 | 83.9 * |
| 51 | The teacher should encourage the use of representations to communicate the problems’ results | 87.5 * | 12.5 | 95.7 * | 4.3 |
| 52 | The teacher should promote the use of representations because they are the ideas that the student has about the problem | 98.2 * | 1.8 | 96.8 * | 3.2 |
| 53 | The teacher should foster the use of multiple representations only with younger students or with the student who does not understand | 41.1 | 58.9 * | 31.2 | 68.8 * |
| 54 | The teacher should encourage its use at the stage of understanding the problem | 67.9 * | 32.1 | 61.3 * | 38.7 |
| 55 | The teacher should encourage the use of representations throughout across the resolution process | 91.1 * | 8.9 | 95.7 * | 4.3 |
| 56 | The teacher should encourage the use of personal and spontaneous representations because they prompt the transition to mathematical or formal representations | 100 * | 0 | 97.8 * | 2.2 |
| 57 | The teacher should encourage the use of the student’s own representation | 92.9 * | 7.1 | 92.5 * | 7.5 |
| 58 | The teacher should encourage the use of more than one representation in one PS process | 98.2 * | 1.8 | 97.8 * | 2.2 |
* Intended response.
A majority of both groups (over 89% of GWo and over 90% of GW except for one item at 84%) demonstrated appropriate knowledge for 10 of the 13 factors. These factors included that manipulatives help students to visualize and manipulate relationships and ideas and are necessary for the solution process, the teacher should promote the use of multiple representations, and representations can be understood as students’ ideas. In addition, 59% of GWo and 69% of GW showed appropriate knowledge regarding the targeting of representations not only with young children or those who struggle with their PS process. In addition, 68% of GWo and 61% of GW would encourage the use of representations in the understanding phase. However, 70% of both groups inappropriately agreed that the representations help students to write the calculations in an orderly and clean way.
Overall:
- The PTs of both groups demonstrated similar level of knowledge of resources, suggesting little difference in the knowledge between them despite differences in exposure to formal knowledge on PS.
- Many of both groups could not correctly identify whether representations will help students to systematically and clearly write their calculations while solving the problem.
6. Discussion and Implications
This study offers a comprehensive investigation of PTs’ PS knowledge for teaching that is not usually considered in other studies. Building on Chapman’s [3] framework of PS knowledge for teaching, it addressed PTs’ knowledge of: (1) PS learning consisting of student as a problem-solver, PS as a worthwhile task, non-cognitive factors related to PS, and (2) PS teaching consisting of PS teaching approaches, discourse in PS, stuck state in PS, PS assessment, and PS resources. The PTs were required to respond to several questionnaire items that involved different ways of viewing these categories of knowledge that provided insights of the depth of their PS knowledge at the end of their teacher education program. As described in our theoretical framework section, these items were based on theory regarding appropriate knowledge teachers should hold to meaningfully and effectively engage students in genuine PS. Thus, our findings indicate the strength and limitations in the PTs’ knowledge based on the items they were able to successfully identify or not. We discuss these key findings regarding their knowledge of PS learning and PS teaching and the implications for elementary teacher education.
6.1. Knowledge of PS Learning
The PTs’ pedagogical knowledge related to PS learning refers to their knowledge of factors that can support or hinder students’ learning of PS. The findings indicated that many of the PTs for both the GW and GWo were able to correctly identify many of the factors regarding student as a problem-solver, PS as worthwhile task, and non-cognitive factors that affect PS. However, there were also factors central to supporting students’ learning of PS that they were less successful in identifying. For the most part, both groups of the PTs shared common pedagogical PS knowledge on learning. For some areas the GW was slightly better than the GWo, suggesting that the PS-oriented course had some positive influence on their knowledge. Many aspects of this knowledge were consistent with recommendations in the literature, e.g., [16], with GW being slightly more in line with more of them than GWo. In considering the total items in each category based on performance of a majority of PTs: (1) for both groups, the highest level of knowledge was for problem selection criteria; (2) the second level of knowledge was for PS strategies and use of strategies, with GW much stronger than GWo; (3) the third level of knowledge was for successful solvers’ characteristics, importance of problem posing, and non-cognitive factors, with both groups performing about the same; and (4) the weakest areas for both groups were PS model and novice problem solvers. When considered based on all participants’ performance, both groups demonstrated similar level of appropriate knowledge for areas such as successful-solvers’ characteristics, problem selection criteria and the importance of problem posing, but the GWo demonstrated a lesser level than the GW on knowledge about strategies and non-cognitive factors that presented the greatest difficulty for them.
Both groups also demonstrated some inappropriate knowledge for every category of knowledge of PS learning. The combination of appropriate and inappropriate knowledge resulted in some conflicts or contradictions in their knowledge. They showed the most conflicts in knowledge for the categories of PS as a worthwhile task and non-cognitive factors; for example, the strategies they claimed to know least or would not use are related to authentic PS processes [12] and their understanding of PS process as both linear and cyclical is problematic. This result may stem from the difficulties Spanish PTs encounter in their own PS proficiency [38] and the challenge to help them to make appropriate changes to their thinking for some aspects of the knowledge of PS learning given that the extra PS training received by the GW did not lead to significant difference compared to the GWo regarding contradictory knowledge.
6.2. Knowledge of PS Teaching
The PTs’ pedagogical knowledge related to PS teaching refers to their knowledge of factors of instruction that could support or limit students’ learning of PS. The findings indicated that many of the PTs for both the GW and GWo were able to correctly identify many of the factors regarding PS teaching approaches, discourse in PS, stuck state in PS, PS assessment, and PS resources. However, there were also factors central to meaningful instruction to support students’ learning of PS that they were not successful in identifying. For the most part, both groups of the PTs shared common knowledge on PS teaching. Many aspects of this knowledge were consistent with recommendations in the literature, e.g., [3,16], with GW being slightly more in line with more of them than GWo. In considering the total items in each category based on majority performance: (1) the highest level of knowledge for both groups equally was for discourse in PS teaching; (2) the second level of knowledge was for PS resources, with GWo being stronger than GW; (3) the third level of knowledge for both group equally was stuck state in PS; (4) the fourth level of knowledge for both group equally was for assessment; and (5) the weakest area for both groups was PS teaching approaches, with the GWo being weaker than GW.
Both groups also demonstrated some inappropriate knowledge for every category of knowledge. The items they performed worst on involved agreeing that: the student’s ability to identify keywords should be assessed and the teacher should exemplify solution and explain explicitly ways to solve problems (for more of the GWo than GW); PS is a linear process going from stage to stage (for less of the GWo and GW). Most of both groups associated a computational error with not understanding the problem. Overall, the difficulty of the GWo focused on knowledge of PS teaching approaches and assessment of PS while the difficulty of the GW focused on knowledge about PS teaching approaches and resources for PS.
The combination of appropriate and inappropriate knowledge resulted in some conflicts or contradictions in the PTs’ knowledge that are related to teaching actions and would limit student’ learning of PS. For example, contradictions for both groups of PTs included low acceptance of discussion of mathematical concepts embodied in problems and high acceptance of resolving each problem before the students face it. They placed importance to incorrect calculations in students’ solutions and that teachers should help by asking questions about how the calculations were performed suggesting that calculations are more important than understanding, which conflicts with their agreement that it is important to discuss the underlying mathematics and the solution processes. They also agreed that it is appropriate to evaluate understanding of the problem, use of mathematical knowledge, and appropriate beliefs, which conflicted with their agreement that they would evaluate the use of keywords in word problems, a strategy that does not consider a real reflection and understanding of the problem. In addition, while the PTs demonstrated knowledge related to teaching for, about, and through PS, which could overlap in classroom reality, as suggested by Schroeder and Lester [23], there were also contradictions. For example, the GWo showed less knowledge for characteristics regarding teaching for and about PS and both groups tended to point to teaching through PS as the “most” appropriate, as suggested by some authors [16]. These findings suggest the challenge to help PTs to make appropriate changes to their thinking for some aspects of the knowledge of PS teaching given that the extra PS training received by the GW did not lead to significant difference compared to the GWo regarding contradictory knowledge and in particular, PS teaching approaches, which was the most difficult for both groups to identify.
7. Conclusions on PTs’ Pedagogical PS Knowledge
Collectively, the PTs demonstrated a combination of different levels of knowledge of PS learning and teaching. The GW performed best for problem selection and PS strategies and use of strategies, followed by discourse, resources, and assessment, while GWo performed best for problem selection and resources followed by discourse and assessment. Areas they performed moderately on were, for both groups, knowledge of novice problem solvers, PS models, problem posing, and stuck state in PS, and for the GWo, also PS strategies and use of strategies. Areas they performed the worst on were non-cognitive factors and teaching approaches for both groups, but with the GWo being worse than the GW for teaching approaches. They performed best on teaching through PS, followed by teaching about PS, followed by teaching for PS, with GW a little better than GWo for some items for all three.
The PTs also demonstrated conflicts or contradictions in their knowledge, which were especially acute for teaching approaches. One possible explanation for the contradictions is the combination of the items on the questionnaires. The pattern of the PTs’ responses suggests that they tended to respond appropriately to questions that did not require deep understanding of PS or when the ideas were put forward in a general way about PS that they could make sense of without deep thinking. However, for specific ideas or to questions that asked them to indicate a concrete action that required deeper thinking their responses tended to be inappropriate and in conflict with their response to parallel ideas of questions that were simpler for them. Thus, the combination of items of different ways of thinking about the same idea resulted in contradictory responses, suggesting a lack of deep understanding for some categories of knowledge and/or lack of awareness of the conflict.
A second possible explanation for the contradictions is limitation to their approach to learning. The contradictions suggest that the PTs had pre-existing knowledge and beliefs based on past experiences with PS, which they considered to be appropriate. Therefore, they did not replace this knowledge, but added new knowledge to it in a way that both seemed appropriate for them. Thus, their overall knowledge suggests a combination of a traditional understanding of PS pedagogy in which PS is a linear and unproblematic process directed by the teacher and a cyclic problematic process directed by the student as problem solver. The implication is that, as part of their learning, the PTs did not engage in a process of reflecting on their knowledge to develop awareness of their thinking and understanding of the nature and impact of conflicting knowledge on learning and teaching PS. Therefore, their traditional ideas about PS and its teaching, such as, PS strategies must be explicitly taught or that solving problems is to perform an algorithmic procedure, contradicted the knowledge they acquired in their education courses regarding genuine PS and the need to explore the underlying mathematics in the problems. Thus, their approach to learning should focus not only on knowing the characteristics of the different categories of knowledge but also on reflecting on their thinking and what it means to their actions as future teachers.
In addition to contradictions, there was a disconnect between practical knowledge and the theoretical knowledge of teaching PS that the PTs demonstrated based on their education courses, which they held in a way that may not be transferred easily to their teaching. In particular, the PTs’ knowledge did not seem to have an organizing structure consistent with the pedagogical PS triangle of our theoretical framework that we considered to be necessary for effective teaching of PS. The triangle indicates two-directional relationships between student and PS, teacher and PS, and teacher and student that form the basis for the teaching of PS. Since a contradiction was reflected in at least one case in all components of the triangle, the implication is that there are conflicts and challenges in the relationships that distort the triangle. Thus, the PTs’ likely did not hold sufficient appropriate knowledge for these relationships to be effectively implemented in their teaching.
A limitation of these conclusions is that they are based on the PTs’ responses to the questionnaires, which do not provide the PTs’ explanations of their thinking regarding the contradictions, in particular. The questionnaires also did not specifically address the pedagogical PS triangle relationships but the elements included in each component of the triangle. Future research should consider both the contradictions and the relationships to understand them from the PTs’ perspectives.
Implications for Teacher Education
The findings suggest that a teacher education program that includes engaging PTs in PS explicitly through a formal course on PS and/or implicitly through PS activities integrated in mathematics education courses could help many PTs to develop or demonstrate appropriate pedagogical knowledge of PS, but with some limitations to the knowledge that include misconceptions or contradictions. Since such contradictions could result from lack of awareness of pre-existing knowledge and beliefs, teacher education should provide the PTs with experiences to develop awareness and understanding of the contradictions. The examples of contradictions in this study could form a basis for the PTs to compare and reflect on their knowledge and impact on their teaching of PS. The implication is that such limitations in their knowledge need to be explicitly addressed in the education programs or PS courses to draw the PTs’ attention to the contradictions in their thinking and the impact they could have on their teaching of PS.
The findings also provide examples of areas PTs may not have deep understanding of that require attention in teacher education in a specific and not general way; for example, using activities that target these areas, such as providing opportunities for them to: analyze and discuss students’ PS to allow them to become comfortable with methods and solutions that are different from their own; articulate how they give meaning to teaching PS; explore PS phases and strategies with connection to related classroom practices; and apply strategies to formulate an accurate metacognitive knowledge base.
In general, the study suggests that PTs should not only know theoretical knowledge but also practical knowledge of PS that should be organized and connected as proposed in the pedagogical PS triangle. Specifically, our findings suggest that the PTs’ knowledge might not be organized in a way that would make it useful to teach PS effectively. Our pedagogical PS triangle could provide a basis in planning activities to help the PTs to organize their knowledge appropriately.
Finally, while commenting on the pedagogical approaches used in the teacher education program and PS course the PTs in this study experienced are beyond the scope of this chapter, the findings imply that there should be a focus on inquiry and reflection and not only on engaging PTs in learning theory and solving problems in order to help them to expand their understanding of problems and PS. There should also be more focus on knowledge models developed from PS processes perspectives, such as the one proposed by Chapman [3] or Foster and collaborators [39] because the transversal nature of the processes would help the PTs make compatible connections in their knowledge in a natural way.
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ministry of Science, Innovation and Universities (Spain) who financed the research project PGC2018-095765-B-I00 (PROFESTEM), and a Ph.D. grant awarded by Chile’s ANID (folio 72170314).
Institutional Review Board Statement
This study did not require ethical approval.
Informed Consent Statement
Informed consent was obtained from all subjects involved in this research.
Data Availability Statement
Data available on request due to restrictions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ball, D.L.; Thames, M.H.; Phelps, G. Content knowledge for teaching: What makes it special? J. Teach. Educ. 2008, 59, 389–407. [Google Scholar] [CrossRef] [Green Version]
- Lin, F.-L.; Rowland, T. Pre-Service and in-service mathematics teachers’ knowledge and professional development. In The Second Handbook of Research on the Psychology of Mathematics Education; Gutiérrez, Á., Leder, G.C., Boero, P., Eds.; Sense: Rotterdam, The Netherlands, 2016; pp. 481–520. [Google Scholar] [CrossRef]
- Chapman, O. Mathematics teachers’ knowledge for teaching problem solving. LUMAT 2015, 3, 19–36. [Google Scholar] [CrossRef]
- García, M.; Llinares, S. Los procesos matemáticos como contenido. El caso de la prueba matemática. In Didáctica de la Matemática en Educación Primaria; Castro, E., Ed.; Síntesis: Madrid, Spain, 2001; pp. 105–122. [Google Scholar]
- NCTM. Principles and Standards for School Mathematics; NCTM: Reston, VA, USA, 2000. [Google Scholar]
- Weber, K.; Leikin, R. Recent advances in research on problem solving and problem posing. In The Second Handbook of Research on the Psychology of Mathematics Education; Gutiérrez, Á., Leder, G.C., Boero, P., Eds.; Sense: Rotterdam, The Netherlands, 2016; pp. 353–382. [Google Scholar] [CrossRef]
- Lester, F.K. Thoughts about research on mathematical problem-solving instruction. Maths Entht. 2013, 10, 245–278. [Google Scholar]
- Schoenfeld, A.H. Learning to think mathematically: Problem solving, metacognition and sense making in mathematics. In Handbook for Research on Mathematics Teaching and Learning; Grows, D., Ed.; Macmillan: New York, NY, USA, 1992; pp. 334–370. [Google Scholar] [CrossRef] [Green Version]
- Mason, J. When is a problem...? “When” is actually the problem! In Posing and Solving Mathematical Problems; Felmer, P., Pehkonen, E., Kilpatrick, J., Eds.; Springer: New York, NY, USA, 2016; pp. 263–285. [Google Scholar] [CrossRef]
- Schoenfeld, A.H. Problematizing the didactic triangle. ZDM 2012, 44, 587–599. [Google Scholar] [CrossRef]
- Kaur, B. Difficulties with problem solving in mathematics. Math Educ. 1997, 2, 93–112. [Google Scholar]
- Mason, J.; Burton, L.; Stacey, K. Thinking Mathematically, 2nd ed.; Pearson: Essex, UK, 2010. [Google Scholar]
- Posamentier, A.S.; Krulik, S. Problem-Solving Strategies for Efficient and Elegant Solutions: A Resource for the Mathematics Teacher; Corwin Press: Thousand Oaks, CA, USA, 1998. [Google Scholar]
- Schoenfeld, A.H. Mathematical Problem Solving; Academic Press: Orlando, FL, USA, 1985. [Google Scholar]
- NCTM. Principles to Action: Ensuring Mathematical Success for All; NCTM: Reston, VA, USA, 2014. [Google Scholar]
- Lester, F.K.; Cai, J. Can mathematical problem solving be taught? Preliminary answers from 30 years of research. In Posing and Solving Mathematical Problems; Felmer, P., Pehkonen, E., Kilpatrick, J., Eds.; Springer: New York, NY, USA, 2016; pp. 117–135. [Google Scholar] [CrossRef]
- Poólya, G. How to Solve It; University Press: Princeton, NJ, USA, 1971. [Google Scholar]
- Brown, S.I.; Walter, M.I. The Art of Problem Posing; Lawrence Erlbaum: Mahwah, NJ, USA, 2005. [Google Scholar]
- Silver, E.A. On mathematical problem posing. Lear Math 1994, 14, 19–28. [Google Scholar]
- Buchanan, N.K. Factors contributing to mathematical problem-solving performance: An exploratory study. Educ. Stu. Math 1987, 18, 399–415. [Google Scholar] [CrossRef]
- Silao, I.V. Factors affecting the mathematics problem solving skills of Filipino pupils. Int. J. Sci. Res. Pub. 2018, 8, 487–497. [Google Scholar]
- Rott, B. Teachers’ Behaviors, Epistemological Beliefs, and Their Interplay in Lessons on the Topic of Problem Solving. Int. J. Sci. Math Educ. 2020, 18, 903–924. [Google Scholar] [CrossRef]
- Schroeder, T.L.; Lester, F.K. Developing understanding in mathematics via problem solving. In New Directions for Elementary School Mathematics. 1989 Yearbook; Trafton, P.R., Shulte, A.P., Eds.; NCTM: Reston, VA, USA, 1989; pp. 31–42. [Google Scholar]
- Chapman, O. Mathematics teachers’ ways of supporting students’ learning of problem solving. In A Life’s Time for Mathematics Education and Problem Solving; Stein, M., Ed.; WTM Verlag: Borsdorf, Germany, 2017; pp. 45–69. [Google Scholar]
- Sullivan, P.; Mousley, J.; Jorgensen, R. Tasks and pedagogies that facilitate mathematical problem solving. In Mathematical Problem Solving. Yearbook 2009; Kaur, B., Yeap, B.H., Kapur, M., Eds.; World Scientific Publishing and Association of Mathematics Educators: Singapore, 2009; pp. 17–42. [Google Scholar]
- Charles, R.I.; Lester, F.K.; O’Daffer, P.G. How to Evaluate Progress in Problem Solving; NCTM: Reston, VA, USA, 1987. [Google Scholar]
- Rosli, R.; Goldsby, D.; Capraro, M.M. Assessing students’ mathematical problem-solving and problem-posing skills. Soc. Sci. 2013, 9, 54–60. [Google Scholar] [CrossRef] [Green Version]
- Kelly, C.A. Using manipulatives in mathematical problem solving: A performance-based analysis. Math Ent. 2006, 3, 184–193. [Google Scholar]
- Smith, R.P. Representation in school mathematics: Children’s representations of problems. In A Research Companion to Principles and Standards for School Mathematics; Kilpatrick, J., Ed.; NCTM: Reston, VA, USA, 2003; pp. 263–274. [Google Scholar]
- Son, J.; Lee, M.Y. Exploring the Relationship Between Preservice Teachers’ Conceptions of Problem Solving and Their Problem-Solving Performances. Int. J. Sci. Math Educ. 2021, 19, 129–150. [Google Scholar] [CrossRef]
- Capraro, M.M.; An, S.A.; Ma, T.; Rangel-Chavez, A.F.; Harbaugh, A. An investigation of preservice teachers’ use of guess and check in solving a semi open-ended mathematics problem. J. Math Behav. 2012, 31, 105–116. [Google Scholar] [CrossRef]
- Karp, A. Analyzing and attempting to overcome prospective teachers’ difficulties during problem-solving instruction. J. Math. Teach. Educ. 2010, 13, 121–139. [Google Scholar] [CrossRef]
- Lee, H.S. Facilitating students’ problem solving in a technological context: Prospective teachers’ learning trajectory. J. Math. Teach. Educ. 2005, 8, 223–254. [Google Scholar] [CrossRef]
- González, G.; Eli, J.A. Prospective and in-service teachers’ perspectives about launching a problem. J. Math. Teach. Educ. 2017, 20, 159–201. [Google Scholar] [CrossRef]
- Metallidou, P. Pre-service and in-service teachers’ metacognitive knowledge about problem-solving strategies. Teach. Teach. Educ. 2009, 25, 76–82. [Google Scholar] [CrossRef]
- Fink, A. How to Ask Survey Questions; Sage Publications: Thousand Oaks, CA, USA, 2003. [Google Scholar]
- Pinóeiro, J.L.; Chapman, O.; Castro-Rodrióguez, E.; Castro, E. Exploring prospective primary school teachers’ mathematical problem-solving knowledge. In SEMT19. Opportunities in Learning and Teaching Elementary Mathematics; Novotnaó, J., Moraovaó, H., Eds.; Charles University: Prague, Czech Republic, 2019; pp. 305–315. [Google Scholar]
- Nortes, R.; Nortes, A. Resolución de problemas, errores y dificultades en el grado de maestro de primaria. Rev. Investig. Educ. 2016, 34, 103–117. [Google Scholar] [CrossRef] [Green Version]
- Foster, C.; Wake, G.; Swan, M. Mathematical knowledge for teaching problem solving: Lessons from lesson study. In Proceedings of the Joint Meeting of PME 38 and PME-NA 36, Vancouver, Canada, 15–20 July 2014; Oesterle, S., Liljedahl, P., Nicol, C., Allan, D., Eds.; PME: Vancouver, BC, Canada, 2014; Volume 3, pp. 97–104. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).