Abstract
In this paper, we present a fractal (self-similar) model of acoustic propagation in a porous material with a rigid structure. The fractal medium is modeled as a continuous medium of non-integer spatial dimension. The basic equations of acoustics in a fractal porous material are written. In this model, the fluid space is considered as fractal while the solid matrix is non-fractal. The fluid–structure interactions are described by fractional operators in the time domain. The resulting propagation equation contains fractional derivative terms and space-dependent coefficients. The fractional wave equation is solved analytically in the time domain, and the reflection and transmission operators are calculated for a slab of fractal porous material. Expressions for the responses of the fractal porous medium (reflection and transmission) to an acoustic excitation show that it is possible to deduce these responses from those obtained for a non-fractal porous medium, only by replacing the thickness of the non-fractal material by an effective thickness depending on the fractal dimension of the material. This result shows us that, thanks to the fractal dimension, we can increase (sometimes by a ratio of 50) and decrease the equivalent thickness of the fractal material. The wavefront speed of the fractal porous material depends on the fractal dimension and admits several supersonic values. These results open a scientific challenge for the creation of new acoustic fractal materials, such as metamaterials with very specific acoustic properties.
1. Introduction
A fractal medium [1] is a medium that presents a self-similarity at different scales. Many real-world phenomena exhibit limited or statistical fractal properties [2]. It is not necessary that these objects have the same structure at all scales, they can be approximately self-similar, or they can be self-similar only for discrete values of the scale belonging to a segment where (resp ) is the smallest (resp the largest) scale present in the object [3].
Fractal media can be modeled as measurable metric sets with non-integer dimensions [4,5,6,7,8]. The non-integer Hausdorff dimension [1] is a basic property of fractals. Isotropic fractal material can be characterized by the relation between the mass M of a ball region V of fractal material
where is the characteristic size of fractal media [7,8]. D is the mass dimension of the fractal medium.
The anisotropy of fractal materials can be taken into account by using a power law relation for the mass of the parallelepiped region in the form
is the non-integer dimension along the axis; i = 1, 2, 3; and , , and represent three edges that meet at one vortex. The parameter describes the increase in the mass of the medium when the size of the parallelepiped increases along one axis, and the other sizes of the parallelepiped along the other axes do not change. The fractal mass dimension of the anisotropic fractal medium is given by .
A fractal material can be defined as a medium with a non-integer mass dimension (Equations (1) and (2)). Although the non-integer dimension does not fully reflect all the physics of the fractal medium, it is considered an important property of fractal media.
Different methods based [9,10,11,12,13,14] on a fractal analysis approach have been developed; however, the solution of fractals differential equations for real fractal materials problems is very limited, because of the poor development of this field of mathematics [7,8].
Carpinteri et al. [15,16,17] suggested interesting models with fractional derivatives (so-called local derivatives) of non-integer orders with respect to spatial coordinates for the description of fractal materials. The concern with these models noted by Tarasov [7,8] is that there are not enough differential equations with these fractional derivatives that are solved for various fractal material problems.
Continuum space models of fractal media with fractional integrals have been developed [18,19,20,21]. The kernels of the fractional integrals are defined by the power law density of states [21]. Many applications of these models exist in mechanics and physics. Ostoja-Starzewski and colleagues [22,23,24,25] have suggested a generalization of fractional-integral continuum models for anisotropic fractal media.
The concept of a fractional space (non-integer powers of coordinates) was proposed in the articles [26,27]. Calcagni et al. [28,29,30] developed the fractional space approach well and it was generalized to anisotropic media using fractional multi-spaces [31].
There have been several interpretations [7] of fractional phase space, the first interpretation deriving from dimensional regularization formulae [26], the second from the fractional measure of phase [27,32]. In a third interpretation, the fractional phase space is described by fractional powers of coordinates and moments. Finally, the last interpretation deals with the fractional phase space as a power law type phase space of non-Hamiltonian systems. There are two forms for differentiation in the fractional space approach: (1) classical derivatives with respect to fractional powers of coordinates [26,27,32], and (2) fractional derivatives of non-integer orders with respect to coordinates. Confusion [28,29,30] arises from the use of the term “fractional space” as notified in [7]. Indeed, this term is used for the effective space (where integration and differentiation of integer orders for these spaces are used) and whose coordinates are non-integer powers of coordinates of the physical space. The fractional space coordinates are considered as effective coordinates (via density of states factors) which are fractional powers of the real space coordinates of the physical system.
Wilson [33], Stillinger [34], and Collins [35] have developed an interesting approach based on integration and differentiation on non-integer spaces. Integration in these spaces is used for dimensional regularization in physics domains such as quantum theory [35,36,37] and in physical kinetics [38,39]. Laplace scalar operators were proposed by Stillinger [34], and Palmer and Stavrinou [40], for non-integer dimensional spaces and have been successfully used in various areas of quantum mechanics and physics [34,40,41,42,43,44,45,46], electrodynamics [47,48], scattering processes, and [49] general relativity [50,51]. The generalizations of the gradient, divergence, curl, and Laplace vector operators for fractional and non-integer spaces to describe anisotropic fractal media are not taken into account by the product measure approach in [34,40]. These generalizations were given in the work of Tarasov [7,8]. Balankin et al. [52] develop the differential vector calculus based on the notion of metric derivative. The authors of [6] suggest two possible definitions of vector differential operators in fractional space.
In this work, we use the fractal model and the concept of the gradient operator introduced by Tarasov [7,8] to describe the acoustic propagation in a fractal porous medium with a rigid structure, in the high frequency domain. The propagation equation is derived in the time domain and solved analytically using the Laplace transformation. A discussion on the impact of the fractal dimension on the propagation is given.
2. Product Measure
Palmer and Stavrinou [40] suggested the product measure approach for non-integer dimensional spaces where each orthogonal coordinate has its own dimension. The method developed by Tarasov [7,8] is a modification of Stillinger’s [34] and Svozils’s [53] methods for the product measure approach. Using the product measure approach for , the single-variable measures with point coordinates , , and are
where is a non-integer (fractional) dimension of the line. The absolute value of x in is taken in order to consider the positive and negative values of x.
The following effective set of coordinates is introduced [7] for the non-integer dimensional space approach:
which is connected with the single-variable measure [34,40]:
with
which is the density of states defined by the measure for integration in non-integer dimensional space. It is possible [7] to obtain the expression of lengths using (6):
which is the non-integer dimensional sphere volume.
The differential operator that takes into account the density of states is given by
These derivatives are not fractional derivatives, nor fractal derivatives [7].
Tarasov [7] defines the Nabla operator using the effective coordinates by
where is the multi-index, and is defined by (6).
Using the expression (9) of the nabla operator in non-integer dimensional space, we will try to rewrite the basic equations of acoustics in a porous medium with a rigid structure and to solve the propagation equation and derive the reflection and transmission operators.
3. Acoustic Equations for Propagation in Rigid Porous Material
In the free fluid, the Euler equation is given by [54]
where is the fluid density, is the acoustic velocity field, and p the pressure acoustic field. The second constitutive relation between pressure and velocity is given by
where K is the compressibility modulus. The two relations (10) and (11) are the basic equations of acoustics, for free fluid.
Using Equations (10) and (11), it is easy to derive the wave equation
where is the velocity of sound in free fluid.
Consider the acoustic propagation in a homogeneous and isotropic porous material saturated with air, such as the porous foams or fibrous materials used for passive acoustic control (noise reduction). In such materials, the solid structure remains immobile and the acoustic wave propagates only in the fluid (air) that saturates the porous medium. We consider the equivalent fluid model [55], which is a simplified case of the general Biot [56,57] model, in which the structure vibrates. The fluid/structure interactions are described by the dynamic tortuosity for viscous effects [58] and the dynamic compressibility for thermal exchanges [55,59]. In the frequency domain, the acoustic fields satisfy the following equivalent-fluid macroscopic equations [55]:
In these equations, . and are the Fourier transforms of and , respectively, thereby obtaining the Helmholtz equation in a porous medium in the presence of visco-thermal losses within the framework of the theory of equivalent fluid:
where the phase velocity is given by .
In the time domain [54,60], the constitutive relations (13) for a porous medium are given by
where and are the tortuosity and compressibility operators [54,60].
The propagation equation in the time domain is given by
This wave equation describes the losses and the memory effects in the porous medium due to the fluid–structure interactions. The operators and express the visco-thermal interactions between the fluid (air) and the structure.
4. Fractal Porous Material and Fractional Calculus
A fractal medium is considered as a medium with non-integer mass dimension [7,8]. One of the main characteristic properties of fractal materials is the fractal (non-integer) dimension. We distinguish three cases of scale invariance in fractal porous media as reported by Balankin et al. [61]; (1) porous media in which the solid matrix is fractal, while the fluid pore space is non-fractal, such as Menger’s sponge and fractal aggregates; (2) porous media in which the fluid pore space is fractal, while the solid matrix is non-fractal, such as media with a fractal networks of pores or fractures, or Menger’s sponge; and (3) porous materials with fractal fluid/solid interfaces, e.g., fracture surfaces. In this work, we are in the second case in which the solid is non-fractal while the fluid saturating the porous medium is fractal, i.e., the fluid presents the property of self similarity according to relation (1).
In this section, we will write the equations of acoustics in a fractal porous medium using the gradient operator (Equation (9)). In this case, Equations (15) become
The propagation of sound in porous materials with a rigid structure depends on the frequency domain studied [55]. The high and low frequencies are defined by comparing the viscous and thermal skin thickness and with pore radius r. In the asymptotic domain (high frequencies), the skin thicknesses become narrower and the viscous effects are concentrated in a small volume small volume near the frame and [55,59].
In the high-frequency range, the dynamic tortuosity and compressibility are given by [55,58]
where is the tortuosity, the viscous characteristic length, the thermal characteristic length, and the adiabatic constant. In the time domain, the expressions of the temporal operators in the asymptotic domain (high frequency range) are given by [54,60]
where is the Dirac function. In this model, the time convolution of with a function is interpreted as a semi-derivative operator according to the definition of the fractional derivative of order given in Samko and coll [62],
where is the gamma function.
For a propagation along the x axis, the constitutive relations (15) will be given by
where is a fractional derivative following the definition (20). The differential operator is given by relation (8).
The coefficients A and B are given by
c is the front wave velocity in a non fractal (no self similarity) porous materials. By replacing by its expression (Equation (6)), the propagation Equation (23) in a fractal porous material is given by
where
The front wave velocity in the fractal porous material is given by
which shows that the speed of the wavefront in the fractal material is self-similar.
5. Solution of Fractional Propagation Equation in Fractal Porous Material
In this section, we will try to solve the propagation Equation (24) in the Laplace domain, using the initial conditions
we note the Laplace transform of defined by
The Laplace transform of , Equation (23) becomes
where
By replacing the expression of given in Equation (6), we obtain
To explicit the solution to Equation (28), we proceed to the function change: where is a parameter to be determined. Equation (28) becomes
by tacking , Equation (29) is reduced to
which is transformed by the variable change , into
which is a differential equation of Bessel, its general solution being given by
where and are the modified Bessel functions of index .
The solution to Equation (30) is
The solution to Equation (28) is the given by
which can be written as:
where and are two new constants given by
The boundary conditions are
By taking the finite solution at infinity, which corresponds to the physical solution to our problem:
where is the Laplace transform of the incident signal .
The calculation of the inverse Laplace transform of a mathematical form similar to relation (35) is given in the case of a non-fractal porous materials [63] by the following Green function:
where
and
is the Green function of the medium. In the time domain, the expression of the acoustic pressure inside the medium is obtained by doing the time convolution of the Green function of the medium with the incident signal .
6. Slab of Fractal Porous Material
The geometry of the problem is given in Figure 1. A slab of fractal porous material occupies the region .

Figure 1.
Geometry of the problem.
Consider an incident sound wave launched in the region . In the region on the left of the material, the expression of the acoustic wave is the sum of the incident and reflected fields
where is the velocity in the free fluid , is the field in the region , is the incident field, and the reflection operator. In the region , the transmitted field is given by
is the front wave velocity in the fractal porous material given by Equation (25), and (x,t) is the field in the region .
The Laplace transform of and is given by
where and are, respectively, the Laplace transforms of and . represents the Laplace transform of (incident field). and are the Laplace transforms of the reflection and transmission operators, respectively.
It is assumed the following continuity relations at the boundary of the material
The expression of the acoustic pressure inside the fractal porous material is given by
where sinh is the hyperbolic sine function. The expression (42) admits as development:
The general solution of the fractional wave equation in the fractal porous material is given by
where is the Green function of the fractal porous medium given by Equation (36).
7. Reflection and Transmission Coefficients
To simulate waves reflected and transmitted by a porous material of non-integer dimensional space, it is necessary to calculate the reflection and transmission coefficients. The boundary conditions at the interfaces and of the flow velocity are needed. In regions (1) () and (2) (), the Euler equation is written as
where and are the acoustic velocity fields in regions (1) and (2), respectively. Note that the spatial derivative in the Euler equation in the region corresponding to the fractal porous material is given by Equation (8). The tortuosity operator is equal to 1 in the free space (region (1); ).
The flow continuity equation at is given by
where is the porosity of the fractal porous material. From (45)–(47) we can write
It is easier to perform the calculations in the Laplace domain. Equation (48) can be written in the Laplace domain as
where is the Laplace transform of . Using Equation (39), we obtain
and
Equation (49) gives
Equation (52) can be simplified to
At the interface , the Euler equation and the continuity of the flow velocity equation lead to the equation
which is written in the Laplace domain as
By replacing and by their expressions, we obtain
The equation system constituted by Equations (53) and (56) allows the calculation of the reflection and transmission coefficients and . This system can be written as
The expressions of the reflection and transmission coefficients can be developed as
Theses expressions take into account the n-multiple reflections inside the fractal porous material. By considering only the first reflections at the interfaces and ;
In the time domain, we obtain the following expressions of the reflection and transmission operators for a fractal porous material:
When the fractal dimension is equal to 1; (), we find the non-fractal case, the expressions of the reflection and transmission operators become
We find exactly the same expressions of reflection and transmission obtained for the case of classical (non-fractal) porous media [60].
Comparing the results for the fractal (Equation (61)) and non-fractal (Equation (62)) cases, we can conclude that the change in the expressions of the reflection and transmission operators amounts to replacing the thickness of the material L (in the non-fractal case) with the thickness in the fractal case. This result could have been predicted using the effective coordinate relation (4) where we find the effective thickness of the fractal medium as a function of the thickness of the non-fractal medium.
Figure 2 shows the variation of the equivalent thickness in the fractal porous material as a function of the fractal dimension . The different curves with distinct colors correspond to values of the thickness L of the non-fractal porous material. When the value of the fractal dimension is equal to 1 (), the equivalent thickness in the porous fractal material is equal to the thickness of the porous non-fractal material (). For thickness L = 0.01 m (blue curve), the value of the equivalent thickness varies from its lowest value ( m, for ), to its maximum value ( m, for ). We see here that the value of the equivalent thickness varies from m to m when changing the value of the fractal dimension () from 1 to 0. This result is very interesting and shows that it is possible to increase the value of the equivalent thickness by a ratio of 50, which will have the effect of significantly increasing the acoustic attenuation in the fractal porous material. For the thicknesses ( m and m), corresponding to the red and green figures, respectively, we notice that the value of the equivalent thickness is more important for low values of the fractal dimension, but with a less important ratio than for the blue curve corresponding to the value of m. We notice that for values above (black curve), the trend changes for the variation of as a function of the fractal dimension, indeed the variation of the equivalent thickness is not important for m. However, for higher thicknesses (i.e., m and m), the trend of the variation of as a function of is totally reversed, i.e., the equivalent thickness now increases with the fractal dimension, which is not the case for low values of L. This study on the equivalent length as a function of the fractal dimension is very interesting because it shows us that it is possible to predict the acoustic properties of a fractal porous material just by acting on its fractal dimension; one can thus increase or decrease the thickness of a porous material “virtually” just by increasing or decreasing the value of its fractal dimension, and it is possible in certain cases to have gains of the order of 50 as for the thickness m, which is a considerable advance.
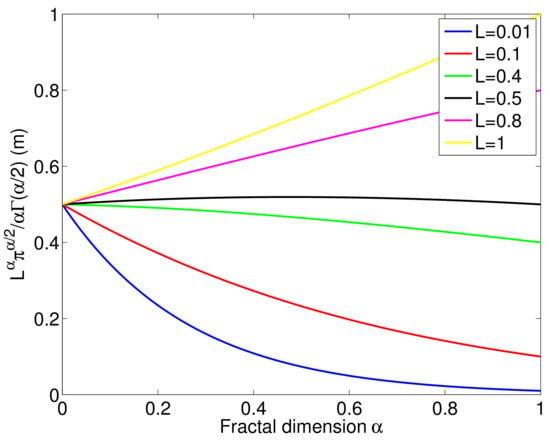
Figure 2.
Variation of the equivalent thickness () in the fractal material as a function of the fractal dimension.
Let us now study the effect of the wavefront speed (Equation (25)) as a function of the fractal dimension (Figure 3). Let us recall again here that for the wavefront velocity in the fractal porous material is equal to the wavefront velocity in the non-fractal porous material . Here, in this example we have the tortuosity equal to and m/s.
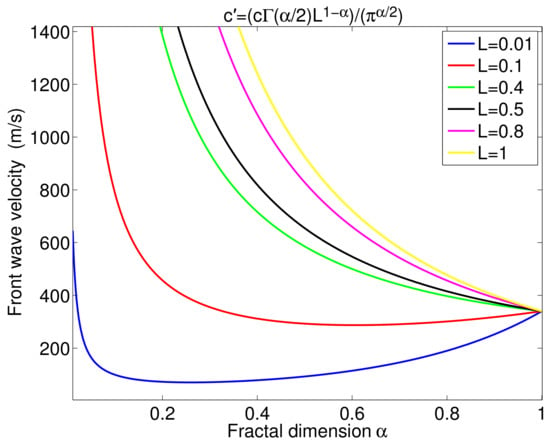
Figure 3.
Variation of the front wave velocity in the fractal material as a function of the fractal dimension.
For thicknesses m and m, by decreasing the value of the fractal dimension , the wavefront velocity of the fractal material decreases (Figure 3), making the material more resistive and less permeable. For very low values of , the velocity tends to large values, which is due to the mathematical properties of the function when x tends to zero. For thicknesses greater than m, we notice that the wavefront velocity increases rapidly with the fractal dimension, reaching supersonic values [64,65]. Let us recall that in classical non-fractal porous materials [54,55,58,59,60,63], the speed of the wavefront is always lower than the speed of sound in air, however we see here that for fractal porous materials, this speed can be higher than the speed of sound in air (supersonic speed), which constitutes an interesting novelty for porous materials.
The results obtained here challenge us for several reasons. We have analytical expressions in the time domain for the reflected and transmitted waves (knowing the incident signal and the properties of the fractal porous medium), which allows us to solve the direct problem and thus predict the propagation of ultrasonic waves in fractal porous media modeled as non-integer dimensional materials in space, but also to predict the reflected and transmitted waves.
Knowing expressions (58) and (59), it is now possible to solve the inverse problem, which would allow us to obtain the properties of the fractal porous material knowing the incident, reflected and/or transmitted fields. We can see what effect the fractal dimension has on the propagation and attenuation of reflected and transmitted waves.
This study on acoustic propagation in fractal porous materials has revealed several very interesting physical phenomena: the fractal porous material can be modeled as a classical non-fractal porous material but with an effective thickness that depends on the fractal dimension. By acting on this dimension, it is possible to increase or decrease the effective thickness of the fractal material depending on the value of the thickness of the non-fractal material. It is also possible to generate a wavefront velocity that can be supersonic, which confers unusual and very interesting physical and acoustic properties to these materials. This result opens up very interesting perspectives for the development of new acoustic materials and metamaterials with particular acoustic properties by acting on the self-similarity and fractality of the material.
8. Conclusions
In this paper, we used the Tarasov model [7] to describe the ultrasonic propagation in a porous material with a rigid structure in the time domain. The acoustic equations were written for a fractal porous material with a rigid structure, using the concept of the nabla operator in a non-integer dimensional medium. We obtained a fractional order propagation equation with non-constant coefficients, depending on the thickness, which is a consequence of the self-similarity of the material and thus of its fractal nature. The fluid–structure interactions were described by fractional operators in the time domain to model the visco-thermal losses in the porous medium. The propagation equation was solved analytically in the time domain by making transformations in the Laplace domain. The problem of a layer of porous material was treated by taking into account the two interfaces of the material, thus making it possible to derive the reflection and transmission operators in the time domain. The results obtained allowed us to conclude that a fractal porous material can be considered as a non-fractal porous material, but with a effective thickness depending on the fractal dimension. By varying the fractal dimension, we can have effective thicknesses that increase by a factor of 50, which would allow for significant acoustic attenuation in the material. This effective thickness of the porous fractal material can increase or decrease with the fractal dimension; this all depends on the value of the thickness of the porous non-fractal material. The velocity of the wavefront in the fractal medium also depends on its fractal dimension and we have shown that this velocity can have supersonic values. These results are very promising for the study of fractal porous materials, especially for applications in metamaterials giving them particular physical and acoustic properties. These works are for the moment theoretical with analytical and numerical results, we hope in the future to make experimental applications on fractal porous materials.
Author Contributions
Writing—original draft preparation, Z.E.A.F., M.F., E.O. and C.D.; analysis, analytical calculations and processing of results, Z.E.A.F., M.F., N.O.O., E.O. and C.D.; writing—review and editing, Z.E.A.F., M.F., N.O.O., E.O. and C.D.; resources, Z.E.A.F., M.F., E.O. and C.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mandelbrot, B.B. The Fractal Geometry of Nature, updated and augmented ed.; W. H. Freeman: New York, NY, USA, 1983; 468p. [Google Scholar]
- Barnsley, M.F. Fractals Everywhere; Morgan Kaufmann: San Mateo, CA, USA, 1993. [Google Scholar]
- Williams, J.K.; Dawe, R.A. Fractals: An overview of potential applications to transport in porous media. Transp. Porous Media 1986, 1, 201–209. [Google Scholar] [CrossRef]
- Falconer, K.F. The Geometry of Fractal Sets; Cammbridge University Press: Cammbridge, UK, 1985. [Google Scholar]
- Feder, J. Fractals; Plenum Press: New York, NY, USA, 1988. [Google Scholar]
- Balankin, A.S. Fractional space approach to studies of physical phenomena on fractals and in confined low-dimensional systems. Chaos Solitons Fractals 2020, 132, 109572. [Google Scholar] [CrossRef]
- Tarasov, V.E. Anisotropic Fractal Media by Vector calculus in non-integer dimensional space. J. Math. Phys. 2014, 55, 083510. [Google Scholar] [CrossRef]
- Tarasov, V.E. Vector calculus in non-integer dimensional space and itss applications to fractal media. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 360–374. [Google Scholar] [CrossRef]
- Kugami, J. Analysis on Fractals; Cammbridge University Press: Cammbridge, UK, 2001. [Google Scholar]
- Strichartz, R.S. Differential Equations on Fractals; Princeton University Press: Princeton, NJ, USA; Oxford, UK, 2006. [Google Scholar]
- Strichartz, R.S. Analysis on Fractals. Not. Am. Math. Soc. 1999, 10, 1199–1208. [Google Scholar]
- Harrison, J. Flux across nonsmooth boundaries and fractal Gauss/Geren/Stokes’ theorems. J. Phys. A 1999, 32, 5317–5328. [Google Scholar] [CrossRef]
- Kumagai, T. Recent developments of analysis on fractals. In Selected Papers on Analysis and Related Topics; Amercian Mathematical Society Series 2; American Mathematical Society: Providence, RI, USA, 2008; Volume 223, pp. 81–96. [Google Scholar]
- Derfel, G.; Grabner, P.; Vogl, F. Laplace operators on fractals and related functional equations. J. Phys. A 2012, 45, 463001. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B.; Cornetti, P. Static-kinematic duality and the principle of virtual work in the mechanics of fractal media. Comput. Methods Appl. Mech. Eng. 2001, 191, 3–19. [Google Scholar] [CrossRef]
- Carpinteri, A.; Cornetti, P. A fractional calculus approach to the description of stress and strain localization in fractal media. Chaos Solitons Fractals 2002, 13, 85–94. [Google Scholar] [CrossRef]
- Carpinteri, A.; Chiaia, B.; Cornetti, O. On the mechanics of quasi-brittle materials with a fractal microstructure. Eng. Fract. Mech. 2003, 15, 2321–2349. [Google Scholar] [CrossRef]
- Tarasov, V.E. Continuum medium model for fractal media. Phys. Lett. A 2005, 336, 167–174. [Google Scholar] [CrossRef]
- Tarasov, V.E. Wave equation for fractal solid string. Mod. Phys. Lett. B 2005, 15, 721–728. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional hydrodynamic equations for fractal media. Ann. Phys. 2005, 318, 286–307. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particules, Fields and Media; Springer: New York, NY, USA, 2011. [Google Scholar]
- Demmie, P.N.; Ostoja-Starzewski, M. Waves in fractal media. J. Elast. 2011, 104, 187–204. [Google Scholar] [CrossRef]
- Joumaa, H.; Ostoja-Starzewski, M. Acoustic-elastoodynamic interaction in isotropic fractal media. Eur. Phys. J. Spec. Top. 2013, 222, 1951–1960. [Google Scholar] [CrossRef]
- Ostoja-Starzewski, M. Electromagnetism on anisotropic fractals. Zeitschrift für Angewandte Mathematik and Physik (J. Appl. Math. Mech.) 2013, 64, 381–390. [Google Scholar]
- Ostoja-Starzewski, M.; Li, J.; Joumaa, H.; Demmie, P.N. From fractal media to continuum mechanics. Zeitschrift für Angewandte Mathematik and Physik 2014, 94, 373–401. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional generalisation of Liouville equations. Chaos 2004, 14, 123–127. [Google Scholar] [CrossRef][Green Version]
- Tarasov, V.E. Fractional Liouville and BBGKI equations. J. Phys. Conf. Ser. 2005, 7, 17–33. [Google Scholar] [CrossRef]
- Calcagni, G. Quandtum filed theory, gravity and cosmology in a fractal universe. J. High Energy Phys. 2010, 120, 120–158. [Google Scholar] [CrossRef]
- Calcagni, G. Geometry of fractional spaces. Adv. Theor. Math. Phys. 2012, 16, 549–644. [Google Scholar] [CrossRef]
- Calcagni, G.; Nardelli, G. Momentum transforms and Laplacians in fractional spaces. Adv. Theor. Math. Phys. 2012, 16, 1315–1348. [Google Scholar] [CrossRef]
- Calcagni, G.; Nardelli, G. Spectral dimension and diffusion in multi-scale spacetimes. Phys. Rev. D 2013, 88, 124025. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional systems and fractional Bogoliubov hierarchy equations. Phys. Rev. E 2005, 71, 0111102. [Google Scholar] [CrossRef]
- Wilson, K.G. Quandtum field—Theory models in less than 4 dimensions. Phys. Rev. D 1973, 10, 2911–2926. [Google Scholar] [CrossRef]
- Stillinger, F.H. Axiomatic basis for spaces with non-integer dimensions. J. Math. Phys. 1977, 18, 1224–1234. [Google Scholar] [CrossRef]
- Collins, J.C. Renormalization; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- ’t Hooft, G.; Veltman, M. Regularization and renormalization og gauge fields. Nucl. Phys. B 1972, 44, 189–213. [Google Scholar] [CrossRef]
- Leibbrandt, G. Introduction to the technique of dimensional regularization. Rev. Mod. Phys. 1975, 47, 849–876. [Google Scholar] [CrossRef]
- Wilson, K.G.; Fisher, M.E. Critical exponents in 3.99 dimensions. Phys. Rev. Lett. 1972, 28, 240–243. [Google Scholar] [CrossRef]
- Wilson, K.G.; Kogut, J. The renormalization group and the ϵ expansion. Phys. Rep. 1974, 12, 75–199. [Google Scholar] [CrossRef]
- Palmer, C.; Stavrinou, P.N. Equations of motion in a non-integer-dimensional space. J. Phys. A 2004, 37, 6987–7003. [Google Scholar] [CrossRef]
- He, X.-F. Excitons in anisotropic solids: The model of fractional-dimensional space. Phys. Rev. B 1991, 43, 2063–2069. [Google Scholar] [CrossRef]
- De Dios-Leyva, M.; Bruno-Alfonso, A.; Matos-Abiague, A.; Oliveira, L.E. Fractional dimensional space and applications in quantum-confined semiconducting heterostructures. J. Appl. Phys. 1997, 82, 3155–3157. [Google Scholar] [CrossRef]
- Thilagham, A. Pauli bloking effects in quantum wells. Phys. Rev. B 1999, 59, 3027–3032. [Google Scholar] [CrossRef]
- Muslih, S.I.; Agrawal, O.P. A scaling method and its applications to problems in fractional dimensional space. J. Math. Phys. 2009, 50, 123501. [Google Scholar] [CrossRef]
- Muslih, S.I.; Agrawal, O.P. Shrödinger equation in fractional space. In Fractional dynamics and Control; Baleanu, D., Tenreiro Machado, J.A., Luo, A.C.J., Eds.; Springer: New York, NY, USA, 2012; Chapter 17; pp. 209–215. [Google Scholar]
- Muslih, S.I.; Baleanu, D. Fractional multipoles in fractional space. Nonlinear Anal. Real World Appl. 2007, 8, 198–203. [Google Scholar] [CrossRef]
- Zubair, M.; Mughal, M.J.; Naqvi, Q.A. Electromagnetic Fileds and Waves in Fractional Dimensional Space; Springer: Berlin, Germany, 2012. [Google Scholar]
- Zubair, M.; Mughal, M.J.; Naqvi, Q.A. An exact solution of the spherical wave equation in D-dimensional fractional space. J. Electromagn. Waves Appl. 2011, 25, 1481–1491. [Google Scholar] [CrossRef]
- Lucena, L.S.; da Silva, L.R.; Tateishi, A.A.; Lenzi, M.K.; Ribeiro, H.V.; Lenzi, E.K. Solutions for a fractional diffusion equation with noninteger dimensions. Nonlinear Anal. Real World Appl. 2012, 13, 1955–1960. [Google Scholar] [CrossRef]
- Sadallah, M.; Muslih, S.I.; Baleanu, D. Equations of motion for Einstein’s field in non-integer dimensional space. Czechoslov. J. Phys. 2006, 56, 323–328. [Google Scholar] [CrossRef]
- Sadallah, M.; Muslih, S.I. Solution of the equations of motion for Einstein’s field in fractional D dimenion space-time. Int. J. Theor. Phys. 2009, 48, 3312–3318. [Google Scholar] [CrossRef]
- Balankin, A.S.; Bory-Reyes, J.; Shapiro, M. Towards a physics on fractals: Differential vector calculus in three-dimensional continuum with fractal metric. Physica A 2016, 444, 345–359. [Google Scholar] [CrossRef]
- Svozil, K. Quantum field theory on fractal spacetime: A new regularization method. J. Phys. A 1987, 20, 3861–3875. [Google Scholar] [CrossRef]
- Fellah, Z.E.A.; Depollier, C. Transient acoustic wave propagation in rigid porous media: A time-domain approach. J. Acoust. Soc. Am. 2000, 107, 683–688. [Google Scholar] [CrossRef]
- Allard, J.F. Propagation of Sound in Porous Media: Modeling Sound Absorbing Materials; Chapman and Hall: London, UK, 1993. [Google Scholar]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Johnson, D.L.; Koplik, J.; Dashen, R. Theory of dynamic permeability and tortuosity in fluid-saturated porous media. J. Fluid Mech. 1987, 176, 379–402. [Google Scholar] [CrossRef]
- Lafarge, D.; Lemarinier, P.; Allard, J.-F.; Tarnow, V. Dynamic compressibility of air in porous structures at audible frequencies. J. Acoust. Soc. Am. 1997, 102, 1995–2006. [Google Scholar] [CrossRef]
- Fellah, Z.E.A.; Fellah, M.; Lauriks, W. Direct and inverse scattering of transient acoustic waves by a slab of rigid porous material. J. Acoust. Soc. Am. 2003, 113, 61–72. [Google Scholar] [CrossRef] [PubMed]
- Balankin, A.S.; Valdivia, J.-C.; Marquez, J.; Susarrey, O.; Solorio-Avila, M.A. Anomalous diffusion of fluid momentum and Darcy-like law for laminar flow in media with fractal porosity. Phys. Lett. A 2016, 380, 2767–2773. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1993; pp. 93–112. [Google Scholar]
- Fellah, Z.E.A.; Fellah, M.; Lauriks, W.; Depollier, C.; Chapelon, J.Y.; Angel, Y.C. Solution in time domain of ultrasonic propagation equation in a porous material. Wave Motion 2003, 38, 151–163. [Google Scholar] [CrossRef]
- Tarasov, V.E. Acoustic waves in fractal media: Non-integer dimensional spaces approach. Wave Motion 2016, 63, 18–22. [Google Scholar] [CrossRef]
- Fellah, M.; Fellah, Z.E.A.; Berbiche, A.; Ogam, E.; Mitri, F.G.; Depollier, D. Transient ultrasonic wave propagation in porous material of non-integer space dimension. Wave Motion 2017, 72, 276–286. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).