The Mathematics of Quasi-Diffusion Magnetic Resonance Imaging
Abstract
1. Introduction
2. Theory
2.1. Quasi-Diffusion Imaging
2.2. General Properties of the Mittag–Leffler Function
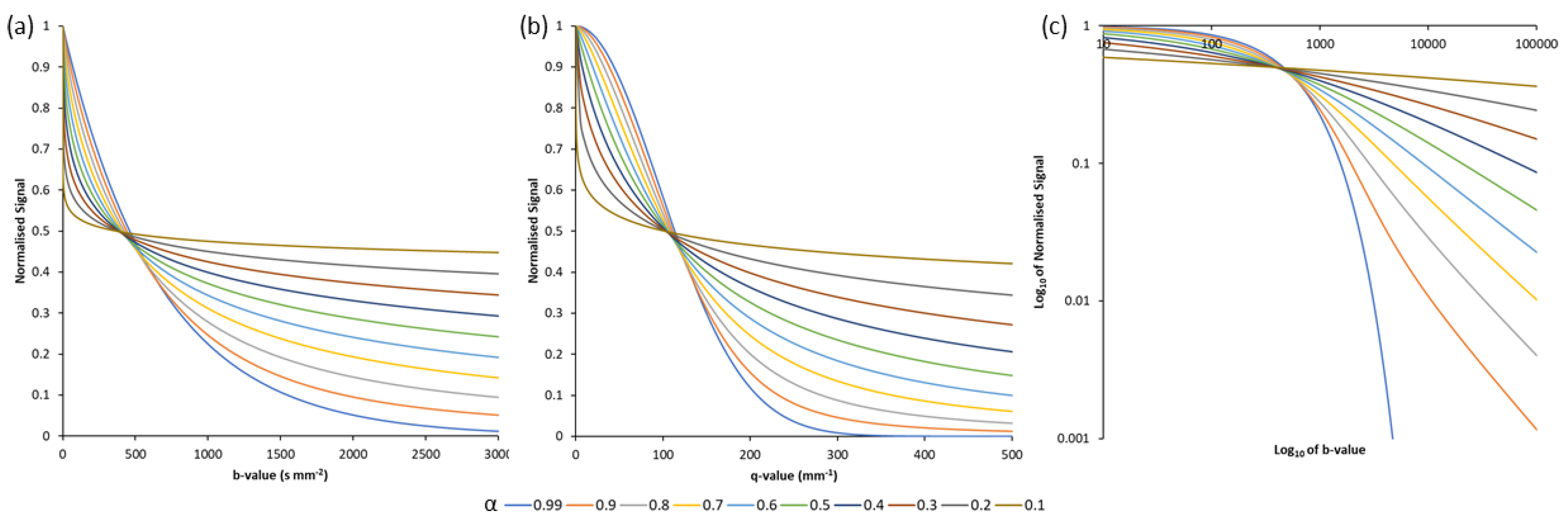
2.3. Asymptotic Properties of the Quasi-Diffusion Characteristic Equation
2.4. The Laplace Transform of the Quasi-Diffusion Characteristic Equation
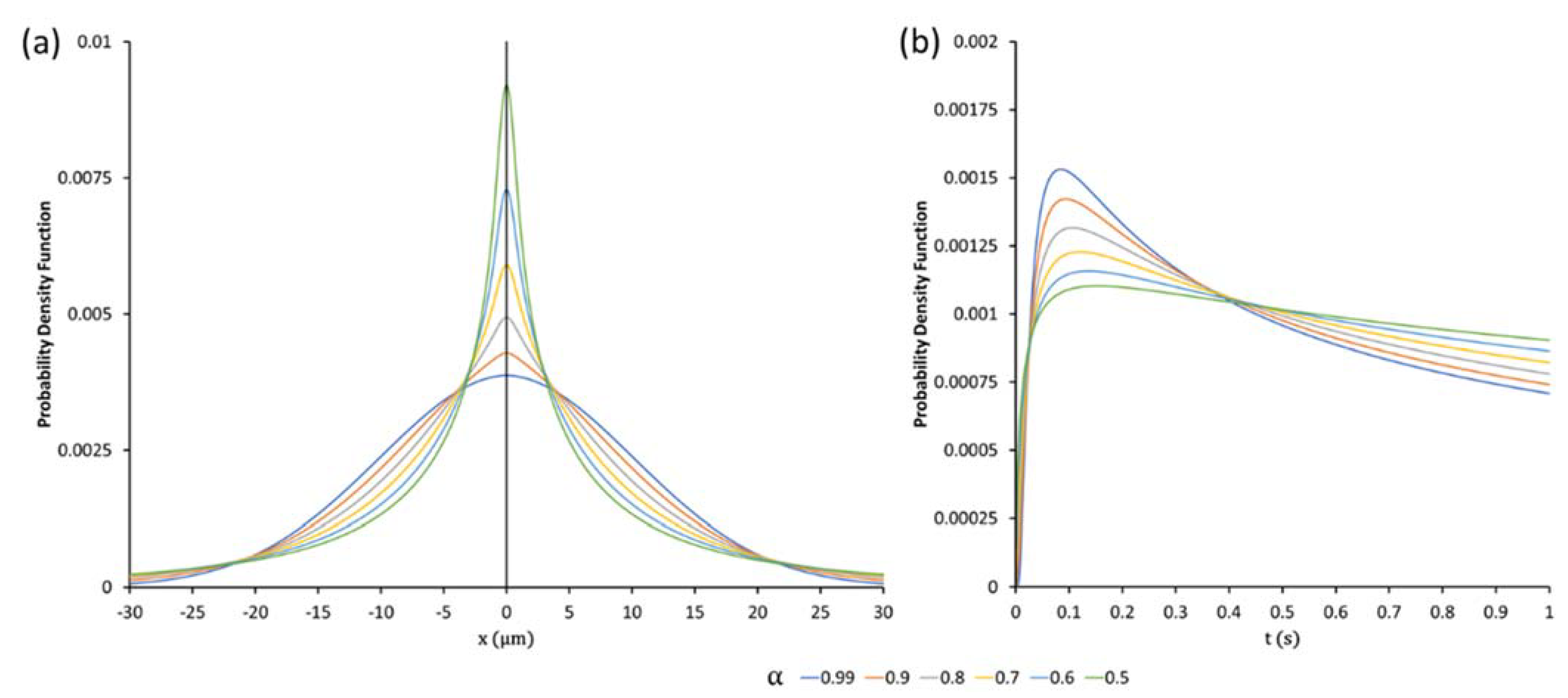
2.5. The Quasi-Diffusion Propagator
2.6. Application of Quasi-Diffusion MRI to Mean Apparent Propagator Imaging
3. Examples
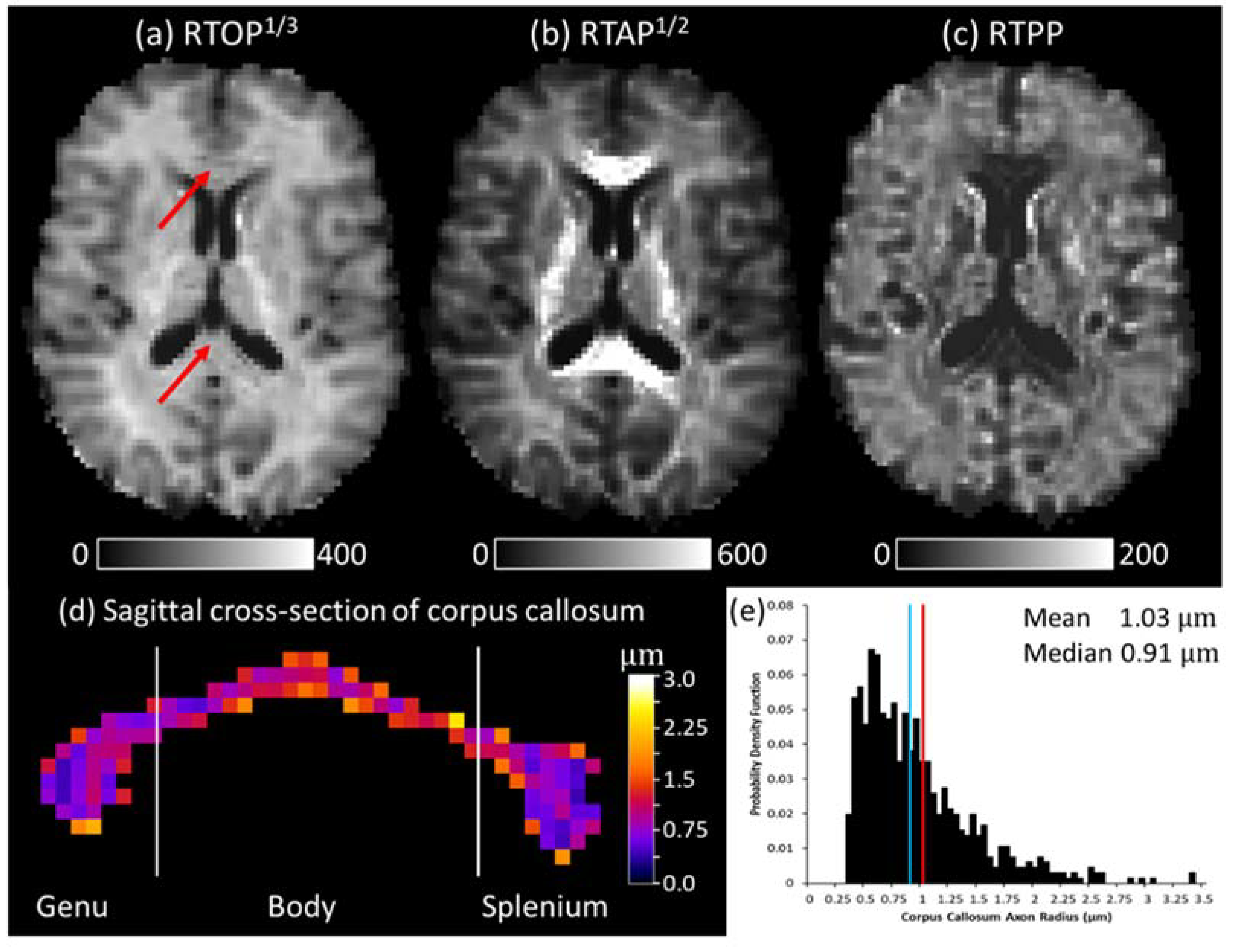
3.1. Quasi-Diffusion Mean Apparent Propagator Imaging of the Corpus Callosum
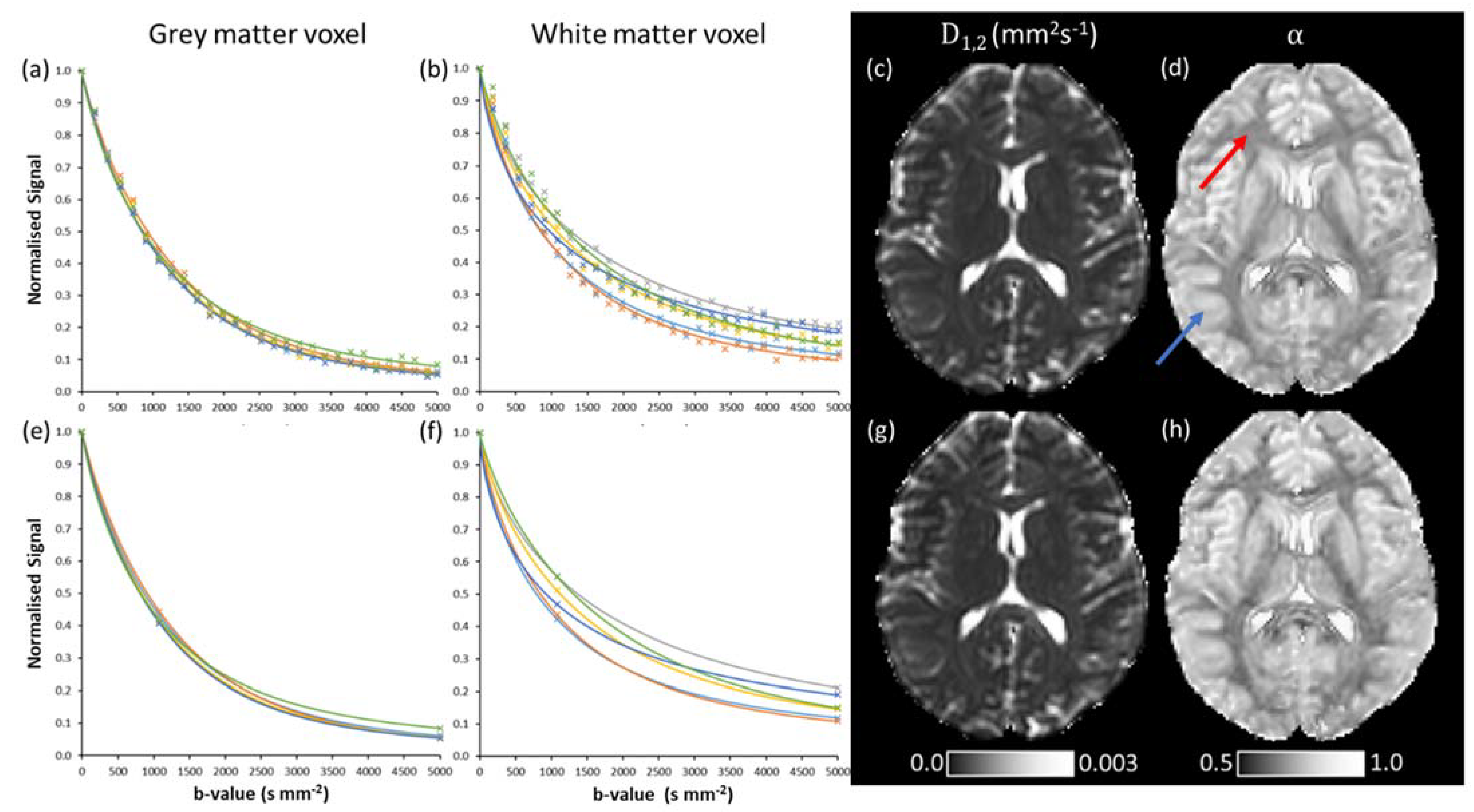
3.2. Quasi-Diffusion Imaging of Brain Tumour
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Diffusion Magnetic Resonance Imaging Data
Appendix A.1. Human Participants
Appendix A.2. Acquisition of Diffusion Magnetic Resonance Imaging Data
References
- Barrick, T.R.; Spilling, C.A.; Ingo, C.; Madigan, J.; Isaacs, J.D.; Rich, P.; Jones, T.L.; Magin, R.L.; Hall, M.G.; Howe, F.A. Quasi-Diffusion Magnetic Resonance Imaging (QDI): A Fast, High b-Value Diffusion Imaging Technique. NeuroImage 2020, 211, 116606. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The Random Walk’s Guide to Anomalous Diffusion: A Fractional Dynamics Approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Continuous Time Random Walk, Mittag–Leffler Waiting Time and Fractional Diffusion: Mathematical Aspects. In Anomalous Transport; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008; pp. 93–127. ISBN 978-3-527-62297-9. [Google Scholar]
- Meerschaert, M.; Scheffler, H.P. Continuous time random walks and space-time fractional differential equations. In Basic Theory; Kochubei, A., Luchko, Y., Eds.; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019; pp. 385–406. ISBN 978-3-11-057162-2. [Google Scholar]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S. Applications to Stochastic Models. In Mittag–Leffler Functions, Related Topics and Applications; Gorenflo, R., Kilbas, A.A., Mainardi, F., Rogosin, S., Eds.; Springer Monographs in Mathematics; Springer: Berlin/Heidelberg, Germany, 2020; pp. 339–379. ISBN 978-3-662-61550-8. [Google Scholar]
- Jones, D.K. Diffusion MRI; Oxford University Press: Oxford, UK, 2010; ISBN 978-0-19-970870-3. [Google Scholar]
- Johansen-Berg, H.; Behrens, T.E.J. Diffusion MRI: From Quantitative Measurement to In Vivo Neuroanatomy; Academic Press: Cambridge, MA, USA, 2013; ISBN 978-0-12-405509-4. [Google Scholar]
- Grebenkov, D.S. From the Microstructure to Diffusion NMR, and Back. In Diffusion NMR of Confined Systems; RSC Publishing: Cambridge, UK, 2016; Chapter 3; pp. 52–110. [Google Scholar]
- Novikov, D.S.; Kiselev, V.G.; Jespersen, S.N. On Modeling. Magn. Reson. Med. 2018, 79, 3172–3193. [Google Scholar] [CrossRef] [PubMed]
- Afzali, M.; Pieciak, T.; Newman, S.; Garyfallidis, E.; Özarslan, E.; Cheng, H.; Jones, D.K. The Sensitivity of Diffusion MRI to Microstructural Properties and Experimental Factors. J. Neurosci. Methods 2021, 347, 108951. [Google Scholar] [CrossRef]
- Callaghan, P.T. Principles of Nuclear Magnetic Resonance Microscopy; Clarendon Press: Oxford, UK, 1993; ISBN 978-0-19-853997-1. [Google Scholar]
- Hall, M.G. The MR Physics of Advanced Diffusion Imaging. In Proceedings of the Computational Diffusion MRI; Fuster, A., Ghosh, A., Kaden, E., Rathi, Y., Reisert, M., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 1–20. [Google Scholar]
- Magin, R.L.; Abdullah, O.; Baleanu, D.; Zhou, X.J. Anomalous Diffusion Expressed through Fractional Order Differential Operators in the Bloch–Torrey Equation. J. Magn. Reson. 2008, 190, 255–270. [Google Scholar] [CrossRef] [PubMed]
- Bennett, K.M.; Schmainda, K.M.; Bennett, R.; Rowe, D.B.; Lu, H.; Hyde, J.S. Characterization of Continuously Distributed Cortical Water Diffusion Rates with a Stretched-Exponential Model. Magn. Reson. Med. 2003, 50, 727–734. [Google Scholar] [CrossRef] [PubMed]
- Hall, M.G.; Barrick, T.R. From Diffusion-Weighted MRI to Anomalous Diffusion Imaging. Magn. Reson. Med. 2008, 59, 447–455. [Google Scholar] [CrossRef]
- Palombo, M.; Gabrielli, A.; De Santis, S.; Cametti, C.; Ruocco, G.; Capuani, S. Spatio-Temporal Anomalous Diffusion in Heterogeneous Media by Nuclear Magnetic Resonance. J. Chem. Phys. 2011, 135, 034504. [Google Scholar] [CrossRef]
- Capuani, S.; Palombo, M.; Gabrielli, A.; Orlandi, A.; Maraviglia, B.; Pastore, F.S. Spatio-Temporal Anomalous Diffusion Imaging: Results in Controlled Phantoms and in Excised Human Meningiomas. Magn. Reson. Imaging 2013, 31, 359–365. [Google Scholar] [CrossRef][Green Version]
- Bueno-Orovio, A.; Teh, I.; Schneider, J.E.; Burrage, K.; Grau, V. Anomalous Diffusion in Cardiac Tissue as an Index of Myocardial Microstructure. IEEE Trans. Med. Imaging 2016, 35, 2200–2207. [Google Scholar] [CrossRef]
- Ingo, C.; Magin, R.L.; Colon-Perez, L.; Triplett, W.; Mareci, T.H. On Random Walks and Entropy in Diffusion-Weighted Magnetic Resonance Imaging Studies of Neural Tissue. Magn. Reson. Med. 2014, 71, 617–627. [Google Scholar] [CrossRef] [PubMed]
- Karaman, M.M.; Sui, Y.; Wang, H.; Magin, R.L.; Li, Y.; Zhou, X.J. Differentiating Low- and High-Grade Pediatric Brain Tumors Using a Continuous-Time Random-Walk Diffusion Model at High b-Values. Magn. Reson. Med. 2016, 76, 1149–1157. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.; Zhou, X.J. Diffusion MRI of Cancer: From Low to High b-Values. J. Magn. Reson. Imaging JMRI 2019, 49, 23–40. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Z.; Merkitch, D.; Karaman, M.M.; Zhang, J.; Sui, Y.; Goldman, J.G.; Zhou, X.J. High-Spatial-Resolution Diffusion MRI in Parkinson Disease: Lateral Asymmetry of the Substantia Nigra. Radiology 2019, 291, 149–157. [Google Scholar] [CrossRef]
- Gatto, R.G.; Ye, A.Q.; Colon-Perez, L.; Mareci, T.H.; Lysakowski, A.; Price, S.D.; Brady, S.T.; Karaman, M.; Morfini, G.; Magin, R.L. Detection of Axonal Degeneration in a Mouse Model of Huntington’s Disease: Comparison between Diffusion Tensor Imaging and Anomalous Diffusion Metrics. Magn. Reson. Mater. Phys. Biol. Med. 2019, 32, 461–471. [Google Scholar] [CrossRef]
- Jensen, J.H.; Helpern, J.A.; Ramani, A.; Lu, H.; Kaczynski, K. Diffusional Kurtosis Imaging: The Quantification of Non-Gaussian Water Diffusion by Means of Magnetic Resonance Imaging. Magn. Reson. Med. 2005, 53, 1432–1440. [Google Scholar] [CrossRef]
- Jensen, J.H.; Helpern, J.A. MRI Quantification of Non-Gaussian Water Diffusion by Kurtosis Analysis. NMR Biomed. 2010, 23, 698–710. [Google Scholar] [CrossRef] [PubMed]
- Özarslan, E.; Koay, C.G.; Basser, P.J. Remarks on Q-Space MR Propagator in Partially Restricted, Axially-Symmetric, and Isotropic Environments. Magn. Reson. Imaging 2009, 27, 834–844. [Google Scholar] [CrossRef]
- Özarslan, E.; Shemesh, N.; Koay, C.G.; Cohen, Y.; Basser, P.J. NMR Characterization of General Compartment Size Distributions. New J. Phys. 2011, 13, 15010. [Google Scholar] [CrossRef]
- Özarslan, E.; Koay, C.G.; Shepherd, T.M.; Komlosh, M.E.; İrfanoğlu, M.O.; Pierpaoli, C.; Basser, P.J. Mean Apparent Propagator (MAP) MRI: A Novel Diffusion Imaging Method for Mapping Tissue Microstructure. NeuroImage 2013, 78, 16–32. [Google Scholar] [CrossRef] [PubMed]
- Mao, J.; Zeng, W.; Zhang, Q.; Yang, Z.; Yan, X.; Zhang, H.; Wang, M.; Yang, G.; Zhou, M.; Shen, J. Differentiation between High-Grade Gliomas and Solitary Brain Metastases: A Comparison of Five Diffusion-Weighted MRI Models. BMC Med. Imaging 2020, 20. [Google Scholar] [CrossRef]
- Le, H.; Zeng, W.; Zhang, H.; Li, J.; Wu, X.; Xie, M.; Yan, X.; Zhou, M.; Zhang, H.; Wang, M.; et al. Mean Apparent Propagator MRI Is Better Than Conventional Diffusion Tensor Imaging for the Evaluation of Parkinson’s Disease: A Prospective Pilot Study. Front. Aging Neurosci. 2020, 12. [Google Scholar] [CrossRef]
- Boscolo Galazzo, I.; Brusini, L.; Obertino, S.; Zucchelli, M.; Granziera, C.; Menegaz, G. On the Viability of Diffusion MRI-Based Microstructural Biomarkers in Ischemic Stroke. Front. Neurosci. 2018, 12. [Google Scholar] [CrossRef]
- Roberts, T.A.; Hyare, H.; Agliardi, G.; Hipwell, B.; d’Esposito, A.; Ianus, A.; Breen-Norris, J.O.; Ramasawmy, R.; Taylor, V.; Atkinson, D.; et al. Noninvasive Diffusion Magnetic Resonance Imaging of Brain Tumour Cell Size for the Early Detection of Therapeutic Response. Sci. Rep. 2020, 10, 9223. [Google Scholar] [CrossRef] [PubMed]
- Novikov, D.S.; Kiselev, V.G. Effective Medium Theory of a Diffusion-Weighted Signal. NMR Biomed. 2010, 23, 682–697. [Google Scholar] [CrossRef] [PubMed]
- Novikov, D.S.; Fieremans, E.; Jensen, J.H.; Helpern, J.A. Random Walks with Barriers. Nat. Phys. 2011, 7, 508–514. [Google Scholar] [CrossRef] [PubMed]
- Novikov, D.S.; Jensen, J.H.; Helpern, J.A.; Fieremans, E. Revealing Mesoscopic Structural Universality with Diffusion. Proc. Natl. Acad. Sci. USA 2014, 111, 5088–5093. [Google Scholar] [CrossRef] [PubMed]
- Cherstvy, A.G.; Safdari, H.; Metzler, R. Anomalous Diffusion, Nonergodicity, and Ageing for Exponentially and Logarithmically Time-Dependent Diffusivity: Striking Differences for Massive versus Massless Particles. J. Phys. Appl. Phys. 2021, 54, 195401. [Google Scholar] [CrossRef]
- Assaf, Y.; Blumenfeld-Katzir, T.; Yovel, Y.; Basser, P.J. Axcaliber: A Method for Measuring Axon Diameter Distribution from Diffusion MRI. Magn. Reson. Med. 2008, 59, 1347–1354. [Google Scholar] [CrossRef] [PubMed]
- Assaf, Y.; Basser, P.J. Composite Hindered and Restricted Model of Diffusion (CHARMED) MR Imaging of the Human Brain. NeuroImage 2005, 27, 48–58. [Google Scholar] [CrossRef] [PubMed]
- Alexander, D.C.; Hubbard, P.L.; Hall, M.G.; Moore, E.A.; Ptito, M.; Parker, G.J.M.; Dyrby, T.B. Orientationally Invariant Indices of Axon Diameter and Density from Diffusion MRI. NeuroImage 2010, 52, 1374–1389. [Google Scholar] [CrossRef]
- Zhang, H.; Schneider, T.; Wheeler-Kingshott, C.A.; Alexander, D.C. NODDI: Practical in Vivo Neurite Orientation Dispersion and Density Imaging of the Human Brain. NeuroImage 2012, 61, 1000–1016. [Google Scholar] [CrossRef]
- Li, J.-R.; Nguyen, H.T.; Van Nguyen, D.; Haddar, H.; Coatléven, J.; Le Bihan, D. Numerical Study of a Macroscopic Finite Pulse Model of the Diffusion MRI Signal. J. Magn. Reson. 2014, 248, 54–65. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Grebenkov, D.; Van Nguyen, D.; Poupon, C.; Le Bihan, D.; Li, J.-R. Parameter Estimation Using Macroscopic Diffusion MRI Signal Models. Phys. Med. Biol. 2015, 60, 3389–3413. [Google Scholar] [CrossRef]
- Mainardi, F.; Luchko, Y.; Pagnini, G. The Fundamental Solution of the Space-Time Fractional Diffusion Equation. arXiv 2007, arXiv:cond-mat0702419. [Google Scholar]
- Mainardi, F.; Pagnini, G. Space-Time Fractional Diffusion: Exact Solutions and Probabilistic Interpretation. In The Waves and Stability in Continuous Media; World Scientific: Porto Ercole, Italy, 2002; pp. 296–301. [Google Scholar]
- Bazhlekova, E. Subordination Principle for Space-Time Fractional Evolution Equations and Some Applications. Integral Transform. Spec. Funct. 2019, 30, 431–452. [Google Scholar] [CrossRef]
- Bazhlekova, E.; Bazhlekov, I. Subordination Approach to Space-Time Fractional Diffusion. Mathematics 2019, 7, 415. [Google Scholar] [CrossRef]
- Luchko, Y. Subordination Principles for the Multi-Dimensional Space-Time-Fractional Diffusion-Wave Equation. arXiv 2018, arXiv:180204752. [Google Scholar] [CrossRef]
- Boyadjiev, L.; Luchko, Y. Multi-Dimensional α-Fractional Diffusion–Wave Equation and Some Properties of Its Fundamental Solution. Comput. Math. Appl. 2017, 73, 2561–2572. [Google Scholar] [CrossRef]
- Luchko, Y. Entropy Production Rate of a One-Dimensional Alpha-Fractional Diffusion Process. Axioms 2016, 5, 6. [Google Scholar] [CrossRef]
- Luchko, Y. Entropy Production Rates of the Multi-Dimensional Fractional Diffusion Processes. Entropy 2019, 21, 973. [Google Scholar] [CrossRef]
- Berberan-Santos, M.N. Properties of the Mittag–Leffler Relaxation Function. J. Math. Chem. 2005, 38, 629–635. [Google Scholar] [CrossRef]
- Mainardi, F. On Some Properties of the Mittag-Leffler Function , Completely Monotone for with . Discret. Contin. Dyn. Syst. B 2014, 19, 2267–2278. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; World Scientific: Porto Ercole, Italy, 2010; ISBN 978-1-908978-57-8. [Google Scholar]
- Ingo, C.; Magin, R.L.; Parrish, T.B. New Insights into the Fractional Order Diffusion Equation Using Entropy and Kurtosis. Entropy 2014, 16, 5838–5852. [Google Scholar] [CrossRef] [PubMed]
- Spilling, C.A.; Howe, F.A.; Barrick, T.R. Quasi-Diffusion Magnetic Resonance Imaging (QDI): Optimisation of Acquisition Protocol. In Proceedings of the International Society for Magnetic Resonance in Medicine Virtual Conference & Exhibition, Paris, France, 8–13 October 2020; p. 4391. [Google Scholar]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag-Leffler Functions and Their Applications. J. Appl. Math. 2011, 2011, 1–51. [Google Scholar] [CrossRef]
- Mainardi, F. Why the Mittag-Leffler Function Can Be Considered the Queen Function of the Fractional Calculus? Entropy 2020, 22, 1359. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S. The Classical Mittag-Leffler Function. In Mittag-Leffler Functions, Related Topics and Applications; Gorenflo, R., Kilbas, A.A., Mainardi, F., Rogosin, S., Eds.; Springer Monographs in Mathematics; Springer: Berlin/Heidelberg, Germany, 2020; pp. 19–62. ISBN 978-3-662-61550-8. [Google Scholar]
- Mainardi, F. Fractional Relaxation-Oscillation and Fractional Diffusion-Wave Phenomena. Chaos Solitons Fractals 1996, 7, 1461–1477. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S. Applications to Deterministic Models. In Mittag-Leffler Functions, Related Topics and Applications; Gorenflo, R., Kilbas, A.A., Mainardi, F., Rogosin, S., Eds.; Springer Monographs in Mathematics; Springer: Berlin/Heidelberg, Germany, 2020; pp. 281–337. ISBN 978-3-662-61550-8. [Google Scholar]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S. Mittag-Leffler Functions, Related Topics and Applications; Springer: Berlin/Heidelberg, Germany, 2020; ISBN 978-3-662-61549-2. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Montreaux, Switzerland; Philadelphia, PA, USA, 1993; ISBN 978-2-88124-864-1. [Google Scholar]
- Mainardi, F.; Pagnini, G.; Saxena, R.K. Fox H Functions in Fractional Diffusion. J. Comput. Appl. Math. 2005, 178, 321–331. [Google Scholar] [CrossRef]
- Panagiotaki, E.; Walker-Samuel, S.; Siow, B.; Johnson, S.P.; Rajkumar, V.; Pedley, R.B.; Lythgoe, M.F.; Alexander, D.C. Noninvasive Quantification of Solid Tumor Microstructure Using VERDICT MRI. Cancer Res. 2014, 74, 1902–1912. [Google Scholar] [CrossRef]
- Ingo, C.; Barrick, T.R.; Webb, A.G.; Ronen, I. Accurate Padé Global Approximations for the Mittag-Leffler Function, Its Inverse, and Its Partial Derivatives to Efficiently Compute Convergent Power Series. Int. J. Appl. Comput. Math. 2017, 3, 347–362. [Google Scholar] [CrossRef]
- Hall, M.G.; Barrick, T.R. Two-Step Anomalous Diffusion Tensor Imaging. NMR Biomed. 2012, 25, 286–294. [Google Scholar] [CrossRef]
- Veraart, J.; Nunes, D.; Rudrapatna, U.; Fieremans, E.; Jones, D.K.; Novikov, D.S.; Shemesh, N. Nonivasive Quantification of Axon Radii Using Diffusion MRI. eLife 2020, 9. [Google Scholar] [CrossRef] [PubMed]
- Bai, J.; Varghese, J.; Jain, R. Adult Glioma WHO Classification Update, Genomics, and Imaging: What the Radiologists Need to Know. Top. Magn. Reson. Imaging 2020, 29, 71–82. [Google Scholar] [CrossRef]
- Hu, L.S.; Hawkins-Daarud, A.; Wang, L.; Li, J.; Swanson, K.R. Imaging of Intratumoral Heterogeneity in High-Grade Glioma. Cancer Lett. 2020, 477, 97–106. [Google Scholar] [CrossRef]
- Veraart, J.; Fieremans, E.; Novikov, D.S. On the Scaling Behavior of Water Diffusion in Human Brain White Matter. NeuroImage 2019, 185, 379–387. [Google Scholar] [CrossRef] [PubMed]
- Reiter, D.A.; Adelnia, F.; Cameron, D.; Spencer, R.G.; Ferrucci, L. Parsimonious Modeling of Skeletal Muscle Perfusion: Connecting the Stretched Exponential and Fractional Fickian Diffusion. Magn. Reson. Med. 2021, 86, 1045–1057. [Google Scholar] [CrossRef]
- Yablonskiy, D.A.; Bretthorst, G.L.; Ackerman, J.J.H. Statistical Model for Diffusion Attenuated MR Signal. Magn. Reson. Med. 2003, 50, 664–669. [Google Scholar] [CrossRef]
- Magin, R.L.; Rawash, Y.Z.; Berberan-Santos, M.N. Analyzing Anomalous Diffusion in NMR Using a Distribution of Rate Constants. In Fractional Dynamics and Control; Springer: Berlin, Germany, 2012; pp. 263–274. [Google Scholar]
- Oshio, K.; Shinmoto, H.; Mulkern, R.V. Interpretation of Diffusion MR Imaging Data Using a Gamma Distribution Model. Magn. Reson. Med. Sci. MRMS Off. J. Jpn. Soc. Magn. Reson. Med. 2014, 13, 191–195. [Google Scholar] [CrossRef] [PubMed]
- Borlinhas, F.; Loução, R.; Conceição, R.C.; Ferreira, H.A. Gamma Distribution Model in the Evaluation of Breast Cancer Through Diffusion-Weighted MRI: A Preliminary Study. J. Magn. Reson. Imaging JMRI 2019, 50, 230–238. [Google Scholar] [CrossRef]
- Togao, O.; Chikui, T.; Tokumori, K.; Kami, Y.; Kikuchi, K.; Momosaka, D.; Kikuchi, Y.; Kuga, D.; Hata, N.; Mizoguchi, M.; et al. Gamma Distribution Model of Diffusion MRI for the Differentiation of Primary Central Nerve System Lymphomas and Glioblastomas. PLoS ONE 2020, 15, e0243839. [Google Scholar] [CrossRef]
- Özarslan, E.; Basser, P.J. MR Diffusion—“Diffraction” Phenomenon in Multi-Pulse-Field-Gradient Experiments. J. Magn. Reson. 2007, 188, 285–294. [Google Scholar] [CrossRef] [PubMed]
- Avram, L.; Özarslan, E.; Assaf, Y.; Bar-Shir, A.; Cohen, Y.; Basser, P.J. Three-Dimensional Water Diffusion in Impermeable Cylindrical Tubes: Theory versus Experiments. NMR Biomed. 2008, 21, 888–898. [Google Scholar] [CrossRef] [PubMed]
- Westin, C.-F.; Knutsson, H.; Pasternak, O.; Szczepankiewicz, F.; Özarslan, E.; van Westen, D.; Mattisson, C.; Bogren, M.; O’Donnell, L.J.; Kubicki, M.; et al. Q-Space Trajectory Imaging for Multidimensional Diffusion MRI of the Human Brain. NeuroImage 2016, 135, 345–362. [Google Scholar] [CrossRef] [PubMed]
- Topgaard, D. Multidimensional Diffusion MRI. J. Magn. Reson. 2017, 275, 98–113. [Google Scholar] [CrossRef] [PubMed]
- Tuch, D.S. Q-Ball Imaging. Magn. Reson. Med. 2004, 52, 1358–1372. [Google Scholar] [CrossRef]
- Wedeen, V.J.; Hagmann, P.; Tseng, W.-Y.I.; Reese, T.G.; Weisskoff, R.M. Mapping Complex Tissue Architecture with Diffusion Spectrum Magnetic Resonance Imaging. Magn. Reson. Med. 2005, 54, 1377–1386. [Google Scholar] [CrossRef]
- Wedeen, V.J.; Wang, R.P.; Schmahmann, J.D.; Benner, T.; Tseng, W.Y.I.; Dai, G.; Pandya, D.N.; Hagmann, P.; D’Arceuil, H.; de Crespigny, A.J. Diffusion Spectrum Magnetic Resonance Imaging (DSI) Tractography of Crossing Fibers. NeuroImage 2008, 41, 1267–1277. [Google Scholar] [CrossRef]
- Jeurissen, B.; Tournier, J.-D.; Dhollander, T.; Connelly, A.; Sijbers, J. Multi-Tissue Constrained Spherical Deconvolution for Improved Analysis of Multi-Shell Diffusion MRI Data. NeuroImage 2014, 103, 411–426. [Google Scholar] [CrossRef]
- Kamagata, K.; Andica, C.; Hatano, T.; Ogawa, T.; Takeshige-Amano, H.; Ogaki, K.; Akashi, T.; Hagiwara, A.; Fujita, S.; Aoki, S. Advanced Diffusion Magnetic Resonance Imaging in Patients with Alzheimer’s and Parkinson’s Diseases. Neural Regen. Res. 2020, 15, 1590–1600. [Google Scholar] [CrossRef]
- Nagaraja, N. Diffusion Weighted Imaging in Acute Ischemic Stroke: A Review of Its Interpretation Pitfalls and Advanced Diffusion Imaging Application. J. Neurol. Sci. 2021, 425, 117435. [Google Scholar] [CrossRef]
- Raja, R.; Rosenberg, G.; Caprihan, A. Review of Diffusion MRI Studies in Chronic White Matter Diseases. Neurosci. Lett. 2019, 694, 198–207. [Google Scholar] [CrossRef] [PubMed]
- Delouche, A.; Attyé, A.; Heck, O.; Grand, S.; Kastler, A.; Lamalle, L.; Renard, F.; Krainik, A. Diffusion MRI: Pitfalls, Literature Review and Future Directions of Research in Mild Traumatic Brain Injury. Eur. J. Radiol. 2016, 85, 25–30. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrick, T.R.; Spilling, C.A.; Hall, M.G.; Howe, F.A. The Mathematics of Quasi-Diffusion Magnetic Resonance Imaging. Mathematics 2021, 9, 1763. https://doi.org/10.3390/math9151763
Barrick TR, Spilling CA, Hall MG, Howe FA. The Mathematics of Quasi-Diffusion Magnetic Resonance Imaging. Mathematics. 2021; 9(15):1763. https://doi.org/10.3390/math9151763
Chicago/Turabian StyleBarrick, Thomas R., Catherine A. Spilling, Matt G. Hall, and Franklyn A. Howe. 2021. "The Mathematics of Quasi-Diffusion Magnetic Resonance Imaging" Mathematics 9, no. 15: 1763. https://doi.org/10.3390/math9151763
APA StyleBarrick, T. R., Spilling, C. A., Hall, M. G., & Howe, F. A. (2021). The Mathematics of Quasi-Diffusion Magnetic Resonance Imaging. Mathematics, 9(15), 1763. https://doi.org/10.3390/math9151763





