Abstract
The article provides an overview of research focusing on pre- and in-service teacher education, conducted in the Czech Republic by teams of researchers of which the authors were members. It employs the methodology of a qualitative meta-analysis of studies aimed at distinguishing key areas of research and their main results. Twenty-one studies were analyzed, 11 of which targeted pre-service teachers and 10 in-service teachers. The article briefly describes the historical and cultural context that informs mathematics education in the Czech Republic. It also elaborates on key theoretical concepts shared by the studies analyzed, including teachers’ pedagogical content knowledge, competence and pedagogical reflection. The meta-analysis uncovered a common core of the studies in their focus on the process of professionalization for mathematics teachers in its three dimensions: professional vision, professional knowledge, and professional action. Six core research strands are identified within the group of studies: lesson study as a means of developing teachers’ pedagogical content knowledge; joint reflection; professional vision and its development; culture of problem solving and teacher development; problem posing to support subject-didactic competence and teachers’ competencies for content and language integrated learning and culturally responsive teaching. The article outlines the methodology and main results of the studies in each research strand and discusses their implications. Finally based on the meta-analysis, a discussion of the core concepts of teacher reflection, problem solving and problem posing is developed.
1. Introduction
Both pre- and in-service teacher education have been the center of attention of ma-thematics education research in the Czech Republic for a long time. As the prominent Czech psychologist, Helus stated:
“A successful effort to change the school is only possible if the teacher becomes its leading agent. It is related to answering questions that focus on his/her competences and responsibility, on his/her appropriate good condition, on updating his/her pre-service and lifelong education.” [1] (p. 38).
The aim of this article is to provide an insider perspective on research carried out in the Czech Republic, with a focus on teacher education. Any research is always embedded within the country’s own tradition, and thus we first outline the historical background to our study. John Amos Comenius’s legacy has influenced mathematics teacher education and research in the Czech Republic, and we therefore begin by outlining its core features. We then outline developments in the didactics of mathematics in the second half of the 20th century, when the modern didactics of mathematics was established as a discipline in Czechoslovakia (the Czech Republic was established in 1993 when Czechoslovakia split into two independent countries). We show that mathematics and its didactics have always been tightly connected and that prominent mathematicians played an active role in establishing the didactics of mathematics and development of mathematics teacher education.
Section 3 outlines the data and methodology used in our study. We analyze selected studies on teacher education conducted in the Czech Republic and distinguish the core concepts and theories in which they are embedded, which mostly concern knowledge, skills and competences that a teacher of mathematics needs. These concepts are summarized in the ensuing section on the theoretical background. The core of the article presents the six research strands revealed by our analysis. We describe each strand briefly, outlining its methodology, main results and implications. In the discussion section, we focus on the common core of the studies, which lies in the concept of reflection that underlies much of the research on teacher education in the Czech Republic. Finally, the follow-up work and implications are briefly summarized.
2. Historical Background
2.1. Comenius as the Founder of Czech Educational Traditions
Education is one of the topics that winds its way through the history of the place we live in like Ariadne’s red thread through the minotaur’s labyrinth. The 14th century witnessed the foundation of the first university in central Europe in Prague by the Roman Emperor and Czech king Charles IV. Education was a focus of attention during the time of the Jan Hus reform movement and the legacy was taken over by the protestant Unity of the Brethren. Let us recollect here that the philosopher, pedagogue and theologian John Amos Comenius (1592–1670), considered to be the father of modern European didactical tradition and sometimes referred to as the teacher of nations, was born in the territory of today’s Czech Republic, in the Margraviate of Moravia. Comenius introduced a number of educational concepts and innovations (see, e.g., [2]). He was also the proponent of the idea that education should be comprehensive and structured into four levels, the first three compulsory for all children, the fourth for the gifted ones. Discussing teachers, he stated:
“The teacher is required... 1. to know himself what he should to teach to others (as no one can teach what he knows little about); 2. to be able to teach others what he himself knows (in other words, to be a gifted teacher and be able patiently to survive ignorant pupils and also to banish ignorance efficiently, etc.); finally, 3. to want to teach what he knows and can teach, in other words, to be active and diligent and long to bring others to the source of light in which he himself delights.’’ [3] (p. 16, our translation).
Comenius’s thinking about education was connected to the idea of a reform of humanity. He tried to find an integrating factor that would combine or integrate everything that was necessary for a better life for all people. A human being becomes human only through education, and thus the main task of education is to transform a being into a human being. That is how he came upon the idea of Pansofia, which was understood as an integration of knowledge. In order to reform humanity, along the lines of his Pansophic ideal, Comenius realized the importance of setting up proper didactic and pedagogical methods to create a more suitable environment for children to learn, eventually transforming the human condition. In short, he believed that proper education for all would be the first step for a better world.
Comenius’s synthesizing work Didactica magna (“The Great Didactic” [3]) was written as a practical and theoretical handbook for educators. In this book, he systematically shows that education must take into account the natural development of children. He proposes simple and quite practical principles on how children of different ages should be taught. In addition, he describes appropriate ways of teaching different types of subjects [4].
What is crucial to realize with respect to modern pedagogy and didactics and to this article on mathematics teacher education is Comenius’s respect for knowledge. His idea was that to bring about a social reform and better society is to educate people and to find ways of handing over the knowledge of the world (Pansofia) in a comprehensible way. It may well be the imprint of the Comenius tradition that has made Czech research in the field of mathematics education respectful to mathematics as such, taking into account both subject knowledge and pedagogical content knowledge (in the sense used in [5]), fully aware that teachers on all levels, including preschool and primary education must master both the content and the teaching methods.
2.2. Beginnings and Development of Basic Research and Establishment of the Didactics of Mathematics in Czechoslovakia
In the early 1960s, similarly to other countries, preparation for the reconstruction of mathematics teaching started in Czechoslovakia. Related activities took place within the framework of the professional organization called the Union of Czechoslovak Mathematicians and Physicists—a society attached to the Czechoslovak Academy of Sciences. Primary and secondary school teachers were guided by the efforts to reconstruct, modernize, and improve mathematics education (in short, to create a complex in which various components would respect each other: purely mathematical content, didactic and psychological aspects, consideration of applications and others) [6]. Teachers regularly met and cooperated in regional groups.
These activities became the starting point for designing and conducting basic research, which is tightly linked with the constitution and development of the didactics of mathematics, as basic research is “essentially experimental didactics and the theory of teaching mathematics is enriched by its results. On the contrary, in carrying out basic research, all previous results from the theory and practice of teaching mathematics are used.” [7] (p. 584). Basic research was planned to provide a foundation for the reform of mathematics education. The aim and task of the didactics of mathematics were to determine the content and methods of teaching and learning of mathematics, and to look for effective ways of assessment. In 1963, experimental (primary) schools were established that were not selective and were used to conduct pedagogical research. The teaching followed an original curriculum and was supported by special teaching texts. This enabled a new way of working in mathematics lessons called a “mathematical laboratory”.
To coordinate the research, a division for the didactics of mathematics was established (later known as the Department for the Didactics of Mathematics of the Institute of Mathematics of the Czechoslovak Academy of Sciences) with a small number of internal staff and a large circle of external collaborators (university educators, especially from faculties preparing teachers, and teachers from the experimental schools). From the very beginning, the activities of the division focused on the theoretical and experimental solution of issues related to the objectives, content and methods of mathematical education at the experimental schools. Issues surrounding the creation of a promising model of mathematics teaching were addressed [6,8]. The activities of the division were understood as long-term and continuous.
2.3. Support for Mathematics Education from “Pure” Mathematics
It is a tradition in the Czech Republic that prominent mathematicians show keen interest in the level of mathematics education and aim at improving it. Examples include such luminaries such as V. Kořínek and J. Kurzweil. Another prominent mathematician, E. Čech, was the author of several textbooks for secondary schools, about which Kuřina later wrote: “In my opinion, a school in the spirit of Čech should: 1. Cultivate pupils’ activity and develop their interest in mathematics. 2. Awaken the love of mathematics and work. 3. Develop pupils’ language and their ability to think independently. 4. Introduce mathematics as a system. 5. Not only teach but also make sure the children/pupils learn.” [9] (p. 15, our translation).
2.4. Teachers and Reconstruction of Mathematics Education
Since the first reflections on the modernization of mathematics teaching in the early 1960s, the need to focus on teacher training and the development of teachers’ competencies was emphasized in Czechoslovakia. For example, weekly training camps focusing on theory and practice (content and methods) were organized for teachers of experimental schools by the division. The Union of Czechoslovak Mathematicians and Physicists also played a significant role in the process by involving experts in the field of mathematics (and physics). Seminars for in-service teachers were held by the Union since the early 1960s. In the following years, the Union (since 1993 it was called the Union of Czech Mathematicians and Physicists) regularly organized lectures, workshops, conferences, etc., for teachers and other pedagogical staff. These conferences continue to be held regularly [10]. Conferences and projects bringing together teachers of mathematics and researchers from the field of teacher education have become the driving force behind changes in mathematics education.
3. Data and Methods
As stated above, the aim of this article was to provide an insider perspective on research conducted into teacher education in the Czech Republic. This is possible because the authors represent institutions that carry out a substantial portion of the countrywide research into mathematics education. The article is a product of a qualitative meta-analysis of selected studies published within the field of mathematics teacher education by research teams that included the authors.
For our analysis, we first listed all the studies conducted and published by the research teams, and identified common themes arising from their aims and research questions. We identified the topic of professionalization of teachers as a key theme, and selected 21 related studies for further analysis. These studies addressed either pre- (PST) (sometimes, we will call them simply “students”) or in-service teacher (IST) development (see Table 1).

Table 1.
Overview of studies included in the meta-analysis.
Second, we focused on the theoretical frameworks of the studies, and distinguished the main concepts and theories within which they were embedded. These are summarized in Section 4, and provide a common theoretical framework for all the studies in question. Most of the studies are informed by well-established international theories and concepts, including pedagogical content knowledge, pedagogical reflection and teachers’ competences. Some of them use an influential conceptualization by the Czech psychologist, Helus, in relation to teachers’ competences, and thus, in Section 4.2, we briefly explain how this is related to internationally known theories.
Next, the studies were divided into groups according to their aims. We distinguished six strands of research, namely, lesson study as a means to develop teachers’ pedagogical content knowledge, joint reflection, professional vision and its development, culture of problem solving and teachers’ development, problem posing to support subject-didactic competence, teachers’ competence in content and language integrated learning and in culturally responsive teaching. Each strand is represented by one or more studies that were then analyzed in terms of their methodology and results. The six strands are described in Section 5 via an outline of their methodology, main results and their implications. Rather than presenting the studies one by one, we present them holistically, focusing on how the studies inform our overarching theme of investigating the professionalism of teachers.
4. Theoretical Background
The quality of teachers’ knowledge and skills is regarded as a significant variable that influences the quality of education. The European Commission analysis (e.g., [32]) required coherent, high-quality and relevant teacher education programs that respond effectively to evolving needs.
From the theoretical perspective, there are different ways to structure and determine the results of learning and education processes (not only in teacher education). In the teacher education literature, the terms knowledge, skills and competences appear most often in the categorization of learning outcomes. They are further differentiated depending on culture and language. For example, in France, a distinction is made between savoir and savoir-faire (knowledge and skills); in German-speaking countries, the terms Fachkompetenz, Methoden-kompetenz, Personalkompetenz and Sozialkompetenz (professional competence, methodological competence, personal competence and social competence) are used for a teacher’s education outputs, while in English-speaking countries, different types of knowledge are defined in the categorization of learning outcomes [33]. At the same time, the terms cognitive competence, functional competence and social competence are sometimes used.
Shulman’s concept of subject matter knowledge being unique to teaching [5] and teachers’ competences constitute a core idea that is present in the theoretical backgrounds of all the studies we analyzed.
4.1. Knowledge of Content and Pedagogical Content Knowledge
Shulman specified seven categories of a knowledge base for teaching [5]: knowledge of content; knowledge of curriculum; pedagogical content knowledge; knowledge of pedagogy; knowledge of learners and learning; knowledge of contexts of schooling; knowledge of educational philosophies, goals and objectives. Content knowledge and its relations to pedagogical content knowledge (PCK) have attracted the particular attention of researchers in mathematics education for a long time. Shulman’s content knowledge component includes knowledge “beyond knowledge of the facts or concepts of a domain” [5] (p. 9). According to Shulman, teachers should have knowledge of the substantive structures of a discipline, “the variety of ways in which the basic concepts and principles of the discipline are organized to incorporate its facts”, and of the syntactic structure, which is “the set of ways in which truth or falsehood, validity or invalidity, are established” [5] (p. 9). PCK is “the category most likely to distinguish the understanding of the content specialist from that of the pedagogue” [5] (p. 8). It comprises the most useful forms of the representation of ideas, the most powerful analogies, illustrations, examples, explanations and demonstrations—in short, the most useful ways of representing and formulating the subject that make it comprehensible to others. PCK also includes an understanding of what makes the learning of specific topics easy or difficult: the conceptions and preconceptions that pupils of different ages and backgrounds bring with them to the learning of those most frequently taught topics and lessons [5] (p. 9). In the European context, we used the term “the didactic of the school subject”.
This distinction of the knowledge teachers need for successful teaching was taken up by other authors in mathematics education. For example, Fennema and Franke [34] proposed their own model of teachers’ mathematics knowledge. It includes four categories: knowledge of mathematics, context specific knowledge, pedagogical knowledge and knowledge of learners’ cognition in mathematics. Fennema and Franke [34] stressed that the four components of teachers’ knowledge influenced one another. An important characteristic of the model is that each component of teachers’ knowledge is situated in a classroom context.
Many follow-up studies focused on the analysis of selected aspects of mathematical knowledge necessary for teaching in more detail. The theory of mathematical knowledge for teaching [35] has become particularly influential. Ball and her colleagues distinguish other domains specific for mathematics teaching in Shulman’s content knowledge (horizon content knowledge and specialized content knowledge) and PCK. They emphasize that the subdomains of PCK relate to the mathematical content taught.
4.2. Teachers’ Competences
Teachers’ competences are stressed when analyzing teachers’ work in the Czech educational context. The term “to have a competence” is used in the situation of having sufficient knowledge, skills or strength to succeed in the teaching profession. It is an amalgam of knowledge and skills that allows a teacher to act and react in a qualified manner in a pedagogical situation. The word knowledge in the Czech language refers to knowing something and does not include the use of this knowledge.
For us, Helus’ [2] conception is particularly relevant as it captures different facets of (mathematics) teachers’ work and forms the basis of their self-confidence. It consists of four basic competencies:
- (a)
- Competence related to pupils (namely creating conditions for the development of pupils’ abilities and skills by designing procedures for an effective pedagogical intervention, etc.).
- (b)
- Subject-didactic competence encompassing mastery of the scientific basis of teaching a subject and didactic creativity (i.e., the ability to keep the subject matter up to date in its cognitive, motivational and social significance).
- (c)
- Pedagogical-organizational competence aimed at creating an effective educational environment, together with a supportive and stimulating climate.
- (d)
- Competence in qualified pedagogical (self-)reflection with an emphasis on the analysis of the teacher’s own thinking and dealing with pupils in a way that is suited to their ability (abbreviated text from [2], pp. 38–39, our translation).
The structure of competences defined by Helus is different from knowledge as defined by Shulman [5] or Ball et al. [35]. The competence related to pupils is defined as a standalone category. Its equivalent can be found in Shulman’s [5] knowledge of learners and learning and also in the definition of Ball et al. [35], where its relation to content is emphasized (knowledge of content and pupils). The pedagogical-organizational competence defined by Helus [2] is equivalent to Ball’s knowledge of content and teaching [35] and Shulman’s knowledge of teaching [5]. What we find important for our considerations in this article is subject-didactic competence, consisting of a skilled orientation towards the educational meaning of teaching a specific subject. We believe that this is to a great extent equivalent to the definition of PCK. However, it emphasizes the connection between content and teaching more. PCK also includes the competence in qualified pedagogical (self-)reflection. This is defined by Helus as a standalone category, which he regards as crucially important for how a teacher organizes their personal development and lifelong learning [2]. The competence of reflecting on one’s activity is considered to be a determining feature of a teacher’s professionalism. Krainer [36] suggested four dimensions of the teacher’s professional practice: action, autonomy, reflection and networking. Their mutual relations can be captured by the diagram in Figure 1.
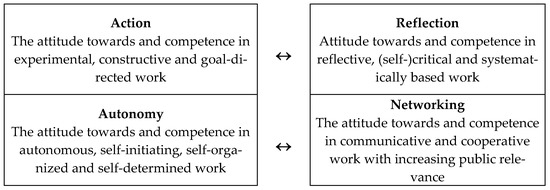
Figure 1.
Dimensions of teacher’s professional practice (schematized by the authors of this article according to Krainer [36]).
Krainer [36] notes that these are contrasting and unified dimensions, with more emphasis on action and autonomy and less attention on reflection and networking, although systematic reflection on one’s activity, of decision processes and of pedagogical situations, is considered to be the key to transition from an intuitive to a conscious and justified action [37,38,39]. Jaworski [40] proposes investigation of reflexive pairs, one of which is “inquiry and reflection”. Mason [41] stresses the importance of reflection:
“When recalling, reflecting on, or reconstructing some incident or event, one readily recalls what was marked. … Intentional reflection and reconstruction enhance the possibility of being sufficiently awake at some future moment so as to be able to respond freshly rather than to react habitually to the situation while it develops.” [41] (p. 41).
Reflection is seen as a prerequisite of future noticing/marking, noticing-in-the-moment and reaction in the classroom. Similarly, van Es and Sherin argue that “learning to notice is one important dimension within the process of reflection” [42] (p. 247). The concept of teachers’ professional vision is tightly connected to noticing. Its definitions vary across studies; however, they mostly distinguish two subprocesses within it—noticing and knowledge-based reasoning. For example, for Sherin, Russ and Colestock noticing is “professional vision in which teachers selectively attend to events that take place and then draw on existing knowledge to interpret these noticed events” [43] (pp. 80–81).
To sum up, the six strands of research on teacher education in the Czech Republic we distinguished among are embedded within the concept of competence in general and teachers’ competence to reflect in particular. We will first present an overview of the studies to show their common core and how they build on one another. Then, their main results and implications will be summarized.
5. Six Strands of Research on Teacher Education in the Czech Republic
Practice-based programs have been increasingly used in teacher education. In the work presented below, we utilized two particular types: (a) programs based on the design of the lesson study (LS) [44,45] in which teachers jointly prepare, conduct and reflect on “a research lesson” (see also [46,47,48]); (b) programs based on the use and reflection on videos of mathematics lessons taught by both unknown teachers and by the participants themselves in video-based courses (sometimes called video-clubs, VC, e.g., [49,50,51]). LS and VC share important characteristics that make them effective means for developing knowledge, beliefs and skills of both pre- and in-service teachers. They are rooted in the practice of teaching as the participants reflect on their own teaching or the teaching of others. Artifacts of practice such as videos of teaching, lesson plans, pupils’ work, etc., are used to help participants to reflect on teaching and pupils’ learning using their experience, knowledge and skills [52]. Both types of programs are rooted in a situated perspective on cognition and learning [53], in which professional learning communities play a leading role. These communities can enhance teachers’ professional knowledge and improve their practice [54]. Finally, both focus on developing teaching that is aimed at conceptual understanding.
When implementing both types of programs, we came across major differences in how the participants interpreted the learning situations. This awakened our research interest and resulted in a number of research studies. The first focus area of our research studies was directly inspired by the Japanese LS. A team led by Vondrová investigated the possibilities of implementing LS in Czech conditions (Section 5.1). The cooperation of Hošpesová and Tichá with in-service teachers was designed similarly to LS and provided data documenting the professional development of the participating teachers (Section 5.2).
The principle of LS was also used by Vondrová and her collaborators in pre-service secondary teacher education. It turned out that there were major differences in the pre-service teachers’ ability to notice important issues in a teaching-learning situation. This ability to notice seemed to be a (for us hidden) part of their emerging PCK. Thus, Vondrová and her colleagues set out to explore the question of what it was the students attended to in a teaching/learning situation and how they interpreted it (Section 5.3). This research was followed by several studies on the topic of noticing, carried out by Vondrová and her collaborators with lower secondary pre-service teachers.
While these research studies focused on (joint) reflection per se, another group of studies used joint reflection as part of their research design. Two of the studies focus on problem solving (Section 5.4) and problem posing (Section 5.5) and their impact on teachers’ professional development. In both, joint reflection was the final phase, supporting the main objective and providing space for data collection.
The research that focused on linguistic issues in mathematics classrooms, the integration of teaching mathematics and a foreign language, and teaching mathematics in linguistically and culturally heterogeneous classrooms cast light on what is needed in pre-service and in-service teacher education. Even teachers of mathematics can no longer expect that they will be teaching in culturally and linguistically heterogeneous classes, and need to be equipped with tools that will enable them to plan and conduct lessons with learners whose mother tongue is not the language of instruction; in some situations (CLIL), the language of instruction is not the mother tongue even for the teacher. The ability to reflect on what is happening during lessons is crucially important if teachers are to be successful in the adaptation and modification of their teaching and teaching materials (Section 5.6).
5.1. Developing Teachers’ Pedagogical Content Knowledge via Lesson Study
The studies presented in this section connected the above two practice-based types of teacher education (namely, LS and VC).
5.1.1. Data and Methods
The study with in-service teachers focused on a year-long course (see [11] for more detail). Video-based tasks of the teaching of others were embedded at its beginning to ease the pressure put on the teachers by a new and unfamiliar format of work. For Czech teachers, this is mostly the pressure of the need to cooperate on lesson preparation, to open their classroom to others and to learn to provide constructive feedback on their colleagues’ teaching. Next, the LS cycle was implemented as faithfully to the Japanese LS as possible. Finally, the second video-based part was implemented, in which the teachers reflected on their own teaching. Four out of five teams of teachers (N = 13) participated in a research study whose aim was to find out how they perceived their participation in the program and whether there was any development in their noticing phenomena related to the teaching of mathematics. The data consisted of the teachers’ responses to a pre- and post-task (a written reflection on a whole mathematics lesson on video), their responses to other tasks set within the course (including reflections on their own and others’ teaching), and field notes from common sessions.
A LS framework was also utilized in a semester-long video-intervention with pre-service teachers [13]. In the ‘own video’ group, the students jointly prepared, realized and reflected on mathematics lessons. The whole work is described in more detail in Section 5.3.
5.1.2. Selected Results
During her work with in-service teachers, Vondrová [11] investigated how the video-based part of the program helped them to form a professional community, which is a necessary prerequisite for a LS cycle. The shared responsibility for the research lesson, which was jointly planned and enacted, reduced any anxiety on the part of the teacher teaching the lesson about being observed by others.
Vondrová et al. [12] did not find measurable outcomes in terms of the teachers’ development of noticing skill; however, the teachers’ perception was different. They repeatedly reported gains in their professional knowledge and skills, and in their ability to reflect on teaching. The cooperative planning process encouraged them to think through the plan thoroughly, recognizing possible hurdles to overcome and factors to be taken into account to a greater extent than when planning a lesson individually. The teachers could not merely suggest attractive tasks but had to think carefully about how to structure them towards the goal, and thus they learned most by trying to formulate the goal for their research lessons. Moreover, they had to negotiate the teaching approach for research lessons, which we find equally valuable. In the Czech Republic, there is no shared idea of the features of mathematics teaching that are aimed at conceptual understanding (nor even a shared idea that this understanding should be targeted; the image of teaching for some teachers is rather procedural), and reaching agreement can be an arduous task for some teachers.
In the study with pre-service teachers, the main results were remarkably consistent with those obtained in the study with in-service teachers. The shared responsibility for the lesson reduced the anxiety they felt when they first learned that their teaching would be video-recorded, and while hardly any development in their noticing skills was found [14], the students saw it differently and emphasized the development of their skills to reflect on the video-lesson in the final questionnaire.
5.2. Joint Reflection in Primary School Teachers’ Professional Development
As stated above, the ability to reflect on one’s teaching has been one of the focuses of the Czech research community. An example is Tichá and Hošpesová’s study [17], which was conceived within the framework of the project Understanding of Mathematics Classroom Culture in Different Countries. An important characteristic of the project was that in addition to researchers, in-service mathematics teachers participated. The aim was to answer the following research questions: Do teachers’ competences in self- and joint-reflection lead to the development of more sensitive approaches to pupils’ ways of thinking and the ability to use them in teaching? What stages did the participants’ reflections go through? How did joint reflection influence the participating teachers’ professional competences?
5.2.1. Data and Methods
The project team video recorded several primary mathematics lessons. The videos became the initial material used to explain how reflection works and to practice its techniques. The framework of the team’s work was very similar to that of the LS: (a) discussion was conducted on the mathematical background of the selected topic and its possible didactic elaboration; (b) a pair of cooperating teachers planned and conducted mathematics lessons on this topic in their classes; (c) individual reflection on the recording was done by all members of the team with the underlying theme of “what I would like to discuss with others/to show to other teachers”; (d) the team organized a joint meeting, in which teachers and researchers watched the video together and reflected on what was happening in the classroom. This discussion was recorded.
The research took a qualitative methodological approach. In the analysis of the recorded joint reflections, the aim was to register noteworthy incidents. The reflections of different participants on the same incident in the lesson were compared. The development of (a) the performance and reflections of individual teachers and (b) the social and professional climate in the group were followed. The features that showed improvement or a possible lack of competence of the teachers were identified.
5.2.2. Selected Results
Using joint reflection as a method for the development of various teacher competences, Tichá and Hošpesová [17] determined some changes in the participating teachers’ attitudes to the work on the project and assessment of their own competences. These changes can be divided into three stages:
- -
- Self-confidence concerning the content and methods of mathematics teaching at the beginning of their research program;
- -
- Uncertainty about their competences, which originated after several discussions;
- -
- Ambition to change their practice, to improve subject-didactic competences and to better understand pupils’ cognition of mathematics.
The level of reflection developed in several stages that were mutually connected and demonstrated professional growth. The first joint reflections had the nature of a simple dialogue with intuitive observations such as “I liked/disliked this”, in which the teachers mostly spoke about their feelings. The teachers who had taught the lesson welcomed the opportunity to study (also individually before the discussion) the video recording of their pupils’ work in detail. They appreciated the opportunity to see what was happening in their class in more detail. This opportunity contributed greatly to the development of their pedagogical-psychological competence. In the discussion, they referred repeatedly to the work of particular pupils. Other teachers from the team who participated in the planning of the lesson focused, above all, on how the teacher conducting the lesson interpreted the topic, the kind of mathematics problems used, how she asked questions and reacted to pupils’ answers, etc. It seemed they studied the teacher’s performance from the point of view of “how would I teach it?”.
The reflection gradually evolved and the teachers started to focus more on improving their teaching by using effective methods to teach specific content. Their analysis of teaching was getting deeper, focusing on goals, methods and content. This had a positive impact on the planning and implementation of their own teaching experiments.
5.3. Professional Vision of Pre-Service Teachers
This section focuses on studies that target the professional vision of (mostly) pre-service mathematics teachers. They make a closely related series in which each study builds on the previous one. Thus, the studies will not be described individually in terms of their methodology and results, but rather by their short summaries, denoting what was new in them. The studies referred to in Section 5.3.1 focus on measuring noticing skills, while those in Section 5.3.2 explore a specific way of developing these skills.
5.3.1. Measuring Noticing Skills
When preparing her first study on the ability to see events in a lesson, Vondrová realized it fitted well into a strand of research on teacher noticing and professional vision. In her first study on noticing, she asked pre-service teachers (N = 70) and in-service teachers (N = 49) to comment on six short carefully selected teaching/learning situations from mathematics lessons captured on video [15]. It transpired that both types of participants rarely commented on details of the lesson content and that pre-service teachers tended to see the pupils in the videos as active even at times when the in-service teachers agreed that the pupils were rather passive. Pre-service teachers tended to focus more on the teacher in the video.
In subsequent studies, Vondrová and her team were looking for an answer to the question of what pre-service teachers focused on in a mathematics lesson on the video (targeting their selective attention) and/or how they reasoned about it (aiming at their knowledge-based reasoning and depth of their reflection). The participants were asked to write a written reflection on the video. On the one hand, some international results were confirmed (for example, that pre-service teachers tend to provide general comments rather than specific ones and do not give enough attention to pupils and the content of the lesson, see [16,17,18,19]). On the other hand, two aspects that were rather neglected in research on noticing at that time were brought to the fore: the focus on important moments in a mathematics lesson (i.e., situations pertinent to the quality of the lesson) and on what was called mathematics-specific phenomena, i.e., phenomena that could be observed, explained, inferred or interpreted in relation to either mathematical or didactic issues pertaining to the teaching or learning of mathematics (as opposed to the teaching and learning of other subjects) [18]. Vondrová et al. found that pre-service teachers tended to notice phenomena that were not identified as important by experts, and that there was hardly any development in their demonstrated ability to notice mathematics-specific phenomena during their entire master’s studies [20,21]. Nor was there any development in shifting attention from the teacher to pupils or from pedagogy to content, or in shifting away from evaluation to interpretation of what they observed [16].
This underlined the importance of the question of how to develop pre-service teachers’ noticing and reasoning skills.
5.3.2. Developing Noticing and Reasoning Skills via Video-Interventions
Beginning with the seminal work by Sherin and van Es [52], studies showed that video-interventions (or video-clubs) are an effective way of developing pre- and in-service teachers’ noticing and reasoning skills. In their first study in this area, Simpson, Vondrová and Žalská [16] confirmed that even a short video-intervention led pre-service teachers to an increased focus on pupils and content and that they became more specific in their comments on the videoed lesson. However, unlike in some other studies, the video-intervention did not lead to an increased interpretation of what was noticed; the pre-service teachers’ comments remained at the level of description and evaluation.
Thus, Vondrová and her team set out to explore their hypothesis that the reason for this divergent result might be that while the pre-service teachers in the study by Simpson et al. [16] observed the teaching of others, in interventions that were effective in the development of interpretation, the participants observed their own teaching. The researchers organized video-interventions (this time with pre-service teachers of five subjects, not only mathematics) of two types, ‘public video’ vs. ‘own video’, and compared them against the comparison group, who did not work with any video (public group: N = 23. Own video: N = 21. Comparison group: N = 16. The pre- and post-task was again a reflective one. The pre-service teachers saw the lesson from the subject they studied. A number of other data were collected: initial and final questionnaires, field notes, recordings of discussions in sessions and the pre-service teachers‘ responses to the tasks set within the video-intervention (see [13] for more detail)). The ‘public video’ group watched videos of lessons taught by other teachers who were unknown to the participants, while in the ‘own video’, the students jointly prepared, conducted and reflected on lessons in the way LS methodology prescribes.
However, the results did not confirm the above hypothesis. There were no important discernible differences between video conditions [14]. Moreover, unlike in the first study by Simpson, Vondrová and Žalská [16], Vondrová et al. found hardly any development in pre-service teachers’ noticing and reasoning skills, even though the conditions of the two rounds of video-interventions were very similar. In an attempt to see whether the above conclusion was an artefact of choice of data (pre-service teachers’ written responses to a video lesson), the authors analyzed other data to look for possible signs of the participants’ learning or possible reasons for their ‘not learning’ [13]. They examined the students’ responses to questionnaires and their work during the (recorded) video-intervention sessions and their responses to reflective tasks.
When comparing the data from the two rounds of video-interventions, a possible explanation for the divergent result was found in the pre-service teachers’ initial level of noticing skills. The participants in the second study started from the position where those in the first study had finished. Thus, the question arises if there is a ‘sweet spot’ in which video interventions of the kind that was organized support the development of professional vision [14]. While it has been acknowledged that unless people have developed a baseline vision, they cannot build on it (e.g., [55]), the study [14] further showed that there might be a limit to how video may allow further development of participants with a well-developed professional vision.
Perhaps expectations for the development of noticing and reasoning skills in a video-intervention might have been too high for pre-service teachers who had no experience of teaching. A specific observation framework might have helped them to focus their attention on more salient aspects of teaching.
Vondrová et al. [13] came to some more intriguing conclusions. Not only the initial skills but also intraindividual differences must be taken into account when considering the effect of a video-intervention on pre-service teachers’ development. Moreover, the pre-service teachers from both types of video-intervention, and regardless of the subject they studied, spoke enthusiastically about their learning from the video-intervention (e.g., they reported having learned to connect the noticed moments to the whole of the lesson and how they impacted achieving the lesson aims; in their own view, they learned to focus on pupils). It also transpired that the question of which type of video-intervention was more suitable for teacher education did not really make sense. Each type was valuable in its own right for the pre-service teachers. Thus, the pre-service teachers from the ‘own video’ groups valued the opportunity to teach and to see themselves from a different perspective, whereas those from the ‘public video’ groups appreciated having seen a range of teaching approaches and topics in the video. Regardless of the type of video observed, the participants spoke highly about the aspects in which the video-interventions were grounded: the use of video, reflective tasks and discussions in the sessions.
5.4. Culture of Problem Solving and Teachers’ Growth
Studies confirm the positive effect of the teachers’ enthusiasm for teaching mathematics on the quality of their pupils’ motivation to learn and on their understanding of school mathematics (see, e.g., [56]). In this section, we present the research project that examined the impact of the use of heuristic strategies for problem solving on participating teachers’ mathematics instruction and on strengthening their PCK, specialized content knowledge (in the sense used in [35]), enthusiasm and teaching strategies [22,57]. One aim of the study was to influence teachers’ and pupils’ perception of mathematical problems, namely, from seeing them as a tool to identify ‘strong’ and ‘weak’ pupils towards seeing them as activating and motivating components of school mathematics teaching [58]. The use of heuristic strategies in problem solving processes was expected to be a key driver of this change. The project was conceived as an instrument to characterize pupils’ approaches to solving mathematics problems on the individual and class levels ([59] within the framework of the concept of the culture of problem solving (CPS) introduced in the Theory of Didactical Situations in Mathematics [33]).
Eisenmann et al.’s study [22] is part of the above project. It focuses on the systematic use of heuristic strategies (in the sense of [59,60]) in solving problems on the school mathematics level. Three classes from three secondary schools in the Czech Republic participated in it. All three teachers involved in the study were engaged teachers who invest a lot of energy in their teaching and life-long learning. They and their pupils were involved in problem solving via heuristic strategies for a 16-month period. The research team created 160 problems that were suitable for solving by heuristic strategies and the teachers themselves decided which problems they integrated in their teaching. The researchers followed changes in teachers’ behavior and beliefs in response to preparing and putting into practice didactical situations that systematically offered their pupils the opportunity to use heuristic strategies.
5.4.1. Data and Methods
The cooperation of the researchers with the participating teachers was systematic. The teacher collected the pupils’ worksheets with the solutions and evaluated them. During regular meetings, the teacher and a member of the research team reflected jointly on all pupils’ outputs, the teacher’s field notes and the strategies used by pupils when solving the problems. The teachers also wrote a brief self-reflection once a week. The members of the research team had access to the pupils’ worksheets and used them to enrich the existing problems by new procedures that were developed spontaneously in the lessons. Researchers regularly observed selected lessons, some being video-recorded and reflected on. One of the aims of this process was to uncover pupils’ attitudes to problem solving and teachers’ teaching styles [22]. Structured interviews were organized at the end of the study during which the teachers answered questions related to the pupils’ and teachers’ relationship to problems, changes in pupils and changes in the teacher and opinions on individual strategies. The interviews were recorded and their protocols were analyzed.
5.4.2. Selected Results
By the end of the long-term study, the teachers lowered their demands on the accuracy and correctness in their pupils’ oral and written communication in favor of understanding the problem solving procedures. They showed more tolerance to variety in pupils’ solutions. They acknowledged a change in their attitude to mathematics teaching to using constructivist and inquiry-based approaches. They grew more interested in pupils’ thinking processes while solving problems. One of the most important results in this area is that the teachers started to pose their own problems, with the aim of helping the pupils to better understand heuristic strategies.
5.5. Supporting Subject-Didactic Competence Through Problem Posing
In the previous section, we discussed how improvements in the culture of problem solving led to teachers’ development. Experience from teaching pre-service primary teachers and from cooperation with in-service teachers shows that problem posing is similarly important; this idea was already stressed by Freudenthal and Polya in the 1960s; later by [61,62,63,64] and many others. Singer et al. [65] summarized the main trends of problem posing in school mathematics and investigated the impact of different techniques of problem posing on pre-service teachers. Researchers in the Czech Republic conducted a number of research studies with pre- and in-service teachers in this area (e.g., [23,24]).
Undoubtedly, teachers must be able to pose problems because they do so every day. However, problem posing in teacher education should not be a mere “drill and skill” process. On the contrary, the effect of systematic problem posing also lies in the realization of one’s own erroneous conceptions, of mistakes and gaps in knowledge. This aspect requires a deeper understanding.
The research on problem posing reported here followed previous studies by Tichá [66] that focused on the pre-service teachers’ ability “to see mathematics” in real life. Tichá was interested in the acquisition of knowledge and skills and their immediate application: in “contextual knowledge”, in the awareness of sense, purpose, conditions and relations (why, when and where I do something). For that purpose, it was necessary to study and handle real situations (naturally of varying levels of mathematical content). The authenticity of learning is important, and thus a focus on solving “real-life problems” that are meaningful and can be described as applications, or at least as problems with the nature of applications (see [66] for more detail) is required.
The second source of this strand of research are studies that deal with grasping a situation [67,68]. By grasping a situation, the authors understand in particular the following thinking processes: perception of the situation; detection of the key objects, phenomena and relations; setting of a specific direction of grasping the situation (aiming at a selected topic or a particular method of solution); construction of a model that enables problems of a graded difficulty to be posed to pupils; formulation of questions and other problems “sprouting” from the situation.
After 2010, Tichá and Hošpesová conducted several small-scale empirical studies related to problem posing in the education of primary school teachers (see, for example, [23,24,25]). Pre-service and in-service teachers were asked to pose problems with fractions in different settings and reflected on this activity in writing or orally. The following questions were targeted: (a) What shortcomings can be identified in the problems posed? (b) How are the problems posed perceived by pre-service and in-service teachers? (c) What relations are there between the quality of the problems posed and perception of this activity by their authors?
5.5.1. Data and Methods
In the analyzed studies, problem posing was initiated in several contexts (similarly to [64]):
- (a)
- Containing specified data (namely, ½ and 3/4) [23,24];
- (b)
- Solvable by a given calculation (namely, “Pose a task (several tasks) that can be solved by calculation: 1/4 × 2/3”) [25].
The studies had a qualitative design. In the first phase, the pre-service teachers posed problems. In the second phase, they solved the problems independently. The third phase took place as independent work at home, during which the pre-service teachers reflected on the problems. In the study [25], the fourth phase was introduced, in which the joint reflection was conducted and videotaped. The problems posed (their comprehensibility, solvability, whether they corresponded to the assignment or their “attractiveness”), written self-reflections of pre-service teachers and video-recordings of joint reflection were analyzed.
5.5.2. Selected Results
The problems posed by pre-service and in-service teachers showed that the process of problem posing uncovers various mistakes, defects, misconceptions or even failures to carry out basic arithmetical operations. The participants of the study lacked the ability to use different interpretations and representations of fractions; they were too far anchored in the domain of natural numbers and in additive structures. When asked to pose more than one problem, a stereotypical nature of the problems posed (fraction as an operator, quantity, etc.) could be observed. The choice of contexts or environments (discreet or continuous) was also stereotypical. The problems were very often “textbook-like”.
Interestingly, while the teachers accepted joint reflection on pupils’ problem-solving, some teachers refused problem posing, because they did not consider it as an activity suitable for their pupils (it distracts from “appropriate, genuine mathematics oriented on mastering of craftsmanship—carrying out calculations”), they were afraid that their training was not sufficient to enable them inclusion of these activities in their teaching, they objected that it would require intellectually and time demanding planning, and some of the teachers were hindered by the fact they would not know how to evaluate problem posing.
Tichá and Hošpesová also asked the participants to reflect in writing [23] or orally during a joint meeting [25] on what problem posing and joint reflection on the problems brought them. The aim was to find out if they realized that they, as primary teachers, needed solid content knowledge. The participants described problem posing as more challenging than problem solving; they emphasized how surprising the variety of interpretations of the same issue could be and how important the wording of a problem was. In the concluding discussion, the participants often stated that it was quite easy to pose many problems of the same type. What they found difficult was to create “cascades” of problems of increasing/decreasing difficulty and to pose several problems in which the fraction would be in a different role (operator, ratio, quantity, etc.).
5.6. Teachers’ Competences for Content and Language Integrated Learning (CLIL) and for Culturally Responsive Teaching
As a consequence of globalization, the beginning of the 21st century saw an increased research interest in the field of teaching mathematics in culturally and linguistically heterogeneous classrooms. The sixth research strand we identified responds to this interest, and targets the teacher’s skills to teach a subject through a foreign language (Section 5.6.1) and to teach in a culturally responsive way (Section 5.6.2).
5.6.1. Pre-Service CLIL Teachers’ Skills with a Focus on Lesson Planning Skills
The study conducted by Novotná, Hadj-Moussová and Hofmannová [26] focused on skills needed to teach mathematics through the medium of the English language. Specifically, they targeted the skills needed to overcome inner barriers, whose negative effect may be multiplied if the instruction is in L2 (L1 refers to the mother tongue, L2 to the language of instruction different from L1). These barriers can be both cognitive and affective. The authors suggest two types of support that the CLIL teacher may offer to pupils to overcome the barriers [26]. The verbal–visual-metacognitive support deals with content and requires the teacher to be competent in providing scaffolding in the form of, e.g., advance organizers, auditory and visual stimuli, gestures, etc. The peer-affective support concerns learners and requires the teacher to be competent in, e.g., showing sensitivity to individual learners’ needs, building their interdependence in both content and language and encouraging cooperative learning, as peer support is equally important as instruction in CLIL. Teacher’s praise, immediate feedback and reinforcement and further encouragement influence the CLIL process in a positive way and constitute a means to overcome affective barriers [26].
Following this preliminary study, Moraová and Novotná [27] focused on skills of pre-service teachers of mathematics when planning CLIL teaching mathematics lessons. As already stated, lesson planning is a key teacher competence. Lesson planning for CLIL lessons is more complex due to the attention that has to be paid to the language goal. The study investigated whether future teachers were aware of this demand and whether they possessed the skills necessary to plan an effective CLIL mathematics lesson.
Within a university course, pre-service teachers were first introduced to the aspects of a mathematics CLIL lesson (such lessons have mathematics and language objectives and should aim at the development of higher order thinking skills and the 4Cs of CLIL according to Coyle—content, communication, cognition and culture [69]) and then each presented a short CLIL activity. This was followed by joint reflection and feedback from the lecturers and the fellow students. The aim of this process was to draw their attention to the merits and shortcomings of the activities prepared and elicit alternative scenarios.
The analysis of 16 lesson plans showed that the pre-service teachers were in general able to plan a lesson that could be efficiently taught in L2, but also revealed some shortcomings. Most of the language goals suggested by the students targeted the acquisition of terminology and keywords only, and little attention was paid to language as the means of communication. An exception were three lesson plans in which their authors showed an ability to formulate meaningful language goals, e.g., “to practice Zero Conditional”. These students realized that pupils were not expected to learn definitions in L2 but to use the language in natural communication situations. On the other hand, ten out of sixteen students planned activities that could potentially develop higher order thinking skills and many also included some communicative activity in the lesson plan [27].
5.6.2. Mathematics Teacher Education for Teaching in Culturally and Linguistically Heterogeneous Classes
The European project, multiculturalism, migration, mathematics education and language, aimed to provide teacher educators and teachers with materials and teaching modules that would allow them to address adequately the needs of their classes in terms of multicultural and language aspects in the teaching and learning of mathematics. The project team made a survey of the needs of in-service mathematics teachers when teaching in culturally and linguistically heterogeneous classrooms [29]. They also proposed and piloted materials suitable for teaching mathematics in these classrooms [28,70].
The question arises of what support teachers need to be able to adapt the existing materials to the needs and conditions of a particular class. Moraová, Novotná and Favilli [30] investigated whether pre- and in-service teachers needed detailed lesson plans to be able to teach in culturally and linguistically diverse classes or whether it would suffice if they are given a learning environment with an outline of its possible uses in teaching. They used the concept of substantial learning environments developed by Wittmann [71], who posits that good teaching material for teachers and pupils should have a simple starting point and a lot of possible investigations or extensions.
The participants were shown ornaments from different cultures (such as Native Indian, Indian, Polynesian, Arabic, etc.) and asked to think of as many mathematical concepts and topics that could be developed in this environment as possible. It transpired that they worked creatively in this environment and proposed a number of problems requiring the application of, e.g., Pythagoras’ theorem, line symmetry, rotation and translation, geometrical figures and their properties, tessellation, etc. An important part of the workshop conducted with the participants was joint reflection on the proposed materials, which gave them an opportunity to reflect on the materials and especially their modifications for particular classes. The authors concluded that their suggested means of developing the teachers’ competence to adapt, develop and create teaching materials for a specific group of learners is a promising one.
6. Discussion and Conclusions
In this article, we summarized Czech research focusing on building and developing a knowledge base for teaching mathematics and subject-didactic competence, through different methods. Generally, the goal of the studies included in the meta-analysis was to uncover efficient ways of contributing to teachers’ professional development and evaluating their influence. We distinguished among six strands of research and described them in the previous section. The scheme in Figure 2 depicts another way to summarize the studies we analyzed. The process of teachers’ professionalism can be seen as consisting of three mutually connected dimensions [72], each of which is studied individually not only in the studies analyzed but also in international research. The dimension of professional vision was present in our studies focusing on the ability to notice and the ability to (jointly) reflect (Section 6.1). The dimension of professional knowledge is represented by the studies focusing on problem solving and problem posing (Section 6.2). The dimension of professional action is not a sole focus in any of the studies analyzed but is present in some via a task for pre- and in-service teachers to design a lesson and conduct it with pupils (Section 6.2).
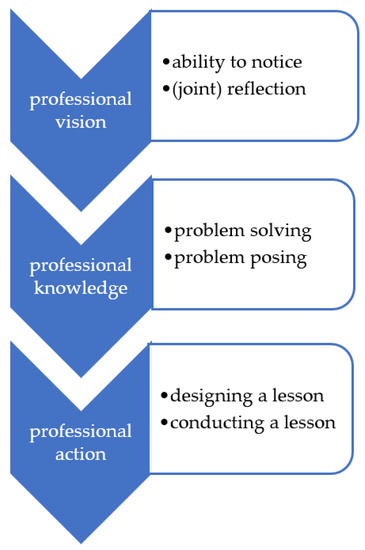
Figure 2.
Three dimensions of a teacher’s professionalism [72] and its projection in the analyzed studies (schematized by the authors of this article).
The process of reflection permeates all the dimensions. Regarding professional vision, there is the reflection on what one observes in a teaching–learning situation, whether as class teacher or observer. In the dimension of professional knowledge, there is reflection on the content and its didactic elaboration. In the dimension of professional action, there is reflection on one’s own teaching.
6.1. Professional Vision and Related Concepts
Professional vision provides the basis for a professional’s (teacher’s) decision-making in a teaching–learning situation. It encompasses how the teacher perceives the situation, how he/she thinks about it and which conclusions he/she reaches. Professional vision is also a key requirement of successful initial teacher education and professional development of in-service teachers, because it involves shifting attention to features of the situation relevant to the specialized goals of teaching.
The studies analyzed used different concepts in their theoretical frameworks, which, under closer scrutiny, seem to be very tightly connected or even overlap. The concept of professional vision is tightly connected with the ability to notice, while reflection seems to be a common denominator of both these concepts. The process of elaborating the experience and perception of both oneself and others enables pre- and in-service teachers to learn and develop as teachers. The studies analyzed showed that the ability to notice is influenced by the experience gained by the analysis of lessons (of mathematics) supported by the knowledge of mathematics education concepts and the process of reflection.
The studies confirmed that long-term interventions supported by videos positively impact the participants’ ability to notice and reflect. In particular, their focus of attention changes in the light of the experience gained. The in-service teachers reflecting on their own teaching primarily notice the pupils’ reactions and activity in the lesson. Only later do they begin to notice their own teaching. At first, the teachers’ observations are more impressionistic and only later do they focus more deeply on the interpretation of subject matter and their conceptions of teaching or assessment. The in-service teachers who observe a lesson given by someone else comment on didactic planning, methods used and communication with the pupils in the lesson [31]. They consequently learn to compare the intended plan of the lesson with its real course [12]. It transpired that they learn more deeply if they have an opportunity to reflect on the teaching within a group of colleagues (lesson study, video-club). Moreover, reflection needs to be given enough space and the skill of qualified reflection has to be learned [17,38].
The above has also been confirmed for pre-service teachers in the studies analyzed. For pre-service teachers, it is difficult to notice and comment on moments important from the point of mathematics education [15]; they tend to notice phenomena that are not identified as important by experts; they often adopt a general pedagogical view, for example, how to support pupils’ active participation in lessons [19]. Vondrová et al. introduced a notion of mathematics-specific phenomena by matching the students’ comments against what the researchers view as important issues in the lessons and developing a framework to further characterize the nature of the observations [16]. Surprisingly, when pre-service teachers’ skills at the beginning and end of their master’s studies were compared, there was hardly any development in their demonstrated ability to notice the mathematics-specific phenomena [20,21] or in shifting attention from the teacher to pupils and from pedagogy to content or in shifting away from evaluation to interpretation of what they observed [17].
It is not surprising that both the ability to notice and to reflect is closely connected to the participants’ knowledge and attitudes [31]. The level of joint reflection in a group of teachers depends on whether there is a teacher or an expert who turns the group’s attention to important moments in the lesson. This shows that qualified reflection is based on deep PCK.
The common conclusion to our studies is that an opportunity to observe and reflect on video recordings of teaching, sometimes alone, but mainly in cooperation with colleagues/peers, brings the in-service and pre-service teachers new insight into the processes in the classroom and into individual pupils’ thinking [17]. While teaching, teachers must solve various problems (not only didactical) without having the time to think about them. The subsequent reflection gives the teachers an opportunity to return to their teaching from a more detached point of view, in tranquility, and allows them to think more deeply about their teaching in the broader contexts of their professional values and beliefs, intentions, goals, ideas and expectations, thus preparing them for similar situations they will face in the future.
A prerequisite condition for successful joint reflection is the willingness of all participants to focus in depth on teaching. It is necessary to record as much information about teaching as possible (video recordings, transcripts, etc.). Although this is increasingly less technically demanding, it is still time-consuming and is not often employed as a component of regular professional development. What is crucially important is supporting a safe atmosphere in the group conducting self- and joint reflection. Pre-service teachers have to reduce the fear of expressing themselves in front of others. In in-service training courses, teachers often express their doubts about the possibility of using joint reflections in everyday practice. For some teachers (regardless of their age), it is very difficult to take part in discussions and to express their opinion. Their low self-evaluation may also have a negative influence [12,17].
6.2. Professional Knowledge and Professional Action (Problem Solving and Problem Posing)
In mathematics teaching, problem solving is the most important method for working with pupils. Many authors consider problem posing to be no less important and thus we consider PCK connected to problem posing and problem solving to be an important part of mathematics teachers’ professional knowledge. The studies analyzed understood problem solving and problem posing to be an educational tool of mathematics education.
Problem solving and the use of heuristic strategies in teaching mathematics in school is included in both pre- and in-service courses in the mathematics education programs. The studies in this area relate particularly to two aspects of a teacher’s professional development: professional knowledge [23,24,25] and professional action (for some of the studies) [17,22,26].
While in pre-service courses, the main focus is on future teachers’ selection of heuristic strategies for specific problems given to them by the educator [26], in in-service courses, the participants’ main task is to pose problems that support the use of different heuristic strategies [22]. Our studies have shown that joint reflection on pupils’ solutions of a problem and posing of similar problems may be regarded both as one of the goals of mathematics teachers’ education and as the means of achieving this goal. The reflected process of problem solving and problem posing and the resulting knowledge may also represent a diagnostic tool, one of the methods of assessing the level of the authors’ knowledge, or possibly specific manifestations of misunderstanding and their causes [24]. Moreover, it was observed that problem posing may motivate participants in the activity to strive to deepen their knowledge (while posing the problem) and recognize their weaknesses (in the subsequent discussion). This proved to be true especially for in-service teachers, because it challenges them to deepen their own knowledge.
In the studies in which a close cooperation between teachers and researchers, and reflections on teachers’ productions played a significant role, we observed signs of the development in teachers’ autonomy in both knowledge and action. At first, the teachers were afraid of their own weaknesses, misconceptions and gaps in knowledge and expected feedback from the researcher (“tell me what’s right” [22]). The mathematics problems they posed did not correspond to the requirements or were imprecise [24]. The first experience with joint reflection on problems posed was not always pleasant and some teachers approached the experience with anxiety. With more experience gained with the process of problem posing and reflection on its products, teachers increased their efforts to deepen their own knowledge and became more willing to offer their problems for reflection. By the end of the long-term cooperation, some teachers became independent in didactic processing of the mathematical content of the curriculum. They acquired the skill to modify the problems as needed. Joint reflection challenged the teachers to make a decision to create a set of problems stimulating pupils’ inquiry and use them with pupils in their own classes to support pupils’ understanding [27,28].
6.3. Methodological Issues
There are two main focuses of the research studies we analyzed. In the first, the education of mathematics teachers was targeted. The studies took into account specific needs of mathematics as a predominantly deductively built subject; that is, they aimed at specific mathematics content (for example, mathematics in general [14,15], fractions [18,23,24] and problem solving [22]). The second type of studies focused on the competences of teachers who face current challenges such as heterogeneous classes, pupils with special needs [26,27] or multicultural issues [29,30].
Some studies describe the level of competence of pre- or in-service teachers [15,18,19,20,27,29], while the rest include an intervention with the goal of supporting the development of competences needed for the teaching of mathematics and evaluating the impact of the intervention. This is a complex issue, and thus it is no surprise that the studies have different designs and did not all manage to eliminate or control all the variables that influence the intervention and the measurement of gains caused by it. Some studies are of a descriptive nature and describe the goal, content and course of the intervention [26,28,30]. Others target the specific learning gains of their participants [11,12,16,17,22,23,24,25,31], while only some of them utilize a pre–post design [13,14,16,21]. While the descriptive studies only bring forward tentative conclusions based on the observations of researchers and eclectic artefacts, the other types of studies include robust findings.
Despite the variability of research designs, we can conclude that all the studies that included an intervention found a positive impact of their parameters of interest. In some studies, this impact was found by quantitative means, and in all of them, it was confirmed by a qualitative analysis of the participants’ productions. However, the positive evaluation of the interventions could be connected to the pre- and in-service teachers’ preferences for professional development that includes concrete examples from teaching practice as such. This was a characteristic of nearly all the studies we analyzed.
Another finding particular to some of the studies lies in the discrepancy between the perceived and measured development of teachers’ competences and knowledge. The tools they used did not fully capture the progress that the participants felt. Thus, the question of appropriate tools of assessment of the influence of different types of interventions comes to the fore.
6.4. Implications and Follow-Up Research Work
The six strands of research presented in the article have not been completed and research is continuing. Video-based interventions remain a focus of research. They are organized with future elementary teachers and include reflecting on videos of teaching from different subjects. A lesson study cycle is also included. Professional vision research continues with a study comparing the competence of pre- and in-service teachers and also experts in the field. As the above studies confirmed, the cooperation with colleagues and/or researchers leads to the improvement of the subject-didactic and pedagogical competences of the participants. Researchers are also participants in research and they are learning as well. Thus, teacher educators’ learning has become the focus of our attention too.
While ample research has been carried out with pre-service teachers in the Czech Republic, there is a lack of research with in-service teachers. This will become a focus of our future efforts. The same applies to more general questions that have been targeted in research but cannot be seen as completed. In particular, how can we assess the benefits of different activities in the pre- and in-service teachers’ education not only in respect to professional development of the participants but the influence on their teaching? What lies behind differences in the types of problems teachers pose and lessons they teach? Finding answers to these questions remains a focus of researchers and the future will certainly pose new challenges.
Naturally, our research has practical implications in our work with both pre- and in-service teachers. We utilized artefacts of practice in our courses (such as video-recordings of lessons or scenarios of teaching-learning situations). In the project learning hyperspace for formative assessment and inquiry based science and mathematics teaching (South Bohemia University in České Budějovice, Czech Republic), most of the teaching modules were based on a video recording of the teaching. In the project enhancement of research excellence in mathematics teacher knowledge (Charles University, Prague, Czech Republic), we utilized a lesson study methodology.
To sum up, the article brings an insider perspective on research on teacher education conducted in the Czech Republic. It presents some of the results of studies that investigated practice-based courses and these could serve as a starting point for further research. However, the studies also highlighted the merits and prerequisites for successful implementation of such courses and these could provide inspiration for teacher educators thinking about using them in their practice. The results could inform leaders of mathematics education courses in university teacher training departments. Some results are applicable more broadly and across disciplines.
We began our article with a quote from J. A. Comenius on what a teacher should know and we end with a quote about the need for his/her professional development: “Our teachers must not be similar to columns at roads that only show where to go but do not go by themselves”.
Author Contributions
Conceptualization, A.H. and J.N.; methodology, A.H. and N.V.; investigation, A.H., J.N., N.V., H.M., M.T.; writing—original draft preparation, A.H., J.N., N.V., H.M., M.T.; writing—review and editing, A.H. and N.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research study has been financially supported by the project of the TECHNOLOGY AGENCY of the Czech Republic (Reg. No. TL02000368) and project PROGRES Q17, “Teacher Preparation and the Teaching Profession in the Context of Science and Research” funded by Charles University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Helus, Z. Four theses on school reform. Pedagogika 2001, 51, 25–41. (In Czech) [Google Scholar]
- Comenius, J.A. The Great Didactic [Didactica Magna]; Keatinge, M.W., Ed.; Russell & Russell: New York, NY, USA, 1967; Available online: https://web.archive.org/web/20140202105252/ (accessed on 27 February 2021).
- Komenský, J.A. Analytical Didactics; Brno: Tvořivá škola, Czech Republic, 2004. (In Czech) [Google Scholar]
- Pikkarainen, E. Signs of Reality: The Idea of general Bildung by J. A. Comenius. In Theories of Bildung and Growth: Connections and Controversies between Continental Educational Thinking and American Pragmatism; Siljander, P., Kivelä, A., Sutinen, A., Sense, B., Eds.; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2012; pp. 19–29. [Google Scholar] [CrossRef]
- Shulman, L.S. Those who understand: Knowledge growth in teaching. Educ. Res. 1986, 15, 4–14. [Google Scholar] [CrossRef]
- Vyšín, J. About basic research and the work of the Section for the Modernization of Mathematics Teaching. Mat. a Fyzika ve Škole 1979, 10, 104–112. (In Czech) [Google Scholar]
- Vyšín, J. Genetic method in teaching mathematics. Mat. a Fyzika ve Škole 1976, 6, 582–593. (In Czech) [Google Scholar]
- Vyšín, J. Research work in the theory of mathematics education. PMFA 1973, 18, 32–38. (In Czech) [Google Scholar]
- Kuřina, F. Mathematics as a Pedagogical Problem: My Didactical Creed; Hradec Králové: Gaudeamus, Czech Republic, 2016. (In Czech) [Google Scholar]
- Novotná, J.; Tichá, M.; Vondrová, N. Czech and Slovak research in didactics of mathematics: Tradition and a glance at present state. In European Traditions in Didactics of Mathematics; Blum, W., Artigue, M., Mariotti, M.A., Strässer, R., van den, M.-P., Eds.; Springer Open: Berlin/Heidelberg, Germany, 2019; pp. 187–212. [Google Scholar] [CrossRef]
- Vondrová, N. Lesson Study, enhanced with video-based tasks, in the education of mathematics teachers: Lesson Study in the middle. In Supporting teachers: Improving instruction. Examples of Research-Based Teacher Education; Janík, T., Delehefte, I.M., Zehetmeier, S.M., Eds.; Waxmann Publishing House: New York, NY, USA, 2019; pp. 129–151. [Google Scholar]
- Vondrová, N.; Cachová, J.; Coufalová, J.; Krátká, M. “Lesson study” in the Czech context: How teachers perceived their participation and what influence it had on their noticing mathematics education phenomena. Pedagogika 2016, 66, 427–442. (In Czech) [Google Scholar] [CrossRef][Green Version]
- Vondrová, N.; Novotná, M.; Pavlasová, L.; Robová, J.; Stará, J.; Uličná, K. Video-Interventions: Bridges between Theory and Practice in Pre-Service Teachers’ Development; Karolinum: Praha, Czech Republic, 2020. [Google Scholar]
- Simpson, A.; Vondrová, N. Developing pre-service teachers’ professional vision with video interventions: A divergent replication. J. Educ. Teach. 2019, 45, 567–584. [Google Scholar] [CrossRef]
- Stehlíková, N. Interpretation of some mathematics education phenomena by pre-service and in-service teachers. Pedagogika 2010, 60, 303–313. (In Czech) [Google Scholar]
- Simpson, A.; Vondrová, N.; Žalská, J. Sources of shifts in pre-service teachers’ patterns of attention: The roles of teaching experience and of observational experience. J. Math. Teach. Educ. 2018, 21, 607–630. [Google Scholar] [CrossRef]
- Tichá, M.; Hošpesová, A. Qualified pedagogical reflection as a way to improve mathematics education. J. Math. Teach. Educ. 2006, 9, 129–156. [Google Scholar] [CrossRef]
- Vondrová, N.; Žalská, J. Do pre-service teachers attend to mathematics specific phenomena when observing mathematics teaching on video? Orb. Sch. 2012, 6, 85–101. [Google Scholar] [CrossRef]
- Pavlasová, L.; Stará, J.; Vondrová, N.; Novotná, M.; Robová, J.; Uličná, K. Selective attention of pre-service teachers and the nature of their interpretations. Pedagogika 2018, 68, 5–24. (In Czech) [Google Scholar] [CrossRef][Green Version]
- Vondrová, N.; Žalská, J. Ability to notice mathematics specific phenomena: What exactly do pre-service teachers attend to? Orb. Sch. 2015, 9, 77–101. [Google Scholar] [CrossRef]
- Vondrová, N. The effect of a video-based intervention on the knowledge-based reasoning of future mathematics teachers. In Invited Lectures from the 13th International Congress on Mathematical Education; Kaiser, G., Ed.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 699–717. [Google Scholar]
- Eisenmann, P.; Novotná, J.; Přibyl, J.; Břehovský, J. The development of a culture of problem solving with secondary students through heuristic strategies. Math. Educ. Res. J. 2015, 27, 535–562. [Google Scholar] [CrossRef]
- Tichá, M.; Hošpesová, A. Developing teachers’ subject didactic competence through problem posing. Educ. Stud. Math. 2013, 83, 133–143. [Google Scholar] [CrossRef]
- Hošpesová, A.M.; Tichá, M. Problem posing in primary school teacher training. In Mathematical Problem Posing: From Research to Effective Practice; Singer, F.M., Ellerton, N., Cai, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 433–447. [Google Scholar] [CrossRef]
- Tichá, M.; Hošpesová, A. Problem Posing and Development of Pedagogical Content Knowledge in Pre-Service Teacher Training. In Proceedings of CERME 6; Lyon, I.N.R.P., Ed.; Institut National de Recherche Pédagogiqu: Lyon, France, 2010; pp. 1941–1950. Available online: www.inrp.fr/editions/cerme6 (accessed on 1 March 2021).
- Novotná, J.; Hadj-Moussová, Z.; Hofmannová, M. Teacher training for CLIL—Competences of a CLIL teacher. In International Symposium Elementary Maths Teaching SEMT ’01. Proceedings; Novotná, J., Hejný, M., Eds.; Charles University, Faculty of Education: Prague, Czech Republic, 2001; pp. 121–126. [Google Scholar]
- Moraová, H.; Novotná, J. How do pre-service teachers of mathematics plan their CLIL mathematics lessons? In Proceedings of the 14th International Conference Efficiency and Responsibility in Education 2017; Houška, M., Ed.; Czech University of Life Sciences Prague: Prague, Czech Republic, 2017; pp. 262–269. [Google Scholar]
- Moraová, H.; Novotná, J. Mathematics lessons in culturally and linguistically heterogeneous classrooms. In Proceedings of the 15th International Conference Efficiency and Responsibility in Education 2018; Fejfar, J., Fejfarová, M., Flégl, M., Houška, M., Husák, J., Krejčí, I., Urbancová, H., Eds.; Czech University of Life Sciences Prague: Prague, Czech Republic, 2018; pp. 221–228. [Google Scholar]
- Ulovec, A.; Moraová, H.; Favilli, F.; Grevholm, B.; Novotná, J.; Piccione, M. Multiculturalism in theory and teachers’ practice. In International Symposium Elementary Maths Teaching SEMT ’13. Proceedings; Novotná, J., Moraová, H., Eds.; Univerzita Karlova, Pedagogická Fakulta: Praha, Czech Republic, 2013; pp. 322–330. [Google Scholar]
- Moraová, H.; Novotná, J.; Favilli, F. Ornaments and tessellations—encouraging creativity in mathematics classroom. In Mathematical Creativity and Mathematical Giftedness: Enhancing Creative Capacities in Mathematically Promising Students; Singer, M., Ed.; Springer: Cham, Switzerland, 2018; pp. 253–284. [Google Scholar] [CrossRef]
- Hošpesová, A.; Tichá, M.; Macháčková, J. Differences and similarities in (qualified) pedagogical reflection. In Proceedings of CERME5; Pitta-Pantazi, D., Philippou, G., Eds.; University of Cyprus: Nicosia, Cyprus, 2005; pp. 1906–1915. [Google Scholar]
- Scheerens, J.; Hendriks, M.; Luyten, H.; Sleegers, P.; Steen, R. Teachers’ Professional Development: Europe in International Comparison. An Analysis of Teachers’ Professional Development Based on the OECD’s Teaching and Learning International Survey (TALIS); European Commission Publication: Luxembourg, Belgium, 2010. [Google Scholar] [CrossRef]
- Brousseau, G. Theory of Didactical Situations in Mathematics; Dordrecht: Kluwer, Switzerland, 1997. [Google Scholar]
- Fennema, E.; Franke, M.L. Teachers’ knowledge and its impact. In Handbook of Research on Mathematics Teaching and Learning; Grows, D.A., Ed.; MacMillan: New York, NY, USA, 1992; pp. 147–165. [Google Scholar]
- Ball, D.L.; Thames, M.H.; Phelps, G. Content knowledge for teaching: What makes it special? J. Teach. Educ. 2008, 59, 389–407. [Google Scholar] [CrossRef]
- Krainer, K. Some considerations on problems and perspectives of in service mathematics teacher education. In 8th International Congress on Mathematics Education: Selected Lectures; Alsina, C., Ed.; SAEM Thales: Seville, Spain, 1996; pp. 303–321. [Google Scholar]
- Švec, V. Student’s self-reflection during the undergraduate didactic education. Pedagogika 1996, 46, 266–276. (In Czech) [Google Scholar]
- Scherer, P.; Steinbring, H. The Professionalisation of Mathematics Teachers’ Knowledge—Teachers Commonly Reflect Feedbacks to Their Own Instruction Activity. 2003. Available online: http://www.dm.unipi.it/~didattica/CERME3/WG11/papers_pdf/TG11_Scherer.pdf (accessed on 10 March 2021).
- Climent, N.; Carrillo, J. Developing and researching professional knowledge with primary teachers. In CERME 2. European Research in Mathematics Education II, Part 1; Novotná, J., Ed.; Charles University, Faculty of Education: Prague, Czech Republic, 2001; pp. 269–280. [Google Scholar]
- Jaworski, B. Research practice into/influencing mathematics teaching and learning development: Towards a theoretical framework based on co-learning partnerships. Educ. Stud. Math. 2003, 54, 249–282. [Google Scholar] [CrossRef]
- Mason, J. Noticing: Roots and branches. In Mathematics Teacher Noticing: Seeing through Teachers’ Eyes; Sherin, M.G., Jacobs, V.R., Philipp, R.A., Eds.; Taylor & Francis: New York, NY, USA; London, UK, 2011; pp. 35–50. [Google Scholar]
- van Es, E.A.; Sherin, M.G. Mathematics teachers’ ‘learning to notice’ in the context of a video club. Teach. Teach. Educ. 2008, 24, 244–276. [Google Scholar] [CrossRef]
- Sherin, M.G.; Russ, R.S.; Colestock, A.A. Assessing mathematics teachers’ in-the-moment noticing. In Mathematics Teacher Noticing: Seeing through Teachers’ Eyes; Sherin, M.G., Jacobs, V.R., Philipp, R.A., Eds.; Taylor & Francis: London, UK, 2011; pp. 79–94. [Google Scholar]
- Fujii, T. Designing and adapting tasks in lesson planning: A critical process of Lesson Study. ZDM 2016, 48, 411–423. [Google Scholar] [CrossRef]
- Lawrence, C.A.; Chong, W.H. Teacher collaborative learning through the lesson study: Identifying pathways for instructional success in a Singapore high school. Asia Pac. Educ. Rev. 2010, 11, 565–572. [Google Scholar] [CrossRef]
- Lewis, J.M.; Fischman, D.; Riggs, I.; Wasserman, K. Teacher learning in Lesson Study. Mont. Math. Enthus. 2013, 10, 583–620. [Google Scholar]
- Pang, M.F. The use of learning study to enhance teacher professional learning in Hong Kong. Teach. Educ. 2006, 17, 27–42. [Google Scholar] [CrossRef]
- White, A.L.; Lim, C.S. Lesson study in Asia Pacific classrooms: Local responses to a global movement. ZDM 2008, 40, 915–925. [Google Scholar] [CrossRef]
- Beisiegel, M.; Mitchell, R.; Hill, H.C. The design of video-based professional development: An exploratory experiment intended to identify effective features. J. Teach. Educ. 2018, 69, 69–89. [Google Scholar] [CrossRef]
- Borko, H.; Jacobs, J.; Eiteljorg, E.; Pittman, M.E. Video as a tool for fostering productive discussions in mathematics professional development. Teach. Teach. Educ. 2008, 24, 417–436. [Google Scholar] [CrossRef]
- Jacobs, V.R.; Lamb, L.L.C.; Philipp, R.A. Professional noticing of children’s mathematical thinking. J. Res. Math. Educ. 2010, 41, 169–202. [Google Scholar] [CrossRef]
- Sherin, M.G.; van Es, E.A. Using video to support teachers’ ability to notice classroom interactions. J. Technol. Teach. Educ. 2005, 13, 475–491. [Google Scholar]
- Putnam, R.T.; Borko, H. What do new views of knowledge and thinking have to say about research on teacher learning? Educ. Res. 2000, 29, 4–15. [Google Scholar] [CrossRef]
- Little, J.W. Locating learning in teachers’ communities of practice: Opening up problems of analysis in records of everyday work. Teach. Teach. Educ. 2002, 18, 917–946. [Google Scholar] [CrossRef]
- Star, J.; Lynch, K.; Perova, N. Using video to improve preservice mathematics teachers’ abilities to attend to classroom features: A replication study. In Mathematics Teacher Noticing: Seeing through Teachers’ Eyes; Sherin, M.G., Jacobs, V.R., Philipp, A.R., Eds.; Taylor & Francis: New York, NY, USA, 2011; pp. 117–133. [Google Scholar]
- OECD. Teacher enthusiasm. In PISA 2018 Results (Volume III): What School LIFE means for Students’ Lives; OECD Publishing: Paris, France, 2020; pp. 87–95. [Google Scholar] [CrossRef]
- Eisenmann, P.; Novotná, J.; Přibyl, J. Culture of solving problems—One approach to assessing students’ culture of mathematics problem solving. In Aplimat 2014—13th Conference on Applied Mathematics; Ve-lichová, D., Ed.; Publishing House of STU: Bratislava, Slovak, 2014; pp. 115–122. [Google Scholar]
- Brousseau, G.; Novotná, J. La culture scolaire des problèmes de mathé-matiques. In Les Didactiques et Leurs Rapports à l‘ Enseignement et à la Formation. Quel Statut Epistémologique de Leurs Modèles et de Leurs Résultats? Sarrazy, B., Ed.; AFIRSE: Bordeaux, France, 2008; Available online: http://people.fjfi.cvut.cz/novotant/jarmila.novotna/2008Brousseau_Novotna.pdf (accessed on 15 March 2021).
- Polya, G. How to Solve It: A New Aspect of Mathematical Method; Princeton University Press: Princeton, NJ, USA, 2004. [Google Scholar]
- Schoenfeld, A.H. Mathematical Problem Solving; Academic Press Inc: London, UK, 1985. [Google Scholar]
- Kilpatrick, J. Problem formulating: Where do good problems come from? In Cognitive Science and Mathematics Education; Schoenfeld, A.H., Ed.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1987; pp. 123–147. [Google Scholar]
- Silver, E.A.; Cai, J. An analysis of arithmetic problem posing by middle school students. J. Res. Math. Educ. 1996, 27, 521–539. [Google Scholar] [CrossRef]
- English, L.D. The development of fifth-grade children’s problem-posing abilities. Educ. Stud. Math. 1997, 34, 183–217. [Google Scholar] [CrossRef]
- Pittalis, M.; Christou, C.; Mousolides, N.; Pitta-Pantazi, D. A structural model for problem posing. In Proceedings of 28th PME; Hoines, M.J., Bishop, A.J., Eds.; Bergen University College: Bergen, Norway, 2004; pp. 49–56. [Google Scholar]
- Singer, F.M.; Ellerton, N.; Cai, J. Mathematical Problem Posing: From Research to EFFECTIVE practice; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Tichá, M. Auf den Spuren der Entdeckung der Mathematik in der Alltagssituationen. In Beiträge zum Mathematikunterricht. Vorträge auf der 35. Tagung für Didaktik der Mathematik; Haiser, G., Ed.; Franzbecker: Hildesheim/Berlin, Germany, 2001; pp. 616–619. [Google Scholar]
- Koman, M.; Tichá, M. On travelling together and sharing expenses. Teach. Math. Appl. 1998, 17, 117–122. [Google Scholar]
- Tichá, M.; Koman, M. Towards developing teachers’ ability for grasping situations. In Proceedings of the International Conference “Teachers and their University Education at the Turn of the Millennium”; Kohnová, J., Ed.; Charles University: Praha, Czech Republic, 2000; pp. 300–306. [Google Scholar]
- Coyle, D. Theory and planning for effective classrooms: Supporting students in content and language integrated learning contexts. In Learning through a Foreign Language: Models, Methods and Outcomes; Masih, J., Ed.; CILT: London, UK, 1999; pp. 46–62. [Google Scholar]
- Moraová, H.; Novotná, J.; Favilli, F. Teaching mathematics in culturally heterogeneous classrooms: What do teachers really need? E-pedagogium 2015, 1, 34–44. (In Czech) [Google Scholar] [CrossRef]
- Wittmann, E.C. Mathematics education as a “Design Science”. Educ. Stud. Math. 1995, 29, 355–374. [Google Scholar] [CrossRef]
- Minaříková, E.; Janík, T. Teachers’ professional vision: Exploring and clarifying the concept. Pedagog. Orientace 2012, 22, 181–204. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).