Abstract
International large-scale assessments (ILSAs) provide several measures as a representation of educational outcomes, the so-called plausible values, which are frequently interpreted as a representation of the ability range of students. In this paper, we focus on how this information should be incorporated into the estimation of efficiency measures of student or school performance using data envelopment analysis (DEA). Thus far, previous studies that have adopted this approach using data from ILSAs have used only one of the available plausible values or an average of all of them. We propose an approach based on the fuzzy DEA, which allows us to consider the whole distribution of results as a proxy of student abilities. To assess the extent to which our proposal offers similar results to those obtained in previous studies, we provide an empirical example using PISA data from 2015. Our results suggest that the performance measures estimated using the fuzzy DEA approach are strongly correlated with measures calculated using just one plausible value or an average measure. Therefore, we conclude that the studies that decide upon using one of these options do not seem to be making a significant error in their estimates.
1. Introduction
Since the pioneering work carried out in the early days of educational economics, the exploration of the educational and societal factors that affect educational attainment has attracted the interest of researchers working in this field. Several authors have named this educational effectiveness research [1,2], which in recent years has been growing rapidly due to the development of new learning methods and the use of information technologies [3,4].
In this context, the rich and extensive information provided by large-scale international assessments (hereafter ILSAs) has become a very useful tool for analyzing the performance of education systems around the world and promoting reforms of national education policies [5,6]. Although the Program for International Student Assessment (PISA) conducted by the OECD is undoubtedly the best known, several other studies can also be included within this group, including the Trends in International Mathematics and Science Study (TIMSS) and the Progress in International Reading Literacy Study (PIRLS), both coordinated by the International Association for the Evaluation of Educational Achievement (IEA).
The technical complexities of these large-scale assessments often create multiple challenges for applied researchers when analyzing their data [7] (Sjøberg [8] described the data generated by PISA as a playground for psychometricians). In this paper, we focus on the construction of measures representing the competences of students, a very relevant issue that has been generating enormous interest in the recent literature [9]. On this issue, it is widely assumed that the competences of students cannot be measured with a simple score derived from the answers provided by students in standardized tests, but by several values randomly obtained from the distribution function of test results, known in the psychometric literature as plausible values. These values should be interpreted as the representation of the ability range for each student [10], which is very difficult to measure in a precise way.
The procedure for handling these values in econometric analyses (where they are frequently included as the dependent variable) is well known for users of these databases, since technical reports and user manuals of international databases describe it in detail [11,12,13]. As we explain in Section 2.2, this procedure requires estimating the model several times: once using each of the plausible values, and then by computing the average of the estimates. However, this issue has been overlooked in studies using these data to estimate efficiency measures of performance using frontier methods, such as data envelopment analysis (DEA) (this nonparametric approach is the most used in these types of studies due to its greater flexibility [14]), which allows the best practices that can serve as benchmarks for the rest to be identified. Such studies have become increasingly common due to restrictions on increasing public spending in education in most countries; thus, policy makers and researchers are very interested in identifying the references that can provide them with some guidelines to improve student and school outcomes without spending more money in educational resources.
In this framework, plausible values are often used as the output measures representing educational outcomes. Nevertheless, researchers often forget that, when selecting a single plausible value or the average of all available plausible values, some of the available information about students’ abilities is overlooked. This is because, in contrast to econometric analysis, when applying traditional frontier methods, it is not possible to account for the fact that the plausible values represent a distribution of results and, therefore, out measures are imprecise.
In this paper, we intend to bridge this knowledge gap by proposing an innovative way of dealing with imprecise data in output measures when applying frontier methods to data from ILSAs. This approach is based on the notion of fuzziness [15] and, more precisely, we rely on the so-called fuzzy DEA (FDEA), which allows for the consideration of the whole distribution of test scores into the estimation of efficiency measures. Among all the many existing approaches to implement FDEA [16], we apply the methodology proposed by Kao and Liu [17], which basically transforms the fuzzy “radial” DEA model to several conventional DEA models by applying the so-called α-cut procedure.
We apply this technique to assess the performance of Spanish students participating in PISA 2015. In our model, we include three outputs (test scores in mathematics, reading and sciences) that are treated as fuzzy in an FDEA model since they are represented by ten different plausible values. Since the estimated efficiency measures are represented using membership functions, it is possible to provide more precise information for decision making.
The research problem that we intend to solve is whether the consideration of all the information provided by plausible values can lead to different results than those obtained when using traditional methods, which only incorporate limited information to represent educational output. Thus, the efficiency estimates derived from the application of the FDEA approach are compared with the estimates obtained with the traditional DEA method using one single plausible value or the average of plausible values.
The remainder of the paper is organized as follows. In Section 2, we explain the concept of plausible values and some guidelines for handling them in empirical studies. Section 3 introduces the necessary notation and background of the proposed FDEA methodology. Subsequently, in Section 4, we explain the main characteristics of our dataset and the variables selected for our empirical analysis. In Section 5, we present and discuss the main results comparing the estimates obtained with the proposed FDEA approach with those obtained with the traditional DEA approach. Finally, we present the main conclusions in Section 6.
2. Plausible Values and How to Use Them in Empirical Analyses
2.1. What Are Plausible Values?
Measuring cognitive outcomes is one of the main concerns of international large-scale assessments, such as PISA, TIMSS or PIRLS. The assessment instrument often includes multiple questions or items and is carried out in a limited period of time with the aim of providing comparable information about the ability of students and their knowledge in different domains, such as reading, mathematics or science. They rely on a complex psychometric design that involves considering different sub-domains within each subject area. This results in an enormous amount of test material to be covered, since it is not possible to ask every pupil all the available questions. Therefore, all the tested items are divided into multiple blocks or clusters. Since test administration can only take place during a maximum of two hours (this limitation on testing time is based on considerations with respect to reducing student burden, minimizing interruptions in the school schedule and other financial and/or time constraints), students are randomly assigned to complete one particular test booklet, each of which includes a subset of tested items consisting of items from one or more clusters; thus, he/she responds to only a fraction of what constitutes the total assessment pool [18].
As pupils answer only a limited number of questions from the total test item pool, the measurement of individual proficiency is achieved with a substantial amount of measurement error [19]. Thus, traditional methods of estimating individual proficiency would result in biased or inconsistent variance estimates. As an alternative to this problem, plausible value methods are employed as a viable technique to generate proficiency estimates from the limited fraction of administered cognitive items and student background information. Since student ability is not directly observed, it is a latent variable (or latent ability) that could be treated as a missing value; thus, it is necessary to use multiple imputation methods [20,21] to estimate the distribution of proficiency for each student in each subject area (see [22,23,24] for further details).
Plausible values can be defined as several random values drawn from the distribution of proficiency estimates [11,25]. They are used by applied researchers for different purposes, such as estimating the plausible range and the location of proficiency for groups of students or exploring the relationship between proficiency and various social and educational variables in secondary analysis. However, it is worth mentioning that plausible values are not individual scores in the traditional sense and should, therefore, not be analyzed as multiple indicators of the same score or latent variables [26].
In practice, five plausible values are reported for each student in overall mathematics and science (TIMSS) and another five for each student in overall reading (PIRLS), since this number is sufficient for the accurate estimation of population-level statistics [27]. However, in recent years, some of the large-scale assessment surveys have increased the number of plausible values with the aim of providing better estimates of the variability when a large amount of imputation is required. For example, ten plausible values were used for PISA 2015 and PISA 2018 for each domain (mathematics, reading and science) [28], while only five plausible values were used for PISA 2000 to PISA 2012. There are very few studies that have provided justifications for increasing the number of plausible values used beyond five. One of the few exceptions is the recent work by Bibby [29], which concludes that the sample size has a larger impact on the estimations of population parameters than an increase in the number of plausible values used. The reported plausible values are in scale scores with a mean of 500 and standard deviation of 100 overall, across all participating countries.
2.2. How to Use Plausible Values in Secondary Analyses
Researchers should be aware that secondary analyses should be performed independently on each of the available plausible values so that they can provide appropriate estimates of population statistics, such as means and variances [30]. Specifically, the correct procedure for handling the plausible values provided in the international achievement databases can be divided into four steps, based on the original work of [20]: (i) estimate the statistic/model of interest five times (or ten in the last waves of PISA) using each of the plausible values to obtain five (or ten) separate parameter estimates (β_pv) and the corresponding estimates of the sampling error (σ_pv); (ii) calculate the average of those estimates; (iii) estimate the magnitude of the imputation error; and (iv) calculate the value of the final standard error by combining the average sampling error and the imputation error (note that the secondary analysis model is typically a subset of the latent regression model used to generate the plausible values [31]). Finally, the final parameter estimates and their standard error can be used to conduct hypothesis tests and construct confidence intervals following the usual methods. In order to facilitate the correct implementation of this procedure in secondary analyses, most software specialized in data processing has specific routines or commands to perform estimations with plausible values (for instance, PV [32] or REPEST [33] in Stata).
Although this procedure is clearly described in technical reports and user manuals of different international large-scale assessments, in some empirical studies dealing with plausible values, it is common to find two different shortcuts in the implementation of secondary analyses with econometric techniques, both of which are incorrect. First, analysts often choose to use just one of the five plausible values. With this option, the standard errors of the statistics of interest are generally underestimated, as the uncertainty associated with the measurement of proficiency distributions is ignored. However, PISA analysts indicate that using one or five plausible values in a large sample does not really make a substantial difference [34]. In fact, during the exploratory phase of the data, statistical analyses can be based on a single plausible value, although it is highly recommended to use all the available values in order to improve the accuracy of the estimates, even for large samples.
The second shortcut employed by some authors is to calculate the average of the existing plausible values (five or ten) and use it as if it were the only available estimate of student performance. The main problem with the calculation of this average value as a proxy for performance is that standard errors are severely underestimated (particularly if only a single plausible value is being used), which might lead to misleading results. Therefore, the mean of the available plausible values should never be used in empirical analyses with econometric techniques [19].
2.3. Plausible Values in Efficiency Analyses
In contrast to the existing clear instructions for secondary studies with econometric techniques, the way to proceed when using frontier methods in empirical studies exploiting data from ILSAs generates much more doubt for researchers. In these studies, test scores (or rather plausible values) achieved by students in different domains are usually identified as proxies for the educational output (see Cordero et al. [35] for a review). However, they follow different criteria to deal with plausible values. The most common option consists of using only one plausible value [36,37,38,39,40], usually the first of all available values, i.e., the first shortcut identified in the previous section. Likewise, other studies follow the second shortcut and use the average of all plausible values to estimate efficiency measures [41,42]. Finally, there is a more cumbersome process, which implies estimating one efficiency score for each plausible value and, subsequently, calculating the average efficiency score [43,44].
The main problem of all the aforementioned alternatives is that none of them explicitly considers the fact that the output measures are imprecise since they treat plausible values as crisp values (precise measurements) when they are actually representing a distribution of results. The results obtained from using these crisp values may not adequately reflect the performance of the units evaluated because some of the available information about students’ abilities is overlooked.
The present study attempts to shed light on this issue by exploring the extent to which the use of these procedures may affect the results and, more specifically, present an innovative method that allows the incorporation of data on the whole distribution of results into the estimation of efficiency measures of educational performance. This method is described in depth in the following section.
3. Methodology
First, we provide a brief description of the traditional DEA model, before going on to explain the method we propose to use in our empirical analysis. Therefore, let us consider n DMUs to be evaluated (such as students within our frame of reference). DMUj consumes , amounts of inputs to generate , , amounts of outputs. From the data, it is possible to construct an estimation of the underlying technology from which the DMUs were generated. The technology represents the set of all feasible input–output bundles [45]. Data Envelopment Analysis provides the following estimator of the technology under variable returns to scale (VRS):
Technical inefficiency can then be calculated as the distance from a DMU to the border of the estimated technology. This distance is usually implemented in practice through two types of approaches: input-oriented models and output-oriented models. For convenience, we only present the output-oriented DEA approach, since this is what we use in our practical example, on the premise that students are always trying to improve their results. Output-oriented models assume that each DMU strives to maximize outputs while using the same level of inputs. Among the existing output-oriented models, the output-oriented radial model is probably the most famous. This approach keeps the inputs of the assessed unit constant but equi-proportionally augments the bundle of outputs. In this way, the output-oriented radial model assuming variable returns to scale for evaluating the unit can be mathematically implemented through the following linear optimization program.
The optimal value of the above program is the efficiency scores associated with the unit . It can be proved that , and with signaling, that the evaluated DMU is technically efficient. Otherwise, , and there is leeway for improving the outputs while using the same level of inputs.
Additionally, the dual program of (2) is the following linear program:
Usual approaches assume that input and output values are precise information (also called “crisp”). However, it may be that the observed values of the variables (inputs and outputs) are imprecise. Within the framework of our research, we elaborate in Section 2 on how student abilities cannot be defined by a unique value (test score), but rather a range or distribution from which we extract different random values. These values (or their average) are frequently used in model (2) to solve the “crisp” traditional DEA radial model. However, they may not necessarily be the most appropriate representation of students’ abilities, especially if there is a high spread or variation in the distribution of results. Therefore, it might happen that two students presenting similar values for a single plausible value (or even similar average plausible values) may exhibit a differing pattern with respect to the unobserved distribution of results; so, when it comes to technical efficiency, they could be categorized differently.
Data imprecision may be included in DEA efficiency models through Fuzzy Data Envelopment Analysis (FDEA), where scores in different competences are included as fuzzy numbers, as opposed to crisp numbers, in the DEA model. Emrouznejad et al. [46] provide a taxonomy and review of the FDEA methods in six categories and that can be found in the literature, namely, the fuzzy ranking approach, the fuzzy random/type-2 fuzzy set, the tolerance approach, the fuzzy arithmetic, the possibility approach, and the α-level based approach. Among them, the α-level based approach is probably the most popular FDEA model. In particular, the one proposed by Kao and Liu [17] is the most popular and the most applied in empirical studies. Consequently, this is the option we use in our analysis. We now review the main characteristics of this approach.
The model of Kao and Liu [17] is based on the notion of α-cuts, also known as α-possibility level sets, and the transformation of the FDEA model into a set of standard crisp DEA models. In this framework, and represent the α-cut of and , respectively. Additionally, represents the membership function, which quantifies the degree of truth of the element. Each α-cut somehow represents a confidence interval for the considered input or output value.
Given that crisp inputs and outputs can be represented as degenerated membership functions with only one value in their domain, we can assume that all inputs and outputs are fuzzy. In this way, the dual of the output-oriented radial model, i.e., model (3), can be formulated as follows:
Additionally, the efficiency score is also a fuzzy number due to the nature of the data used in the model. That fuzzy number is linked to a membership function. Kao and Liu’s model allows this membership function to be calculated from different α-cuts. Next, given a certain level α (), we show how the lowest and the highest values of the corresponding α-cut for the membership function of can be calculated. In particular, the lowest value is determined through program (5):
In model (5), note that the inputs of the evaluated DMU and the outputs of all other units were set to their greatest values, while the outputs of the assessed unit and the inputs of all other DMUs were set to their lowest values. This is the essence of the approach by Kao and Liu [17]. Regarding the highest value of the corresponding α-cut, it can be implemented through model (6):
Models (5) and (6) allow the interval to be determined for different values of α ().
Finally, ranking units to ascertain better performance is a procedure of interest in efficiency analysis. In the case of the Fuzzy Data Envelopment Analysis, there are a few approaches that could be applied. In this paper, again following [1], we implemented the following index:
where and .
4. Data and Variables
We used data from PISA 2015 in our empirical study. PISA is a triennial study that provides international comparative data on the performance of 15-year-old students in three main domains (in each cycle, one of the domains is in focus, with reading in 2000 and 2009, mathematics in 2003 and 2012, and science in 2006 and 2015) (reading, science and mathematics). In addition, this database contains information about many potential factors that might affect those results, such as variables representing student family background, home resources, school environment or class characteristics (in total, there are more than two hundred variables, including the original variables and the composite indexes constructed from the original information). This information is derived from the responses given by students and school principals to different questionnaires [11].
We selected students as the unit of analysis because they represent the group for which we have imprecise measures of educational output approximated by plausible values. Moreover, there are some additional reasons. First, if we consider that the main purpose pursued in education is the improvement of results, it makes sense that students represent the evaluated units, since they are the ones who must develop their skills based on the resources they have at their disposal [47]. Second, if the observations were aggregated at the school level, the fact that the level of resource utilization by students may differ according to their characteristics cannot be taken into account [48]. Additionally, using school-level averages does not consider the existing dispersion of the data, which may result in inaccurate measures of performance, especially regarding the identification of efficient units [49] For the purpose of our study, we used a representative dataset for Spain, composed of 6700 students from 201 schools (the original dataset includes 6378 students, but we excluded 38 students due to the absence of data in some variables).
With regard to the selection of input variables, we followed a very restrictive efficiency notion that consists of using only one input representing student socioeconomic background as a proxy for the academic quality of the student (this approach is also used in other previous studies [41,50]). Specifically, the input at student level was measured by the students’ socioeconomic background (ESCS): an index of the economic, social and cultural status of students created by PISA analysts that captures a range of aspects of a student’s family and home background and combines information on parents’ education and occupations and cultural possessions at home. The first variable is the higher educational level of any of the students’ parents according to the International Standard Classification of Education (ISCED). The second variable is the highest occupational status of any of the students’ parents according to the International Socio-economic Index of Occupational Status (ISEI [51]). The third variable is an index of educational possessions related to household economy. This indicator is continuous and is positively correlated with output variables. Using this single input, we evaluated the extent to which a student is making the most of his/her potential abilities, considering his/her socioeconomic background as a proxy for this concept, or to which his/her performance is below the expected level.
Since the ESCS index presented negative values (the values of the PISA index of economic, social and cultural status were standardized to a mean of zero for the total population of students in OECD countries), the values of this variable were rescaled by adding the maximum negative value to all of them; thus, all the new quantities were positive. As a result, the variable fulfils the requirement of isotonicity (i.e., ceteris paribus, more input implies equal or higher level of output), which allows us to preserve the desirable property of translation invariance [52]. This variable was treated as crisp in our empirical analysis.
Output variables are represented by students´ test scores in the three domains assessed by PISA (mathematics, reading and science). For each domain, PISA 2015 provides ten plausible values; thus, we can define our output by using different alternatives that we intend to compare. Thus, we can use a single crisp value for each domain, which in turn could consist of the use of only one plausible value (e.g., PV1MATH, PV1READ or PV1SCIE) or the mean of all the available plausible values (). The other alternative is to treat them as fuzzy numbers. This possibility implies considering the existing variation among different plausible values, which can be higher or lower for each of the observations, as shown in Table 1, for two randomly selected students.

Table 1.
Statistics of fuzzy variables for two randomly selected students.
As a preliminary step to the application of the approach suggested by Kao and Liu [17], we need to model the values of the three variables representing the output (PVMATH, PVREAD and PVSCIE) as a particular fuzzy number. To this end, we estimated a kernel function for each student from the data corresponding to each variable. We also calculated the skewness coefficient for each kernel, obtaining values close to zero, which is indicative that the kernel functions are quite symmetrical. This implies that the mean values of the distributions are close to the median and the mode. Figure 1 presents several examples of the shape of the estimated kernel functions for the PVMATH variable for different students.
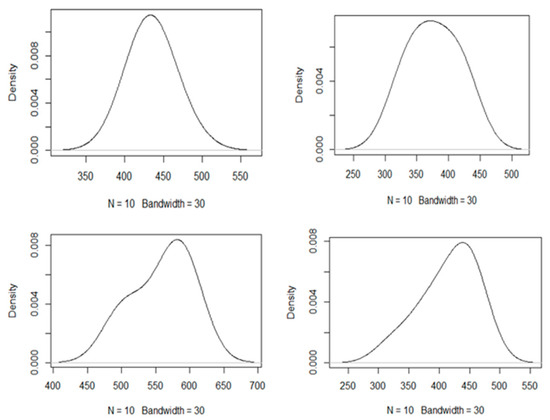
Figure 1.
Examples of kernel functions for the PVMATH variable.
Kao and Liu’s approach determines the α-cut for each value α, with 0 < α ≤ 1. The α-cut corresponds to an interval. To this end, the y-axis in the kernel must be rescaled so that the maximum is equal to one for the rescaled kernel function. For example, if we consider student #1635 from the data sample, we obtain different intervals (α-cuts) for the values α = 0.7, α = 0.8, α = 0.9 and α = 1. The corresponding α-cuts are shown in Table 2. Given the set of α-cuts, we may determine the membership function of the fuzzy efficiency score of each DMU (student), following the steps described in Section 3. Table 3 reports the descriptive statistics for all the variables employed in our study.

Table 2.
α-cuts for student 1635 (randomly selected).

Table 3.
Descriptive statistics.
5. Results
In this section, we illustrate the potential divergences that might arise in efficiency measures depending on how we deal with plausible values by applying different approaches to the data from PISA. We chose three alternative methods (the resolution of these approaches was carried out by programming algorithms with R software [53]). First, we estimated a standard DEA using ESCS as our input and the mean values of all the plausible values for each domain as our outputs, i.e., treating PVMATH, PVREAD and PVSCIE as crisp (Model A). Second, we also treated PVMATH, PVREAD and PVSCIE as crisp, but we calculated a standard DEA for each set of plausible values (ten values), once more including ESCS as the only input (Model B) (these estimations were conducted using the R package “lpSolveAPI” [54]). Both estimations are relatively simple, since we only need to solve linear programming models. Finally, we obtained fuzzy efficiency estimates using the approach by Kao and Liu [17] for different α-cuts (α = 0.7, 0.8, 0.9 and 1) incorporating PVMATH, PVREAD and PVSCIE as fuzzy numbers through kernel functions and ESCS as a crisp input variable (Model C) (we also estimated efficiency scores for other values (e.g., α = 0.1, 0.2, 0.3, 0.4, 0.5 and 0.6), but we do not report these results because the intervals are too wide). This is much more complex, since it is necessary to previously estimate the kernel functions of each of the fuzzy variables (PVMATH, PVREAD and PVSCIE) (we obtained these estimates using the “density” function, implemented within the R stats package [53], opting for the use of the “Gaussian” smoothing method). Once the kernels were estimated, we performed the α-cuts on the kernels, generating, for each fuzzy variable and for each α, an interval of values. Next, we created a database for each α-cut with the interval data of all the fuzzy variables and incorporated the information of the rest of the crisp variables. Finally, after obtaining these databases, we applied the fuzzy linear programming model (5) and (6) of Kao and Liu [17] (again, this was also solved using the R package “lpSolveAPI” [54]), which allowed us to obtain, for each student, the values of the efficiency associated with each α.
Table 4 reports the main descriptive statistics of efficiency estimates for each alternative. For Model 3, we present for each α both the lowest and the highest values of the confidence interval for the fuzzy efficiency score. Therefore, we obtained intervals as . Moreover, we also calculated the index I0 (Equation (7)), which reflects a summary of the different results determined for the set of αs. We assume variable returns to scale and an output orientation in all estimations.

Table 4.
Descriptive statistics of efficiency scores for different approaches.
From our results, we observe that, in general terms, the average scores calculated with the traditional DEA are similar to the estimated values obtained with fuzzy DEA for . Indeed, the correlation among them is higher than 0.9 (and statistically significant) in all cases, as we can see in Table 5. In our opinion, this is due to two main reasons. First, considering , it yields the mode of the data for each variable and student as the corresponding α-cut. Second, the modes are generally close to the means of the data in this real example due to the symmetry of the data distributions. Consequently, the results of programs (5) and (6) for are identical and generate an optimal value (score) very similar to the optimal value of model (2), where PVMATH, PVREAD and PVSCIE are incorporated as crisp variables. Of course, in the case of asymmetric data distributions, the efficiency scores for the traditional model and for could be different.

Table 5.
Correlation coefficients among efficiency scores estimated with different approaches.
Although we note that the values of the index I0 are highly correlated with the rest of scores calculated using traditional DEA, it is also noteworthy that their mean values are significantly lower. This can be observed more clearly if we examine the divergences for students presenting a high dispersion in output data. In Table 6, we report the estimated scores for all the considered alternatives for students with the highest values of standard deviation in the fuzzy variables. Here, we can see that the standard DEA tends to overestimate the level of inefficiency, since their efficiency scores are clearly higher than the value of the index I0. The information displayed in this table also highlights that there is a high level of variation across efficiency scores calculated with each set of plausible values, that cannot be detected when plausible values are aggregated (Model A).

Table 6.
Efficiency scores for students with the highest dispersion in their plausible values.
If we focus on students identified as efficient according to standard DEA models, which are presented in Table 7, we detect that most of them present an index I0 higher than one and, for almost a half, are not considered as efficient in the fuzzy DEA model for α = 1. Moreover, some students are fuzzy efficient exclusively for α = 1, but the upper bound of the α-cuts for all other possible levels is greater than one. Thus, we cannot be totally sure that these students are performing efficiently, although this would be the conclusion to be drawn from an analysis performed with a standard DEA. Therefore, our results suggest that the consideration of all the variability reported by the different plausible values using an FDEA model may modify the conclusions obtained to a certain extent, at least as far as the identification of efficient units is concerned.

Table 7.
Efficient units according to the traditional DEA compared to efficiency scores with other alternatives (FDEA and each PV).
6. Conclusions
In this paper, we used a novel method to incorporate all the information provided by the plausible values available in international large-scale educational databases as an approximation of educational output to estimate efficiency measures. Specifically, we applied the fuzzy DEA approach proposed by Kao and Liu [17]. This methodology provides more precise information than conventional methods, such as DEA, which only allows for incorporating a part of the available information about students as proxies of educational output. Therefore, the main objective of this research was to determine the extent to which having this additional information on the units evaluated can change the results in terms of identifying best practices and ranking units. In order to be able to make this comparison, we applied both methods to assess the performance of a sample of Spanish students participating in PISA 2015.
Our results reveal that the estimated measures of performance obtained with the fuzzy DEA approach present high levels of correlation with the efficiency scores calculated using traditional DEA models. Therefore, in principle, when researchers use only one plausible value or aggregate values into a single aggregate measure, they obtain similar results to those obtained if they were to consider the whole distribution of results, represented by all the available plausible values that are expressed by a kernel function within our framework. This can be considered as a positive result for practitioners using traditional frontier methods in this area, since it appears that not considering all available information on students’ abilities does not seem to generate relevant biases in the estimated efficiency measures.
However, we also found some noteworthy divergences among the estimated scores with both alternatives. First, we noticed that standard DEA may overestimate the level of inefficiency for some students, especially those with a higher dispersion in their results, i.e., plausible values more different from each other. Second, we also observed that a high proportion of units identified as efficient in standard DEA models are not identified as efficient in the fuzzy DEA model; thus, we cannot be completely sure that units identified as being efficient by traditional DEA are actually efficient.
In view of the above, we claim that empirical studies using microdata from international comparative surveys for estimating measures of performance using DEA should try to account for the existing variation among plausible values as a representation of the output (test scores). Otherwise, there might be an overestimation of the level of inefficiency of some units as well as a misidentification of efficient units, which could also affect the measures of the remaining evaluated units, since they are commonly used as references in DEA.
Finally, we would like to mention that we are aware that our study presents a series of limitations that should lead us to interpret the results with some caution. Probably the most important of these limitations is that we only incorporated one input variable in our empirical analysis, which is not very common in efficiency studies. However, this decision was made in an attempt to minimize the potential problems of loss of discriminatory power of nonparametric techniques, such as DEA or FDEA. Another potential limitation arises from the fact that in our application, we only used data referring to one country (Spain), so it would be advisable to extend the scope of the study to a broader context considering information on other countries. In the same way, it could also be interesting to use more recent information, such as the data available in PISA 2018, although in principle, this change would not be relevant since the newest wave of this survey offers the same number of plausible values for each student (10). Finally, it is also worth mentioning that we only used one of the multiple existing models to implement FDEA, Kao and Liu´s procedure; thus, a potential extension of the present study could be to applied other alternative FDEA approaches to test the robustness of our results.
Author Contributions
Conceptualization, J.A. and J.M.C.; Methodology, J.A.; Data curation, L.O.; writing—original draft preparation, J.A., J.M.C. and L.O.; writing—review and editing, J.A., J.M.C. and L.O. All authors have read and agreed to the published version of the manuscript.
Funding
J. Aparicio and L. Ortiz thank the financial support of the Spanish Ministry of Science and Innovation and the State Research Agency under grant PID2019-105952GB-I00/AEI/10.13039/501100011033, and Jose M. Cordero also acknowledges the support from the Spanish Ministry of Science and Innovation and the State Research Agency through grant ECO2017-83759-P/AEI/10.13039/501100011033 and the Regional government of Extremadura (Junta de Extremadura) through grant GR18106.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data used in this paper are publicly available in the OECD website: https://www.oecd.org/pisa/data/2015database/, accessed on 4 July 2021.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reynolds, D.; Teddlie, C. The International Handbook of School Effectiveness Research; Routledge: London, UK, 2002. [Google Scholar]
- Creemers, B.; Kyriakides, L. The Dynamics of Educational Effectiveness; Routledge: London, UK, 2008. [Google Scholar]
- Ergüzen, A.; Erdal, E.; Ünver, M.; Özcan, A. Improving Technological Infrastructure of Distance Education through Trustworthy Platform-Independent Virtual Software Application Pools. Appl. Sci. 2021, 11, 1214. [Google Scholar] [CrossRef]
- Dospinescu, O.; Dospinescu, N. Perception Over E-Learning Tools in Higher Education: Comparative Study Romania and Moldova. In Proceedings of the IE 2020 International Conference, Madrid, Spain, 20–23 July 2020; Volume 10. [Google Scholar]
- Gustafsson, J.-E. Effects of International Comparative Studies on Educational Quality on the Quality of Educational Research. Eur. Educ. Res. J. 2008, 7, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Fischman, G.E.; Topper, A.M.; Silova, I.; Goebel, J.; Holloway, J.L. Examining the influence of in-ternational large-scale assessments on national education policies. J. Educ. Policy 2019, 34, 470–499. [Google Scholar] [CrossRef]
- Rutkowski, L.; Gonzalez, E.; Joncas, M.; von Davier, M. International large-scale assessment data: Issues in secondary analysis and reporting. Educ. Res. 2010, 39, 142–151. [Google Scholar] [CrossRef]
- Sjøberg, S. PISA and ‘real life challenges’: Mission impossible? In PISA According to PISA: Does PISA Keep What It Promises; LIT: Wien, Vienna, 2007; pp. 241–263. [Google Scholar]
- Sáez-López, J.-M.; Domínguez-Garrido, M.-C.; Medina-Domínguez, M.-D.-C.; Monroy, F.; González-Fernández, R. The Competences from the Perception and Practice of University Students. Soc. Sci. 2021, 10, 34. [Google Scholar] [CrossRef]
- Mislevy, R.J.; Beaton, A.E.; Kaplan, B.; Sheehan, K.M. Estimating Population Characteristics From Sparse Matrix Samples of Item Responses. J. Educ. Meas. 1992, 29, 133–161. [Google Scholar] [CrossRef]
- OECD. PISA 2015 Technical Report; PISA, OECD Publishing: Paris, France, 2016. [Google Scholar]
- Boston College: TIMSS & PIRLS International Study Center. Methods and Procedures in TIMSS 2015. 2016. Available online: http://timssandpirls.bc.edu/publications/timss/2015-methods.html (accessed on 21 May 2021).
- Foy. TIMSS 2015 User Guide for the International Database. TIMSS & PIRLS; International Study Center, International Association for the Evaluation of Educational Achievement: Boston, MA, USA, 2017. [Google Scholar]
- De Witte, K.; López-Torres, L. Efficiency in education: A review of literature and a way forward. J. Oper. Res. Soc. 2017, 68, 339–363. [Google Scholar] [CrossRef]
- Zadeh, L. The concept of a linguistic variable and its application to approximate reasoning—I. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Hatami-Marbini, A.; Emrouznejad, A.; Tavana, M. A taxonomy and review of the fuzzy data en-velopment analysis literature: Two decades in the making. Eur. J. Oper. Res. 2011, 214, 457–472. [Google Scholar] [CrossRef]
- Kao, C.; Liu, S.-T. Fuzzy efficiency measures in data envelopment analysis. Fuzzy Sets Syst. 2000, 113, 427–437. [Google Scholar] [CrossRef]
- Berezner, A.; Adams, R.J. Why large-scale assessments use scaling and item response theory. In Implementation of Large-Scale Education Assessments; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2017. [Google Scholar]
- von Davier, M.; Gonzalez, E.; Mislevy, R. Plausible values: What are they and why do we need them? IERI Monogr. Ser. Issues Methodol. Large-Scale Assess. 2009, 2, 9–36. [Google Scholar]
- Rubin, D.B. Multiple Imputation for Nonresponse in Surveys; John Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- Schafer, J.L. Multiple Imputation in Multivariate Problems When the Imputation and Analysis Models Differ. Stat. Neerl. 2003, 57, 19–35. [Google Scholar] [CrossRef]
- Von Davier, M.; Sinharay, S. Analytics in international large-scale assessments: Item response the-ory and population models. In Handbook of International Large-Scale Assessment: Background, Technical Issues, And Methods of Data Analysis; Chapman and Hall/CRC: London, UK, 2013; pp. 155–174. [Google Scholar]
- Marsman, M.; Maris, G.K.J.; Bechger, T.M.; Glas, C.A.W. What can we learn from plausible val-ues? Psychometrika 2016, 81, 274–289. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laukaityte, I.; Wiberg, M. Using plausible values in secondary analysis in large-scale assessments. Commun. Stat. Theory Methods 2016, 46, 11341–11357. [Google Scholar] [CrossRef]
- Wu, M. The role of plausible values in large-scale surveys. Stud. Educ. Eval. 2005, 31, 114–128. [Google Scholar] [CrossRef]
- Mislevy, R.J. Should “multiple imputations” be treated as “multiple indicators”? Psychometrika 1993, 58, 79–85. [Google Scholar] [CrossRef]
- Luo, Y.; Dimitrov, D.M. A Short Note on Obtaining Point Estimates of the IRT Ability Parameter With MCMC Estimation in Mplus: How Many Plausible Values Are Needed? Educ. Psychol. Meas. 2019, 79, 272–287. [Google Scholar] [CrossRef]
- OECD. PISA 2018 Technical Report; PISA, OECD Publishing: Paris, France, 2019. [Google Scholar]
- Bibby, Y. Plausible Values: How Many for Plausible Results? Ph.D. Thesis, University of Melbourne, Melbourne, Australia, 2020. [Google Scholar]
- Goldstein, H. International comparisons of student attainment: Some issues arising from the PISA study. Assess. Educ. Princ. Policy Pract. 2004, 11, 319–330. [Google Scholar] [CrossRef]
- Braun, H.; von Davier, M. The use of test scores from large-scale assessment surveys: Psychometric and statistical considerations. Large-Scale Assess. Educ. 2017, 5, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Macdonald, K. PV: Stata Module to Perform Estimation with Plausible Values; Statistical Software Compo-nents S456951; College Department of Economics: Boston, MA, USA, 2019. [Google Scholar]
- Avvisati, F.; Keslair, F. REPEST: Stata Module to Run Estimations with Weighted Replicate Samples and Plausible Values; Statistical Software Components; College Department of Economics: Boston, MA, USA, 2020. [Google Scholar]
- OECD. PISA Data Analysis Manual, SPSS Second Edition; OECD Publishing: Paris, France, 2009. [Google Scholar]
- Cordero, J.M.; Polo, C.; Santín, D.; Simancas, R. Efficiency measurement and cross-country differ-ences among schools: A robust conditional nonparametric analysis. Econ. Model. 2018, 74, 45–60. [Google Scholar] [CrossRef]
- De Witte, K.; Kortelainen, M. What explains the performance of students in a heterogeneous envi-ronment? Conditional efficiency estimation with continuous and discrete environmental variables. Appl. Econ. 2013, 45, 2401–2412. [Google Scholar] [CrossRef]
- Agasisti, T.; Zoido, P. Comparing the Efficiency of Schools Through International Benchmarking: Results From an Empirical Analysis of OECD PISA 2012 Data. Educ. Res. 2018, 47, 352–362. [Google Scholar] [CrossRef]
- Agasisti, T.; Zoido, P. The efficiency of schools in developing countries, analysed through PISA 2012 data. Socio-Econ. Plan. Sci. 2019, 68, 100711. [Google Scholar] [CrossRef]
- Aparicio, J.; Cordero, J.M.; Pastor, J.T. The determination of the least distance to the strongly effi-cient frontier in Data Envelopment Analysis oriented models: Modelling and computational aspects. Omega 2017, 71, 1–10. [Google Scholar] [CrossRef]
- Aparicio, J.; Cordero, J.M.; Gonzalez, M.; Lopez-Espin, J.J. Using non-radial DEA to assess school efficiency in a cross-country perspective: An empirical analysis of OECD countries. Omega 2018, 79, 9–20. [Google Scholar] [CrossRef]
- Cordero, J.M.; Prior, D.; Simancas, R. A comparison of public and private schools in Spain using robust nonparametric frontier methods. Central Eur. J. Oper. Res. 2015, 24, 659–680. [Google Scholar] [CrossRef] [Green Version]
- Cordero, J.M.; Santín, D.; Simancas, R. Assessing European primary school performance through a conditional nonparametric model. J. Oper. Res. Soc. 2017, 68, 364–376. [Google Scholar] [CrossRef]
- De Jorge, J.; Santin, D. Determinantes de la eficiencia educativa en la Unión Europea. Hacienda Pública Española 2010, 193, 131–155. [Google Scholar]
- Crespo-Cebada, E.; Pedraja-Chaparro, F.; Santín, D. Does school ownership matter? An unbiased efficiency comparison for regions of Spain. J. Prod. Anal. 2014, 41, 153–172. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Ineffi-ciencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef] [Green Version]
- Emrouznejad, A.; Tavana, M.; Hatami-Marbini, A. The State of the Art in Fuzzy Data Envelopment Analysis. In Performance Measurement with Fuzzy Data Envelopment Analysis; Springer: Berlin/Heidelberg, Germany; pp. 1–48.
- Waldo, S. On the use of student data in efficiency analysis: Technical efficiency in Swedish upper sec-ondary school. Econ. Educ. Rev. 2007, 26, 173–185. [Google Scholar] [CrossRef]
- Santin, D. La medición de la eficiencia de las escuelas: Una revisión crítica. Hacienda Pública Española 2006, 177, 57–82. [Google Scholar]
- Aparicio, J.; Cordero, J.M.; Ortiz, L. Measuring efficiency in education: The influence of imprecision and variability in data on DEA estimates. Socio-Econ. Plan. Sci. 2019, 68, 100698. [Google Scholar] [CrossRef]
- Thieme, C.; Prior, D.; Tortosa-Ausina, E. A multilevel decomposition of school performance using robust nonparametric frontier techniques. Econ. Educ. Rev. 2013, 32, 104–121. [Google Scholar] [CrossRef] [Green Version]
- Ganzeboom, H.; De Graaf, P.M.; Treiman, D.J. A standard international socio-economic index of occupational status. Soc. Sci. Res. 1992, 21, 1–56. [Google Scholar] [CrossRef] [Green Version]
- Cooper, W.W.; Seiford, L.M.; Tone, K. Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- R Core Team. Package “Stats.”. RA Lang. Environment Stat. Comput. Vienna, Austria: R Foundation for Statistical Computing. 2021. Available online: https://www.R-project.org (accessed on 21 October 2020).
- Konis, K.; Konis, M.K. Package ‘lpSolveAPI’. 2020. Available online: https://cran.r-project.org/web/packages/lpSolveAPI/lpSolveAPI.pdf (accessed on 21 October 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).