Infinitely Smooth Polyharmonic RBF Collocation Method for Numerical Solution of Elliptic PDEs
Abstract
:1. Introduction
2. The Polyharmonic Radial Basis Function Collocation Method
2.1. The Governing Equation
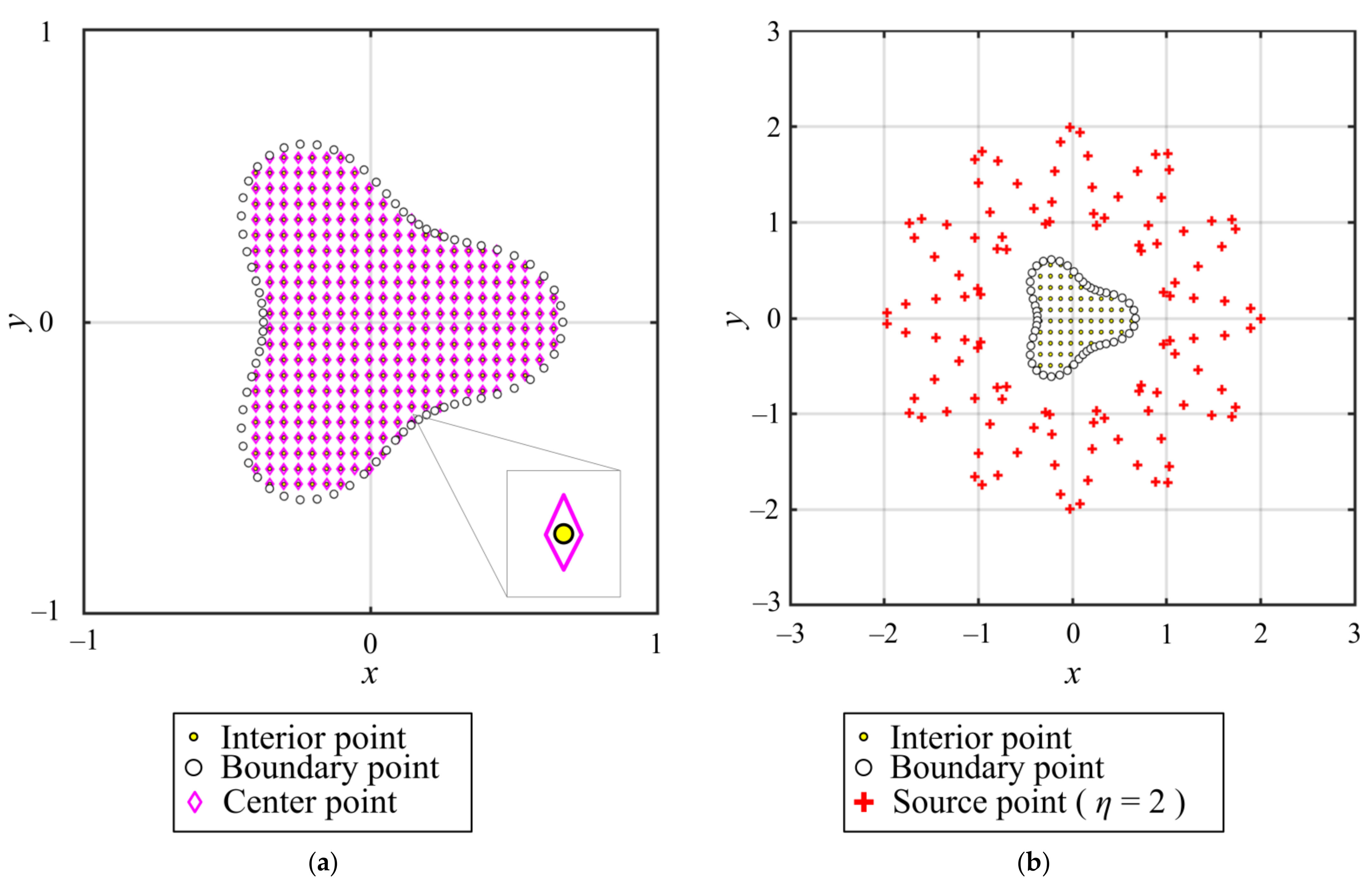
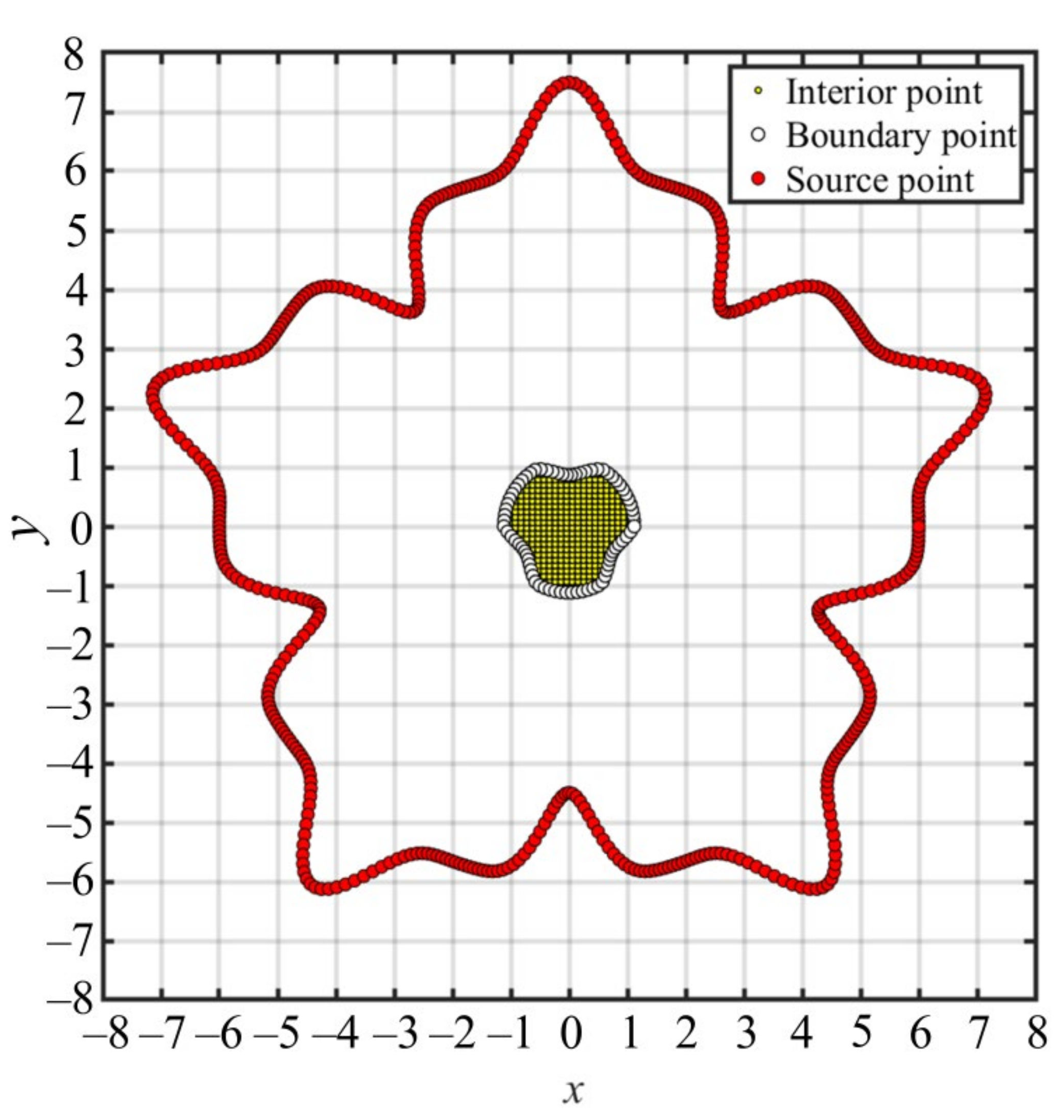
2.2. The Fictitious Sources
3. Convergence Analysis
4. Numerical Examples
4.1. The Seismic Wave Propagation Problem
4.2. The Groundwater Flow Problem
4.3. The Unsaturated Flow Problem
4.4. The Groundwater Contamination Problem
5. Conclusions
- (1)
- We convert the piecewise smooth PRBF into an infinitely smooth PRBF using source points collocated outside the domain. The distance between the interior point and fictitious source is, therefore, greater than zero. The PRBF and its derivatives in the governing equation always have the characteristics of global infinite differentiability and smoothness. Accordingly, techniques to deal with the singularity in the original PRBF are no longer required.
- (2)
- To clarify the possible influences for the positions of the sources on the accuracy, an analysis was conducted to evaluate the accuracy versus the shapes and positions of sources. The results show that the error may grow with the increase of the dilation parameter. However, results from all cases reveal that we may obtain accurate results with the use of an arbitrary value in the range of 1.5 to 5 for the dilation parameter. Nevertheless, the error may increase while the larger dilation parameter is adopted. However, it reveals that we could still obtain better accuracy than original PS even in the worst case. Furthermore, it appears that the accuracy may be less sensitive to the order k from the numerical results. It is found that accurate results with order k in the range of 3 to 10 were acquired.
- (3)
- The seismic wave propagation problem, groundwater flow problem, unsaturated flow problem, and groundwater contamination problem were investigated to show the robustness and accuracy of the proposed approach. From the results, the proposed infinitely smooth PRBF could provide much more accurate solutions than the conventional PRBF even with the optimal order.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, C.Y.; Ku, C.Y.; Huang, C.C.; Lin, D.G.; Yeih, W.C. Numerical solutions for groundwater flow in unsaturated layered soil with extreme physical property contrasts. Int. J. Nonlinear Sci. Numer. Simul. 2015, 16, 325–335. [Google Scholar] [CrossRef]
- Vu, T.D.; Ni, C.F.; Li, W.C.; Truong, M.H.; Hsu, S.M. Predictions of groundwater vulnerability and sustainability by an integrated index-overlay method and physical-based numerical model. J. Hydrol. 2021, 596, 126082. [Google Scholar] [CrossRef]
- Gu, Y. Meshfree methods and their comparisons. Int. J. Comput. Methods 2005, 2, 477–515. [Google Scholar] [CrossRef]
- Hon, Y.C.; Chen, W. Boundary knot method for 2D and 3D Helmholtz and convection–diffusion problems under complicated geometry. Int. J. Numer. Methods Eng. 2003, 56, 1931–1948. [Google Scholar] [CrossRef] [Green Version]
- Ling, L.; Opfer, R.; Schaback, R. Results on meshless collocation techniques. Eng. Anal. Bound. Elem. 2006, 30, 247–253. [Google Scholar] [CrossRef] [Green Version]
- Xiong, J.; Wen, J.; Liu, Y.-C. Localized boundary knot method for solving two-dimensional Laplace and Bi-Harmonic equations. Mathematics 2020, 8, 1218. [Google Scholar] [CrossRef]
- Li, P.W. Space–time generalized finite difference nonlinear model for solving unsteady Burgers’ equations. Appl. Math. Lett. 2020, 114, 106896. [Google Scholar] [CrossRef]
- Chen, W.; Fu, Z.J.; Chen, C.S. Recent Advances in Radial Basis Function Collocation Methods; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Ma, Z.; Li, X.; Chen, C.S. Ghost point method using RBFs and polynomial basis functions. Appl. Math. Lett. 2021, 111, 106618. [Google Scholar] [CrossRef]
- Fornberg, B.; Natasha, F. Solving PDEs with radial basis functions. Acta Numer. 2015, 24, 215. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.S.; Karageorghis, A.; Dou, F. A novel RBF collocation method using fictitious centres. Appl. Math. Lett. 2020, 101, 106069. [Google Scholar] [CrossRef]
- Hardy, R. Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 1971, 76, 1905–1915. [Google Scholar] [CrossRef]
- Gu, J.; Jung, J.H. Adaptive Gaussian radial basis function methods for initial value problems: Construction and comparison with adaptive MQ RBF methods. J. Comput. Appl. Math. 2020, 381, 113036. [Google Scholar] [CrossRef]
- Beatson, R.K.; Light, W.A. Fast evaluation of radial basis functions: Methods for two-dimensional polyharmonic splines. IMA J. Numer. Anal. 1997, 17, 343–372. [Google Scholar] [CrossRef]
- Madych, W.R.; Nelson, S.A. Polyharmonic cardinal splines. J. Approx. Theory 1990, 60, 141–156. [Google Scholar] [CrossRef] [Green Version]
- Xiang, S.; Bi, Z.Y.; Jiang, S.X.; Jin, Y.X.; Yang, M.S. Thin plate spline radial basis function for the free vibration analysis of laminated composite shells. Compos. Struct. 2011, 93, 611–615. [Google Scholar] [CrossRef]
- Tsai, C.C.; Cheng, A.D.; Chen, C.S. Particular solutions of splines and monomials for polyharmonic and products of Helmholtz operators. Eng. Anal. Bound. Elem. 2009, 33, 514–521. [Google Scholar] [CrossRef]
- Sarra, S.A.; Sturgill, D. A random variable shape parameter strategy for radial basis function approximation methods. Eng. Anal. Bound. Elem. 2009, 33, 1239–1245. [Google Scholar] [CrossRef]
- Biazar, J.; Hosami, M. An interval for the shape parameter in radial basis function approximation. Appl. Math. Comput. 2017, 315, 131–149. [Google Scholar] [CrossRef]
- Segeth, K. Polyharmonic splines generated by multivariate smooth interpolation. Comput. Math. Appl. 2019, 78, 3067–3076. [Google Scholar] [CrossRef]
- Fasshauer, G.E. RBF collocation methods as pseudospectral methods. WIT Trans. Model. Simul. 2005, 39, 10. [Google Scholar]
- Krowiak, A. Radial basis function-based pseudospectral method for static analysis of thin plates. Eng. Anal. Bound. Elem. 2016, 71, 50–58. [Google Scholar] [CrossRef]
- Fasshauer Gregory, E.; Mccourt Michael, J. Stable evaluation of Gaussian radial basis function interpolants. SIAM J. Sci. Comput. 2012, 34, 737–762. [Google Scholar] [CrossRef]
- Gholampour, F.; Hesameddini, E.; Taleei, A. A global RBF-QR collocation technique for solving two-dimensional elliptic problems involving arbitrary interface. Eng. Comput. 2020, 1–19. [Google Scholar] [CrossRef]
- Gonzalez-Rodriguez, P.; Bayona, V.; Moscoso, M.; Kindelan, M. Laurent series based RBF-FD method to avoid ill-conditioning. Eng. Anal. Bound. Elem. 2015, 52, 24–31. [Google Scholar] [CrossRef] [Green Version]
- Bayona, V.; Flyer, N.; Fornberg, B.; Barnett, G.A. On the role of polynomials in RBF-FD approximations: II. Numerical solution of elliptic PDEs. J. Comput. Phys. 2017, 332, 257–273. [Google Scholar] [CrossRef] [Green Version]
- Shcherbakov, V.; Larsson, E. Radial basis function partition of unity methods for pricing vanilla basket options. Comput. Math. Appl. 2016, 71, 185–200. [Google Scholar] [CrossRef]
- Cavoretto, R.; De Marchi, S.; De Rossi, A.; Perracchione, E.; Santin, G. Partition of unity interpolation using stable kernel-based techniques. Appl. Numer. Math. 2017, 116, 95–107. [Google Scholar] [CrossRef] [Green Version]
- Rashidinia, J.; Fasshauer, G.E.; Khasi, M. A stable method for the evaluation of Gaussian radial basis function solutions of interpolation and collocation problems. Comput. Math. Appl. 2016, 72, 178–193. [Google Scholar] [CrossRef]
- Wright, G.B.; Fornberg, B. Stable computations with flat radial basis functions using vector-valued rational approximations. J. Comput. Phys. 2017, 331, 137–156. [Google Scholar] [CrossRef] [Green Version]
- De Marchi, S.; Martínez, A.; Perracchione, E. Fast and stable rational RBF-based partition of unity interpolation. J. Comput. Appl. Math. 2019, 349, 331–343. [Google Scholar] [CrossRef]
- Bawazeer, S.A.; Baakeem, S.S.; Mohamad, A.A. New approach for radial basis function based on partition of unity of Taylor series expansion with respect to shape parameter. Algorithms 2021, 14, 1. [Google Scholar] [CrossRef]
- Ku, C.Y.; Liu, C.Y.; Xiao, J.E.; Hsu, S.M. Multiquadrics without the shape parameter for solving partial differential equations. Symmetry 2020, 12, 1813. [Google Scholar] [CrossRef]
- Ku, C.Y.; Liu, C.Y.; Xiao, J.E.; Hsu, S.M.; Yeih, W. A collocation method with space–time radial polynomials for inverse heat conduction problems. Eng. Anal. Bound. Elem. 2021, 122, 117–131. [Google Scholar] [CrossRef]
- Cao, L.; Qin, Q.H.; Zhao, N. An RBF–MFS model for analysing thermal behaviour of skin tissues. Int. J. Heat Mass Transf. 2010, 53, 1298–1307. [Google Scholar] [CrossRef]
- Mai-Duy, N.; Tran-Cong, T. Indirect RBFN method with thin plate splines for numerical solution of differential equations. CMES Comp. Model. Eng. Sci. 2003, 4, 85–102. [Google Scholar]
- Li, J.; Zhai, S.; Weng, Z.; Feng, X. H-adaptive RBF-FD method for the high-dimensional convection-diffusion equation. Int. Commun. Heat Mass Transf. 2017, 89, 139–146. [Google Scholar] [CrossRef]


















| Optimum Order | Dilation Parameter | MAE | RMSE | ||
|---|---|---|---|---|---|
| The conventional PRBF | 7 | - | |||
| The proposed method | Case I | 1 | 5 | ||
| Case II | 1 | 5 | |||
| Case III | 1 | 5 | |||
| Case IV | 1 | 5 | |||
| Case V | 1 | 5 | |||
| Case VI | 1 | 5 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.-Y.; Ku, C.-Y.; Hong, L.-D.; Hsu, S.-M. Infinitely Smooth Polyharmonic RBF Collocation Method for Numerical Solution of Elliptic PDEs. Mathematics 2021, 9, 1535. https://doi.org/10.3390/math9131535
Liu C-Y, Ku C-Y, Hong L-D, Hsu S-M. Infinitely Smooth Polyharmonic RBF Collocation Method for Numerical Solution of Elliptic PDEs. Mathematics. 2021; 9(13):1535. https://doi.org/10.3390/math9131535
Chicago/Turabian StyleLiu, Chih-Yu, Cheng-Yu Ku, Li-Dan Hong, and Shih-Meng Hsu. 2021. "Infinitely Smooth Polyharmonic RBF Collocation Method for Numerical Solution of Elliptic PDEs" Mathematics 9, no. 13: 1535. https://doi.org/10.3390/math9131535
APA StyleLiu, C.-Y., Ku, C.-Y., Hong, L.-D., & Hsu, S.-M. (2021). Infinitely Smooth Polyharmonic RBF Collocation Method for Numerical Solution of Elliptic PDEs. Mathematics, 9(13), 1535. https://doi.org/10.3390/math9131535









