A Constrained Markovian Diffusion Model for Controlling the Pollution Accumulation

Abstract

This work presents a study of a finite-time horizon stochastic control problem with restrictions on both the reward and the cost functions. To this end, it uses standard dynamic programming techniques, and an extension of the classic Lagrange multipliers approach. The coefficients considered here are supposed to be unbounded, and the obtained strategies are of non-stationary closed-loop type. The driving thread of the paper is a sequence of examples on a pollution accumulation model, which is used for the purpose of showing three algorithms for the purpose of replicating the results. There, the reader can find a result on the interchangeability of limits in a Dirichlet problem.

1. Introduction

The aim of pollution accumulation models is to study the management of some goods to be consumed by a society. It is generally accepted that such consumption generates two byproducts: a social utility, and pollution. The difference between the utility and the disutility associated with the pollution is known as social welfare. The theory developed in this work enables the decision maker to find a consumption policy that maximizes an expected social welfare for the society, subject to a constraint that may represent, for example, that some costs of cleaning the environment are not to exceed some given quantity along time.

This paper deals with the problem of finding optimal controllers and values for a class of diffusions with unbounded coefficients on a finite-time horizon under the total payoff criterion subject to restrictions. It uses standard dynamic programming tools, the Lagrange multipliers approach, and a result on the interchangeability of limits in a Bellman equation. The driving thread of the paper is a sequence of examples on a pollution accumulation model, which is used for the purpose of showing how to replicate the theoretical results of the work.

The origin of the use of the optimal control theory in the context of stochastic diffusions on a finite-time horizon can be traced back to the works of Howard (see [1]), Fleming (see, for instance, [2,3,4]), Kogan (see [5]), and Puterman (cf. [6]). However, the stochastic optimization problem with constraints was attacked only in the late 90s and early 2000s, when some financial applications demanded the consideration of these models, under the hypothesis that the coefficients of all: the diffusion itself, the reward function, and the restrictions, are bounded (see, for Example [7,8,9,10]). Constrained optimal control under the discounted and ergodic criteria was studied in the seminal paper of Borkar and Ghosh (see [11]), the work of Mendoza-Pérez, Jasso-Fuentes, Prieto-Rumeau and Hernández-Lerma (see [12,13]), and the paper by Jasso-Fuentes, Escobedo-Trujillo and Mendoza-Pérez [14]. In fact, these works serve as an inspiration to pursue an extension of their research to the realm of non-stationary strategies.

Although this is not the first time that the problem of pollution accumulation has been studied from the point of view of dynamic optimization (for example, [15] uses an LQ model to describe this phenomenon, [16] deals with the average payoff in a deterministic framework, [17,18] extend the approach of the former to a stochastic context, and [19] uses a stochastic differential game against nature to characterize the situation), this paper contributes to the state-of-the-art by adding constraints to the reward function, and by taking into consideration a finite-time horizon. Moreover, this work profits from this fact by proposing a simulation scheme to test its analytic results. However, it would not be possible to find a suitable Lagrange multiplier for such simulations without the results presented in Example 3, and Theorem 2, below.

The relevance of this work lies in the applicability of its analytic results in a finite-time interval. Unlike the models under infinite-time criteria (i.e., discounted and average payoffs; and the refinements of the latter), which focus on finding optimal controllers in the set of (Markovian) stationary strategies, the criterion at hand considers as well the more general set of (Markovian) non-stationary strategies. This fact implies that the functional form of the Bellman equation includes a time-dependent term, and that the feedback controllers will depend explicitly on the time argument. Since the coefficients of the diffusions involved in this study are assumed to be unbounded, all of the points in ${\mathbb{R}}^n$ will be attainable, and a verification result will be needed to ensure the existence of a solution to the Bellman equation that remains valid for all $(t,x)$ in $[0;T]\times {\mathbb{R}}^n$, where T will be the horizon.

Significance and contributions.

• This paper presents an application of two classic tools: the Lagrange multipliers approach, and Bellman optimization in a finite horizon for diffusions with possibly unbounded coefficients. This fact represents a major technical contribution with respect to the existing literature.
• This study illustrates its results by means of the full development and implementation of an example on control of pollution accumulation. It also gives actual algorithms which can be used for the replication of the results presented along its pages.
• This work lies within the framework of dynamic optimization. However, it considers a broader class of coefficients than, for instance, [15]. As is the case of [16], it presents a pollution accumulation model. However, it focuses on a stochastic context (as in [17,18]), with the difference that the present project does so in a finite-time horizon, and with restrictions on both the reward and the cost functions.

The rest of the paper is divided as follows. The next section gives the generalities of the model under consideration, i.e., the diffusion that drives the control problem, the total payoff criterion, the restrictions on the cost and the control policies at hand. Example 1 introduces the pollution model. Section 3 deals with the actual (analytic and simulated) solution of the problem. Examples 2, 3, 4, Lemma 2, Theorem 2 and Example 5 illustrate the analytic technique and serve the purpose of comparing it with some numeric simulations. Finally, Section 4 is devoted to the presentation of the final Remarks.

This section concludes by introducing some notation for spaces of real-valued functions on an open set ${\mathbb{R}}^n$. The space ${\mathcal{W}}^{\ell ,p}\left({\mathbb{R}}^n\right)$ stands for the Sobolev space consisting of all real-valued measurable functions h on ${\mathbb{R}}^n$ such that $D^{\alpha }h$ exists for all $\left|\alpha \right|\le \ell$ in the weak sense, and it belongs to ${\mathcal{L}}^p\left({\mathbb{R}}^n\right)$, where

$$D^{\alpha }h:=\frac{{\partial }^{\left|\alpha \right|}h}{\partial x_1^{{\alpha }_1},\cdots ,\partial x_n^{{\alpha }_n}}with\alpha =({\alpha }_1,\cdots ,{\alpha }_n),and\left|\alpha \right|:=\sum _{i=1}^n{\alpha }_i.$$

Moreover, ${\mathcal{C}}^{\kappa }\left({\mathbb{R}}^n\right)$ is the space of all real-valued continuous functions on ${\mathbb{R}}^n$ with continuous ℓ-th partial derivative in $x_i\in \mathbb{R}$, for $i=1,...,N$, $\ell =0,1,...,\kappa$. In particular, when $\kappa =0$, ${\mathcal{C}}^0\left({\mathbb{R}}^n\right)$ stands for the space of real-valued continuous functions on ${\mathbb{R}}^n$. Now, ${\mathcal{C}}^{\kappa ,\eta }\left({\mathbb{R}}^n\right)$ is the subspace of ${\mathcal{C}}^{\kappa }\left({\mathbb{R}}^n\right)$ consisting of all those functions h such that $D^{\alpha }h$ satisfies a Hölder condition with exponent $\eta \in ]0;1]$, for all $\left|\alpha \right|\le \kappa$; that is, there exists a constant $K_0$ such that

$$|D^{\alpha }h\left(x\right)-D^{\alpha }h\left(y\right)|\le K_0{|x-y|}^{\eta }.$$

Define

$${\mathcal{W}}^{1,\ell ;p}([0;T]\times {\mathbb{R}}^n):=\{h:[0;T]\times {\mathbb{R}}^n\to \mathbb{R},h(t,·)\in {\mathcal{W}}^{\ell ;p}\left({\mathbb{R}}^n\right)andh(·,x)\in C^1\left([0;T]\right)\}.$$

The space ${\mathcal{W}}^{1,\ell ;p}([0;T]\times {\mathbb{R}}^n)$ is assumed to be endowed with the topology of ${\mathcal{W}}^{\ell ;p}([0;T]\times {\mathbb{R}}^n)$. Similarly, $p\in [1;\infty [$ in ${\mathcal{C}}^{1;\kappa }\left({\mathbb{R}}^n\right)$ and ${\mathcal{L}}^p([0;T]\times {\mathbb{R}}^n)$.

2. Preliminaries

This work studies a finite-horizon optimal control problem with restrictions. In concrete, let $(\mathsf{\Omega },\mathcal{F},\left\{{\mathcal{F}}_t:t\ge 0\right\})$ be a measurable space. Let there also be an ${\mathcal{F}}_t$-adapted stochastic differential system of the form

$$\mathrm{d}x\left(t\right)=b\left(x\right(t),u(t\left)\right)\mathrm{d}t+\sigma \left(x\right(t\left)\right)\mathrm{d}W\left(t\right),x\left(0\right)=x,t\ge 0,$$

(1)

where $b:{\mathbb{R}}^n\times U\to {\mathbb{R}}^n$ and $\sigma :{\mathbb{R}}^n\to {\mathbb{R}}^{n\times d}$ are the drift and diffusion coefficients, respectively; and $W(·)$ is a d-dimensional standard Brownian motion. Here, the set $U\subset {\mathbb{R}}^m$ is a Borel set called the action (or control) set. Moreover, let $u(·)$ be a U-valued stochastic process representing the controller’s action at each time $t\ge 0$.

Now, the profit that an agent can obtain from its activity in the system is measured with the performance index:

$$J_T(t,x,u,r):={\mathbb{E}}_x^u\left[{\int }_t^{T}r\left(s,x\left(s\right),u\left(s\right)\right)\mathrm{d}s+r_1(T,x\left(T\right))\right],$$

(2)

where r and $r_1$ are the running and terminal rewards, respectively; and the symbol ${\mathbb{E}}_x^u[·]$ stands for the conditional expectation of · given that $x\left(t\right)=x$, and the agent uses the sequence of controllers u.

The goal is to maximize (2) subject to a finite-horizon cost index of the operation:

$$\begin{array}{c}\hfill J_T(t,x,u,c):={\mathbb{E}}_x^u\left[{\int }_t^{T}c\left(s,x\left(s\right),u\left(s\right)\right)\mathrm{d}s+c_1(T,x\left(T\right))\right]\\ \hfill \le {\mathbb{E}}_x^u\left[{\int }_t^T\theta \left(s,x\left(s\right)\right)\mathrm{d}s+{\theta }_1(T,x\left(T\right))\right],\end{array}$$

(3)

where c is a running-cost rate, $c_1$ is a terminal cost rate function; $\theta$ is a running constraint-rate function, and ${\theta }_1$ is a terminal constraint-rate function. Observe that as the running reward-rate function r depends on the action of the controller; the running constraint-rate $\theta$ is independent of such variable.

The following is an assumption on the coefficients of the differential system (1).

Hypothesis (H1a).

The control set U is compact.

Hypothesis (H1b).

The drift coefficient $b(x,u)$ is continuous on ${\mathbb{R}}^n\times U$, and $x\mapsto b(x,u)$ satisfies a local Lipschitz condition on ${\mathbb{R}}^n$, uniformly on U; that is, for each $R>0$, there exists a constant $K_1\left(R\right)>0$ such that for all $\left|x\right|,\left|y\right|\le R$

$$\underset{u\in U}{sup}|b(x,u)-b(y,u)|\le K_1\left(R\right)|x-y|.$$

Hypothesis (H1c).

The diffusion coefficient σ satisfies a local Lipschitz condition on ${\mathbb{R}}^n$; that is, for each $R>0$, there exists a constant $K_2\left(R\right)>0$ such that for all $\left|x\right|,\left|y\right|\le R$; that is, there exists a positive constant $K_2$ such that for all $x,y\in {\mathbb{R}}^n.$

$$|\sigma \left(x\right)-\sigma \left(y\right)|\le K_2\left(R\right)|x-y|.$$

Hypothesis (H1d).

The matrix $a\left(x\right):=\sigma \left(x\right){\sigma }^{\prime }\left(x\right)$ satisfies auniform ellipticitycondition, i.e., for some constant $K_3>0$,

$$y^{\prime }a\left(x\right)y\ge K_3{\left|y\right|}^{2}for allx,y\in {\mathbb{R}}^n.$$

Remark 1.

The local Lipschitz conditions on the drift and diffusion coefficients referred to in Hypothesis 1b–1c, along with the compactness of the control set U, stated in Hypothesis 1a, yield that for each $R>0$, there exists a number $K_4\left(R\right)\ge K_1\left(R\right)+K_2\left(R\right)$ such that

$$\underset{u\in U}{sup}\left|b(x,u)\right|+\left|\sigma \left(x\right)\right|\le K_4\left(R\right)(1+|x\left|\right)$$

for all $\left|x\right|\le R.$

For $u\in U$, and $h(t,·)\in {\mathcal{W}}^{2,p}\left({\mathbb{R}}^n\right)$ for all $t\ge 0$, define:

$$\begin{array}{ccc}\hfill {\mathbb{L}}^{u}h(t,x)& :=& ⟨\nabla h(t,x),b\left(x,u\right)⟩+\frac{1}{2}\mathrm{Tr}\left[\left[\mathbb{H}h\right(t,x\left)\right]a\left(x\right)\right]\hfill \\ & =& \sum _{i=1}^n{b}_i\left(x,u\right){\partial }_{x_i}h(t,x)+\frac{1}{2}\sum _{i,j=1}^n{a}_{ij}\left(x\right){\partial }_{x_i{x}_j}^{2}h(t,x),\hfill \end{array}$$

(4)

with $a(·)$ as in Hypothesis 1d, and $\nabla h$, $\mathbb{H}$ representing the gradient and the Hessian matrix of h with respect to the state variable x, respectively.

The main application of this work is the pollution accumulation model. Although it will be possible to solve this problem within the realm of pure feedback strategies, this is not always the case. As a consequence, the set of actions needs to be widened.

Control Policies. Let $\mathbb{M}$ be the family of measurable functions $f:[0;T]\times {\mathbb{R}}^n\to U$. A strategy $u\left(t\right):=f(t,x(t\left)\right)$, for some $f\in \mathbb{M}$ is called a Markov policy.

Definition 1.

Let $(U,\mathcal{B}(U\left)\right)$ be a measurable space, and $\mathcal{P}\left(U\right)$ be the family of probability measures supported on U. Arandomized policyis a family $\pi :=({\pi }_t:t\ge 0)$ of stochastic kernels on $\mathcal{B}\left(U\right)\times {\mathbb{R}}^n$ satisfying:

(a) 

for each $t\ge 0$ and $x\in {\mathbb{R}}^n$, ${\pi }_t(·|x)\in \mathcal{P}\left(U\right)$ such that ${\pi }_t\left(U\right|x)=1,$ and for each $D\in \mathcal{B}\left(U\right)$, ${\pi }_t\left(D\right|·)$ is a Borel function on ${\mathbb{R}}^n$; and

(b) 

for each $D\in \mathcal{B}\left(U\right)$ and $x\in {\mathbb{R}}^n$, the function ${\pi }_t\left(D\right|x)$ is a Borel-measurable in $t\ge 0$.

The set of randomized policies is denoted by Π.

Observe that every $f\in \mathbb{M}$ can be identified with a strategy in $\mathsf{\Pi }$ by means of the $\mathcal{P}\left(U\right)$-valued trajectory ${\delta }_f$, where ${\delta }_f$ represents the Dirac measure at f. When the controller operates policies $\pi =({\pi }_t:t\ge 0)\in \mathsf{\Pi }$, both the drift coefficient b, and the operator ${\mathbb{L}}^u$ defined in (1) and (4), respectively, are written as

$$b(x,{\pi }_t):={\int }_{U}b(x,u){\pi }_t\left(\mathrm{d}u\right|x),{\mathbb{L}}^{{\pi }_t}\nu (t,x):={\int }_U{\mathbb{L}}^u\nu (t,x){\pi }_t\left(\mathrm{d}u\right|x).$$

Under Hypothesis (H1a)–(H1d) and Remark 1, for each policy $\pi \in \mathsf{\Pi }$ there exists an almost surely unique strong solution $x^{\pi }(·)$ of (1), which is a Markov-Feller process. Furthermore, for each policy $\pi =({\pi }_t:t\ge 0)\in \mathsf{\Pi },$ the operator ${\partial }_t\nu (t,x)+{\mathbb{L}}^{{\pi }_t}\nu (t,x)$ becomes the infinitesimal generator of the dynamics (1) (for more details, see the arguments in [20] (Theorem 2.2.7)). Moreover, by the same reasoning of Theorem 4.3 in [20], for each $\pi \in \mathsf{\Pi }$, the associated probability measure ${\mathbb{P}}^{\pi }(t,x,·)$ of $x^{\pi }(·)$ is absolutely continuous with respect to Lebesgue’s measure for every $t\ge 0$ and $x\in {\mathbb{R}}^n$. Hence, there exists a transition density function $p^{\pi }(t,x,y)\ge 0$ such that

$${\mathbb{P}}^{\pi }(t,x,B)={\int }_B{p}^{\pi }(t,x,y)\mathrm{d}y,$$

for every Borel set $B\subset {\mathbb{R}}^n$.

Topology of relaxed controls. The set $\mathsf{\Pi }$ is topologized as in [21]. Such a topology renders $\mathsf{\Pi }$ a compact metric space, and it is determined by the following convergence criterion (see [20,21,22]).

Definition 2

(Convergence criterion). It will be said that the sequence $\left({\pi }^m:m=1,2,...\right)$ in Πconverges to$\pi \in \mathsf{\Pi }$, and such convergence is denoted as ${\pi }^m\stackrel{W}{\to }\pi$, if and only if

$$\begin{array}{c}\hfill {\int }_{{\mathbb{R}}^n}{\int }_0^T{\int }_{U}g(t,x)h(t,x,u){\pi }_t^m\left(\mathrm{d}u\right|x)\mathrm{d}t\mathrm{d}x\to \\ \hfill {\int }_{{\mathbb{R}}^n}{\int }_0^{T}g(t,x){\int }_{U}h(t,x,u){\pi }_t\left(\mathrm{d}u\right|x)\mathrm{d}t\mathrm{d}x.\end{array}$$

(5)

for all $g\in {\mathcal{L}}^1([0;T]\times {\mathbb{R}}^n)$, and $h\in {\mathcal{C}}_b([0;T]\times {\mathbb{R}}^n\times U)$, i.e., in the set of continuous and bounded functions on $[0;T]\times {\mathbb{R}}^n\times U$. Denoting $h(t,x,{\pi }_t)$ by ${\int }_{U}h(t,x,u){\pi }_t\left(\mathrm{d}u\right|x)$ for each $\pi =({\pi }_t:t\ge 0)\in \mathsf{\Pi }$, the convergence referred to in (5) reduces to

$${\int }_{{\mathbb{R}}^n}{\int }_0^{T}g(t,x)h(t,x,{\pi }_t^m)\mathrm{d}t\mathrm{d}x\to {\int }_{{\mathbb{R}}^n}{\int }_0^{T}g(t,x)h(t,x,{\pi }_t)\mathrm{d}t\mathrm{d}x.$$

Throughout this work, the convergence in $\mathsf{\Pi }$ is understood in the sense of the convergence criterion introduced in Definition 2.

The following Definition is this work’s version of the polynomial growth condition quoted in, for instance [18].

Definition 3.

Given a polynomial function of the form $w\left(x\right)=1+{\left|x\right|}^k$ (with $k\ge 2$), and $x\in {\mathbb{R}}^n$, let the normed linear space ${\mathcal{B}}_w([0;T]\times {\mathbb{R}}^n)$ be that which consists of all real-valued measurable functions ν on $[0;T]\times {\mathbb{R}}^n$ with finite w-norm given by

$${\Vert \nu \Vert }_w:=\underset{(t,x)\in [0;T]\times {\mathbb{R}}^n}{sup}\frac{\left|\nu \right(t,x\left)\right|}{w\left(x\right)}.$$

Remark 2.

(a) 

Observe that for any function $\nu \in {\mathcal{B}}_w([0;T]\times {\mathbb{R}}^n)$:

$$\left|\nu (t,x)\right|\le {\Vert \nu \Vert }_{w}w\left(x\right)={\Vert \nu \Vert }_w{(1+|x|}^k).$$

This last inequality implies that any function $\nu \in {\mathcal{B}}_w([0;T]\times {\mathbb{R}}^n)$ satisfies the polynomial growth condition.

(b) 

Assuming that the initial data $x\left(s\right)=x$ has finite absolute moments of every order (i.e., ${\mathbb{E}\left|x\left(s\right)\right|}^k<\infty$ for each $k=1,2,\dots$)—see [23] [Theorem 4.2], gives that

$${\mathbb{E}\left|x\left(t\right)\right|}^k\le C_k{(1+\mathbb{E}|x\left(s\right)|}^k),s\le t\le T,$$

where the constant $C_k$ depends on k, $T-s$, and the constant $K_1$ is as in Hypothesis (H1b).

(c) 

In the application developed throughout this paper, the constant initial data $x\left(s\right)=x$ is considered. Then ${\mathbb{E}\left|x\left(t\right)\right|}^k$ also has finite moments of every order (see Proposition 10.2.2 in [18]). Therefore, ${\mathbb{E}\left|x\left(t\right)\right|}^k\le C_k{(1+|x|}^k).$

Now, hypotheses on the reward, cost and constraint rates from (2) and (3) are stated. These are very standard, and represent an extension of the ones used in classic works, such as p. 157 in [23] (Chapter VI.3) and p. 130 in [24] (Chapter 3).

Hypothesis (H2a).

The functions $r,c:[0;T]\times {\mathbb{R}}^n\times U\to \mathbb{R}$ are continuous, and locally Lipschitz on ${\mathbb{R}}^n$, uniformly on U; that is, for each $R>0$, there exists a constant $K_5\left(R\right)>0$ such that for all $\left|x\right|,\left|y\right|\le R$

$$\underset{(t,u)\in [0;T]\times U}{sup}|r(t,x,u)-r(t,y,u)|+\underset{(t,u)\in [0;T]\times U}{sup}|c(t,x,u)-c(t,y,u)|\le K_5\left(R\right)|x-y|.$$

Hypothesis (H2b).

$r(·,·,u)$ and $c(·,·,u)$ are in ${\mathcal{B}}_w([0;T]\times {\mathbb{R}}^n)$ uniformly on U; in other words, there exists $M>0$ such that for all $(t,x)\in [0;T]\times {\mathbb{R}}^n$,

$$\underset{(t,u)\in [0;T]\times U}{sup}\left|r(t,x,u)\right|+\underset{(t,u)\in [0;T]\times U}{sup}\left|c(t,x,u)\right|\le Mw\left(x\right).$$

Hypothesis (H2c).

The terminal reward and cost rates $r_1(·,·),c_1(·,·)\in {\mathcal{B}}_w([0;T]\times {\mathbb{R}}^n)$; andthe running and terminal constraint rates$\theta (·,·),{\theta }_1(·,·)\in {\mathcal{B}}_w([0;T]\times {\mathbb{R}}^n)$ are non-negative measurable functions which are locally Lipschitz on $[0;T]\times {\mathbb{R}}^n$, i.e., for each $R>0$, there exists a constant ${\tilde{K}}_5\left(R\right)>0$ such that for all $\left|x\right|,\left|y\right|\le R$,

$$\begin{array}{ccc}& & \underset{t\ge 0}{sup}\left[\left|r_1(t,x)-r_1(t,y)\right|+\left|c_1(t,x)-c_1(t,y)\right|\right]\hfill \\ & & +\underset{t\ge 0}{sup}\left[\left|\theta (t,x)-\theta (t,y)\right|+\left|{\theta }_1(t,x)-{\theta }_1(t,y)\right|\right]\hfill \\ & \le & {\tilde{K}}_5\left(R\right)|x-y|.\hfill \end{array}$$

For $\pi =({\pi }_t:t\ge 0)\in \mathsf{\Pi }$ the reward and cost rates are written as

$$r(t,x,{\pi }_t):={\int }_{U}r(t,x,u){\pi }_t\left(\mathrm{d}u\right|x),c(t,x,{\pi }_t):={\int }_{U}c(t,x,u){\pi }_t\left(\mathrm{d}u\right|x).$$

(6)

To complete this section, the main application of this work is introduced. It consists of a pollution accumulation model. This application is inspired by the one presented in [17,18], and satisfies Hypotheses 1a–1d and 2a–2c.

Example 1.

Fix the probability space $(\mathsf{\Omega },\mathcal{F},\{{\mathcal{F}}_t:t\ge 0\},\mathbb{P})$, and let $T>0$ be a given time horizon. Consider the pollution process defined by the controlled diffusion

$$\mathrm{d}x\left(s\right)=\left[u\right(s)-\eta x(s\left)\right]\mathrm{d}s+\sigma \mathrm{d}W\left(s\right),x\left(t\right)=x>0,$$

(7)

for $s\in [t;T]$, where $0\le u\left(t\right)\le \gamma <\frac{\eta }{2}$. Here $u\left(s\right)$ represents the consumption flow at time $t\ge 0$, and γ is certain consumption restriction imposed by, for instance worldwide protocols. Additionally, the number $\eta \in ]0;1]$ is the rate of pollution decay.

It is easy to see that the coefficients of (7) meet Hypothesis (H1a)–(H1c). A simple calculation yields that $K_3\ge {\sigma }^2-c$ for any $c\in ]0;{\sigma }^2[$.

Now, a simulation of the trajectories of the Itô’s diffusion (1) is presented. To this end, the extension of Euler’s method for solving first order differential equations known asEuler-Maruyama’s method(see, for instance [25] and Chapter 1 in [26]) is used. This technique is suitable for diffusions that meet Hypothesis (H1a)–(H1d). The focus is on the comparison between Vasicek’s model for interest rates in finance (see, for instance Chapter 5 in [27]):

$$\mathrm{d}x\left(s\right)=[\mu -\eta x(s\left)\right]\mathrm{d}s+\sigma \mathrm{d}W\left(s\right),x\left(t\right)=x>0,$$

(8)

with $s\in [t;T]$, and Kawaghuchi–Morimoto’s model (7).

Let $z^N:\{0,1,...,N\}\times \mathsf{\Omega }\to {\mathbb{R}}^n$, $N\in \mathbb{N}$, be the Euler-Maruyama approximations for the stochastic differential Equation (1), recursively defined by $z_0^N:=x$ and

$$z_{n+1}^N:=z_n^N+b(z_n^N,u_n)\frac{T}{N}+\sigma \left(z_n^N\right)\left(W_{\frac{(n+1)T}{N}}-W_{\frac{nT}{N}}\right)$$

for all $n\in \{0,1,...,N\}$, with $N\in \mathbb{N}$.

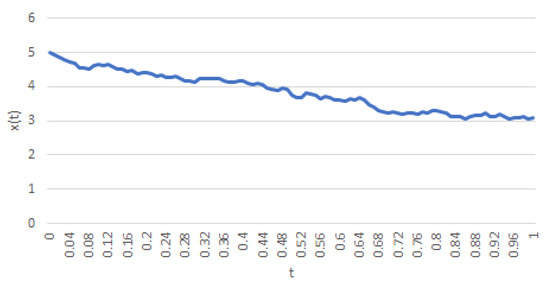
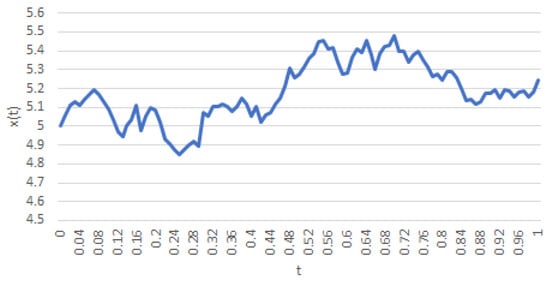
In Figure 1 and Figure 2, observe that Kawaguchi-Morimoto’s process allows one to choose a deterministic (implicit) function of t, whereas Vasicek’s series features what is known in the literature asmean reversion. The latter fact is clear from the choice of a constant parameter μ.

Figure 1. A realization of a trajectory of (7) with $x_0=5$, $\eta =1$, $\sigma \equiv 0.5$, $u\left(t\right)=\sqrt{x\left(t\right)}$, $T=1$, and $N=100$.

Figure 2. A realization of a trajectory of (8) with $x_0=5$, $\eta =1$, $\sigma \equiv 0.5$, $\mu =5$, $T=1$, and $N=100$.

Let $h\in {\mathcal{W}}^{1,2;p}([0;T]\times \mathbb{R})$. After (4), the infinitesimal generator of (7) is given by

$$h_t(t,x)+{\mathbb{L}}^{u}h(t,x)=h_t(t,x)+(u-\eta x)h_x(t,x)+\frac{1}{2}{\sigma }^2{h}_{xx}(t,x).$$

The polynomial function $w\left(x\right)=x^2+x+1$ satisfies Definition 3. Please note that this function does not depend on the time argument t.

The reward-rate function used in further developments represents the social welfare, is given by $r:[0;T]\times \mathbb{R}\times U\to \mathbb{R}$, and is defined as:

$$r(t,x,u):=F\left(u\right)-a·x,$$

(9)

where $F\in {\mathcal{C}}^2\left(\mathbb{R}\right)$ stands for the social utility of the consumption u, and $a·x$ stands for the social disutility (so to speak) of the pollution stock x, for $a>0$ fixed. It is assumed that

$$\left\{\begin{array}{cc}{F}^{\prime }\ge 0,& F^{\prime \prime }\le 0,\\ F^{\prime }(\infty )=F\left(0\right)=0,& F^{\prime }(0+)=F(\infty )=\infty .\end{array}\right.$$

(10)

The cost rate function will be given by

$$c(t,x,u):=c_{1}x+c_{2}ufor all(t,x,u)\in [0;T]\times \mathbb{R}\times U,$$

(11)

with $c_1>0$, and $c_2\in \mathbb{R}$ satisfying

$$c_1+\eta c_2>0.$$

(12)

Since the pollution stock x depends on the time variable $t\ge 0$, the functions defined in (9) and (11) also depend on this variable.

The running constraint-rate function has the form

$$\theta (t,x):=\frac{c_{1}x}{\eta }+q,for all(t,x)\in [0;T]\times \mathbb{R},$$

(13)

where q is a positive constant. (Here, as with the reward and cost functions, it is assumed that x implicitly depends on t.) Theterminalconstraint, cost and reward rates will be fixed at a level of zero. It is not difficult to see that if F meets Hypothesis (H2a)–(H2c), then so do the social welfare, the cost rate and the running constraint functions.

3. A Finite-Horizon Control Problem with Constraints

This section is devoted to the introduction of the study of the finite-horizon problem with constraints.

Definition 4.

For each $\pi \in \mathsf{\Pi }$ and $T\ge t,$ thetotal expected reward, cost and constraint rates over the time interval $[t;T]$ given that $x\left(t\right)=x$are, respectively,

$$\begin{array}{ccc}\hfill J_T(t,x,\pi ,r)& :=& {\mathbb{E}}_x^{\pi }\left[{\int }_t^{T}r\left(s,x\left(s\right),{\pi }_s\right)\mathrm{d}s+r_1(T,x\left(T\right))\right],\hfill \\ \hfill J_T(t,x,\pi ,c)& :=& {\mathbb{E}}_x^{\pi }\left[{\int }_t^{T}c\left(s,x\left(s\right),{\pi }_s\right)\mathrm{d}s+c_1(T,x\left(T\right))\right],\hfill \\ \hfill {\overline{\theta }}_T(t,x,\pi )& :=& {\mathbb{E}}_x^{\pi }\left[{\int }_t^T\theta \left(s,x\left(s\right)\right)\mathrm{d}s+{\theta }_1(T,x\left(T\right))\right],\hfill \end{array}$$

with $r\left(s,x\left(s\right),{\pi }_s\right)$ and $c\left(s,x\left(s\right),{\pi }_s\right)$ as in (6).

The proof of the next result is an extension of [28] [Proposition 3.6].

Lemma 1.

Hypothesis (H2a)–(H2c) imply that the total expected reward $J_T(t,x,\pi ,r)$, the total expected cost $J_T(t,x,\pi ,c)$, and the constraint rate ${\overline{\theta }}_T(t,x,\pi )$ belong to the space ${\mathcal{B}}_w([0;T]\times {\mathbb{R}}^n)$. In fact, for every $(t,x)\in [0;T]\times {\mathbb{R}}^n$,

$$\begin{array}{ccc}\hfill \underset{\pi \in \mathsf{\Pi },t\in [0;T]}{sup}\left|J_T(t,x,\pi ,r)\right|& \le & M_2(T,t)w\left(x\right),\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill \underset{\pi \in \mathsf{\Pi },t\in [0;T]}{sup}\left|J_T(t,x,\pi ,c)\right|& \le & M_2(T,t)w\left(x\right),\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill \underset{\pi \in \mathsf{\Pi },t\in [0;T]}{sup}\left|{\overline{\theta }}_T(t,x,\pi )\right|& \le & M_2(T,t)w\left(x\right),\hfill \end{array}$$

(16)

where $M_2(T,t):=M\left(C_k(T-t)+(T-t)+C_k\right)$.

Proof Proof of Lemma 1.

The proof is presented only for $J_T(t,x,\pi ,r)$, for the line of reasoning is the same for $J_T(t,x,\pi ,c)$ and ${\overline{\theta }}_T(t,x,\pi )$. By Hypothesis (H2b), it is known that for every $(t,x)\in [0;T]\times {\mathbb{R}}^n$,

$$\begin{array}{ccc}\hfill \left|J_T(t,x,\pi ,r)\right|& =& \left|{\mathbb{E}}_x^{\pi }{\int }_t^{T}r(s,x\left(s\right),{\pi }_s)\mathrm{d}s+r_1(T,x\left(T\right))\right|\hfill \\ & \le & M\left[{\int }_t^T{\mathbb{E}}_x^{\pi }w\left(x^{{\pi }_s}\left(s\right)\right)\mathrm{d}s+w\left(x\left(T\right)\right)\right].\hfill \end{array}$$

Now, Remark 2(b)–(c) gives that

$$\left|J_T(t,x,\pi ,r)\right|\le M\left(C_k{\left(\right|x|}^k+1)(T-t)+(T-t)+C_k{\left(\right|x|}^k+1)\right).$$

Letting $M_2(T,t):=M\left(C_k(T-t)+(T-t)+C_k\right)$ yields the result. □

For each $T>0$, and $x\in {\mathbb{R}}^n$, assume that the (running and terminal) constraint functions $\theta (·,·)$ and ${\theta }_1(·,·)$ are given, and that they satisfy Hypothesis 2c. In this way, let

$${\mathcal{F}}_{{\theta }_T}^{t,x}:=\{\pi \in \mathsf{\Pi }:J_T(t,x,\pi ,c)\le {\overline{\theta }}_T(t,x,\pi )\}.$$

To avoid trivial situations, it is assumed that this set is not empty (see Remark 3.8 in [14]). To formally introduce what is meant when talking about the maximization of (2) subject to (3), the finite-horizon problem with constraints is defined.

Definition 5.

A policy ${\pi }^{*}\in \mathsf{\Pi }$ is said to be optimal for thefinite-horizon problem with constraints(FHPC) with initial state $x\in {\mathbb{R}}^n$ if ${\pi }^{*}\in {\mathcal{F}}_{{\theta }_T}^{t,x}$ and, in addition,

$$J_T\left(t,x,{\pi }^{*},r\right)=\underset{\pi \in {\mathcal{F}}_{{\theta }_T}^{t,x}}{sup}{J}_T\left(t,x,\pi ,r\right).$$

In this case, $J_T^{*}(t,x,r):=J_T(t,x,{\pi }^{*},r)$ is called theT-optimal rewardfor the FHPC.

Example 2

(Example 1 continued). One intends to find a strategy ${\pi }^{*}\in \mathsf{\Pi }$ that maximizes the total expected reward

$$J_T\left(t,x,\pi ,r\right)={\mathbb{E}}_x^{\pi }\left[{\int }_t^T(F\left({\pi }_s\right)-ax\left(s\right))\mathrm{d}s\right]$$

(17)

subject to

$$\begin{array}{c}\hfill J_T\left(t,x,\pi ,c\right)={\mathbb{E}}_x^{\pi }\left[{\int }_t^T(c_{1}x\left(s\right)+c_2{\pi }_s)\mathrm{d}s\right]\\ \hfill \le {\mathbb{E}}_x^{\pi }\left[{\int }_t^T\left(\frac{c_{1}x\left(s\right)}{\eta }+q\right)\mathrm{d}s\right]=:{\overline{\theta }}_T\left(t,x,\pi \right).\end{array}$$

(18)

That is, find ${\pi }^{*}\in \mathsf{\Pi }$ such that $J_T\left(t,x,{\pi }^{*},r\right):=\underset{\pi \in {\mathcal{F}}_{{\theta }_T}^{t,x}}{sup}{J}_T\left(t,x,\pi ,r\right).$

3.1. Lagrange Multipliers

To solve the FHPC, the Lagrange multipliers approach and the dynamic programming technique are used to transform the original FHPC into an unconstrained finite-horizon problem, parametrized by the so-named Lagrange multipliers. To do this, take $\lambda \le 0$ and consider the new (running and terminal) reward rates

$$\begin{array}{ccc}\hfill r^{\lambda }(t,x,u)& :=& r(t,x,u)+\lambda \left(c(t,x,u)-\theta (t,x)\right),\hfill \\ \hfill r_1^{\lambda }\left(x\left(T\right)\right)& :=& r_1(T,x\left(T\right))+\lambda \left(c_1(T,x\left(T\right))-{\theta }_1\left(x\left(T\right)\right)\right).\hfill \end{array}$$

Using the same notation from (6), write

$$r^{\lambda }(t,x,{\pi }_t):=r(t,x,{\pi }_t)+\lambda (c(t,x,{\pi }_t)-\theta (t,x)),\pi =({\pi }_t:t\ge 0)\in \mathsf{\Pi }.$$

Observe also that for each $\lambda <0$, $r^{\lambda }(·,·,{\pi }_t)\in {\mathcal{B}}_w([0;T]\times {\mathbb{R}}^n)$ uniformly in $\mathsf{\Pi }$, and $r_1^{\lambda }\le w$. Indeed,

$$\begin{array}{ccc}\hfill |r^{\lambda }(t,x,{\pi }_t)|& \le & |r(t,x,{\pi }_t)|+|\lambda \left|\right|c(t,x,{\pi }_t)|+|\lambda \left|\right|\theta (t,x)|\hfill \\ \hfill & \le & Mw\left(x\right)+M\left|\lambda \right|w\left(x\right)+\left|\lambda \right|\left|\theta \right(t,x\left)\right|\hfill \\ \hfill & \le & \left(M+M\left|\lambda \right|+\left|\lambda \right|·{\parallel \theta \parallel }_w\right)w\left(x\right)=N^{\lambda }w\left(x\right),\hfill \\ \hfill |r_1^{\lambda }\left(x\left(T\right)\right)|& \le & (M+M|\lambda |+|\lambda |\parallel {\theta }_1{\parallel }_w)w\left(x\right)=N_1^{\lambda }w\left(x\right),\hfill \end{array}$$

where $N^{\lambda }:=M+M\left|\lambda \right|+\left|\lambda \right|·{\parallel \theta \parallel }_w$, $N_1^{\lambda }:=M+M\left|\lambda \right|+\left|\lambda \right|·\parallel {\theta }_1{\parallel }_w$, and M as in Hypothesis (H2b).

It is natural to let, for all $(t,x)\in [0;T]\times {\mathbb{R}}^n$,

$$J_T(t,x,\pi ,r^{\lambda }):={\mathbb{E}}_x^{\pi }\left[{\int }_t^T{r}^{\lambda }(s,x\left(s\right),{\pi }_s)\mathrm{d}s+r_1^{\lambda }(T,x\left(T\right))\right].$$

Notice that

$$J_T(t,x,\pi ,r^{\lambda })=J_T(t,x,\pi ,r)+\lambda \left[J_T(t,x,\pi ,c)-{\overline{\theta }}_T(t,x,\pi )\right].$$

(19)

Example 3

(Examples 1 and 2 continued). The performance index for the FHUP is given by

$$J_T(t,x,\pi ,r^{\lambda })={\mathbb{E}}_x^{\pi }{\int }_t^T\left[F\left({\pi }_s\right)-ax\left(s\right)+\lambda \left(c_{1}x\left(s\right)+c_2{\pi }_s-\frac{c_{1}x\left(s\right)}{\eta }-q\right)\right]\mathrm{d}s.$$

(20)

Return now to Example 1, where a single trajectory of the processes (7) and (8) for certain parameters were simulated, and the policy $u\left(t\right)=\sqrt{x\left(t\right)}$, for (7); and $u\left(t\right)=\mu$, for (8). One’s aim is to compute (20) for a fixed value of $\lambda <0$, when the utility function derived from the consumption is given by $F\left(u\right)=\sqrt{u}$, by means of Monte Carlo simulation. To this end, the following pseudocodes are presented.

Walkthrough of Algorithm 1.This pseudocode’s goal is to compute the integral inside (20).

• Line 1 initializes the process.
• Line 2 emphasizes the fact that $\lambda <0$ is supposed to be given.
• In lines 3–11, the algorithm decides if it will work with (7), or with (8).
• Line 12 sets $F=\sqrt{u}$ and $D=a·x$, and computes initial values for r, c and θ according to (9), (11) and (13), respectively.
• Line 13 computes the integrand in (20) for the initial step.
• The while loop in lines 15–30 does the following:

  -

  For each step, lines 16–24 decide between (7) and (8).

  -

  Lines 25–26 implement Euler–Matuyama’s method.

  -

  Line 27 updates the values of F, D, r, c and θ,

  -

  Line 28 updates the value of the integrand.

• Line 31 computes the integral in (20).

Walkthrough of Algorithm 2.The purpose of this pseudocode is to compute a 95%-confidence interval for the expectation of the result of Algorithm 1 according to Monte Carlo’s method.

• Line 1 calls Algorithm 1 N times.
• Line 2 computes an average of the iterations just performed.
• Line 3 computes the sample mean of the iterations.
• The Algorithm uses the results of lines 2–3 to return the desired interval.

Algorithm 1: Integral algorithm

Algorithm 1 receives the initial value $x_0$, the step size $\mathrm{d}t$, the time horizon T, and the parameters of the diffusion (7) (resp. (8)) to calculate the (Itô) integral inside the expectation operator in (20) when the process (7) (resp. (8)) is used; then, Algorithm 2 iterates this process and returns the average of such iteration, thus approximating the value of (20). These algorithms require a negative and constant value of the Lagrange multiplier. Later, in Example 5, a modification of Algorithm 1 that solves this situation will be proposed. For the sake of illustration, take the parameter values from Example 1 (that is $x_0=5$, $\eta =1$, $\sigma \left(x\right)\equiv 0.5$, $\mu =5$, $T=1$, and $N=100$), and use Algorithms 1 and 2 to compute an approximation to the value of (20) when one considers the diffusion (8) (that is, the diffusion (7) with $u\left(t\right)\equiv \mu )$ for all $t\ge 0$). Additionally, take

$$\gamma =0.4,c_1=0.1,c_2=0.05,q=0.0195,anda=1.25.$$

Algorithm 2: 95%-confidence interval for the expectation of an Itô’s integral using Monte Carlo’s method.

In this case, an arbitrary value of ${\lambda }_0=-40$ is used. Taking 10,000 simulations, these values yield averages around

$$\begin{array}{ccc}\hfill J_T(0,5,u,r^{{\lambda }_0})& \approx & -6.6549064 and\hfill \\ \hfill J_T(0,5,\mu ,r^{{\lambda }_0})& \approx & -13.235737,\hfill \end{array}$$

for (7), and (8), respectively.

Let $\tau$ be any stopping time valued in $[t;T]$, and $\phi \in {\mathcal{W}}^{1,2;p}([0;T]\times {\mathbb{R}}^n)\cap {\mathcal{B}}_w([0;T]\times {\mathbb{R}}^n)$. Should $p>n$, an application of Itô’s Lemma to $\phi (T\wedge \tau ,x(T\wedge \tau \left)\right)$ yields the following result.

Proposition 1.

Suppose that Hypotheses 1 and 2 are met. Fix $\pi \in \mathsf{\Pi }$ and $\lambda \le 0$; assume that there is a function $\phi \in {\mathcal{W}}^{1,2;p}([0;T]\times {\mathbb{R}}^n)\cap {\mathcal{B}}_w([0;T]\times {\mathbb{R}}^n)$ satisfying:

$$r^{\lambda }(t,x,{\pi }_t)+{\partial }_t\phi (t,x)+{\mathbb{L}}^{{\pi }_t}\phi (t,x)=0,forallx\in [0;T]\times {\mathbb{R}}^n,$$

(21)

with boundary condition $\phi (T,x\left(T\right))=r_1^{\lambda }\left(x\left(T\right)\right).$ Then

$$\phi (t,x)=J_T(t,x,{\pi }_t,r^{\lambda }).$$

(22)

Moreover, if the equality in (21) is replaced by “≤” or “≥”, then (22) holds with the corresponding inequality.

Notice that Proposition 1 does not assert the existence of a function that satisfies (21) (this is the purpose of Proposition 2 below). It rather motivates the definition of the finite-horizon unconstrained problem.

Definition 6.

A policy ${\pi }^{*}\in \mathsf{\Pi }$ for which

$$J_T(t,x,{\pi }^{*},r^{\lambda })=\underset{\pi \in \mathsf{\Pi }}{sup}{J}_T(t,x,\pi ,r^{\lambda })=:J_T^{*}(t,x,r^{\lambda })forall(t,x)\in [0;T]\times {\mathbb{R}}^n,$$

(23)

is called finite-horizon optimalfor thefinite-horizon unconstrained problem(FHUP), and $J_T^{*}(·,·,r^{\lambda })$ is referred to as thefinite-horizon optimal rewardfor the FHUP.

The first part of the following result is an extension of Proposition 1 and the verification result Theorem 3.5.2(i) in [29] to the realm of Sobolev spaces. The proof of the second part mimics that of Theorem 3.5.2(ii) in [29].

Proposition 2.

Suppose that Hypotheses 1 and 2 are met. Then:

(i) 

For each fixed $\lambda \le 0$ and all $t\in [0;T]$, the finite-horizon optimal reward $J_T^{*}(·,·,·,r^{\lambda })$ defined in (23) belongs to ${\mathcal{W}}^{1,2;p}([0;T]\times {\mathbb{R}}^n)\cap {\mathcal{B}}_w([0;T]\times {\mathbb{R}}^n)$, and verifies the total reward Hamilton-Jacobi-Bellman (HJB) equation; that is,

$$\begin{array}{c}\hfill 0=\underset{\pi \in \mathsf{\Pi }}{sup}\left\{r^{\lambda }(t,x,\pi )+{\partial }_t{J}_T^{*}(t,x,r^{\lambda })+{\mathbb{L}}^{\pi }{J}_T^{*}\left(t,x,r^{\lambda }\right)\right\}forall(t,x)\in [0;T]\times {\mathbb{R}}^n.\end{array}$$

(24)

with boundary condition $J_T^{*}(T,x\left(T\right),r^{\lambda })=r_1^{\lambda }\left(x\left(T\right)\right)$. Conversely, if some function $\phi \in {\mathcal{W}}^{1,2;p}([0;T]\times {\mathbb{R}}^n)\cap {\mathcal{B}}_w([0;T]\times {\mathbb{R}}^n)$ verifies (24) with boundary condition $\phi (T,x\left(T\right))=r_1^{\lambda }\left(x\left(T\right)\right)$, then $\phi (t,x)=J_T^{*}(t,x,r^{\lambda })$ for all $(t,x)\in [0;T]\times {\mathbb{R}}^n$.

(ii) 

If there exists a Markovian policy $f^{*}\in \mathbb{M}$ (depending on λ) that maximizes the right-hand-side of (24), i.e.,

$$0=r^{\lambda }(t,x,f^{*})+{\partial }_t{J}_T^{*}(t,x,r^{\lambda })+{\mathbb{L}}^{f^{*}}{J}_T^{*}(t,x,r^{\lambda }),forall(t,x)\in [0;T]\times {\mathbb{R}}^n;$$

and this policy is such that the boundary condition $J_T^{*}(T,x\left(T\right),r^{\lambda })=r_1^{\lambda }(T,x\left(T\right))$ is met as well, then this policy is a finite-horizon optimal policy for the FHUP.

Use the former result to introduce the HJB equation for the FHUP for the examples presented along the paper.

Example 4

(Examples 1–3 continued). The HJB equation for the FHUP is given by:

$$\left\{\begin{array}{cc}{h}_t(t,x)+\underset{y\in [0;\gamma ]}{sup}\left\{F\left(y\right)-ax+\lambda \left[c_{1}x+c_{2}y-\frac{c_{1}x}{\eta }-q\right]+{\mathbb{L}}^{y}h(t,x)\right\}=0,\hfill & for t<T;\hfill \\ h(T,x)=0,\hfill \end{array}\right.$$

(25)

where $h\in {\mathcal{C}}^{1,2}([0;T]\times \mathbb{R})$; and

$${\mathbb{L}}^{y}h(t,x)=(y-\eta x)h_x\left(t,x\right)+\frac{1}{2}{\sigma }^2{h}_{xx}(t,x).$$

According to Proposition 2, a solution of the HJB equation (25) yields the finite-horizon optimal reward $J_T^{*}(t,x,r^{\lambda })$ and the optimal policy ${\pi }^{*}$ for the FHUP over the interval $[t;T]$.

Now use Definition 6 and Propositions 1 and 2 to set expressions for the optimal performance index, policies, and constraint rates from the examples presented along this work.

Lemma 2

(Examples 1–4 continued). Let Λ and $\mathcal{I}$ be the Lebesgue’s measure and the indicator function, respectively. Consider the planning horizon $[t;T]$ and assume the conditions in (7), (9)–(13) hold. Then,

(i) 

For every $x>0$ and $\lambda \le 0$, the value function $J_T^{*}(t,x,r^{\lambda })$ in (23), becomes

$$J_T^{*}(t,x,r^{\lambda })=m_1\left[1-{\mathrm{e}}^{-\eta (T-t)}\right]x+m_2\left(t\right),$$

(26)

where

$$\begin{array}{ccc}\hfill m_1& :=& \frac{a}{\eta }+\frac{\lambda c_1}{{\eta }^2}-\frac{\lambda c_1}{\eta },\hfill \end{array}$$

(27)

$$\begin{array}{c}{m}_2\left(t\right):=-\lambda q(T-t)+\left(F\left(\gamma \right)+\lambda \gamma c_2\right)\mathsf{\Lambda }\left(\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\}\right)\hfill \\ +{\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_{\lambda }\left(y\right)\right\}}\left(F\left(I\left(a_{\lambda }\left(y\right)\right)\right)+\lambda c_{2}I\left(a_{\lambda }\left(y\right)\right)+k_1\left[1-{\mathrm{e}}^{-\eta (T-y)}\right]I\left(a_{\lambda }\left(y\right)\right)\right)\mathrm{d}y\hfill \\ +m_1\gamma {\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\right\}}\left[1-{\mathrm{e}}^{-\eta (T-y)}\right]\mathrm{d}y,\hfill \end{array}$$

(28)

and $a_{\lambda }\left(t\right):=-\lambda c_2-m_1\left[1-{\mathrm{e}}^{-\eta (T-t)}\right]$, and $I(·)$ is the inverse of $F^{\prime }(·)$. Moreover, this policy turns out to be optimal for the FHUP; i.e., it is such that (24) holds.

(ii) 

Define

$$f^{\lambda }\left(t\right):=\left\{\begin{array}{cc}I\left(a_{\lambda }\left(t\right)\right)\hfill & \mathrm{if}{F}^{\prime }\left(\gamma \right)<a_{\lambda }\left(t\right),\hfill \\ \gamma \hfill & \mathrm{if}{F}^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(t\right).\hfill \end{array}\right.$$

(29)

For every $x>0$ and $\lambda \le 0$, the total expected reward, cost and constraint, respectively $J_T(t,x,f^{\lambda }\left(t\right),r)$, $J_T(t,x,f^{\lambda }\left(t\right),c)$, and ${\overline{\theta }}_T(t,x,f^{\lambda }\left(t\right))$; defined in Example 2, take the form

$$\begin{array}{c}\hfill J_T(t,x,f^{\lambda }\left(t\right),r)\\ \hfill ={\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_{\lambda }\left(y\right)\right\}}\left[F\left(I\left(a_{\lambda }\left(y\right)\right)\right)-\frac{aI\left(a_{\lambda }\left(y\right)\right)}{\eta }-a\frac{\eta x-I\left(a_{\lambda }\left(y\right)\right)}{\eta }{\mathrm{e}}^{-\eta (t-y)}\right]\mathrm{d}y\\ \hfill +\left[F\left(\gamma \right)-\frac{a\gamma }{\eta }\right]\mathsf{\Lambda }\left(\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\right\}\right)\\ \hfill -a\frac{\eta x-\gamma }{{\eta }^2}\left[{\mathrm{e}}^{-\eta [T-t]}-1\right]{\mathcal{I}}_{\{t:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(t\right)\}},\end{array}$$

(30)

$$\begin{array}{c}\hfill J_T(t,x,f^{\lambda }\left(t\right),c)=\\ \hfill {\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_{\lambda }\left(y\right)\right\}}\left[c_1\left[\frac{I\left(a_{\lambda }\left(y\right)\right)}{\eta }+\frac{\eta x-I\left(a_{\lambda }\left(y\right)\right)}{\eta }{\mathrm{e}}^{-\eta (t-y)}\right]+c_{2}I\left(a_{\lambda }\left(y\right)\right)\right]\mathrm{d}y\\ \hfill +\left[\frac{c_1\gamma }{\eta }+c_2\gamma \right]\mathsf{\Lambda }\left(\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\right\}\right)\\ \hfill -c_1\frac{\eta x-\gamma }{{\eta }^2}\left[{\mathrm{e}}^{-\eta [T-t]}-1\right]{\mathcal{I}}_{\{t:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(t\right)\}},\end{array}$$

(31)

$$\begin{array}{c}\hfill {\overline{\theta }}_T(t,x,f^{\lambda }\left(t\right))\\ \hfill ={\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_{\lambda }\left(y\right)\right\}}\left[\frac{c_{1}I\left(a_{\lambda }\left(y\right)\right)}{{\eta }^2}+c_1\frac{\eta x-I\left(a_{\lambda }\left(y\right)\right)}{{\eta }^2}{\mathrm{e}}^{-\eta (t-y)}\right]\mathrm{d}y\\ \hfill +\frac{c_1\gamma }{{\eta }^2}\mathsf{\Lambda }\left(\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\right\}\right)-c_1\frac{\eta x-\gamma }{{\eta }^3}\left[{\mathrm{e}}^{-\eta [T-t]}-1\right]{\mathcal{I}}_{\{t:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(t\right)\}}\\ \hfill +q(T-t).\end{array}$$

(32)

Proof Proof of Lemma 2.

(i)

Start by making an informed guess of the solution of (25). Namely

$$h(t,x):=p\left(t\right)x+m_2\left(t\right).$$

(33)

Observe that $h_t(t,x)=p^{\prime }\left(t\right)x-m_2^{\prime }\left(t\right)$, $h_x(t,x)=p\left(t\right),$ and $h_{xx}(t,x)=0$. The substitution of these expressions in (25) yields

$$\begin{array}{c}\hfill x\left(-a+\lambda c_1-\frac{\lambda c_1}{\eta }-\eta p\left(t\right)+p^{\prime }\left(t\right)\right)+\underset{0\le u\le \gamma }{sup}\left\{F\left(u\right)+\lambda c_{2}u+up\left(t\right)\right\}-\lambda q-m_2^{\prime }\left(t\right)\\ \hfill =0,\end{array}$$

This means that

$$\begin{array}{ccc}\hfill -a+\lambda c_1-\frac{\lambda c_1}{\eta }-\eta p\left(t\right)+p^{\prime }\left(t\right)& =& 0,\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill \underset{0\le u\le \gamma }{sup}\left\{F\left(u\right)+\lambda c_{2}u+up\left(t\right)\right\}-\lambda q-m_2^{\prime }\left(t\right)& =& 0,\hfill \end{array}$$

(35)

Impose the terminal condition $p\left(T\right)=0$ to (34) to obtain

$$p\left(t\right)=m_1\left[1-{\mathrm{e}}^{-\eta (T-t)}\right],$$

where $k_1$ is as in (27). Now, from (35), write

$$\begin{array}{ccc}\hfill m_2^{\prime }\left(t\right)& =& -\lambda q+\underset{0\le u\le \gamma }{sup}\left\{F\left(u\right)+\lambda c_{2}u+up\left(t\right)\right\}\hfill \\ & =& -\lambda q+\underset{0\le u\le \gamma }{sup}\left\{F\left(u\right)+\lambda c_{2}u+u{m}_1\left[1-{\mathrm{e}}^{-\eta (T-t)}\right]\right\}.\hfill \end{array}$$

(36)

To find the supremum of the expression inside the braces, use a standard calculus argument to see that at a critical point u:

$$F^{\prime }\left(u\right)+\lambda c_2+m_1\left[1-{\mathrm{e}}^{-\eta (T-t)}\right]=0.$$

(37)

Next, since by (10), $F^{\prime }\left(u\right)\ge 0$, it turns out that

$$q\lambda c_2+m_1\left[1-{\mathrm{e}}^{-\eta (T-t)}\right]\le 0.$$

(38)

Then, from (37):

$$F^{\prime }\left(u\right)=-\lambda c_2-m_1\left(1-{\mathrm{e}}^{-\eta (T-t)}\right)=:a_{\lambda }\left(t\right)\ge 0,$$

and

$$f^{\lambda }\left(t\right):=\left\{\begin{array}{cc}I\left(a_{\lambda }\left(t\right)\right)\hfill & \mathrm{if}{F}^{\prime }\left(\gamma \right)<a_{\lambda }\left(t\right),\hfill \\ \gamma \hfill & \mathrm{if}{F}^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(t\right).\hfill \end{array}\right.$$

With this in mind, (36) turns into

$$m_2^{\prime }\left(t\right)=-\lambda q+F\left(f^{\lambda }\left(t\right)\right)+\lambda c_2{f}^{\lambda }\left(t\right)+m_1\left[1-{\mathrm{e}}^{-\eta (T-t)}\right]f^{\lambda }\left(t\right).$$

Finally, $m_2\left(t\right)=-\lambda q(T-t)+{\int }_t^T\left(F\left(f^{\lambda }\left(y\right)\right)+\lambda c_2{f}^{\lambda }\left(y\right)+m_1\left[1-{\mathrm{e}}^{-\eta (T-y)}\right]f^{\lambda }\left(y\right)\right)\mathrm{d}y$, which equals

$$\begin{array}{ccc}\hfill & \hfill & -\lambda q(T-t)\hfill \\ \hfill & \hfill & +{\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_{\lambda }\left(y\right)\right\}}\left(F\left(f^{\lambda }\left(y\right)\right)+\lambda c_2{f}^{\lambda }\left(y\right)+m_1\left[1-{\mathrm{e}}^{-\eta (T-y)}\right]f^{\lambda }\left(y\right)\right)\mathrm{d}y\hfill \\ & \hfill & +{\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\right\}}\left(F\left(f^{\lambda }\left(y\right)\right)+\lambda c_2{f}^{\lambda }\left(y\right)+m_1\left[1-{\mathrm{e}}^{-\eta (T-y)}\right]f^{\lambda }\left(y\right)\right)\mathrm{d}y\hfill \\ \hfill & =\hfill & -\lambda q(T-t)\hfill \\ \hfill & \hfill & +{\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_{\lambda }\left(y\right)\right\}}\left(F\left(I\left(a_{\lambda }\left(y\right)\right)\right)+\lambda c_{2}I\left(a_{\lambda }\left(y\right)\right)+m_1\left[1-{\mathrm{e}}^{-\eta (T-y)}\right]I\left(a_{\lambda }\left(y\right)\right)\right)\mathrm{d}y\hfill \\ & \hfill & +{\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\right\}}\left(F\left(\gamma \right)+\lambda c_2\gamma +m_1\left[1-{\mathrm{e}}^{-\eta (T-y)}\right]\gamma \right)\mathrm{d}y\hfill \\ \hfill & =\hfill & -\lambda q(T-t)\hfill \\ \hfill & \hfill & +{\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_{\lambda }\left(y\right)\right\}}\left(F\left(I\left(a_{\lambda }\left(y\right)\right)\right)+\lambda c_{2}I\left(a_{\lambda }\left(y\right)\right)+m_1\left[1-{\mathrm{e}}^{-\eta (T-y)}\right]I\left(a_{\lambda }\left(y\right)\right)\right)\mathrm{d}y\hfill \\ \hfill & \hfill & +\left(F\left(\gamma \right)+\lambda \gamma c_2\right)\mathsf{\Lambda }\left(\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\}\right)\hfill \\ \hfill & \hfill & +m_1\gamma {\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\right\}}\left[1-{\mathrm{e}}^{-\eta (T-y)}\right]\mathrm{d}y,\hfill \end{array}$$

where $\mathsf{\Lambda }(·)$ stands for Lebesgue’s measure. Therefore, from (33), obtain

$$h(t,x):=p\left(t\right)x+m_2\left(t\right)=J_T^{*}(t,x,r^{\lambda })=J_T(t,x,f^{\lambda }\left(t\right),r^{\lambda }).$$

This proves (26)–(28). The optimality of (29) for the FHUP (20) follows from Proposition 2(ii).

(ii)

To see that (30) holds, use (17) to write

$$\begin{array}{ccc}\hfill J_T(t,x,f^{\lambda }\left(t\right),r)& =& {\mathbb{E}}_x^{f^{\lambda }}\left[{\int }_t^T(F\left(f^{\lambda }\left(y\right)\right)-ax\left(y\right))\mathrm{d}y\right]\hfill \\ & =& {\int }_t^T(F\left(f^{\lambda }\left(y\right)\right)-a{\mathbb{E}}_x^{f^{\lambda }}\left[x\left(y\right)\right])\mathrm{d}y.\hfill \end{array}$$

Here, the interchange of integrals is possible due to the finiteness of the interval $[t;T]$, and Fubini’s rule. Now, since the solution of the controlled diffusion process (7) is given by

$$\begin{array}{c}\hfill x\left(t\right)={\mathrm{e}}^{-\eta (t-t_0)}\left[x+\frac{f^{\lambda }}{\eta }\left({\mathrm{e}}^{\eta (t-t_0)-1}\right)+\sigma {\int }_{t_0}^T{\mathrm{e}}^{\eta (s-t_0)}dW\left(s\right)\right],\end{array}$$

where $x\left(t_0\right)=x$ and its expected value is

$$\begin{array}{c}\hfill {\mathbb{E}}_x^{f^{\lambda }}\left[x\left(t\right)\right]=\frac{f^{\lambda }}{\eta }+\frac{\eta x-f^{\lambda }}{\eta }{\mathrm{e}}^{\eta (t-t_0)}.\end{array}$$

Now, by (29) observe that the former equals:

$$\begin{array}{ccc}& & J_T(t,x,f^{\lambda }\left(t\right),r)\hfill \\ & =& {\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_{\lambda }\left(y\right)\right\}}F\left(f^{\lambda }\left(y\right)\right)\mathrm{d}y\hfill \\ & & +{\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\right\}}F\left(f^{\lambda }\left(y\right)\right)\mathrm{d}y-a{\mathbb{E}}_x^{f^{\lambda }}\left[{\int }_t^{T}x\left(y\right)\mathrm{d}y\right]\hfill \\ & =& {\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_{\lambda }\left(y\right)\right\}}F\left(I\left(a_{\lambda }\left(y\right)\right)\right)\mathrm{d}y\hfill \\ & & +{\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\right\}}F\left(\gamma \right)\mathrm{d}y-a{\mathbb{E}}_x^{f^{\lambda }}\left[{\int }_t^{T}x\left(y\right)\mathrm{d}y\right]\hfill \\ & =& {\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_{\lambda }\left(y\right)\right\}}F\left(I\left(a_{\lambda }\left(y\right)\right)\right)\mathrm{d}y\hfill \\ & & +F\left(\gamma \right)\mathsf{\Lambda }\left(\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\right\}\right)-a{\mathbb{E}}_x^{f^{\lambda }}\left[{\int }_t^{T}x\left(y\right)\mathrm{d}y\right]\hfill \\ & =& {\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_{\lambda }\left(y\right)\right\}}F\left(I\left(a_{\lambda }\left(y\right)\right)\right)\mathrm{d}y\hfill \\ & & +F\left(\gamma \right)\mathsf{\Lambda }\left(\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\right\}\right)\hfill \\ & & -a{\int }_t^T\left[\frac{f^{\lambda }\left(y\right)}{\eta }+\frac{\eta x-f^{\lambda }\left(y\right)}{\eta }{\mathrm{e}}^{-\eta (y-t)}dy\right]\hfill \\ & =& {\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_{\lambda }\left(y\right)\right\}}\left[F\left(I\left(a_{\lambda }\left(y\right)\right)\right)-\frac{aI\left(a_{\lambda }\left(y\right)\right)}{\eta }-a\frac{\eta x-I\left(a_{\lambda }\left(y\right)\right)}{\eta }{\mathrm{e}}^{-\eta (y-t)}\right]\mathrm{d}y\hfill \\ & & +\left[F\left(\gamma \right)-\frac{a\gamma }{\eta }\right]\mathsf{\Lambda }\left(\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\right\}\right)\hfill \\ & & +a\frac{\eta x-\gamma }{{\eta }^2}\left[{\mathrm{e}}^{-\eta [T-t]}-1\right]{\mathcal{I}}_{\{t:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(t\right)\}}.\hfill \end{array}$$

To prove (31), use the two leftmost members in (18), and proceed as above to put:

$$\begin{array}{ccc}& & J_T(t,x,f^{\lambda }\left(t\right),c)\hfill \\ & =& {\int }_t^T(c_1{\mathbb{E}}_x^{f^{\lambda }}\left[x\left(s\right)\right]+c_2{\mathbb{E}}_x^{f^{\lambda }}\left[f^{\lambda }\left(s\right)\right]\mathrm{d}s\hfill \\ & =& c_1{\int }_t^T\left[\frac{f^{\lambda }\left(y\right)}{\eta }+\frac{\eta x-f^{\lambda }\left(y\right)}{\eta }{\mathrm{e}}^{-\eta (y-t)}\right]dy+c_2{\mathbb{E}}_x^{f^{\lambda }}\left[{\int }_t^T{f}^{\lambda }\left(y\right)\mathrm{d}y\right]\hfill \\ & =& {\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_{\lambda }\left(y\right)\right\}}\left[c_1\left[\frac{I\left(a_{\lambda }\left(y\right)\right)}{\eta }+\frac{\eta x-I\left(a_{\lambda }\left(y\right)\right)}{\eta }{\mathrm{e}}^{-\eta (y-t)}\right]+c_{2}I\left(a_{\lambda }\left(y\right)\right)\right]\mathrm{d}y\hfill \\ & & +\left[\frac{c_1\gamma }{\eta }+c_2\gamma \right]\mathsf{\Lambda }\left(\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\right\}\right)\hfill \\ & & -c_1\frac{\eta x-\gamma }{{\eta }^2}\left({\mathrm{e}}^{-\eta [T-t]}-1\right){\mathcal{I}}_{\{t:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(t\right)\}}.\hfill \end{array}$$

Finally, by the two rightmost members of (18), write

$$\begin{array}{ccc}& & {\overline{\theta }}_T(t,x,f^{\lambda }\left(t\right))\hfill \\ & =& {\mathbb{E}}_x^{f^{\lambda }}\left[{\int }_t^T\frac{c_1}{\eta }x\left(s\right)\mathrm{d}s\right]+q(T-t)\hfill \\ & =& {\int }_t^T\frac{c_1}{\eta }{\mathbb{E}}_x^{f^{\lambda }}\left[x\left(s\right)\right]\mathrm{d}s+q(T-t)\hfill \\ & =& {\int }_t^T\frac{c_1}{\eta }\left[\frac{f^{\lambda }\left(y\right)}{\eta }+\frac{\eta x-f^{\lambda }\left(y\right)}{\eta }{\mathrm{e}}^{-\eta (y-t)}\right]\mathrm{d}s+q(T-t)\hfill \\ & =& {\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_{\lambda }\left(y\right)\right\}}\left[\frac{c_{1}I\left(a_{\lambda }\left(y\right)\right)}{{\eta }^2}+c_1\frac{\eta x-I\left(a_{\lambda }\left(y\right)\right)}{{\eta }^2}{\mathrm{e}}^{-\eta (y-t)}\right]\mathrm{d}y\hfill \\ & & +\frac{c_1\gamma }{{\eta }^2}\mathsf{\Lambda }\left(\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(y\right)\right\}\right)\hfill \\ & & -c_1\frac{\eta x-\gamma }{{\eta }^3}\left[{\mathrm{e}}^{-\eta [T-t]}-1\right]{\mathcal{I}}_{\{t:F^{\prime }\left(\gamma \right)\ge a_{\lambda }\left(t\right)\}}+q(T-t).\hfill \end{array}$$

This proves (32).

The proof is now complete. □

Remark 3.

The equality

$$\begin{array}{ccc}\hfill h(t,x)& =& J_T^{*}(t,x,r^{\lambda })\hfill \\ & =& J_T(t,x,f^{\lambda }\left(t\right),r)+\lambda \left[J_T\left(t,x,f^{\lambda }\left(t\right),c\right)-{\overline{\theta }}_T\left(t,x,f^{\lambda }\left(t\right)\right)\right]\hfill \end{array}$$

follows from (30)–(32).

3.2. From an Unconstrained Problem, to a Problem with Restrictions

This section starts with an important observation on the set of strategies which will be used.

Remark 4.

For each $\lambda \le 0$, define ${\mathsf{\Pi }}^{\lambda }:=\{\pi =({\pi }_t:t\ge 0)\in \mathsf{\Pi }:0=r^{\lambda }(t,x,{\pi }_t)+{\partial }_t{J}_T^{*}(t,x,r^{\lambda })+{\mathbb{L}}^{{\pi }_t}{J}_T^{*}(t,x,r^{\lambda })$ for all $(t,x)\in [0;T]\times {\mathbb{R}}^n;$ and $J_T^{*}(T,x\left(T\right),r^{\lambda })=r_1^{\lambda }\left(x\left(T\right)\right)\}.$

Since $\mathbb{M}$ can be thought of as a subset of Π, Proposition 2(ii) ensures that the set ${\mathsf{\Pi }}^{\lambda }$ is nonempty.

Lemma 3.

Let $\left({\lambda }_m\right)$ be a sequence in $]-\infty ;0]$ converging to some ${\lambda }^{*}\le 0$, and assume that there exists a sequence $\left({\pi }^{{\lambda }_m}\right)\subset {\mathsf{\Pi }}^{{\lambda }_m}$ for each $m\ge 1$ that converges to a policy $\pi \in \mathsf{\Pi }$. Then $\pi \in {\mathsf{\Pi }}^{{\lambda }^{*}}$; that is, π satisfies

$$0=r^{{\lambda }^{*}}(x,{\pi }_t)+{\partial }_t{J}_T^{*}(t,c,r^{{\lambda }^{*}})+{\mathbb{L}}^{{\pi }_t}{J}_T^{*}(t,x,r^{{\lambda }^{*}})forall(t,x)\in [0;T]\times {\mathbb{R}}^n.$$

Proof 

(Proof of Lemma 3.). Recall Definition 2. Take an arbitrary sequence $\left({\pi }^m\right)\subset {\mathsf{\Pi }}^{\lambda }$ such that ${\pi }^m\stackrel{W}{\to }\pi$. Observe that Proposition 2 ensures that for each $m\ge 1$, $J_T(t,x,r^{{\lambda }_m})$ satisfies:

$$0=r^{{\lambda }_m}(t,x,{\pi }_t^m)+{\partial }_t{J}_T^{*}(t,x,r^{{\lambda }_m})+{\mathbb{L}}^{{\pi }_t^m}{J}_T^{*}(t,x,r^{{\lambda }_m})forall(t,x)\in [0;T]\times {\mathbb{R}}^n.$$

In terms of the operator ${\widehat{\mathbb{L}}}_{{\lambda }_m}^{{\pi }_t^m}$, defined in (A4), the former relation reduces to

$$0={\widehat{\mathbb{L}}}_{{\lambda }_m}^{{\pi }_t^m}{J}_T^{*}(t,x,r^{{\lambda }^{*}})forall(t,x)\in [0;T]\times {\mathbb{R}}^n,$$

(39)

for the special case $v_1\equiv r$, $v_3\equiv c$, $\rho (t,x,u)\equiv \theta (t,x)$, ${\pi }_t^m\equiv {\pi }_t^{{\lambda }_m}$, $h_m(t,x)\equiv J_T^{*}(t,x,r^{{\lambda }_m})$, and ${\lambda }_m$ constant. A verification that the hypotheses of Appendix A follows. Specifically, part (a) trivially follows from (39). Then, the focus will be on checking that part (b) of Theorem A1 is met. To do that, for some $R>0$, take the ball $B_R:=\{x\in {\mathbb{R}}^n:\left|x\right|<R\}$. By [30] [Theorem 9.11], there exists a constant $C_0$ (depending on R) such that for a fixed $p>n$:

$$\begin{array}{ccc}& & \parallel J_T^{*}(·,·,r^{{\lambda }_m}){\parallel }_{{\mathcal{W}}^{1,2;p}([0;T]\times B_R)}\hfill \\ & \le & C_0\left(\parallel J_T^{*}(·,·,r^{{\lambda }_m}){\parallel }_{{\mathcal{L}}^p([0;T]\times B_{2R})}+{\parallel r^{{\lambda }_m}(·,·,{\pi }_{·}^m)\parallel }_{{\mathcal{L}}^p([0;T]\times B_{2R})}\right)\hfill \\ & \le & C_0\left(M_2{(T,t)\parallel w\parallel }_{{\mathcal{L}}^p([0;T]\times B_{2R})}+M{\parallel w\parallel }_{{\mathcal{L}}^p([0;T]\times B_{2R})}\right)\hfill \\ & \le & C_0\left(M_2(T,t)+M\right)T{\left|{\overline{B}}_{2R}\right|}^{1/p}\underset{x\in {\overline{B}}_{2R}}{max}w\left(x\right)<\infty ,\hfill \end{array}$$

where $|{\overline{B}}_{2R}|$ represents the volume of the closed ball with radius $2R$; M and $M_2(x,T,t)$ are the constants in Hypothesis (H2b), and in (14), respectively.

Notice that conditions (c) to (f) from Theorem A1 trivially hold, and that condition (g) is given as a part of the hypotheses just presented. Then, one can claim the existence of a function $h^{{\lambda }^{*}}\in W^{1,2;p}([0;T]\times B_R)$ together with a subsequence $\left(m_k\right)$ such that $J_T^{*}(·,·,r^{{\lambda }_{m_k}})=J_T^{*}(·,·,{\pi }_{·}^{m_k},r^{{\lambda }_{m_k}})\to h^{{\lambda }^{*}}(·,·)$uniformly in $[0;T]\times B_R$ and pointwise on $[0;T]\times {\mathbb{R}}^n$ as $k\to \infty$ and ${\pi }^m\stackrel{W}{\to }\pi$. Furthermore, $h^{{\lambda }^{*}}$ satisfies:

$$0=r^{{\lambda }^{*}}(t,x,{\pi }_t)+{\mathbb{L}}^{{\pi }_t}{h}^{{\lambda }^{*}}(t,x),for(t,x)\in [0;T]\times B_R.$$

Since the radius $R>0$ was arbitrary, one can extend the analysis to all of $x\in {\mathbb{R}}^n$. Thus, Proposition 1 asserts that $h^{{\lambda }^{*}}(t,x)$ coincides with $J_T^{*}(t,x,r^{{\lambda }^{*}})$. This proves the result. □

Lemma 3 gives, in particular, the continuity of the mapping ${\pi }_t\to J_T(t,x,{\pi }_t,r^{\lambda })$.

Lemma 4.

Assume the hypotheses of Proposition 1. Then:

(a) 

For each fixed $(t,x)\in [0;T]\times {\mathbb{R}}^n$, $\lambda \le 0$, and $\eta \in \mathbb{R}$ under which $\lambda +\eta \le 0$:

$$\begin{array}{ccc}\eta \left[J_T(t,x,{\pi }_t^{\lambda },c)-{\overline{\theta }}_T(t,x,{\pi }_t^{\lambda })\right]\hfill & \le \hfill & J_T^{*}(t,x,r^{\lambda +\eta })-J_T^{*}(t,x,r^{\lambda })\hfill \\ \hfill & \le \hfill & \eta \left[J_T(t,x,{\pi }_t^{\lambda +\eta },c)-{\overline{\theta }}_T(t,x,{\pi }_t^{\lambda +\eta })\right].\hfill \end{array}$$

(40)

(b) 

The mapping $\lambda \mapsto J_T^{*}(t,x,r^{\lambda })$ is differentiable on $]-\infty ;0[$, for any $(t,x)\in [0;T]\times {\mathbb{R}}^n$; in fact, for each $\lambda <0$,

$$\frac{\partial J_T^{*}(t,x,r^{\lambda })}{\partial \lambda }=J_T(t,x,{\pi }_t^{\lambda },c)-{\overline{\theta }}_T(t,x,{\pi }_t^{\lambda }).$$

(41)

Proof Proof of Lemma 4.

(a)

Observe that from (19), (23), and the definition of $r^{\lambda +\eta }$, one can assert that

$$\begin{array}{c}\hfill J_T^{*}(t,x,r^{\lambda +\eta })\ge J_T(t,x,{\pi }_t^{\lambda },r^{\lambda +\eta })\\ \hfill =J_T(t,x,{\pi }_t^{\lambda },r)+\left(\lambda +\eta \right)\left[J_T(t,x,{\pi }_t^{\lambda },c)-{\overline{\theta }}_T(t,x,{\pi }_t^{\lambda })\right].\end{array}$$

(42)

On the other hand, Proposition 2(ii) and the definition of ${\pi }^{\lambda }\in {\mathsf{\Pi }}^{\lambda }$ yield the equality

$$\begin{array}{c}\hfill J_T^{*}(t,x,r^{\lambda })=J_T(t,x,{\pi }_t^{\lambda },r^{\lambda })\\ \hfill =J_T(t,x,{\pi }_t^{\lambda },r)+\lambda \left[J_T(t,x,{\pi }_t^{\lambda },c)-{\overline{\theta }}_T(t,x,{\pi }_t^{\lambda })\right].\end{array}$$

(43)

Subtracting (43) from (42) yields

$$J_T^{*}(t,x,r^{\lambda +\eta })-J_T^{*}(t,x,r^{\lambda })\ge \eta \left[J_T(t,x,{\pi }_t^{\lambda },c)-{\overline{\theta }}_T(t,x,{\pi }_t^{\lambda })\right].$$

(44)

Applying analogous arguments to those given in the above procedure, but taking $J_T^{*}(t,x,r^{\lambda })$ and the policy ${\pi }^{\lambda +\eta }$, it is possible to obtain

$$J_T^{*}(t,x,r^{\lambda +\eta })-J_T^{*}(t,x,r^{\lambda })\le \eta \left[J_T(t,x,{\pi }_t^{\lambda +\eta },c)-{\overline{\theta }}_T(t,x,{\pi }_t^{\lambda +\eta })\right].$$

(45)

Hence (a) follows by combining (44) and (45).

(b)

By (15) and (16):

$$|J_T(t,x,{\pi }_t^{\lambda +\eta },c)-{\overline{\theta }}_T(t,x,{\pi }_t^{\lambda +\eta })|\le M_{2}w\left(x\right).$$

Therefore, the continuity of $\lambda \mapsto J_T^{*}(·,·,r_{\alpha }^{\lambda })$ follows by letting $\eta \to 0$ in all of the terms of (40). Now let $(t,x)\in [0,\infty [\times {\mathbb{R}}^n$ and $\lambda <0$ be fixed, and consider a sequence of negative numbers $\left({\eta }_m\right)$ such that ${\eta }_m\uparrow 0$ together with its associated sequence of policies $\left({\pi }^{\lambda +{\eta }_m}\right)$, where ${\pi }^{\lambda +{\eta }_m}\in {\mathsf{\Pi }}^{\lambda +{\eta }_m}$ for each m. From the compactness of the metric space $\mathsf{\Pi }$, there exists a subsequence $\left({\pi }^{\lambda +{\eta }_{m_k}}\right)$ and $\pi \in \mathsf{\Pi }$ such that ${\pi }^{\lambda +{\eta }_{m_k}}\stackrel{W}{\to }\pi$ as $k\to \infty$. From Lemma 3, $\pi$ belongs to ${\mathsf{\Pi }}^{\lambda }$, so, denote it by ${\pi }^{\lambda }:=\pi$. By Lemma 3, the mapping ${\pi }_t\mapsto J_T(t,x,{\pi }_t,v)$ is also continuous on $\mathsf{\Pi }$, with $v(t,x,u)=c(t,x,u)-\theta (t,x)$. Please note that $J_T(t,x,{\pi }_t,v)=J_T(t,x,{\pi }_t,c)-{\overline{\theta }}_T(t,x,{\pi }_t)$, which gives

$$\begin{array}{c}\hfill J_T\left(t,x,{\pi }_t^{\lambda +{\eta }_{m_k}},c\right)-{\overline{\theta }}_T\left(t,x,{\pi }_t^{\lambda +{\eta }_{m_k}}\right)\\ \hfill \to J_T\left(t,x,{\pi }_t^{\lambda },c\right)-{\overline{\theta }}_T\left(t,x,{\pi }_t^{\lambda }\right),\\ \hfill for(t,x)\in [0;\infty [\times {\mathbb{R}}^{n}ask\to \infty .\end{array}$$

Therefore, from part (a) of this result, it turns out that the limit

$$\underset{k\to \infty }{lim}\frac{J_T^{*}(t,x,r^{\lambda +{\eta }_{m_k}})-J_T^{*}(t,x,r^{\lambda })}{{\eta }_{m_k}}=J_T(t,x,{\pi }_t^{\lambda },c)-{\overline{\theta }}_T(t,x,{\pi }_t^{\lambda }),$$

(46)

for $(t,x)\in [0;\infty [\times {\mathbb{R}}^n.$ Similarly, if one considers a sequence of positive real numbers $\left({\eta }_m\right)$ such that $\lambda +{\eta }_m\le 0$, it is possible to prove that there exists a subsequence $\left(\lambda +{\eta }_{m_k}\right)$ such that (46) holds. This proves that $\lambda \mapsto J_T^{*}(t,x,r^{\lambda })$ is differentiable on $]-\infty ;0]$, with derivative given by (41).

□

The following is the main result of this section. It shows how to compute optimal policies for the FHPC.

Theorem 1.

Let Hypotheses 1 and 2 hold, and consider a point $(t,x)\in [0;T]\times {\mathbb{R}}^n$ fixed. Then:

(a) 

If ${\lambda }_{t,x}^{*}<0$ is a critical point of $J_T^{*}(t,x,r^{\lambda })$; that is, if the derivative in (41) equals zero at $\lambda ={\lambda }_{t,x}^{*}$, then every ${\pi }^{{\lambda }^{*}}=\left({\pi }_t^{{\lambda }_{t,x}^{*}}:t\ge 0\right)\in {\mathsf{\Pi }}^{{\lambda }^{*}}$ is optimal for the FHPC, and

$$J_T(t,x,{\pi }^{{\lambda }_{t,x}^{*}},c)={\overline{\theta }}_T(t,x,{\pi }^{{\lambda }_{t,x}^{*}}).$$

Moreover, $J_T^{*}(t,x,r^{{\lambda }_{t,x}^{*}})$ is the optimal value for the FHPC which in turn coincides with $J_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}},r)$. In addition,

$$J_T^{*}(t,x,r^{{\lambda }_{t,x}^{*}})=\underset{\lambda <0}{inf}{J}_T^{*}(t,x,r^{\lambda }).$$

(47)

(b) 

Case ${\lambda }_{t,x}^{*}=0$: If ${\pi }^0=\left({\pi }_t^0:t\ge 0\right)\in {\mathsf{\Pi }}^0$ satisfies $J_T(t,x,{\pi }_t^0,c)\le {\overline{\theta }}_T(t,x,{\pi }_t^0)$; i.e., ${\pi }^0\in {\mathcal{F}}_{{\theta }_T}^{t,x}$, then this policy is optimal for the FHPC. Moreover, $J_T^{*}(t,x,r^0)=J_T^{*}(t,x,r)$ becomes the optimal value for the FHPC and it coincides with $J_T(t,x,{\pi }^0,r)$. Furthermore,

$$J_T^{*}(t,x,r^0)=\underset{\lambda \le 0}{min}{J}_T^{*}(t,x,r^{\lambda }).$$

(48)

Proof Proof of Theorem 1.

(a)

Since ${\lambda }_{t,x}^{*}<0$ is a critical point of $J_T^{*}(t,x,r^{\lambda })$, the relation (41) yields:

$$\begin{array}{c}\hfill \frac{\partial J_T^{*}(t,x,r^{\lambda })}{\partial \lambda }{|}_{\lambda ={\lambda }_{t,x}^{*}}\\ \hfill =J_T\left(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}},c\right)-{\overline{\theta }}_T\left(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}}\right)=0forevery{\pi }_t^{{\lambda }^{*}}\in {\mathsf{\Pi }}^{{\lambda }^{*}}.\end{array}$$

(49)

Thus, using (19) and (49), it can be said that:

$$\begin{array}{ccc}{J}_T(t,x,{\pi }^{{\lambda }_{t,x}^{*}},r^{{\lambda }_{t,x}^{*}})\hfill & =\hfill & J_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}},r)+{\lambda }_{t,x}^{*}\left[J_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}},c)-{\overline{\theta }}_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}})\right]\hfill \\ \hfill & =\hfill & J_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}},r).\hfill \end{array}$$

(50)

Moreover, given that ${\pi }^{{\lambda }^{*}}$ is in ${\mathsf{\Pi }}^{{\lambda }^{*}}$, Proposition 2(ii) and Remark 4 yield

$$J_T^{*}(t,x,r^{{\lambda }_{t,x}^{*}}):=\underset{\pi \in \mathsf{\Pi }}{sup}{J}_T(t,x,{\pi }_t,r^{{\lambda }_{t,x}^{*}})=J_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}},r^{{\lambda }_{t,x}^{*}}).$$

(51)

On the other hand, observe that for all $\pi \in {\mathcal{F}}_{{\theta }_T}^{t,x},$$J_T(t,x,{\pi }_t,c)-{\overline{\theta }}_T(t,x,{\pi }_t)\le 0$, implying that ${\lambda }_{t,x}^{*}[J_T(t,x,{\pi }_t,c)-\overline{\theta }(t,x,{\pi }_t)]\ge 0$. This last inequality, together with (19), (23), (50) and (51), leads to

$$\begin{array}{ccc}{J}_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}},r)\hfill & =\hfill & J_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}},r^{{\lambda }_{t,x}^{*}})=J_T^{*}(t,x,r^{{\lambda }_{t,x}^{*}})\ge J_T(t,x,{\pi }_t,r^{{\lambda }_{t,x}^{*}})\hfill \\ \hfill & =\hfill & J_T\left(t,x,{\pi }_t,r\right)+{\lambda }_{t,x}^{*}\left[J_T(t,x,{\pi }_t,c)-{\overline{\theta }}_T(t,x,{\pi }_t)\right]\hfill \\ \hfill & \ge \hfill & J_T\left(t,x,{\pi }_t,r\right)forall\pi \in {\mathcal{F}}_{{\theta }_T}^{t,x}.\hfill \end{array}$$

(52)

Therefore,

$$\begin{array}{ccc}\hfill J_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}},r)& \ge & \underset{\pi \in {\mathcal{F}}_{{\theta }_T}^{t,x}}{sup}{J}_T\left(t,x,{\pi }_t,r\right).\hfill \end{array}$$

(53)

Finally, by (49):

$$J_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}},c)={\overline{\theta }}_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}}),$$

yielding that ${\pi }^{{\lambda }^{*}}$ is in ${\mathcal{F}}_{{\theta }_T}^{t,x}$. This fact, along with (52) and (53), gives that

$$\begin{array}{ccc}\hfill J_T^{*}(t,x,r^{{\lambda }_{t,x}^{*}})& =& J_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}},r)=\underset{\pi \in {\mathcal{F}}_{{\theta }_T}^{t,x}}{sup}{J}_T\left(t,x,{\pi }_t,r\right);\hfill \end{array}$$

that is, ${\pi }^{{\lambda }^{*}}$ is optimal for the FHPC, and $J_T^{*}(t,x,r^{{\lambda }_{t,x}^{*}})$ coincides with the optimal reward for the FHPC.

To prove (47), observe that for each $\lambda <0$ and for all ${\pi }^{\lambda }\in {\mathsf{\Pi }}^{\lambda }$, Proposition 1 gives

$$J_T^{*}(t,x,r^{\lambda })\ge J_T(t,x,{\pi }_t,r^{\lambda })=J_T(t,x,{\pi }_t,r)+\lambda \left[J_T(t,x,{\pi }_t,c)-{\overline{\theta }}_T(t,x,{\pi }_t)\right]$$

for all $\pi \in \mathsf{\Pi }$, $(t,x)\in [0;\infty [\times {\mathbb{R}}^n$, in particular, taking $\pi :={\pi }^{{\lambda }_{t,x}^{*}}$ in the latter expression, and observing that the second term is zero (see (49)) yield

$$\begin{array}{ccc}\hfill J_T^{*}(t,x,r^{\lambda })& \ge & J_T(t,x,{\pi }_t^{{\lambda }^{*}},r)+\lambda \left[J_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}},c)-{\overline{\theta }}_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}})\right]\hfill \\ & =& J_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}},r)+{\lambda }_{t,x}^{*}\left[J_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}},c)-{\overline{\theta }}_T(t,x,{\pi }_t^{{\lambda }_{t,x}^{*}})\right]\hfill \\ & =& J_T^{*}(t,x,r^{{\lambda }_{t,x}^{*}}).\hfill \end{array}$$

Since $\lambda <0$ was an arbitrary negative constant, then (47) holds.

(b)

It is clear that ${\lambda }_{t,x}^{*}=0$ implies $r(t,x,{\pi }_t)=r^0(t,x,{\pi }_t)$, for all $(t,x)\in [0;\infty [\times {\mathbb{R}}^n$ and $\pi \in \mathsf{\Pi }$. Since ${\mathsf{\Pi }}^0$ is nonempty (see Remark 4), Proposition 2(ii) ensures that ${\pi }^0\in {\mathsf{\Pi }}^0$ is optimal for the FHUP ($\lambda =0$). Given that ${\pi }^0\in {\mathcal{F}}_{{\theta }_T}^{t,x}$, then ${\pi }^0$ is optimal for the FHPC. Therefore,

$$J_T^{*}(t,x,r^0)=J_T(t,x,{\pi }_t^0,r)=\underset{\pi \in {\mathcal{F}}_{{\theta }_T}^{t,x}}{sup}{J}_T(t,x,{\pi }_t,r).$$

Moreover, since $J_T(t,x,{\pi }_t^0,c)\le {\overline{\theta }}_T(t,x,{\pi }_t^0)$, one can take $\eta <0$. From (40):

$$0\le \eta \left[J_T(t,x,{\pi }_t^0,c)-{\overline{\theta }}_T(t,x,{\pi }_t^0)\right]\le J_T^{*}(t,x,r^{\eta })-J_T^{*}(t,x,r^0).$$

This yields $J_T^{*}(t,x,r^0)\le J_T^{*}(t,x,r^{\eta })$, for all $\eta <0$. Therefore, (48) follows trivially.

□

Theorem 2

(Examples 1–4, and Lemma 2 continued). Assume that $K>0$ and let $z>0$ fixed such that for all $t\in [0;T]$

$$\begin{array}{c}\hfill \left[{\mathrm{e}}^{-\eta [T-t]}-1\right]\left(-\frac{c_{1}K}{{\eta }^2}-\frac{c_{1}z}{\eta }-\frac{c_{2}K}{\eta }+\frac{c_{1}K}{{\eta }^3}+\frac{c_{1}z}{{\eta }^2}\right)\\ \hfill +{\mathrm{e}}^{-\eta (T-t)}(T-t)\left(\frac{c_{1}K}{\eta }-\frac{c_{1}K}{2{\eta }^2}\right)-q(T-t)=0,\end{array}$$

(54)

and

$$0<K{\mathrm{e}}^{-\eta (T-t)}<\gamma$$

(55)

(a) 

If $F^{\prime }\left(K{\mathrm{e}}^{-\eta (T-t)}\right)>-m_1\left(1-{\mathrm{e}}^{-\eta (T-t)}\right),$ then the mapping $\lambda \mapsto J_T^{*}(t,z,r^{\lambda })$ admits a critical point ${\lambda }_t^{*}\equiv {\lambda }_t^{*}\left(z\right)<0$ satisfying

$$\begin{array}{c}\hfill a_{{\lambda }_t^{*}}\left(t\right)=-{\lambda }_t^{*}{c}_2-m_1\left(1-{\mathrm{e}}^{-\eta (T-t)}\right)=F^{\prime }\left(K{\mathrm{e}}^{-\eta (T-t)}\right),\end{array}$$

(56)

where $m_1$ is as in (27). Hence, every ${\pi }^{{\lambda }_t^{*}}\in {\mathsf{\Pi }}^{{\lambda }_t^{*}}$ is optimal for the constrained control problem and $J_T(t,z,{\pi }^{{\lambda }_t^{*}},c)={\overline{\theta }}_T(t,z,{\pi }^{{\lambda }_t^{*}})$; in particular, the corresponding $f^{{\lambda }_t^{*}}\in \mathbb{M}\cap {\mathsf{\Pi }}^{{\lambda }^{*}}$ defined in (29) becomes the policy

$$f\left(t\right):=K{\mathrm{e}}^{-\eta (T-t)},$$

(57)

and the optimal value for the FHPC is given by

$$\begin{array}{c}\hfill J_T(t,z,r^{{\lambda }_t^{*}})=J_T(t,z,f^{{\lambda }_t^{*}},r)\\ \hfill ={\int }_t^{T}F\left(K{\mathrm{e}}^{-\eta (T-y)}\right)\mathrm{d}y+\frac{aK}{{\eta }^2}\left({\mathrm{e}}^{-\eta (T-t)}-1\right)\\ \hfill -\frac{az}{\eta }\left({\mathrm{e}}^{-\eta [T-t]}-1\right)+\frac{K}{\eta }{\mathrm{e}}^{-\eta (T-t)}(T-t).\end{array}$$

(58)

Moreover,

$$\begin{array}{ccc}& & J_T(t,z,f^{{\lambda }_t^{*}}\left(t\right),c)-{\overline{\theta }}_T(t,z,f^{{\lambda }_t^{*}}\left(t\right))\hfill \\ & =& \left[{\mathrm{e}}^{-\eta [T-t]}-1\right]\left(-\frac{c_{1}K}{{\eta }^2}-\frac{c_{1}z}{\eta }-\frac{c_{2}K}{\eta }+\frac{c_{1}K}{{\eta }^3}+\frac{c_{1}z}{{\eta }^2}\right)\hfill \\ & & +{\mathrm{e}}^{-\eta [T-t]}[T-t]\left(\frac{c_{1}K}{\eta }-\frac{c_{1}K}{2{\eta }^2}\right)-q[T-t]=0.\hfill \end{array}$$

(b) 

If $F^{\prime }\left(K{\mathrm{e}}^{-\eta (T-t)}\right)\le -m_1\left[1-{\mathrm{e}}^{-\eta (T-t)}\right],$ then

$$f^0\left(t\right)=I\left(-m_1\left[1-{\mathrm{e}}^{-\eta (T-t)}\right]\right)\in [0;\gamma ]$$

defines a policy which belongs to ${\mathsf{\Pi }}^0$ and $J_T(t,z,f^0\left(t\right),c)\le {\overline{\theta }}_T(t,z,f^0\left(t\right))$; that is $f^0\in \mathbb{M}\cap {\mathsf{\Pi }}^0$. Moreover, $f^0$ is an optimal policy for the FHPC with optimal value

$$\begin{array}{c}\hfill J_T^{*}(t,z,r^0)=J_T^{*}(t,z,r)=J_T^{*}(t,z,f^0\left(t\right),r)\\ \hfill ={\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_{\lambda }\left(y\right)\right\}}\left[F\left(I\left(a_0\left(y\right)\right)\right)-\frac{aI\left(a_0\left(y\right)\right)}{\eta }-a\frac{\eta z-I\left(a_0\left(y\right)\right)}{\eta }{\mathrm{e}}^{-\eta (y-t)}\right]\mathrm{d}y.\end{array}$$

(59)

Proof Proof of Theorem 2.

(a)

Consider ${\lambda }_t^{*}\in \mathbb{R}$ from (56). Then it satisfies the following inequality too

$${\lambda }_t^{*}:=\frac{-F^{\prime }\left(K{\mathrm{e}}^{-\eta (T-t)}\right)-m_1\left[1-{\mathrm{e}}^{-\eta (T-t)}\right]}{c_2}<0.$$

(60)

From (55):

$$0<K{\mathrm{e}}^{-\eta (T-t)}<\gamma .$$

Since $F^{\prime }(·)$ is a strictly decreasing function, then

$$F^{\prime }\left(\gamma \right)<F^{\prime }\left(K{\mathrm{e}}^{-\eta (T-t)}\right)=a_{{\lambda }_t^{*}}\left(t\right).$$

Hence, from (29), $f^{{\lambda }_t^{*}}\left(t\right)=I\left(a_{{\lambda }_t^{*}}\left(t\right)\right)\in {\mathsf{\Pi }}^{{\lambda }^{*}}$ takes the form (57). On the other hand, from Lemma 4(b), the mapping $\lambda ⟼J_T^{*}(t,z,r^{\lambda })$ is differentiable in ${\lambda }_t^{*}<0$, with

$$\frac{\partial J_T^{*}(t,z,r^{\lambda })}{\partial \lambda }{|}_{\lambda ={\lambda }_t^{*}}=J_T(t,z,{\pi }^{{\lambda }^{*}},c)-{\overline{\theta }}_T(t,z,{\pi }^{{\lambda }^{*}})forall{\pi }^{{\lambda }^{*}}\in {\mathsf{\Pi }}^{{\lambda }_t^{*}}.$$

In particular, if one considers ${\pi }^{{\lambda }_t^{*}}:=f^{{\lambda }_t^{*}}$ as given by (57), and then replaces it in (31) and (32), one obtains that $J_T(t,z,f^{{\lambda }_t^{*}},c)={\overline{\theta }}_T(t,z,f^{{\lambda }_t^{*}})$ using the condition (54), i.e., ${\lambda }_t^{*}$ is a critical point of the function $\lambda \mapsto J_T^{*}(t,z,r^{\lambda })$. Thus, from Theorem 1(b), every ${\pi }^{{\lambda }_t^{*}}\in {\mathsf{\Pi }}^{{\lambda }^{*}}$ is an optimal policy for the control problem with constraints, and $J_T(t,z,{\pi }^{{\lambda }_t^{*}},c)={\overline{\theta }}_T(t,z,{\pi }^{{\lambda }_t^{*}})$, with optimal value $J_T^{*}(t,z,r^{{\lambda }_t^{*}})=J_T(t,z,{\pi }^{{\lambda }_t^{*}},r)=J_T(t,z,f^{{\lambda }_t^{*}},r)$.

(b)

Observe that

$$\begin{array}{c}\hfill F^{\prime }\left(\gamma \right)<F^{\prime }\left(K{\mathrm{e}}^{-\eta (T-t)}\right)\le -m_1\left[1-{\mathrm{e}}^{-\eta (T-t)}\right]=a_0\left(t\right),\end{array}$$

(61)

which implies that

$$I\left(a_0\left(t\right)\right)=I\left(-m_1[1-{\mathrm{e}}^{-\eta (T-t)}]\right)\le K{\mathrm{e}}^{-\eta (T-t)}<\gamma .$$

(62)

From (29), it follows that $f^0\left(t\right)=I\left(a_0\left(t\right)\right)\in \mathbb{M}\cap {\mathsf{\Pi }}^0$. Moreover, by (61)–(62)

$$\begin{array}{ccc}\hfill & \hfill & J_T\left(t,z,f^0,c\right)-{\overline{\theta }}_T\left(t,z,f^0\right)\hfill \\ & =\hfill & \left(1-\frac{1}{\eta }\right){\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_0\left(y\right)\right\}}\left[\frac{c_{1}I\left(a_0\left(y\right)\right)}{\eta }+c_1\frac{\eta z-I\left(a_0\left(y\right)\right)}{\eta }{\mathrm{e}}^{-\eta (y-t)}\right]\mathrm{d}y\hfill \\ \hfill & \hfill & +c_2{\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_0\left(y\right)\right\}}I\left(a_0\left(y\right)\right)\mathrm{d}y-q(T-t)\hfill \\ \hfill & \le \hfill & \left(1-\frac{1}{\eta }\right){\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_0\left(y\right)\right\}}\left[\frac{c_{1}K{\mathrm{e}}^{-\eta (T-y)}}{\eta }+c_1\frac{\eta z-K{\mathrm{e}}^{-\eta (T-y)}}{\eta }{\mathrm{e}}^{-\eta (y-t)}\right]\mathrm{d}y\hfill \\ \hfill & \hfill & +c_2{\int }_{\left\{y\in [t;T]:F^{\prime }\left(\gamma \right)<a_0\left(y\right)\right\}}K{\mathrm{e}}^{-\eta (T-y)}\mathrm{d}y-q(T-t)\hfill \\ \hfill & =\hfill & \left({\mathrm{e}}^{-\eta (T-t)}-1\right)\left(-\frac{c_{1}K}{{\eta }^2}-\frac{c_{1}z}{\eta }-\frac{c_{2}K}{\eta }+\frac{c_{1}K}{{\eta }^3}+\frac{c_{1}z}{{\eta }^2}\right)\hfill \\ \hfill & \hfill & +{\mathrm{e}}^{-\eta [T-t]}(T-t)\left(\frac{c_{1}K}{\eta }-\frac{c_{1}K}{2{\eta }^2}\right)-q(T-t)=0,\hfill \end{array}$$

(63)

that is, $J_T\left(t,x,f^0,c\right)-{\overline{\theta }}_T\left(t,x,f^0\right)\le 0$. Hence, Theorem 1(b) ensures that $f^0$ is an optimal policy for the FHPC with optimal value $J_T^{*}(t,z,r)=J_T(t,z,f^0,r)$. Henceforth, replacing $f^0$ into (30), one easily deduces (59).

□

Remark 5.

If the opposite condition in (54) occurs, then the existence of a critical point of the mapping $\lambda \mapsto J_T^{*}(t,z,r^{\lambda })$ implies necessarily that

$$F^{{}^{\prime }}\left(\gamma \right)\ge a_0\left(t\right)=-m_1\left[1-{\mathrm{e}}^{-\eta (T-t)}\right]and{f}^{\lambda }\left(t\right)=\gamma forall\lambda \le 0.$$

In this case, every $\lambda \le 0$ is a critical point of $\lambda \to J_T^{*}(t,z,r^{\lambda })$ and $f^{\lambda }\left(t\right)=\gamma$ is an optimal policy for the FHPC. To avoid this trivial situation, under the fact $F^{{}^{\prime }}(\infty )=0$, choose γ large enough such that

$$F^{{}^{\prime }}\left(\gamma \right)<-m_1\left[1-{\mathrm{e}}^{-\eta (T-t)}\right].$$

Now use Theorem 2 to propose a modification of Algorithm 1 to compute the integral inside (20). Observe that it is no longer needed to include the computation of the Vasicek process (8) because the optimal values of the controllers $f^{{\lambda }^{*}}$—given by (57), and the Lagrange multipliers ${\lambda }_t^{*}$—given by (60)- are non-stationary along time.

Example 5

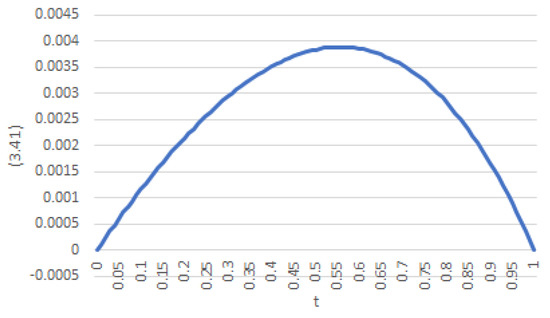
(Examples 1–4, Lemma 2, and Theorem 2 continued). Algorithms 2 and 3 can be used to compare the Monte Carlo simulations for the integral inside the expectation operator (20) with the results (formula (58)) from Theorem 2. To this end, recall from Example 1, the choice made for the parameters of (7) (that is: $x_0=5$, $\sigma \left(x\right)\equiv 0.5$, $\eta =1$ and $T=1$). In addition, choose constants that meet (12): these are $a=1.25$, $\gamma =1$, $c_1=0.1$, $c_2=0.05$, and $q=0.0195$. With this configuration, condition (54) holds for all $t\in [0;1]$ with an error of, at most $0.004$ (see Figure 3). With all these in mind, formula (58) in Theorem 2 yields an optimal value for the FHPC of

$$J_1^{*}(0,5,r^{{\lambda }_t^{*}})=J_1^{*}(0,5,f^{{\lambda }_t^{*}},r)=-3.58813.$$

(64)

Figure 3. Error in the approximation of (57).

Algorithm 3: Integral algorithm

The use of Algorithms 2 and 3 (with 10,000 simulations) gives optimal values for the FHUP around

$$J_1^{*}(0,5,r^{{\lambda }_t^{*}})\approx -3.3231104.$$

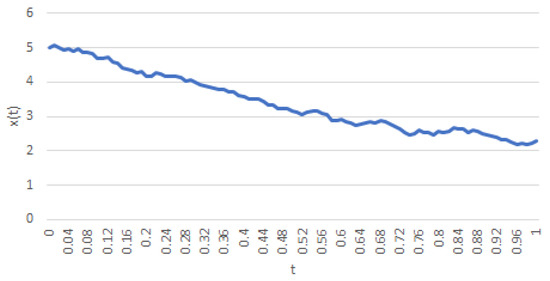
The relative error implied by the latter numeric expression and (64) is about 7.3%. The step size used, along with the error involved in hypothesis (54) explain this difference. Figure 4 shows the resulting pollution stock along time when the optimal strategy is implemented.

Figure 4. A realization of a trajectory of (7) with $x_0=5$, $\eta =1$, $\sigma \left(x\right)\equiv 0.5$, $u\left(t\right)=f^{{\lambda }^{*}}\left(t\right)$, $T=1$, and $N=100$.

4. Concluding Remarks

This paper studies a stochastic system on a finite-time horizon under the criterion of the total performance with restrictions with unbounded coefficients of all: the diffusion, the reward and the constraints. The results have been illustrated by means of a sequence of examples, a Lemma and a Theorem. The approach is based on the use of some classic dynamic programming tools, and the Lagrange multipliers technique for optimization with restrictions.

The results of this work represent a natural extension of the ones introduced in [12], to the non-stationary case. All these can also be applied to the control of pollution accumulation as presented in [17,18]. An additional contribution of this presentation is given by the optimal controllers –and objective function- for a finite-time horizon under constraints. Moreover, this work used the tools presented in [25], and the Monte Carlo simulation technique to test its analytic findings. This represents a major implication of this work concerning the current methodology for resource management and consumption when pollution has an active role. Indeed, the model presented along this paper can be used for the purpose of decision-making when the social welfare, and the cost and rewards constraints are known and parametrized.

A plausible extension of this paper could be related to looking for optimal controllers on a random horizon with a constrained performance index, in the fashion of [31].